Дифференциальное и интегральное исчисления для втузов, т.2
Дифференциальное и интегральное исчисления для втузов, т.2
ОглавлениеПРЕДИСЛОВИЕ К ДЕВЯТОМУ ИЗДАНИЮГЛАВА XIII.  (n) = f(x) (n) = f(x)§ 18. Некоторые типы дифференциальных уравнений второго порядка, приводимых к уравнениям первого порядка. Задача о второй космической скорости § 19. Графический метод интегрирования дифференциального уравнения второго порядка § 20. Линейные однородные уравнения. Определения и общие свойства § 21. Линейные однородные уравнения второго порядка с постоянными коэффициентами § 22. Линейные однородные уравнения n-го порядка с постоянными коэффициентами § 23. Неоднородные линейные уравнения второго порядка § 24. Неоднородные линейные уравнения второго порядка с постоянными коэффициентами § 25. Неоднородные линейные уравнения высших порядков § 26. Дифференциальное уравнение механических колебаний § 27. Свободные колебания. Векторное и комплексное изображение гармонических колебаний § 28. Вынужденные колебания § 29. Системы обыкновенных дифференциальных уравнений § 30. Системы линейных дифференциальных уравнений с постоянными коэффициентами § 31.  Понятие о теории устойчивости Ляпунова. Поведение траектории дифференциального уравнения в окрестности особой точки Понятие о теории устойчивости Ляпунова. Поведение траектории дифференциального уравнения в окрестности особой точки§ 32. Приближенное решение дифференциальных уравнений первого порядка методом Эйлера § 33. Разностный метод приближенного решения дифференциальных уравнений, основанный на применении формулы Тейлора.. Метод Адамса § 34. Приближенный метод интегрирования систем дифференциальных уравнений первого порядка Упражнения к главе XIII ГЛАВА XIV. КРАТНЫЕ ИНТЕГРАЛЫ § 2. Вычисление двойного интеграла § 3. Вычисление двойного интеграла (продолжение) § 4. Вычисление площадей и объемов с помощью двойных интегралов § 5. Двойной интеграл в полярных координатах § 7. Вычисление площади поверхности § 9. Момент инерции площади плоской фигуры § 10. Координаты центра масс площади плоской фигуры § 11. Тройной интеграл § 12. Вычисление тройного интеграла § 13. Замена переменных в тройном интеграле § 14.  Момент инерции и координаты центра масс тела Момент инерции и координаты центра масс тела§ 15. Вычисление интегралов, зависящих от параметра Упражнения к главе XIV ГЛАВА XV. КРИВОЛИНЕЙНЫЕ ИНТЕГРАЛЫ И ИНТЕГРАЛЫ ПО ПОВЕРХНОСТИ § 2. Вычисление криволинейного интеграла § 3. Формула Грина § 4. Условия независимости криволинейного интеграла от пути интегрирования § 5. Поверхностный интеграл § 6. Вычисление поверхностного интеграла § 7. Формула Стокса § 9. Оператор Гамильтона. Некоторые его применения Упражнения к главе XV ГЛАВА XVI. РЯДЫ § 1. Ряд. Сумма ряда § 2. Необходимый признак сходимости ряда § 3. Сравнение рядов с положительными членами § 4. Признак Даламбера § 5. Признак Коши § 6. Интегральный признак сходимости ряда § 7. Знакочередующиеся ряды. Теорема Лейбница § 8. Знакопеременные ряды. Абсолютная и условная сходимость § 9. Функциональные ряды § 10. Мажорируемые ряды § 11. Непрерывность суммы ряда § 12. Интегрирование и дифференцирование рядов § 13.  Степенные ряды. Интервал сходимости Степенные ряды. Интервал сходимости§ 14. Дифференцирование степенных рядов § 15. Ряды по степеням x-a § 16. Ряды Тейлора и Маклорена § 17. Примеры разложения функций в ряды § 18. Формула Эйлера § 19. Биномиальный ряд § 20. Разложение функции ln(1+x) в степенной ряд. Вычисление логарифмов § 21. Вычисление определенных интегралов с помощью рядов § 22. Интегрирование дифференциальных уравнений с помощью рядов § 24. Ряды с комплексными членами § 25. Степенные ряды с комплексной переменной § 26. Решение дифференциального уравнения первого порядка методом последовательных приближений (метод итераций) § 27. Доказательство существования решения дифференциального уравнения. Оценка погрешности при приближенном решении § 28. Теорема единственности решения дифференциального уравнения Упражнения к главе XVI ГЛАВА XVII. РЯДЫ ФУРЬЕ § 2. Примеры разложения функций в ряды Фурье § 3. Одно, замечание о разложении периодической функции в ряд Фурье § 4.  Ряды Фурье для четных и нечетных функций Ряды Фурье для четных и нечетных функций§ 5. Ряд Фурье для функции с периодом 2l § 6. О разложении непериодической функции в ряд Фурье § 7. Приближение в среднем заданной функции с помощью тригонометрического многочлена § 8. Интеграл Дирихле § 9. Сходимость ряда Фурье в данной точке § 10. Некоторые достаточные условия сходимости ряда Фурье § 11. Практический гармонический анализ § 12. Ряд Фурье в комплексной форме § 13. Интеграл Фурье § 14. Интеграл Фурье в комплексной форме § 15. Ряд Фурье по ортогональной системе функций § 16. Понятие о линейном функциональном пространстве. Аналогия между разложением функций в ряд Фурье и разложением векторов Упражнения к главе XVII ГЛАВА XVIII. УРАВНЕНИЯ МАТЕМАТИЧЕСКОЙ ФИЗИКИ § 1. Основные типы уравнений математической физики § 2. Вывод уравнения колебаний струны. Формулировка краевой задачи. Вывод уравнений электрических колебаний в проводах § 3. Решение уравнения колебаний струны методом разделения переменных (методом Фурье) § 4.  Уравнение распространения тепла в стержне. Формулировка краевой задачи Уравнение распространения тепла в стержне. Формулировка краевой задачи§ 5. Распространение тепла в пространстве § 6. Решение первой краевой задачи для уравнения теплопроводности методом конечных разностей § 8. Задачи, приводящие к исследованию решений уравнения Лапласа. Формулировка краевых задач § 9. Уравнение Лапласа в цилиндрических координатах. Решение задачи Дирихле для кольца с постоянными значениями искомой функции на внутренней и внешней окружностях § 10. Решение задачи Дирихле для круга § 11. Решение задачи Дирихле методом конечных разностей Упражнения к главе XVIII ГЛАВА XIX. ОПЕРАЦИОННОЕ ИСЧИСЛЕНИЕ И НЕКОТОРЫЕ ЕГО ПРИЛОЖЕНИЯ § 1. Начальная функция и ее изображение § 2. Изображение функций … § 3. Изображение функции с измененным масштабом независимой переменной. Изображение функций sin at, cos at § 4. Свойство линейности изображения § 5. Теорема смещения § 6. Изображение функций … § 7. 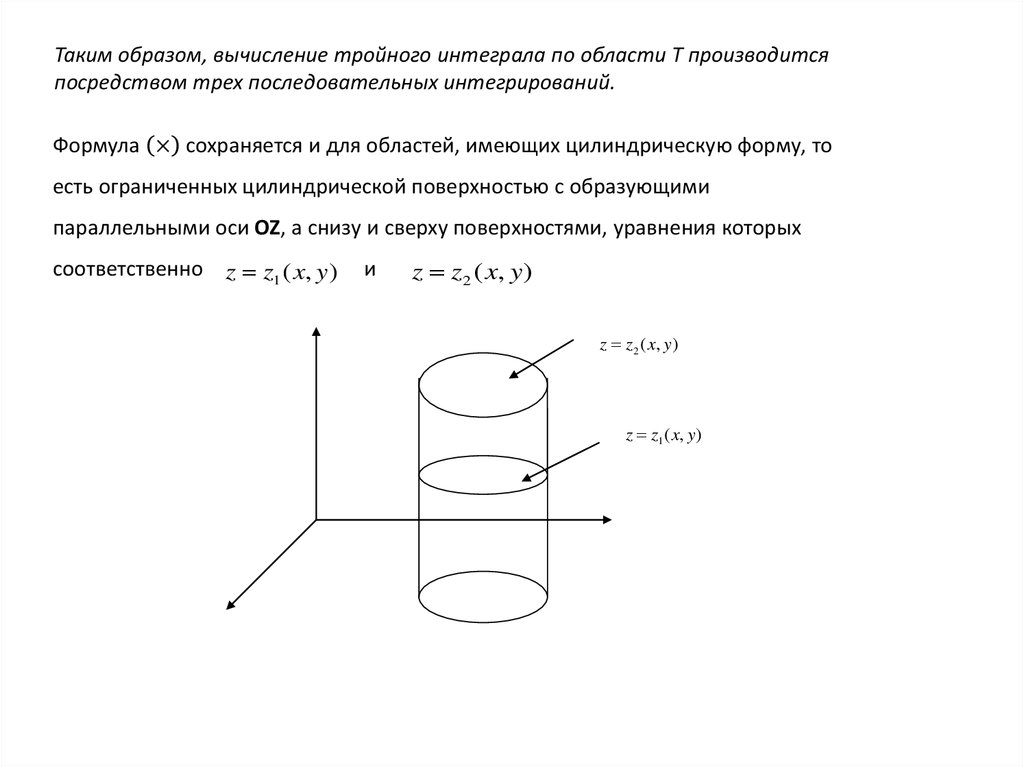 Дифференцирование изображения Дифференцирование изображения§ 8. Изображение производных § 9. Таблица некоторых изображений § 10. Вспомогательное уравнение для данного дифференциального уравнения § 11. Теорема разложения § 12. Примеры решения дифференциальных уравнений и систем дифференциальных уравнений операционным методом § 13. Теорема свертывания § 14. Дифференциальные уравнения механических колебаний. Дифференциальные уравнения теории электрических цепей § 15. Решение дифференциального уравнения колебаний § 16. Исследование свободных колебаний § 17. Исследование механических и электрических колебаний в случае периодической внешней силы § 18. Решение уравнения колебаний в случае резонанса § 19. Теорема запаздывания § 20. Дельта-функция и ее изображение Упражнения к главе XIX ГЛАВА XX. ЭЛЕМЕНТЫ ТЕОРИИ ВЕРОЯТНОСТЕЙ И МАТЕМАТИЧЕСКОЙ СТАТИСТИКИ § 1. Случайное событие. Относительная частота случайного события. Вероятность события. Предмет теории вероятностей  Классическое определение вероятности и непосредственный подсчет вероятностей Классическое определение вероятности и непосредственный подсчет вероятностей§ 3. Сложение вероятностей. Противоположные случайные события § 4. Умножение вероятностей независимых событий § 5. Зависимые события. Условная вероятность. Полная вероятность § 6. Вероятность гипотез. Формула Байеса § 7. Дискретная случайная величина. Закон распределения дискретной случайной величины § 8. Относительная частота и вероятность относительной частоты при повторных испытаниях § 9. Математическое ожидание дискретной случайной величины § 10. Дисперсия. Среднеквадратичное отклонение. Понятие о моментах § 11. Функции от случайных величин § 12. Непрерывная случайная величина. Плотность распределения непрерывной случайной величины. Вероятность попадания случайной величины в заданный интервал § 13. Функция распределения, или интегральный закон распределения. Закон равномерного распределения вероятностей § 14. Числовые характеристики непрерывной случайной величины § 15. 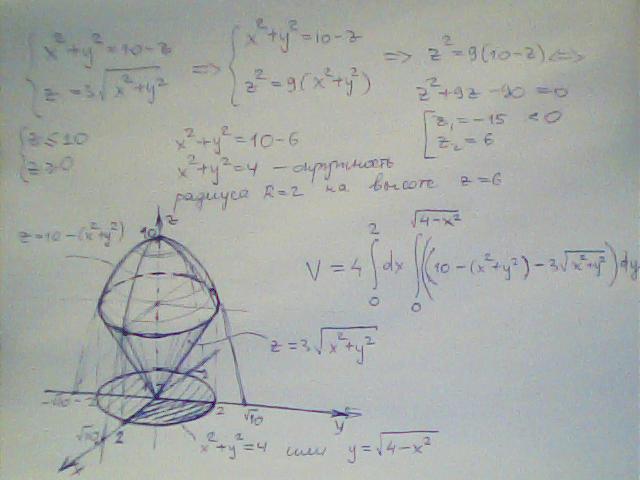 Нормальный закон распределения. Математическое ожидание нормального распределения Нормальный закон распределения. Математическое ожидание нормального распределения§ 16. Дисперсия и среднеквадратичное отклонение случайной величины, подчиненной нормальному закону распределения § 17. Вероятность попадания значения случайной величины в заданный интервал. Функция Лапласа. Интегральная функция распределения для нормального закона § 18. Вероятное (срединное) отклонение или срединная ошибка § 19. Выражение нормального закона распределения через срединное отклонение. Приведенная функция Лапласа § 20. Правило трех сигм. Шкала вероятностей распределения ошибок § 21. Среднеарифметическая ошибка § 22. Мера точности. Соотношение между характеристиками распределения ошибок § 23. Двумерная случайная величина § 24. Нормальный закон распределения на плоскости § 26. Вероятность попадания двумерной случайной величины в эллипс рассеивания § 27.  Задачи математической статистики. Статистический материал Задачи математической статистики. Статистический материал§ 28. Статистический ряд. Гистограмма § 29. Определение подходящего значения измеряемой величины § 30. Определение параметров закона распределения. Теорема Ляпунова. Теорема Лапласа Упражнения к главе XX ГЛАВА XXI. МАТРИЦЫ. МАТРИЧНАЯ ЗАПИСЬ СИСТЕМ И РЕШЕНИЙ СИСТЕМ ЛИНЕЙНЫХ ДИФФЕРЕНЦИАЛЬНЫХ УРАВНЕНИЙ § 1. Линейные преобразования. Матрица § 2. Общие определения, связанные с понятием матрицы § 3. Обратное преобразование § 4. Действия над матрицами. Сложение матриц § 5. Преобразование вектора в другой вектор с помощью матрицы § 6. Обратная матрица § 7. Нахождение матрицы, обратной данной § 8. Матричная запись системы линейных уравнений § 9. Решение системы линейных уравнений матричным методом § 10. Ортогональные отображения. Ортогональные матрицы § 11. Собственный вектор линейного преобразования § 12. Матрица линейного преобразования, при котором базисные векторы являются собственными векторами § 13.  Преобразование матрицы линейного преобразования при переходе от одного базиса к другому Преобразование матрицы линейного преобразования при переходе от одного базиса к другому§ 14. Квадратичные формы и их преобразования § 15. Ранг матрицы. Существование решений системы линейных уравнений § 16. Дифференцирование и интегрирование матриц § 17. Матричная запись системы дифференциальных уравнений и решений системы дифференциальных уравнений с постоянными коэффициентами § 18. Матричная запись линейного уравнения n-го порядка § 19. Решение систем линейных дифференциальных уравнений с переменными коэффициентами методом последовательных приближений с использованием матричной записи Упражнения к главе XXI ПРИЛОЖЕНИЯ |
1.2.7. Вычисление тройного интеграла в декартовых координатах
Естественные науки / Специальные главы высшей математики / 1.2.7. Вычисление тройного интеграла в декартовых координатах
Пусть в пространстве XYZ задано тело V. Известно, что масса его задается формулой:
Известно, что масса его задается формулой:
,
где f(P)=f(x, y, z) – плотность.
Введем прямоугольную сетку с целью выражения бесконечно малого объема dv, разбив тело V системой параллельных плоскостей (рис. 1.19), получим:
. (1.61)
Тройной интеграл теперь записывается так:
(1.62)
Чтобы свести тройной интеграл к трехкратному (повторному), поступаем так, как это было изложено для двойного интеграла. Предположим, что тело V ограничено поверхностями z = z1(x, y) – снизу и z = z2(x, y) – сверху и цилиндрической поверхностью с боков (её может не быть). Функции z1(x, y) и z2(x, y) заданы в области D – проекции тела V на плоскость оси xОz. Каждая прямая, параллельная оси Оz и проходящая через внутреннюю точку D, пересекает границу V в двух точках – точке входа на z = z1(x, y) и точке выхода на поверхность z = z2(x, y) (рис. 1.20).
Каждая прямая, параллельная оси Оz и проходящая через внутреннюю точку D, пересекает границу V в двух точках – точке входа на z = z1(x, y) и точке выхода на поверхность z = z2(x, y) (рис. 1.20).
Возьмем бесконечно малый элемент с высотой dz и проекцией на плоскость xОy, его масса будет:
.
Чтобы найти массу «столбика» надо «просуммировать» все такие элементы:
.
Для определения массы всего тела V, нужно «просуммировать» массы всех «столбиков»:
. (1.63)
Сравнение (1.63) с (1.62) дает формулу:
(1.64)
Методическое руководство
Расстановка пределов обычно проводится в следующем порядке: внешний интеграл имеет постоянные пределы а и b; далее для внутреннего двойного интеграла — от точки входа до точки выхода ; для внутреннего тройного интеграла — от точки входа до точки выхода.
Отметим, что имеет место операция изменения порядка интегрирования.
Первым вычисляют внутренний интеграл для тройного, результат подводят под внутренний интеграл для двойного и последним вычисляют обычный определенный интеграл, получают число. Таким образом, тройной интеграл трехкратным интегрированием сводится к определенному интегралу.
Пример 1
Вычислить:
Пример 2
Найти объем тела, ограниченного плоскостями и (рис. 1.21).
Решение. Согласно формуле (1.46) имеем:
.
Тогда, применяя порядок как в (1.64), получим:
Пример 3
Тело, ограничено поверхностями и . Плотность массы тела в каждой точке равна аппликате точки: . Найти массу тела.
Решение. При вычислении двойного интеграла часто удобно прибегать к полярным координатам. По (1.64) имеем:
По (1.64) имеем:
.
Найдем проекцию D тела V на xОy (рис. 1.22).
Решим совместно уравнения:
– круг радиуса R = 1.
Тогда
Как найти объем твердого тела между двумя поверхностями вращения Для чайников
Исследуйте книгу Купить на Amazon
Если вы хотите найти объем твердого тела, которое падает между двумя разными поверхностями вращения, вы можете использовать для этого метод мясорубки. Метод мясорубки лучше всего работает с твердыми телами, имеющими одинаковое поперечное сечение. Вот план:
Найдите выражение, которое представляет площадь случайного поперечного сечения твердого тела через x .
Используйте это выражение для построения определенного интеграла (в терминах d x ), представляющего объем твердого тела.
Вычислите этот интеграл.

Хитрость заключается в том, чтобы найти способ описать кольцевидную площадь поперечного сечения как разность двух интегралов: один интеграл, описывающий всю форму, минус другой, описывающий отверстие.
Например, предположим, что вы хотите найти объем тела, показанного здесь.
Твердое тело в форме вазы между двумя поверхностями вращения.
Это твердое тело похоже на чашу, перевернутую на бок. Внешний край представляет собой тело вращения вокруг оси x для функции
.Внутреннее ребро представляет собой тело вращения вокруг оси x для функции
Вот как решить эту проблему:
Найдите выражение, представляющее площадь случайного поперечного сечения твердого тела.
То есть найдите площадь круга радиусом
и вычесть площадь круга с радиусом
Используйте это выражение для построения определенного интеграла, представляющего объем твердого тела.
Пределы интегрирования 0 и 4:
Решить интеграл:
Теперь оцените это выражение:
Вот еще одна задача: найти объем показанного здесь твердого тела.
Еще одно твердое тело, образовавшееся между двумя поверхностями вращения.
Это тело падает между поверхностью вращения y = ln x и поверхностью вращения
ограничено снизу y = 0 и сверху y = 1.
Поперечное сечение этого твердого тела показано в правой части рисунка: круг с отверстием посередине.
Обратите внимание, однако, что это поперечное сечение перпендикулярно оси y . Чтобы использовать метод мясной нарезки, поперечное сечение должно быть перпендикулярно оси x . Измените задачу, используя инверсию:
Возникшая проблема показана на этом рисунке.
Используйте инверсию, чтобы повернуть задачу из более раннего рисунка, чтобы вы могли использовать метод мясной нарезки.
Теперь вы можете использовать метод мясорубки для решения проблемы:
Найдите выражение, представляющее площадь случайного поперечного сечения твердого тела.
То есть найдите площадь круга с радиусом e x и вычтите площадь круга с радиусом
Это просто геометрия.
 Помните, что площадь круга равна π r 2 :
Помните, что площадь круга равна π r 2 :Используйте это выражение для построения определенного интеграла, представляющего объем твердого тела.
Пределы интегрирования 0 и 1:
Оценка интеграла:
Таким образом, объем этого твердого тела составляет примерно 9,179 кубических единиц.
Эта статья из книги:
- Исчисление II для чайников,
Об авторе книги:
Марк Зегарелли, репетитор по математике и писатель с 25-летним профессиональным опытом, доставляет удовольствие кристально ясно излагать техническую информацию — и весело — для средних читателей. Он автор Логика для чайников и Базовая математика и предварительная алгебра для чайников .Эта статья можно найти в категории:
- Calculus,
Жидкий-таблица-Google Suce
AlleshoppingBildervideoSmapsNewsbücher
. g.g.gpate Shoption 9000.g.g.gpatemoptemoptemoptec жидкие › теги › итерация
g.g.gpate Shoption 9000.g.g.gpatemoptemoptemoptec жидкие › теги › итерацияГенерирует HTML-таблицу. Должен быть заключен в открывающий
Язык шаблонов Liquid — с открытым исходным кодом
shopify.github.io › Liquid
Liquid — это язык шаблонов с открытым исходным кодом, созданный Shopify и написанный на Ruby. Это основа тем Shopify и используется для загрузки динамического контента …
Итерация · Шаблон · Варианты Liquid · Введение
Объекты Liquid: tablerow — Shopify.dev
shopify.dev › docs › API › ликвидные › объекты › tablerow
В шаблоне: Доступ к объекту возможен непосредственно в определенных шаблонах или в разделах или блоках, включенных в шаблон. Например, вы можете получить доступ к …
Имя
Все запросы
Все запросы
Заполнение таблицы жидким шаблоном путем перебора массива . ..
..
stackoverflow.com потребуется реализовать шаблоны Liquid с помощью Liquid.js, и мне интересно, почему я не могу получить базовую таблицу, отображаемую при повторении …
Интеллектуальный способ создания таблиц с помощью Liquid из файла CSV?
Как получить все товары в шаблоне .liquid с помощью Shopify?
Переменная HTML шаблона Liquid — переполнение стека
Не удалось получить значение из пользовательской таблицы на портале PowerApps
Вернуться к тексту на stackoverflow.com
Liquid tablerow: Генерирует HTML-таблицу в Shopify — AVADA | Блог
blog.avada.io › shopify › devdocs › generate-an-ht…
08.01.2022 · Таким образом, таблица HTML может разложить все данные на строки и столбцы ячеек, такие как текст, изображения, ссылки , другие таблицы и т.д. Необходимая форма …
Строка таблицы | LiquidJS
Liquidjs.com › теги › tablerow
14.02.2023 · LiquidJS — это простой, выразительный и безопасный шаблонизатор, совместимый с Shopify / Github Pages, на чистом JavaScript.
Основное использование · Параметры · столбцы
Как получить данные из таблицы и отобразить их в пользовательском шаблоне жидкости
powerusers.microsoft.com › td-p
Как получить данные из таблицы и отобразить их в пользовательском жидком шаблоне. 06.07.2021 06:25. bishwaroopdey_0-1625577774772.png.
Работа с шаблонами Liquid — Power Apps | Microsoft Learn
Learn.Microsoft.com › … › Power Apps
12.10.2022 · Узнайте, как использовать Liquid, язык шаблонов с открытым исходным кодом, на своих порталах.
Ähnliche Fragen
Что такое шаблон Liquid?
Shopify все еще использует Liquid?
Насколько сложно научиться Ликвиду?
Что такое базовый код Liquid?
Ресурс для создания тем Shopify с помощью Liquid
www.shopify.com › партнеры › shopify-cheat-sheet
Эта памятка представляет собой интерактивный справочник по языку шаблонов Liquid, который поможет вам создавать шаблоны электронной коммерции на Shopify.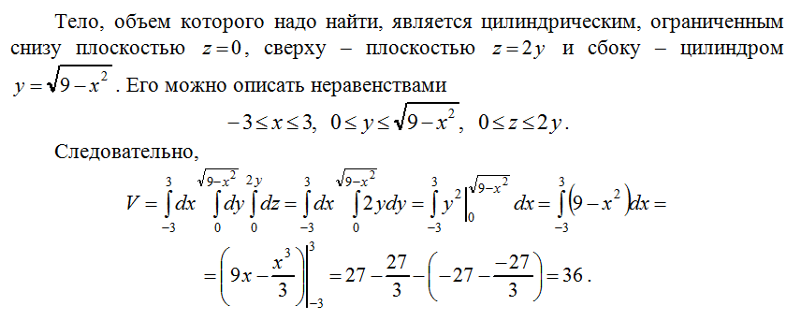


 Помните, что площадь круга равна π r 2 :
Помните, что площадь круга равна π r 2 :