Математика: Справ. материалы
Математика: Справ. материалы
ОглавлениеСЛОВО К УЧАЩИМСЯГЛАВА I. ЧИСЛА § 1. Натуральные числа 2. Арифметические действия над натуральными числами. 3. Деление с остатком. 4. Признаки делимости. 5. Разложение натурального числа на простые множители. 6. Наибольший общий делитель нескольких натуральных чисел. 7. Наименьшее общее кратное нескольких натуральных чисел.  8. Употребление букв в алгебре. Переменные. § 2. Рациональные числа 10. Равенство дробей. Основное свойство дроби. Сокращение дробей. 11. Приведение дробей к общему знаменателю. 12. Арифметические действия над обыкновенными дробями. 13. Десятичные дроби. 14. Арифметические действия над десятичными дробями. 15. Проценты. 16. Обращение обыкновенной дроби в бесконечную десятичную периодическую дробь. 17. Обращение бесконечной десятичной периодической дроби в обыкновенную дробь. 18. Координатная прямая. 19. Множество рациональных чисел. § 3. Действительные числа 21. Действительные числа. Числовая прямая. 22 Обозначения некоторых числовых множеств. 23. Сравнение действительных чисел. 25. Числовые промежутки. 26. Модуль действительного числа. 27. Формула расстояния между двумя точками координатной прямой. 28. Правила действий над действительными числами. 29. Свойства арифметических действий над действительными числами. 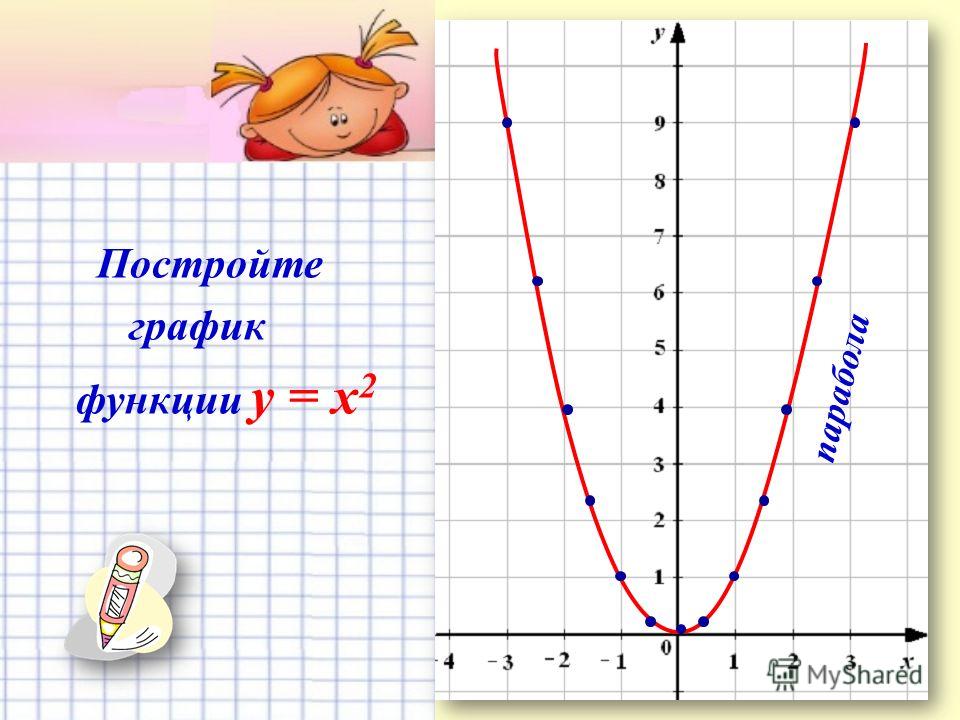 30. Пропорции. 31. Целая часть числа. Дробная часть числа. 32. Степень с натуральным показателем. 33. Степень с нулевым показателем. Степень с отрицательным целым показателем. 34. Стандартный вид положительного действительного числа. 35. Определение арифметического корня. 36. Корень нечетной степени из отрицательного числа. 37. Степень с дробным показателем. 38. Свойства степеней с рациональными показателями. 39. Приближенные значения чисел. Абсолютная и относительная погрешности. 40. Десятичные приближения действительного числа по недостатку и по избытку. 41. Правило извлечения квадратного корня из натурального числа. 42. Понятие о степени с иррациональным показателем. 43. Свойства степеней с действительными показателями. § 4. Комплексные числа 45. Арифметические операции над комплексными числами. 46. Алгебраическая форма комплексного числа. ГЛАВА II. АЛГЕБРАИЧЕСКИЕ ВЫРАЖЕНИЯ 49.  3.112. Построение графика функции y = f(x-m)+n 113. График квадратичной функции. 114. Способы построения графика квадратичной функции 115. Построение графика функции y = f(kx). 116. Сжатие и растяжение графиков тригонометрических функций. 117. График гармонического колебания ГЛАВА IV. ТРАНСЦЕНДЕНТНЫЕ ВЫРАЖЕНИЯ § 12. Преобразование выражений, содержащих переменную под знаком логарифма 119. Определение логарифма положительного числа по данному основанию. 120. Свойства логарифмов. 121. Переход к новому основанию логарифма. 122. Логарифмирование и потенцирование. 123. Десятичный логарифм. Характеристика и мантисса десятичного логарифма. § 13. Формулы тригонометрии и их использование для преобразования тригонометрических выражений 125. Формулы сложения и вычитания аргументов. 126. Формулы приведения. 127. Соотношения между тригонометрическими функциями одного и того же аргумента. 128. Формулы двойного угла. 129. Формулы понижения степени.  130. Преобразование суммы тригонометрических функций в произведение. 131. Преобразование произведения тригонометрических функций в сумму. 132. Преобразование выражения a cos t + b sin t к виду A sin (t + a). 133. Примеры преобразований выражений, содержащих обратные тригонометрические функции. ГЛАВА V. УРАВНЕНИЯ И СИСТЕМЫ УРАВНЕНИЙ § 14. Уравнения с одной переменной 135. Равносильность уравнений. 136. Линейные уравнения. 137. Квадратные уравнения. 138. Неполные квадратные уравнения. 139. Теорема Виета. 140. Системы и совокупности уравнений. 142. Понятие следствия уравнения. Посторонние корни. 143. Уравнения с переменной в знаменателе. 144. Область определения уравнения. 145. Рациональные уравнения. 146. Решение уравнения p(x) = 0 методом разложения его левой части на множители. 147. Решение уравнений методом введения новой переменной. 148. Биквадратные уравнения.  149. Решение задач с помощью составления уравнений. 150. Иррациональные уравнения. 151. Показательные уравнения. 152. Логарифмические уравнения. 153. Примеры решения показательно-логарифмических уравнений. 154. Простейшие тригонометрические уравнения. 155. Методы решения тригонометрических уравнений. 156. Универсальная подстановка (для тригонометрических уравнений). 157. Метод введения вспомогательного аргумента (для тригонометрических уравнений). 158. Графическое решение уравнений. 159. Уравнения с параметром. § 15. Уравнения с двумя переменными 161. График уравнения с двумя переменными. 162. Линейное уравнение с двумя переменными и его график. § 16. Системы уравнений 164. Решение систем двух уравнений с двумя переменными методом подстановки. 165. Решение систем двух уравнений с двумя переменными методом сложения. 167. Графическое решение систем двух уравнений с двумя переменными. 168. Исследование системы двух линейных уравнений с двумя переменными.  169. Решение систем двух уравнений с двумя переменными методами умножения и деления. 170. Системы показательных и логарифмических уравнений. 171. Системы тригонометрических уравнений с двумя переменными. 172. Системы трех уравнений с тремя переменными. 173. Решение задач с помощью составления систем уравнений. Глава VI. НЕРАВЕНСТВА 175. Графическое решение неравенств с одной переменной. 176. Линейные неравенства с одной переменной. 177. Системы неравенств с одной переменной. 178. Совокупность неравенств с одной переменной. 179. Дробно-линейные неравенства. 180. Неравенства второй степени. 181. Графическое решение неравенств второй степени. 182. Неравенства с модулями. 183. Решение рациональных неравенств методом промежутков. 184. Показательные неравенства. 185. Логарифмические неравенства. 186. Иррациональные неравенства. 187. Решение тригонометрических неравенств. 188.  Неравенства и системы неравенств с двумя переменными.§ 18. Доказательство неравенств 190. Синтетический метод доказательства неравенств. 191. Доказательство неравенств методом от противного. 192. Использование неравенств при решении уравнений. ГЛАВА VII. ЭЛЕМЕНТЫ МАТЕМАТИЧЕСКОГО АНАЛИЗА § 19. Числовые последовательности 194. Способы задания последовательности. 195. Возрастание и убывание последовательности. 196. Определение арифметической прогрессии. 197. Свойства арифметической прогрессии 198. Определение геометрической прогрессии. 199. Свойства геометрической прогрессии. 200. Понятие о пределе последовательности. 201. Вычисление пределов последовательностей. 202. Сумма бесконечной геометрической прогрессии при |q| § 20. Предел функции 204. Вычисление пределов функции при х->оо. 205. Предел функции в точке. Непрерывные функции. 206. Вертикальная асимптота. 207. Вычисление пределов функций в точке. § 21.  Производная и ее применения209. Определение производной. 210. Формулы дифференцирования. Таблица производных. 211. Дифференцирование суммы, произведения, частного. 213. Физический смысл производной. 214. Вторая производная и ее физический смысл. 215. Касательная к графику функции. 216. Применение производной к исследованию функций на монотонность. 217. Применение производной к исследованию функций на экстремум. 218. Отыскание наибольшего и наименьшего значений непрерывной функции на отрезке. 219. Отыскание наибольшего или наименьшего значения непрерывной функции на незамкнутом промежутке. 220. Задачи на отыскание наибольших или наименьших значений величин. 221. Применение производной для доказательства тождеств. 222. Применение производной для доказательства неравенств. 223. Общая схема построения графика функции. § 22. Первообразная и интеграл 225. Таблица первообразных. 226.  Правила вычисления первообразных.227. Интеграл. 228. Связь между интегралов и первообразной (формула Ньютона—Лейбница). 229. Правила вычисления интегралов. 230. Использование интеграла для вычисления площадей плоских фигур. ГЕОМЕТРИЯ. ГЛАВА I. ГЕОМЕТРИЧЕСКИЕ ФИГУРЫ НА ПЛОСКОСТИ 2. Точка. Прямая. 3. Определения. Аксиомы. Теоремы. § 2. Основные свойства простейших геометрических фигур 5. Луч. 6. Окружность. Круг. 7. Полуплоскость. 8. Угол. Градусная мера угла. 9. Смежные и вертикальные углы. 10. Центральные и вписанные углы. 11. Параллельные прямые. 12. Признаки параллельности прямых. 13. Перпендикулярные прямые. 14. Касательная к окружности. 15. Треугольники. 16. Равенство треугольников. 17. Равнобедренный треугольник. 18. Сумма углов треугольника. 19. Прямоугольный треугольник. Теорема Пифагора. 20. Окружности, вписанные в треугольник и описанные около треугольника. § 3. Геометрические построения на плоскости  Простейшие задачи на построение.23. Геометрическое место точек на плоскости. § 4. Четырехугольники 25. Параллелограмм. 26. Прямоугольник. Ромб. Квадрат. 27. Трапеция. § 5. Многоугольники 29. Выпуклые многоугольники. 30. Правильные многоугольники. 31. Длина окружности. § 6. Решение треугольников 33. Соотношения между сторонами и углами в прямоугольном треугольнике. 34. Теорема косинусов. Теорема синусов. 35. Решение треугольников. § 7. Площади плоских фигур 37. Площади многоугольников. 38. Площади подобных фигур. 39. Площадь круга. ГЛАВА II. Прямые и плоскости в пространстве § 9. Параллельность прямых и плоскостей 42. Параллельность прямой и плоскости. 43. Параллельные плоскости. § 10. Перпендикулярность прямых и плоскостей 45. Перпендикуляр и наклонная к плоскости. 46. Перпендикулярность плоскостей. ГЛАВА III. ТЕЛА В ПРОСТРАНСТВЕ § 11. Многогранники 48. Многогранные углы. Многогранники.  49. Призма. Параллелепипед. Куб. 50. Пираприда. 51. Правильные многогранники. § 12. Тела вращения 53. Конус. 54. Шар. § 13. Изображение пространственных фигур на плоскости 56. Ортогональное проектирование. 57. Геометрическое место точек в пространстве. § 14. Объемы тел 59. Объем параллелепипеда, призмы и пирамиды. 60. Объем цилиндра и конуса. 61. Общая формула объемов тел вращения. § 15. Площади поверхностей тел 63. Понятие площади поверхности. 64. Площади поверхностей тел вращения. ГЛАВА IV. ДЕКАРТОВЫ КООРДИНАТЫ § 16. Координаты на плоскости и в пространстве 66. Координаты середины отрезка. § 17. Уравнения фигур на плоскости 68. Пересечение двух окружностей. 69. Уравнение прямой. 70. Пересечение прямой и окружности. § 18. Уравнения фигур в пространстве 72. Уравнение сферы. 73. Взаимное расположение сферы и плоскости. 74. Пересечение двух сфер. ГЛАВА V. РЕОБРАЗОВАНИЯ ФИГУР 76.  Понятие движения.§ 20. Подобие фигур 78. Подобные фигуры. ГЛАВА VI. ВЕКТОРЫ 80. Понятие вектора. 81. Координаты вектора. § 22. Операции над векторами 83. Умножение вектора на число. Коллинеарные векторы. 84. Скалярное произведение векторов. ПРИЛОЖЕНИЯ ГЕОМЕТРИЯ |
8 класс. Алгебра. Квадратичная функция. Функция у = к/х. — Преобразования графика квадратичной функции.
Комментарии преподавателяКак построить график функции у = f (x + t), если известен график функции у = f(x)
Конкретизируем задачу.
Дано:
Кривая ; график этой функции нам известен
(действительное число)
Построить:
Это и есть задача нашего урока. Рассмотрение этой задачи начнем с простейших примеров.
Пример 1. Построить а) у = (х – 1)2; б) у = (х + 1)2
Дано:
у = х2(графиком данной функции является парабола (рис.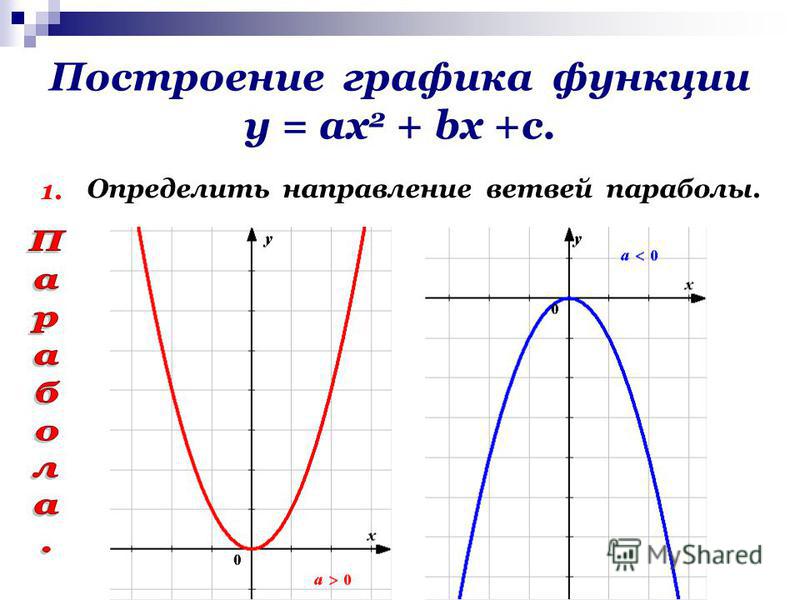
1).
Рис. 1. Парабола
Решение:
Поясним характер кривых, их взаимное расположение поясним с помощью таблицы.
|
х |
-2 |
-1 |
0 |
1 |
2 |
|
у = х2 |
4 |
1 |
0 |
1 |
4 |
|
у = (х – 1)2 |
9 |
4 |
1 |
0 |
1 |
|
у = (х – 1)2 |
1 |
0 |
1 |
4 |
9 |
Строим график функции у = (х – 1)2 (рис.
2):
Рис. 2. График функции у = (х – 1)2
Следует заметить, что кривая а) была получена сдвигом на 1 единицу вправо. Кривая же б) будет получена сдвигом на 1 единицу влево (что можно проверить, поставив полученные в таблице точки на координатную прямую) (рис. 3):
Рис. 3. Сдвиг графика
Заметим еще раз, что если к х прибавляется 1 единица, то сдвиг исходной прямой идет влево вдоль оси Ох, а если отнимается – то сдвиг графика идет вправо.
Вспомнить, когда сдвиг идет направо, а когда – налево, нам помогает самая характерная точка параболы – вершина параболы.
Значение у = 0 достигается этими функциями (рис. 4):
при х = 0, если у = х2
при х = 1, если у = (х – 1)2
при х = -1, если у = (х + 1)2
Рис. 4. Случаи, когда у = 0
Если у нас у = (х – 1)2, то кривая сдвигается на 1 единицу вправо.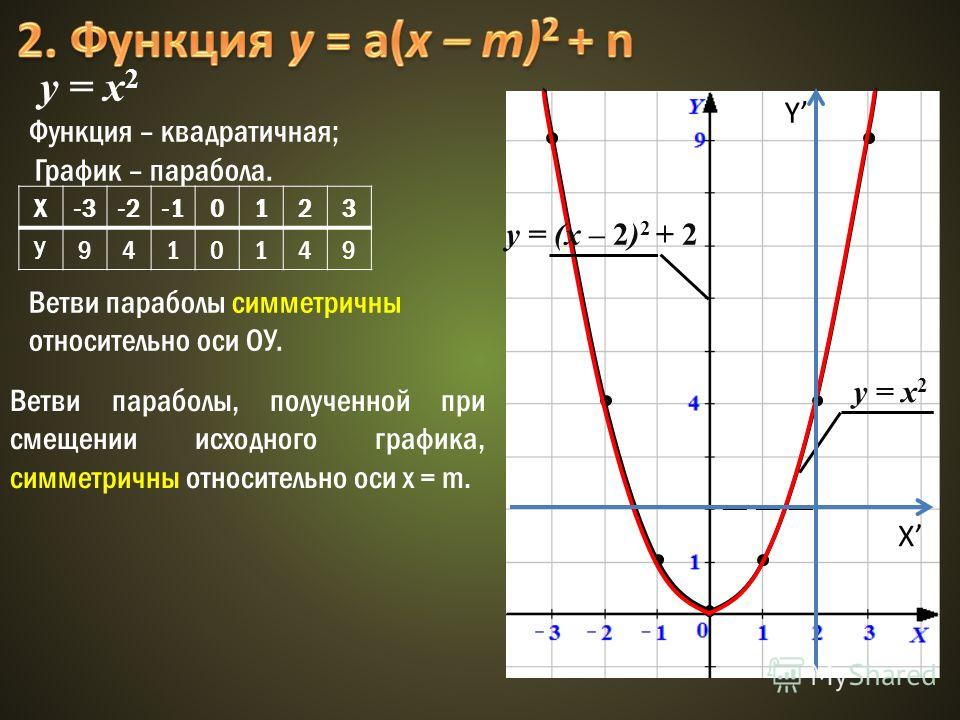
Если у нас у = (х + 1)2, то кривая сдвигается на 1 единицу влево.
Мы рассмотрели конкретный случай с конкретными числами. Но вместо чисел, можно взять любое действительное число; вместо функции у = х2можно взять любую функцию. Получим важное правило.
Чтобы получить у = f(x + t), надо кривую у = f(x):
— сдвинуть на единиц вправо, если t < 0,
— сдвинуть на единиц влево, если t > 0
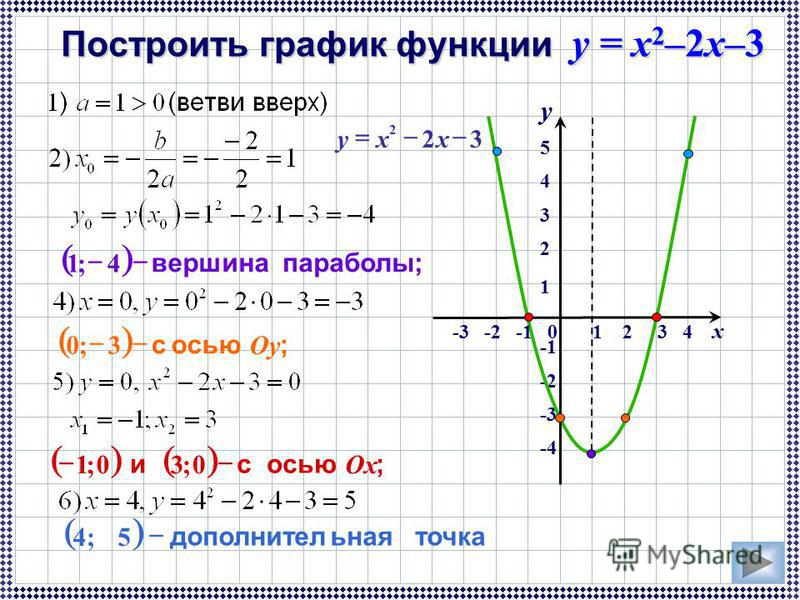
Как построить график функции у = f (x) + m, если известен график функции у = f(x)
На прошлом уроке мы научились график функции . Сейчас же наша задача – научиться строить график функции . Рассмотрим пример:
Дано:
у = х2(графиком данной функции будет парабола) (рис. 1)
Рис. 1. Иллюстрация к задаче
Построить:
а) у = х2 + 1
б) у = х2 — 1
Решение: Поясним характер кривых, их взаимное расположение поясним с помощью таблицы:
|
х |
0 |
1 |
-1 |
2 |
-2 |
|
у = х2 |
0 |
1 |
1 |
4 |
4 |
|
у = х2 + 1 |
1 |
2 |
2 |
5 |
5 |
|
у = х2 – 1 |
-1 |
0 |
0 |
3 |
3 |
Строим график функции у = х2 + 1 (рис.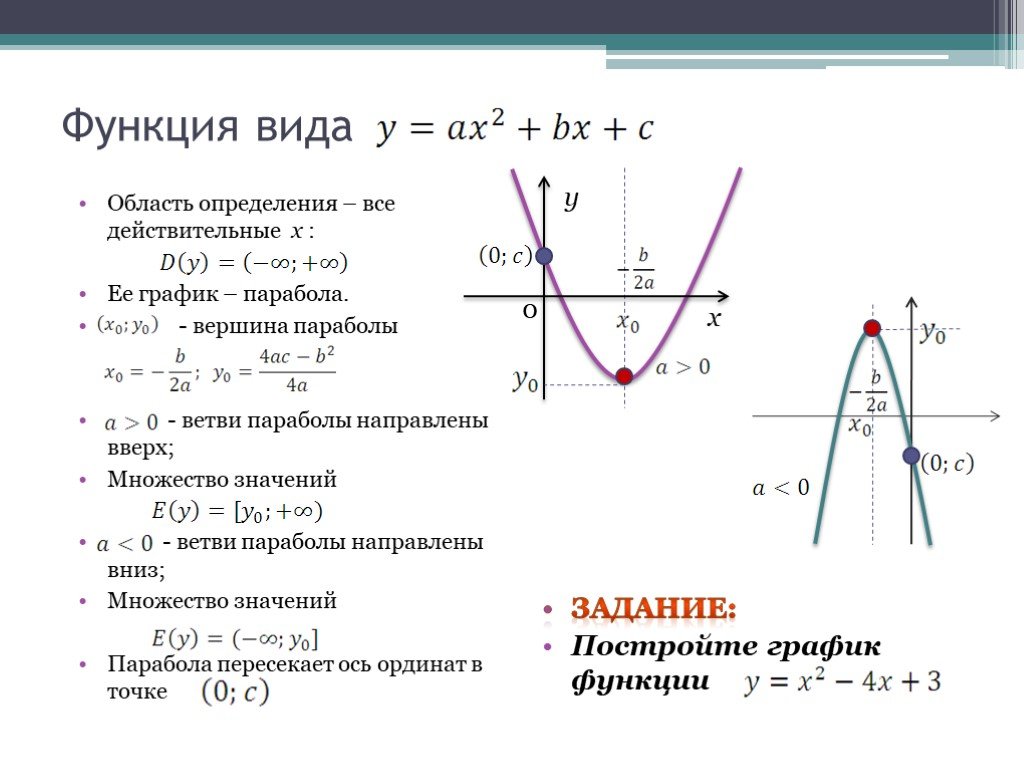
2):
Рис. 2. График функции у = х2 + 1
График этой функции получается с помощью сдвига вверх на 1 единицу графика исходной функции.
График же следующей функции мы получим сдвигом исходной функции вниз на 1 единицу (рис. 3):
Рис. 3. График функции у = х2 – 1
Итак, чтобы построить график функции у = х2 + 1, надо график исходной функции сдвинуть на 1 единицу вверх. Чтобы построить график функции у = х2 – 1, необходимо график исходной функции сдвинуть на 1 единицу вниз.
Сдвиги вверх и вниз приводят к изменению множества значений. Множество значений иллюстрирует эти сдвиги:
;
;
Мы рассмотрели частный случай, когда к х2 прибавляли или отнимали единицу. Отсюда следует правило:
Правило построения не изменится при . Правило также не изменится, если мы возьмем любую другую функцию.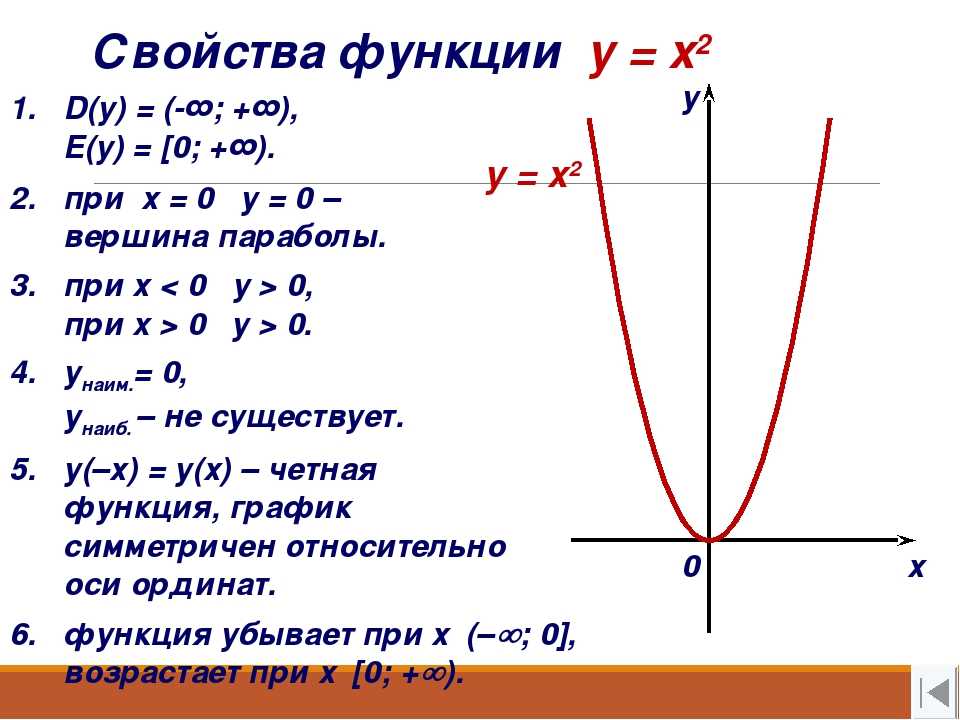
Сформулируем важное для нас правило:
Чтобы получить у = f(х) + m, надо кривую у = f(x):
— сдвинуть на единиц вверх, если m > 0,
— сдвинуть на единиц вниз, если m < 0
Рисунок отображает графически данное правило (рис. 4):
Рис. 4. Иллюстрация правила
На этом уроке вы узнаете, как построить график функции у = f (x + t) + m, если известен график функции у = f(x)Построение графика y = f (x + t) + m через повторение правил на построение y = f(x + t) и y = f(x) + m
Мы умеем строить график функции y = f(x+t), если известен график функции y = f(x).
Правило построения графиков функции y = f(x+t):
y = f(x+t)
y = f(х) сдвигаем:
— при на единиц
— при на единиц
Правило построения графиков функции y = f(x) + m:
y = f(x) + m
y = f(х) сдвигаем:
— при на единиц
— при на единиц
Пример.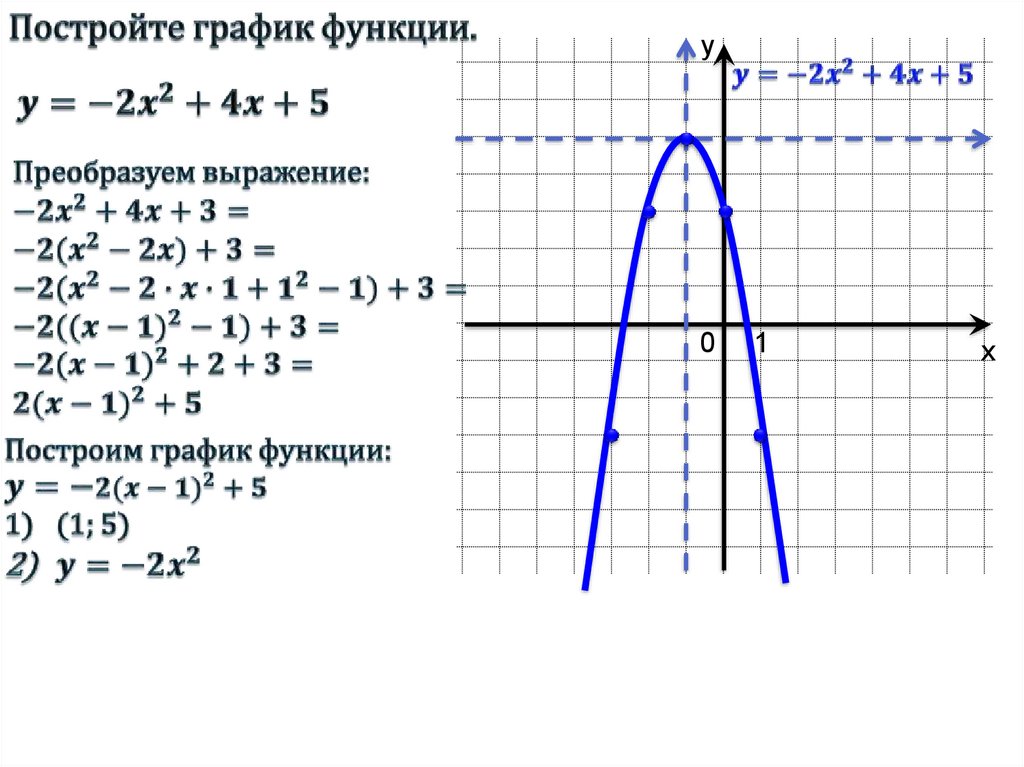
Построить график функции
Дано:
Решение. 1. Сначала мы должны построить график функции вида в нашем случае это .
Так как -1 < 0, то, соответственно, график сдвигается вдоль оси Ох вправо на 1 единицу (рис. 1).
Рис. 1. График функции
2. Теперь построим :
Так как , а 2 > 0, то график, полученный в предыдущем действии, мы сдвигаем вверх 2 единицы (рис. 2).
Рис. 2. График функции
Этот график и будет графиком требуемой функции. Точка пересечения с осями – (0; 3).
Пример решен.
В данном примере числа -1 и 2 можно заменить на параметры t и m соответственно.
Функцию также можно заменить на любую другую функцию. В результате можно сформулировать правило построения графика функции у = f (x + t) + m:
Чтобы получить кривую , надо кривую сдвинуть:
— при на |t| единиц
— при на |t| единиц
— при на |m| единиц
— при на |m| единиц
Источник конспекта:http://interneturok.
ru/ru/school/algebra/8-klass/kvadratichnaya-funkciya-funkciya-ykxb/kak-postroit-grafik-funktsii-u-f-x-l-m-esli-izvesten-grafik-funktsii-u-f-x?konspekt
http://interneturok.ru/ru/school/algebra/8-klass/kvadratichnaya-funkciya-funkciya-ykxb/kak-postroit-grafik-funktsii-u-f-x-m-esli-izvesten-grafik-funktsii-u-f-x?konspekt
http://interneturok.ru/ru/school/algebra/8-klass/kvadratichnaya-funkciya-funkciya-ykxb/kak-postroit-grafik-funktsii-u-f-x-l-esli-izvesten-grafik-funktsii-u-f-x?konspekt
Источник видео: http://www.youtube.com/watch?v=87ZIEIqyN6s
3.4 Снаряды, параболы и непараболы
Вернемся к Галилею.
Напомним из Урока 2, что Галилей экспериментально подтвердил, что объекты, падающие (точнее, катящиеся) под действием гравитации, ускоряются с постоянной скоростью. Данные о расстояниях, выпавших через равные промежутки времени, имеют постоянные двойные разности.
Теперь мы понимаем, что Галилей был прав, утверждая, что данные следуют квадратному выражению: высота падающего объекта определяется формулой вида 92+bt+c\)
где количество времени, в течение которого объект падал.
Чудесно!
Когда объект подбрасывается в воздух, он совершает два движения:
i) он движется горизонтально с постоянной скоростью (при условии, что влиянием сопротивления воздуха можно пренебречь.
ii) его вертикальная высота изменяется в соответствии с этим квадратичным уравнением формула.
U-образная кривая, которую можно увидеть как траекторию брошенного объекта, как мы только что показали, является формой графика квадратного уравнения.
Параболы
Греческие ученые древних времен классифицировали целый ряд специальных кривых, следующих определенным геометрическим свойствам. Одной из таких кривых является парабола , о которой мы упоминали в Уроке 1. Она строится следующим образом.
Нарисуйте на странице фиксированную точку \(F\) (называемую фокусом ) и фиксированную линию \(L\) (называемую направляющей ). Тогда парабола с этим фокусом и директрисой есть множество всех точек плоскости, одинаково удаленных от \(F\) и \(L\), как показано.
Студентка Элизабет Гербер построила параболу на пробковой доске, используя веревки и кнопки.
Посмотрите в конце этих заметок некоторые ее дополнительные работы.
Легенда гласит, что Архимед Сиракузский (288–212 гг. до н. э.) предложил построить на скалах острова огромные параболические зеркала, чтобы фокусировать солнечные лучи на приближающихся вражеских деревянных кораблях и поджигать их. Греческие ученые знали, что параболическая форма имеет геометрическое свойство фокусировать параллельные лучи света.
Можно построить параболическую кривую, сложив бумагу.
Нарисуйте точку на пару дюймов выше нижнего края страницы для фокуса \(F\) и представьте линию нижнего края как направляющую \(L\).
Теперь поднимите нижний край и совместите одну точку на нем с точкой \(F\). Сделайте складку и разверните.
Сделайте это еще примерно 50 раз, поднимая разные точки вдоль нижнего края до точки \(F\) и каждый раз делая линию сгиба.
Эти линии сгиба очерчивают кривую, и эта кривая — парабола!
| В СТОРОНЕ: Вот как можно показать, что кривая, которую мы видим, имеет геометрическое свойство быть параболой. Для ясности покажем, что каждая линия сгиба, которую мы создаем, является касательной к параболе. Таким образом, набор всех линий сгиба дает набор всех касательных линий к параболе. Предположим, что точка \(P\) на направляющей поднята на \(F\), чтобы получилась показанная пунктирная линия сгиба. По симметрии складывания каждая точка на линии сгиба находится на таком же расстоянии от \(F\), как и от \(P\). В частности, точка \(T\) непосредственно над \(P\) на линии сгиба равноудалена от \(P\) и \(F\). Мы видим тогда, что \(T\) удовлетворяет геометрическому условию нахождения на параболе с фокусом \(F\) и направляющей \(L\). Каждая линия сгиба имеет по крайней мере одну точку на параболе с фокусом и направляющей . Рассмотрим любую другую точку \(R\) на линии сгиба. Пусть \(a\) будет его расстоянием от \(F\), которое равно его расстоянию от \(P\), и пусть \(b\) будет его расстоянием от \(L\). Мы видим, что \(b \neq a\) ( \(b\) катет прямоугольного треугольника, а \(a\) гипотенуза, и они не могут быть равны). Итак, \(R\) , а не удовлетворяет геометрическому условию нахождения на параболе с фокусом \(F\) и направляющей \(L\). Каждая линия сгиба имеет только одну точку на параболе с фокусом и направляющей . 92+bx+c\). Это кажется осуществимым? 1. Сложите параболу из бумаги . 2. Отметьте одинаковые интервалы вдоль нижнего края и измерьте высоту от нижнего края до кривой, как показано на рисунке. Это дает последовательность значений.
3. Рассчитайте таблицу разностей для этих данных. 4. С учетом человеческой ошибки разумно ли говорить, что у вас есть постоянные двойные различия?
ЗАДАЧА: Предположим, что мы расположили объекты в координатной плоскости так, что направляющая \(L\) представляет собой горизонтальную линию \(k\) единиц ниже оси \(x\) (и поэтому уравнение \(y=-k\)) и фокусом \(F\) является точка \(k\) единиц выше по вертикальной оси (и поэтому имеет координаты \((0,k)\)). Превратите геометрическое условие для точки \(P=(x,y)\) в параболу с фокусом \(F\) и направляющей \(L\) в алгебраическое условие. Является ли это алгебраическое условие квадратным уравнением? 92+bx+c\) и вовсе не очевидно, что эти две кривые являются или даже должны быть одними и теми же. Ошибочный шаг ГалилеяДавайте продолжим изучение U-образных кривых, которые мы наблюдаем в природе. Галилей заметил, что форма цепи, висящей между двумя полюсами, соответствует U-образной кривой, и задался вопросом, следует ли она также основной квадратичной формуле. Он подозревал, что да.
ЗАДАНИЕ:1. Повесьте на доску кусок легкой цепи. 2. С помощью линейки проведите горизонтальную линию и отметьте вдоль нее равные промежутки. Измерьте показанные горизонтальные высоты и соберите последовательность значений данных. 3. Используя разностные методы, найдите квадратную формулу для высот вдоль цепи.
НЕ ЧИТАЙТЕ СЛЕДУЮЩИЙ РАЗДЕЛ, ПОКА НЕ ПОПРОБУЕТЕ ЭТО ЗАНЯТИЕ САМИ И ПОСМОТРИТЕ САМИ. (Следующие спойлеры!)
Несомненно, в ваших данных есть неточности из-за человеческого фактора, а рассчитанные вами первая и вторая разности не являются постоянными. Вернитесь назад и попытайтесь собрать более точные и достоверные данные.
Но вы обнаружите, что вторые различия все же не постоянны. И как бы вы ни старались, при все более и более точных измерениях вы не сможете увидеть постоянной разницы в секундах.
Получается, что U-образные кривые висящих цепей просто равны не квадратичный. И ваши данные говорят вам об этом! Форма кривой висящей цепи известна как цепная кривая (от латинского catena для цепи). Только в 1691 году математики нашли точную формулу для этой кривой, и она сильно отличается от квадратного выражения!
В завершение этого урока позвольте мне указать, что у вас есть практическая возможность проверить, действительно ли определенные U-образные кривые имеют квадратичную структуру.
РАСШИРЕННОЕ ЗАДАНИЕ 1: Является ли арка ворот Сент-Луиса квадратичной кривой? Узнайте, сделав замеры на фотографии арки. РАСШИРЕННОЕ ЗАДАНИЕ 2: Задается ли полуокружность квадратным выражением? Узнайте это, обведя крышку кастрюли на листе бумаги и проведя измерения с помощью линейки. РАСШИРЕННОЕ ЗАДАНИЕ 3: Форма радуги, заданная квадратным выражением. Найдите фотографию радуги и соберите с нее данные. РАСШИРЕННОЕ ЗАДАНИЕ 4: Действительно ли траектория снаряда квадратична (или сопротивление воздуха оказывает существенное влияние на форму траекторий)? Найдите серию фотографий баскетбольного мяча или другого подбрасываемого предмета и измерьте высоту мяча на фотографиях через равные промежутки времени.
Комментарий: Вот это шок. Траектория снаряда по поверхности планеты — даже без атмосферы, которая позволяет избежать сопротивления воздуха — никогда не бывает квадратичной по своей природе! Движение брошенного предмета в идеальных условиях на самом деле представляет собой дугу эллипса, еще одну другую кривую, идентифицированную греческими учеными древности. Основное предположение на уроках физики состоит в том, что Земля плоская и что гравитация всегда направлена в одном направлении. Но на сферической планете направление «притяжения» гравитации всегда направлено к центру планеты, и это направление меняется по мере движения объекта.
Привет Элизабет Г. и ее брату Виктору Г.С помощью инструментов геометрии – биссектрисы угла, равноудаленности, наклона перпендикулярных прямых – Элизабет и ее брат смогли найти формулу для наклона касательной линия к параболе, та же самая формула, которую дает исчисление. Им также удалось доказать, что параллельные лучи света действительно отражаются от параболической поверхности и встречаются в ее фокусе.
Присоединяйтесь к обсуждению в Facebook и Twitter и поделитесь этой страницей, используя кнопки ниже. Представление трансформаций на плоскости с использованием, например, прозрачных пленок и программного обеспечения для геометрии; описывать преобразования как функции, которые принимают точки на плоскости в качестве входных данных и дают другие точки в качестве выходных данных. Сравните преобразования, которые сохраняют расстояние и угол, с теми, которые этого не делают (например, перемещение по сравнению с горизонтальным растяжением). | СС | ГСГ | HSG-СО | HSG-CO.APopular Tutorialsin Представление преобразований на плоскости с использованием, например, прозрачных пленок и программного обеспечения для создания геометрии; описывать преобразования как функции, которые принимают точки на плоскости в качестве входных данных и дают другие точки в качестве выходных данных. Сравните преобразования, которые сохраняют расстояние и угол, с теми, которые этого не делают (например, перемещение по сравнению с горизонтальным растяжением).
|
Будьте честны в том, что вы заметили.
Не стесняйтесь попробовать эти четыре примера.
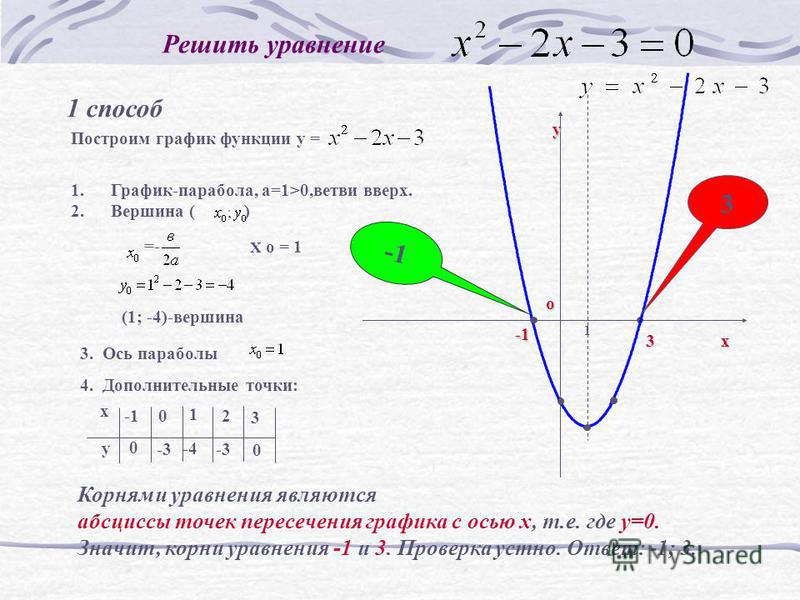
Этот урок покажет вам, что делает их особенными!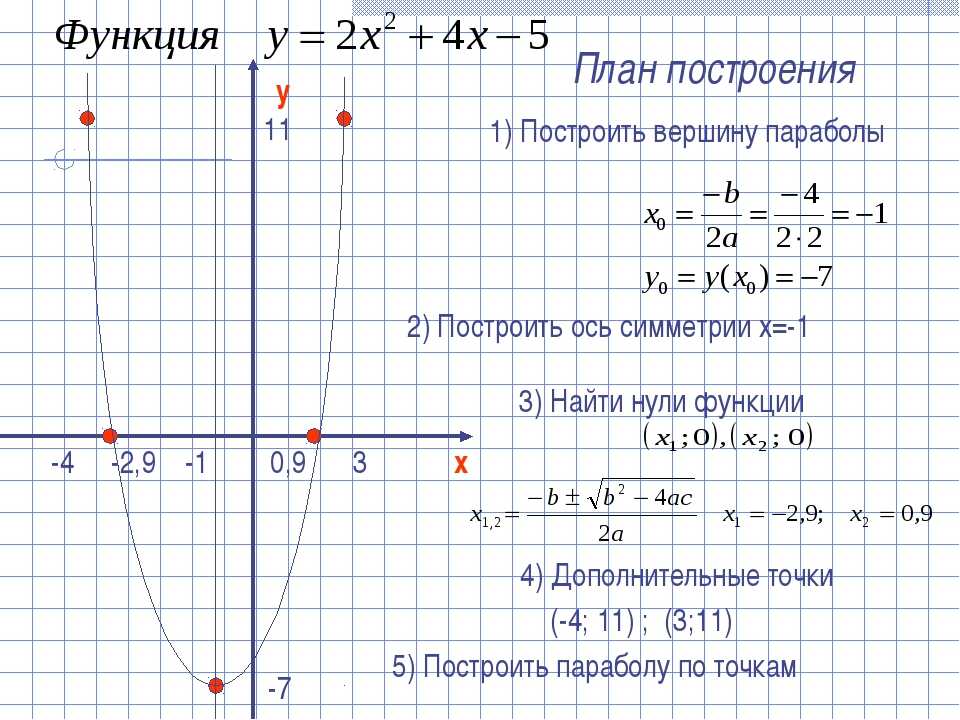
Затем просто соедините точки, чтобы создать новую фигуру. Посмотрите этот процесс в действии, посмотрев этот урок!
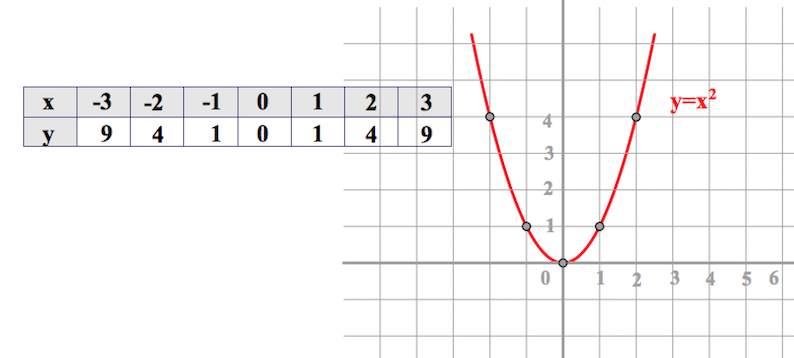Затем просто соедините точки, чтобы создать новую фигуру. Этот урок покажет вам, как!