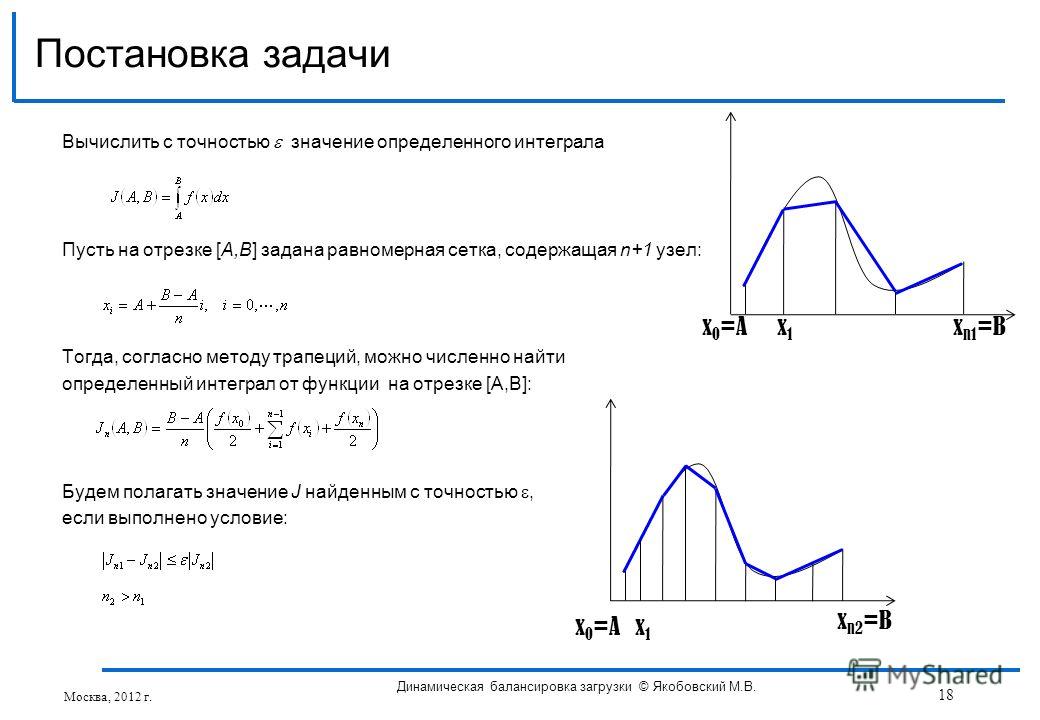
korowin5_1
С учетом сказанного имеет место разложение
(6.13)
называемое рядом Тейлора функции f(x) в точке х0.
Если в (6.13) положить х0 = 0, то получим ряд
(6.14)
который является частным случаем ряда Тейлора и называется рядом Маклорена.
1. f(x) = ln x в окрестности точки х0 = 1.
2. f(x) =2x в окрестности точки х0 = 2.
Решение
1. Вычислим значения функции ln x и ее производных в точке х0 = 1 и воспользуемся разложением (5.13):
f(x) = ln x , f(1) = ln 1 = 0;
;
;
;
;
=24;
……………
Тогда
,
или
2.
Найдем значения функции 2х и ее
производных в точке х0 = 2.
. . . . . . . . . .
Подставляя полученные выражения в формулу (6.13), получим искомое разложение:
или
Пример 2. Разложить в ряд Маклорена функцию f(x) = ex.
Решение. Найдем значения функции ex и ее производных в точке x0 =0.
Известно, что
и, следовательно, .
Тогда из формулы (6.14) получим
.
Аналогично можно получить разложения
;
;
(R, 1 < x < 1).
Последнее
разложение называется биномиальным
рядом.
В
случае, когда
натуральное число,
= n
N,
этот ряд представляет собой формулу бинома
Ньютона.
.
Пример 3. Разложить в ряд Маклорена функцию .
Решение. В разложении
заменим t на – х2, получим
или
.
Разложить в ряд Маклорена функции:
97. 98.
99. 100.
101. 102.
103. 104.
Разложить в ряд Тейлора функции в окрестности заданных точек
107.
108.
109. x0 = 2
110.
,
x0 =
§6. Применение степенных рядов
к приближенным вычислениям
1. Приближенные вычисления значений функций
Вычисление приближенного значения функции f(x) основано на использовании приближенного равенства f(x) Sn(x), где Sn(x) – частичная сумма степенного ряда, в который раскладывается данная функция. Для определения погрешности найденного приближенного значения, нужно оценить сумму отброшенных членов ряда или его остатка rn(x).
Известно, что погрешность приближенного равенства
(6.15)
определяется оценочной формулой , т.е. сумма отброшенных слагаемых в разложении функции ех меньше величины при 0 < x < n +1.
Пример
1. Вычислить
число е с точностью до 0,001.
Решение. Воспользуемся приближенным равенством (6.15), положив в нем х = 1, тогда . Из формулы оценки остатка ряда rn(x) при х = 1 получим
.
Число членов частичной суммы ряда, обеспечивающее необходимую точность приближения, определим из неравенства rn < 0,001 или < 0,001, т. е. n! n > 1000. Отсюда видно, что достаточно взять n = 6, так как 6! 6 = 720 7 + 4320 > 1000. Следовательно,
.
Слагаемые суммы необходимо вычислять с точностью до четвертого знака после запятой, чтобы при суммировании не получить погрешности, превышающей 0,001.
То есть
2,0000 + 0,5000 0,1667 0,0417 0,0083 0,0014 2,7181 |
Таким
образом, е
2,7181.
Пример 2. Вычислить с точностью до 0,00001.
Решение. Положим в приближенном равенстве (6.15) , тогда получим
.
Выражение в правой части равенства представляет собой частичную сумму знакочередующегося ряда, удовлетворяющего признаку Лейбница. Поэтому допускаемая при отбрасывании членов ряда погрешность не превосходит модуля первого из отброшенных слагаемых.
Нетрудно видеть, что < 0,00001.
Следовательно, необходимая точность будет достигнута, если частичную сумму составить из пяти слагаемых, т. е.
.
Производя вычисления, окончательно получаем .
2. Приближенные вычисления определенных интегралов
Пример 3. Вычислить с точностью до 0,001.
Решение.
Воспользуемся разложением функции
в
ряд Маклорена (см. Пример 2).
Тогда можно записать
Здесь учтено, что для достижения необходимой точности вычисления интеграла, достаточно ограничиться пятью слагаемыми, так как 0,0008 < 0,001.
111. Вычислить с точностью до 0,00001.
112. Вычислить с точностью до 0,00001.
113. Вычислить ln 1,04 с точностью до 0,0001.
114. Вычислить с точностью до 0,0001.
115. Вычислить ln 0,98 с точностью до 0,001.
116. Вычислить cos 180 с точностью до 0,0001.
117. Вычислить sin 90 с точностью до 0,0001.
118. Вычислить с точностью до 0.001.
119. Вычислить с точностью до 0,0001.
120.
Вычислить с точностью до 0,001.
121. Вычислить с точностью до 0,0001.
ОГЛАВЛЕНИЕ Глава I. ВВЕДЕНИЕ В АНАЛИЗ 2 Глава II. ПРЕДЕЛЫ 4Глава III. ДИФФЕРЕНЦИРОВАНИЕ 17
§1. Производная функции ……………………………………………….17
§2. Дифференциал функции 29
§3. Исследование функций и построение графиков 32
§4. Функции нескольких переменных 48
§5. Экстремумы функции двух переменных 53
Глава IV. ИНТЕГРИРОВАНИЕ 59
§ 1. Первообразная и неопределенный интеграл 59
§ 2. Методы интегрирования 60
§ 3. Определенный интеграл 67
§ 4. Методы вычисления определенного интеграла 70
§ 5. Приближенное вычисление определенных интегралов 74
§
6.
Геометрические приложения определенного
интеграла 79
§ 7. Несобственные интегралы 83
Глава V. ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ 86
§ 1. Основные понятия и определения 86
§ 2. Дифференциальные уравнения первого порядка…………………. 86
§ 3. Дифференциальные уравнения второго порядка 99
§ 4. Приложения дифференциальных уравнений 105
Глава VI. РЯДЫ 109
§ 1. Числовые ряды 109
§ 2. Знакопеременные ряды 118
§ 3. Функциональные ряды 121
§ 4. Степенные ряды 123
§ 5. Ряд Тейлора 128
§ 6. Применение степенных рядов к приближенным вычислениям 132
137
«Приближенные методы вычисления определенных интегралов»
ТЕМА: Приближенные
методы вычисления определенных интегралов.
ЦЕЛЬ: рассмотреть приближенные методы вычисления интегралов на основании геометрического смысла интеграла.
ЗАДАЧИ:
образовательные:
— изучение приближенных методов вычисления определенных интегралов: метода прямоугольников и метода трапеций, параболических трапеций;
— формирование умений и навыков вычисления определенных интегралов методами прямоугольников и трапеций, параболических трапеций;
воспитательные:
– воспитание самостоятельности, инициативности, решительности, уверенности в себе, стремления к творческому поиску и исследовательской деятельности;
развивающие:
– развитие концентрации внимания, абстрактно-логического мышления,
ТИП:
МЕТОДЫ ОБУЧЕНИЯ: проблемное изложение учебного материала.
ВНУТРИДИСЦИПЛИНАРНЫЕ СВЯЗИ
Дифференциальное исчисление.
Дифференциал функции и его приложение к приближенным вычислениям.
Интегральное исчисление.
и определенный интегралы, методы их решений.
МЕЖДИСЦИПЛИНАРНЫЕ СВЯЗИ
1. Дисциплина «Естествознание».
Современные естественнонаучные знания о мире.
2.5. Вещество и поле, их взаимодействие.
2. Дисциплина «Экономическая статистика».
Отражение результатов производства.
МАТЕРИАЛЬНОЕ ОБЕСПЕЧЕНИЕ: презентация, раздаточный материал.
Студент должен
знать:
формулы приближенного вычисления определенного интеграла:
— формулу прямоугольников;
— формулу трапеций;
— формулой параболических трапеций ( формула Симпсона).
уметь:
— вычислять определенные интегралы приближенно методами прямоугольников и трапеций, параболических трапеций.
ХОД ЗАНЯТИЯ
1. Организационный момент
Решение многих технических задач
сводится к вычислению определённых интегралов, точное выражение которых сложно,
требует длительных вычислений и не всегда оправдано практически.
Здесь бывает
вполне достаточно их приближённого значения.
Очень часто приходится вычислять определённые интегралы, для которых невозможно найти первообразную. В этом случае применяют приближённые методы вычисления определённых интегралов. Иногда приближённый метод применяют и для “берущихся” интегралов, если вычисление по формуле Ньютона-Лейбница не рационально.
2. Сообщение темы, целей занятия
Преподаватель объявляет тему занятия, привлекает студентов к постановке целей и задач занятия.
3. Мотивация
Чтобы вдохновиться на изучение нового материала, вспомним о полезности интеграла.
Выясним, в чем состоит экономический смысл интеграла:
Экономический смысл интеграла
Z(t) — функция производительности труда от времени
V(t) — функция объема произведенной продукции от времени
Z(t) =V'(t)
V(t) — первообразная Z(t)
Объем произведенной продукции есть первообразная производительности труда
Применение интеграла в естествознании.
Перемещение за ограниченный интервал времени – это определенный интеграл скорости по времени:
Для нахождения работы необходимо найти определенный интеграл функции силы по перемещению:
4. Актуализация опорных знаний.
а) фронтальный опрос.
1. Что называют неопределенным интегралом функции ?
2. Что называют определенным интегралом от a до b функции ?
3. В чем состоит геометрический смысл определенного интеграла?
4) Какие два метода интегрирования вы знаете?
5) Какие вопросы можно задать об этих двух методах? (выбранный студент опрашивает группу о том, на чем основан метод непосредственного интегрирования и в каких случаях применяется метод замены переменной).
6) Что называют прямоугольником? Начертите изображение прямоугольника и запишите формулу его площади.
7) Выполните те же задания, но для трапеции.
б) тестирование по теме “Интеграл”.
Вариант 1.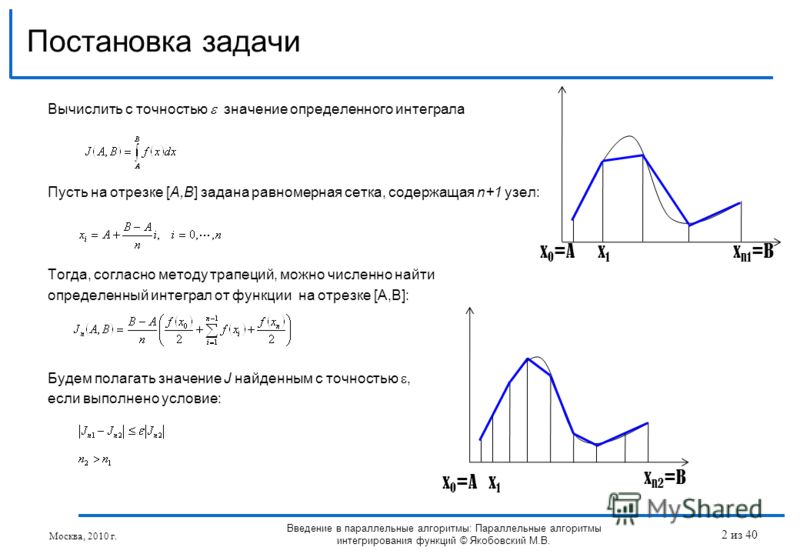
1) Вычислите:
Ответ: а) 27 б) 24 в) 18 г) 21
Ответ: а) -2 б) 2 в) -3 г) 3
Ответ: а) 26/3 б) 28/3 в) 15/2 г) 47/6
2) Найдите интеграл:
Ответ: а) 1.5 б) 2/3 в) -2/3 г) не существует.
3) При каком значении “а” выполняется равенство ?
Ответы: а) 2/3 б) 8/3 или -2 в) 2 или -1/3 г) -3
4) Вычислите площадь фигуры, ограниченной графиками функций: у=f(x), y=0, Y=-x2+x+2
Ответы: а) 13/3 б) 29/6 в) 16/3 г) 4,5
Вариант 2.
1) Вычислите:
Ответы: а) 25/3 б) 28/3 в) 26/3 г) 29/3
Ответы: -3.5 б) 1.5 в) -1.5 г) -3.5
Ответ: а) 22/9 б) -14/9 в) -22/9 г) 14/9
2) Найдите интеграл.
Ответ: а) 0 б) -12 в) не существует. Г) 12
3) При каком значении “а” выполняется равенство ?
Ответы: а) 2, -13/3 б) -4 в) 4, -5/2 г) -3,9/4
Вычислите площадь фигуры, ограниченной графиками функций: у=f(x), y=0, Y=-x2+4x-3
Ответы: а) 4/3 б) -1,5 в) 11/6 г)7/6
5.
Формирование
новых знаний и способов действий
Организация деятельности
Предполагается, проводить работу 3-мя группами.
1-я группа – работает над формулой приближенного интегрирования — формулой прямоугольников
2-я группа – работает над формулой приближенного интегрирования – формулой трапеций
3-я группа – работает над формулой приближенного интегрирования – формулой параболических трапеций ( формула Симпсона)
Описание
Под непосредственным интегрированием понимают такой способ
интегрирования, при котором данный интеграл путем тождественных преобразований
подынтегральной функции и применения свойств неопределенного интеграла
приводится к одному или нескольким табличным интегралам. Но вычислить интеграл
непосредственным интегрированием удается далеко не всегда, а иногда это связано
с большими трудностями. В этих случаях вычисление определенного интеграла по
формуле Ньютона – Лейбница либо невозможно, либо затруднительно, поэтому
прибегают к различным методам приближенного интегрирования.
Вычислить интеграл точно по формуле Ньютона – Лейбница с целью оценки погрешности при приближенном вычислении этого же интеграла.
Все три группы одновременно вычисляют интеграл :
Пример 1
= .
Блок 1
Разделим интервал интегрирования на равных частей (частичных интервалов) и заменим данную трапецию ступенчатой фигурой, состоящей из прямоугольников, опирающихся на частичные интервалы, причем высоты этих прямоугольников равны значениям функции в начальных или конечных точках частичных интервалов. Значение площади этой фигуры и будет давать приближенное значение искомого интеграла .
Если обозначить значения функции в точках деления через , то будем иметь следующую формулу — формулу прямоугольников :
или
Блок 2
Оставим
разбиение интервала прежним,
но заменим теперь каждую дугу линии ,
соответствующую частичному интервалу . хордой, соединяющей конечные точки этой
дуги. Таким образом, заменяем данную криволинейную трапецию прямолинейными.
Площадь каждой трапеции, построенной на частичном интервале, равна полусумме
площадей , соответствующих этому интервалу прямоугольников. Суммируя все эти
площади, получим формулу трапеций :
Блок 3
Разобьем интервал на равных частей , но предположим, что – четное число: . Заменим дугу линии , соответствующую интервалу , дугой параболы, ось которой параллельна оси ординат и которая проходит через следующие три точки дуги: начальную точку дуги , среднюю точку , конечную точку . Площадь данной трапеции приближенно равна сумме площадей получающихся параболических трапеций и выражается формулой :
1 группа
Решает пример 1 по формуле прямоугольников : при
Таблица расчетов :
0 | 1 | 2 | 3 | 4 | 5 |
|
0 | 0. | 0.4 | 0.6 | 0.8 | 1 | |
1 | 0,9615 | 0,8621 | 0,7353 | 0,6098 | 0,5 |
22 группа
Решает пример 1 по формуле трапеций : при
Таблица расчетов :
0 | 1 | 2 | 3 | 4 | 5 |
|
0 | 0. | 0.4 | 0.6 | 0.8 | 1 | |
1 | 0,9615 | 0,8621 | 0,7353 | 0,6098 | 0,5 |
23 группа
Решает пример 1 по формуле параболических трапеций : при
Таблица расчетов :
0 | 1 | 2 | 3 | 4 |
|
0 | |||||
1 |
Занесем итоги расчета в таблицу и сравним:
значение интеграла | абсолютная погрешность | относительная погрешность |
|
формула Н-Л | 0,7854 | ||
фор-ла прям-ков | 0,8337 | 6,1 % | |
фор-ла трапеций | 0,7837 | ||
фор-ла Симпсона | 0,7854 | 0 | 0 |
= 6,1 %
Вывод : гипотеза о том, что с
помощью формул численного интегрирования можно вычислять определенные интегралы
подтвердилась.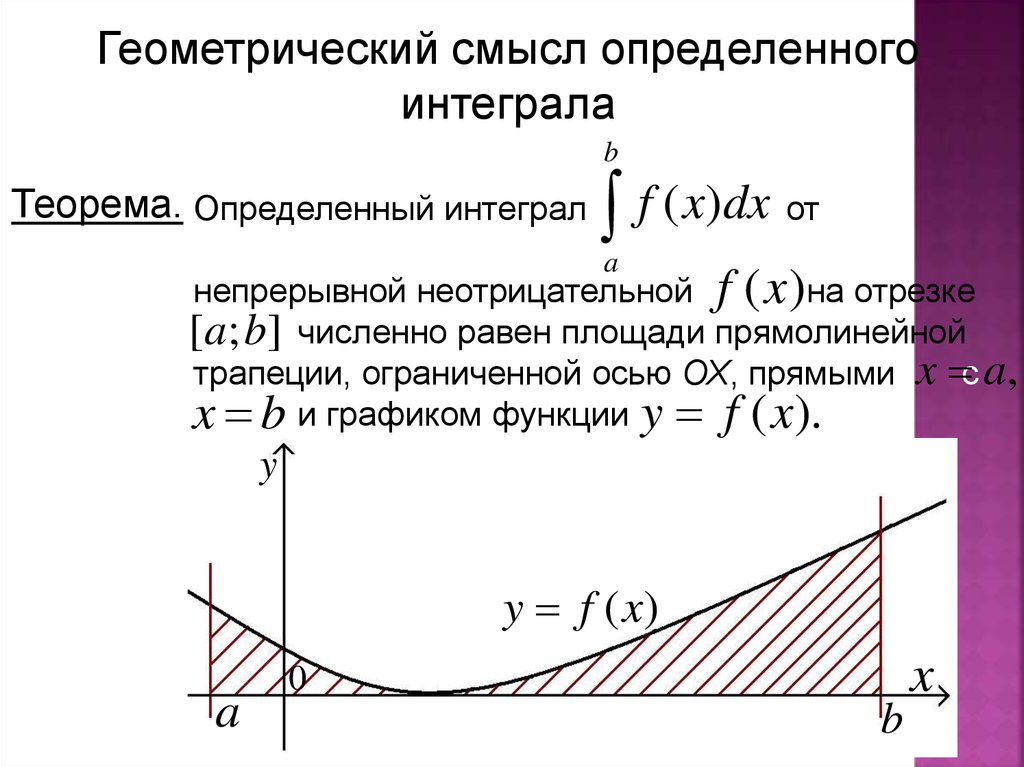
Однако, при одном и том же значении формула
Симпсона дает лучшее приближение.
6. Закрепление материала
Пример 1. Вычислить по формуле прямоугольников . Найти абсолютную и относительную погрешности вычислений.
Решение:
Разобьём отрезок [a, b] на несколько (например, на 6) равных частей. Тогда а = 0, b = 3 ,
х k = a + k х
х0 = 2 + 0* = 2 х1 = 2 + 1* = 2,5 х2 = 2 + 2* =3
х3 = 2 + 3 * = 3,5 х4 = 2 + 4* = 4 х5 = 2 + 5 * = 4,5
f (x0) = 22 = 4
f (x 1 ) = 2 ,52 = 6,25
f (x 2 ) = 32 = 9
f (x 3 ) = 3,52 = 12,25
f (x 4 ) = 42 = 16
f (x 5 ) = 4,52 = 20,25
х 2 2,5 3 3,5 4 4,5
у 4 6,25 9 12,25 16 20,25
По формуле (1):
Для того, чтобы вычислить относительную погрешность вычислений, надо найти точное значение интеграла:
Пример 2.Вычислить приближенно определенный
интеграл по формуле трапеций.
Результаты округлить до трёх знаков после
запятой.
а) Разбив отрезок интегрирования на 3
части.
б) Разбив отрезок интегрирования на 5 частей.
Решение:
а)
По условию отрезок интегрирования нужно разделить на 3 части, то есть .
Вычислим длину каждого отрезка разбиения: .
Параметр ,
напоминаю, также называют шагом.
Сколько будет точек (узлов
разбиения)? Их будет на одну больше, чем количество
отрезков:
Ну а общая формула трапеций сокращается до
приятных размеров:
Для расчетов можно использовать обычный
микрокалькулятор:
Обратите внимание, что, в соответствии с условием задачи, все вычисления следует округлять до 3-го знака после запятой.
Окончательно:
б) Разобьём отрезок интегрирования на 5 равных частей, то есть . Увеличивая количество отрезков, мы увеличиваем точность вычислений.
Если ,
то формула трапеций принимает следующий вид:
Найдем шаг разбиения:
,
то есть, длина каждого промежуточного отрезка равна 0,6.
При чистовом оформлении задачи все
вычисления удобно оформлять расчетной таблицей:
В первой строке записываем «счётчик»
Как формируется вторая строка– сначала записываем нижний предел интегрирования , остальные значения получаем, последовательно приплюсовывая шаг .
В результате:
Если для 3 отрезков разбиения приближённое значение составило, то для 5 отрезков . Таким образом, с большой долей уверенности можно утверждать, что, по крайне мере .
Пример 3
Вычислить приближенно определенный
интеграл по формуле Симпсона с точностью до 0,001. Разбиение начать с двух
отрезков
Решение: Начинаем решать. Если у нас два
отрезка разбиения ,
то узлов будет на один больше: .
И формула Симпсона принимает весьма компактный вид:
Вычислим шаг разбиения:
Заполним расчетную таблицу:
В верхнюю строку записываем «счётчик» индексов
Во второй строке сначала пишем нижний
предел интегрирования ,
а затем последовательно приплюсовываем шаг .
В третью строку заносим значения подынтегральной функции. Например, если , то . Сколько оставлять знаков после запятой? Действительно, в условии опять об этом ничего не сказано. Принцип тот же, что и в методе трапеций, смотрим на требуемую точность: 0,001. И прибавляем дополнительно 2-3 разряда. То есть, округлять нужно до 5-6 знаков после запятой.
В результате:
Первичный результат получен. Теперь удваиваем количество
отрезков до четырёх: .
Формула Симпсона для данного разбиения принимает следующий вид:
Вычислим шаг разбиения:
Заполним расчетную таблицу:
Таким образом:
Найдём абсолютное значение разности между
приближениями:
Правило Рунге для метода Симпсона очень
вкусное. Если при использовании метода средних
прямоугольников и метода трапеций нам даётся «поблажка» в одну треть, то
сейчас – аж в одну пятнадцатую:
,
и точность здесь уже не страдает:
Рассмотрим другое решение, где придётся
сделать дополнительный шаг: так как больше
требуемой точности: ,
то необходимо еще раз удвоить количество отрезков: .
Формула Симпсона растёт, как на дрожжах:
Вычислим шаг:
И снова заполним расчетную таблицу:
Таким образом:
Оцениваем погрешность:
Погрешность меньше требуемой точности: . Осталось взять наиболее точное приближение , округлить его до трёх знаков после запятой и записать:
Ответ: с точностью до 0,001
Приведенные правила численного интегрирования помогают решать прикладные задачи.
Прикладная задача
Ширина реки равна 20м; промеры глубины в некотором поперечном ее сечении через каждые 2м дали следующую таблицу :
0 | 2 | 4 | 6 | 8 | 10 | 12 | 14 | 16 | 18 | 20 |
|
0. | 0,5 | 0,9 | 1,1 | 1,3 | 1,7 | 2,1 | 1,5 | 1,1 | 0,6 | 0,2 |
2Расстояние (в метрах) от одного из берегов обозначено через , соответствующая глубина реки ( также в метрах) – через Требуется найти площадь поперечного сечения реки.
По формуле Симпсона находим :
7. Контроль усвоения, обсуждение допущенных ошибок и их коррекция. Самостоятельная работа студентов:
Вариант 1
Вариант 2
Обсуждение
решения.
8. Подведение итогов занятия
Обобщаются новые знания, делаются выводы студентами о достигнутых целях. Отмечаются активные студенты.
9. Домашнее задание
Студенты записывают домашнее задание, преподаватель объясняет способ его выполнения.
Домашнее задание:
Вычислить интеграл приближенно методами: 1) прямоугольников; 2) трапеций и точно – по формуле Ньютона-Лейбница; найти абсолютные погрешности приближений:
Литература
1. Пахомова Н.Ю. Метод учебного проекта в образовательном учреждении: Пособие для учителей и студентов пед.вузов, — М:АРКТИ, 2005г.
2. Чечель И.Д Исследовательский проекты в практике обучения. «Практика административной работы в школе» , 6/2003 г.
3. Богомолов Н.В. Практические задания по математике. — М.:Высшая школа, 1990.
4.
Бермант А. Ф.,
Араманович И. Г. Краткий курс математического анализа для втузов.
— М.: Наука,
1967.
О вычислении определенных интегралов с помощью вычисления неопределенных интегралов
Введение
Как известно, с помощью определенных интегралов ученые исследовали многие практические задачи, такие как вычисление площади, ограниченной некоторыми функциями или прямыми линиями , объемы некоторых различных фигур, объемы тел вращения, расстояния между объектами, энергия сигналов, землетрясений и др. (см., например, [1, с. 169–222, 2, 3]). Исследование определенных интегралов тесно связано с нахождением решения начальной задачи для ОДУ. Поэтому для построения методов вычисления определенных интегралов были привлечены такие известные ученые, как Ньютон, Коттес, Гаусс, Чебышев, Симпсон, Адамс и др. (см., например, [4, 5]). Учеными построены различные формулы для вычисления определенных интегралов, имеющие различную точность.
А также известно, что для получения более точных результатов при вычислении определенных интегралов применялось уменьшение размера шага, что приводит к увеличению объема расчетных работ.
А известно, что первый прямой метод решения начальной задачи для ОДУ был построен Эйлером с использованием простейшей формы квадратурной формулы. Принимая во внимание, что порядок точности метода Эйлера равен 1 (единице), поэтому для построения более точных методов, чем метод Эйлера, специалисты предложили использовать интерполяционные полиномы с высокой точностью при построении методов вычисления определенные интегралы (см., например, [6, 7]). Но вот для построения более точных методов предложили использовать метод неизвестных коэффициентов. А для исследования определенных интегралов методом подынтервалов с помощью этого сравнивали полученные здесь результаты с известными. 9b {f(x)dx},$$
(1)
здесь достаточно гладкая функция f ( x ) определена в интервале \([x_0,b]\). Для построения методов вычисления определенного интеграла (1) обозначим через \(f_i\) значения функции f ( x ) в узловых точках \(x_{i}=x_{ 0}+ih\) \((i=0,1,\ldots ,N)\).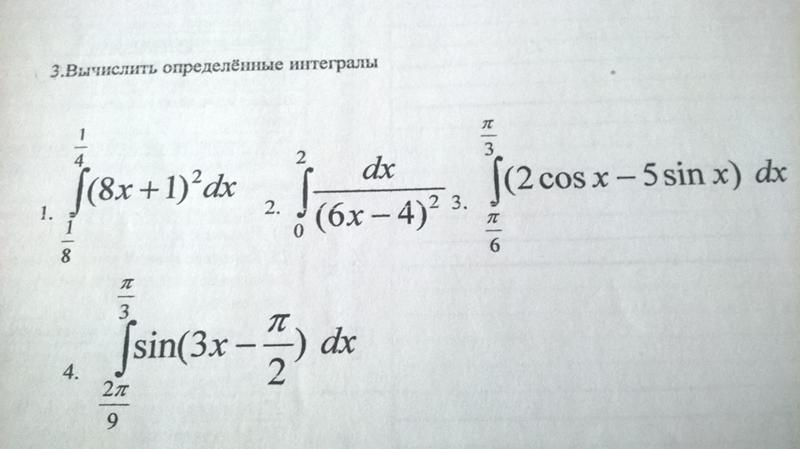
{x_{i+1}} {f(s)ds}, (i=0,1,\ldots ,N- 1).$$
(4)
Используя это равенство, ученые построили методы решения задачи (3) с разными порядками точности. Здесь мы предложили использовать конечно-разностные методы и применили их для решения задач (3) и (4), а также построили методы прямого (расширенного) и гибридного типов для вычисления определенного интеграла (1).
Построение конечно-разностных методов
Как известно, одним из популярных методов решения задачи (3) является конечно-разностный или многошаговый метод, который можно представить в следующем виде: 9k {\beta _{i}f_{n+i}}$$
(5)
$$(n=0,1,\ldots ,N-l; l=\max (s,k)).$ $
Этот метод исследовался некоторыми авторами (см., например, [8,9,10,11,12,13,14]). Отметим, что метод (5) в случае \(s=k\) принципиально исследован Далквистом [8] и показал, что если метод (5) устойчив в случае \(s=k\) и имеет степень p тогда \(p\le 2[k/2]+2\) и для всех значений порядка k существуют устойчивые методы с максимальными степенями.
Здесь мы используем известное определение степени зачатия и устойчивости, предложенное Далквистом [8]. 9{p+1}),\quad h\rightarrow 0.$$
Здесь p — целое число.
Следует отметить, что все известные методы типа (5) подчиняются закону Дальквиста. Но в работе [13] доказано существование устойчивых методов типа (5) со степенью \(p=k+m+1\) (для значений \(k\ge {3m}, m=k-s \)). Методы с таким же свойством были построены и другими авторами (см., например, [14,15,16]). Принимая во внимание это свойство методов прямого скачка, рассмотрим здесь применение методов прямого скачка к решению задачи (3). Поэтому предположим, что \(s
Но для вычисления \(y(x_{N})\) методами прямого перехода нам необходимо использовать некоторые значения функции f ( x ) за пределами рассматриваемого сегмента.
Используя границы \(p\le {k+m+1}\) \((m\le {[k/3]})\), получаем, что для построения более точных устойчивых методов значение k нужно выбирать больше. Например, если \(k\ge 9\), то можно построить устойчивый метод типа (5) со степенью \(p\le {k+4}\) . Как известно, для повышения точности метода (5) необходимо повышение точности начальных значений \(y_{j}\) \((j=0,1,\ldots ,k-1)\) . Поэтому ученые обсудили использование другой схемы для построения устойчивых методов с высокими степенями. Для этой цели предлагается использовать интерполяционные полиномы Гаусса, Чебышева, Лабботто и др. В результате чего появились новые методы. Эти методы остались от гибридных методов и в простом виде могут быть записаны следующим образом (см., например, [17,18,19{l+1}}{(l+1)!}\alpha _{i}}\nonumber \\&l=1,2,\ldots ,p-1.
\end{aligned}$$
(9)
Используя решение нелинейной системы (9), можно построить устойчивые методы типа (8). Заметим, что в системе (9) есть \(p+1\) уравнений и \(4k+3-m\) неизвестных. Если система (9) имеет решение в случае \(p+1=4k+3-m\), то получаем, что существуют методы типа (8) со степенью \(p=4k+2-m \). Обычно методы со степенью \(p=4k+2-m\) непригодны. Докажите, что существуют устойчивые методы для \(k>2\) со степенью \(p\le {3k+2+m}\). Но отсюда не следует, что \(P_{\max }=3k+2+m\)\((k\ge{3m})\). Система (8) является нелинейной, поэтому найти некоторые условия существования единственного решения непросто.
Следовательно, существование устойчивых методов типа (9) с максимальными степенями нам неизвестно. Эти свойства нелинейной системы алгебраических уравнений были встречены при исследовании методов Гаусса и Чебышева. Поэтому для нахождения узловых точек Гаусса авторы использовали известные многочлены (см., например, [4, с. 189–199, 25, с. 463–469]). Но здесь мы для нахождения решения системы (9) воспользовались программой Mathcad и в ряде случаев получили существование решения системы (9) в случае \(p>3k+2+m\).
k {\ gamma _ {i} y»_ {n + i}}, $ $ 9l {\gamma _{i}f’_{n+i}}.$$
(13)
Принимая во внимание, что функция f ( x ) известна, получаем это, используя методом (13) можно вычислить значение определенного интеграла (1). Метод (13) основательно исследовался некоторыми авторами (см., например, [28,29,30,31]). Если метод (13) устойчив и имеет степень p , то существуют методы со степенью \(p\le {2k+2}\) (в случае \(s=k=l\) ) и существуют методы со степенью \(p>2k+2\) в остальных случаях.
Следует отметить, что понятие устойчивости для метода (13) зависит от значений коэффициентов \(\beta _{i}\) \((i=0,1,\ldots ,k)\) . Если выполняются условия \(|\beta _{0}|+|\beta _{1}|+\cdots +|\beta _{s}|\ne 0\), то понятие устойчивости метода ( 13) определяется как устойчивость метода (5). Но в случае \(|\beta _{0}|+|\beta _{1}|+\cdots +|\beta _{s}|=0\) метод (13) называется устойчивым , если корни многочлена \(\rho (\lambda )\) лежат в единичной окружности, на границе которой нет кратных корней без двукратного корня \(\lambda =1\).
Очевидно, что в этом случае степень метода (13) будет такой же, как и степень метода (5). Для простоты положим в равенстве (13) \(s=k=l\). Как отмечалось выше, в этом случае существуют устойчивые методы со степенью \(p=2k+2\), если \(|\beta _{0}|+|\beta _{1}|+\cdots +|\beta _{s}|\ne 0\) выполняется. Нетрудно понять, что с помощью метода (13) можно определить значение \(y_{n+k}\), если значения \(y_{j}\) \((j=0, 1,\ldots ,k-1)\) известны. Для решения этой проблемы предлагается использовать следующий метод: 9{(j)}}.$$
(14)
Из этой формулы можно получить разложение Тейлора для значения \(k=1\). В этом случае получают одношаговый метод, который всегда можно применить к вычислению определенного интеграла (1), так что \(y_{0}=0\). Таким образом, используя описанный способ, мы можем построить методы предиктора-корректора с различными степенями для вычисления значений \(y_{j}\) \((j=0,1,\ldots ,k-1)\) и значения \(y_{n+k}\) \((n=0,1,\ldots ,N-k;x_{N}=x_{0}+Nh)\).
Для построения устойчивых методов типа (13) (в случае \(s=k=l\)) будем считать определяемыми значения коэффициентов метода (13).
Как было отмечено выше, для определения значений коэффициентов метода (13) можно использовать метод неизвестных коэффициентов. И в этом случае получить систему алгебраических уравнений, аналогичную системе (9). Но здесь мы хотим представить способ нахождения значений коэффициентов для метода (13), при использовании которого объем вычислительной работы меньше вычислительной работы, получаемой при решении системы, аналогичной системе (9{(3)} =С. \end{aligned}$$
Здесь константа C есть коэффициент при главной части в разложении остаточного члена построенных методов. Эквиваленты системы (9) и (16) можно найти в работе [25].
Заметим, что в случае \(k=2\) линейную часть метода (13) можно представить в виде: \(y_{n+2}-y_{n}\). В этом случае при замене ч на ч / 2 из указанной линейной части получим: \(y_{n+1}-y_{n}\). Таким образом, таким образом построили одношаговый метод, аналогичный гибридным методам. Эту схему можно обобщить следующим образом: 9l {\gamma _{i}f’_{n+i}}.
$$
(17)
Для получения одношагового метода из метода (17) достаточно выбрать размер шага h в виде h / k . Следует отметить, что метод (17) может быть неустойчивым при значениях \(k>2\). Но получение одноступенчатой формы, которая будет стабильной.
Построение некоторых простых методов и их применение к вычислению определенных интегралов
Сначала рассмотрим построение устойчивых методов типа (5). Как известно, для случая \(s=k\) можно построить устойчивые методы со степенью \(p\le 8\), имеющей явный и неявный тип для \(k\le 6\). Поэтому рассмотрим случай, когда \(s
$$y_{n+ 1}=y_{n}+h(5f_{n}+8f_{n+1}-f_{n+2})/12.$$
(18)
А теперь положим \(k= 3\) и \(m=2\), то получим:
$$y_{n+1}=y_{n}+h(9f_{n}+19f_{n+1}-5f_{n+2} +f_{n+3})/24.
$$
(19)
Но для случая \(k=4\) и \(m=3\) устойчивый метод можно записать так:
$ $y_{n+1}=y_{n}+h(251f_{n}+646f_{n+1}-264f_{n+2}+106f_{n+3}-19f_{n+4})/720.$$
(20)
Метод (19) имеет степень \(p=4\), а метод (20) имеет степень \(p=5\) . В [11] доказано, что для коэффициентов \(|\beta _{k-m+i}|>|\beta _{k-m+i+1}|\) и \(\beta _{k-m} >0\) (для \(\alpha _{km}>0\) ), \(\beta _{km+i}\beta _{km+i+1}<0\) если коэффициенты удовлетворяют условию: \(\beta _{k-m+i}\ne 0\), \(\beta _{k-m+i+1}\ne 0\). Описанные выше методы удовлетворяют этим условиям.
Применение методов (18) и (20) к вычислению интеграла (1) очень просто, поскольку известно \(y_{0}\). Теперь рассмотрим случай \(k=3\) и \(m=1\). В этом случае метод с максимальной степенью можно записать в виде:
$$y_{n+2}=(8y_{n+1}+11y_{n})/19+h(10f_{n}+57f_{n+1}+24f_{n+2}-f_{ n+3})/57.$$
(21)
Этот метод устойчив и имеет степень \(p=5\). Если в этом методе размер шага ч заменить на ч / 2, то получим:
$$y_{n+2}=(8y_{n+1}+11y_{n})/19+h (10f_{n}+57f_{n+1/2}+24f_{n+1}-f_{n+3/2})/114.
$$
(22)
Метод (22) сложнее метода (20), так что в методе (22) участвует член \(y_{n 1/2}\). Чтобы найти это значение, можно использовать метод (19) или метод (20). Но если рассмотреть случай \(m=0\) и \(k=2\), то получим следующий устойчивый метод со степенью \(p=4\):
$$y_{n+2}=y_{ n}+h(f_{n+2}+4f_{n+1}+f_{n})/3,$$
и в этом методе после замены h на h / 2 получаем:
$$y_{n+1}=y_{n}+h(f_{n+1}+4f_{n+1/2}+f_{n})/6,$$
(23)
, который можно применить для вычисления интеграла (1) в отдельной форме. Теперь рассмотрим построение устойчивого метода типа (8) и положим \(k=1\). В этом случае из метода (8) можно получить устойчивые методы разного порядка точности. Например, метод со степенью \(p=6\) можно записать так:
$$y_{n+1}=y_{n}+h(f_{n}+f_{n+1})/12+5h(f_{n+\alpha }+f_{n+1-\alpha })/12,\,\,\,\,\, \alpha =1/2-\sqrt{5}/10.$$
(24)
Этот метод является неявным. В этом случае явный метод со степенью \(p=5\) можно записать так:
$$\begin{aligned}&y_{n+1}=y_{n}+hf_{n}/9+ h((16+\sqrt{6})f_{n+3/5-\alpha}+(16-\sqrt{6})f_{n+3/5+\alpha})/36,\nonumber \ \&\quad \alpha =\sqrt{6}/10.
\end{aligned}$$
(25)
Если предположить, что \(\beta _{i}=0\) \((i=0,1,\ldots ,k)\), то можно доказать что существуют устойчивые методы со степенью \(p=2k+2\). В случае \(k=1\) метод со степенью \(p=4\) имеет следующий вид:
$$\begin{aligned}&y_{n+1}=y_{n}+h(f_{n+l}+f_{n+1-l})/2,\nonumber \\&\quad l =1/2-\sqrt{3}/6. \end{aligned}$$
(26)
А теперь рассмотрим построение многошаговых методов второй производной. Как отмечалось выше, если эти методы устойчивы, то степень этих методов удовлетворяет условию \(p\le {2k+2}\). Сначала поставим \(s=k=l\) и \(k=1\). Тогда из метода (18) можно получить следующие методы (см., например, [27,28,29,30]): 9{3}f»_{(\xi )}/6. \end{aligned}$$
(29)
Обратите внимание, что метод (27) неявный, метод (29) явный, но метод (28) в зависимости от его применения может быть явным или неявным. В нашем случае метод (28) является явным, поскольку функция f ( x ) не зависит от функции y ( x ).
{2}(-3f’_{n+2 }-40f’_{n+1}+3f’_{n})/240. \end{выровнено}$$ 9{1} {exp{(\lambda {s}})ds}.$$
(37)
Эта задача была сведена к решению задачи: \(y'(x)=exp{(\lambda { x})}\) \(y(0)=0\), точное решение которого можно записать в виде: \(y(x)=exp{(\lambda {x})}-1\). Эта задача была решена с помощью методов прямого скачка (17)–(20), гибридных методов (24)–(26) и многошаговых методов с множественными производными (27), (35) и (36). Для сравнения полученных результатов была решена рассматриваемая задача для различных значений \(\lambda\) и \(h=0,1\).
Результаты вычисления данного определенного интеграла сведены в таблицы 1 и 2.
Таблица 1 Результаты решения примера в случае \(\lambda =\pm 1\)Полная таблица
Таблица 2 Результаты решения примера в случае \(\lambda =\pm 5\)Полная таблица
Для построения устойчивых методов с высокими степенями предложено три пути. И дали некоторые из конкретных методов прямого скачка, гибридного и многошагового типов вторых производных, которые были сравнены путем их применения для решения примера (37).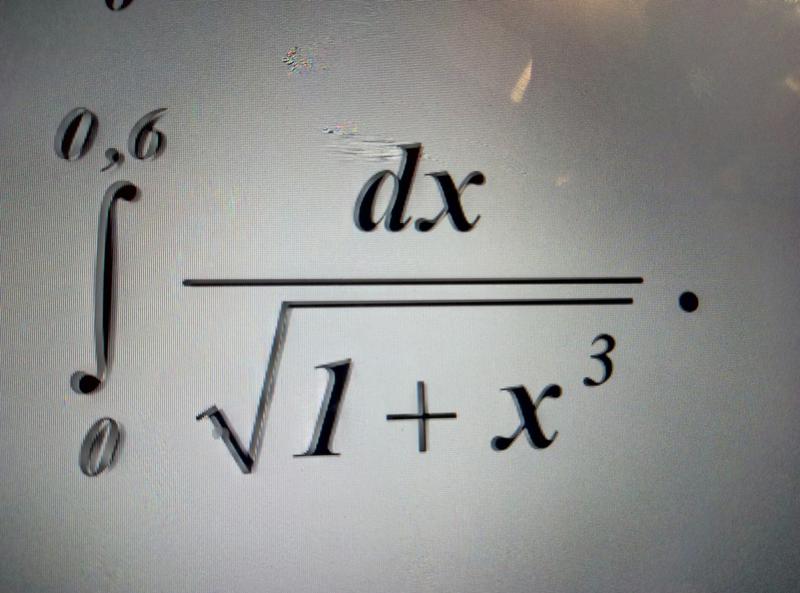
9{y} {f(x,t)dt}.$$
Заключение
Как было отмечено выше, здесь описаны некоторые способы вычисления определенного интеграла и их применение к вычислению двойных интегралов. Дано некоторое сравнение методов, рекомендованных для вычисления определенных интегралов. Показали, что поведение ошибок при использовании методов зависит от их типа. Для этого воспользовались результатами, полученными для шага \(h=0,1\), которые сведены в таблицы 1 и 2. А также показали, что ошибки в основном зависят от свойств решения рассматриваемых задач. . Как видно из таблицы 2, результаты, полученные методами прямого скачка для \(h=0,1\) и \(m=5\), не являются удовлетворительными и не могут считаться нормальными. Но результаты, полученные для шага \(h=0,1\) и \(m=1\), можно считать нормальными. Надеемся, что описанный выше метод найдет свое широкое применение при решении научных и технических задач. Чтобы показать преимущества описанного здесь метода, было рассмотрено применение вышеупомянутого метода для вычисления двукратно определенных интегралов.
А для вычисления значений конкретных двойных интегралов были применены предложенные здесь методы. С учетом полученных здесь результатов оба метода представляют как теоретический, так и практический интерес. Этот метод является новым направлением в вычислении определенных интегралов, и мы верим, что он найдет своих последователей.
Вычисление площади под кривой с помощью сумм Римана
Площадь под кривой
Дана функция $f(x)$, где $f(x) \ge 0$ на интервале $a \le x \le b $ исследуется площадь области, которая находится под графиком $f(x)$ и выше интервала $[a, b]$ на оси $x$. Например, заштрихованная фиолетовым цветом область ниже — это область над интервалом $[-1,10]$ и под графиком функции $f$. Такую область часто называют «площадью под кривой».
Поскольку область под кривой имеет такую странную форму, вычислить ее площадь слишком сложно. Но вычислить площадь прямоугольников просто. Давайте упростим нашу жизнь, представив, что область состоит из набора прямоугольников.
Чтобы превратить область в прямоугольники, мы будем использовать ту же стратегию, что и при использовании прямого Эйлера для решения дифференциальных уравнений в чистом времени.
Как показано на следующем рисунке, мы делим интервал $[a,b]$ на $n$ подинтервалов длины $\Delta x$ (где $\Delta x$ должно быть равно $(b-a)/n$). Мы помечаем концы подынтервалов $x_0$, $x_1$ и т. д., так что самая левая точка равна $a=x_0$, а самая правая точка — $b=x_n$. На рисунке показан случай с четырьмя подынтервалами.
Следующий шаг — сделать вид, что $f(x)$ не меняется на каждом подынтервале. Мы будем измерять $f(x)$ в левой части подинтервала и игнорировать любые изменения в $f$ на протяжении подинтервала. В результате мы делаем вид, что область под $f$ состоит из набора прямоугольников, по одному на каждый подинтервал. Возможно, это грубое приближение, но оно позволяет легко вычислить площадь.
Пронумеруем $n$ подинтервалов как $i=0,1,2, \ldots, n-1$. Тогда левый конец подынтервала с номером $i$ равен $x_i$, а его правый конец равен $x_{i+1}$.
Мы представляем себе, что высота $f$ на всем подынтервале равна $f(x_{i})$, значению $f$ в левой конечной точке. Поскольку ширина прямоугольника равна $\Delta x$, его площадь равна $f(x_{i})\Delta x$. 9{n-1} f(x_{i}) \Delta x.
\label{left_riemann}
\end{выравнивание}
Эта сумма называется суммой Римана.
Сумма Римана является лишь приближением к фактической площади под графиком $f$. Для улучшения аппроксимации можно увеличить количество подинтервалов $n$, что приведет к уменьшению ширины подинтервала $\Delta x= (b-a)/n$. Чтобы узнать, что происходит, когда $n$ становится все больше и больше, вы можете использовать следующий апплет.
Площадь через левую сумму Римана. Площадь под графиком $f(x)$ (синяя кривая на левой панели) на интервале $[a,b]$ вычисляется с помощью левой суммы Римана. Левая сумма Римана $n$ подынтервалов изображается прямоугольниками, на которые наложен график $f$. На правой панели показаны площади прямоугольников $\hat{A}(x)$ от $a$ до $x$, изображенные в виде зеленой кривой.
Площадь на всем интервале $[a,b]$ равна величине $\hat{A}(b)$. Чтобы исследовать поведение $\hat{A}$, вы можете перемещать розовые точки по кривой и вершинам прямоугольников. При перемещении розовых точек выделяется прямоугольник, а в правом верхнем углу отображается расчет его площади. Площадь каждого прямоугольника равна значению $f$ в его левой конечной точке, умноженному на ширину подынтервала $\Delta x$. Текущая сумма площади $\hat{A}(x)$ увеличивается на площадь прямоугольника, когда вы перемещаете розовые точки вправо на один прямоугольник. Если вы установите флажок «точно», истинная площадь под графиком $f$ заштрихована красным слева, а правая панель отображает график (красным цветом) истинной площади $A(x)$ под $f $ от $a$ до $x$. Истинная площадь справа от выделенного прямоугольника вычисляется вместе с ошибкой между истинной площадью и соответствующей площадью, рассчитанной с помощью суммы Римана. Значения $A(x)$ и $\hat{A}(x)$ являются площадями под $f$ только для случая, когда $f(x) \ge 0$.
92+12$, выпишите все четыре члена суммы Римана с $n=4$, которая оценивает площадь под графиком $f$ на интервале $[a,b]=[-2,7]$. Подставьте числа из $f$, оцененные в левых конечных точках, и рассчитайте эту оценку площади. Эта оценка должна согласовываться с тем, что вы вычисляете с помощью приведенного выше апплета для этой функции и четырех подынтервалов.
Что произойдет, если вы будете увеличивать $n$ все дальше и дальше? Если разделить интервал $[-2,7]$ на 100 подинтервалов длины $\Delta x = 0,09$, какова оценка площади под графиком $f$? Как насчет $n=1000$ и $\Delta x=0,009$? Сходится ли оценка площади при увеличении $n$? Чтобы посмотреть на эту сходимость, проверьте, меняются ли оценки все меньше и меньше по мере того, как вы продолжаете удваивать число $n$ подынтервалов.
Определенный интеграл
По мере увеличения и увеличения $n$ (и уменьшения и уменьшения $\Delta x$) значение суммы Римана \eqref{left_riemann} должно приближаться к одному числу. Это единственное число называется 9b f(x)dx$, что является просто числом.
{n-1} f(x_{i+1}) \Delta x.
\label{right_riemann}
\end{выравнивание}
Единственное отличие от левой суммы Римана \eqref{left_riemann} состоит в том, что мы вычисляем $f$ в интервале $i$ на правом конце $x_{i+1}$.
Поскольку $f$ действительно меняется в течение подинтервала, мы ожидаем, что левая сумма Римана даст другую площадь, чем правая сумма Римана. Чем правая сумма Римана отличается от левой суммы Римана? Приведенный ниже апплет позволит вам поэкспериментировать. Когда вы увеличиваете число интервалов $n$, сходится ли оценка площади к одному числу? Похоже ли это число на то же, что и левая сумма Римана?
Площадь через правую сумму Римана. Площадь под графиком $f(x)$ (синяя кривая на левой панели) на интервале $[a,b]$ вычисляется с помощью правой суммы Римана. Правая сумма Римана из $n$ подынтервалов изображается прямоугольниками, на которые наложен график $f$. На правой панели показаны площади прямоугольников $\hat{A}(x)$ от $a$ до $x$, изображенные в виде зеленой кривой.
Площадь на всем интервале $[a,b]$ равна величине $\hat{A}(b)$. Чтобы исследовать поведение $\hat{A}$, вы можете перемещать розовые точки по кривой и вершинам прямоугольников. При перемещении розовых точек выделяется прямоугольник, а в правом верхнем углу отображается расчет его площади. Площадь каждого прямоугольника равна произведению $f$ на его правом конце на ширину подынтервала $\Delta x$. Текущая сумма площади $\hat{A}(x)$ увеличивается на площадь прямоугольника, когда вы перемещаете розовые точки вправо на один прямоугольник. Если вы установите флажок «точно», истинная площадь под графиком $f$ заштрихована красным слева, а правая панель отображает график (красным цветом) истинной площади $A(x)$ под $f $ от $a$ до $x$. Истинная площадь справа от выделенного прямоугольника вычисляется вместе с ошибкой между истинной площадью и соответствующей площадью, рассчитанной с помощью суммы Римана. Значения $A(x)$ и $\hat{A}(x)$ являются площадями под $f$ только для случая, когда $f(x) \ge 0$.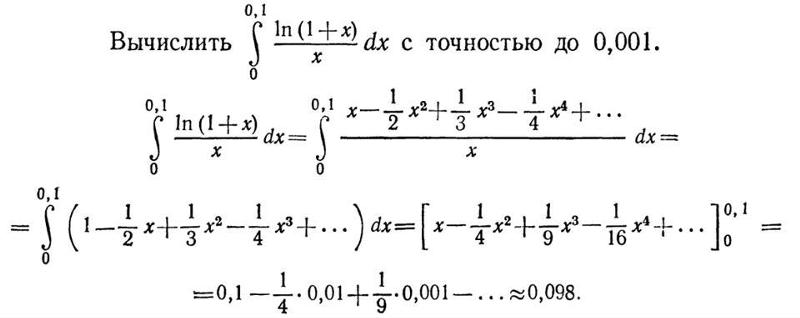
9bf(t)dt$, а соответствующий неопределенный интеграл равен $\int f(t)dt$.
Чтобы сделать наш прямой результат Эйлера похожим на задачу оценки площади, давайте использовать $A(t)$ для переменной в дифференциальном уравнении с чистым временем, записав его как $\diff{A}{t}=f( т)$. Если мы сделаем начальным условием $A(a)=0$, то Форвард Эйлер аппроксимирует решение $A(t)$, т. е. первообразную $A(t)=\int f(t)dt$, имеющую $ А(а)=0$. Сравнивая сумму, которую мы написали для Forward Euler (уравнение (8) со страницы Forward Euler), и левую сумму Римана \eqref{left_riemann}, мы должны быть в состоянии убедиться, что они одинаковы, когда начальное условие равно нулю. 9бф(т)дт$. Но если вы переименуете некоторые переменные, то расчет по существу будет таким же, как расчет прямого Эйлера. Ниже мы сделали апплет, который вы можете преобразовать между случаем расчета площади и случаем прямого Эйлера, который, как мы надеемся, прояснит параллель.
Алгоритм Эйлера или аппроксимация площади суммой Римана.
Демонстрация связи между приближением Эйлера к дифференциальному уравнению с чистым временем и вычислением площади под кривой. Когда установлен флажок «площадь», площадь под графиком $f(t)$ (синяя кривая на левой панели) на интервале $[a,b]$ вычисляется с помощью суммы Римана. Сумма Римана $n$ подынтервалов изображается прямоугольниками, на которые наложен график $f$. Когда вы перемещаете розовые точки, область прямоугольников слева подсвечивается, и эта площадь $\hat{A}(t)$ отображается как функция $t$ зеленой кривой на правой панели. Когда поле «площадь» снято, показано решение дифференциального уравнения с чистым временем $\diff{A}{t}=f(t)$ с помощью алгоритма Эйлера. Остаются только вершины прямоугольников, которые образуют приближение к $f$, постоянное на каждом подынтервале. Зеленая кривая на правой панели остается, но ее интерпретация представляет собой приближенное решение дифференциального уравнения, в котором наклон остается постоянным на каждом подинтервале. Этот наклон показан серыми линиями: постоянной на наклоне на левой панели и касательной на правой панели.
В отличие от расчета площади, начальное условие $A(a)$ можно изменить, перетащив синюю точку на правой панели или введя значение в поле. В любом из режимов показаны расчеты для $\hat{A}(t)$ для текущего подинтервала, а также точное решение и соответствующая ошибка, когда установлен флажок «точно». Точное решение также показано красной кривой, а для площадного случая — красной штриховкой области под $f(t)$.
Дополнительная информация об апплете.
Одним из важных различий между прямым вычислением Эйлера и вычислением площади является начальное условие. Для расчета площади мы суммируем площадь, начиная с $A(a)=0$. С Forward Euler у нас может быть произвольное начальное условие $A(a)$, которое вы можете изменить, только сняв флажок с опции «площадь» в апплете.
Обязательно ли для вычисления площади под кривой сохранять $A(a)=0$? Или, если мы допустим, что $A(a)$ будет другим значением, сможем ли мы по-прежнему оценить площадь по результату? Использование другого значения $A(a)$ для прямого расчета Эйлера означает, что он оценивает другую первообразную (поскольку начальное условие определяет произвольную константу).
Как получить площадь области под графиком $f$ независимо от используемой первообразной? 9{n-1}f(t_i)\Дельта t.
\label{fe_sum}
\end{выравнивание}
Возьмем это уравнение, устремим $n$ к бесконечности, чтобы переписать уравнение в терминах определенного интеграла от $f$, который представляет собой площадь под кривой. Отсюда определите, как можно определить площадь по оценке $A(b)$ с помощью прямого Эйлера с любым начальным условием $A(a)$. Вы должны проверить, работает ли ваш метод, попробовав разные значения с помощью апплета.
Область отрицательных функций?
При использовании сумм Римана для вычисления площади математические формулы имеют смысл, даже если $f$ отрицательно. Отрицательные значения не должны быть проблемой, поскольку мы показали, что расчет такой же, как и при использовании прямого Эйлера. При работе с Forward Euler наличие отрицательной функции не было проблемой. 92+12$, выпишите все четыре члена суммы Римана с $n=4$, которая оценивает площадь под графиком $f$ на интервале $[a,b]=[-2,7]$.
Подставьте числа из $f$, оцененные в левых конечных точках, и рассчитайте эту оценку площади.
Правая сумма
- Покажите, что правая сумма Римана дает разные оценки площади для малых значений $n$, например, для случая $n=4$, который вы вычислили выше.
- При увеличении числа интервалов $n$ оценка площади сходится к одному числу? Похоже ли это число на то же, что и левая сумма Римана?
Форвард Эйлер и площадь
- Начав с суммы уравнения \eqref{fe_sum} для прямого Эйлера, устремите $n$ к бесконечности, чтобы переписать уравнение в терминах определенного интеграла от $f$, который является площадью под кривой.
