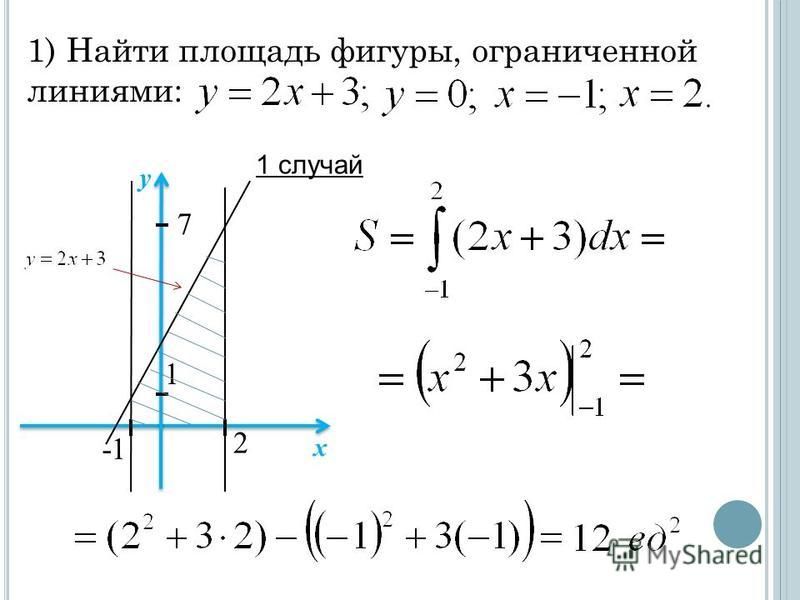
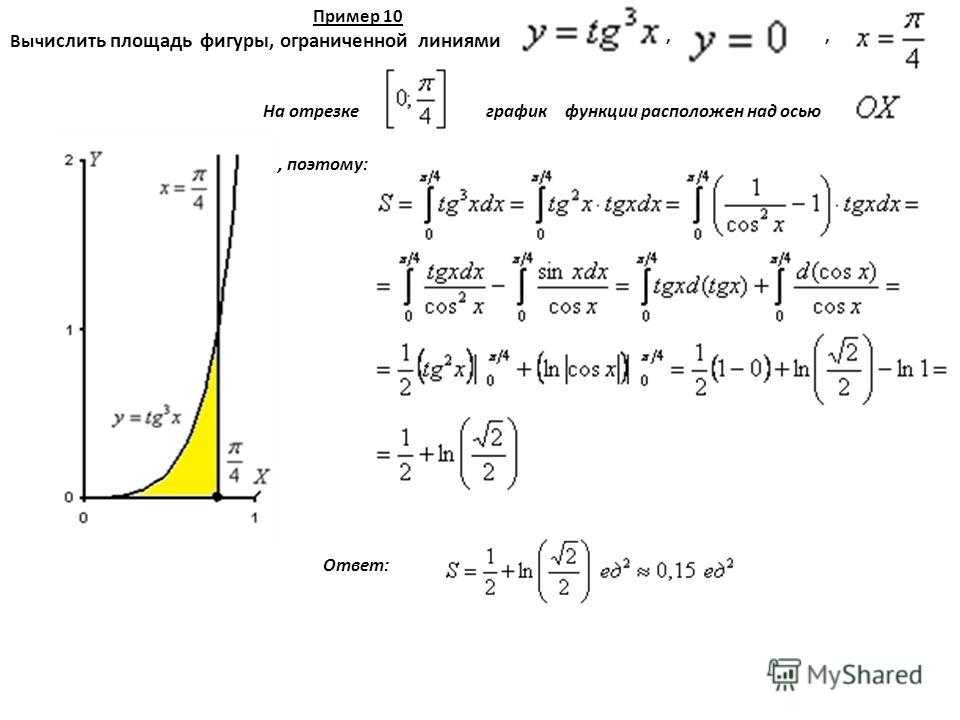
Вычисление площадей фигур с помощью интеграла
Похожие презентации:
Элементы комбинаторики ( 9-11 классы)
Применение производной в науке и в жизни
Проект по математике «Математика вокруг нас. Узоры и орнаменты на посуде»
Знакомство детей с математическими знаками и монетами
Тренажёр по математике «Собираем урожай». Счет в пределах 10
Методы обработки экспериментальных данных
Лекция 6. Корреляционный и регрессионный анализ
Решение задач обязательной части ОГЭ по геометрии
Дифференциальные уравнения
Подготовка к ЕГЭ по математике. Базовый уровень Сложные задачи
Вычисление площадей фигур
с помощью интеграла
11 класс
Криволинейной трапецией
называется фигура, ограниченная
отрезками прямых х = а, х = b, y = 0
и графиком непрерывной функции y = f(x),
такой, что f(x)≥0 на отрезке [a;b]
и f(x)>0 при x (а;b).
Отрезок [a;b] называется
основанием трапеции.
Формула Ньютона – Лейбница
криволинейной
трапеции
Вычислить площадь
криволинейной трапеции
Площадь фигуры равна сумме
площадей криволинейных
трапеций
Площадь фигуры равна разности
площадей криволинейных трапеций
Площадь фигуры вычисляется как
разность площадей криволинейных
трапеций на отрезке [a;b]
Если функции у = f(x) и
непрерывны на отрезке [а;b]
и
на (a;b), то
Искомая площадь фигуры равна
площади фигуры, симметричной
данной относительно оси Ох
• Если f(x) 0 на
отрезке [a; b], то
площадь
криволинейной
трапеции равна
Задача. Вычислить площадь фигуры, ограниченной
параболой
, осью Ох и прямой, проходящей
через точки (4;0) и (1;3).
Решение.
Фигура состоит из криволинейной
трапеции и прямоугольного
треугольника.
Задача. Вычислить площадь фигуры, ограниченной
параболой
, осью Ох и прямой, проходящей
через точки (4;0) и (1;3).
Решение.
 Подставив в уравнение
Подставив в уравнениепрямой y = kx + b координаты
заданных точек, получим систему
уравнений:
откуда найдём k = — 1, b = 4.
Уравнение прямой АВ: y = 4 — x.
Задача. Найти площадь фигуры, ограниченной
линиями
Решение. Точки пересечения
заданных линий: О(0;0), К(6;0), Р(4;2)
Фигура состоит из криволинейной
трапеции и прямоугольного
треугольника.
Задача. Найти площадь фигуры, ограниченной
графиками функций y = x2 , y = 2х – x2 и осью Ох.
Решение. Найдём абсциссы
точек пересечения этих
графиков из уравнения
Искомая площадь равна сумме
площадей криволинейных
трапеций
Задача. Найти площадь фигуры, ограниченной
графиками функций ,
осями абсцисс и ординат.
Решение. Функция
возрастает, а у = — x+3
убывает на R, поэтому их
графики имеют только
одну общую точку.
Задача. Найти площадь фигуры, ограниченной
графиками функций y = x2 — 2x + 2 и y = — x2+ 6
Решение.
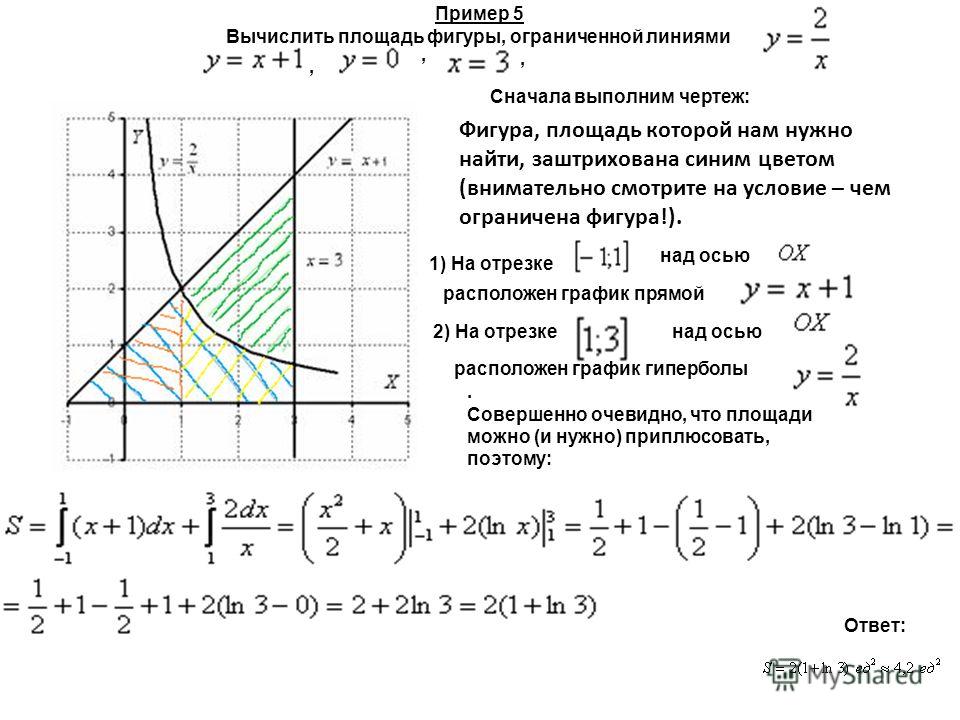 Найдём абсциссы
Найдём абсциссыточек пересечения этих
графиков из уравнения
Искомая площадь равна
разности площадей
криволинейных трапеций
Задача. Найти площадь фигуры, ограниченной
графиками функций y = x2 +1 и y = x + 3
Решение. Найдём абсциссы
точек пересечения этих
графиков из уравнения
Искомая площадь равна
разности площадей двух
криволинейных трапеций,
опирающихся на отрезок [-1;2].
Задача. Найти площадь фигуры,
ограниченной графиками функций y = x3
и y=
Решение. Найдём точки
пересечения этих графиков. Их
координаты удовлетворяют
системе уравнений:
Откуда находим пределы
интегрирования, а затем
площадь фигуры по формуле:
Задача. Найти площадь фигуры, ограниченной ,
линиями
,
Решение.
–
Задача. Найдите площадь фигуры,
ограниченной линиями
Решение.
Задача. Найти площадь фигуры, ограниченной
линиями y = (x + 3)(3 – x), y = 4 и x = 3
Решение.
График функции y = (x + 3)(3 – x)
или
Координаты вершины параболы
В(1;4)
Искомая площадь равна разности
площадей криволинейных трапеций
Задача.
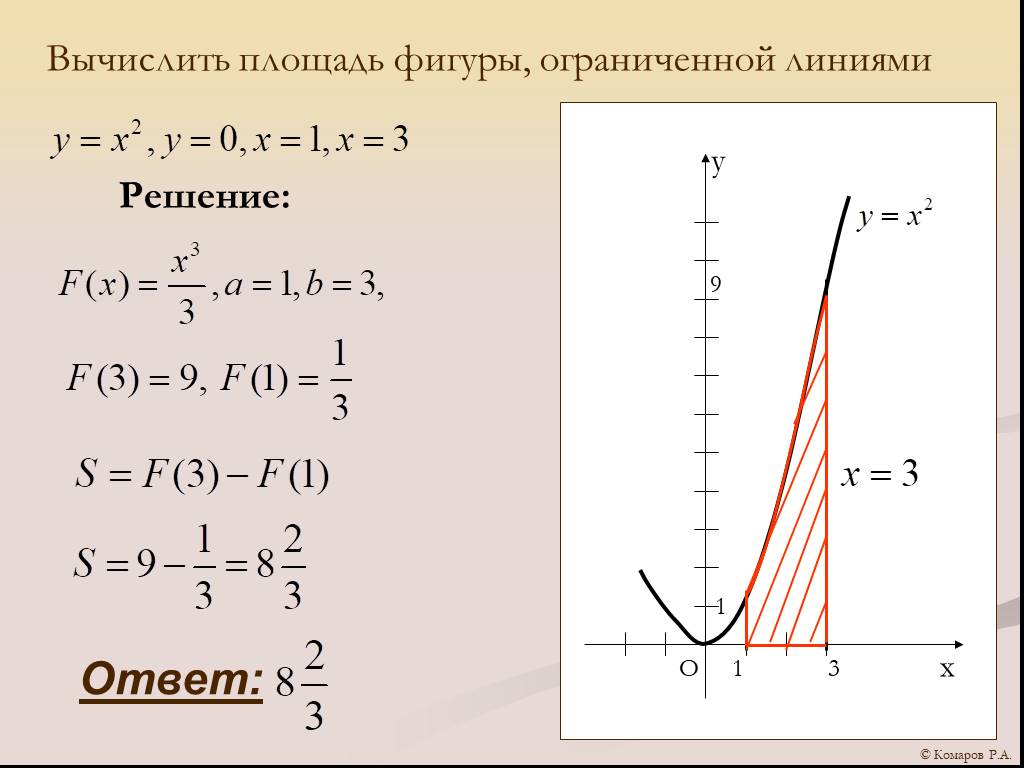 Найти площадь фигуры,
Найти площадь фигуры,ограниченной графиком функции
и осями координат
Решение.
Заданная фигура
представляет собой
криволинейную
трапецию, лежащую
«ниже» оси Ох.
Задача. Вычислить площадь фигуры,
ограниченной параболой
и прямой, проходящей через точки (4;0) и (0;4).
Решение. Первый способ.
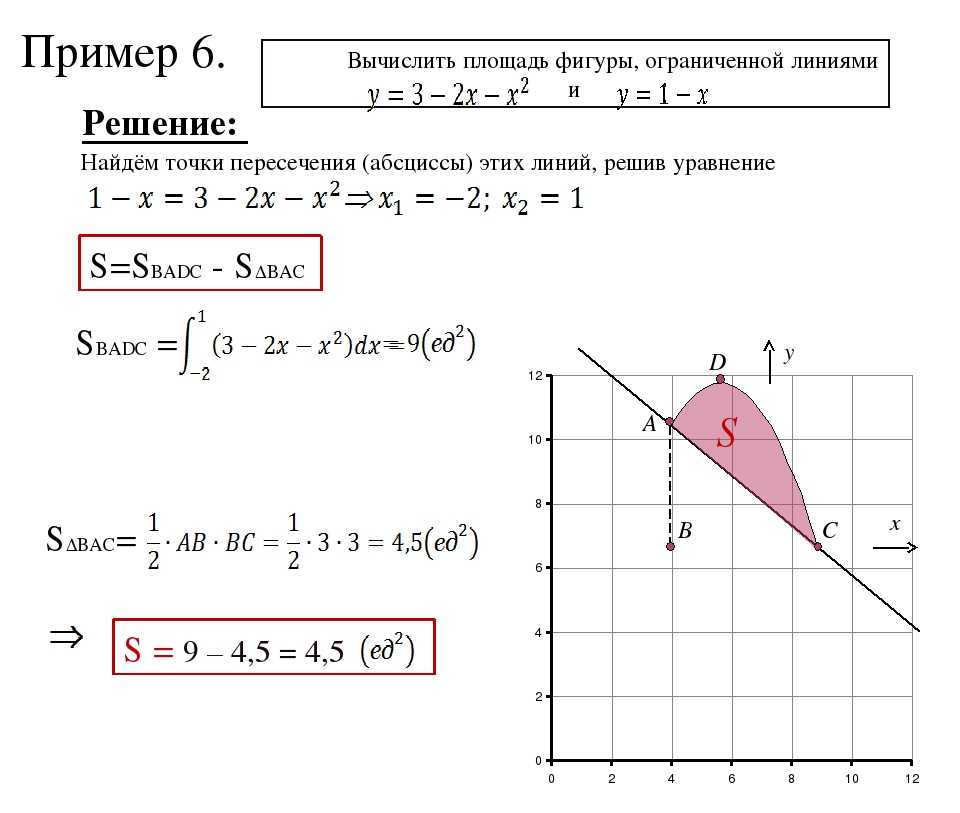
Задача. Вычислить площадь фигуры, ограниченной
параболой
и прямой, проходящей
через точки (4;0) и (0;4).
Решение. 2 способ.
Подставив в уравнение прямой y = kx + b
систему уравнений:
откуда найдём k = — 1, b = 4.
Уравнение прямой АВ:
y = — x + 4.
Задача. Найти площадь фигуры, ограниченной
параболами
Задача. Найти площадь фигуры, ограниченной
графиками функций
Решение. Найдём абсциссы
точек пересечения этих
графиков из уравнения
Искомая площадь равна
разности площадей
криволинейных трапеций
По рисункам 31 – 36 назвать из каких фигур
состоит фигура , площадь которой вычисляется, и
указать пределы интегрирования.

Литература
1. Ю.М. Колягин, М.В. Ткачёва, и др. Под редакцией Жижченко А.Б. Алгебра и начала
математического анализа 11 класс. Учебник для общеобразовательных
учреждений. Базовый и профильный уровень.
2.Программы по математике для общеобразовательных учреждений 2008 год.
English Русский Правила
Как решить задачу: Площадь фигур, ограниченных графиками
Площадь фигур, ограниченных графиками
Ребята! Вот Вы и познакомились с тем, как при помощи интегрирования находить площади криволинейных фигур.
Теперь Вы умеете находить площадь подграфика, если график функции лежит в верхней полуплоскости. Это важное дополнение.
Формула эта называется формулой Ньютона-Лейбница.
Надо найти точки пересечения прямой с параболами, чтобы определить границы трапеций, т.е. пределы интегрирования. Для этого приравниваем правые части и решим уравнения:
Из четырёх получившихся значений выбираем нужные два. Это х=1 и х=(-1+√5)/2. 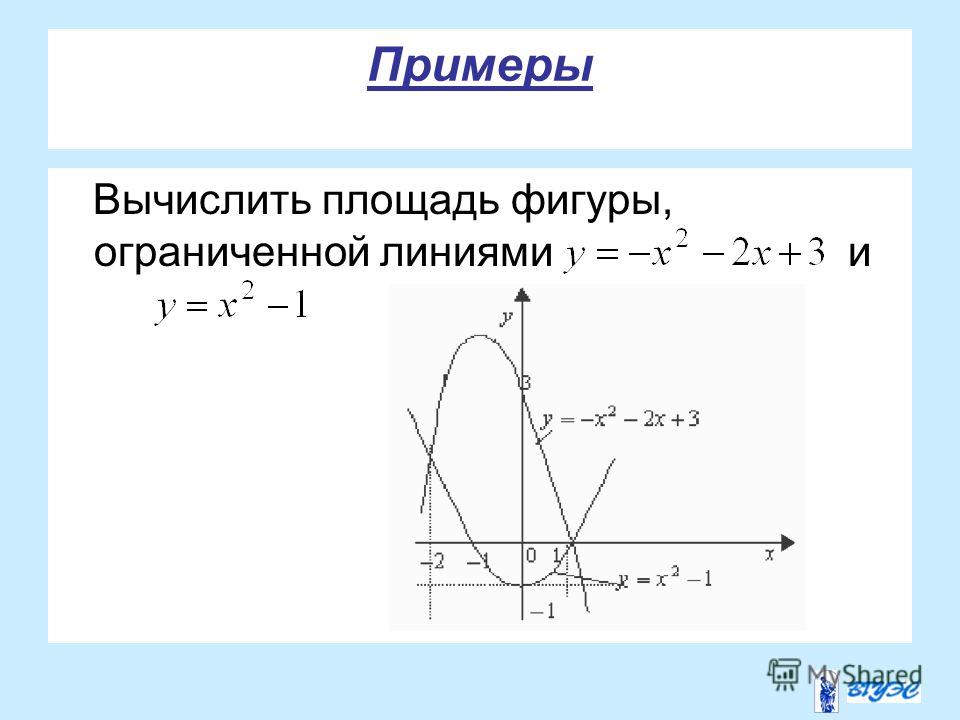 |
© MathOnline.um-razum.ru
© MathOnline.um-razum.ru
Следующее Предыдущее Главная страница
Онлайн-калькулятор площади между кривыми с пошаговыми инструкциями и решением
Введение в калькулятор площади между кривыми
Калькулятор площади между двумя кривыми представляет собой онлайн-инструмент для расчета площади между двумя кривыми. Используя пределы, он использует определенные интегралы для вычисления площади, ограниченной двумя кривыми. Это дает вам быстрый способ сделать расчеты, а не делать их вручную.
В исчислении площадь под кривой определяется интегралами. Точно так же площадь, ограниченную двумя кривыми, можно вычислить с помощью интегралов. Мы представляем онлайн-инструмент, который поможет вам быстро найти площадь под двумя кривыми. Этот инструмент может сэкономить вам время и энергию, которые вы тратите на ручные вычисления.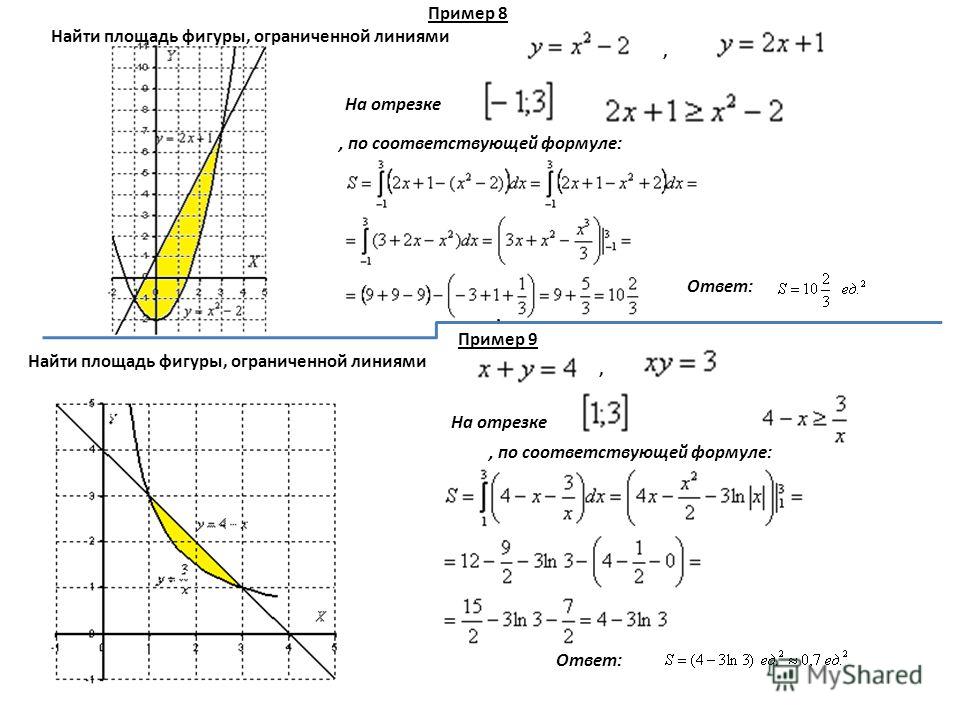
Как найти площадь между двумя кривыми калькулятором с шагами?
Калькулятор области между кривыми с шагами — это расширенный математический калькулятор, использующий концепцию интеграции в бэкенде. Вы можете легко найти этот инструмент в Интернете. Для этого выполните указанные шаги;
- Используйте основное ключевое слово для поиска инструмента в нужном браузере.
- Ваша поисковая система выдаст вам разные результаты. Выберите площадь между двумя калькуляторами кривых из этих результатов.
- На странице сайта будет список встроенных инструментов.
- Выберите нужный инструмент из списка. Или вы также можете использовать наши различные инструменты, такие как калькулятор площади под графиком.
Формула, используемая калькулятором областей, ограниченных кривыми
Площадь между двумя кривыми является одним из основных понятий исчисления. Он определяется как пространство, ограниченное двумя кривыми между двумя точками.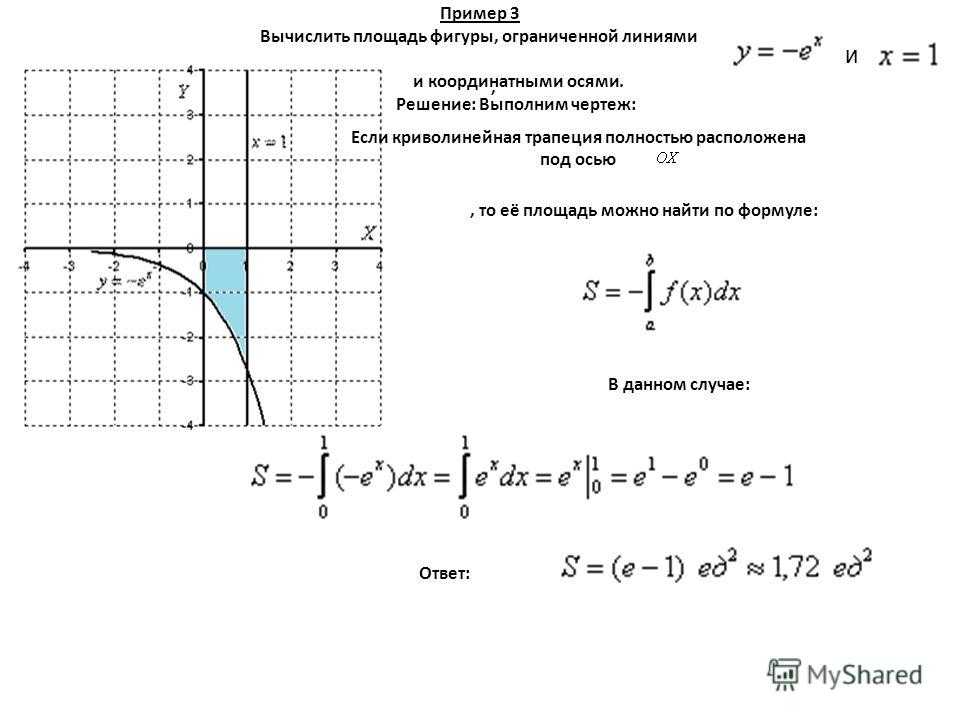 Разность интегралов между двумя функциями используется для вычисления площади под двумя кривыми. Например, первая кривая определяется f(x), а вторая определяется g(x). Таким образом, общая площадь между f(x) и g(x) на интервале (a,b) равна: 9b_a[f(x)-g(x)]dx$$
Разность интегралов между двумя функциями используется для вычисления площади под двумя кривыми. Например, первая кривая определяется f(x), а вторая определяется g(x). Таким образом, общая площадь между f(x) и g(x) на интервале (a,b) равна: 9b_a[f(x)-g(x)]dx$$
Где
- f(x) и g(x) — две кривые.
- ∫ b a — интегральный символ.
- dx — коэффициент интеграла.
Приведенная выше формула используется калькулятором площади между двумя кривыми, чтобы предоставить вам быстрое и простое решение.
Как использовать калькулятор площади, ограниченной кривыми?
С помощью этого инструмента легко выполнять расчеты. Только вы должны следовать данным шагам. Эти шаги помогут вам найти площадь, ограниченную двумя кривыми, шаг за шагом.
- Введите функцию первой и второй кривых в поле ввода. Этот шаг заключается в входе в функции ввода.
- Выберите из меню определенный или неопределенный интеграл.
 Если площадь ограничена двумя точками, выберите определенный интеграл. В противном случае можно использовать неопределенный интеграл.
Если площадь ограничена двумя точками, выберите определенный интеграл. В противном случае можно использовать неопределенный интеграл. - В случае определенного интеграла запишите значение верхней и нижней границ.
- Теперь выберите переменную интегрирования, т. е. x, y или z.
- Просмотрите введенное значение и нажмите кнопку расчета.
После нажатия кнопки расчета область между калькулятором кривых и шагами предоставит быстрые результаты.
Зачем использовать калькулятор площади, охватываемой двумя кривыми?
Интеграция и дифференцирование — два важных понятия в исчислении. Калькулятор площади, ограниченной кривыми, — лучший онлайн-инструмент для легкого пошагового расчета. Он надежен как для математиков, так и для студентов и помогает им в решении реальных задач.
Основной причиной использования этого инструмента является простота и быстрота расчетов. Используя этот онлайн-инструмент, вы также можете получить визуальную интерпретацию данного интеграла.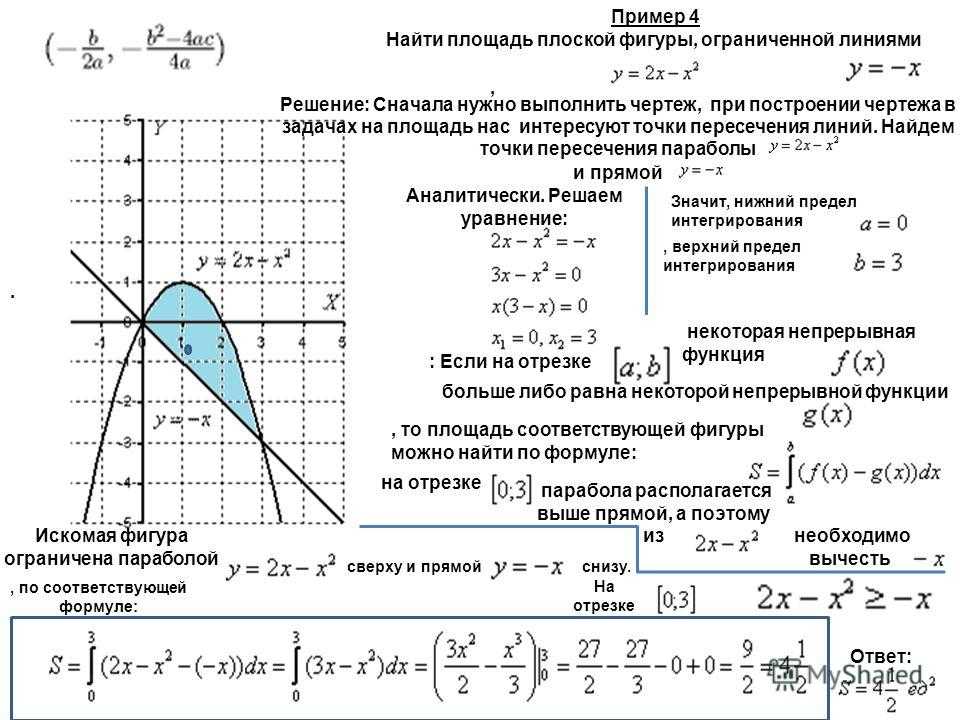 Он также предоставляет вам все возможные промежуточные шаги вместе с графиком интеграла. Поэтому лучше всего использовать этот инструмент.
Он также предоставляет вам все возможные промежуточные шаги вместе с графиком интеграла. Поэтому лучше всего использовать этот инструмент.
Преимущества использования Калькулятора площади между 4 кривыми
Нахождение площади, ограниченной двумя кривыми, — долгая и сложная процедура. Таким образом, использование онлайн-инструмента может помочь найти простые решения. Все, что вам нужно, чтобы иметь хороший интернет и несколько кликов для этого. Использование этого онлайн-калькулятора даст вам следующие преимущества:
- Это экономит время, предоставляя вам область под двумя кривыми в течение нескольких секунд.
- Он имеет удобный интерфейс, так что вы можете легко его использовать.
- Он предоставляет вам все возможные промежуточные шаги, визуальное представление, сумму Римана, а также определенные и неопределенные интегралы всего за несколько кликов.
- Позволяет практиковаться на разных примерах.
- Это бесплатный онлайн-калькулятор, поэтому вам не нужно платить.

Надеемся, вам понравится пользоваться самым передовым и востребованным инструментом интегралов. Многочисленные инструменты также доступны в интегральном калькуляторе, чтобы помочь вам интегрироваться. Вы также можете использовать сходящийся или расходящийся калькулятор, чтобы легко выучить интегралы.
Часто задаваемые вопросы
Как найти площадь области между двумя кривыми?
Площадь области между двумя кривыми можно рассчитать с помощью определенных интегралов. Для этого необходимо проинтегрировать разность обеих функций, а затем подставить значения верхней и нижней границ. Формула для расчета площади между двумя кривыми: 9b_a [f(x)-g(x)]dx$$
Что такое целая площадь?
Целая площадь представляет собой сумму площадей бесконечно малых частей, на которые делится фигура или кривая. Его можно вычислить, используя определенные и неопределенные интегралы.
Каково правило расчета площади?
Площадь — это мера общего пространства внутри поверхности или формы.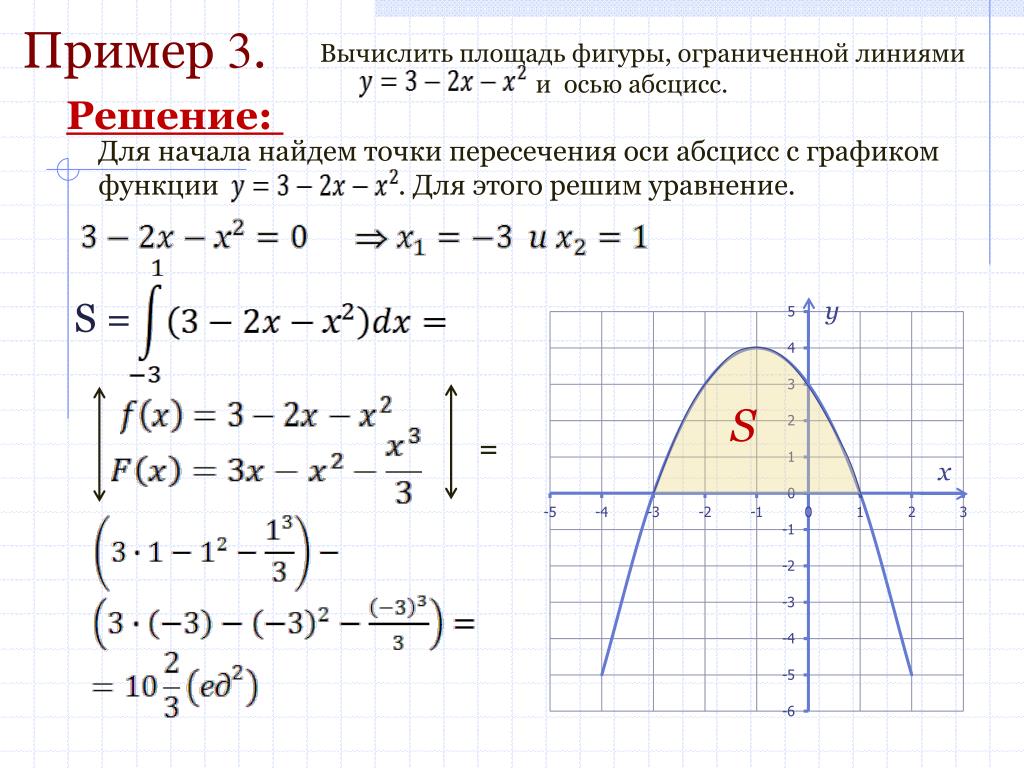 Чтобы вычислить площадь прямоугольника или квадрата, умножьте ширину и высоту. А площадь под кривой можно вычислить, найдя площади всех небольших частей и сложив их вместе.
Чтобы вычислить площадь прямоугольника или квадрата, умножьте ширину и высоту. А площадь под кривой можно вычислить, найдя площади всех небольших частей и сложив их вместе.
Калькулятор площади под кривой • С шагами и графиком!
Знакомство с калькулятором площади под кривой
Чтобы найти площадь под кривой, вам необходимо знать понятия интегралов. Однако какая техника интеграла требует ответа на то, как найти площадь под кривой? Это вопрос, который возникает, когда вы думаете о площади или о теле неправильной формы. Но здесь калькулятор интеграла площади кривой, который обеспечивает точную оценку площади конкретной области под кривой.
Калькулятор площади под графиком — это онлайн-инструмент для оценки площади. Этот онлайн-инструмент отображает область для заданной функции кривой с заданными пределами за несколько секунд. Калькулятор площади под кривой делает расчет быстрее и точнее. Калькулятор площади под двумя кривыми рассчитывает безрисковый расчет с понятными расчетами.
Что такое калькулятор площади под кривой?
Калькулятор площади интеграла — это инструмент, который использует этот метод для вычисления площади определенных интегралов между верхним и нижним пределами. В основном калькулятор площади под интегральной кривой используется для нахождения площадей неправильных фигур.
Этот калькулятор поможет вам решить уравнения и даст более быстрые и точные результаты.
Формула, используемая калькулятором площади интеграла
Калькулятор площади под двумя кривыми вычисляет определенные интегралы с пошаговыми инструкциями. Этот калькулятор использует следующую формулу с пошаговыми инструкциями для решения задач:
Здесь
a & b верхний и нижний пределы
F(x) заданная функция кривой. 90 \;=\; 0 — \frac{16}{4} \;=\; -4 $$
Таким образом, площадь равна 4 .
Когда мы сложим эти два разделенных интеграла, мы получим площадь под графиком как 8 единиц .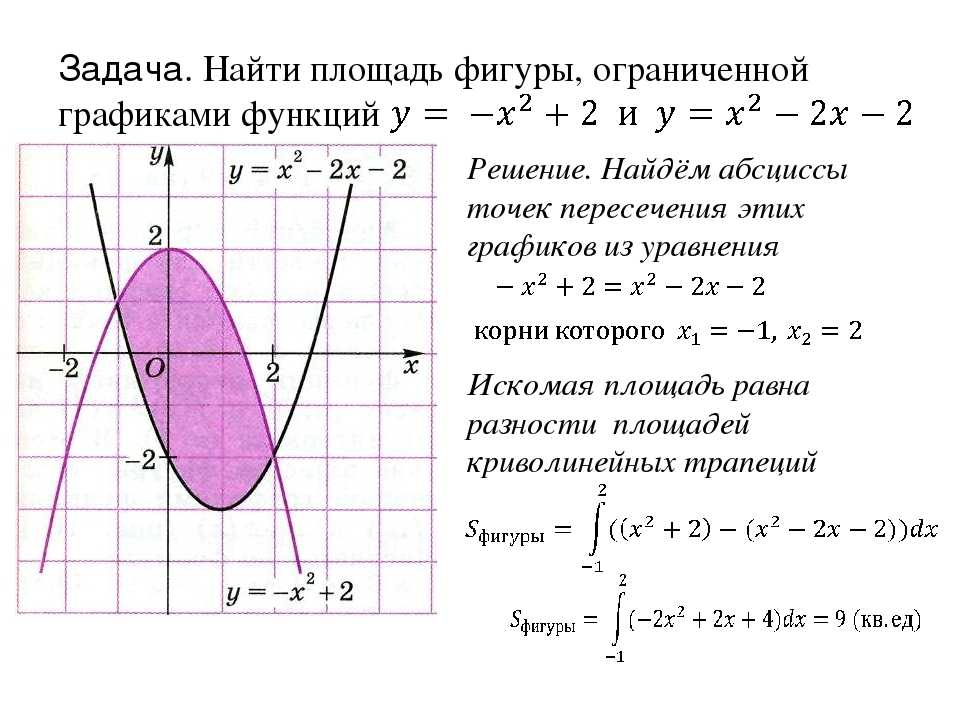
Как использовать калькулятор площади под графиком?
Калькулятор площади под кривой с шагами находит площадь под кривой с помощью интегрирования, следуя этим рекомендациям.
Вывод:
На странице результатов этот интегральный калькулятор площади предоставит:
- Визуальное представление интегральной функции.
- Площадь определенного региона со всеми возможными промежуточными шагами.
Как получить онлайн-калькулятор интеграла площади?
Чтобы найти площадь под калькулятором кривой с шагами, выполните следующие шаги:
Шаг 1: Прежде всего, введите ключевые слова в строку поиска.
Шаг 2: Google показывает вам несколько предложений по искомым калькуляторам.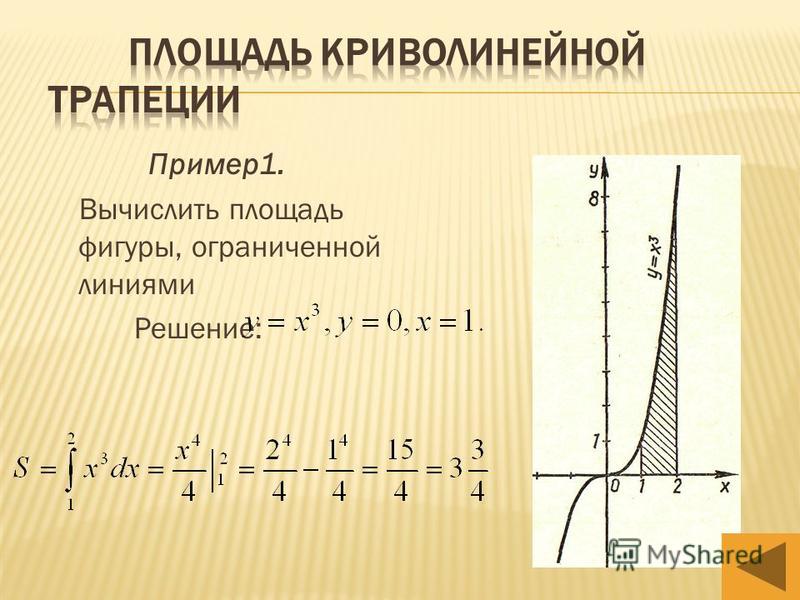
Шаг 3: Теперь выберите Калькулятор интегралов из предложений Google.
Преимущества калькулятора площади под кривой
Калькулятор площади области под кривой имеет следующие преимущества:
- Калькулятор интеграла площади под кривой рассчитает задачи всего за несколько минут и решит кривую функции шаг за шагом.
- Это экономящий время инструмент для решения области неправильных фигур и форм.
- Это убережет вас от сложных и лихорадочных ручных вычислений.
- Этот онлайн-калькулятор предоставляет бесплатное решение без каких-либо затрат.
- Калькулятор площади под 2-мя кривыми вычисляет площади различных определенных и неопределенных функций.
- В области под графиком калькулятора отображаются результаты в виде графиков, возможных промежуточных шагов, действительных и мнимых частей и альтернативной формы определенных и неопределенных интегралов.


 Числа a и b называются пределами интегрирования — нижним и верхним. Как видим, неважно, в какой полуплоскости лежит график функции, главное, что одна функция — верхняя, а другая — нижняя.
Числа a и b называются пределами интегрирования — нижним и верхним. Как видим, неважно, в какой полуплоскости лежит график функции, главное, что одна функция — верхняя, а другая — нижняя.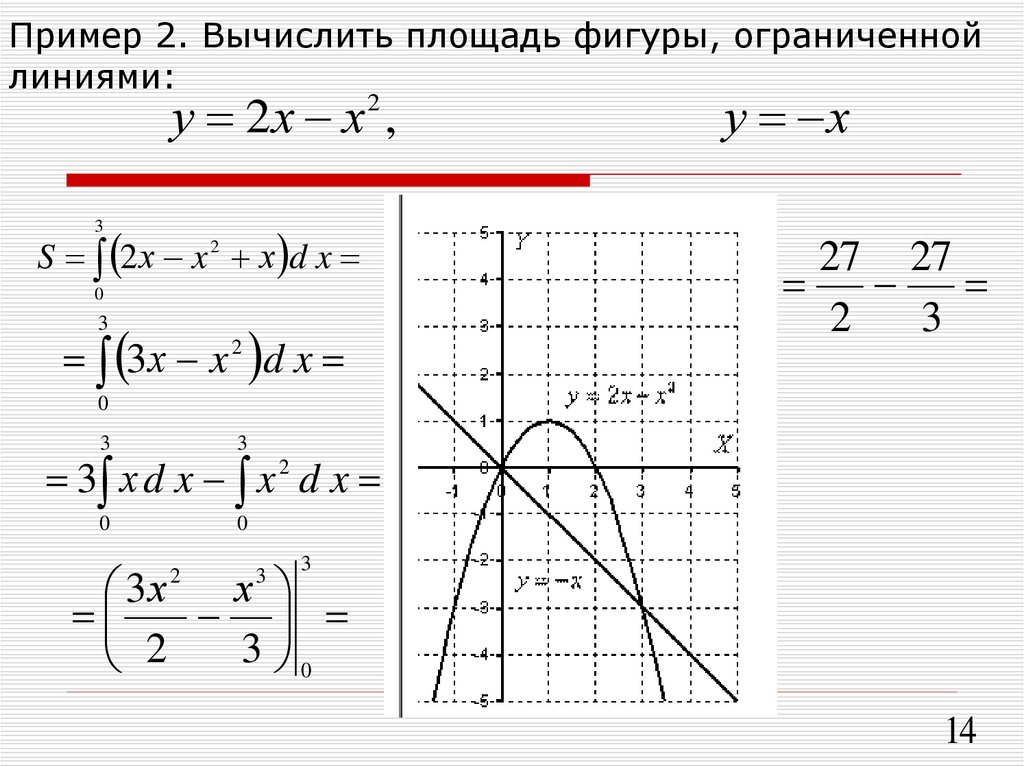
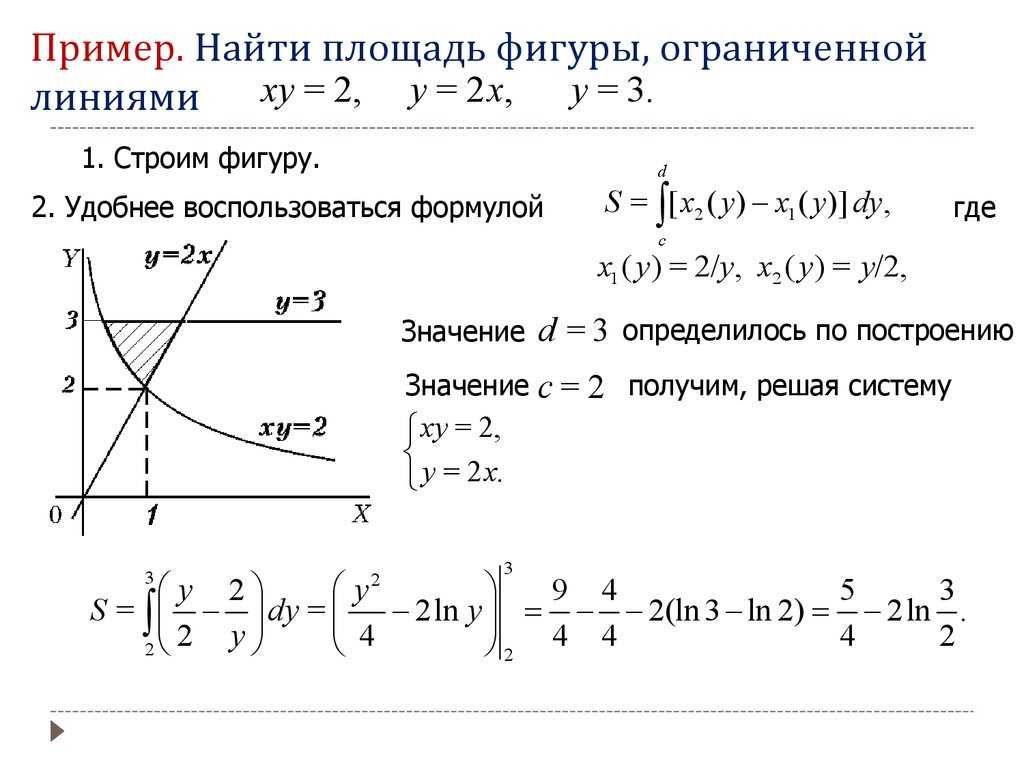 Если площадь ограничена двумя точками, выберите определенный интеграл. В противном случае можно использовать неопределенный интеграл.
Если площадь ограничена двумя точками, выберите определенный интеграл. В противном случае можно использовать неопределенный интеграл.