Приложения тройного интеграла: Механические приложения тройного интеграла / Тройной интеграл / 3dstroyproekt.ru

Краткий курс высшей математики

Краткий курс высшей математики

Шнейдер В. Е. и др. Краткий курс высшей математики. Учеб. пособие для втузов. М., «Высш. школа», 1972. 640 с. Данное учебное пособие предназначено для студентов вечерних факультетов втузов и заводов-втузов. Оно в основном охватывает весь материал, предусмотренный обязательной программой. Достаточное количество решенных примеров и задач способствует лучшему усвоению теоретического материала. Оглавление ПРЕДИСЛОВИЕ ГЛАВА I. МЕТОД КООРДИНАТ. ПОНЯТИЕ ФУНКЦИИ § 1. ДЕЙСТВИТЕЛЬНЫЕ ЧИСЛА. КООРДИНАТЫ ТОЧКИ НА ПРЯМОЙ 2. Геометрическое изображение действительных чисел. Координаты точки на прямой 3. Абсолютная величина действительного числа 4. Расстояние между двумя точками на прямой § 2. КООРДИНАТЫ НА ПЛОСКОСТИ И В ПРОСТРАНСТВЕ 2. Расстояние между двумя точками на плоскости 3. Деление отрезка в данном отношении 4. Координаты точки в пространстве 5. Расстояние между двумя точками в пространстве § 3. УГОЛ МЕЖДУ ДВУМЯ ОСЯМИ. ПОЛЯРНЫЕ КООРДИНАТЫ 2. Полярные координаты 3. Зависимость между декартовыми и полярными координатами § 4. ФУНКЦИОНАЛЬНАЯ ЗАВИСИМОСТЬ 2. Понятие функции 3. График функции 4. Способы задания функций 5. Основные элементарные функции и их графики 6. Сложные функции. Элементарные функции 7. Целые и дробно-рациональные функции 8. Функции четные и нечетные. Периодические функции § 5. УРАВНЕНИЕ ЛИНИИ 2. Нахождение уравнения линии по ее геометрическим свойствам § 6 ПРЕОБРАЗОВАНИЕ КООРДИНАТ 2. Поворот осей координат ГЛАВА II. АНАЛИТИЧЕСКАЯ ГЕОМЕТРИЯ НА ПЛОСКОСТИ § 1. ПРЯМАЯ 2. Уравнение прямой с угловым коэффициентом 3. Уравнение прямой, параллельной оси ординат 4. Общее уравнение прямой и его частные случаи 5. Точка пересечения прямых. Построение прямой по ее уравнению 6. Вычисление угла между двумя прямыми. Условия параллельности и перпендикулярности двух прямых 7. Уравнение прямой, проходящей через данную точку в заданном направлении 8. Пучок прямых 9. Уравнение прямой, проходящей через две данные точки 10. Расстояние от точки до прямой § 2. КРИВЫЕ ВТОРОГО ПОРЯДКА 2. Окружность 3. Эллипс 4. Гипербола 5. Парабола 6. Окружность, эллипс, гипербола и парабола как конические сечения 7. Упрощение уравнения кривой второго порядка. График квадратного трехчлена 8. Уравнение равносторонней гиперболы, асимптоты которой приняты за оси координат 9. График дробно-линейной функции 10. Преобразование уравнения кривой второго порядка, не содержащего члена с произведением координат ГЛАВА III. ЭЛЕМЕНТЫ ЛИНЕЙНОЙ И ВЕКТОРНОЙ АЛГЕБРЫ § 1. ЭЛЕМЕНТЫ ТЕОРИИ ОПРЕДЕЛИТЕЛЕЙ 2. Определитель третьего порядка 3. Понятие об определителях высших порядков § 2. СИСТЕМЫ УРАВНЕНИЙ ПЕРВОЙ СТЕПЕНИ 2. Однородная система двух уравнений первой степени с тремя неизвестными 3. Система трех уравнений первой степени с тремя неизвестными 4. Однородная система трех уравнений первой степени с тремя неизвестными § 3. ЭЛЕМЕНТЫ ВЕКТОРНОЙ АЛГЕБРЫ 2. Линейные операции над векторами 4. Проекция вектора на ось и составляются вектора по оси 5. Разложение вектора на составляющие по осям координат 6. Направляющие косинусы вектора 7. Условие коллинеарности двух векторов 8. Скалярное произведение 9. Выражение скалярного произведения через проекции перемножаемых векторов 10. Косинус угла между двумя векторами 11. Векторное произведение 12. Выражение векторного произведения через проекции перемножаемых векторов 13. Смешанное произведение трех векторов 14. Геометрический смысл смешанного произведения 15. Условие компланарности трех векторов § 4. МАТРИЦЫ И ДЕЙСТВИЯ НАД НИМИ 2. Равенство матриц. Действия над матрицами 3. Обратная матрица 4. Матричная запись и матричное решение системы уравнений первой степени § 5. ЛИНЕЙНЫЕ ОТОБРАЖЕНИЯ 2. Преобразование координат 3. Приведение квадратичной формы к каноническому виду 4. Упрощение общего уравнения кривой второго порядка ГЛАВА IV. АНАЛИТИЧЕСКАЯ ГЕОМЕТРИЯ В ПРОСТРАНСТВЕ § 1. ПЛОСКОСТЬ 2. Нормальный вектор плоскости. Уравнение плоскости, проходящей через данную точку 3. Общее уравнение плоскости и его частные случаи 4. Построение плоскости по ее уравнению 5. Угол между плоскостями. Условия параллельности и перпендикулярности двух плоскостей 6. Точка пересечения трех плоскостей § 2. ПРЯМАЯ В ПРОСТРАНСТВЕ 2. Общие уравнения прямой 3. Векторное уравнение прямой. Параметрические уравнения прямой 4. Канонические уравнения прямой 5. Уравнения прямой, проходящей через две точки 6. Угол между двумя прямыми. Условия параллельности и перпендикулярности прямых § 3. Прямая и плоскость в пространстве 2. Точка пересечения прямой с плоскостью 3. Расстояние от точки до плоскости 4. Пучок плоскостей § 4. ПОВЕРХНОСТИ ВТОРОГО ПОРЯДКА 2. Цилиндрические поверхности 3. Конические поверхности 4. Поверхность вращения 6. Гиперболоиды 7. Параболоиды ГЛАВА V. ТЕОРИЯ ПРЕДЕЛОВ § 1. ПРЕДЕЛ ФУНКЦИИ 2. Предел функции при х -> -оо 3. Предел функции при х->х0 4. Бесконечно малые функции. Ограниченные функции 5. Бесконечно большие функции и их связь с бесконечно малыми функциями 6. Основные теоремы о пределах 7. Предел функции при x -> 0 8. Последовательность. Число e 9. Натуральные логарифмы 10. Сравнение бесконечно малых функций § 2. НЕПРЕРЫВНЫЕ ФУНКЦИИ 2. Операции над непрерывными функциями. Непрерывность элементарных функций 3. Свойства функций, непрерывных на сегменте 4. Понятие об обратной функции 5. Обратные тригонометрические функции 6. Показательная и логарифмическая функции 7. Понятие о гиперболических функциях ГЛАВА VI. ДИФФЕРЕНЦИАЛЬНОЕ ИСЧИСЛЕНИЕ ФУНКЦИЙ ОДНОЙ ПЕРЕМЕННОЙ 1. Приращение аргумента и приращение функции 2. Определение непрерывности функции с помощью понятии приращения аргумента и приращения функции 3. Задачи, приводящие к понятию производной 4. Определение производной и ее механический смысл 5. Дифференцируемость функции 6. Геометрический смысл производной 7. Производные некоторых основных элементарных функций 8. Основные правила дифференцирования 9. Производная обратной функции 10. Производные обратных тригонометрических функций 11. Производная сложной функции § 12. Производные гиперболических функций 13. Производная степенной функции с любым показателем 14. Сводная таблица формул дифференцирования 15. Неявные функции и их дифференцирование 16. Уравнения касательной а нормали к кривой 17. Графическое дифференцирование § 2. ПРОИЗВОДНЫЕ ВЫСШИХ ПОРЯДКОВ 1. Нахождение производных высших порядков 2. Механический смысл второй производной § 3. ДИФФЕРЕНЦИАЛ ФУНКЦИИ 2. Производная как отношение дифференциалов 3. Дифференциал суммы, произведения и частного функций 4. Дифференциал сложной функции. Инвариантность формы дифференциала 5. Применение дифференциала к приближенным вычислениям 6. Дифференциалы высших порядков § 4. ФУНКЦИИ, ЗАДАННЫЕ ПАРАМЕТРИЧЕСКИ, И ИХ ДИФФЕРЕНЦИРОВАНИЕ 2. Дифференцирование функций, заданных параметрически § 5. ВЕКТОРНАЯ ФУНКЦИЯ СКАЛЯРНОГО АРГУМЕНТА 2. Векторная функция скалярного аргумента и ее производная 3. Уравнения касательной прямой и нормальной плоскости к пространственной кривой 4. Механический смысл первой и второй производных векторной функции скалярного аргумента § 6. НЕКОТОРЫЕ ТЕОРЕМЫ О ДИФФЕРЕНЦИРУЕМЫХ ФУНКЦИЯХ 2. Теорема Ролля 3. Теорема Лагранжа 4. Правило Лопиталя § 7. ПРИЛОЖЕНИЕ ПРОИЗВОДНОЙ К ИССЛЕДОВАНИЮ ФУНКЦИЙ И ПОСТРОЕНИЮ ГРАФИКОВ 2. Максимум и минимум функции 3. Достаточный признак существования экстремума, основанный на знаке второй производной 4. Отыскание наибольшего и наименьшего значений функции 5. Применение теории максимума и минимума к решению задач 6. Выпуклость и вогнутость графика функции. Точки перегиба 7. Асимптоты графика функции 8. Общая схема исследования функции и построение ее графика § 8. ПРИБЛИЖЕННОЕ РЕШЕНИЕ УРАВНЕНИЙ 2. Уточнение найденных значений корней методом хорд и касательных § 9. ИНТЕРПОЛЯЦИОННАЯ ФОРМУЛА ЛАГРАНЖА ГЛАВА VII. НЕОПРЕДЕЛЕННЫЙ ИНТЕГРАЛ § 1. НЕОПРЕДЕЛЕННЫЙ ИНТЕГРАЛ И ЕГО СВОЙСТВА 2. Геометрический смысл неопределенного интеграла 3. Таблица основных интегралов 4. Основные свойства неопределенного интеграла § 2. ОСНОВНЫЕ МЕТОДЫ ИНТЕГРИРОВАНИЯ 2. Интегрирование методом замены переменной 3. Интегрирование по частям § 3. ИНТЕГРИРОВАНИЕ РАЦИОНАЛЬНЫХ ФУНКЦИЙ 2. Рациональные дроби. Выделение правильной рациональной дроби 3. Интегрирование простейших рациональных дробей 4. Разложение правильной рациональной дроби на простейшие дроби 5. Метод неопределенных коэффициентов 6. Интегрирование рациональных дробей § 4. Интегрирование тригонометрических функций 2. Рациональные функции двух переменных 3. Интегралы вида § 5. ИНТЕГРИРОВАНИЕ НЕКОТОРЫХ ИРРАЦИОНАЛЬНЫХ ФУНКЦИЙ 2. Интеграл вида 3. Интегралы видов 4. Интегралы вида § 6. ОБЩИЕ ЗАМЕЧАНИЯ О МЕТОДАХ ИНТЕГРИРОВАНИЯ. ИНТЕГРАЛЫ, НЕ БЕРУЩИЕСЯ В ЭЛЕМЕНТАРНЫХ ФУНКЦИЯХ 2. Понятие об интегралах, не берущихся в элементарных функциях ГЛАВА VIII. ОПРЕДЕЛЕННЫЙ ИНТЕГРАЛ § 1. ЗАДАЧИ, ПРИВОДЯЩИЕ К ОПРЕДЕЛЕННОМУ ИНТЕГРАЛУ 2. Задача о работе переменной силы § 2. ОПРЕДЕЛЕННЫЙ ИНТЕГРАЛ 2. Свойства определенного интеграла 3. Производная интеграла по переменной верхней границе 4. Формула Ньютона—Лейбница 5. Замена переменной в определенном интеграле 6. Интегрирование по частям в определенном интеграле § 3. ГЕОМЕТРИЧЕСКИЕ И ФИЗИЧЕСКИЕ ПРИЛОЖЕНИЯ ОПРЕДЕЛЕННОГО ИНТЕГРАЛА 2. Вычисление площади в полярных координатах 3. Вычисление объема тела по известным поперечным сечениям 4. Объем тела вращения 5. Длина дуги кривой 6. Дифференциал дуги 7. Площадь поверхности вращения 8. Общие замечания о решении задач методом интегральных сумм § 4. КРИВИЗНА ПЛОСКОЙ КРИВОЙ 2. Вычисление кривизны 3. Радиус кривизны. Круг кривизны. Центр кривизны 4. Эволюта и эвольвента § 5. НЕСОБСТВЕННЫЕ ИНТЕГРАЛЫ 2. Интегралы от разрывных функций 3. Признаки сходимости несобственных интегралов § 6. ПРИБЛИЖЕННЫЕ МЕТОДЫ ВЫЧИСЛЕНИЯ ОПРЕДЕЛЕННЫХ ИНТЕГРАЛОВ 2. Метод трапеций 3. Метод параболических трапеций (метод Симпсона) ГЛАВА IX. ДИФФЕРЕНЦИАЛЬНОЕ ИСЧИСЛЕНИЕ ФУНКЦИЙ НЕСКОЛЬКИХ ПЕРЕМЕННЫХ § 1. ФУНКЦИИ НЕСКОЛЬКИХ ПЕРЕМЕННЫХ 2. График функции двух переменных 3. Функции трех и большего числа переменных § 2. Предел функции нескольких переменных. Непрерывность функции. Точки разрыва 2. Непрерывность функции нескольких переменных 3. Понятие области 4. Точки разрыва 5. Свойства функций, непрерывных в ограниченной замкнутой области § 3. ЧАСТНЫЕ ПРОИЗВОДНЫЕ 2. Геометрический смысл частных производных функции двух переменных 3. Частные производные высших порядков § 4. ПОЛНЫЙ ДИФФЕРЕНЦИАЛ ФУНКЦИИ НЕСКОЛЬКИХ ПЕРЕМЕННЫХ 2. Полный дифференциал функции 3. Приложение полного дифференциала к приближенным вычислениям § 5. Дифференцирование сложных и неявных функций 2. Инвариантность формы полного дифференциала 3. Дифференцирование неявных функций § 6. СКАЛЯРНОЕ ПОЛЕ 2. Производная по направлению 3. Градиент 4. Касательная плоскость а нормаль к поверхности 5. Геометрический смысл полного дифференциала функции двух переменных § 7. ЭКСТРЕМУМ ФУНКЦИЙ ДВУХ ПЕРЕМЕННЫХ 2. Наибольшее и наименьшее значения функции двух переменных ГЛАВА X. КРАТНЫЕ И КРИВОЛИНЕЙНЫЕ ИНТЕГРАЛЫ § 1. ДВОЙНОЙ ИНТЕГРАЛ 2. Двойной интеграл. Теорема существования 3. Свойства двойного интеграла 4. Вычисление двойного интеграла в декартовых координатах 5. Вычисление двойного интеграла в полярных координатах 6. Приложения двойного интеграла § 2. ТРОЙНОЙ ИНТЕГРАЛ 2. Тройной интеграл и его свойства 3. Вычисление тройного интеграла в декартовых координатах 4. Вычисление тройного интеграла в цилиндрических координатах 5. Приложения тройного интеграла § 3. КРИВОЛИНЕЙНЫЙ ИНТЕГРАЛ 2. Задача о работе. Криволинейный интеграл 3. Вычисление криволинейного интеграла 4. Формула Остроградского — Грина 5. Независимость криволинейного интеграла от пути интегрирования 6. Отыскание первообразной по полному дифференциалу 7. Криволинейный интеграл по длине дуги ГЛАВА XI. РЯДЫ § 1. ЧИСЛОВЫЕ РЯДЫ 2. Геометрическая прогрессия 3. Простейшие свойства числовых рядов 4. Необходимый признак сходимости ряда 5. Достаточные признаки сходимости знакоположительных рядов 6. Знакопеременные ряды 7. Остаток ряда и его оценка § 2. ФУНКЦИОНАЛЬНЫЕ РЯДЫ 2. Правильно сходящиеся функциональные ряды и их свойства § 3. СТЕПЕННЫЕ РЯДЫ 2. Свойства степенных рядов 3. Ряды по степеням разности х-а 4. Разложение функций в степенные ряды. Ряд Тейлора 5. Разложение некоторых элементарных функций в ряды Тейлора и Маклорена § 4. ПРИЛОЖЕНИЕ РЯДОВ К ПРИБЛИЖЕННЫМ ВЫЧИСЛЕНИЯМ 2. Приближенное вычисление интегралов § 5. ПОНЯТИЕ О ФУНКЦИИ КОМПЛЕКСНОЙ ПЕРЕМЕННОЙ. СТЕПЕННЫЕ РЯДЫ В КОМПЛЕКСНОЙ ОБЛАСТИ 2. Числовые ряды с комплексными членами 3. Степенные ряды в комплексной области § 6. РЯДЫ ФУРЬЕ 2. Ряд Фурье 3. Сходимость ряда Фурье 4. Ряды Фурье для четных и нечетных функций 5. Разложение в ряд Фурье функций с периодом 2l ГЛАВА XII. ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ § 1. ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ ПЕРВОГО ПОРЯДКА 2. Дифференциальные уравнения первого порядка 3. Уравнения с разделяющимися переменными 4. Однородные уравнения 5. Линейные уравнения 6. Уравнение в полных дифференциалах 7. Особые решения 8. Приближенное решение дифференциальных уравнений первого порядка методом Эйлера § 2. ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ ВТОРОГО ПОРЯДКА 2. Простейшие уравнения второго порядка, допускающие понижение порядка 3. Понятие о дифференциальных уравнениях высших порядков § 3. ЛИНЕЙНЫЕ ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ ВТОРОГО ПОРЯДКА 2. Линейные однородные дифференциальные уравнения второго порядка 3. Линейные неоднородные дифференциальные уравнения второго порядка 4. Метод вариации произвольных постоянных § 4. ЛИНЕЙНЫЕ ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ ВТОРОГО ПОРЯДКА С ПОСТОЯННЫМИ КОЭФФИЦИЕНТАМИ 2. Линейные неоднородные дифференциальные уравнения второго порядка с постоянными коэффициентами 3. Приложение линейных дифференциальных уравнений второго порядка к изучению механических и электрических колебаний § 5. ЛИНЕЙНЫЕ ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ ВЫСШИХ ПОРЯДКОВ 2. Линейные дифференциальные уравнения n-го порядка с постоянными коэффициентами § 6. ИНТЕГРИРОВАНИЕ ДИФФЕРЕНЦИАЛЬНЫХ УРАВНЕНИЙ С ПОМОЩЬЮ РЯДОВ § 7. ПОНЯТИЕ О СИСТЕМАХ ДИФФЕРЕНЦИАЛЬНЫХ УРАВНЕНИЙ 2. Системы линейных дифференциальных уравнений с постоянными коэффициентами ПРИЛОЖЕНИЕ 1. ИНТЕРПОЛЯЦИОННАЯ ФОРМУЛА НЬЮТОНА ПРИЛОЖЕНИЕ 2. МЕТОД НАИМЕНЬШИХ КВАДРАТОВ

20.4. Приложения тройных интегралов

ОбъемОбластиВыражается формулой

(20.12)

В сферических координатах этот интеграл имеет вид

(20.13)

А в цилиндрических координатах

Если тело занимает объемИ- плотность его в — точке

, то масса тела равна

(20.15)

Координаты центра тяжести тела вычисляются по формулам

(20.16)

Где— масса тела.

Моменты инерции тела относительно координатных плоскостей определяются интегралами

Момент инерции тела относительно оси Ои определяется интегралом

Где— расстояние точкиТела от осиВ частности, моменты инерции

Тела относительно координатных осейОпределяются формулами

(20. 17)

Момент инерции тела относительно начала координат определяется формулой  Очевидно, верны следующие соотношения:

Ньютоновым потенциалом тела в точкеНазывается интеграл

(20.18)

Где— объем тела,- плотность тела,

Материальная точка массыПритягивается телом с силой, проекции которой На оси координатРавны:

Пример 20.9. Найти объем тела, ограниченного поверхностями

Данное тело ограничено сферами радиусовИЦентрами в начале координат и конусом с вершиной в начале координат и осью, совпадающей с осью Оно расположено над плоскостьюСечение этого тела плоскостьюИзображено на рис. 20.3.

Для вычисления объема тела перейдем к сферическим координатам по формулам (20.9). Уравнение сферыПримет видТак как

Аналогично преобразуется уравнение второй сферы. Уравнение конусаПримет видПотому что

Откуда

По формуле (20.13) находим

Пример 20.10. Вычислить объем тела, ограниченного поверхностями

Рис. 20. 3  Рис. 20.4

Данное тело ограничено сферойИ параболоидом вращения

; сечение тела плоскостьюИзображено на рис. 20.4. Для вычисления объема тела перейдем к цилиндрическим координатам по формулам (20.7). В цилиндрических координатах получаем(уравнение сферы),

(уравнение параболоида). Отметим, что при постоянных значенияхИВнутри тела z изменяется от(для точкиПересечения с поверхностью параболоида)

До(для точкиПересечения с верхней частью поверхности сферы).

При постоянномИзменяется от 0 (для точек, лежащих на оси) до наибольшего значения в точках линии пересечения данных поверхностей, так как с возрастаниемДля поверхности параболоида возрастает, а для шара убывает (что видно из уравнений поверхностей). Для линии пересечения поверхностей ИИмеемОткуда

(второй корень дает мнимые значения для р). Следовательно, для точек линии пересеченияВнутри тела р изменяется от 0 до. Заметив еще, что

Ф изменяется от 0 до 2тс, по формуле (20.14) получим

Пример 20. 11. Вычислить объем тела, ограниченного эллипсоидом

При наличии выраженияВ уравнении поверхности по

Лезен переход к обобщенным сферическим координатам по формулам (20.11). Якобиан в этом случае равен

Уравнение данной поверхности в новых координатах примет вид(ибо

, поэтому

Для данного телаИзменяется от 0 до 1. Заметив, чтоПо

Формуле (20.6) получим

Итак,В частном случае, приПолучаем объем ша

Ра

Замечание. Поскольку эллипсоидсимметричен относительно координатных плоскостей, то можно найти объемЧасти данного тела. При вычислении интеграла нужно иметь в виду, что в этом случае

От предыдущих.

Пример 20.12. Найти массу шараЕсли плотность в

Каждой точке обратно пропорциональна расстоянию ее до начала координат.

Пусть- произвольная точка данного шара, тогда ее расстояниеДо

Начала координат выражается формулойПоэтому плотностьВ

Соответствиис условием задачи определяется формулой

, где- коэффициент пропорциональности. По

Формуле (20.15) имеем

Где областьОтраничена сферойДля вычисления данного

Интеграла перейдем к сферическим координатам по формулам (20.9). Подынтегральная функция, а уравнение сферы примет вид

По формуле (20.10) находим

Пример 20.13. Найти центр тяжести шара если плотность в каждой точке его обратно пропорциональна расстоянию до начала координат.

Воспользуемся формулами (20.16). Масса m была определена в предыдущей задаче (см. пример 20.12). Из соображений симметрии следует, чтоНайдем

Замечание. КоординатыМожно получить с помощью

Первых двух формул (20.16).

Следовательно,

Пример 20.14. Вычислить момент инерции однородного куба относительно одного из его ребер.

Начало прямоугольной декартовой системы координат поместим в одной из вершин куба, а оси направим вдоль трех взаимно перпендикулярных ребер. Обозначим черезРебро куба и найдем его момент инерции относительно оси воспользовавшись третьей из формул (20.17). Так как куб является однородным, то в указанных формулах можно положить:

Гпава 21

КРИВОЛИНЕЙНЫЕ ИНТЕГРАЛЫ

< Предыдущая		Следующая >

Что представляет собой тройной интеграл? — Криста Кинг Математика

Может быть трудно представить себе, что представляет собой тройной интеграл, поэтому в этом видео мы ответим на вопрос: «Что я нахожу, когда вычисляю тройной интеграл?»

Чтобы ответить на этот вопрос, мы сравним тройной интеграл с двойным интегралом, чтобы мы точно поняли, как перейти от двойных интегралов к тройным интегралам. Каждая часть двойного интеграла, такая как интеграл, границы или пределы интегрирования, функция, которая является подынтегральной функцией, и дифференциал (обычно dydx) будут переведены в соответствующую часть тройного интеграла.

Тройной интеграл интересен тем, что его можно использовать двумя способами. Напротив, одиночные интегралы находят только площадь под кривой, а двойные интегралы находят только объем под поверхностью. Но тройные интегралы можно использовать для 1) нахождения объема, как и двойной интеграл, и 2) нахождения массы, когда объем интересующей нас области имеет переменную плотность.

Таким образом, тройные интегралы позволяют нам делать больше, чем мы могли сделать с двойными интегралами. Мы можем добавить дополнительное измерение переменной плотности внутри объема и, основываясь на этой переменной плотности, найти массу объема, в отличие от возможности найти только объем, чем мы были ограничены в двойной интеграл.

Если мы хотим описать двойные и тройные интегралы словами, мы можем сказать, что для двойного интеграла мы интегрируем функцию многих переменных f(x,y) по области R, которая определена для x на интервале [a ,b] и для y на интервале [c,d], используя вертикальные срезы объема, чтобы найти общий объем под поверхностью f(x,y), но над плоскостью xy.

Напротив, мы можем сказать, что для тройного интеграла мы интегрируем многомерную функцию плотности f(x,y,z) для объема B, которая определена для x на интервале [a,b] и для y на интервале [c, d] и для z на интервале [r, s], разрезав объем в трех направлениях, чтобы получить крошечные кусочки (или коробки) объема, чтобы найти общую массу объема.

тройных интеграла можно использовать для 1) нахождения объема, как и двойной интеграл, и 2) нахождения массы, когда объем интересующей нас области имеет переменную плотность.

Из этого видео вы узнаете:

0:15 // Повторение того, что представляет собой двойной интеграл
1:22 // Тройной интеграл имеет два применения (объем и масса)
1:45 // Как использовать тройной интеграл для нахождения объема
8:59 // Почему тройной интеграл делает больше, чем двойной интеграл
11:19 // Как использовать тройной интеграл для нахождения массы, когда объем имеет переменную плотность

Хотите узнать больше о множественных интегралах? У меня есть пошаговый курс для этого.

😃

Узнать больше

Изучайте математикуКриста Кинг 29 августа 2017 г. тройной интеграл, интегралы, тригонометрические тождества

0 лайков

Чем полезны тройные интегралы | Майк Бенешан

Photo by Tommaso Urli on Unsplash

Вы можете почувствовать ужас в комнате, когда ученики осознают, что существуют двойных интегралов и тройных интегралов . Интегралы, которые многие студенты помнят только как «странно выглядящие S-элементы», уже были достаточно сложными. Из 5 стадий математической скорби первой является отрицание: они умоляют: «Это ошибка, верно? Почему две этих странных букв S?» После этого наступает второй этап, гнев: «Когда нам когда-нибудь понадобится использовать это в реальной жизни!?» (Третий этап — торг, когда они спрашивают у меня ответы на свой тест по математическому анализу.)

Я здесь, чтобы объяснить, зачем нам нужны тройные интегралы (и вообще интегралы) в реальной жизни.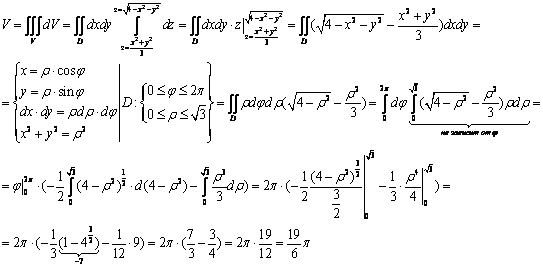 Когда я впервые взялся за многомерное исчисление, меня тоже парализовал страх перед страшной тройкой S, и я понимаю, что поначалу концепция кажется абстрактной чепухой. Но тройные интегралы действительно полезны! Сначала мы собираемся разобрать это, объяснив, почему нам нужны одиночные интегралы, затем двойные интегралы, а затем тройные интегралы.

Для простых фигур у нас есть четкие формулы для нахождения площади:

Изображение автора

Но как мы должны найти площадь этих фигур?

Изображение автора

Ответ заключается в том, что мы можем использовать интеграл. Один простой способ описать интеграл состоит в том, что это площадь под некоторой кривой, и обычно мы используем интеграл, чтобы найти площадь странных форм.

Допустим, мы хотим найти площадь под странной кривой, которая выглядит так:

Изображение автора

Измерить точную площадь сложно, поэтому вы можете решить,Вместо этого 0039 аппроксимирует площадь под кривой.

Пока вы ломаете голову над тем, как примерно определить площадь, вы можете мечтать о более простых формах, таких как прямоугольники. Ах да, прямоугольники с их легко вычисляемыми площадями высоты, умноженной на ширину.

«Подождите, — думаете вы, — почему бы нам не аппроксимировать площадь под кривой, нарисовав кучу прямоугольников под кривой, найдя площади этих прямоугольников и сложив все маленькие области, вот так :”

Изображение автора

Это хорошая идея и приличное приближение. Наша приблизительная площадь будет равна сумме площадей всех зеленых прямоугольников.

Каждый прямоугольник будет иметь одинаковую ширину для облегчения вычислений. Ширина равна величине, которую мы назовем Δx (концептуально Δx — это изменение x). Высота каждого прямоугольника разная, но она задается функцией f(x), представленной изогнутой черной линией в верхней части диаграммы.

Чтобы было понятно, что все высоты разные, мы можем сказать, что 1-й прямоугольник слева имеет высоту f(x₁), 2-й прямоугольник имеет высоту f(x₂) и так далее. В общем случае i-й прямоугольник имеет высоту f(xᵢ).

Площадь прямоугольника равна произведению высоты на ширину, поэтому площадь одного из прямоугольников равна f(xᵢ)*Δx.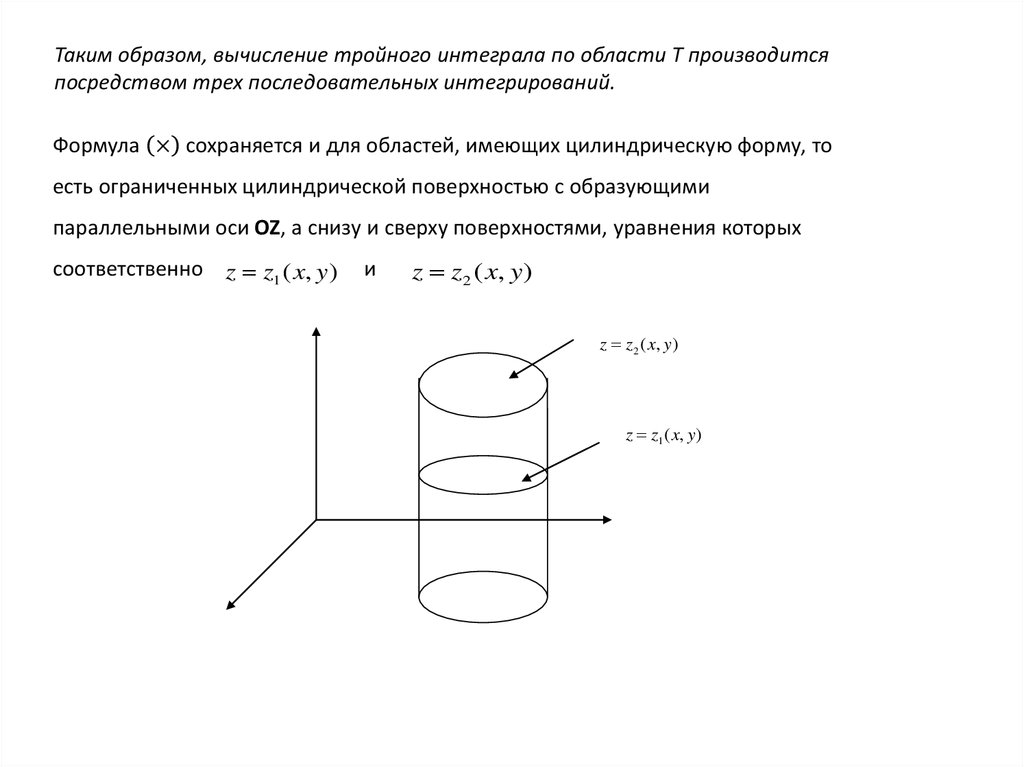 Если просуммировать все площади прямоугольников, то получим приблизительную площадь под кривой.

Но наша аппроксимация не настолько точна — между нашими прямоугольниками и кривой есть куча промежутков. Мы могли бы сделать аппроксимацию более точной, увеличив количество прямоугольников, например так:

Изображение автора

Обратите внимание, что Δx, изменение x, теперь меньше. Кроме того, эта сумма является более точной, чем предыдущая. Мы можем продолжать делить график на все более тонкие прямоугольники, чтобы сделать нашу сумму еще более точной. В конце концов, когда количество прямоугольников приближается к бесконечности (и ширина каждого прямоугольника приближается к 0), приблизительная область становится ближе к фактической области . То, что начиналось как грубое приближение, теперь очень точно!

Эта сумма называется интегралом . Интеграл записывается так:

Символ интеграла ∫ выглядит как большая буква S, потому что, когда немецкий чувак по имени Готфрид Лейбниц разрабатывал исчисление, он думал об интеграле как о бесконечной сумме . «dx» представляет Δx, ширину каждого прямоугольника, которая теперь бесконечно мала. «dx» называется дифференциал . f(x) — это просто та же функция, что и раньше (черная линия).

Вот как мы используем один интеграл. Мы интегрируем по 1 переменной, в данном случае x. Двигаясь вдоль оси X, мы получаем сумму множества невероятно тонких прямоугольников. Чем меньше ширина, тем точнее наша аппроксимация. Вот как мы находим площадь под кривой.

Для двумерных фигур у нас есть площадь , а для трехмерных фигур у нас есть объем . Как и прежде, у нас есть красивые, аккуратные формулы для объемов некоторых трехмерных фигур:

Изображение автора

Но найти объемы этих трехмерных фигур гораздо сложнее:

Изображение автора

Излишне говорить, что нелегко найти объем собаки, похожего на губку предмета и/или какой-то голубой сдутый волейбольный мяч. Как мы должны найти объем этих странных фигур? Чтобы найти объем, мы будем использовать двойной интеграл .

Допустим, я хочу найти объем этой буханки ананасового хлеба:

Изображение с Викисклада. xyz-axes добавлены мной. Кокосовая стружка добавлена ​​пекарем.

Как и раньше, мы можем начать с аппроксимации громкости. Вместо того, чтобы делить график на прямоугольники, мы могли бы начать с деления этого толстого хлеба на ломтики по оси Y:

Изображение автора

Каждый ломтик имеет одинаковую ширину; назовем эту ширину Δy. Если сложить площади всех ломтиков, то получится примерный объем батона. И, как и раньше, по мере того, как мы делим буханку на все более тонкие ломтики (по мере того, как Δy все ближе и ближе к 0), аппроксимация объема буханки становится все более и более точной.

Нам просто нужно сложить площади всех ломтиков хлеба. Единственная проблема в том, что вычислить объем ломтика хлеба не так-то просто. Если мы посмотрим на отдельный срез, вы заметите, что он сам по себе имеет странную форму:

Изображение с Викисклада. Ось Y выглядит как точка, потому что с этой точки зрения ось Y идет прямо к вам. Вы также заметите, что вместо ломтика ананасового хлеба я использую ломтик цельнозернового пшеничного хлеба без потери универсальности.

Нам нужно приблизительно определить площадь этого ломтика хлеба, и мы можем сделать это, разделив его на несколько прямоугольников. Другими словами, чтобы найти площадь одного ломтика, мы должны выполнить один интеграл, как в предыдущем разделе:

Чтобы найти площадь одного ломтика хлеба, мы интегрируем по оси x, складывая крошечные прямоугольники. Затем, возвращаясь к буханке, мы интегрируем по оси Y, чтобы сложить площади всех ломтиков.

По существу, чтобы найти объем буханки ананасового хлеба, мы берем интеграл интегралов: мы берем сумму ломтиков, где каждый ломтик сам по себе является суммой прямоугольников. Конечно, «интеграл от интегралов» писать неуклюже, поэтому мы просто назовем его 9.0039 двойной интеграл , а пишем так:

Воу! Это двойной интеграл, во всем. Что это значит?

«dy» — это ширина ломтика хлеба (поскольку каждый ломтик расположен вдоль оси y), а «dx» — ширина прямоугольника внутри ломтика хлеба (поскольку каждый прямоугольник в ломтике расположен по оси x). -ось). f(x,y) относится к верхней части буханки. Это связано с тем, что высота буханки в некоторой точке (координата z) является функцией от координаты x этой точки и y-координата , так что это f(x,y).

Итак, теперь самое интересное: тройные интегралы. Мы уже рассмотрели одинарные и двойные интегралы. Надеюсь, понятно, почему они могут быть полезны: хотя это не единственное их применение, они могут помочь нам найти площади и объемы неправильных 2-D и 3-D форм!

Вы можете догадаться, что здесь есть образец, который выглядит примерно так:

• С одинарными интегралами мы интегрируем по одному измерению, чтобы найти площадь двумерной фигуры.
• С помощью двойных интегралов мы интегрируем по двум измерениям, чтобы найти объем трехмерной фигуры.
• С помощью тройных интегралов мы интегрируем по трем измерениям, чтобы найти объем… четырехмерной формы?

И вы были бы правы! Тройной интеграл используется для нахождения объема четырехмерной фигуры. Это звучит невозможно. «Мы не живем в четырехмерном пространстве, Марк», — можете сказать вы. «Как они могут быть полезны, если четырехмерных форм не существует!» Ну, во-первых, меня зовут Майк, а не Марк. Но во-вторых, я могу объяснить, как тройные интегралы полезны в реальном мире. Чтобы увидеть это, нам нужно изменить то, как мы думаем об измерениях.

Сколько измерений в фотографии?

Вернемся ненадолго к двойным интегралам. Вы когда-нибудь видели термограмму? Это одна из тех фотографий, сделанных с помощью тепловизионной камеры, где разные цвета представляют разные температуры. Обложка альбома Брокхэмптона Iridescence представляет собой термограмму. Есть еще термограмма кота.

Фотографии являются двухмерными, но каждая точка на термографическом фото имеет связанное с ней «тепло». Поскольку тепло измеряется численно (с температурой), мы можем точно сказать, что каждой точке на термографической фотографии соответствует число: 9.0004 Легенда относится к температуре (Изображение автора).

Как видно из легенды справа, синие пятна могут иметь теплотворную способность «15», а более красные пятна могут иметь теплотворную способность «28».

Мы можем даже превратить эту фотографию в 3D-график, где высота (координата z) соответствует теплу (так что 30-градусная точка на фотографии будет выше, чем 15-градусная точка):

Изображение автора

Итак, вот вопрос: как мне найти всего количества тепла по всей этой фотографии? Ответ заключается в том, что мы используем двойной интеграл! Мы интегрируем по оси x и оси y и суммируем температуру по всей фотографии. Общее количество теплоты равно том трехмерного графика выше.

Это может показаться запутанным, поскольку фотография двумерная, а, как упоминалось ранее, для нахождения объема трехмерной формы используются двойные интегралы. Но нам нужно изменить то, как мы думаем об «измерениях». Обычно мы думаем об измерениях как о пространственных измерениях: на вашей кухне вы можете перемещаться в трех пространственных измерениях. Однако «размер» на самом деле просто относится к значению, связанному с точкой. Измерение не обязательно должно быть направлением в пространстве. Например, взгляните на этот график количества пассажиров рейса с 1949–1961:

Изображение автора

Эта гистограмма имеет два измерения, но это не совсем x и y. Два измерения — «Дата» и «Пассажиры», и так уж получилось, что дата откладывается по оси x, а количество пассажиров — по оси y.

В термограмме есть 2 пространственных измерения, а также 3-е измерение тепла. Тепло — это секрет 3-го измерения, что означает, что мы можем рассматривать фотографию как трехмерный объект и использовать двойной интеграл.

Тройные интегралы в реальном мире

Итак, вернемся к тройным интегралам. Допустим, у вас есть спальня в форме коробки. Вентиляционное отверстие может находиться только в одном углу комнаты, чтобы тепло не распространялось равномерно по всей комнате. Температура будет высокой возле вентиляционного отверстия, низкой в ​​углу, противоположном вентиляционному отверстию, и так далее. Тепло в любой заданной точке комнаты определяется некоторой функцией f(x,y,z) (это функция координат x, y и z некоторой точки комнаты).

Если я хочу добавить все тепло в комната , как бы я это сделал?

Очевидно, что в комнате есть 3 пространственных измерения. Но опять же, температура также считается измерением, поскольку это число, связанное с точкой. Итак, эта задача имеет место в 4 измерениях: ширина, длина, высота и температура .

Так как есть 4 измерения, мы будем использовать тройной интеграл!

Начнем с визуализации комнаты. Вот как может выглядеть трехмерная термограмма трехмерной комнаты:

Каждая сторона этой «комнаты» на самом деле представляет собой двухмерную термограмму, сделанную ранее. Я отредактировал его, чтобы он выглядел как трехмерная термограмма комнаты.

Как было сказано ранее, если вы посмотрите на прямоугольник, то увидите, что температура является функцией точных координат x, y и z точки внутри прямоугольника. Эта функция есть f(x,y,z).

Начнем с интегрирования по оси Z, разделив коробку на множество срезов, параллельных земле: , но помните, температура это тоже измерение. На самом деле я взял комнату и нарезал ее на кучу двухмерных термограмм. И как мы уже говорили, двухмерную термограмму можно превратить в трехмерный график:

Изображение автора

Далее мы проинтегрируем по y, разделив термограмму на множество маленьких кусочков, как мы сделали с буханкой ананасового хлеба:

Изображение автора

Наконец, мы возьмем каждый кусочек и разделим его на части. маленьких прямоугольников вдоль оси X:

Изображение автора

Делая это, мы можем точно суммировать все тепло в этой квадратной комнате. Разбиваем помещение на термограммы по оси z, затем делим термограммы на срезы по оси y, затем делим срезы на прямоугольники по оси x. Берем сумму суммы сумм, интеграл интегралов интегралов (удачи говорят, что в 3 раза быстрее). Мы называем это тройной интеграл . Записывается так:

«dz» — это изменение z, «dy» — изменение y, а «dx» — изменение x. Функция f(x,y,z) — это функция, которая сообщает вам температуру в некоторой точке комнаты.

Используя этот тройной интеграл, мы можем найти общее количество тепла в трехмерной комнате. Если «размерность» может означать что-то иное, чем пространственное измерение, мы понимаем, что у тройных интегралов есть множество применений. Мы могли бы найти полную инерцию над некоторым трехмерным объектом или гравитационное притяжение баскетбольного мяча.

Короче говоря:

• Измерение в математических целях не обязательно должно относиться к пространству. Он может относиться к любому числовому значению, такому как температура, инерция или влажность.
• В одном интеграле мы интегрируем по 1 переменной, чтобы найти площадь двумерной фигуры.
• В двойном интеграле мы интегрируем две переменные, чтобы найти объем трехмерной фигуры.
• В тройном интеграле мы интегрируем по трем переменным, чтобы найти объем четырехмерной фигуры.

  No related posts.