Интегральные функции:
- Si(x)
- Интегральный синус от x
- Ci(x)
- Интегральный косинус от x
- Shi(x)
- Интегральный гиперболический синус от x
- Chi(x)
- Интегральный гиперболический косинус от x
В выражениях можно применять следующие операции:
- Действительные числа
- вводить в виде 7.
 3
3- — возведение в степень
- x + 7
- — сложение
- x — 6
- — вычитание
- 15/7
- — дробь
Другие функции:
- asec(x)
- Функция — арксеканс от x
- acsc(x)
- Функция — арккосеканс от x
- sec(x)
- Функция — секанс от x
- csc(x)
- Функция — косеканс от x
- floor(x)
- Функция — округление x в меньшую сторону (пример floor(4.5)==4.0)
- ceiling(x)
- Функция — округление x в большую сторону (пример ceiling(4.5)==5.0)
- sign(x)
- Функция — Знак x
- erf(x)
- Функция ошибок (или интеграл вероятности)
- laplace(x)
- Функция Лапласа
- asech(x)
- Функция — гиперболический арксеканс от x
- csch(x)
- Функция — гиперболический косеканс от x
- sech(x)
- Функция — гиперболический секанс от x
- acsch(x)
- Функция — гиперболический арккосеканс от x
Постоянные:
- Число «Пи», которое примерно равно ~3.
 14159..
14159.. - e
- Число e — основание натурального логарифма, примерно равно ~2,7183..
- i
- Комплексная единица
- oo
- Символ бесконечности — знак для бесконечности
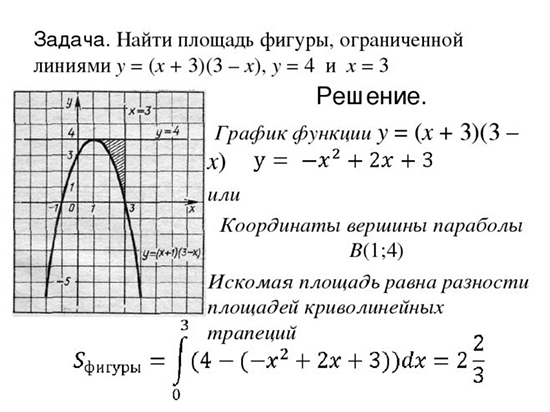
Вычислить площадь фигуры, ограниченную линиями.
Пример 1:
С помощью определённого интеграла вычислить площадь области D, ограниченной заданными линиями.
Решение от преподавателя:
Пример 2:
Вычислить площадь плоской фигуры, ограниченной заданными кривыми. Сделать чертеж области.
Решение от преподавателя:
Пример 3:
Вычислить площадь фигуры, ограниченной линиями
Решение от преподавателя:
Пример 4:
Решение от преподавателя:
Пример 5:
Найти площадь фигуры, ограниченной линиями
построить схематический чертеж в декартовых координатах.
Решение от преподавателя:
Пример 6:
Сделать чертеж области, ограниченной заданными линиями. Вычислить площадь полученной фигуры
Решение от преподавателя:
Построим область, площадь которой необходимо найти, заштрихуем искомую фигуру.
Затем найдём ординаты точек пересечения кривой и прямой.
Для этого приравняем правые части уравнений
и прямой
и решим полученное квадратное уравнение
Корни этого уравнения
Применим формулу:
Вычислим искомую площадь:
Ответ:
Пример 7:
Вычислить площадь фигуры, ограниченной линиями:
используя двойной интеграл.
Решение от преподавателя:
Пример 8:
Найти площадь плоской фигуры с помощью двойного интеграла:
Решение от преподавателя:
Пример 9:
Вычислить площадь фигуры, ограниченной осями координат играфиком функции
Решение от преподавателя:
Пример 10:
Решение от преподавателя:
Пример 11:
Найти площадь фигуры, ограниченной графиком функции прямыми .
Решение от преподавателя:
Пример 12:
Вычислить (с точностью до двух знаков после запятой) площадь фигуры, ограниченной указанными линиями.
Решение от преподавателя:
Пример 13:
Вычислить площадь фигуры, ограниченной линиями.
Решение от преподавателя:
Пример 14:
Вычислить площадь фигуры ограниченную линиями:
y=sinx, y = cosx, x = 0.
Решение от преподавателя:
Расмотрим два случая:
а) точка
Согласно критерию Лебега, функция интегрируема, если существует конечное число точек разрыва (в данном случае 1)
б) входит
Пример 15:
Вычислить площадь фигуры, ограниченной линиями.
Решение от преподавателя:
Пример 16:
Вычислить площадь фигуры, ограниченной графиками функций:
Решение от преподавателя:
Пример 17:
Вычислить площадь фигуры, ограниченной линиями:
Решение от преподавателя:
Пример 18:
Найти площадь фигуры, ограниченной линиями
построить схематический чертеж в декартовых координатах.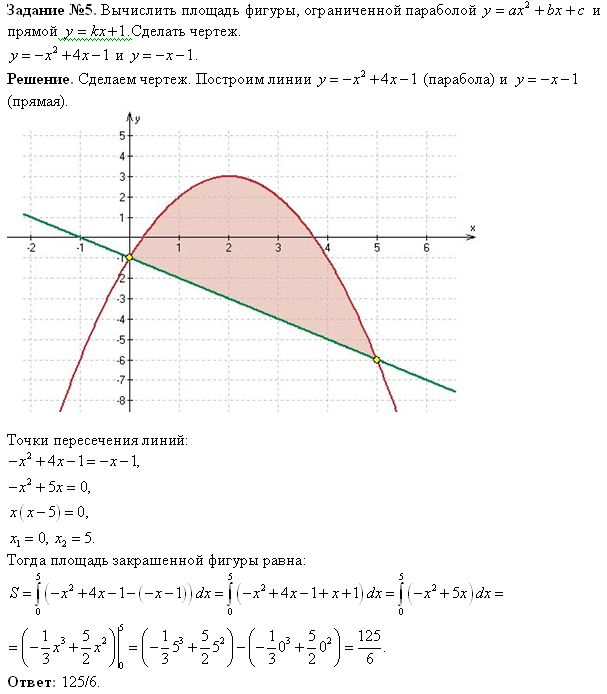
Решение от преподавателя:
Пример 19:
Вычислить площади фигур, ограниченных графиками функций.
Решение от преподавателя:
Пример 20:
Вычислить площадь фигуры, ограниченной осями координат и графиком функции:
Решение от преподавателя:
Пример 21:
Вычислить площади фигур, ограниченных графиками функций.
Решение от преподавателя:
Пример 22:
Вычислить площадь фигуры, ограниченной линиями используя двойной интеграл.
Решение от преподавателя:
=0,5238 кв. ед.
Пример 23:
Вычислить площадь фигуры, ограниченной линиями x2 = y +2 и y =-x.
Решение от преподавателя:
y=x2 — 2 и y =-x
Построим графики функций:
Пример 24:
Вычислите площадь фигуры, ограниченной линиями:
y=4x-x2 ; y=0
Решение от преподавателя:
Вначале построим фигуру, ограниченную данными линиями:
Искомая площадь находится по формуле
Ответ: Площадь искомой фигуры 32/3 (ед2).
Пример 25:
Найти площадь фигуры, ограниченной линиями:
Решение от преподавателя:
Построим фигуру:
Находим точки пересечения:
Искомая площадь состоит из двух одинаковых частей, поэтому достаточно найти площадь одной из них и умножить на 2:
Ответ:
Пример 26:
Вычислить площадь фигуры, ограниченной линиями и расположенной в первой четверти координатной плоскости. Сделать чертеж.
Решение от преподавателя:
Сначала сделаем схематичный чертёж. Построим график функции
Искомую площадь вычислим при помощи определённого интеграла.
Ответ:
Пример 27:
Вычислить площадь фигуры, ограниченной линиями:
Решение от преподавателя:
Пример 28:
Вычислить площадь фигуры, ограниченной параболой , прямой .
Решение от преподавателя:
Пример 29:
Найти площадь фигуры, ограниченной линиями:
Решение от преподавателя:
Пример 30:
Вычислить площадь фигуры, ограниченной графиками функций
Решение от преподавателя:
Пример 31:
Найти площадь фигуры, ограниченной линией:
Решение от преподавателя:
Пример 32:
Найти площадь фигуры, ограниченной линиями:
Решение от преподавателя:
Пример 33:
Найти площадь фигуры, ограниченной линиями:
Решение от преподавателя:
Работа вам нужна срочно.
 Не волнуйтесь, уложимся!
Не волнуйтесь, уложимся!Заполните, пожалуйста, данные для автора:
- 22423 авторов готовы помочь тебе.
- 2402 онлайн
вопросы: найдите площадь фигуры, ограниченной параболой, а парабола дана, наш X равен 2 y в квадрате, а X равен 1 минус 3 Y + 2 найдите площадь, которую они обе покрывают, чтобы они были окружены по этой параболе так что я сделал это нарисовал параболу вы сделали координатные оси и есть парабола и пометили несчастный теперь вы видите что это Х равно 1 минус 3 на 4 и Х равно равно минус 2 y в квадрате, чтобы найти площадь ограниченной фигуры, поэтому из диаграммы мы можем видеть, что все это представляет собой площадь, ограниченную параболой, поэтому в основном мы должны вычислить мы должны вычислить эту площадь, поэтому для этого что что вы собираетесь сделать, это мы собираемся вычислить площадь, ограниченную Воробьем, то есть X, равно 1 минус квадрат A, и вычесть площадь, ограниченную притчей 1 -2, как вызвать вы должны se
как это это прямоугольная коробка и это маленькая прямоугольная коробка это но теперь мы должны рассчитать площадь дивана в этом месяце делая это либо мы находим размеры этого и вычисляем площадь либо иначе мы можем вычислить площадь весь прямоугольный блок и минус эта часть, так что в основном мы делаем C, используя ту же концепцию, что и вы, поэтому, когда мы вычисляем площадь, ограниченную параболой, она дает всю площадь, которая покрывается в нашем случае, например, это 1-3 вайшнавов, интегрируйте это когда мы интегрируем эту притчу из пределов 12, какой бы ограниченный вы ни хотели найти, область должна дать всю эту область, которая оказывается в левой части этого сайта сейчас, и аналогично для этого — белый для голосовых вызовов от 0 к нему будет включен вся часть слева, поэтому, когда область притяжения ограничена квадратом 1 минус 3 y, а мой пенис притягивает область, ограниченную США этим малым квадратом минус 2 y, мы получаем площадь, необходимую для этого, чтобы сначала найти это
точки, где эти две, чтобы мы могли рассчитать, откуда и где найти угловой диван, делая то, что нам нужно, чтобы найти точку пересечения Итак, уравнения: X равно 1 минус 3 y квадрат и и X равно равно минус 2 y в квадрате sunao см. оба уравнения с обоими уравнениями 1 минус 3 y в квадрате равно минус 2 y в квадрате, поэтому, когда мы возьмем это слева, это станет одним минус y в квадрате равно нулю, поэтому почему появляется сперма чтобы быть одним, поэтому отсюда, почему из вас выходит -1, и это два значения того, почему теперь Forex Forex поместит значение Y, так что это от x дано нам 1 минус 3 y квадратный закон в обоих вопрос Вы можете видеть, что это было именно так, в основном, когда у вас есть -11, значение x будет выглядеть так, как будто вы будете использовать один год, поэтому X равно 1 минус 3 в одном квадрате
оба уравнения с обоими уравнениями 1 минус 3 y в квадрате равно минус 2 y в квадрате, поэтому, когда мы возьмем это слева, это станет одним минус y в квадрате равно нулю, поэтому почему появляется сперма чтобы быть одним, поэтому отсюда, почему из вас выходит -1, и это два значения того, почему теперь Forex Forex поместит значение Y, так что это от x дано нам 1 минус 3 y квадратный закон в обоих вопрос Вы можете видеть, что это было именно так, в основном, когда у вас есть -11, значение x будет выглядеть так, как будто вы будете использовать один год, поэтому X равно 1 минус 3 в одном квадрате
эта концепция X равна 1 минус 3 X получается -2, так что теперь мы идем отсюда, мы можем сказать, что две координаты, потому что тогда координаты станут -2 -1 и -2 Паван, так что это верхнее часть равна -2 кам — одна, а нижняя — -2 -1, поэтому мы получили наши значения, теперь мы должны вычислить это для этого, что мы собираемся сделать, это ограниченная область, так что теперь, если вы видите, что это площадь вдоль линии вдоль оси x, симметричная с обеих сторон, в основном область, расположенная ниже оси x, аналогична той, что находится над осью x, поэтому, что мы можем сделать, мы можем найти любой из них и просто удвоить x 2 получит всю область то же самое, чтобы сделать вашу поддержку, скажем, эту область, ограниченную областью, ограниченную
парабола равна 2 x 2 X, поэтому мы должны интегрировать эту область от 0, потому что она не равна нулю, да, она равна нулю, потому что мы интегрируем ее по координатам y y, поэтому в основном от Y, если вы видите, что она идет от от нуля до единицы вычисляется значение Y, поэтому от 0 до 1 лакха для расчета, поэтому из пределов от нуля до единицы теперь то, что внешнее уравнение будет один минус 3 y в квадрате, так что это приведет к 1 минус 3 Y — из них уравнения шахтеров минус 2 y в квадрате, так что в DY, так что это вопрос, который мы должны решить только области гитары, супер делая 2 в 10 до 11 — 3 y в квадрате + 2 y в квадрате DY, так что получается
Tu в 2021 году 1 минус y в квадрате на DY, так что теперь вы разделите студентов на 2021 Divine -2 в 2021 y в квадрате sunao aap для расчета решит эти Integra, поэтому, когда мы решим это kaun sa Ab To 12 vi от 0 до 1 минус 2 в кубе y на 3 от 0 до 1 12 футов значения нуля в одном, так что это выйдет 20 и 21 — 0 — 2 в это приведет к 1 на 3 минус ноль, поэтому, когда вы так на этом концерте к Bittu это будет становится слишком y3, поэтому, когда cal становится 6 — 2y 3, поэтому ответ считается равным 4 на 3 квадратных единицы
MathScene — Интеграция — Урок 3
MathScene — Интеграция — Урок 3| 2010 Расмус Эф и Джанн Сак | Интеграция |
Урок 3
Области между графиками функции
Области, ограниченные графиками функций, можно найти интегрированием.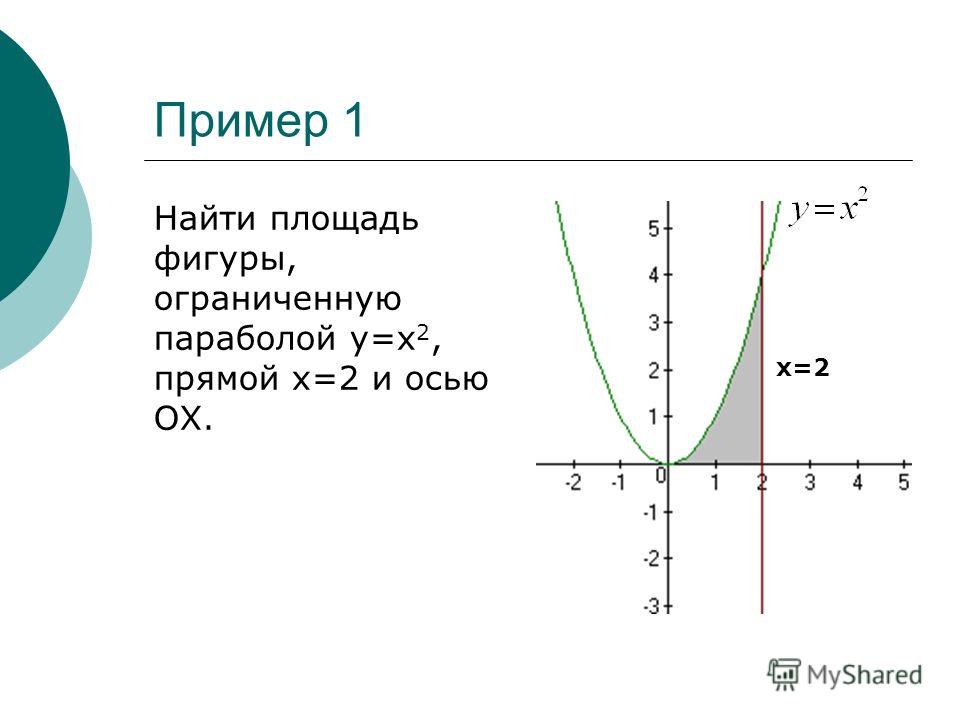 Для
Например, мы найдем площадь, ограниченную двумя графиками f(x) = x 2 + 5x 3
и у = х.
Для
Например, мы найдем площадь, ограниченную двумя графиками f(x) = x 2 + 5x 3
и у = х.
Это площадь, показанная в калькуляторе:
Начнем с нахождение точек пересечения двух графиков, чтобы дать нам границы площади:
х 2 + 5х 3 = х
х 2 + 4х 3 = 0 Упрощать.
(x 2 4x + 3) = 0 1 из-за скобки.
(x 1)(x 3) = 0 Факторизация .
(х 2 4x + 3) = 0
(x 1)(x 3) = 0
Точками пересечения являются x = 1 и x = 3. Они лежат на прямой y = x, поэтому координаты y совпадают с координатами x, то есть (1, 1) и (3, 3).
Нам нужно только
используйте координаты x для вычисления площади между каждой кривой и осью x.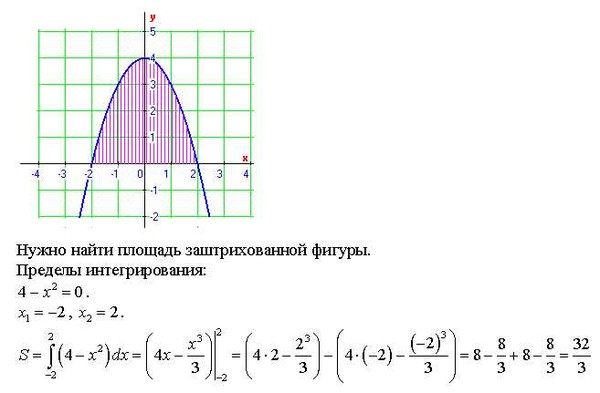
Интеграл дает площадь между осью x и функцией е (х) = х 2 + 5x 3 на интервале от 1 до 3.
Это заштрихованная область графика ниже
Таким же образом это площадь между y = x и x — на одном интервале. Снова на графике показана площадь найденный.
Если мы соединим эти два графика, мы увидим, что область, которую мы хотим найти, является разница между двумя вышеперечисленными.
Итак, мы просто нужно взять разницу между двумя интегралами, чтобы найти площадь, которую мы требовать.
|
 На диаграмме показана новая ситуация.
На диаграмме показана новая ситуация.Точки пересечения остаются прежними, так как мы добавили 2 к обеим сторонам уравнение. Ниже приведены расчеты, если вы не уверены!
x 2 + 5x 5 = x 2
х 2 + 4х 3 = 0 Упростить .
(x 2 4x + 3) = 0
(x 1)(x 3) = 0 Факторизация.
И снова решения x = 1 и x = 3. Интегрируя таким же образом, вы можете видеть, что 2 снова упрощается, поэтому мы имеем тот же результат, что и раньше.
Это означает что при вычислении площади между кривыми нам не нужно беспокоиться о независимо от того, находится ли область выше или ниже оси x, метод всегда один и тот же.
Площадь ограничен сверху графиком е(х) и ниже по графику g(x): Границы х = а и х = б являются решениями уравнения f(x) = g(x) |
Пример 1
Найдите площадь между параболой f(x) = x 2 4 и линия у = х 2.
Начнем с решение уравнения x 2 4 = x 2 найти площадь границы
х 2 4 = х 2
x 2 4 х + 2 = 0
х 2 х 2 = 0
(х + 1)(х 2) = 0
Решения: х = 1 х = 2,
Это хорошая идея, чтобы посмотреть на график и область, вовлеченную в калькулятор.
Мы видим, что линия ограничивает область выше, поэтому мы вычитаем интеграл от парабола от линии.
Пример 2
Найдите площадь, заключенную между графиками f(x) = sin x и g(x) = cos x.
на интервале 0 ≤ x < 2p
Калькулятор показывает нам площадь, которую мы собираемся найти.
Мы снова должны начнем с поиска точек пересечения двух графиков.
Решение уравнения
грех х = потому что х.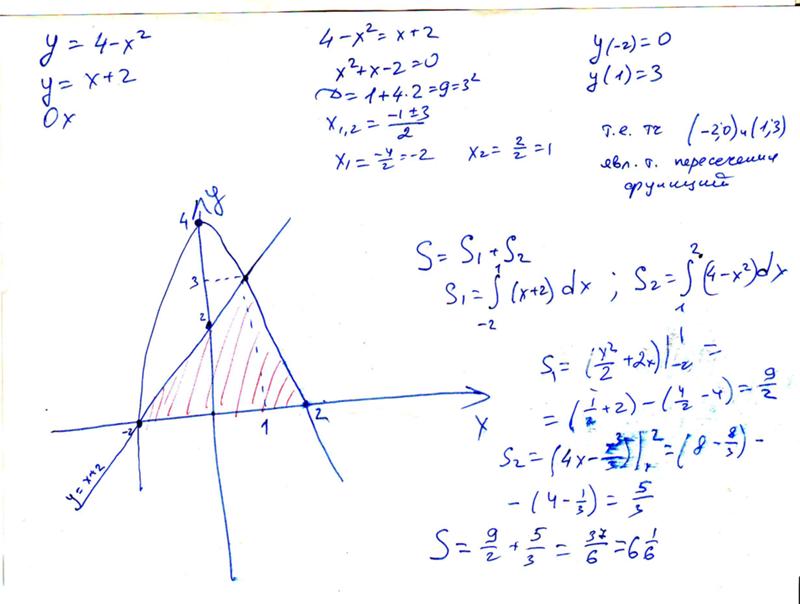
sin x/cos x = 1 Разделить на cos х
тангенс х = 1
х = коричневый 1 1 = /4 + номер
Это означает что х = /4 и х = 5/4 на интервале 0 ≤ x < 2
График f(x) = sin x лежит над графиком g(x) = cos x на всех интервал между точками пересечения, поэтому расчеты площади выглядят как следует:
Сейчас потому что /4 = грех / 4 «=» и cos 5/4 = грех 5/4 «=»
Таким образом, точное значение площади равно
.Пример 3
Найдите площадь, ограниченную графиками прямой y = 3x + 1 и многочлен f(x) = ⅓ x 3 2x 2 + 3x + 1.
Сначала график рисуется с помощью калькулятора. Следующие значения окна должны работать
Вот график:
Теперь вычисляем точки пересечения.

 3
3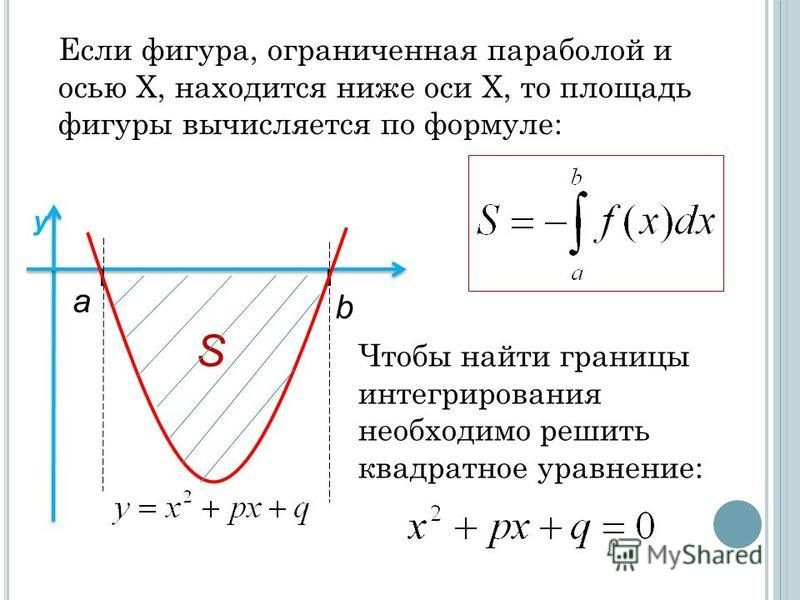 14159..
14159..