Как построить график функции y = f (x+l) и y = f (x)+m, если известен график функции y = f(x). 8-й класс
- Ефименко Вера Николаевна, учитель математики
Разделы: Математика
Класс: 8
Цели:
- повторить правила построения и свойства графиков функций у = x2, , , у =| x |;
- выяснить правила построения графиков функций у = f (x + l) и у = f (x) + m;
- развить умение строить графики функций;
- развивать познавательную активность учащихся.
Оборудование: интерактивная доска,
проектор, презентация к уроку.
ХОД УРОКА
1. Организационный момент
2. Устная работа (Приложение. Слайды 2-8.)
Задание: Графики каких функций
изображены на рисунках? (у = x2, у = – x2,
, , ,
, у =| x |, у =
– | x |).
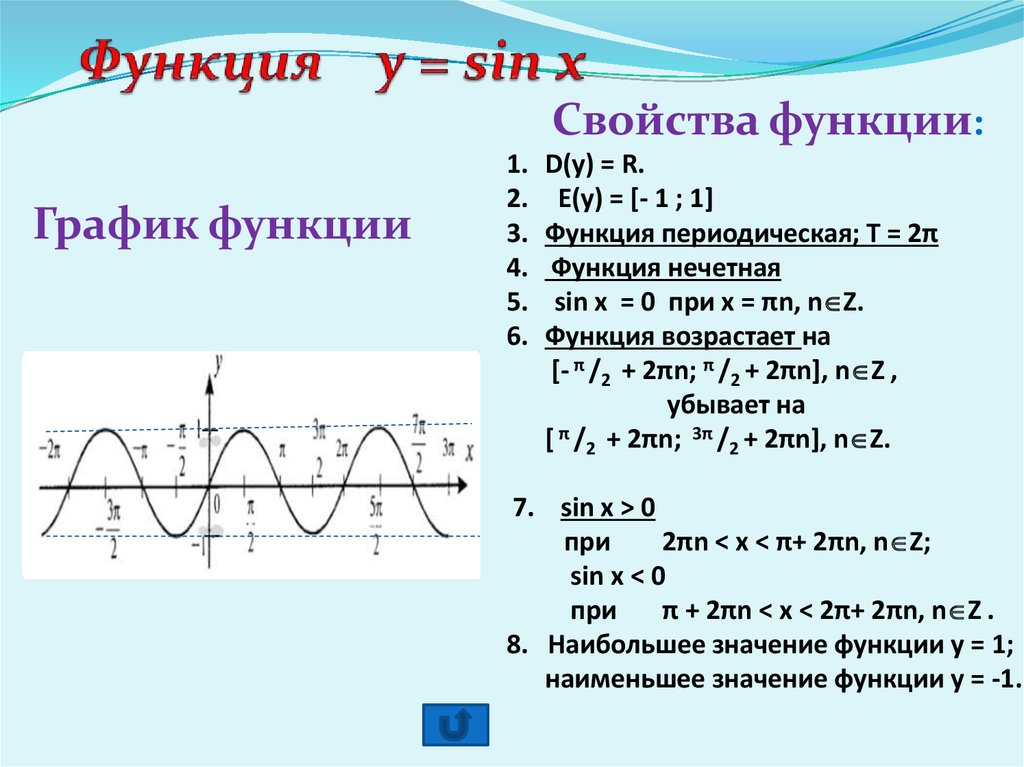
Для каждой из функций сформулировать ее свойства
и правила построения графика функции.
3. Изучение нового материала (Приложение)
На координатной плоскости в тетрадях учащиеся по точкам строят графики функций у = x2 и у = x2 +1. Учащиеся самостоятельно приходят к выводу о сдвиге параболы (параллельном переносе) на 1 единицу вверх. (Слайд 10.)
На координатной плоскости в тетрадях учащиеся по точкам строят графики функций у = x2 и у = x2
– 1.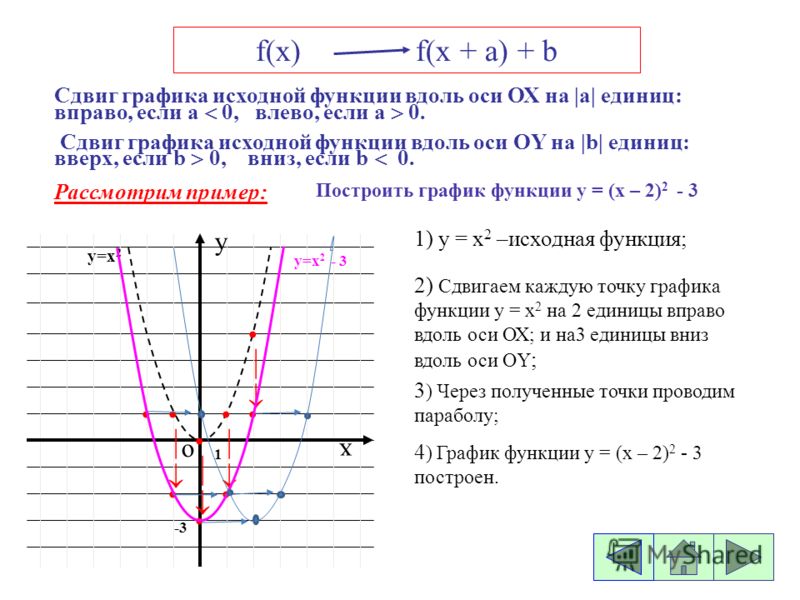 Учащиеся
самостоятельно приходят к выводу о сдвиге
параболы (параллельном переносе) на 1 единицу
вниз. (Слайд 11.)
Учащиеся
самостоятельно приходят к выводу о сдвиге
параболы (параллельном переносе) на 1 единицу
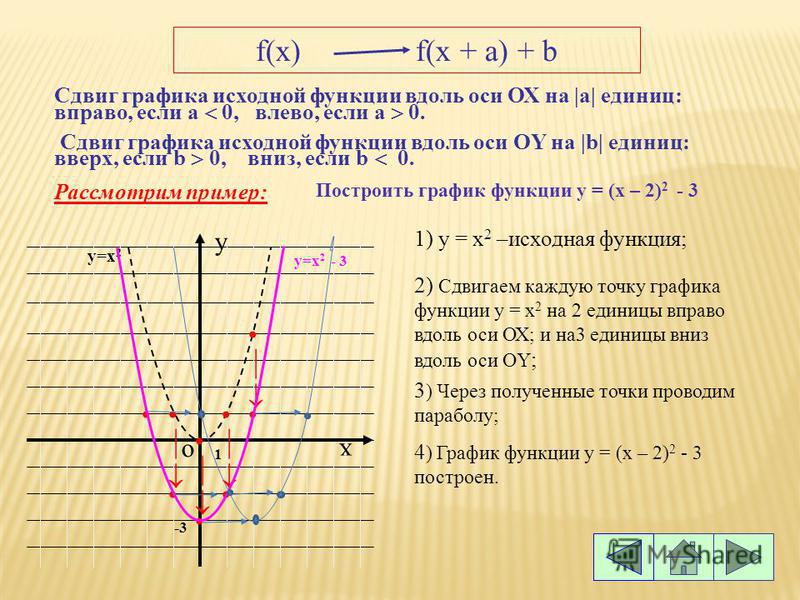
вниз. (Слайд 11.)На координатной плоскости в тетрадях учащиеся по точкам строят графики функций у = x2 и у = (x – 1)2. Учащиеся самостоятельно приходят к выводу о сдвиге параболы (параллельном переносе) на 1 единицу вправо. (Слайд 12.)
На координатной плоскости в тетрадях учащиеся по точкам строят графики функций у = x2 и у = (x + 1)2. Учащиеся самостоятельно приходят к выводу о сдвиге параболы (параллельном переносе) на 1 единицу влево. (Слайд 13.)
С помощью учителя учащиеся формулируют правило построения графика функции у = f (x + l) и графика функции у = f (x) + m
 )
)Затем рассматривается вариант построения графика функции у = f (x + l) и графика функции у = f (x) + m с помощью сдвига графика функции у = f (x), если известен график функции у = f (x) с помощью сдвига осей координат. (Слайды 19-23. Анимация сдвигов осей координат на слайдах помогает лучшему восприятию правила построения графиков.)
Правила построения графиков функций у = f (x + l) и у = f (x) + m записываются в тетрадь.
4. Закрепление материала
№ 19.6, № 20.6, № 19.11(в), № 19.12(в), № 19.13(в), № 19.14(в), № 20.11(в), № 20.12(в), № 20.13(в), № 20.14(в).
5. Домашнее задание
Параграф 19, 20 учебника, № 19.5, № 20.5, № 19.11–19.14(а), № 20.11–20.14(а).
6. Подведение итогов урока
Подготовка школьников к ЕГЭ и ОГЭ (Справочник по математике — Планиметрия
Поиск по сайту:
| Справочник по математике | Алгебра | Координатная плоскость |
Элементарные преобразования графика функции y = f (x ) перечислены в следующей таблице.
| Преобразование | Описание | Рисунок |
y = f (x + c), | В случае c > 0 график функции | |
В случае c < 0 график функции | ||
y = f (x) + c, | В случае c > 0 график функции | |
В случае c < 0 график функции | ||
| y = – f (x) | График функции y = f (x) симметрично отражается относительно оси Ox. | |
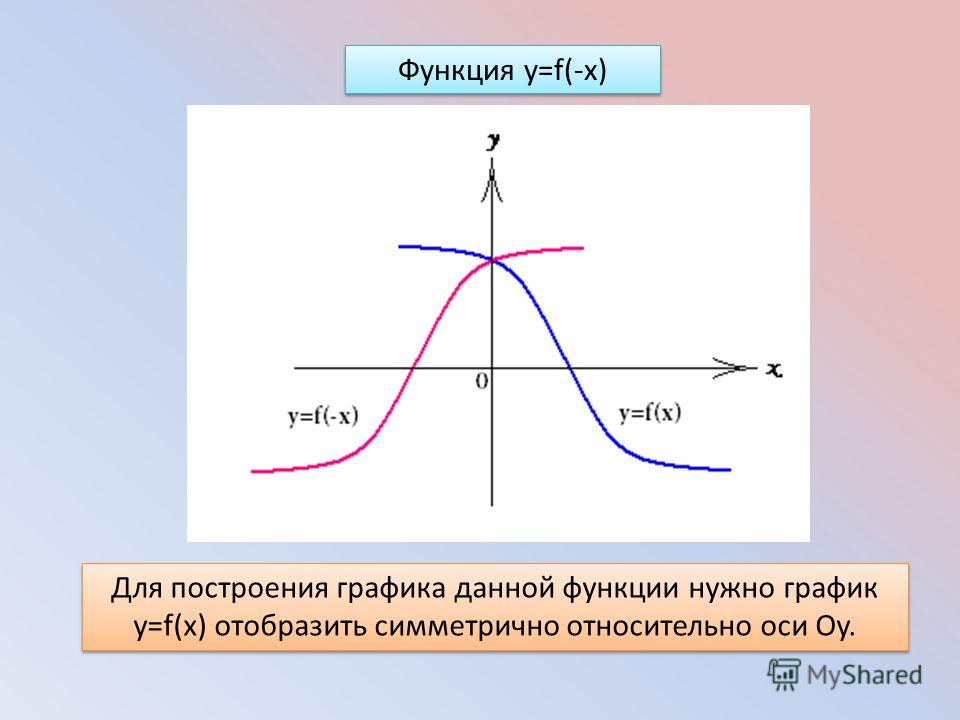
| y = f ( – x) | График функции y = f (x) симметрично отражается относительно оси Oy. | |
| В случае k > 1 происходит | |
В случае 0 < k < 1 происходит растяжение графика функции | ||
В случае – 1 < k < 0 происходит растяжение графика функции | ||
В случае k < – 1 происходит | ||
| В случае k > 1 происходит | |
В случае 0 < k < 1 происходит | ||
В случае – 1 < k < 0 происходит | ||
В случае k < – 1 происходит | ||
| y = | f (x)| | Часть графика функции y = f (x), расположенная в области | |
| y = f (| x|) | Ось Oy является осью симметрии Часть графика функции y = f (x), расположенная в области |
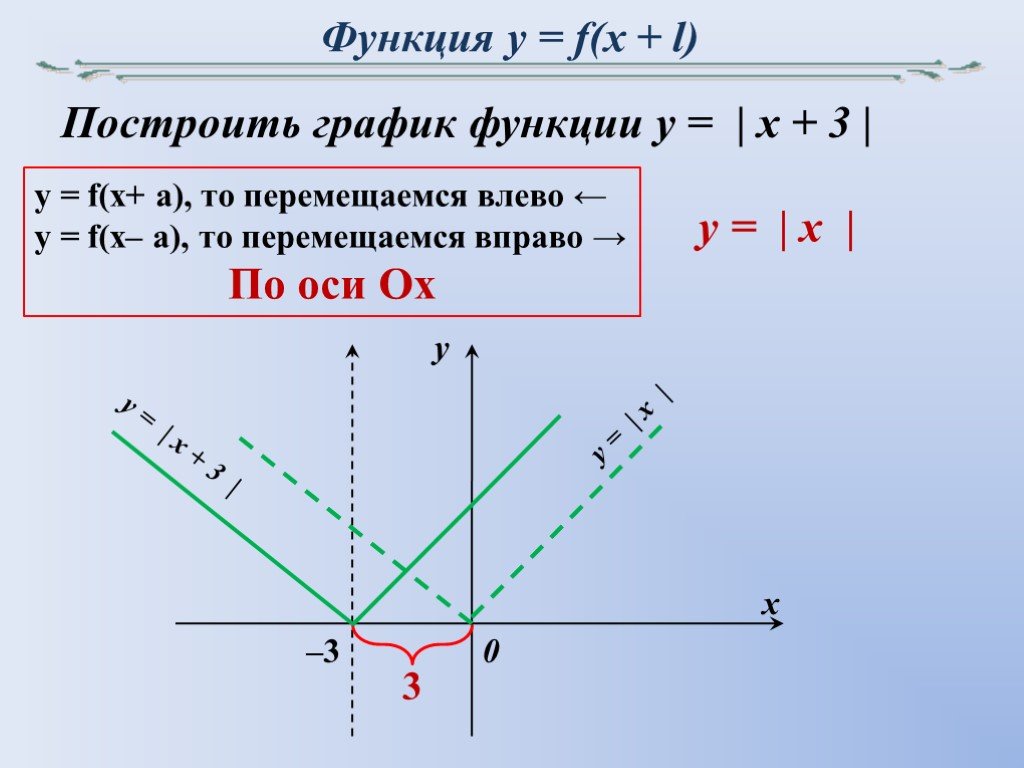
| Преобразование y = f (x + c), где c – число | |
В случае c > 0 график функции y = f (x) переносится влево на расстояние | c | | |
В случае c < 0 график функции y = f (x) переносится вправо на расстояние | c | | |
| Преобразование y = f (x) + c, где c – число | |
В случае c > 0 график функции y = f (x) переносится вверх на расстояние | c | | |
В случае c < 0 график функции y = f (x) переносится вниз на расстояние | c | | |
| Преобразование y = – f (x) | |
График функции y = f (x) симметрично отражается относительно оси Ox. | |
| Преобразование y = f ( – x) | |
График функции y = f (x) симметрично отражается относительно оси Oy. | |
| Преобразование y = f (kx), где k – число | |
В случае k > 1 происходит сжатие графика функции | |
В случае 0 < k < 1 происходит растяжение графика функции y = f (x) в раз от оси Oy. | |
В случае – 1 < k < 0 происходит растяжение графика функции y = f (x) в раз от оси Oy с последующим симметричным отражением графика относительно оси Oy. | |
В случае k < – 1 происходит сжатие графика функции | |
| Преобразование y = k f (x), где k – число | |
В случае k > 1 происходит растяжение графика функции y = f (x) в k раз от оси Ox. | |
В случае 0 < k < 1 происходит сжатие графика функции y = f (x) в раз к оси Ox. | |
В случае – 1 < k < 0 происходит сжатие графика функции y = f (x) в раз к оси Ox с последующим симметричным отражением графика относительно оси Ox. | |
В случае k < – 1 происходит растяжение графика функции y = f (x) в | k | раз от оси Ox с последующим симметричным отражением графика относительно оси Ox. | |
| Преобразование y = | f (x)| | |
Часть графика функции | |
| Преобразование y = f (| x|) | |
Ось Oy является осью симметрии графика функции y = f (| x|). Часть графика функции | |
| Преобразование y = f (x + c), где c – число |
Описание: В случае c > 0 график функции y = f (x) переносится влево на расстояние | c | Рисунок: |
Описание: В случае c < 0 график функции y = f (x) переносится вправо на расстояние | c | Рисунок: |
| Преобразование y = f (x) + c, где c – число |
Описание: В случае c > 0 график функции y = f (x) переносится вверх на расстояние | c | Рисунок: |
Описание: В случае c < 0 график функции y = f (x) переносится вниз на расстояние | c | Рисунок: |
| Преобразование y = – f (x) |
Описание: График функции y = f (x) симметрично отражается относительно оси Ox. Рисунок: |
| Преобразование y = f ( – x) |
Описание: График функции y = f (x) симметрично отражается относительно оси Oy. Рисунок: |
| Преобразование y = f (kx), где k – число |
Описание: В случае k > 1 происходит сжатие графика функции y = f (x) в k раз к оси Oy. Рисунок: |
Описание: В случае 0 < k < 1 происходит растяжение графика функции y = f (x) в раз от оси Oy. Рисунок: |
Описание: В случае – 1 < k < 0 происходит растяжение графика функции y = f (x) в раз от оси Oy с последующим симметричным отражением графика относительно оси Oy. Рисунок: |
Описание: В случае k < – 1 происходит сжатие графика функции y = f (x) в | k | раз к оси Oy с последующим симметричным отражением графика относительно оси Oy. Рисунок: |
| Преобразование y = k f (x), где k – число |
Описание: В случае k > 1 происходит растяжение графика функции y = f (x) в k раз от оси Ox. Рисунок: |
Описание: В случае 0 < k < 1 происходит сжатие графика функции y = f (x) в раз к оси Ox. Рисунок: |
Описание: В случае – 1 < k < 0 происходит сжатие графика функции y = f (x) в раз к оси Ox с последующим симметричным отражением графика относительно оси Ox. Рисунок: |
Описание: В случае k < – 1 происходит растяжение графика функции y = f (x) в | k | раз от оси Ox с последующим симметричным отражением графика относительно оси Ox. Рисунок: |
| Преобразование y = | f (x)| |
Описание: Часть графика функции y = f (x), расположенная в области , остаётся на месте. Рисунок: |
| Преобразование y = f (| x|) |
Описание: Ось Oy является осью симметрии графика функции y = f (| x|). Часть графика функции y = f (x), расположенная в области остаётся на месте. Часть графика функции y = f (| x|), расположенная в области x < 0, получается из части графика, расположенной в области при помощи симметричного отражения относительно оси Oy. Рисунок: |
Примеры элементарных преобразований графика функции y = x2 приведены в следующей таблице.
| Функция | График |
| y = x2 = f (x) | |
y = x2 + 4x + 4 = (x + 2)2 = = f (x + 2) | |
y = x2 – 4x + 4 = (x – 2)2 = = f (x – 2) | |
| y = x2 + 2 = f (x)+ 2 | |
| y = x2 – 2 = f (x) – 2 | |
| y = – x2 = – f (x) | |
| y = 2x2 = 2 f (x) |
Функция: y = x2 = f (x) График: |
Функция: y = x2 + 4x + 4 = График: |
Функция: y = x2 – 4x + 4 = График: |
Функция: y = x2 + 2 = График: |
Функция: y = x2 – 2 = График: |
Функция: y = – x2 = График: |
Функция: y = 2x2 = График: |
Примеры элементарных преобразований графика функции y = x2 – 6 x + 5 приведены в следующей таблице.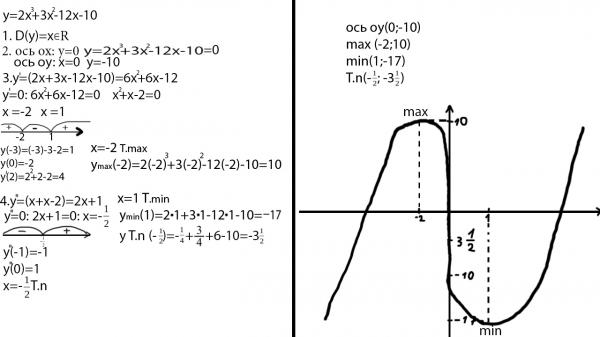
| Функция | График |
| y = x2 – 6x + 5 = = f (x) | |
| y = x2 + 6x + 5 = = f (– x) | |
| y = 4x2 – 12x + 5 = = f (2x) | |
| y = | x2 – 6x + 5| = = | f (x)| | |
| y = x2 – 6 | x| + 5 = = f (| x|) |
Функция: y = x2 – 6x + 5 = График: |
Функция: y = x2 + 6x + 5 = График: |
Функция: y = 4x2 – 12x + 5 = График: |
Функция: y = | x2 – 6x + 5| = График: |
Функция: y = x2 – 6 | x| + 5 = График: |
На сайте можно также ознакомиться с нашими учебными материалами для подготовки к ЕГЭ и ОГЭ по математике.
| До ЕГЭ по математике осталось | |||
| дней | часов | минут | секунд |
|
Мэтуэй | Популярные задачи
92) 9(3x) по отношению к x 92+1| 1 | Найти производную — d/dx | бревно натуральное х | |
| 2 | Оценить интеграл | интеграл натурального логарифма x относительно x | |
| 3 | Найти производную — d/dx | ||
| 21 | Оценить интеграл | ||
| 22 | Найти производную — d/dx | грех(2x) | |
| 23 | Найти производную — d/dx | ||
| 41 | Оценить интеграл | интеграл от cos(2x) относительно x | |
| 42 | Найти производную — d/dx | 1/(корень квадратный из х) | |
| 43 | Оценка интеграла 9бесконечность | ||
| 45 | Найти производную — d/dx | х/2 | |
| 46 | Найти производную — d/dx | -cos(x) | |
| 47 | Найти производную — d/dx | грех(3x) | |
| 68 | Оценить интеграл | интеграл от sin(x) по x | |
| 69 | Найти производную — d/dx | угловой синус(х) | |
| 70 | Оценить предел | ограничение, когда x приближается к 0 из (sin(x))/x 92 по отношению к х | |
| 85 | Найти производную — d/dx | лог х | |
| 86 | Найти производную — d/dx | арктан(х) | |
| 87 | Найти производную — d/dx | бревно натуральное 5х92 |
Поверхности как графики функций
Если $f$ — скалярная функция одной переменной, $f:\R \to \R$ (перепутали?),
тогда графом $f$ называется множество точек $(x,f(x))$ для всех $x$ в области определения $f$. Когда часто называют это
график $y=f(x)$, поскольку мы считаем, что точки лежат в $xy$-плоскости. При нанесении точек на $xy$-плоскость они обычно образуют кривую a точек, например график
$f(x)=\sin x$ показано ниже. 92 \to \R$ таким же образом. График представляет собой набор точек
$(x,y,f(x,y))$ для всех $(x,y)$ в области определения $f$.
Когда часто называют это
график $z=f(x,y)$, так как мы считаем, что точки лежат в
$xyz$-пространство. Вы можете не найти это формальное определение особенно информативным,
но мы можем показать, что график $f(x,y)$ является поверхностью.
Когда часто называют это
график $y=f(x)$, поскольку мы считаем, что точки лежат в $xy$-плоскости. При нанесении точек на $xy$-плоскость они обычно образуют кривую a точек, например график
$f(x)=\sin x$ показано ниже. 92 \to \R$ таким же образом. График представляет собой набор точек
$(x,y,f(x,y))$ для всех $(x,y)$ в области определения $f$.
Когда часто называют это
график $z=f(x,y)$, так как мы считаем, что точки лежат в
$xyz$-пространство. Вы можете не найти это формальное определение особенно информативным,
но мы можем показать, что график $f(x,y)$ является поверхностью.
Функция f принимает два входа, $x$ и $y$, и возвращает одно число, которое мы называем $z$.
Если провести координатные оси $x$-$y$-$z$ стандартным образом,
ось $z$ представляет высоту, и это ключ к построению графика $f(x,y)$.
Если вы выберете точку $(x,y)$ на плоскости $xy$, то $z=f(x,y)$ представляет собой высоту графика в этой точке.
Например, вот график простой функции $g(x,y)=1$.
Независимо от того, какие значения вы выберете для $x$ и $y$,
функция $g$ всегда будет возвращать («высоту») единицу.
Загрузка апплета
Горизонтальная плоскость. График функции $g(x,y)=1$ представляет собой горизонтальную плоскость высотой 1.
Подробнее об апплете.
График функции одной переменной $g(x)$ представляет собой линия с наклоном 1 через начало координат. Можете ли вы представить, что график ее обобщения на две переменные, функция $g(x,y)=x+y$, будет выглядеть? Это будет не линия, а плоскость. Этот график не будет иметь постоянную высоту, равную единице, но вы сможете сделать некоторые наблюдения:
- Если $y=-x$, то $g(x,y)=0$.
- Если $x$ и $y$ оба положительны, то $g(x,y) > 0$.
- Если $x$ и $y$ оба отрицательны, то $g(x,y)
- Если вы зафиксируете $x$ или $y$ и увеличите другую переменную, функция будет возрастать с наклоном, равным единице.
Можете ли вы увидеть, правда ли это на графике?
Загрузка апплета
Наклонная плоскость. График функции $g(x,y)=x+y$ представляет собой наклонную плоскость.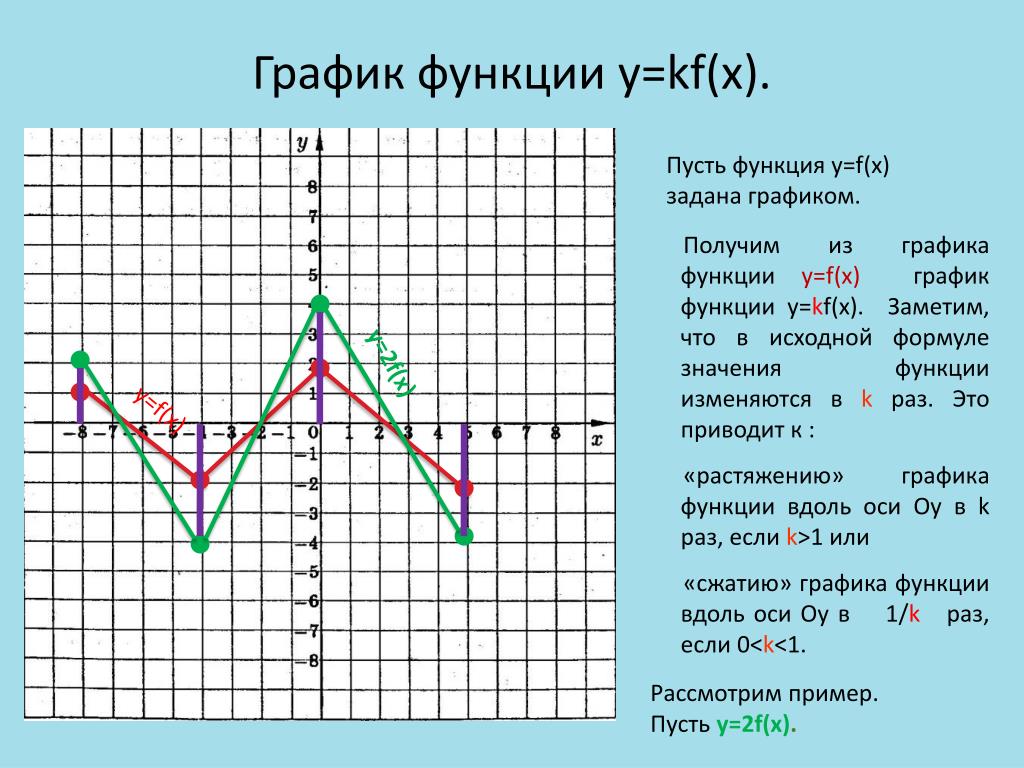



 Часть графика функции y = f (x), расположенная в области y < 0, симметрично отражается относительно оси Ox.
Часть графика функции y = f (x), расположенная в области y < 0, симметрично отражается относительно оси Ox.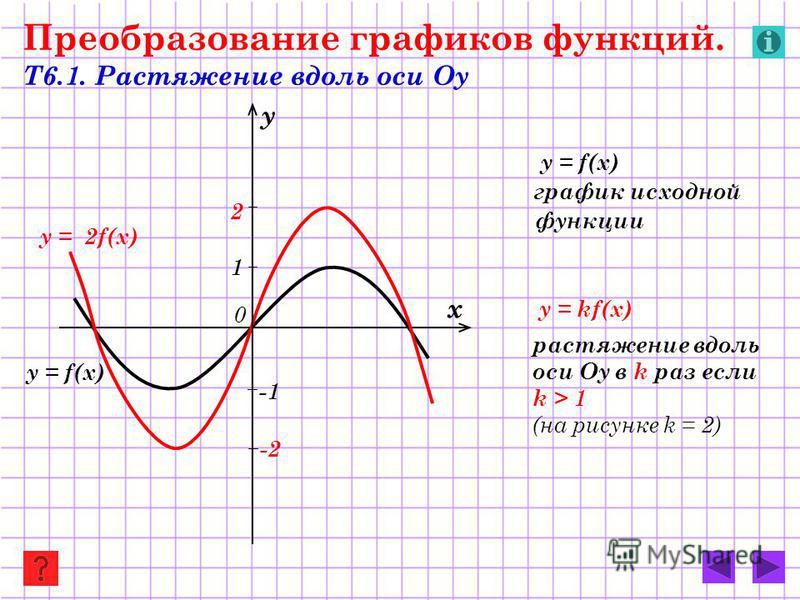

 Часть графика функции y = f (x), расположенная в области y < 0, симметрично отражается относительно оси Ox.
Часть графика функции y = f (x), расположенная в области y < 0, симметрично отражается относительно оси Ox.