Вычислить площадь параллелограмма построенного на векторах а и b: Площадь параллелограмма построенного на векторах

Площадь параллелограмма, построенного на векторах

Содержание:

• Как определить площадь параллелограмма, построенного на векторах
• Что такое модуль векторного произведения
• Как рассчитать площадь обычного параллелограмма
• Пример решения задачи в трехмерном пространстве
• Пример решения в двухмерном пространстве

Содержание

• Как определить площадь параллелограмма, построенного на векторах
• Что такое модуль векторного произведения
• Как рассчитать площадь обычного параллелограмма
• Пример решения задачи в трехмерном пространстве
• Пример решения в двухмерном пространстве

Как определить площадь параллелограмма, построенного на векторах

Определение

Площадь параллелограмма, построенного на векторах, определяется как произведение их длин на синус угла между ними.

Если по условию задачи даны длины этих векторов, то вычисление площади параллелограмм не вызывает затруднений. Для этого необходимо воспользоваться формулой:

\( S=\left|a\right|\times\left|b\right|\times\sin\beta\)

Осторожно! Если преподаватель обнаружит плагиат в работе, не избежать крупных проблем (вплоть до отчисления). Если нет возможности написать самому, закажите тут.

Что такое модуль векторного произведения

Векторным произведением некоторых векторов m и n является третий вектор p.

\(\overline p\;=\left|\overline m\right|\times\left|\overline n\right|\\\)

Определение

Модуль векторного произведения, то есть скаляр вектора p определяется как произведение модулей векторов m и n, на синус лежащего между ними угла α. Это определение записывается математическим языком так:

\(\left|p\right|=\left|m\right|\times\left|n\right|\times\sin\alpha\\\)

Все три эти вектора образуют правую тройку.

Это значит, что если привести их к общему началу из конца третьего вектора (р), то кратчайший поворот от первого вектора (m) ко второму вектору (n) будет совершаться против часовой стрелки.

Допустим, вектора заданы координатами:

\(\overline m=\left\{x_1;y_1;z_1\right\}\\\)

\(\overline n=\left\{x_2;y_2;z_2\right\}\\\)

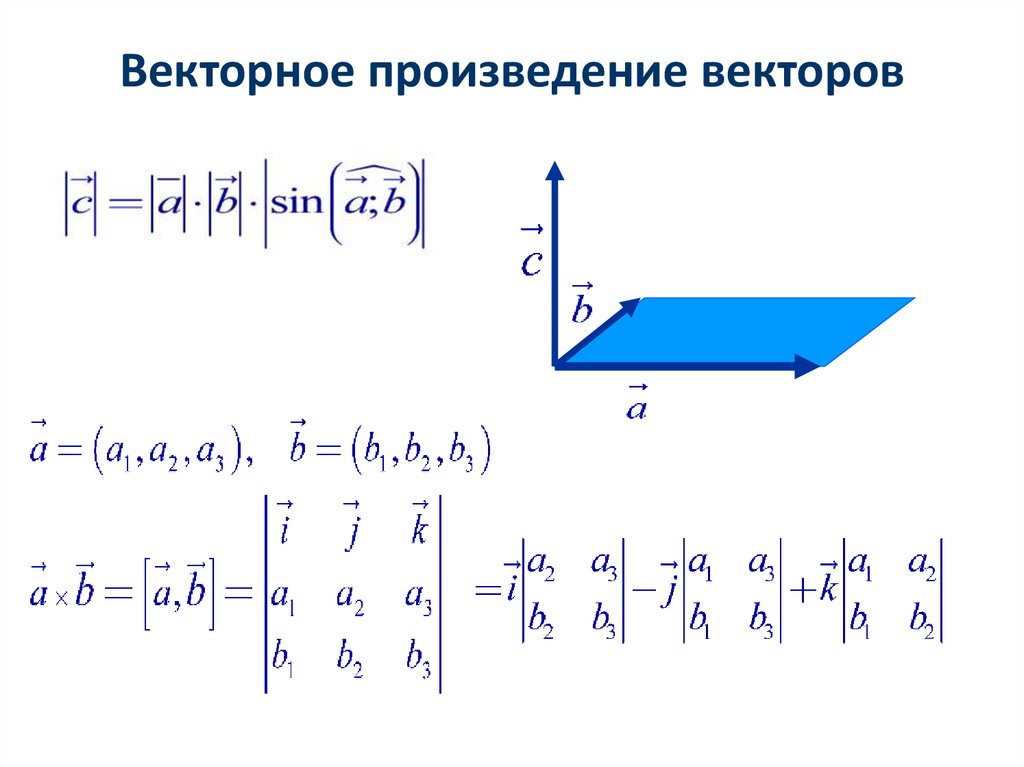
В декартовой системе координат их произведение можно будет вычислить по формуле:

\(\left[m\times n\right]=\left\{y_1\times z_2-y_2\times z_1;z\times x_2-z_2\times x_1;x_2\times y_2-x_2\times y_1\right\}\\\)

Примечание

В этом виде запомнить формулу достаточно сложно. Значительно проще представить ее в другой форме:

\(\left[m\times n\right]=\begin{vmatrix}i&j&k\\x_1&y_1&z_1\\x_2&y_2&z_2\end{vmatrix}\\\\\\\)

Как рассчитать площадь обычного параллелограмма

Пример

Рассмотрим еще один пример. Дан параллелограмм с длиной сторон a – 5 см, b – 6 см и углом между ними равным 30^0\\\\\\. 0=30\times\frac12=15\\\\\\\)

Таким образом, площадь данного параллелограмма равна 15 квадратным сантиметрам.

Пример решения задачи в трехмерном пространстве

Пример

Даны два вектора, а и b, имеющие в декартовой системе следующие координаты:

\(\left\{4,\;2,\;6\right\}\\\\\\\)

\(\left\{4,\;8,\;11\right\}\\\\\\\)

Требуется найти площадь, образуемого ими параллелограмма.

Для решения требуется найти векторное произведение заданных векторов:

\(\left[a\times b\right]=\begin{vmatrix}i&j&k\\4&2&6\\4&8&11\end{vmatrix}=i\begin{vmatrix}2&6\\8&11\end{vmatrix}-j\begin{vmatrix}4&6\\4&11\end{vmatrix}+k\begin{vmatrix}4&2\\4&8\end{vmatrix}=i\left(2\times11-48\right)-j\left(44-24\right)+k\left(32-8\right)=-26i-20j+24k=\left\{-26;-20;24\right\}\\\\\\\)

Для полученного отрезка, имеющего направление, найдем модульное значение. Оно и будет площадью параллелограмма, построенного на векторах а и b. 2}=\sqrt{676+400+576}=\sqrt{1652}\\\\\\\)

После извлечения квадратного корня получаем, что площадь параллелограмма равна 40,64.

Пример решения в двухмерном пространстве

Пример

Вычислить площадь параллелограмма, заданного векторами a и b. Их координаты:

\(\left\{4;\;5\right\}\\\\\\\)

\(\left\{-7;\;8\right\}\\\\\\\)

Оба эти вектора лежат в одной плоскости. Поэтому третью их координату принимаем за 0. Тогда площадь данного параллелограмма будет равна:

\(S=\sqrt{32+35}=\sqrt{67}\approx8.2\\\\\\\)

Насколько полезной была для вас статья?

У этой статьи пока нет оценок.

Выделите текст и нажмите одновременно клавиши «Ctrl» и «Enter»

Поиск по содержимому

векторы площадь параллелограмма

Вы искали векторы площадь параллелограмма? На нашем сайте вы можете получить ответ на любой математический вопрос здесь. Подробное решение с описанием и пояснениями поможет вам разобраться даже с самой сложной задачей и выразить площадь проекции параллелограмма на векторах, не исключение. Мы поможем вам подготовиться к домашним работам, контрольным, олимпиадам, а так же к поступлению в вуз. И какой бы пример, какой бы запрос по математике вы не ввели — у нас уже есть решение. Например, «векторы площадь параллелограмма».

Применение различных математических задач, калькуляторов, уравнений и функций широко распространено в нашей жизни. Они используются во многих расчетах, строительстве сооружений и даже спорте. Математику человек использовал еще в древности и с тех пор их применение только возрастает. Однако сейчас наука не стоит на месте и мы можем наслаждаться плодами ее деятельности, такими, например, как онлайн-калькулятор, который может решить задачи, такие, как векторы площадь параллелограмма,выразить площадь проекции параллелограмма на векторах,вычислите площадь параллелограмма построенного на векторах,вычислить диагонали и площадь параллелограмма построенного на векторах,вычислить площадь параллелограмма построенного на векторах,вычислить площадь параллелограмма построенного на векторах a и b,вычислить площадь параллелограмма построенного на векторах a и b онлайн,вычислить площадь параллелограмма построенного на векторах а и b,вычислить площадь параллелограмма построенного на векторах а и в,вычислить площадь параллелограмма построенного на векторах и,как вычислить площадь параллелограмма построенного на векторах,как найти площадь параллелограмма построенного на векторах,как найти площадь параллелограмма построенного на векторах а и в,найдите площадь параллелограмма построенного на векторах,найти высоту параллелограмма построенного на векторах,найти площадь параллелограмма диагоналями которого служат векторы,найти площадь параллелограмма построенного на векторах,найти площадь параллелограмма построенного на векторах онлайн,обчислити площу паралелограма побудованого на векторах,онлайн калькулятор площадь параллелограмма построенного на векторах,онлайн найти площадь параллелограмма построенного на векторах,параллелограмм построен на векторах a и b,площадь параллелограмма векторы,площадь параллелограмма на векторах,площадь параллелограмма по векторам,площадь параллелограмма построенного на векторах,площадь параллелограмма построенного на векторах найти онлайн,площадь параллелограмма построенного на векторах онлайн калькулятор,площадь параллелограмма через вектора,площадь параллелограмма через векторы,пользуясь параллелограммом построенным на векторах a и b,построить параллелограмм на векторах.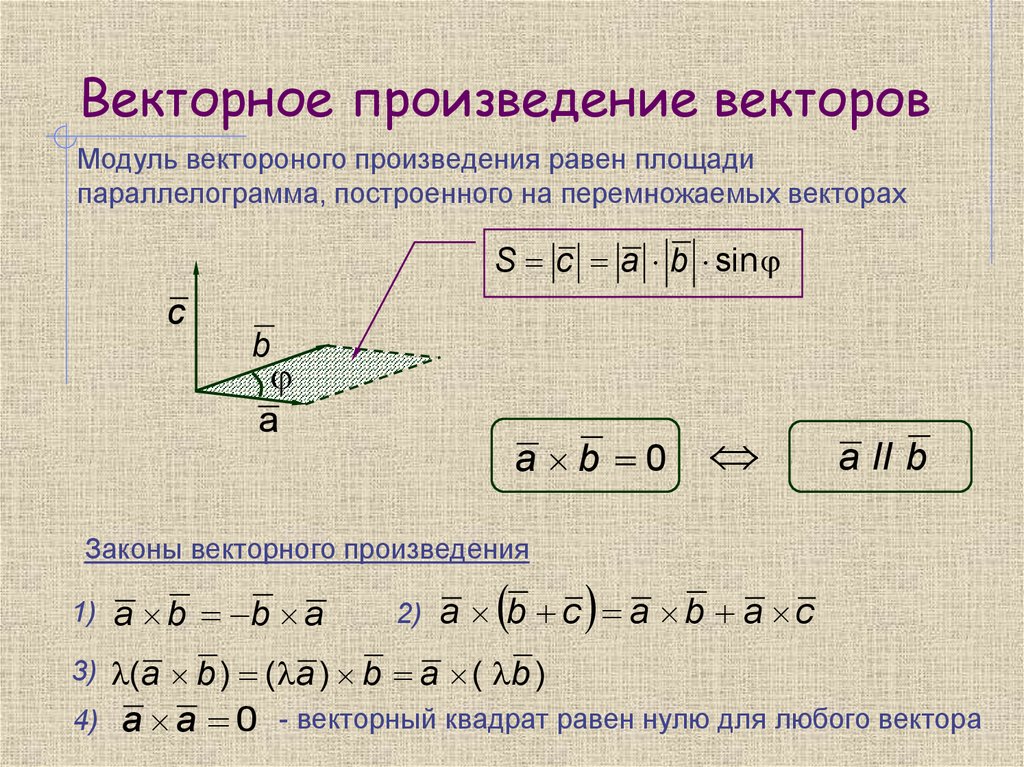

На этой странице вы найдёте калькулятор, который поможет решить любой вопрос, в том числе и векторы площадь параллелограмма. Просто введите задачу в окошко и нажмите «решить» здесь (например, вычислите площадь параллелограмма построенного на векторах).

Решить задачу векторы площадь параллелограмма вы можете на нашем сайте https://pocketteacher.ru. Бесплатный онлайн решатель позволит решить онлайн задачу любой сложности за считанные секунды. Все, что вам необходимо сделать — это просто ввести свои данные в решателе. Так же вы можете посмотреть видео инструкцию и узнать, как правильно ввести вашу задачу на нашем сайте. А если у вас остались вопросы, то вы можете задать их в чате снизу слева на странице калькулятора.

Площадь параллелограмма

Площадь параллелограмма

Часть 3:

Параллелограммы и треугольники

Даны два вектора u и v с общим начальная точка, множество конечных точек векторов s u + t v для 0 £ s , t £ 1 определяется как параллелограмм охватывает u и против .

Мы можем исследовать параллелограмм, натянутый на два вектора в двумерной системе координат. То есть, поскольку системы координат являются плодом нашего коллективного воображения, мы можем вообразить параллелограмм, натянутый на два вектора, находится в системе координат

x’ y’ , где ось x’ параллельна у а ось y’ находится в той же плоскости, что и u и против

(Нажмите и перетащите конечную точку стрелки. Углы указаны в градусах.)

Поскольку и = || и || i и v = || против || ( cos(q) i + sin(q) j ) в системе координат x’ y’ их векторное произведение равно

|| и || || против || ( cos( q) i × i + sin( q) i × j ) || и || || против || sin(q) к

Это приводит к следующей теореме:

Теорема 3. 3: Если q — угол, образованный u и v , то

|| u × v || = || и || || против || sin(q)

Рассмотрим два приложения теоремы 3.3. Во-первых, если и и v параллельны, тогда q = 0 и u × v = 0.

Во-вторых, параллелограмм, натянутый на и и на , можно разрезать на две части. части, образующие прямоугольник с высотой || против || sin( q) и основание || и || ,

Таким образом, площадь параллелограмма, образованного и и и , равна || и |||| против || грех(q) . Действительно, имеем следующее:

Последний результат следует из того, что и — и делят пополам параллелограмм, образованный и и

и .

ПРИМЕР 5    Найдите площадь треугольника с вершинами P ₁ ( 2,2) , P ₂ ( 4,4) , и P _{3 ( 6, ) 3 .}

Решение: Легко видеть, что u = б2,2 с и v = б 4,-1 с . Как векторов в R ³ , имеем u = б2,2,0 с и v = а 4,-1,0 с . Таким образом, их векторное произведение равно

а 0,0, 2·( -1) -4·2 – 0,0,-10 –

Так как треугольник имеет половину площади параллелограмма, образованного u и v , площадь треугольника

Площадь = || u × v || =   0 2 +0 2 +(-10) 2 = 5   единиц 2

ПРИМЕР 6    Найдите площадь треугольника с вершинами P ₁ (3,0,2) , P ₂ (4,6,1) и P 3 1 5,4) .

Решение: Для этого сначала построим векторы u и против :

и  =   П 1 П 2   = б4-3,6-0,1-2 с = а 1,6,-1 № v = Р 1 Р 3   = В0-3,5-0,4-2 с = б-3,5,2 №

В качестве векторов в R ³ теперь мы имеем u = б2,2,0 с и v = а 4,-1,0 с . Таким образом, их векторное произведение равно

. 6·2-5·(-1),(-1)·(-3)-2·1,1·5-(-3)·6 – 17,1,23 –

Поскольку треугольник имеет половину площади параллелограмма, образованного и и и , площадь треугольника равна

Площадь = || u × v || =   17 2 +2 2 +23 2 = 14,335   единиц 2

Рисунок Maple/Javaview

Проверьте свои знания: Какова площадь параллелограмма, натянутого на u и против в примере 6?

Перекрестное произведение — Math Insight

Есть два способа получить произведение пары векторов. Одним из таких методов умножения является перекрестное произведение на , которому посвящена эта страница. Другое умножение — скалярное произведение, которое мы обсуждаем на другой странице.

Перекрестное произведение определено только для трехмерных векторов. Если $\vc{a}$ и $\vc{b}$ — два трехмерных вектора, то их векторное произведение, записанное как $\vc{a} \times \vc{b}$ и произносимое как «a cross b , — еще один трехмерный вектор. Мы определяем этот вектор перекрестного произведения $\vc{a} \times \vc{b}$ следующими тремя требованиями:

1. $\vc{a} \times \vc{b}$ — вектор, перпендикулярный оба $\vc{a}$ и $\vc{b}$.
2. Величина (или длина) вектора $\vc{a} \times \vc{b}$, записанная как $\|\vc{a} \times \vc{b}\|$, представляет собой площадь параллелограмм натянутый на $\vc{a}$ и $\vc{b}$ (т.е. параллелограмм, смежные стороны — это векторы $\vc{a}$ и $\vc{b}$, как показано на рисунке ниже).
3. Направление $\vc{a} \times \vc{b}$ определяется правило правой руки. (Это означает, что если мы согнем пальцы правой рукой от $\vc{a}$ до $\vc{b}$, затем большой палец указывает на направление $\vc{a} \times \vc{b}$.)

На приведенном ниже рисунке показано, как с помощью тригонометрии мы можем вычислить, что площадь параллелограмм, натянутый на $\vc{a}$ и $\vc{b}$, является \начать{выравнивать*} \|\vc{а}\| ~ \|\vc{b}\| \sin\тета, \конец{выравнивание*} где $\тета$ угол между $\vc{a}$ и $\vc{b}$. На рисунке показан параллелограмм с основанием длиной $\|\vc{b}\|$ и перпендикулярная высота $\|\vc{a}\| \sin\тета$.

Эта формула показывает, что величина векторного произведения равна наибольшее, когда $\vc{a}$ и $\vc{b}$ перпендикулярны. С другой стороны, если $\vc{a}$ и $\vc{b}$ параллельны или любой из векторов является нулевой вектор, то векторное произведение является нулевым вектором. (Это хороший Дело в том, что в этих случаях мы получаем нулевой вектор, так что приведенное выше определение по-прежнему имеет смысл. Если векторы параллельны или один вектор является нулевым вектором, тогда не существует уникальной линии перпендикулярно обоим $\vc{a}$ и $\vc{b}$. Но так как есть только один вектор нулевой длины, определение по-прежнему однозначно определяет перекрестное произведение.)

Ниже приведен апплет, который помогает проиллюстрировать, как перекрестное произведение работает. Хотя, по общему признанию, трудно манипулировать точным образом, вы можете убедиться, что перечисленные выше свойства перекрестное произведение удовлетворяется вектором перекрестного произведения, показанным на апплет.

Загрузка апплета

Перекрестное произведение. Вектор $\color{red}{\vc{c}}$ (красный) является векторным произведением векторов $\color{blue}{\vc{a}}$ (синим) и $\color{green}{\vc{b}}$ (зеленым цветом), $\color{red}{\vc{c}} = \color{blue}{\vc{a}} \times \color{ зеленый}{\vc{b}}$. Параллелограмм, образованный параллелограммом $\color{blue}{\vc{a}}$ и $\color{green}{\vc{b}}$, розовый на той стороне, где перекрестное произведение $\color{red}{\ точки vc{c}}$ и фиолетовый цвет на противоположной стороне. Используя мышь, вы можете перетаскивать кончики стрелок векторов $\color{blue}{\vc{a}}$ и $\color{green}{\vc{b}}$, чтобы изменить эти векторы. Посмотрите, как векторное произведение $\color{red}{\vc{c}}$ и параллелограмм изменяются в ответ. (Вы не можете изменить вектор красного перекрестного произведения $\color{red}{\vc{c}}$ напрямую.) Трехмерную перспективу этого графика будет легче воспринимать, если вы будете вращать фигуру, перетаскивая ее рукой. мышь.

Дополнительная информация об апплете.

Обратите внимание, что площадь параллелограмма (и, следовательно, величина векторного произведения) стремятся к нулю при приближении $\vc{a}$ и $\vc{b}$ параллельный (где термин «параллельный» также включает то, что вы может считаться антипараллельным). Вы также можете убедиться, что апплет демонстрирует $\vc{b} \times \vc{a} = — \vc{a} \times \vc{b}$ и $\vc{a} \times \vc{a} = \vc{0}$, которые являются важными свойствами креста. продукт.

Геометрическое определение перекрестного произведения полезно для понимания его свойств.