Вычислить пределы онлайн с подробным решением: Решение пределов · oнлайн с подробным решением

alexxlab / / Разное

Содержание

Правило Лопиталя ℹ️ для вычисления пределов, примеры с подробным решением

Общие сведения

Важным понятием в высшей математике является определение бесконечности. Эта неопределённость обозначается символом ∞. Когда её упоминают, то имеют в виду как бесконечно малое число, так и большое. Для записи предела функций используется знак лимита, например, lim 0k (y). В нижней части указывается аргумент со стрелочкой, обозначающей, к чему именно стремится неопределённость. Если предел известный, то он называется конечным, в ином случае — бесконечным.

Когда нельзя установить, является ограничение бесконечным или конечным, то говорят, что предела для рассматриваемой функции не существует. Это возможно, например, когда ограничение тригонометрической функции стремится к бесконечности. Существует несколько способов вычисления пределов: правило Лопиталя, формулы Тейлера, графический метод, подставление неизвестного в функцию.Указанные способы можно применять для нахождения того или иного предела, но для неопределённости вида 0/0 или ∞/∞, а также вычисления отношений бесконечно малых или больших выражений лучше всего использовать закон Лопиталя.

Состоит он из двух правил:

  • Для бесконечно малых величин. Когда функции k (y) и d (y) можно дифференцировать в некоторой области точки, исключая саму её, при этом в этой окрестности производная выражения неравна нулю, а пределы этих функций равны нулю, то отношение ограничения этих функций будет равно пределу отношения их производных.
  • Для бесконечно больших значений. Если две функции k (y) и d (y) можно дифференцировать по окрестности взятой точки, но при этом её саму исключить, учитывая, что в рассматриваемой окрестности производная d (y) не равняется нулю, то когда функции в этой точке равны бесконечности, предел отношения этих выражений тождественен отношению их производных.

Другими словами, смысл теоремы Лопиталя заключается в том, что когда нужно найти ограничение для двух функций, отношение которых даёт неопределённость 0/0 или ∞/∞, то можно взять производные этих выражений и найти их отношение. Это действие приведёт к получению искомого ответа.

Метод позволяет упростить вычисление сложных показательных степенных функций. Его можно применять и при умножении неопределённостей или их вычитании. Например, 0 * ∞, ∞ — ∞.

Доказательство правила

Лопиталь после знакомства с Бернулли смог систематизировать метод Иоганна и издать в 1696 году книгу «Анализ бесконечно малых», где подробно изложил способы решения задач с неопределённостями. Математически его описание состоит из четырёх пунктов:

  • lim k (y) = lim d (y) = 0 (∞).
  • Графики k (y) и d (y) приближаются к линейному виду.
  • d (y)’ ≠ 0.
  • lim k (y)’ / d (y)’ = lim k (y) / d (y).

Пусть имеется два дифференцируемых выражения, при этом d (y) во всех точках имеет не нулевую производную. При y, стремящемся к a, d стремится к бесконечности. Если предел отношения производных конечного предела или бесконечного равняется числу L, тогда ограничение отношений производных этих функций также будет тождественно этому числу. То есть lim k (y) / d (y) = L, при y → a. Исходя из определения Гейне и Коши, рассматривать можно только монотонные последовательности, которые стремятся к a.

Взяв произвольный ряд, который может расти yn → a, верно утверждать, что в соответствии со следствием теоремы Дарбу и условием d (y)’ ≠ 0, рассматриваемая функция будет строго монотонной. А это означает, что последовательность d (yn) будет такой же. В тоже время из условия lim d (y) = ∞ следует, что d (yn) → ∞. При этом бесконечность может быть как со знаком минус, так и плюс.

Рассмотрим теорему Штольца, а именно отношение: (k (yn+1) — k (yn)) / (d (yn+1) — d (yn)) = k'(Cn) / d'(Cn) = L. Из неё следует, что k (y) / d (y) → L. То есть всегда найдётся такая точка Cn, которая будет принадлежать множеству (Yn+1,Yn). Так как множество стремится к L, то и точка, принадлежащая ему, тоже будет приближаться к L. Поэтому можно утверждать, что и выражение lim k (y) / d (y) → L.

Аналогичным образом первому доказывается и второй случай, когда lim k (y) = lim d (y) = 0. Если предел отношения производных будет L, то ограничения отношений функций будет также равняться этому числу. Из теоремы Дарбу и монотонности получим, что d (Yn) → 0, кроме того k (Yn) → 0. Используя правило Штольце, можно будет утверждать, что k (y) / d (y) → L.

Но на практике часто для решения примеров правило Лопиталя оказывается недостаточным. Это справедливо для заданий, в которых y стремится не к конечному числу, а к бесконечному. Поэтому для таких задач используется следствие из теоремы. Согласно ему, при k → 0 и d → 0, а y → + ∞. Тогда существует предел lim k'(y) / d'(y) = AЄR и предел отношений lim k (y) / d (y) = A. Этот вспомогательный закон очень важен и то же может быть доказан.

Следствие из утверждения

Перед доказательством следствия нужно условиться, что в выражении a будет всегда больше либо равно единице. Это возможно исходя из того, что если a будет меньше единицы, то доказывать нужно будет правило только от единицы до плюс бесконечности. Кроме этого, необходимо ввести замену вида t = 1/y. Она необходима, так как во многом облегчает сведение доказательства к теореме Лопиталя.

Пусть имеется функция K (t), равная k, и D (t), равная d. При этом аргумент последней будет 1/t. Так как по условию правила функции k и d определены на интервале от a до плюс бесконечности, то можно сказать, что функции K и D известны на интервале от нуля до единицы, делённом на a. Это верно из-за того, что если в исходной функции k и d икс подходил достаточно близко к плюс бесконечности, то в силу сделанной ранее замены t будет приближаться к нулю. Если же икс близок к a, то t будет приближаться к значению 1/a.

Так как a больше либо равняется единице, то интервал от нуля до единицы, делённой на a, будет определён корректно. Чтобы воспользоваться теоремой Лопиталя, нужно доказать, что предел lim K'(t) / D'(t) при t, стремящемся к нулю, равняется A. В силу того, что K (t) = k (1/t) и D (t) = d (1/t), можно написать: lim K'(t) / D'(t) = lim k'(1/t)’ / d'(1/t)’ .

Теперь нужно воспользоваться теоремой о производной композиции, условия которой выполнены. Вначале нужно взять производную внутренней функции, а затем внешней. Должно получиться следующее выражение: lim -1/ t 2 k ‘(1/ t) / (-1/ t 2) * d ‘ (1/ t) = lim K ‘(t) / D ‘(t) = lim k ‘(y)/ d (y) = A.

Отсюда можно утверждать, что предел отношений K'(t) / D'(t) будет равняться A. Все условия теоремы Лопиталя выполнены. А это значит, что существует предел отношения функций при t, стремящемся к нулю, равный A. Теперь можно снова применить теорему о пределе композиций и от переменной t перейти обратно к иксу: lim K (t)/D (t) = lim k (y)/(d (y) = A.

Таким образом можно сделать вывод, что требуемое утверждение верно. Использование правила и следствия позволяет выполнить быстрый расчёт неопределённости 0/0 или ∞/∞.

При этом другого вида выражение можно свести к этой неопределённости. Это намного упрощает работу, особенно если необходимо логарифмировать или возводить в степень.

Решение примеров

Закрепить правило лучше всего на соответствующих примерах. Существуют типовые задания, чаще всего встречающиеся на контрольных работах. Например, требуется найти предел отношения натурального логарифма от тангенса икс к котангенсу два икс, когда неизвестное стремится к p /4. Помощь в решении окажет правило Лопиталя, которое при сравнении с альтернативными методами окажется на порядок проще.

Для того чтобы понять, какого вида неопределённость в задании, нужно в числитель и знаменатель подставить p/4. Тогда: ln td p /4 = ln 1 = 0 и ctd p /2 = 0. По правилу можно свести нахождение предела функций к вычислению их производных. Искомый предел: A = lim (lntdy ‘) / (ctd 2 y)’ = lim (ctdy * 1/ cos

2 y) / 2 (-1/ sin 2 2 y) = lim (-sin 2 y)(2 * siny * cosy) = (-½) * lim (sin 2 2 y / siny * cosy) = — ½ * 1/½ = -1. Таким образом, решение будет равняться минус единице.

Пусть есть выражение вида: lim y½ (p — 2 arctd √ y) = A. Нужно определить предел при иксе, стремящемся к плюс бесконечности. Чтобы воспользоваться правилом, исходное выражение нужно привести к дробному виду. Для этого выражение можно переписать как lim (p — 2 arctd √ y) / y½. В этом случае имеет место неопределённость 0/0. Поэтому можно рассматривать отношение производной делимого на делитель: A = lim (2 *(1/1+ y) * ½ * y -½ ) / ½ * y -3/2 = lim 2y/(1+y) = 2 lin 1 /(1+ 1/ y) = 2.

Замечательным случаем является неопределённость вида ∞/∞. Например, требуется найти предел lim k (y) при иксе, стремящемся к бесконечности, где функция k (y) = y /ey. По теореме Лопиталя A = lim (y)’ / (ey)’, а это выражение есть не что иное, как lim 1/ey, равняющийся нулю. Теперь можно рассмотреть пример сложнее.

Пусть дано выражение нормальной функции со степенью: lim yy = A, где A = lim k (y).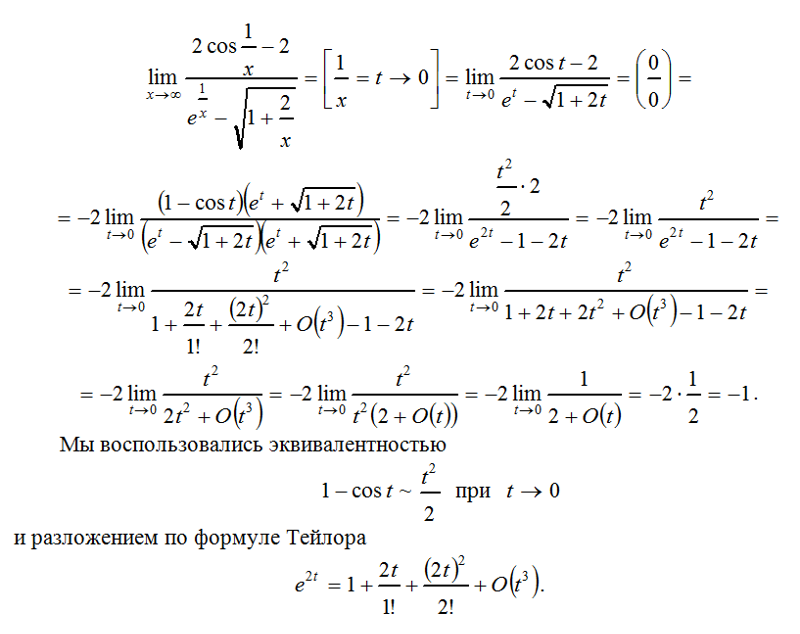 Проэкспоненцируя эту функцию, выражение можно привести к виду: yy = ey *lny. Если найти, к чему стремится показатель экспоненты, то это и будет решением рассматриваемого примера. Можно записать: lim y * lny = lim lny /1/ y = lim (1/ y)/(-1/ y 2 ) = 0. Если предел в показателе экспоненты стремится к нулю, то можно написать, что он будет равняться e0, то есть единице. А это и будет искомый предел: lim k (y) = 1 при иксе, стремящемся к плюс бесконечности.

Закон Лопиталя является хорошим помощником при вычислении особо экзотических пределов. При этом можно попробовать составить выражение, отвечающее условиям правила и из неявного вида функции. Для этого можно использовать раскрытие скобок, дополнительно умножить или разделить функцию на однородный многочлен.

Использование онлайн-калькулятора

Не всегда задания, попадающиеся на практике, довольно легко привести к условию, отвечающему правилу. Да и нередко сама функция настолько умудрённая, что для определения производной понадобится не только проявить внимание и усидчивость, но и затратить довольно много времени. Поэтому в таких случаях есть резон решать задания на онлайн-калькуляторе с подробным решением. Правило Лопиталя отлично поддаётся автоматизированному вычислению.

Такую услугу предлагают более десятка специализированных на математических расчётах сайтов. Доступ к вычислениям предоставляется полностью бесплатно. От пользователя даже не требуется регистрации и указания персональных данных. Работают они на основе алгоритмов, заложенных в программный код используемого онлайн-приложения. Пользователю нужно лишь только подключение к интернету и любой веб-обозреватель.

Все его действия сводятся к введению в предложенную форму условия примера и нажатия кнопки «Рассчитать». После этого программа автоматически вычислит ответ и выведет его на дисплей. При этом в большинстве случаев вместе с ответом приложение отобразит пошаговый расчёт с комментариями. Это позволит потребителю не просто получить готовый ответ, но и разобраться в решении.

Из наиболее популярных сайтов можно выделить следующую пятёрку:

  • Math.semestr.
  • Kontrolnaya-rabota
  • Planetcalc.
  • Math34.
  • Webmath.

Все эти сайты имеют интуитивно понятный интерфейс на русском языке. Кроме предоставления услуги онлайн-калькулятора, на их страницах содержится вся необходимая теория, помогающая понять, как происходит нахождение ответа. А также приведены несколько типовых примеров с подробным решением.

Пользоваться такими сайтами сможет даже пользователь, ничего не понимающий в математическом анализе. Но решая различные примеры, со временем он поймёт суть идеи правила и сможет самостоятельно вычислять пределы функций. При этом такие сайты являются отличным подспорьем как инженерам, проводящим сложные вычисления, так и студентам, проверяющим свои навыки.

Высшая математика онлайн — Стоматология в Химках

Онлайн калькулятор высшей математики

Вы искали высшая математика онлайн? На нашем сайте вы можете получить ответ на любой математический вопрос здесь. Подробное решение с описанием и пояснениями поможет вам разобраться даже с самой сложной задачей и калькулятор онлайн математика, не исключение. Мы поможем вам подготовиться к домашним работам, контрольным, олимпиадам, а так же к поступлению в вуз. И какой бы пример, какой бы запрос по математике вы не ввели — у нас уже есть решение. Например, «высшая математика онлайн».

Применение различных математических задач, калькуляторов, уравнений и функций широко распространено в нашей жизни. Они используются во многих расчетах, строительстве сооружений и даже спорте. Математику человек использовал еще в древности и с тех пор их применение только возрастает. Однако сейчас наука не стоит на месте и мы можем наслаждаться плодами ее деятельности, такими, например, как онлайн-калькулятор, который может решить задачи, такие, как высшая математика онлайн, калькулятор онлайн математика, калькуляторы по математике онлайн, математичний калькулятор, онлайн калькулятор с подробным решением, решение онлайн высшая математика, решить функцию. На этой странице вы найдёте калькулятор, который поможет решить любой вопрос, в том числе и высшая математика онлайн. Просто введите задачу в окошко и нажмите «решить» здесь (например, калькуляторы по математике онлайн).

Где можно решить любую задачу по математике, а так же высшая математика онлайн Онлайн?

Решить задачу высшая математика онлайн вы можете на нашем сайте https://pocketteacher. ru. Бесплатный онлайн решатель позволит решить онлайн задачу любой сложности за считанные секунды. Все, что вам необходимо сделать — это просто ввести свои данные в решателе. Так же вы можете посмотреть видео инструкцию и узнать, как правильно ввести вашу задачу на нашем сайте. А если у вас остались вопросы, то вы можете задать их в чате снизу слева на странице калькулятора.

Наш искусственный интеллект решает сложные математические задания за секунды.

Мы решим вам контрольные, домашние задания, олимпиадные задачи с подробными шагами. Останется только переписать в тетрадь!

Наш искусственный интеллект решает сложные математические задания за секунды.

Www. pocketteacher. ru

11.08.2020 18:51:18

2020-08-11 18:51:18

Источники:

Https://www. pocketteacher. ru/topic/vysshaja-matematika-onlajn

Решение задач онлайн » /> » /> .keyword { color: red; }

Онлайн калькулятор высшей математики

Решение Ваших математических задач в онлайн режиме. Бесплатная версия программы предоставляет Вам только ответы. Если вы хотите увидеть полное решение, Вы должны зарегистрироваться для полной версии.

Другие программы

Основы математики

Онлайн программа решения математических задач предлагает Вам решение в режиме онлайн задач с дробями, корнями, метрическими преобразованиями.
Вы можете найти площадь и объем прямоугольника, окружности, треугольника, трапеции, куба, цилиндра, конуса, пирамиды, шара.
Вы можете упростить, найти значение, объединять и умножать выражения.

Онлайн программа решения задач курса предварительной алгебры (геометрии)

Вы можете решать все задачи с основного раздела математики а также координатных задач, простых уравнений, неравенств, упрощать выражения.
Вы можете подсчитывать выражения, объединить выражения и умножать / делить выражения.

Онлайн программа решения задач по алгебре

Мы рекомендуем Вам зарегистрироваться для этой онлайн программы.
Решите Ваши задачи (уравнения, неравенства, радикалы, построение графиков, решение полиномов) в онлайн режиме.
Если Ваша домашняя работа включает в себя математические уравнения, неравенства, функции, многочлены, матрицы, значит это правильный выбор.

Онлайн программа решения задач по тригонометрии

Находит значения всех типов выражений (синус, косинус, тангенс, котангенс, секанс, косеканс), уравнений, неравенств.
Строит графики тригонометрических функций.
Тригонометрия прямоугольного треугольника.

Онлайн программа решения задач курса предварительной алгебры

Включает в себя все вышеперечисленное функции плюс нахождение пределов (LIM), сумм, матриц.

Онлайн программа решения задач курса высшей математики

Решение задач c определенными, неопределенными интегралами.

Онлайн программа решения статистических задач

Решайте задач с нахождением вероятности, комбинаторные задачи. Статистические задачи — найти среднее (арифметическое, геометрическое, квадратическое) значение, распределение, нормальное распределение, т-распределение.
Онлайн программа успешно проводит тестирование статистических гипотез

© 2005 — 2022
Копирование запрещено! В случае копирования администрация сайта обратится в компетентные органы.

Основы математики

Онлайн программа решения математических задач предлагает Вам решение в режиме онлайн задач с дробями, корнями, метрическими преобразованиями.
Вы можете найти площадь и объем прямоугольника, окружности, треугольника, трапеции, куба, цилиндра, конуса, пирамиды, шара.
Вы можете упростить, найти значение, объединять и умножать выражения.

Вы можете решать все задачи с основного раздела математики а также координатных задач, простых уравнений, неравенств, упрощать выражения.
Вы можете подсчитывать выражения, объединить выражения и умножать / делить выражения.

Находит значения всех типов выражений синус, косинус, тангенс, котангенс, секанс, косеканс, уравнений, неравенств.

Www. math20.com

08.06.2017 5:48:30

2017-06-08 05:48:30

Источники:

Https://www. math20.com/ru/reshenie-zadach-onlain/

Решение математики онлайн. Онлайн калькуляторы по математике » /> » /> .keyword { color: red; }

Онлайн калькулятор высшей математики

Здесь представлены онлайн калькуляторы для решения различных задач по математике. Охватываются такие области математики, как интегралы, производные, пределы, операции с матрицами, задачи по аналитической геометрии, построение графиков онлайн и т. д..

В разделе «Онлайн сервисы» вам предоставлена возможность решать онлайн интегралы, брать производные, пределы, считать ряды практически для любых функций. Решение задач производится автоматически программой и является быстрым и абсолютно бесплатным.

Все калькуляторы выдают ответ с подробным решением. Считайте легко, быстро и надежно вместе с нами.

С помощью онлайн сервиса получите правильный ответ и проверьте своё решение!

    Правила ввода функций и констант Инженерный калькулятор Математический анализ
      Вычислить неопределенный интеграл Вычислить определенный интеграл Вычислить двойной интеграл Вычислить производную Вычислить предел функции Вычислить сумму ряда
      Найти определитель матрицы Найти обратную матрицу
      Решение дифференциальных уравнений Решение квадратных уравнений Решение системы линейных уравнений (метод подстановки) Решение системы линейных уравнений (метод Гаусса) Решение системы линейных уравнений (метод Крамера) Решение системы линейных уравнений (матричный метод)
      Уравнение прямой по двум точкам Уравнение плоскости по трем точкам Расстояние между точкой и прямой Расстояние между точкой и плоскостью
      Скалярное произведение векторов Векторное произведение векторов Смешанное произведение векторов Проверить, образуют ли вектора базис Разложить вектор по базису
      Построить график онлайн

    Закажите работу

    Компания Matematikam. ru предлагает вам свои услуги по решению контрольных работ по математике, физике, теории вероятности!

    Контрольные работы на заказ!

    Только у нас вы найдете одновременно низкие цены, короткие сроки и высокое качество исполнения контрольных работ на заказ. Мы решаем контрольные работы любой сложности. Наши специалисты имеют большой опыт и сердняя оценка, выставляемая клиентами за выполненные работы, составляет 9.75 баллов.

    Заказать работу по физике

    Закажите контрольную по физике или математике на Matematikam. ru и вы получите отличный сервис, полное сопровождение заказа, бесплатные доработки и ответы по работе на любые ваши вопросы и уточнения. Закажите контрольную работу у нас и вы убедитесь — как просто и безопасно может быть получение решения сложной и трудоемкой работы!

    Здесь представлены онлайн калькуляторы для решения различных задач по математике. Охватываются такие области математики, как интегралы, производные, пределы, операции с матрицами, задачи по аналитической геометрии, построение графиков онлайн и т. д..

    В разделе «Онлайн сервисы» вам предоставлена возможность решать онлайн интегралы, брать производные, пределы, считать ряды практически для любых функций. Решение задач производится автоматически программой и является быстрым и абсолютно бесплатным.

    Все калькуляторы выдают ответ с подробным решением. Считайте легко, быстро и надежно вместе с нами.

    С помощью онлайн сервиса получите правильный ответ и проверьте своё решение!

      Правила ввода функций и констант Инженерный калькулятор Математический анализ
        Вычислить неопределенный интеграл Вычислить определенный интеграл Вычислить двойной интеграл Вычислить производную Вычислить предел функции Вычислить сумму ряда
        Найти определитель матрицы Найти обратную матрицу
        Решение дифференциальных уравнений Решение квадратных уравнений Решение системы линейных уравнений (метод подстановки) Решение системы линейных уравнений (метод Гаусса) Решение системы линейных уравнений (метод Крамера) Решение системы линейных уравнений (матричный метод)
        Уравнение прямой по двум точкам Уравнение плоскости по трем точкам Расстояние между точкой и прямой Расстояние между точкой и плоскостью
        Скалярное произведение векторов Векторное произведение векторов Смешанное произведение векторов Проверить, образуют ли вектора базис Разложить вектор по базису
        Построить график онлайн

      Вычислить определенный интеграл.

      Matematikam. ru

      16.03.2018 16:45:43

      2018-03-16 16:45:43

      Источники:

      Https://matematikam. ru/calculate-online/

Раздвигая границы транспорта и технологий

Наша платформа Ultium обеспечивает гибкость, мощность и дальность действия. Мы делаем электромобили для всех.

Посмотрите, как

Имитация аккумулятора 1 и GMC Hummer EV 2 показаны.

  1. Показана имитация батареи. Не пытайтесь. Соблюдайте все предупреждения на этикетках аккумуляторов.
  2. Фактическая серийная модель может отличаться. Начальная доступность Осень 2021.
  3. Фактическая серийная модель может отличаться. Первоначальная доступность в первой половине 2022 г.

Сегодня мы строим безопасное и


более устойчивое будущее.

  • Безопасность транспортных средств

    Благодаря исследованиям, технологиям и пропаганде мы продвигаем наше видение будущего без аварий.

  • Электрификация

    Наша новая платформа Ultium поможет каждому пересесть на электромобиль и приблизить мир к полностью электрическому будущему.

  • Social Impact

    Мы стремимся стать самой инклюзивной компанией в мире, и мы не остановимся, пока не добьемся этого.

Показан демонстрационный грузовик. Фактическое производство будет отличаться. Silverado EV 2024 модельного года будет доступен осенью 2023 года. Показан смоделированный энергетический продукт. Возможны изменения.

GM Energy: мощность, когда она вам нужна

Благодаря подключенным продуктам и услугам GM Energy владельцы электромобилей получают больший контроль над управлением домашним энергопотреблением и расширяют доступ к зарядке электромобилей. Его инструменты и услуги разработаны, чтобы предлагать целостное энергетическое решение для домашних, коммерческих и электрических клиентов, даже помогая смягчить последствия перебоев в подаче электроэнергии в случае необходимости. Ознакомьтесь с решениями GM Energy для клиентов здесь.

Подробнее

Показана опытная модель. Реальная производственная модель может отличаться. Заказы MY23 LYRIQ выполнены. Перейдите на сайт Cadillac.com для получения информации о наличии.

EV LIVE

Узнайте об электромобилях, не выходя из дома

Присоединяйтесь к нам на EV LIVE, пока мы переходим к полностью электрическому будущему. Живите в нашей студии, общайтесь с нашими специалистами по электромобилям и получайте ответы на все свои вопросы об электромобилях в режиме реального времени. Изучите новейшие электромобили GM и все аспекты эксплуатации электромобилей, включая владение, техническое обслуживание, а также домашнюю и общественную зарядку. Независимо от того, где вы находитесь в своем путешествии на электромобиле, эксперты EV LIVE всегда готовы помочь.

Демонстрируются смоделированные, опытные образцы или концептуальные продукты, которые могут быть изменены. Некоторые продукты в настоящее время недоступны или их наличие ограничено. Подробности смотрите на сайтах автомобилей.

Электрификация нашего модельного ряда, по одному удивительному автомобилю за раз

Узнать больше

«Во всем мире один миллиард человек имеет ту или иную форму инвалидности, и это то, с чем большинство из нас столкнется в какой-то момент своей жизни. Поскольку мы стремимся стать самой инклюзивной компанией в мире, вполне логично, что доступность является частью уравнения».

КЭРРИ МОРТОН (она/она) // Главный инженер Центра передового опыта в области доступности

 

Мы ищем искателей приключений и творческих идейных лидеров, которые помогут нам трансформировать мобильность и продвигать полностью электрическое будущее.

  1. Имитация автомобиля. Фактическая производственная модель будет отличаться. Поступит в продажу осенью 2023 г. Показан дополнительный зарядный блок.

Проверка бизнеса | Погоня за бизнесом