Вычислить ранг матрицы с помощью элементарных преобразований онлайн: Онлайн калькулятор. Ранг матрицы

Страница не найдена — ПриМат

По данному адресу ничего не найдено. Попробуйте воспользоваться поиском.

Искать:

© 2012-2016: Нохум-Даниэль Блиндер (11), Анастасия Лозинская (10), Валентин Малявко (8), Елизавета Савицкая (8), Игорь Любинский (8), Юлия Стерлянко (8), Денис Стехун (8), Александр Базан (7), Анна Чалапчий (7), Константин Берков (7), Олег Шпинарев (7), Людмила Рыбальченко (6), Кирилл Волков (6), Татьяна Корнилова (6), Влад Радзивил (6), Максим Швандт (6), Елизавета Снежинская (5), Вадим Покровский (5), Даниил Радковский (5), Влад Недомовный (5), Александр Онищенко (5), Андрей Метасов (5), Денис Базанов (5), Александр Ковальский (5), Александр Земсков (5), Марина Чайковская (5), Екатерина Шибаева (5), Мария Корень (5), Анна Семененко (5), Мария Илларионова (5), Сергей Черкес (5), Алиса Ворохта (5), Валерия Заверюха (5), Игорь Чернега (4), Даниил Кубаренко (4), Ольга Денисова (4), Татьяна Осипенко (4), Яков Юсипенко (4), Ольга Слободянюк (4), Руслан Авсенин (4), Екатерина Фесенко (4), Дмитрий Заславский (4), Алина Малыхина (4), Андрей Лисовой (4), Полина Сорокина (4), Кирилл Демиденко (4), Дмитрий Стеценко (4), Александр Рапчинский (4), Святослав Волков (4), Иван Мясоедов (4), Владислав Стасюк (4), Алёна Гирняк (4), Николай Царев (4), Валентин Цушко (4), Павел Жуков (4), Роман Бронфен-Бова (4), Артём Романча (4), Анна Шохина (4), Иван Киреев (4), Никита Савко (4), Кондрат Воронов (4), Алина Зозуля (4), Иван Чеповский (4), Артем Рогулин (4), Екатерина Мальчик (3), Анатолий Осецимский (3), Иван Дуков (3), Дмитрий Робакидзе (3), Вячеслав Зелинский (3), Данила Савчак (3), Дмитрий Воротов (3), Стефания Амамджян (3), Валерия Сиренко (3), Георгий Мартынюк (3), Виктор Иванов (3), Вячеслав Иванов (3), Валерия Ларикова (3), Евгений Радчин (3), Андрей Бойко (3), Милан Карагяур (3), Александр Димитриев (3), Иван Василевский (3), Руслан Масальский (3), Даниил Кулык (3), Стас Коциевский (3), Елизавета Севастьянова (3), Павел Бакалин (3), Антон Локтев (3), Андрей-Святозар Чернецкий (3), Николь Метри (3), Евелина Алексютенко (3), Константин Грешилов (3), Марина Кривошеева (3), Денис Куленюк (3), Константин Мысов (3), Мария Карьева (3), Константин Григорян (3), Колаев Демьян (3), Станислав Бондаренко (3), Ильдар Сабиров (3), Владимир Дроздин (3), Кирилл Сплошнов (3), Карина Миловская (3), Дмитрий Козачков (3), Мария Жаркая (3), Алёна Янишевская (3), Александра Рябова (3), Дмитрий Байков (3), Павел Загинайло (3), Томас Пасенченко (3), Виктория Крачилова (3), Таисия Ткачева (3), Владислав Бебик (3), Илья Бровко (3), Максим Носов (3), Филип Марченко (3), Катя Романцова (3), Илья Черноморец (3), Евгений Фищук (3), Анна Цивинская (3), Михаил Бутник (3), Станислав Чмиленко (3), Катя Писова (3), Дмитрий Дудник (3), Дарья Кваша (3), Игорь Стеблинский (3), Артем Чернобровкин (3), Виктор Булгаков (3), Дмитрий Мороз (3), Богдан Павлов (3), Игорь Вустянюк (3), Андрей Яроцкий (3), Лаура Казарян (3), Юрий Олейник (2), Кирилл Бондаренко (2), Елена Шихова (2), Татьяна Таран (2), Наталья Федина (2), Настя Кондратюк (2), Никита Гербали (2), Сергей Запорожченко (2), Николай Козиний (2), Георгий Луценко (2), Владислав Гринькив (2), Александр Дяченко (2), Анна Неделева (2), Никита Строгуш (2), Настя Панько (2), Кирилл Веремьев (2), Даниил Мозгунов (2), Андрей Зиновьев (2), Андрей Данилов (2), Даниил Крутоголов (2), Наталия Писаревская (2), Дэвид Ли (2), Александр Коломеец (2), Александра Филистович (2), Евгений Рудницкий (2), Олег Сторожев (2), Евгения Максимова (2), Алексей Пожиленков (2), Юрий Молоканов (2), Даниил Кадочников (2), Александр Колаев (2), Александр Гутовский (2), Павел Мацалышенко (2), Таня Спичак (2), Радомир Сиденко (2), Владислав Шиманский (2), Илья Балицкий (2), Алина Гончарова (2), Владислав Шеванов (2), Андрей Сидоренко (2), Александр Мога (2), Юлия Стоева (2), Александр Розин (2), Надежда Кибакова (2), Майк Евгеньев (2), Евгений Колодин (2), Денис Карташов (2), Александр Довгань (2), Нина Хоробрых (2), Роман Гайдей (2), Антон Джашимов (2), Никита Репнин (2), Инна Литвиненко (2), Яна Юрковская (2), Гасан Мурадов (2), Богдан Подгорный (2), Алексей Никифоров (2), Настя Филипчук (2), Гук Алина (2), Михаил Абабин (2), Дмитрий Калинин (2), Бриткариу Ирина (2), Никита Шпилевский (2), Алексей Белоченко (2), Юлиана Боурош (2), Никита Семерня (2), Владимир Захаренко (2),

РГР по матрицам – Заказать решение расчётно графической работы онлайн

Если у вас нет времени на выполнение заданий по матрицам, вы всегда можете попросить меня, пришлите задания мне в whatsapp, и я вам помогу онлайн или в срок от 1 до 3 дней.

Ответы на вопросы по заказу заданий по матрицам:

Сколько стоит помощь?

• Цена зависит от объёма, сложности и срочности. Присылайте любые задания по любым предметам — я изучу и оценю.

Какой срок выполнения?

• Мне и моей команде под силу выполнить как срочный заказ, так и сложный заказ. Стандартный срок выполнения – от 1 до 3 дней. Мы всегда стараемся выполнять любые работы и задания раньше срока.

Если требуется доработка, это бесплатно?

• Доработка бесплатна. Срок выполнения от 1 до 2 дней.

Могу ли я не платить, если меня не устроит стоимость?

• Оценка стоимости бесплатна.

Каким способом можно оплатить?

• Можно оплатить любым способом: картой Visa / MasterCard, с баланса мобильного, google pay, apple pay, qiwi и т.д.

Какие у вас гарантии?

• Если работу не зачли, и мы не смогли её исправить – верну полную стоимость заказа.

В какое время я вам могу написать и прислать задание на выполнение?

• Присылайте в любое время! Я стараюсь быть всегда онлайн.

Ниже размещён теоретический и практический материал, который вам поможет разобраться в теме

вычисления и решения Матриц, если у вас есть желание и много свободного времени!

Содержание:

1. Ответы на вопросы по заказу заданий по матрицам:
2. Матрицы
3. РГР 1.
4. РГР 2.
5. Определители. Ранг матрицы
6. РГР 3.
7. РГР 4.
8. Обратная матрица. Матричные уравнения
9. РГР 5.
10. РГР 6.

Матрицы

Матрицей называется прямоугольная таблица, элементами которой могут быть вещественные или комплексные числа. Если состоит из строк и столбцов, говорят о матрице порядка элементы которой обозначаются , где Матрицы с равным числом строк и столбцов называют квадратными матрицами порядка Следом квадратной матрицы называется сумма её диагональных элементов, обозначаемая как

Операции с матрицами определяются через операции с их элементами.

Транспонирование матрицы, или замена местами строк и столбцов:

Умножение матрицы на число определяет новую матрицу Сложение двух матриц возможно лишь для матриц одинакового порядка, в результате Произведение определено для двух матриц с порядками т.е. число столбцов первого сомножителя равно числу строк второго сомножителя, а элемент произведения есть .

Отсюда можно определить степень квадратной матрицы

как кратное умножение матрицы на себя. Для различных матриц при возможности вычисления в общем случае Величина называется коммутатором матриц и Матрицы, для которых называют коммутирующими. Так, всегда коммутируют между собой две диагональные квадратные матрицы одного порядка. При использовании ряда Тейлора для функций возможно вычисление функций от квадратных матриц через соответствующие линейные комбинации, образующие ряд.

Некоторые виды матриц имеет своё собственное обозначение из-за особенностей в структуре расположения своих элементов.

Диагональная матрица имеет ненулевые элементы лишь на главной диагонали, поэтому а все остальные элементы равны нулю. Если все то является единичной матрицей порядка с элементами где символ Кронекера. Симметричная матрица обладает свойством а для антисимметричной матрицы, наоборот, в случае комплексных

элементов вводится операция эрмитового сопряжения сочетающая транспонирование и комплексное сопряжение: где черта

обозначает комплексное сопряжение. Матрицы, обладающие свойством

называются эрмитовыми. Заметим, что диагональные элементы эрмитовой матрицы всегда вещественны, а класс симметричных матриц является подмножеством эрмитовых матриц с вещественными элементами. По аналогии с антисимметричной матрицей вводятся антиэрмитовы матрицы, обладающие свойством

Возможно, вас также заинтересует эта ссылка:

Решение задач по матрицам с примерами онлайн

РГР 1.

Вычислить произведение матриц

• Решение:

Данные матрицы имеют порядки поэтому их произведение есть матрица порядка 1×2. Вычислим её элементы:

следовательно,

Возможно, вас также заинтересует эта ссылка:

Помощь по матрицам онлайн

РГР 2.

Вычислить значение многочлена для матрицы

• Решение:

Разложим вначале многочлен на множители, записав Для матричного аргумента это означает, что — единичная матрица соответствующего порядка. Подставив матрицу данную в условии, получим окончательно

Возможно, вас также заинтересует эта ссылка:

Курсовая работа по матрицам заказать готовую онлайн

Определители.

Ранг матрицы

Определителем, или детерминантом квадратной матрицы порядка называется следующая числовая функция от её элементов: для матрицы первого порядка для матрицы 2-го порядка для матриц 3-го порядка и выше детерминант можно определить по индукции при помощи формулы разложения, или раскрытия по строке:

есть дополнительный минор элемента

(черта здесь не обозначает комплексное сопряжение), представляющий собой определитель порядка составленный из элементов исходной матрицы из которой вычеркнуты строка и столбец. Раскрытие определителя производится аналогично. Матрицы с ненулевым определителем называются невырожденными, или неособыми, а при матрица, строки (столбцы) которой становятся при этом линейно зависимыми, называется вырожденной, или особой.

Основные свойства определителей при операциях с элементами матрицы: при перестановке столбцов (строк) меняет знак, при умножении одной строки (столбца) на число весь умножается на это число. При транспонировании матрицы её определитель не меняется. Определитель также не меняется при операции, когда меняется лишь одна строка (столбец) матрицы, к элементам которой прибавляют элементы другой строки (столбца), умноженные на некоторое число.

Действия над элементами матрицы, при которых не изменяется её определитель, называются элементарным преобразованием матрицы. При вычислении определителей справедливы

также равенства

Минором порядка прямоугольной матрицы называется определитель, составленный из элементов некоторых строк и столбцов этой матрицы, при этом Наивысший порядок минора, отличного от нуля, когда все миноры более высоких порядков равны нулю, называется рангом матрицы и обозначается Любой минор с порядком, равным рангу, называется базисным минором данной матрицы. Строки и столбцы, составляющие базисный минор, называются базисными строками и столбцами, и являются линейно независимыми.

Возможно, вас также заинтересует эта ссылка:

Задачи по матрицам с решением

РГР 3.

Вычислить определитель порядка:

• Решение:

Используем метод элементарных преобразований. Вычтем первую строку матрицы из всех остальных, при этом определитель не изменится: Полученный детерминант есть определитель верхней треугольной матрицы, который равен произведению элементов, стоящих на главной диагонали, т.е.

РГР 4.

Показать, что определитель эрмитовой матрицы всегда является вещественным числом.

• Решение:

Эрмитова матрица обладает свойством кроме того, определитель любой квадратной матрицы не меняется при транспонировании,

а комплексное сопряжение элементов матрицы приводит к комплексному сопряжению всего определителя, Комбинируя все эти свойства, мы получаем, что для эрмитовой матрицы т.е. число, равное , является вещественным.

Обратная матрица. Матричные уравнения

Для невырожденной квадратной матрицы можно ввести понятие обратной матрицы удовлетворяющей равенству Элементы обратной матрицы находятся по формуле

Из определения обратной матрицы следует, что При решении матричных уравнений вида

решение находится в виде где есть обратная матрица к матрице

РГР 5.

Найти обратную матрицу для матрицы

• Решение:

Вначале вычисляем определитель матрицы, который в данном случае равен двум. Следовательно, матрица не вырождена и имеет обратную. Далее запишем транспонированную матрицу

матрицу из алгебраических дополнений матрицы и умножим полученную матрицу на число, равное В результате получаем обратную матрицу окончательно имеющую вид

Выполним проверку, вычислив произведение в результате получив единичную матрицу.

Возможно, вас также заинтересует эта ссылка:

• Заказать РГР расчетно-графическую работу

РГР 6.

Найти матрицу из уравнения

• Решение:

Уравнение имеет вид откуда Находим обратную матрицу для матрицы для которой имеем Вычисляя произведение получаем ответ Выполним

проверку, подставив найденную матрицу в исходное уравнение. После вычисления произведения получается матрица, равная матрице в правой части уравнения.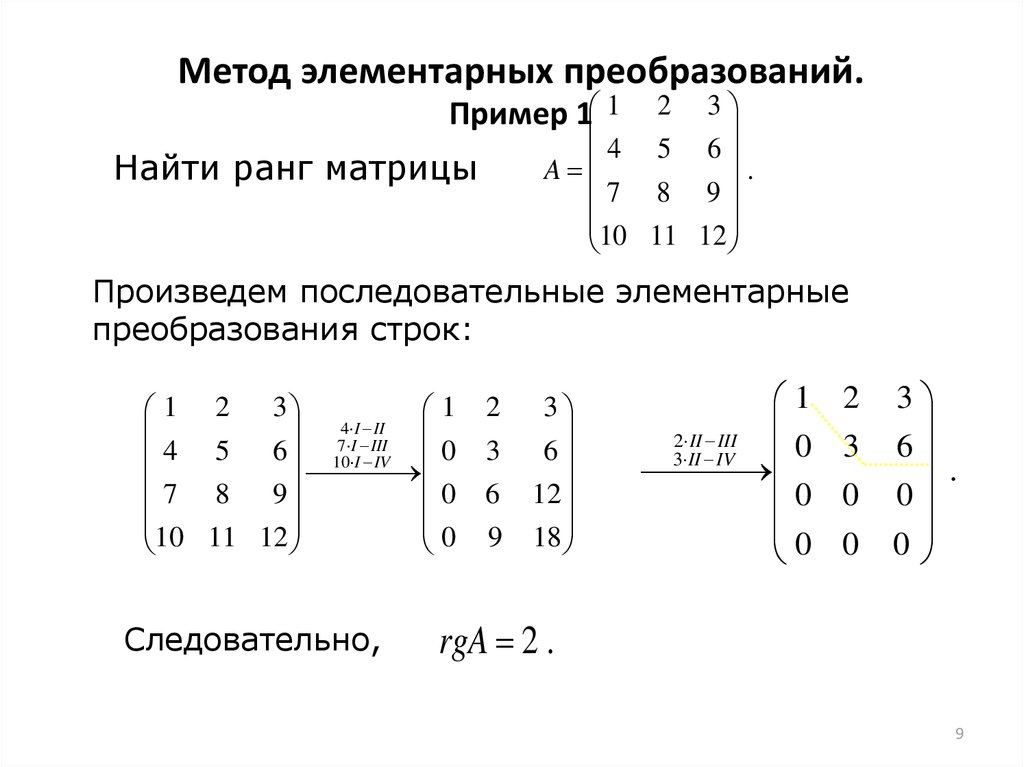

Возможно, вас также заинтересует эта ссылка:

Заказать работу по матрицам помощь в учёбе

линейная алгебра — Нахождение ранга матрицы с помощью операций с элементарными столбцами

спросил 4 года 11 месяцев назад

Изменено 4 года, 11 месяцев назад

Просмотрено 3к раз

$\begingroup$

Я изучаю нахождение ранга матрицы, и в моем учебнике я видел только элементарные операции над строками. Например, для любой матрицы, чтобы найти ее ранг, нам нужно просто использовать элементарные операции со строками, чтобы привести матрицу к форме эшелона строк, и тогда ранг будет просто количеством ненулевых строк. Но можем ли мы также использовать элементарные операции со столбцами, чтобы найти ранг? Например, скажем, у меня есть матрица $3 \times 4$:

$$\begin{bmatrix} a_{11} & a_{12} & a_{13} & a_{14} \\ a_{21} & a_{22} & a_{23} & a_{24} \ \ a_{31} & a_{32} & a_{33} & a_{34} \end{bmatrix}$$ и после использования элементарных операций со столбцами, скажем, я уменьшаю его до:

$$\begin{bmatrix} 0 & 1 & 0 & 0 \\ 0 & 0 & 1 & 0 \\ 0 & 0 & 0 & 1 \end{ bmatrix}$$

Могу ли я заключить, что ранг равен $3$, поскольку имеется три ненулевых строки?

• линейная алгебра
• матрицы

$\endgroup$

0

$\begingroup$

Каждая элементарная операция со строкой соответствует умножению слева на обратимую матрицу, а каждая элементарная операция со столбцом соответствует умножению справа на обратимую матрицу. Таким образом, если вы начали с матрицы $A$ и после $k$ элементарных операций со строками и $\ell$ элементарных операций со столбцами получили матрицу $B$, то

$$B = E_1 \cdots E_k A F_1 \cdots F_\ell$$

где каждая $E_j$ — элементарная операция со строкой, а каждая $F_j$ — элементарная операция со столбцом. Умножение на обратимую матрицу не меняет ранг, поэтому $B$ имеет тот же ранг, что и $A$.

В вашем конкретном примере это действительно означает, что ранг равен $3$.

Подробнее см. в этой статье.

$\endgroup$

$\begingroup$

Если вы выполнили преобразование столбцов правильно, то да, ранг равен 3. Матрица имеет тот же ранг, что и ее транспонирование, поэтому использование операций со столбцами или операций со строками (или их смешивание) работает в любом случае, поскольку вы можете просматривать операции со столбцами как операции со строками при транспонировании.

$\endgroup$

Зарегистрируйтесь или войдите в систему

Зарегистрируйтесь с помощью Google

Зарегистрироваться через Facebook

Зарегистрируйтесь, используя электронную почту и пароль

Опубликовать как гость

Электронная почта

Требуется, но никогда не отображается

Опубликовать как гость

Электронная почта

Требуется, но не отображается

Нажимая «Опубликовать свой ответ», вы соглашаетесь с нашими условиями обслуживания, политикой конфиденциальности и политикой использования файлов cookie

.

Элементарное преобразование матрицы — введение, определение, методы, расчет и примеры решения

Матрица — это прямоугольное расположение чисел, символов или знаков, представляющее набор данных в любой системе. Элементы матрицы расположены в строках и столбцах. Порядок матрицы — это представление количества ее строк и столбцов в виде MxN, где m — количество строк, а n — количество столбцов. Две матрицы называются равными, если они имеют одинаковый порядок и их элементы одинаковы. Существует разница между терминами «равные матрицы» и «эквивалентные матрицы». Эквивалентность двух матриц обозначается символом «~». Две матрицы называются эквивалентными, если одну матрицу можно изменить элементарным преобразованием матрицы, чтобы получить другую матрицу.

Что такое элементарное преобразование матрицы?

Элементарные преобразования — это операции, выполняемые над строками и столбцами матриц для преобразования их в другую форму, чтобы упростить вычисления. Понятие «Что такое элементарные преобразования» используется в методе Гаусса для решения линейных уравнений, определения ступенчатой ​​формы матрицы и других операций, связанных с матричным представлением системы уравнений. Он также используется для нахождения обратных матриц, определителей матриц и решения системы линейных уравнений. Для выполнения элементарных преобразований между любыми двумя матрицами порядок двух матриц должен быть одинаковым.

Элементарные преобразования строк

Преобразования строк выполняются только на основе нескольких наборов правил. Индивидуум не может выполнять какие-либо другие операции со строками, кроме указанных ниже правил. Существует три вида элементарных преобразований строк.

1. Замена строк в матрице: В этой операции вся строка в матрице заменяется другой строкой. Это символически представлено как Ri ↔ Rj, где i и j — два разных номера строки.

2. Масштабирование всей строки с ненулевым числом: Вся строка умножается на одно и то же ненулевое число. Это символически представлено как Ri → k Ri, что указывает на то, что каждый элемент строки масштабируется с коэффициентом «k».

3. Добавить одну строку к другой строке, умноженной на ненулевое число: Каждый элемент строки заменяется числом, полученным путем прибавления его к масштабированному элементу другой строки. Он символически представляется как Ri → Ri + k Rj.

Две матрицы называются эквивалентными по строкам тогда и только тогда, когда одна матрица может быть получена из другой путем выполнения любого из приведенных выше элементарных преобразований строк.

Пример матрицы, эквивалентной строке

1. Покажите, что матрицы A и B эквивалентны строке, если 

\[A=\begin{bmatrix}1 & -1 & 0 \\2 & 1 & 1\end{bmatrix} \textrm{and B}=\begin{bmatrix}3 & 0 & 1 \\0 & 3 & 1\end{bmatrix}\] 

Решение:

Рассмотрим матрицу A.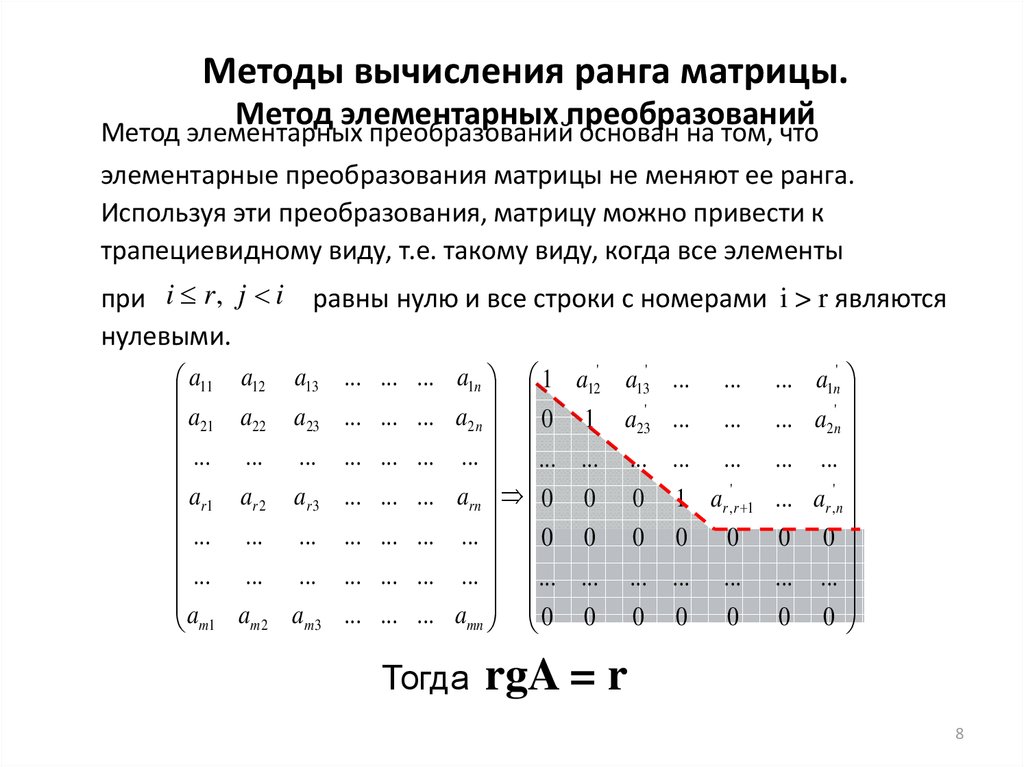 Примените преобразование строк так, чтобы R1 → R1 + Р2

Применение преобразования строки к первой строке, A11 = 1 + 2, A12 = -1 + 1 и A13 = 0 + 1

Таким образом, матрица A будет равна  

\[\begin{bmatrix}3 & 0 & 1 \\2 & 1 & 1\end{bmatrix}\]

Теперь давайте сохраним первую строку и применим преобразование строки ко второй строке, так что

R2 → 3 R2 — R1

Итак, элементы второй строки в A будет дано следующим образом:

A21 = 2 x 3 — 3 = 3

A22 = 1 x 3 — 0 = 3

A23 = 1 x 3 — 1 = 2

Таким образом, матрица A будет равна R1 и примените преобразование строки к R2 так, чтобы R2 → R2 — R1.

A21 = 3 — 3 = 0

A22 = 3 — 0 = 3

A23 = 2 — 1 = 1

Таким образом, матрица A будет равна матрице B.

\[\begin{bmatrix}3 & 0 & 1 \\0 & 3 & 1\end{bmatrix}\]

Отсюда мы можем заключить, что матрицы A и B эквивалентны по строкам.

Элементарные преобразования столбцов

Существует также несколько наборов правил, которым необходимо следовать при выполнении преобразований столбцов. Существует три различных формы преобразования элементарных столбцов. Никакие другие преобразования столбцов, кроме этих трех, не допускаются.

1. Замена столбцов в матрице: В этой операции весь столбец в матрице заменяется другим столбцом. Он символически представлен как Ci ↔ Cj, где i и j — два разных номера столбца.

2. Умножение всего столбца на ненулевое число: Весь столбец умножается или делится на одно и то же ненулевое число. Он символически представлен как Ci → k Ci, что указывает на то, что каждый элемент столбца умножается на коэффициент масштабирования «k».

3. Добавить один столбец к другому столбцу, масштабированному ненулевым числом: Каждый элемент столбца заменяется числом, полученным путем добавления его к масштабированному элементу другого столбца.

   No related posts.