Четверти круга тригонометрия – Тригонометрическая окружность. Подробная теория с примерами.

Содержание

Четверть числовой окружности

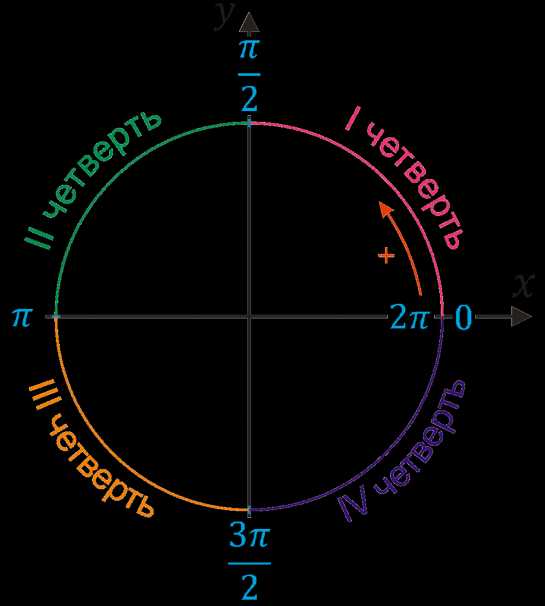
Если посмотреть на числовую окружность, то можно заметить, что оси абсцисс и ординат разбивают ее на четыре части. Эти части называют четвертями и нумеруют в том порядке как их проходят, двигаясь в положительном направлении (против часовой стрелки).

\((\)\(\frac{π}{2}\)\(;π)\)- вторая четверть		\((0;\)\(\frac{π}{2}\)\()\) — первая четверть

\((π;\)\(\frac{3π}{2}\)\()\) — третья четверть		\((\)\(\frac{3π}{2}\)\(;2π)\) — четвертая четверть

Почему так важно определять какой четверти принадлежит угол?

Дело в том, что каждая четверть уникальна в плане знаков тригонометрических функций.

Например, для любого угла из второй четверти — синус положителен, а косинус, тангенс и котангенс отрицательны. А для любого угла из первой четверти — все четыре функции будут положительны.

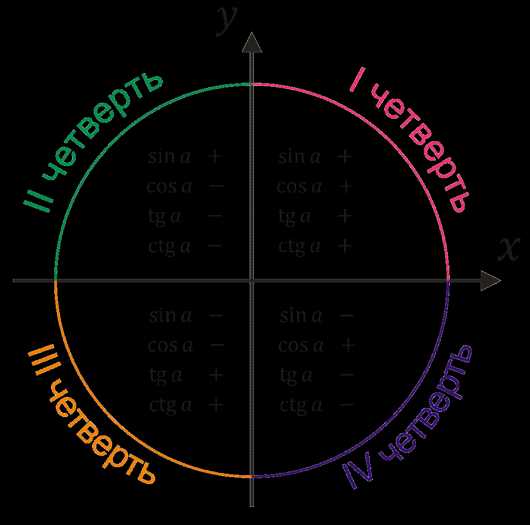
Теперь давайте рассмотрим пример задачи, которую не решить без использования знаний про четверти.

Пример (ЕГЭ):

Найдите \(\sin⁡a\), если \(\cos⁡a=-0,6\) и \(π<a<\)\(\frac{3π}{2}\)		Нам известен косинус, а найти нужно синус того же угла. Какая тригонометрическая формула связывает синус и косинус того же угла? Основное тригонометрическое тождество. Запишем его.
\(\sin^2⁡a+\cos^2⁡a=1\)		Подставим известное, и проведем вычисления.
\(\sin^2⁡a+(-0,6)^2=1\) \(\sin^2⁡a+0,36=1\) \(\sin^2⁡a=0,64\)
\(\sin⁡a=0,8\) или \(\sin⁡a=-0,8\)		У нас два ответа, и оба нам подходят. Но у угла не может быть два синуса! Один лишний! А какой? Вот тут нам и поможет знание о четвертях: обратите внимание, что у нас в условии есть двойное неравенство \(π<a<\) \(\frac{3π}{2}\), то есть угол \(a\) такой, что больше \(π\), но меньше \(\frac{3π}{2}\). Значит он лежит в третьей четверти. А в третьей четверти синус отрицателен. Поэтому верный ответ: \(-0,8\).

Ответ: \(\sin⁡a=-0,8\).

Про непостоянство четвертей:

Важно понимать, что, например, первой четверти принадлежат не только углы от \(0\) до \(\frac{π}{2}\), но и углы от \(2π\) до \(\frac{5π}{2}\), и от \(4π\) до \(\frac{9π}{2}\), и от \(6π\) до \(\frac{13π}{2}\) и так далее. Ведь как только мы заканчиваем полный оборот – кончается четвертая четверть и опять начинается первая.

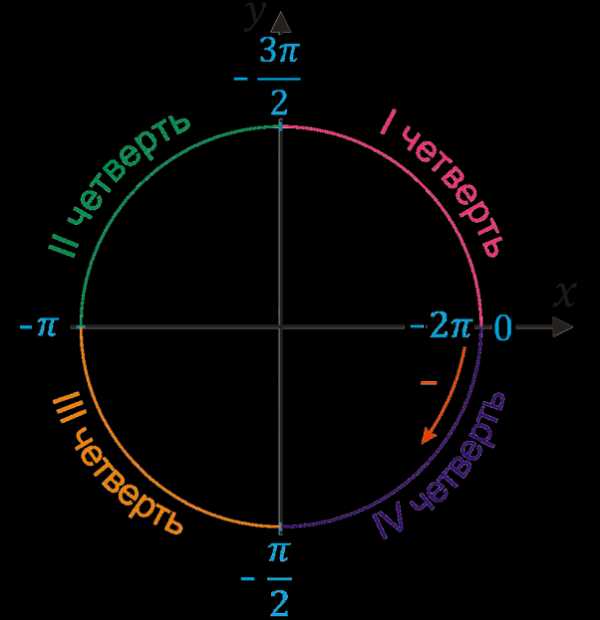
Кроме того, нужно помнить, что углы могут откладываться в отрицательную сторону (по часовой стрелке), и тогда мы попадем в первую четверть только в конце круга. Ведь сначала мы пройдем четвертую четверть, потом в третью и т.д.

\((-π;-\)\(\frac{3π}{2}\)\()\)- вторая четверть		\((-\)\(\frac{3π}{2}\)\(;-2π)\) — первая четверть

\((-\)\(\frac{π}{2}\)\(;-π)\) — третья четверть		\((0;-\)\(\frac{π}{2}\)\()\) — четвертая четверть

Ну и, конечно, мы можем в отрицательную сторону делать обороты, так же как и в положительную.

Смотрите также:
Числовая окружность (шпаргалка)
Тригонометрическая таблица с кругом
Как обозначать точки на числовой окружности

Скачать статью

cos-cos.ru

Числовая окружность, макеты числовой окружности — урок. Алгебра, 10 класс.

Единичная окружность — это окружность, радиус которой принимается за единицу измерения.

Длина единичной окружности \(l\) равна l=2π⋅R=2π⋅1=2π.

Считаем, что R=1.

Если взять π≈3,14, то длина окружности \(l\) может быть выражена числом 2π≈2⋅3,14=6,28.

Будем пользоваться единичной окружностью, в которой проведены горизонтальный и вертикальный диаметры \(CA\) и \(DB\) (см. рис.)

Принято называть дугу \(AB\) — первой четвертью, дугу \(BC\) — второй четвертью, дугу \(CD\) — третьей четвертью, дугу \(DA\) — четвёртой четвертью, причём это открытые дуги, т. е. дуги без их концов.

Длина каждой четверти единичной окружности равна 14⋅2π=π2.

Принято в обозначении дуги на первом месте писать букву, обозначающую начало дуги, а на втором месте писать букву, обозначающую конец дуги.

Для работы с числовой окружностью часто используются два макета числовой окружности.

Каждая из четырёх четвертей числовой окружности разделена на две равные части, и около каждой из полученных восьми точек записано число, которому она соответствует.

Каждая из четырёх четвертей числовой окружности разделена на три равные части, и около каждой из полученных двенадцати точек записано число, которому она соответствует.

Для числовой окружности верно следующее утверждение:

если точка \(M\) числовой окружности соответствует числу \(t\), то она соответствует и числу вида t+2πk,k∈&integers;.

На указанных двух макетах написаны числа, соответствующие точкам при первом обходе числовой окружности в положительном направлении, т. е. на промежутке 0;2π.

Таким образом,

единичная окружность с установленным соответствием между действительными числами и точками окружности называется числовой окружностью.

www.yaklass.ru

Тригонометрический круг

Тригонометрический круг — это окружность с единичным радиусом и центром в начале осей координат, каждая точка которой образует треугольник с точками:

точка в начале осей координат (точка 0;0)
точка на окружности (выбрана нами)
точка на оси X, которая является проекцией выбранной нами точки на эту ось (перпендикуляр к оси X)

Как видно, такой треугольник является прямоугольным, так как из выбранной нами точки на ось абсцисс всегда опускается перпендикуляр. То есть сторона, соединяющая начало координат и выбранную нами точку на тригонометрическом круге ( на приведенном рисунке обозначенную как B, B1. B2, B3) всегда является гипотенузой прямоугольного треугольника, проекция выбранной точки — это катет, а сторона от точки пересечения с осью X образует второй катет.

Угол, который образуется между осью абсцисс (осью X) и гипотенузой треугольника — является углом, для которого и вычисляются значения тригонометрических функций. Этот угол отсчитывается от положительного направления оси абсцисс (оси X) как ноль, далее против часовой стрелки. Таким образом, полный круг составляет 360 градусов или 2π радиан

Чтобы вычислить значение тригонометрической функции для выбранного угла тригонометрического круга достаточно воспользоваться координатами точки, принадлежащей окружности тригонометрического круга. На приведенном выше рисунке, показано вычисление значения синуса для всех углов.

Например, sin α для треугольника OBC (где координаты точки B равны (x,y) ) ,будет равен: y / √ ( x² + y²)

Свойства тригонометрического круга

Если последовательно вычислять значения тригонометрических функций для тригонометрического круга, то становится видно, что результат таких вычислений меняет свой знак в зависимости от того, в какой четверти тригонометрического круга выбрана точка. При этом знак тригонометрической функции в пределах одной и той же четверти сохраняется.

Знаки тригонометрических функций в координатных четвертях в тригонометрическом круге

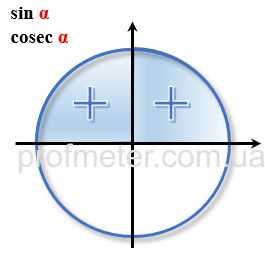
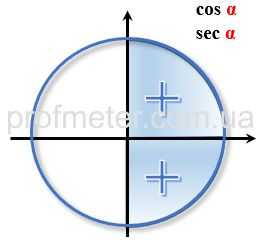
Преобразование углов больше 360 градусов или 2π радиан

Как видно из картинок, после того, как значение угла превысит 360 градусов (или 2π радиан), то результат вычисления значения будет тем же самым. То есть, для того, чтобы привести значение к «нормальному» — нужно вычесть из имеющегося значения 360 градусов или 2π радиан и повторять операцию столько раз, пока результат не станет меньше 360 или 2π.

Тригонометрические соотношения в прямоугольном треугольнике | Описание курса | Радианы и градусы. Радiани i градуси

profmeter.com.ua

Функции угла на тригонометрической окружности, значения функций, четверти. Тест

Вопрос 1. Углом какой четверти является угол 283⁰?

Вопрос 2. Углом какой четверти является угол -20⁰?

Вопрос 3. Углом какой четверти является угол 190⁰?

Вопрос 4. Углом какой четверти является угол 100⁰?

Вопрос 5. Углом какой четверти является угол 800⁰?

Вопрос 6. Углом какой четверти является угол 10000⁰?

Вопрос 7. Найдите в промежутке от 0⁰ до 360⁰ такой угол, чтобы поворот начального радиуса на этот угол совпадал с поворотом на угол 420⁰?

Вопрос 8. Найдите в промежутке от 0⁰ до 360⁰ такой угол, чтобы поворот начального радиуса на этот угол совпадал с поворотом на угол -210

Вопрос 9. Найдите в промежутке от 0⁰ до 360⁰ такой угол, чтобы поворот начального радиуса на этот угол совпадал с поворотом на угол -700⁰?

Вопрос 10. Какое наибольшее значение выражения

Вопрос 11. Какое наименьшее значение выражения ?

Вопрос 12. Какое наибольшее значение выражения ?

Вопрос 13. Какое наименьшее значение выражения ?

Вопрос 14. Какое наибольшее значение выражения ?

Вопрос 15. Какой знак имеет , если

Вопрос 16. Какой знак имеет , если

Вопрос 17. Какой знак имеет , если ?

Вопрос 18. Какой знак имеет , если ?

Вопрос 19.

Какой знак имеет ?

Вопрос 20. Какой знак имеет ?

Вопрос 21. Какой знак имеет ?

Вопрос 22. Какой знак имеет ?

Вопрос 23. Какой знак имеет ?

Вопрос 24. Какой знак имеет ?

Вопрос 25. Какой знак имеет ?

Вопрос 26. Какой знак имеет ?

Вопрос 27. Какой знак имеет выражение ?

Вопрос 28. Какой знак имеет выражение ?

Вопрос 29. Какой знак имеет выражение ?

Вопрос 30. Какой знак имеет выражение ?

Вопрос 31. Углом какой четверти является угол, если ?

Вопрос 32. Углом какой четверти является угол, если ?

Вопрос 33. Углом какой четверти является угол, если ?

Вопрос 34. Углом какой четверти является угол, если ?

Вопрос 35. Углом какой четверти является угол, если ?

Вопрос 36. Углом какой четверти является угол, если ?

Вопрос 37. Найдите градусную меру угла, радианная мера которого

Вопрос 38. Найдите градусную меру угла, радианная мера которого

Вопрос 39. Найдите градусную меру угла, радианная мера которого 0,5 (округлить до градусов)

Вопрос 40. Найдите градусную меру угла, радианная мера которого 10 (округлить до градусов)

Вопрос 41. Найдите градусную меру угла, радианная мера которого 3,1 (округлить до градусов)

Вопрос 42. Найдите градусную меру угла, радианная мера которого 0,2 (округлить до градусов)

Вопрос 43. Углом какой четверти является угол ?

Вопрос 44. Углом какой четверти является угол ?

Вопрос 45. Определите знак выражения

Вопрос 46. Определите знак выражения

Вопрос 47. Определите знак выражения

Вопрос 48. Определите знак выражения

Вопрос 49. Определите знак выражения

Вопрос 50. Определите знак выражения

fizmat.by

Тригонометрия. Единичная окружность

Разделы: Математика, Конкурс «Презентация к уроку»

Презентация к уроку

Загрузить презентацию (322,7 кБ)

Внимание! Предварительный просмотр слайдов используется исключительно в ознакомительных целях и может не давать представления о всех возможностях презентации. Если вас заинтересовала данная работа, пожалуйста, загрузите полную версию.

Цель: научить использовать единичную окружность при решении различных тригонометрических заданий.

В школьном курсе математики возможны различные варианты введения тригонометрических функций. Наиболее удобной и часто используемой является «числовая единичная окружность». Её применение в теме «Тригонометрия» весьма обширно.

Единичная окружность используется для:

– определения синуса, косинуса, тангенса и котангенса угла;
– нахождения значений тригонометрических функций для некоторых значений числового и углового аргумента;
– выведение основных формул тригонометрии;
– выведения формул приведения;
– нахождения области определения и области значений тригонометрических функций;
– определения периодичности тригонометрических функций;
– определения четности и нечетности тригонометрических функций;
– определения промежутков возрастания и убывания тригонометрических функций;
– определения промежутков знакопостоянства тригонометрических функций;
– радианного измерения углов;
– нахождения значений обратных тригонометрических функций;
– решение простейших тригонометрических уравнений;
– решение простейших неравенств и др.

Таким образом, активное осознанное владение учащимися данным видом наглядности дает неоспоримые преимущества для овладения разделом математики «Тригонометрия».

Использование ИКТ на уроках преподавания математики позволяет облегчить овладение числовой единичной окружностью. Конечно, интерактивная доска имеет широчайший диапазон применения, однако не во всех классах она есть. Если же говорить о применении презентаций, то на просторах Интернета и их выбор велик, и каждый педагог может найти наиболее приемлемый вариант для своих уроков.

В чем особенность представляемой мною презентации?

Данная презентация предполагает различные варианты использования и не является наглядностью к конкретному уроку в теме «Тригонометрия». Каждый слайд данной презентации можно использовать обособлено, как на этапе объяснения материала, формирования навыков, так и для рефлексии. При создании данной презентации особое внимание уделялось «читаемости» её с дальнего расстояния, поскольку количество учеников со сниженным зрением постоянно растет. Продумано цветовое решение, логически связанные объекты объединены единым цветом. Презентация анимирована таким образом, чтобы учитель имел возможность комментировать фрагмент слайда, а ученик задать вопрос. Таким образом, данная презентация – это своего рода «подвижные» таблицы. Последние слайды не анимированы и используются для проверки усвоения материала, в ходе решения тригонометрических заданий. Окружность на слайдах максимально упрощена внешне и максимально приближена к изображаемой на тетрадном листе учениками. Это условие я считаю принципиальным. У учащихся важно сформировать мнение о единичной окружности, как о доступном и мобильном (хотя и не единственном) виде наглядности при решении тригонометрических заданий.

Данная презентация поможет педагогам познакомить учеников с единичной окружностью в 9 классе на уроках геометрии при изучении темы «Соотношения между сторонами и углами треугольника». И, конечно, она поможет расширить и углубить навык работы с единичной окружностью при решении тригонометрических заданий у учащихся старшего звена обучения на уроках алгебры.

Слайды 3, 4 поясняют построение единичной окружности; принцип определения местоположения точки на единичной окружности в I и II координатных четвертях; переход от геометрических определений функций синус и косинус (в прямоугольном треугольнике) к алгебраическим на единичной окружности.

Слайды 5-8 поясняют, как найти значения тригонометрических функций для основных углов I координатной четверти.

Слайды 9-11 поясняет знаки функций в координатных четвертях; определение промежутков знакопостоянства тригонометрических функций.

Слайд 12 используется для формирования представлений о положительных и отрицательных значениях углов; знакомством с понятием периодичности тригонометрических функций.

Слайды 13, 14 используются при переходе на радианную меру угла.

Слайды 15-18 не анимированы и используются при решении различных тригонометрических заданий, закрепления и проверки результатов усвоения материала.

Содержание:

Титульный лист.
Целеполагание.
Построение единичной окружности. Основные значения углов в градусной мере.

Определение синуса и косинуса угла на единичной окружности.

Табличные значения для синуса в порядке возрастания.

Табличные значения для косинуса в порядке возрастания.

Табличные значения для тангенса в порядке возрастания.

Табличные значения для котангенса в порядке возрастания.

Знаки функции sin α.

Знаки функции cos α.

Знаки функций tg α и ctg α.

Положительные и отрицательные значения углов на единичной окружности.

Радианная мера угла.

Положительные и отрицательные значения углов в радианах на единичной окружности.

Различные варианты единичной окружности для закрепления и проверки результатов усвоения материала.

12.04.2013

Поделиться страницей:
xn--i1abbnckbmcl9fb.xn--p1ai
No related posts.