Вычитание и сложение – правила, секретные примеры, упражнения, игры

Как объяснить сложение и вычитание чисел?

Повторим важные математические  действия в математике, такие как сложение и вычитание.

Сложение чисел

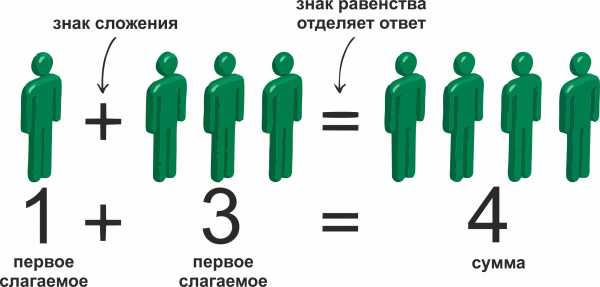
Сложение — это математическое действие. Числа, которые складываются, называются слагаемыми. Результат сложения называется суммой.

Чтобы найти сумму двух чисел, можно воспользоваться числовой прямой. Это самый простой способ. Числа располагают вдоль прямой линии,  что позволяет легко считать их влево и вправо. На рисунке показано, как сложить числа 1 и 3.

 

 

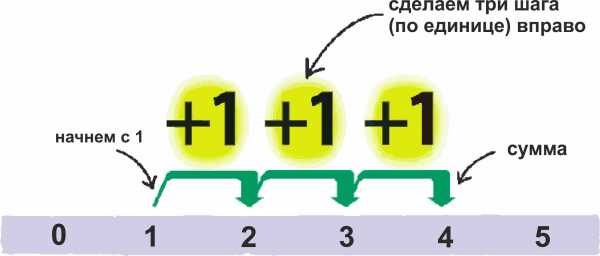
Как объяснить?

На числовой прямой, чтобы найти сумму 1 и 3, встанем на отметку 1 и сделаем три шага вправо, добавляя по единице. В результате
мы окажемся на отметке 4. Это и будет ответ.

 

Что это значит?
Если мы прибавим 3 к 1, получим 4. Иначе говоря, сумма 1 и 3 равна 4.

Сложение многозначных чисел

Числа, которые состоят из нескольких цифр, складываются поразрядно: сначала единицы, затем десятки, потом сотни и т. д. Сумма каждого разряда записывается под ним.

Если сумма состоит из двух цифр, то старшая цифра переносится в следующий разряд.

 

Вычитание чисел

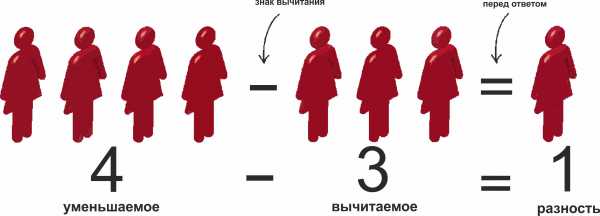
Вычитая одно число из другого, мы находим разницу между ними. Результат называется разностью.

Для вычитания также можно использовать числовую прямую.
Для этого делаем от отметки первого числа столько шагов влево, сколько единиц во втором числе. Здесь из 4 вычитаем 3.

Как объяснить?

На числовой прямой, чтобы вычесть 3 из 4, от отметки числа 4 сделаем три шага влево: сначала к 3, потом к 2 и, наконец, к отметке 1.

Что это значит?
Результат вычитания 3 из 4 равен 1. Иными словами, разность 4 и 3 равна 1.

 

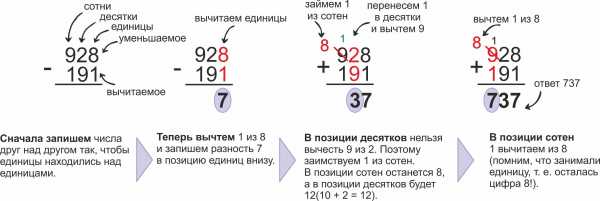
Вычитание многозначных чисел

Числа, которые состоят из нескольких цифр, вычитаются поразрядно: сначала единицы, затем десятки, потом сотни и т. д. При этом иногда приходится заимствовать единицу из следующего (старшего) разряда.

xn--80aakeqfhfoqvpv.xn--p1ai

Вычитание и сложение чисел с переходом через десяток

На данном уроке вы вспомните, как складывать и вычитать числа с переходом через десяток. Решая интересные задания, вы повторите алгоритм сложения и вычитания чисел с переходом через десяток. У вас будет возможность попрактиковать изученный ранее материал вместе с веселыми пчелками.

Тема: Повторение

Урок: Вычитание и сложение чисел с переходом через десяток

Посмотрите на числовой ряд. (рис. 1)

Рис. 1

Как связаны пары чисел между собой? В сумме они дают 10.

Запомните эти пары. (рис. 2)

Рис. 2

Это свойство чисел нам пригодится при решении задач.

9 + 6 = ?

Выполним сложение по частям, для этого разбиваем второе слагаемое 6 на две части так, чтобы первая часть дополняла число 9 до десяти. (рис. 3)

Рис. 3

Первая часть – число 1, вторая часть – все что осталось – 5. (рис. 4)

Рис. 4

Значит, 9 + 6 =  15.

1.      Читаю пример

Первое слагаемое …

Второе слагаемое …

2.      Нахожу число, которое дополнит первое слагаемое до 10. Это число …

3.      Разбиваю второе слагаемое на 2 части … и …

4.      Дополняю первое слагаемое до 10 и прибавляю оставшиеся единицы. 10 + …

5.      Читаю ответ …

Потренируемся в счёте.

Решите примеры и узнайте, с какого цветка пчёлки соберут сладкий нектар. (рис. 5) 

Рис. 5

Решение представлено на рисунке. (рис. 6)

Рис. 6

Если у вас возникли затруднения, повторите состав чисел, это вам обязательно поможет.

А теперь рассмотрим пример на вычитание.

11 – 6 = ?

Находим количество единиц в уменьшаемом – число 11 состоит из 1 десятка и 1 единицы. Разбиваем вычитаемое 6 на две части: первая равна количеству единиц уменьшаемого – 1, вторая – оставшихся единиц – 5. (рис. 7)

Рис. 7

Вычитать будем по частям. Вычитаем первую часть: 11 — 1= 10, а потом из 10 вычитаем 5, равно 5. (рис. 8)

Рис. 8

Значит, 11 – 6 = 5

1.      Читаю пример

Уменьшаемое …

Вычитаемое …

2.      В разряде единиц уменьшаемого число …

3.      Разбиваю вычитаемое на две части … и …

4.      Вычитаю первую часть …, получаю 10, вычитаю из 10 вторую часть …

5.      Читаю ответ.

Закрепим новое знание.

У нас три кошки: рыжая, белая и чёрная. (рис. 9)

 

Рис. 9

У них родились котята. Хотите узнать сколько? Тогда правильно решите примеры и назовите цвет кошки, у которой больше всего котят. (рис. 10)

Рис. 10

Следовательно, больше всех котят у рыжей кошки.

На данном уроке вы вспомнили алгоритм сложения и вычитания чисел с переходом через десяток. Вы закрепили изученный ранее материал, решая веселые задачи, что поможет вам в дальнейшем изучении математики.

 

Список литературы

1. Александрова Л.А., Мордкович А.Г. Математика 1 класс. – М: Мнемозина, 2012.
2. Башмаков М.И., Нефедова М.Г. Математика. 1 класс. – М: Астрель, 2012.
3. Беденко М.В. Математика. 1 класс. – М7: Русское слово, 2012.

 

Дополнительные рекомендованные ссылки на ресурсы сети Интернет

1. Пособия для начальной школы (Источник).
2. Социальная сеть работников образования (Источник).
3. 5klass.net (Источник).

 

Домашнее задание

1. Вспомните алгоритм сложения и вычитания чисел с переходом через десяток.

2. Решите примеры и узнайте, с какого цветка пчёлки соберут сладкий нектар.

3. Решите примеры:

3 + 8 = 6 + 5 = 9 + 7 = 8 + 5=

15 – 6 = 17 – 9 = 14 – 7 = 18 – 9 =

interneturok.ru

Сложение и вычитание величин

При сложении или вычитании однородных величин единицы измерения величин не меняются.

Чтобы найти сумму или разность однородных величин, надо произвести действия над их численными значениями и, к полученному результату, приписать единицу измерения величины.

Пример 1. Найти сумму 37 м + 12 м:

37 + 12 = 49 м

Пример 2. Найти разность 108 км — 69 км:

108 — 69 = 39 км

Если величины состоят из двух единиц измерения, то можно либо сразу произвести действия над их численными значениями, по необходимости переводя промежуточный результат из одной единицы измерения в другую. Либо сначала привести их к одной единице измерения, а потом произвести нужные вычисления.

Пример 1. Найти сумму величин 12 кг 729 гр + 9 кг 435 гр.

Сложение будем производить столбиком. Напишем числа так, чтобы килограммы были записаны под килограммами, а граммы – под граммами.

Складываем единицы граммов

: 9 + 5 = 14 (единиц граммов или 1 десяток граммов и 4 единицы). Пишем под единицами граммов цифру 4 и 1 десяток запоминаем.

Складываем десятки граммов: 2 + 3 = 5 (десятков граммов). К этим 5 десяткам надо прибавить ещё один, который мы получили при сложении единиц: 5 + 1 = 6 (десятков граммов). Пишем под десятками граммов цифру 6.

Складываем сотни граммов: 7 + 4 = 11 (сотен граммов или 1 тысяча граммов и 1 сотня). Пишем под сотнями граммов цифру 1 и 1 тысячу запоминаем.

Складываем единицы килограммов: 2 + 9 = 11 (единиц килограммов). К этим 11 единицам надо прибавить ещё 1, которую мы получили при сложении сотен граммов: 11 + 1 = 12 (единиц килограммов или 1 десяток и 2 единицы). Пишем цифру 2 и 1 десяток запоминаем.

Складываем десятки килограммов: 1 + 0 = 1 (десяток килограммов). К этому десятку надо прибавить ещё один, который мы получили при сложении единиц килограммов: 1 + 1 = 2 (десятка килограммов). Пишем под десятками килограммов цифру 2.

Всего получили 22 кг 164 гр.

Данное выражение можно вычислить по другому: сначала привести обе величины к одной единице измерения:

12 кг 729 гр = 12729 гр

9 кг 435 гр = 9435 гр

а затем численные значения величин можно сложить столбиком:

полученный результат, при необходимости, можно привести обратно к двум единицам измерения:

22164 гр = 22 кг 164 гр

Пример 2. Найти разность величин 9 км 528 м — 6 км 909 м.

Вычитание будем производить столбиком. Напишем числа так, чтобы километры были записаны под километрами, а метры – под метрами:

Всего получили 2 км 619 м.

Данное выражение можно вычислить по другому: сначала привести обе величины к одной единице измерения:

9 км 528 м = 9528 м

6 км 909 м = 6909 м

а затем выполнить вычитание столбиком:

полученный результат, при необходимости, можно привести обратно к двум единицам измерения:

2619 м = 2 км 619 м

naobumium.info

Сложение и вычитание чисел — Excel для Mac

Сложение нескольких чисел в одной ячейке

1. Щелкните любую пустую ячейку и введите знак равенства (=), чтобы начать ввод формулы.

2. После знака равенства введите несколько чисел, разделенных знаком «плюс» (+).

   Например: 50+10+5+3.

3. Нажмите клавишу RETURN.

   Если использовать числа из примера, получается результат 68.

   Примечания: 

   • Если вместо ожидаемого результата отображается дата, выделите ячейку и на вкладке Главная выберите пункт Общий.

Сложение чисел с помощью ссылок на ячейки

Ссылка на ячейку представляет собой букву столбца и номер строки, например А1 или F345. При использовании в формуле ссылки на ячейку вместо значения ячейки можно изменить значение, не меняя формулу.

1. Введите число, например 5, в ячейку C1. Затем введите другое число, например 3, в ячейку D1.

2. В ячейке E1 введите знак равенства (=), чтобы начать ввод формулы.

3. После знака равенства введите C1+D1.

4. Нажмите клавишу RETURN.

   Если использовать числа из примера, получается результат 8.

   Примечания: 

   • Если изменить значение в ячейке C1 или D1 и нажать клавишу RETURN, значение ячейки E1 изменится, даже если формула осталась неизменной.

   • Если вместо ожидаемого результата отображается дата, выделите ячейку и на вкладке Главная выберите пункт Общий.

Быстрое суммирование чисел в строке или столбце

1. Введите несколько чисел в столбец или строку, а затем выделите заполненный диапазон ячеек.

2. В строке состояния найдите значение рядом с надписью строка состоянияСумма. В этом примере будет выведено 86.

Вычитание нескольких чисел в одной ячейке

1. Щелкните любую пустую ячейку и введите знак равенства (=), чтобы начать ввод формулы.

2. После знака равенства введите несколько чисел, разделенных знаком «минус» (–).

   Например: 50-10-5-3.

3. Нажмите клавишу RETURN.

   Если использовать числа из примера, получается результат 32.

Вычитание чисел с помощью ссылок на ячейки

Ссылка на ячейку представляет собой букву столбца и номер строки, например А1 или F345. При использовании в формуле ссылки на ячейку вместо значения ячейки можно изменить значение, не меняя формулу.

1. Введите числа в ячейки C1 и D1.

   Например, введите 5 и 3.

2. В ячейке E1 введите знак равенства (=), чтобы начать ввод формулы.

3. После знака равенства введите C1-D1.

4. Нажмите клавишу RETURN.

   Если использовать числа из примера, получается результат 2.

   Примечания: 

   • Если изменить значение в ячейке C1 или D1 и нажать клавишу RETURN, значение ячейки E1 изменится, даже если формула осталась неизменной.

   • Если вместо ожидаемого результата отображается дата, выделите ячейку и на вкладке Главная выберите пункт Общий.

Сложение нескольких чисел в одной ячейке

1. Щелкните любую пустую ячейку и введите знак равенства (=), чтобы начать ввод формулы.

2. После знака равенства введите несколько чисел, разделенных знаком «плюс» (+).

   Например: 50+10+5+3.

3. Нажмите клавишу RETURN.

   Если использовать числа из примера, получается результат 68.

   Примечание: Если вы видите дату вместо ожидаемого результата, выделите ячейку и на вкладке Главная в группе число нажмите кнопку Общие во всплывающем меню.

Сложение чисел с помощью ссылок на ячейки

Ссылка на ячейку представляет собой букву столбца и номер строки, например А1 или F345. При использовании в формуле ссылки на ячейку вместо значения ячейки можно изменить значение, не меняя формулу.

1. Введите число, например 5, в ячейку C1. Затем введите другое число, например 3, в ячейку D1.

2. В ячейке E1 введите знак равенства (=), чтобы начать ввод формулы.

3. После знака равенства введите C1+D1.

4. Нажмите клавишу RETURN.

   Если использовать числа из примера, получается результат 8.

   Примечания: 

   • Если изменить значение в ячейке C1 или D1 и нажать клавишу RETURN, значение ячейки E1 изменится, даже если формула осталась неизменной.

   • Если вы видите дату вместо ожидаемого результата, выделите ячейку и на вкладке Главная в группе число нажмите кнопку Общие во всплывающем меню.

Быстрое суммирование чисел в строке или столбце

1. Введите несколько чисел в столбец или строку, а затем выделите заполненный диапазон ячеек.

2. На строка состояния, найдите значение параметра рядом с пунктом Сумма =. Итоговое значение 86.

   Если строка состояния не отображается, в меню Вид выберите пункт Строка состояния.

Вычитание нескольких чисел в одной ячейке

1. Щелкните любую пустую ячейку и введите знак равенства (=), чтобы начать ввод формулы.

2. После знака равенства введите несколько чисел, разделенных знаком «минус» (–).

   Например: 50-10-5-3.

3. Нажмите клавишу RETURN.

   Если использовать числа из примера, получается результат 32.

Вычитание чисел с помощью ссылок на ячейки

Ссылка на ячейку представляет собой букву столбца и номер строки, например А1 или F345. При использовании в формуле ссылки на ячейку вместо значения ячейки можно изменить значение, не меняя формулу.

1. Введите числа в ячейки C1 и D1.

   Например, введите 5 и 3.

2. В ячейке E1 введите знак равенства (=), чтобы начать ввод формулы.

3. После знака равенства введите C1-D1.

4. Нажмите клавишу RETURN.

   Если использовать числа из примера, получается -2.

   Примечания: 

   • Если изменить значение в ячейке C1 или D1 и нажать клавишу RETURN, значение ячейки E1 изменится, даже если формула осталась неизменной.

   • Если вы видите дату вместо ожидаемого результата, выделите ячейку и на вкладке Главная в группе число нажмите кнопку Общие во всплывающем меню.

support.office.com

Сложение и вычитание вещественных чисел.

Выполнение арифметических операций над вещественными числами отличается от аналогичных операций над целыми числами.

К началу выполнения арифметического действия операнды операции помещаются в соответствующие регистры АЛУ.

При сложении и вычитании сначала производится подготовительная операция, называемая выравниванием порядков.

В процессе выравнивания порядков мантисса числа с меньшим порядком сдвигается в своем регистре вправо на количество разрядов, равное разности порядков операндов. После каждого сдвига порядок увеличивается на единицу.

В результате выравнивания порядков одноименные разряды чисел оказываются расположенными в соответствующих разрядах обоих регистров, после чего мантиссы складываются или вычитаются.

В случае необходимости полученный результат нормализуется путем сдвига мантиссы результата влево. После каждого сдвига влево порядок результата уменьшается на единицу.

В целом оперции сложения, вычитания чисел представленных в формате с плавающей точкой выполняются в следующей последовательности:

1) Осуществляется сравнение порядков (при этом поскольку в форматах хранятся не сами порядки а смещенные порядки, как целые беззнаковые числа, то их сравнение осуществляется путем вычитания их как целых беззнаковых чисел).

2) Производится выранивание порядков числа с меньшим порядком в сторону числа с большим порядком.

3) Производится алгебраическое сложение.

4) Производится нормализация результатов.

Пример 5. Сложить двоичные нормализованные числа 0.10111•2–1 и 0.11011*210. Разность порядков слагаемых здесь равна

Пример 6. Выполнить вычитание двоичных нормализованных чисел 0.10101*210 и 0.11101*21. Разность порядков уменьшаемого и вычитаемого здесь равна единице, поэтому перед вычитанием мантисса второго числа сдвигается на один разряд вправо:

При сложении, вычитании мантисс может возникнуть нарушение нормализации (денормализация) влево на 1 разряд. Для получения нормализованного результата необходимо мантиссу сдвинуть на 1 разряд вправо, а порядок увеличить на 1.

Может возникнуть переполнение порядков. При сложении мантисс близких по модулю друг к другу, но имеющих разные знаки может возникнуть денормализация впрао на любое число разрядов вплоть до нулей. Если получились все нули, то результату присваевается машинный ноль (потеря значимости).

Если мантисса не нулевая и имеет место денормализация вправо, то для получения нормализованного результата мантисса сдвигается влево на соответствующее число разрядов (пока старшаая разрядная цифра остается равной нулю), а порядок порядок уменьшается на эту величину. В этом случае может возникнуть антипереполнение.

Задание 10.

Самостоятельно выполните в четырехбайтном формате сложение и вычитание двух вещественых чисел, выбранных из таблицы №4, предварительно переведя их в двоичную систему счисления и осуществите проверку результатов в десятичной системе.

Статьи к прочтению:

Системы счисления: Сложение, вычитание и умножение двоичных чисел. Центр онлайн-обучения «Фоксфорд»

Похожие статьи:

• Правило 10. вычитание чисел.

  Для того, чтобы вычисть числа в системе счисления с основанием q, необходимо записать одно под другим столбиком, чтобы разряды вычитаемого располагались…

• Вычитание чисел в дополнительном коде

  ПРАКТИЧЕСКАЯ РАБОТА №3 Изучение принципов выполнения операций сложения и вычитания в двоичной ССЧ Цель работы: изучить принципы выполнения операций…

csaa.ru

Математика для дошкольников. Вычитание и сложение.

Если ваш ребенок уже знаком с цифрами, может называть их, видя на картинках, и умеет их писать, то самое время научить его считать. Умение считать необходимо любому человеку, и чем ранее ребенок освоит счет, тем лучше. Красочные картинки помогут вам в обучении. Но если приступить к обучению с помощью цифр, то это может вызвать некоторые затруднения у малыша.

Дело в том, что цифра для взрослого человека – это нечто абстрактное. Взрослый не ассоциирует конкретное число с каким-либо предметом, он воспринимает его обособленно. Маленький ребенок так не умеет. Для его проще всего воспринимать цифры, связывая их с каким-либо конкретным предметом.

Перед вами шесть карточек, которые помогут вашему ребенку в обучении счету. Три из них посвящены сложению, три – вычитанию. В качестве объектов для сложения и вычитания там использованы изображения предметов, животных, героев мультфильмов, цветов и т.д. Такие занятия будут гораздо более интересными, чем занятия с обычными цифрами. С помощью этих несложных карточек ребенок быстро освоит счет от 1 до 10. Для занятий можно использовать игровую форму. К примеру, вы говорите ребенку, что на столе лежало 5 конфет, но ежик одной угостил зайчика. Сколько конфет осталось у ежика?
 

Сложение

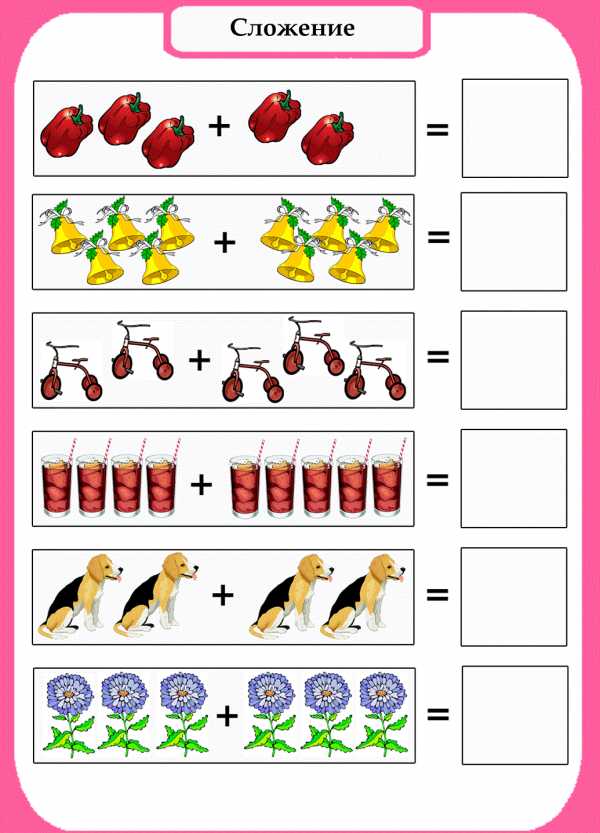
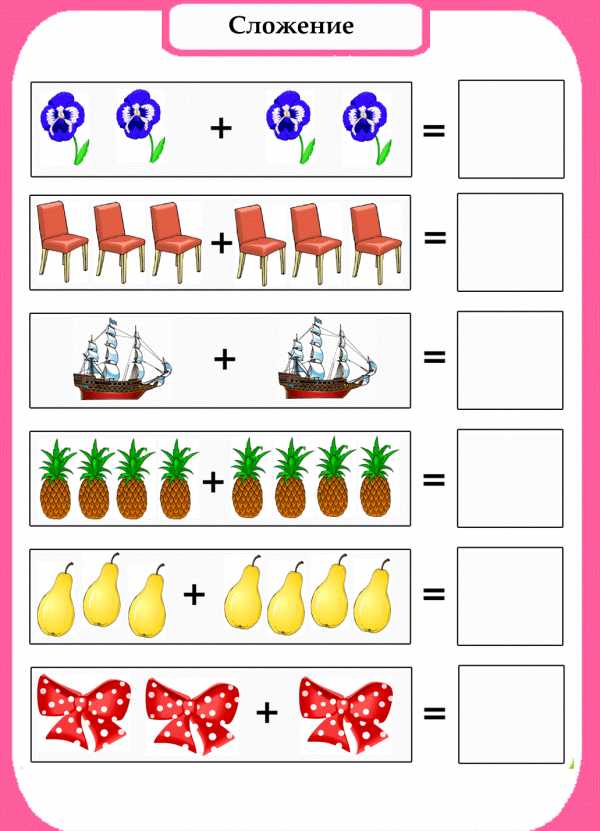
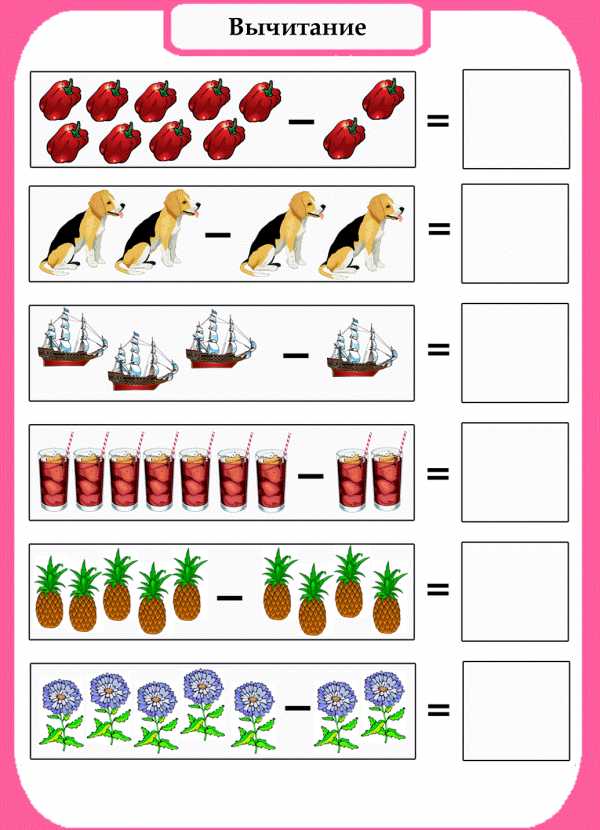
Вычитание

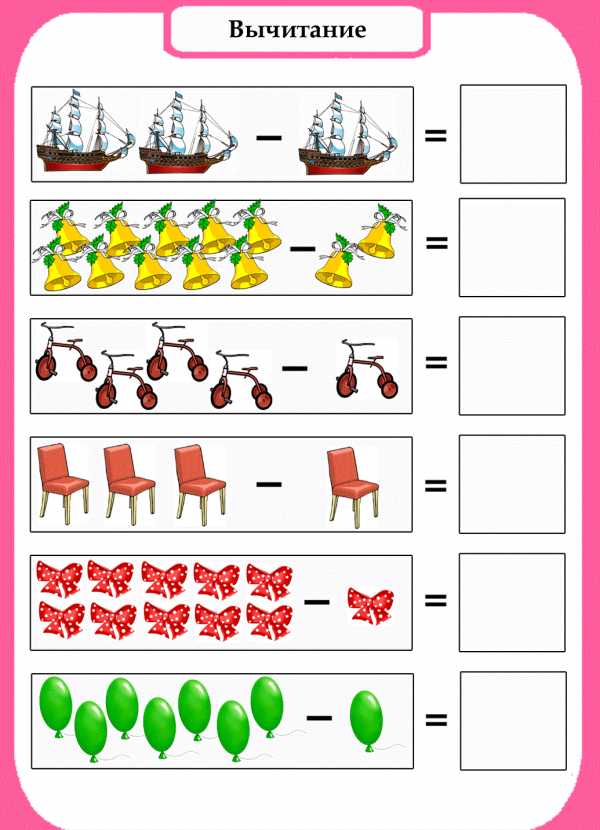
Узнайте, что еще должен знать и уметь ребенок в этом возрасте. 

 

feminissimo.ru

Связь сложения и вычитания — СПИШИ У АНТОШКИ

Какова же общая связь сложения и вычитание натуральных чисел?

Связь сложения с вычитанием заключается в следующем — вычитание является действием ОБРАТНЫМ для сложения. Что же это означает? Чтобы ответить на этот вопрос, давайте рассмотрим пример.

Щенок Антошка смотрит, как на ветке березы сидит 3 синички (с предметов) и 2 воробья (b предметов), он уже знает, что всего на дереве 5 птичек (a предметов).
Схематично можно записать так:  c + b = а (предметов).  Переместительное свойство сложения натуральных чисел позволяет также записать равенство вида b + c = a). Понятно, что если с березы улетит 2 воробья, то останется 3 синички. Запишем схематично a − b = c. Аналогично, если улетит 3 синички, то останется 2 воробья, то есть, a − c = b.

Рассмотренный пример наглядно демонстрирует, что если сумма чисел c и b равна a, то число c является разностью натуральных чисел a и b, а число b – разностью чисел a и c. 

То есть, c  = a − b и b = a − c, если c + b = a.

А также, если нам известно, что сумма двух чисел c и b равна a, то разность a − c равна b, а разность a − b равна c.

Вычитание – это действие, с помощью которого находится одно слагаемое, когда известна сумма и другое слагаемое.

На это определение будем равняться при построении правил, по которым выполняется вычитание двух натуральных чисел.

Вычитание чисел с использованием таблицы сложения натуральных чисел.С помощью Таблицы сложения можно находить не только сумму двух натуральных чисел, не превышающих десяти, но и одно слагаемое, если известна сумма и другое слагаемое. Покажем на примере, как это делается.

Найти неизвестное слагаемое, если известное слагаемое равно 6, а сумма равна 10 (в таблице эти строки и столбцы закрашены зеленым цветом).

Очевидно — нам необходимо просто провести линию до пересечения с искомым ответом, в нашем случае ответ = 4

Вычитание натурального числа из суммы чисел.

Чтобы вычесть натуральное число из суммы двух чисел можно сначала вычислить сумму, после чего из нее вычесть данное натуральное число. 

А можно воспользоваться свойством вычитания натурального числа из суммы двух чисел, если это упростит процесс вычитания. Рассмотрим несколько примеров.

Вычтем из суммы 50 + 8 натуральное число 20. Сумма 50 + 8 представляет собой сумму разрядных слагаемых числа 58. Мы пока не знаем, как из 58 вычесть 20, поэтому будем искать другой вариант решения. Воспользуемся свойством вычитания натурального числа из суммы: так как 20<50 (при необходимости обращайтесь к статье сравнение натуральных чисел), то справедливо равенство (50 + 8) −20 = (50 − 20) + 8. Находим, что 50 − 20 = 30 (5 десятков минус 2 десятка), тогда (50 − 20) + 8 = 30 + 8. Последняя сумма равна 38. Итак, все решение можно записать в виде цепочки равенств следующего вида: (50 + 8)−20 = (50 − 20)+8 = 30 + 8 = 38.

Усложним пример. Выполним вычитание числа 20 из суммы 20 000 + 6 000 + 300 + 50 + 1. Для этого воспользуемся свойством вычитания натурального числа из суммы. Мы без труда можем вычесть число 20 из числа 50, поэтому целесообразно вычитание провести следующим образом:

(20 000 + 6 000 + 300 + 50 + 1) − 20 = 20 000 + 6 000 + 300 + (50 − 20) + 1=20 000 + 6 000 + 300 + 30 + 1 = 26 331.

Вычитание суммы чисел из натурального числа.

Чтобы вычесть сумму двух чисел из данного натурального числа, можно сначала вычислить сумму, после чего провести вычитание. Однако часто удобнее использовать свойство вычитания суммы двух чисел из натурального числа. Рассмотрим несколько примеров.

Вычтем из числа 100 сумму 90+8. По свойству вычитания суммы из натурального числа имеем 100−(90+8)=(100−90)−8. Находим 100−90=10 (10 десятков минус 9 десятков). Осталось лишь закончить вычисление: (100−90)−8=10−8=2.

Приведем еще один пример. Отнимем от числа 17 сумму чисел 8 и 4. Имеем 17 − (8 + 4) = (17 − 8) − 4. Из таблицы сложения находим, что 17 − 8 = 9, тогда (17 − 8) − 4 = 9 − 4 = 5. Кратко решение можно записать так: 17 − ( 8 + 4)=(17 − 8) − 4 = 9 − 4 = 5.

Если вы хотите что-нибудь добавить на сайт «Спиши у Антошки», или у вас остались вопросы после прочтения материала, напишите мне [email protected] я с радостью нацарапаю вам ответ лапкой.

spishy-u-antoshki.ru

No related posts.