Выполнить действия над комплексными числами: Действия с комплексными числами

Действия над комплексными числами

Над комплексными числами можно выполнять следующие действия:

• сложение;
• вычитание;
• умножение;
• деление;
• возведение комплексного числа в степень;
• извлечение корня $n$—й степени из комплексного числа.

Операции сложения и вычитания выполняются для чисел, представленных в алгебраической форме.

Умножение, деление и возведение в степень выполняются для чисел, представленных в любой форме записи.

Извлечение корня выполняется для чисел, представленных в тригонометрической форме.

Определение 1

Запись некоторого комплексного числа $z$ в виде $z=a+bi$ называется алгебраической формой записи (или алгебраической записью) комплексного числа. При этом:

• $a$ — вещественная (действительная) часть;
• $b$ — мнимая часть.

Определение 2

Запись некоторого комплексного числа $z$ в виде $z=r\cdot (\cos \varphi +i\sin \varphi )$ называется тригонометрической формой записи, где число $r$ — модуль комплексного числа $z$, определяемый по формуле $r=|z|=|a+bi|=\sqrt{a^{2} +b^{2} } $, $\varphi $ — аргумент комплексного числа $z$, определяемый по формуле $\varphi =arctg\frac{b}{a} $. {2} } $, $\varphi $ — аргумент комплексного числа $z$, определяемый по формуле $\varphi =arctg\frac{b}{a} $.

Примечание 1

При необходимости извлечения корня из комплексного числа, записанного в показательной форме, необходимо предварительно привести его к тригонометрической форме представления.

Сумма комплексных чисел

Суммой двух заданных комплексных чисел $z_{1} =a_{1} +b_{1} i$ и $z_{2} =a_{2} +b_{2} i$ является комплексное число, которое определяется равенством \[z_{1} +z_{2} =(a_{1} +b_{1} i)+(a_{2} +b_{2} i)=(a_{1} +a_{2} )+(b_{1} +b_{2} )\cdot i.\]

Разность комплексных чисел

Разностью двух заданных комплексных чисел $z_{1} =a_{1} +b_{1} i$ и $z_{2} =a_{2} +b_{2} i$ является комплексное число, которое определяется равенством \[z_{1} -z_{2} =(a_{1} +b_{1} i)-(a_{2} +b_{2} i)=(a_{1} -a_{2} )+(b_{1} -b_{2} )\cdot i.\]

Пример 1

Выполнить действия: 1) $z_{1} +z_{2} $2) $z_{1} -z_{2} $ для заданных комплексных чисел $z_{1} =2+4i$ и $z_{2} =1-3i$.

{2} =2+4i+6=8+4i\]

Пример 3

Выполнить умножение комплексных чисел представленных в тригонометрической форме:

$z_{1} =3\sqrt{3} \cdot (\cos \frac{\pi }{2} +i\cdot \sin \frac{\pi }{2} )$ и $z_{2} =2\cdot (\cos \pi +i\cdot \sin \pi )$.

Решение:

1) По определению имеем: $z_{1} \cdot z_{2} =r_{1} \cdot r_{2} \cdot [\cos (\varphi _{1} +\varphi _{2} )+i\sin (\varphi _{1} +\varphi _{2} )]$

Для исходных чисел получаем:

\[\begin{array}{l} {z_{1} \cdot z_{2} =\left(3\sqrt{3} \cdot (\cos \frac{\pi }{2} +i\cdot \sin \frac{\pi }{2} )\right)\cdot \left(2\cdot (\cos \pi +i \cdot \sin \pi )\right)=6\cdot \sqrt{3} \cdot \left[\cos \left(\frac{\pi }{2} +\pi \right)+i\cdot \sin \left(\frac{\pi }{2} +\pi \right)\right]=} \\ {=6\sqrt{3} \cdot \left(\cos \frac{3\pi }{2} +i\cdot \sin \frac{3\pi }{2} \right)} \end{array}\]

Частное комплексных чисел

Частным двух заданных комплексных чисел $z_{1} =r_{1} \cdot (\cos \varphi _{1} +i\sin \varphi _{1} )$ и $z_{2} =r_{2} \cdot (\cos \varphi _{2} +i \sin \varphi _{2} )$ является комплексное число, которое определяется равенством

\[z_{1} \div z_{2} =\frac{r_{1} }{r_{2} } \cdot [\cos (\varphi _{1} -\varphi _{2} )+i\sin (\varphi _{1} -\varphi _{2} )]. {2} } =\frac{2+3i-1}{1+1} =\frac{1+3i}{2} = \frac{1}{2} +\frac{3}{2} i\]

Пример 5

Выполнить деление комплексных чисел представленных в тригонометрической форме:

$z_{1} =3\cdot \left(\cos \frac{2\pi }{3} +i\cdot \sin \frac{2\pi }{3} \right)$ и $z_{2} =2\cdot (\cos 2\pi +i\cdot \sin 2\pi )$.

Решение:

По определению имеем: $z_{1} \div z_{2} =\frac{r_{1} }{r_{2} } \cdot [\cos (\varphi _{1} -\varphi _{2} )+i\sin (\varphi _{1} -\varphi _{2} )]$

Для исходных чисел получаем:

\[\begin{array}{l} {\frac{z_{1} }{z_{2} } =3\cdot \left(\cos \frac{2\pi }{3} +i\cdot \sin \frac{2\pi }{3} \right)\div \left(2\cdot (\cos 2\pi +i\cdot \sin 2\pi )\right)=\frac{3}{2} \cdot \left[\cos \left(\frac{2\pi }{3} -2\pi \right)+i\cdot \sin \left(\frac{2\pi }{3} -2\pi \right)\right]=} \\ {= \frac{3}{2} \cdot \left(\cos \left(-\frac{4\pi }{3} \right)+i\cdot \sin \left(-\frac{4\pi }{3} \right)\right)} \end{array}\]

Степерь комплексного числа

Степенью порядка $n$ некоторого комплексного числа $z=r\cdot (\cos \varphi +i\sin \varphi )$ является комплексное число, которое определяется равенством

\[z^{n} =r^{n} \cdot (\cos n\varphi +i\sin n\varphi ). {100} \cdot \left(\cos \left(100\cdot \frac{\pi }{2} \right)+i\cdot \sin \left(100\cdot \frac{\pi }{2} \right)\right)=1\cdot \left(\cos 50\pi +i\cdot \sin 50\pi \right)=1\cdot \left(\cos 0+i\cdot \sin 0\right).\]

Корень комплексного числа

Корнем $n$-й степени некоторого комплексного числа $z=r\cdot (\cos \varphi +i\sin \varphi )$ является комплексное число, которое определяется равенством

\[\sqrt[{n}]{z} =\sqrt[{n}]{r} \cdot (\cos \frac{\varphi +2\pi k}{n} +i\sin \frac{\varphi +2\pi k}{n} ),\, \, \, k=0..n-1.\]

Пример 8

Выполнить действие $\sqrt[{3}]{z} $, где $z=4\cdot (\cos \pi +i\cdot \sin \pi )$.

Решение:

Для $k=0$ получаем: $w_{1} =\sqrt[{3}]{z} =\sqrt[{3}]{4} \cdot \left(\cos \frac{\pi }{3} +i\cdot \sin \frac{\pi }{3} \right)$.

Для $k=1$ получаем: $w_{2} =\sqrt[{3}]{z} =\sqrt[{3}]{4} \cdot \left(\cos \frac{\pi +2\pi }{3} +i\cdot \sin \frac{\pi +2\pi }{3} \right)=\sqrt[{3}] {4} \cdot \left(\cos \pi +i\cdot \sin \pi \right)$.

Для $k=2$ получаем: $w_{3} =\sqrt[{3}]{z} =\sqrt[{3}]{4} \cdot \left(\cos \frac{\pi +4\pi }{3} +i\cdot \sin \frac{\pi +4\pi }{3} \right)=\sqrt[{3}] {4} \cdot \left(\cos \frac{5\pi }{3} +i\cdot \sin \frac{5\pi }{3} \right)$.

Действия над комплексными числами в тригонометрической форме

Умножение комплексных чисел. Возьмем два комплексных числа в тригонометрической форме:

Перемножая их, получим:

Таким образом, при умножении комплексных чисел модули их перемножаются:

|а аргументы складываются

Геометрическая интерпретация умножения комплексных чисел.

Пусть требуется умножить комплексное число на комплексное число.

Комплексное число представляется вектором , а комплексное число представляется вектором. Чтобы построить вектор, изображающий комплексное число

надо вектор повернуть на угол против часовой стрелки, если, и по часовой стрелке, если. и«увеличить» его длину в раз (рис. 3).

Так как , то умножение любого числаz на i можно рассматривать как операцию поворота вектора, изображающего число z на угол против движения часовой стрелки.

Рис. 3.

Деление комплексных чисел.

Возьмем два комплексных числа ии разделим на .

Так как деление комплексных чисел рассматривается как действие, обратное умножению, то

Таким образом, при делении комплексных чисел модули делятся, а аргументы вычитаются:

Для построения вектора, изображающего комплексное число , надо вектор повернуть на угол по часовой стрелке, если, и против, если, и «уменьшить» его длину враз.

Деление комплексного числа z на i можно рассматривать как операцию поворота вектора на уголпо часовой стрелке.

Возведение в степень комплексных чисел.

Возведение в степень n (где n — натуральное число) комплексного числа z рассматривается как n-кратное умножение z на самого себя.

Пусть . Тогда

.

т. е. (**)

Таким образом при возведении комплексного числа в степень модуль возводится в эту степень, а аргумент умножается на число, равное показателю степени:

Формулу (**) можно записать:

В частном случае, когда n=1 эта формула имеет вид:

Эта формула называется формулой Муавра.

Извлечение корня из комплексных чисел

Пусть n – натуральное число. Корнем n – степени из комплексного числа называется комплексное число, для которого.

Обозначим его

Давая k значения 0,1,2,…,(n-1)? Получим n различных значений корня. Для значений k=n,n+1… или k=-1, -2,…

и т.д. значения корней будут повторять полученные ранее значения.

Например, при k=0 имеем . Приk=n имеем и т.д.

Обобщая данный частный случай, можно сказать, что геометрически точки, соответствующие различным значениям корня n – й степени из комплексного числа , располагаются в вершинах правильногоn – угольника с центром θ, причем одна из вершин соответствует числу .

Действительная часть комплексного числа обозначается ReZ (ReZ=x), а мнимая часть обозначается символом ImZ (ImZ=y). Следовательно, комплексное число можно записать .

Запись комплексного числа называется алгебраической формой записи.

Комплексное число называется сопряженным с комплексным числоми обозначается.

Каждое комплексное число можно изобразить на плоскости Оху в виде точкиM(x,y) или ее радиус – вектором и обратно, всякая точкаM(x,y) плоскости Оху может быть рассмотрена как геометрический образ комплексного числа .

Таким образом, комплексные числа могут изображаться как точками, так и векторами. Плоскость, на которой изображаются комплексные числа, называется комплексной плоскостью, ось

Ох — действительная ось, ось Оу — мнимая. Модуль числа Z равен расстоянию точки М(х,у), изображающей это число, от начала координат. Введя полярную систему координат, получим , тогда . Выражение называется тригонометрической формой записи комплексного числа Z. Величины r и φ выражаются через х и у (см. рис. 4).

Рис. 4.

и называются соответственно модулем и аргументом комплексного числа . Аргумент φ комплексного числа Z определяется неоднозначно, а с точностью до слагаемого 2πk, где k — любое целое число.

Значение argZ, удовлетворяющее условию 0

называется главным значением аргумента и обозначается символом argZ. В некоторых случаях главным значением аргумента называют значение argZ, удовлетворяющее условию . Еслиr = 0, то комплексное число равно нулю и его аргумент неопределён. Действительное число имеет аргумент 2πk (главное значение аргумента равно нулю), если оно положительное, и (главное значение аргумента равно π^—), если оно отрицательное. Если действительная часть комплексного числа равна нулю

—называется чисто мнимым комплексным числом), то аргумент его равен (главное значение аргумента равно , еслиу > 0 и или; (главное значение аргумента равноили), еслиу < 0. Аргумент комплексного числа, угол φ, считается положительным, если он отсчитывается от положительного направления оси Ох

против часовой стрелки, и отрицательным при противоположном направлении отсчёта.

Пример. Записать в тригонометрической форме следующие комплексные числа:

Решение. Для того, чтобы комплексное число записать в тригонометрической форме, нужно найти его модуль и значение аргумента φ, который связан с координатами хи у следующими формулами , причём ни одна из этих формул в отдельности не позволяет найти φ по заданным х и у.

а) Любое действительное число а можно записать в тригонометрической форме.

1. а > 0, и, если ограничиться главным значением аргумента (k = 0), то .

2. a < 0, и, если ограничиться главным значением аргумента(k = 0), то

Тогда:

и при k=0,

и при k=0.

б) Z = 3i. Так как в этом случае действительная часть равна нулю, то комплексное число находится на оси Оу и r = |3|, а аргумент его равен , если у>0 и

при у < 0. Тогда:

в) 1. . Так кактолежит в первой координатной четверти, асоответствует. Другой способ. Так как, то φ находится в первой координатной четверти и равен. Следовательно

2. .лежит в четвертой четверти (x>0, y<0) и , тогдаили так как, то φ находится в четвертой координатной четверти и равен. Тогда

Для того, чтобы записать комплексное число в показательной форме, используем формулы Эйлера

выражающие показательную функцию через тригонометрическую и обратно. Тогда получим

Используя формулы Эйлера, можно выразить любую целую положительную степень cosx и sinx, а также их произведения в виде суммы членов, содержащих лишь первые степени синусы и косинусы кратных дуг:

Пример. Представить в комплексной форме следующее число:

Решение. Ограничимся главными значениями аргументов.

Пример. Найти значения: и решить уравнения

Решение. Так как

Полагая k=0 и k=1, находим два значения корня

При дальнейших значения k корни будут повторятся.

3) Учитывая, что , получим

При дальнейших значения k корни будут повторятся.

Действия с комплексными числами

Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: Археология Биология Генетика География Информатика История Логика Маркетинг Математика Менеджмент Механика Педагогика Религия Социология Технологии Физика Философия Финансы Химия Экология ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрации Техника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ? Влияние общества на человека Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления

⇐ ПредыдущаяСтр 2 из 4Следующая ⇒ Время проведения –2 часа. Цель работы:отработать навыки выполнения действий с комплексными числами; научиться решать квадратные уравнения, дискриминант которых отрицателен. Вопросы для подготовки к работе: 1. Понятие мнимой единицы; 2. Понятие комплексного числа; 3. Понятие модуля и аргумента комплексного числа; 4. Равенство комплексных чисел; 5. Решение квадратных уравнений, дискриминант которых отрицателен; 6. Действие над комплексными числами в алгебраической форме; 7. Геометрическая интерпретация комплексного числа; 8. Тригонометрическая форма комплексного числа; Содержание работы: 1. Решение квадратных уравнений, дискриминант которых отрицателен; 2. Выполнение действий над комплексными числами; 3. Геометрическая интерпретация комплексного числа; 4. Представление комплексного числа в тригонометрической форме. Литература:[1, с.17-23] Порядок выполнения задания: При выполнении первого задания необходимо учитывать следующее: в комплексных числах можно извлечь квадратный корень из отрицательного числа, так как , где — мнимая единица. Следовательно, в поле комплексных чисел разрешимо любое квадратное уравнение, в том числе с отрицательным дискриминантом. Пример: Решить уравнение Решение: Найдем дискриминант , , следовательно, уравнение имеет мнимые корни, которые находят по формуле Ответ: Для выполнения второго, третьего заданий необходимо уметь применять операции над комплексными числами и знать правило равенства комплексных чисел. Отметим, что с комплексными числами, записанными в алгебраической форме, операции сложения, вычитания и умножения можно производить также, как с действительными биномами, деление выполняют путем умножения делимого и делителя на число, сопряженное делителю. Правило равенства: два комплексных числа равны тогда и только тогда, когда равны их действительные части и равны коэффициенты мнимых частей. Пример: Найдите сумму, разность, произведение, частное двух комплексных чисел Решение: , где Ответ: , , , Пример: Найдите действительные решения уравнения Решение: В соответствии с правилом равенства получаем: Ответ: Для выполнения четвертого, пятого заданий необходимо знать тригонометрическую форму записи комплексного числа и его геометрическую интерпретацию. Геометрическая интерпретация комплексных чисел состоит в том, что каждому комплексному числу ставится в соответствие точка М координатной плоскости таким образом, что действительная часть комплексного числа представляет собой абсциссу (ось называют действительной), а коэффициент при мнимой части – ординату точки (ось называют мнимой). y       b   М     r φ   0   a x   Расстояние от начала системы координат до точки, соответствующей комплексному числу , называют модулем этого числа, который вычисляют по формуле: . Угол между положительной полуосью и лучом называют аргументом комплексного числа . Выражение называют тригонометрической формой комплексного числа. Пример: Изобразить на комплексной плоскости число и записать его в тригонометрической форме. Решение: Комплексному числу соответствует точка плоскости y M 1 r φ   0 X   Для комплексного числа имеем: , (по чертежу). Поэтому в тригонометрической форме комплексное число имеет вид: Ответ: Вариант 1 1. Решить уравнение 1) 2) 3) 4) 2. Выполнить действия над комплексными числами, представив результат в алгебраической форме 1) 2) 3) 4) 5) 6) 7) 3. Найти действительные решения уравнения 1) 2) 4. Изобразите на комплексной плоскости следующие комплексные числа 1) 2) 5. Записать комплексное число в тригонометрической форме   Вариант 2 1. Решить уравнение 1) 2) 3) 4) 2. Выполнить действия над комплексными числами, предствавив результат в алгебраической форме 1) 2) 3) 4) 5) 6) 7) 3. Найти действительные решения уравнения 1) 2) 4. Изобразите на комплексной плоскости следующие комплексные числа 1) 2) 5. Записать комплексное число в тригонометрической форме     Практическая работа № 8 ⇐ Предыдущая1234Следующая ⇒ Читайте также:  Алгоритмические операторы Matlab Конструирование и порядок расчёта дорожной одежды Исследования учёных: почему помогают молитвы? Почему терпят неудачу многие предприниматели? 

Последнее изменение этой страницы: 2016-04-18; просмотров: 1766; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia. su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь — 161.97.168.212 (0.014 с.)

Действия над комплексными числами в алгебраической форме

Математика Действия над комплексными числами в алгебраической форме

просмотров — 1813

Сложение, вычитание, умножение комплексных чисел в алгебраической форме производят по правилам соответствующих действий над многочленами.

Пример 2. Даны комплексные числа z₁ = 2 + 3i, z₂ = 5 – 7i. Найти:

а) z₁ + z₂; б) z₁ – z₂; в) z₁z₂.

Решение.

а) z₁ + z₂ = (2 + 3i) + (5 – 7i) = 2 + 3i + 5 – 7i = (2 + 5) + (3i – 7i) = 7 – 4i; б) z₁ – z₂ = (2 + 3i) – (5 – 7i) = 2 + 3i – 5 + 7i = (2 – 5) + (3i + 7i) = – 3 + 10i; в) z₁z₂ = (2 + 3i)(5 – 7i) = 10 – 17i + 15i – 21i² = 10 – 14i + 15i + 21 = (10 + 21) + (– 14i + 15i) = 31 + i (здесь учтено, что i² = – 1).

Пример 3. Выполнить делœение:

Решение.

а) Имеем

Произведем умножение для делимого и делителя в отдельности:

(2 + 3i)(5 + 7i) = 10 + 14i + 15i + 21i² = – 11 + 29i; (5 – 7i)(5 + 7i) = 25 – 49i² = 25 + 49 = 74.

Итак,

Пример 4. Решите уравнение:

x² – 6x + 13 = 0

Решение. а) Найдем дискриминант по формуле

D = b² – 4ac.

Так как a = 1, b = – 6, c = 13, то

D = (– 6)2 – 4*1*13 = 36 – 52 = – 16;

Корни уравнения находим по формулам

Текст задания

1–7. Вычислите:

1. i⁶⁶; i¹⁴³; i²¹⁶; i¹³⁷. 2. i⁴³ + i⁴⁸ + i⁴⁴ + i⁴⁵. 3. (i³⁶ + i¹⁷)i²³. 4. (i¹³³ + i¹¹⁵ + i²⁰⁰ + i¹⁴²)(i¹⁷ + i³⁶). 5. i¹⁴⁵ + i¹⁴⁷ + i²⁶⁴ + i³⁴⁵ + i¹¹⁷. 6. (i¹³ + i¹⁴ + i¹⁵)i³². 7. (i⁶⁴ + i¹⁷ + i¹³ + i⁸²)(i⁷² – i³⁴).

8–13. Найдите значения x и y из равенств:

8. 7x + 5i = 1 – 10iy. 9. (2x + y) – i = 5 + (y – x)i. 10. x + (3x – y)i = 2 – i. 11. (1 + 2i)x + (3 – 5i)y = 1 – 3i. 12. (2 – i)x + (1 + i)y = 5 – i. 13. (3i – 1)x + (2 – 3i)y = 2 – 3i.

14–21. Произведите сложение и вычитание комплексных чисел:

14. (3 + 5i) + (7 – 2i). 15. (6 + 2i) + (5 + 3i). 16. (– 2 + 3i) + (7 – 2i). 17. (5 – 4i) + (6 + 2i). 18. (3 – 2i) + (5 + i). 19. (4 + 2i) + (– 3 + 2i). 20. (– 5 + 2i) + (5 + 2i). 21. (– 3 – 5i) + (7 – 2i).

22–29. Произведите умножение комплексных чисел:

22. (2 + 3i)(5 – 7i). 23. (6 + 4i)(5 + 2i). 24. (3 – 2i)(7 – i). 25. (– 2 + 3i)(3 + 5i). 26. (1 –i)(1 + i). 27. (3 + 2i)(1 + i). 28. (6 + 4i)*3i. 29. (2 – 3i)(– 5i).

30–37. Выполните действия:

30. (3 + 5i)². 31. (2 – 7i)². 32. (6 + i)². 33. (1 – 5i)². 34. (3 + 2i)³. 35. (3 – 2i)³. 36. (4 + 2i)³. 37. (5 – i)³.

38–43. Выполните действия:

38. (3 + 2i)(3 – 2i). 39. (5 + i)(5 – i). 40. (1 – 3i)(1 + 3i). 41. (7 – 6i)(7 + 6i). 42. (a + bi)(a – bi). 43. (m – ni)(m + ni).

44–55. Выполните делœение:

56–60. Выполните действия:

61 — 64. Решите уравнения:

61. x² – 4x + 13 = 0. 62. x² + 3x + 4 = 0. 63. 2,5x² + x + 1 = 0. 64. 4x² – 20x + 26 = 0.

Практическая работа № 4

Тема: Корни и степени

Цель работы: закрепить знания и умения студентов по освоению применения формул при выполнении вычислений и решении иррациональных уравнений.

Теоритическое обоснование:

— Определение, изображение комплексных чисел. Действия над комплексными числами в алгебраической форме

Комплексные числа На множестве С вводятся понятия функции, предела таким образом, что соответствующие понятия действительного анализа рассматриваются как част­ный случай.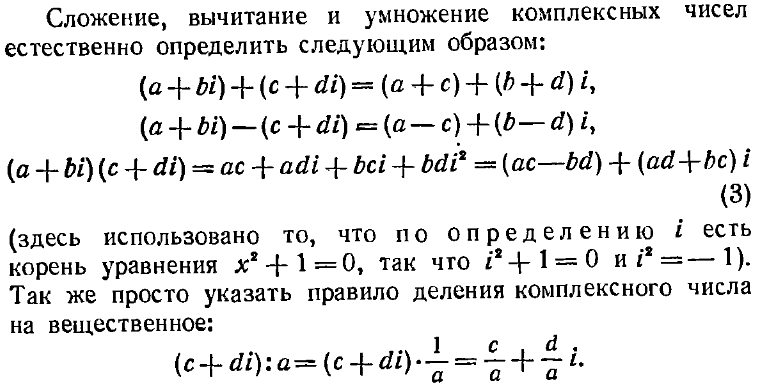 Естественно, при этом сохраняются известные свойства функций действительного переменного:… [читать подробенее]

— Действия над комплексными числами в алгебраической форме

Сложение, вычитание, умножение комплексных чисел в алгебраической форме производят по правилам соответствующих действий над многочленами. Пример 2. Даны комплексные числа z1 = 2 + 3i, z2 = 5 – 7i. Найти: а) z1 + z2; б) z1 – z2; в) z1z2. Решение. а) z1 + z2 = (2 + 3i) + (5 – 7i) = 2 + 3i + 5 – 7i = (2 + 5) + (3i – 7i) =… [читать подробенее]

— Действия над комплексными числами в алгебраической форме.

В алгебраической форме над комплексными числами удобно выполнять следующие операции: · сложение; · вычитание; · умножение; · деление. Сложение, вычитание и умножение комплексных чисел производят по правилам соответствующих действий над многочленами. Пример 42.2. Для… [читать подробенее]

— Действия над комплексными числами в алгебраической форме

Суммой двух комплексных чисел и называется комплексное число . Произведением двух комплексных чисел и называется комплексное число . Вычитание комплексных чисел вводится как операция, обратная сложению; деление комплексных чисел вводится как операция, обратная… [читать подробенее]

Комплексные числа — MATHS HELPER

Комплексными числами называются всевозможные упорядоченные пары $z=(x,y)$ действительных чисел. Множество всех комплексных чисел обозначается символом $\mathbb{C}$.

Действительные числа $x$ и $y$ называются действительной и мнимой частями комплексного числа $z=(x,y)$ и обозначаются символами $\mbox{Re} z$ и $\mbox{Im} z$ соответственно. Два комплексных числа $z_1=(x_1,y_1)$ и $z_2=(x_2,y_2)$ называются равными в том и только в том случае, когда равны их действительные и мнимые части $x_1=x_2$, $y_1=y_2$.

Для комплексных чисел операции сложения и умножения определяются следующим образом:

(1)

\begin{equation} (x_1,y_1)+(x_2,y_2)=(x_1+x_2,y_1+y_2). 2}}\\ \end{array} \right. \end{align}

называется аргументом комплексного числа $z=x+iy\neq0$.

Все аргументы числа $z$ различаются на целые кратные $2\pi$ и обозначаются единственным символом $\mbox{Arg}z$. Каждое значение аргумента совпадает с величиной $\varphi$ некоторого угла, на который следует повернуть ось $Ox$ до совпадения с радиус-вектором $\overline{OM}$ точки $M$ (при этом $\varphi>0$, если поворот совершается против часовой стрелки, и $\varphi<0$ в противном случае).

Значение $\mbox{Arg}z$, удовлетворяющее условию $0\leqslant\mbox{Arg}z<2\pi$ называется главным значением аргумента и обозначается символом $\mbox{arg}z$. В некоторых случаях главным значением аргумента называется значение $\mbox{Arg}z$, удовлетворяющее условию $-\pi<\mbox{Arg}z\leqslant\pi$.
Из соотношения (4) следует, что для всякого комплексного числа $z$ справедливо равенство
$$z=|z|\left(\cos\varphi+i\sin\varphi\right),$$
называемое тригонометрической формой комплексного числа $z$. {i\left(\frac{2\pi}{9}+\frac{2\pi k}{3}\right)}=\sqrt[3]{4}\left(\cos\left(\frac{2\pi}{9}+\frac{2\pi}{3}k\right)\right.+\left.i\sin\left(\frac{2\pi}{9}+\frac{2\pi}{3}k\right)\right),$ где $k=0,\,1,\,2.$
При
$k=0:~\left(\sqrt[3]{a}\right)_0=\sqrt[3]{4}\left(\cos\frac{2\pi}{9}+i\sin\frac{2\pi}{9}\right),$ $k=1:~\left(\sqrt[3]{a}\right)_1=\sqrt[3]{4}\left(\cos\frac{8\pi}{9}+i\sin\frac{8\pi}{9}\right),$ $k=2:~\left(\sqrt[3]{a}\right)_2=\sqrt[3]{4}\left(\cos\frac{14\pi}{9}+i\sin\frac{14\pi}{9}\right).\blacktriangleright$

---

Тема 7. Мнимая единица. Комплексные числа. Действия над комплексными числами — FINDOUT.SU

Поможем в ✍️ написании учебной работы

Имя

Поможем с курсовой, контрольной, дипломной, рефератом, отчетом по практике, научно-исследовательской и любой другой работой

Выберите тип работыЧасть дипломаДипломная работаКурсовая работаКонтрольная работаРешение задачРефератНаучно — исследовательская работаОтчет по практикеОтветы на билетыТест/экзамен onlineМонографияЭссеДокладКомпьютерный набор текстаКомпьютерный чертежРецензияПереводРепетиторБизнес-планКонспектыПроверка качестваЭкзамен на сайтеАспирантский рефератМагистерская работаНаучная статьяНаучный трудТехническая редакция текстаЧертеж от рукиДиаграммы, таблицыПрезентация к защитеТезисный планРечь к дипломуДоработка заказа клиентаОтзыв на дипломПубликация статьи в ВАКПубликация статьи в ScopusДипломная работа MBAПовышение оригинальностиКопирайтингДругое

Нажимая кнопку «Продолжить», я принимаю политику конфиденциальности

1) Мнимая единица. Степень мнимой единицы.

2) Множество комплексных чисел, их геометрическая интерпретация

3) Модуль и аргумент комплексного числа.

4) Действия над комплексными числами в алгебраической форме (сложение, вычитание, умножение, деление, возведение во вторую и третью степень).

5) Элементарные вычисления с помощью МК.

 

х² + 4 = 0       х² = — 4          во множестве R решений нет

                     

Обозначим:

 

   

 

Множество действительных чисел и мнимая единица составляют множество комплексных чисел, тогда

 

i ²³ = i ³ = — i                (23 : 4 = 4  5 + 3)

 

i ²³ = i ²⁰  i ³ = 1  (-i) = — i

 

i ⁴⁸ = i ⁰ = 1      i ¹⁰  i ⁸ i ²  = 1 (-1) = -1 i ¹⁴ = i ² = — 1            i ²⁵ = i ¹ = i

 

i ¹⁰³ = i ³ = — i             2 i ³ — 7 i ⁸ + 5 i ⁹ + 4 i ¹⁰ = — 2 i — 7 + 5 i — 4 = — 11 + 3 i

 

Число Z = a + b i — комплексное число (алгебраическая форма записи)

а — действительная часть числа

b i — мнимая часть числа

a + b i = a1  + b1 i         если а = а1 b = b1

 

a + b i  и  a — b i называются сопряженными

 

 

Например

 

2 — 3 i и 2 + 3 i

 

— 4 — i и — 4 + i ,    т. е. отличаются знаком перед мнимой частью

 

Числа a + b i  и — a — b i   называются противоположными

 

 

Например

 

— 3 — 4 i и 3 + 4 i

 

— 5 + 2 i и 5 — 2 i ,    т.е. отличаются знаками и перед мнимой и перед действительной частями

Комплексные числа изображаются геометрически точкой (a; b) или радиусом — вектором, проведенным к этой точке из начала координат

(-2;3)

Z 1 = 5i Z 2 = 2 Z 3 = — 3i           Z 4 = — 4i

(3;-4)

Z = 3 — 4 i        Z = — 2 + 3 i

 

Изобразите числа:

 

Z = — 7 + 2 i                             Z = — 9 — i

 

Z = — 1 — 4 i                             Z = 12

 

Z = — 5 i                                  Z = 6 i

 

Z = — 4                                   Z = — 3 — 2 i

 

Итак: a + bi

(-a;b)

(a;-b)

(-a;-b)

a  OX                                                                                                                     I ч j > 0 острый

 

b  OY                                                                                                II ч j > 0 тупой j = 180 ⁰ — j₁

 

             III ч j < 0; тупой j = — (180 ⁰ — j₁)

 

                                              IV ч j < 0; острый

 

 

 – модуль комплексного числа

 аргумент комплексного числа

 

Найти модуль и аргумент комплексного числа:

 

а) Z = 5 + 2 i

 

   

 

б)  Z = — 3 + 7 i

 

 

 

 

в) Z = — 5 — i

 

     

 

г) Z = 3 — 5 i

 

      

 

 

Для чисел, состоящих только из мнимой или только действительной частей нахождение  и     упрощается:

 

1) Z = 2             

 

2 = 2 + 0i                 Число находится на «ОХ»

 

2) Z = 3i                               

 

3i = 0 + 3i                          Число находится на «ОУ»

 

 

3) Z = — 4         

 

  Число находится на «ОХ» (влево)

 

4) Z = — 7 i

 

 Число находится на «ОУ» (вниз)

Рассмотрим действия над числами

Сложение

Z ₁ + Z ₂ = (a ₁ + b ₁ i) + (a ₂ + b ₂ i) = a ₁ + b ₁ i + a ₂ + b ₂ i = (a ₁  + a ₂) + (b ₁ + b ₂) i

 

Вычитание

Z ₁ — Z ₂ = (a ₁ + b ₁ i) — (a ₂ + b ₂ i) = a ₁ + b ₁ i — a ₂ — b ₂ i = (a ₁  — a ₂) + (b ₁ — b ₂) i

Умножение

Z ₁ Z ₂ = (a ₁ + b ₁ i) (a ₂ + b ₂ i) = a ₁  a ₂ + b ₁ а ₂ i + a ₁ b ₂ i + b ₁ b ₂ i ² =

 

= a ₁ a ₂  + i (b ₁ а ₂  + a ₁ b ₂) — b ₁ b ₂ = (a ₁ a ₂  — b ₁ b ₂) + (b ₁ а ₂  + a ₁ b ₂) i

Например

1) (3 — 5 i) (- 3 + i) = — 9 + 15 i + 3 i — 5 i ² = — 9 +18 i + 5 = — 4 + 18i;

 

                             т. к. i ² = — 1, то -5 (-1) = 5

 

 

2) (2 — 3 i) (2 + 3 i) = 4 — 9 i ² = 4 + 9 = 13

 

 

( a + b i ) ( a — b i ) = a ² — b ²  i ²   = a ² + b ²

( a + b i ) ( a — b i ) = a 2 + b 2

 Сумма квадратов

 

Сумма квадратов разлагается на множители только во множестве комплексных чисел

Деление

 

 

конкретно на примере:

 

 

Возведение в квадрат, куб (используем формулы сокращенного умножения)

 

Z = ( a + b i ) ² = a ² + 2 a b i + b ² i ² = a ² + 2 a b i — b ²;

 

например:

 

1)  ( — 4 + i ) ² = 16 — 8 i + i ² = 16 — 8 i — 1 = 15 — 8 i

 

2)  ( 2 — 3 i ) ³ = 8 — 3 2² 3 i + 3 2 ( — 3 i ) ² — 27 i ³ = 8 — 36 i + 54 i ² — 27 i ³ =

 

                        = 8 — 36 i — 54 + 27 i = — 46 — 9 i

 

Выполнить действия

 

 

при этих действиях использованы правила: i ³ = — i; i ² = — 1; ( a — b ) ² = a ² — 2 a b + b ² , а теперь разделим, для этого умножим знаменатель на сопряженное ему число ( — 5 + 12 i) , а чтобы дробь не изменилась умножаем и числитель на это число, т. е.

 

 

 

Тема 8. Размещения, перестановки, сочетания. Классическое определение вероятности.

Операции с комплексными числами

Горячая математика

К добавлять два комплексные числа , добавьте действительную часть к действительной части и мнимую часть к мнимой части.

( а + б я ) + ( с + д я ) знак равно ( а + с ) + ( б + д ) я

Пример 1:

( 2 + 7 я ) + ( 3 − 4 я ) знак равно ( 2 + 3 ) + ( 7 + ( − 4 ) ) я знак равно 5 + 3 я

К вычесть два комплексных числа, вычесть действительную часть из действительной части и мнимую часть из мнимой части.

( а + б я ) − ( с + д я ) знак равно ( а − с ) + ( б − д ) я

Пример 2:

( 9 + 5 я ) − ( 4 + 7 я ) знак равно ( 9 − 4 ) + ( 5 − 7 ) я знак равно 5 − 2 я

К умножить два комплексных числа, используйте ФОЛЬГА метод и объединять подобные термины .

( а + б я ) ( с + д я ) знак равно а с + а д я + б с я + б д я 2 знак равно а с + ( а д + б с ) я − б д ( Запомнить я 2 знак равно − 1 ) знак равно ( а с − б д ) + ( а д + б с ) я

Пример 3:

( 3 + 2 я ) ( 5 + 6 я ) знак равно 15 + 18 я + 10 я + 12 я 2 знак равно 15 + 28 я − 12 знак равно 3 + 28 я

К разделять два комплексных числа, умножьте числитель и знаменатель на комплексное сопряженный , расширить и упростить. Затем запишите окончательный ответ в стандартной форме.

а + б я с + д я ⋅ с − д я с − д я знак равно ( а с + б д ) + ( б с − а д ) я с 2 + д 2

Пример 4:

3 + 2 я 4 − 5 я знак равно 3 + 2 я 4 − 5 я ⋅ 4 + 5 я 4 + 5 я знак равно 12 + 15 я + 8 я + 10 я 2 16 + 25 знак равно 2 + 23 я 41 знак равно 2 41 + 23 41 я

Комплексные числа и операции с ними

Введение в комплексные числа

До этого момента квадратный корень из отрицательного числа оставался неопределенным. Например, мы знаем, что −9 не является действительным числом.

−9=? или  ( ?)2= −9

Не существует действительного числа, которое при возведении в квадрат дает отрицательное число. Мы начнем решать эту проблему, определив воображаемую единицу, определяемую как i=-1, где i2=-1., i , как квадратный корень из -1.

             i=−1       и           i2=−1

Чтобы выразить квадратный корень из отрицательного числа через мнимую единицу i , мы используем следующее свойство, где a представляет любое неотрицательное действительное число:

−a=−1⋅a=−1 ⋅a=ia

Таким образом, мы можем записать

−9=−1⋅9=−1⋅9=i⋅3=3i

Если −9=3i, то мы ожидаем, что 3i в квадрате будет равно −9 :

(3i)2=9i2=9(−1)=−9 ✓

Таким образом любой квадратный корень из отрицательного действительного числа может быть записан в терминах мнимой единицы. Такое число часто называют мнимым числом. Квадратный корень из любого отрицательного действительного числа. .

Пример 1

Перепишите в мнимой единице i .

1. −7
2. −25
3. −72

Решение:

1. −7=−1⋅7=−1⋅7=i7
2.  −25=−1⋅25=−1⋅25=i⋅5=5i
3.  −72=−1⋅36⋅2=−1⋅36⋅2=i⋅6⋅2=6i2

Обозначение Примечание : Когда мнимое число включает радикал, мы ставим i перед радикалом. Рассмотрим следующее:

6i2=62i

Поскольку умножение коммутативно, эти числа эквивалентны. Однако в форме 62i воображаемая единица i часто ошибочно интерпретируется как часть подкоренного числа. Чтобы избежать этой путаницы, лучше всего поместить i перед радикалом и использовать 6i2.

Комплексное числоЧисло вида a+bi, где a и b — действительные числа. любое число формы, а+би где a и b — действительные числа. Здесь a называется действительной частью. Действительное число a комплексного числа a+bi. а b называется мнимой частью. Действительное число b комплексного числа a+bi.. Например, 3−4i является комплексным числом с действительной частью 3 и мнимой частью -4. Важно отметить, что любое действительное число также является комплексным числом. Например, 5 — действительное число; его можно записать как 5 + 0i с действительной частью 5 и мнимой частью 0. Следовательно, множество действительных чисел, обозначенное ℝ, является подмножеством множества комплексных чисел, обозначенных ℂ.

ℂ={a+bi|a,b∈ℝ}

Комплексные числа используются во многих областях, включая электронику, технику, физику и математику. В этом учебнике мы будем использовать их, чтобы лучше понять решения таких уравнений, как x2+4=0. По этой причине мы далее исследуем алгебраические операции с ними.

Сложение и вычитание комплексных чисел

Сложение и вычитание комплексных чисел аналогично сложению и вычитанию многочленов с одинаковыми членами. Мы добавляем или вычитаем действительные части, а затем мнимые части.

Пример 2

Добавить: (5−2i)+(7+3i).

Решение:

Добавьте действительные части, а затем добавьте мнимые части.

(5−2i)+(7+3i)=5−2i+7+3i=5+7−2i+3i=12+i

Ответ: 12+i

Чтобы вычесть комплексные числа, мы вычитаем действительные части и вычесть мнимые части. Это согласуется с использованием распределительного свойства.

Пример 3

Вычесть: (10−7i)−(9+5i).

Решение:

Распределите знак минус, а затем соедините одинаковые члены.

(10−7i)−(9+5i)=10−7i−9−5i=10−9−7i−5i=1−12i

Ответ: 1−12i

В общем, при заданных действительных числах a , b , c и d :

(a+bi)+(c+di)=(a+c)+(b+d)i(a+bi)−(c+di )=(a−c)+(b−d)i

Пример 4

Упрощение: (5+i)+(2−3i)−(4−7i).

Решение:

(5+i)+(2−3i)−(4−7i)=5+i+2−3i−4+7i=3+5i

Ответ: 3+5i

Итого , сложение и вычитание комплексных чисел дает комплексное число.

Умножение и деление комплексных чисел

Умножение комплексных чисел аналогично умножению многочленов. Применяется распределительное свойство. Кроме того, мы используем тот факт, что i2=−1, чтобы упростить результат до стандартной формы a+bi.

Пример 5

Умножьте: −6i(2−3i).

Решение:

Начнем с применения свойства распределения.

−6i(2−3i)=(−6i)⋅2−(−6i)⋅3iРаспределить.=−12i+18i2Заменить i2=−1.=−12i+18(−1)Упростить.=−12i−18 =−18−12i

Ответ: −18−12i

Пример 6

Умножьте: (3−4i)(4+5i).

Решение:

(3−4i)(4+5i)=3⋅4+3⋅5i−4i⋅4−4i⋅5iРаспределить.=12+15i−16i−20i2Подставить i2=−1. =12+15i−16i−20(−1)=12−i+20=32−i

Ответ: 32−i

. d :

(a+bi)(c+di)=ac+adi+bci+bdi2=ac+adi+bci+bd(-1)=ac+(ad+bc)i-bd=(ac-bd )+(ad+bc)i

Попробуйте! Упростить: (3−2i)2.

Ответ: 5−12i

(нажмите, чтобы посмотреть видео)

Даны комплексные числа a+bi, их комплексно-сопряженные два комплексных числа, действительные части которых совпадают, а мнимые части противоположны. Если дано a+bi, то его комплексно-сопряженным является a−bi. это а-би. Далее мы исследуем произведение комплексных сопряженных чисел.

Пример 7

Умножьте: (5+2i)(5−2i).

Решение:

(5+2i)(5−2i)=5⋅5−5⋅2i+2i⋅5−2i⋅2i=25−10i+10i−4i2=25−4(−1)=25 +4=29

Ответ: 29

В общем случае произведение комплексно-сопряженных чиселДействительное число, которое получается в результате умножения комплексно-сопряженных чисел: (a+bi)(a−bi)=a2+b2. следующим образом:

(a+bi)(a−bi)=a2−a⋅bi+bi⋅a−b2i2=a2−abi+abi−b2(−1)=a2+b2

Обратите внимание, что результат не задействовать воображаемую единицу; следовательно, это реально. Это приводит нас к очень полезному свойству

(a+bi)(a−bi)=a2+b2

Для деления комплексных чисел мы применяем метод, используемый для рационализации знаменателя. Умножьте числитель и знаменатель на сопряженную часть знаменателя. Затем результат может быть упрощен до стандартной формы a+bi.

Пример 8

Разделить: 12−3i.

Решение:

В этом примере сопряжение знаменателя равно 2+3i. Поэтому мы будем умножать на 1 в виде (2+3i)(2+3i).

12−3i=1(2−3i)⋅(2+3i)(2+3i)=(2+3i)22+32=2+3i4+9=2+3i13

Чтобы записать это комплексное число в стандартной форме, мы используем тот факт, что 13 является общим знаменателем.

2+3i13=213+3i13=213+313i

Ответ: 213+313i

Пример 9

Разделить: 1−5i4+i.

Решение:

1−5i4+i=(1−5i)(4+i)⋅(4−i)(4−i)=4−i−20i+5i242+12=4−21i+5( −1)16+1=4−21i−517=−1−21i17=−117−2117i

Ответ: −117−2117i

d , где c и d не оба 0:

(a+bi)(c+di)=(a+bi)(c+di)⋅(c−di)(c−di) =ac-adi+bci-bdi2c2+d2=(ac+bd)+(bc-ad)ic2+d2=(ac+bdc2+d2)+(bc-adc2+d2)i

Пример 10

Разделить: 8−3i2i.

Решение:

Здесь мы можем думать о 2i=0+2i и, таким образом, мы можем видеть, что его сопряженное число равно −2i=0−2i.

8−3i2i=(8−3i)(2i)⋅(−2i)(−2i)=−16i+6i2−4i2=−16i+6(−1)−4(−1)=−16i−64 =−6−16i4=−64−16i4=−32−4i

Поскольку знаменатель является мономом, мы могли бы умножить числитель и знаменатель на 1 в форме ii и сэкономить несколько шагов, уменьшая в конце.

8−3i2i=(8−3i)(2i)⋅ i  i =8i−3i22i2=8i−3(−1)2(−1)=8i+3−2=8i−2+3−2=− 4i−32

Ответ: −32−4i

Попробуйте! Разделить: 3+2i1−i.

Ответ: 12+52i

(нажмите, чтобы посмотреть видео)

При умножении и делении комплексных чисел мы должны понимать, что правила произведения и частного для радикалов требуют, чтобы оба числа a и b были положительными. Другими словами, если a и bn оба являются действительными числами, то мы имеем следующие правила.

Правило произведения для радикалов:a⋅bn=an⋅bnЧастное правило для радикалов:abn=anbn

Например, мы можем продемонстрировать, что правило произведения верно, когда a и b оба положительны следующим образом: b оба отрицательны, свойство неверно.

−4⋅−9=?362i⋅3i=66i2=6−6=6 ✗

Здесь −4 и −9 не являются действительными числами, и правило произведения радикалов не дает истинного утверждения. Поэтому, чтобы избежать некоторых распространенных ошибок, связанных с этой техникой, убедитесь, что любое комплексное число записано с точки зрения мнимой единицы 9. 0059 i перед выполнением любых операций.

Пример 11

Умножьте: −6⋅−15.

Решение:

Начните с записи радикалов в терминах мнимой единицы i .

−6⋅−15=i6⋅i15

Теперь оба подкоренных числа положительны, и применяется правило произведения для радикалов.

−6⋅−15=i6⋅i15=i26⋅15=(−1)90=(−1)9⋅10=(−1)⋅3⋅10=−310

Ответ: −310

Пример 12

Умножить: −10(−6−10).

Решение:

Начните с записи радикалов в терминах мнимой единицы i, а затем распределите.

−10(−6−10)=i10(i6−10)=i260−i100=(−1)4⋅15−i100=(−1)⋅2⋅15−i⋅10=−215−10i

Ответ: −215−10i

Таким образом, умножение и деление комплексных чисел дает комплексное число.

Попробуйте! Упростить: (2i2)2−(3−i5)2.

Ответ: −12+6i5

(нажмите, чтобы посмотреть видео)

Ключевые выводы

• Воображаемая единица i определяется как квадратный корень из отрицательной единицы. Другими словами, i=-1 и i2=-1.
• Комплексные числа имеют вид a+bi, где a и b — действительные числа.
• Множество действительных чисел является подмножеством комплексных чисел.
• Результатом сложения, вычитания, умножения и деления комплексных чисел является комплексное число.
• Произведение комплексно-сопряженных чисел a+bi и a−bi является действительным числом. Используйте этот факт для деления комплексных чисел. Умножьте числитель и знаменатель дроби на комплексное сопряжение знаменателя, а затем упростите.
• Перед выполнением любых операций убедитесь, что любое комплексное число записано в виде мнимой единицы i .

Тематические упражнения

Часть A: Введение в комплексные числа

Переписать в мнимой единице i .

1. −81

2. −64

3. −−4

4. −−36

5. −20

6. −18

7. −50

8. −48

9. −−45

10. −−8

11. −116

12. −29

13. −0,25

14. −1,44

Запишите комплексное число в стандартной форме a+bi.

15. 5−2−4

16. 3−5−9

17. −2+3−8

18. 4−2−18

19. 3−−246

20. 2+−7510

21. −63−5−12

22. −−72+8−24

Учитывая, что i2=−1 , вычислите следующие степени числа i.

23. i3

24. и4

25. i5

26. i6

27. и15

28. и24

Часть B: Сложение и вычитание комплексных чисел

Выполнение операций.

29. (3+5i)+(7−4i)

30. (6−7i)+(−5−2i)

31. (−8−3i)+(5+2i)

32. (−10+15i)+(15−20i)

33. (12+34i)+(16−18i)

34. (25−16i)+(110−32i)

35. (5+2i)−(8−3i)

36. (7-i)-(-6-9i)

37. (−9−5i)−(8+12i)

38. (−11+2i)−(13−7i)

39. (114+32i)−(47−34i)

40. (38−13i)−(12−12i)

41. (2−i)+(3+4i)−(6−5i)

42. (7+2i)−(6−i)−(3−4i)

43. (13−i)−(1−12i)−(16+16i)

44. (1−34i)+(52+i)−(14−58i)

45. (5−3i)−(2+7i)−(1−10i)

46. (6−11i)+(2+3i)−(8−4i)

47. −16−(3−−1)

48. −100+(−9+7)

49. (1+-1)-(1—1)

50. (3−−81)−(5−3−9)

51. (5−2−25)−(−3+4−1)

52. (-12—1)-(3—49)

Часть C: Умножение и деление комплексных чисел

Выполнение операций.

53. я(1−я)

54. я(1+я)

55. 2и(7−4и)

56. 6и(1−2и)

57. −2i(3−4i)

58. −5i(2−i)

59. (2+i)(2−3i)

60. (3−5i)(1−2i)

61. (1-i)(8-9i)

62. (1+5i)(5+2i)

63. (4+3i)2

64. (−1+2i)2

65. (2−5i)2

66. (5−и)2

67. (1+i)(1−i)

68. (2−i)(2+i)

69. (4−2i)(4+2i)

70. (6+5i)(6−5i)

71. (12+23i)(13−12i)

72. (23−13i)(12−32i)

73. (2−и)3

74. (1−3i)3

75. −2(−2−6)

76. −1(−1+8)

77. −6(10−−6)

78. −15(3−−10)

79. (2−3−2)(2+3−2)

80. (1+−5)(1−−5)

81. (1−3−4)(2+−9)

82. (2−3−1)(1+2−16)

83. (2−3i2)(3+i2)

84. (−1+i3)(2−2i3)

85. −3i

86. 5и

87. 15+4i

88. 13−4i

89. 151−2i

90. 295+2i

91. 20i1−3i

92. 10i1+2i

93. 10-5i3-i

94. 5−2i1−2i

95. 5+10i3+4i

96. 2−4i5+3i

97. 26+13i2−3i

98. 4+2i1+i

99. 3-i2i

100. −5+2i4i

101. 1а-би

102. иа+би

103. 1−−11+−1

104. 1+-91—9

105. −−618+−4

106. −122−−27

Учитывая, что i−n=1 в , вычислите следующие степени числа i.

107. i-1

108. я-2

109. я-3

110. я-4

Выполните операции и упростите.

111. 2i(2−i)−i(3−4i)

112. я(5-я)-3я(1-6я)

113. 5−3(1−i)2

114. 2(1−2i)2+3i

115. (1-i)2-2(1-i)+2

116. (1+i)2−2(1+i)+2

117. (2i2)2+5

118. (3i5)2−(i3)2

119. (2−i)2−(2+i)2

120. (i3+1)2−(4i2)2

121. (11+i)2

122. (11+i)3

123. (а-би)2-(а+би)2

124. (а2+аи+1)(а2-аи+1)

125. Покажите, что и −2i, и 2i удовлетворяют условию x2+4=0.

126. Покажите, что и −i, и i удовлетворяют условию x2+1=0.

127. Покажите, что и 3−2i, и 3+2i удовлетворяют условию x2−6x+13=0.

128. Покажите, что и 5−i, и 5+i удовлетворяют условию x2−10x+26=0.

129. Покажите, что 3, −2i и 2i являются решениями уравнения x3−3×2+4x−12=0.

130. Покажите, что −2, 1−i и 1+i являются решениями уравнения x3−2x+4=0.

Часть D: Дискуссионная доска.

131. Исследуйте и обсудите историю мнимой единицы и комплексных чисел.

132. Как бы вы определили i0 и почему?

133. Узнайте, что значит вычислить абсолютное значение комплексного числа |a+bi|. Проиллюстрируйте свой вывод примером.

134. Исследуйте силы и . Ищите закономерность и делитесь своими выводами.

Ответы

1. 9и

3. −2i

5. 2и5

7. 5i2

9. −3i5

11. и4

13. 0,5i

15. 5−4i

17. −2+6i2

19. 12−63i

21. 512−74i

23. −i

25. и

27. −i

29. 10+i

31. −3−i

33. 23+58i

35. −3+5i

37. −17−17i

39. −12+94i

41. −1+8i

43. −56−23i

45. 2

47. −3+5i

49. 2и

51. 8−14i

53. 1+i

55. 8+14i

57. −8−6i

59. 7−4i

61. −1−17i

63. 7+24i

65. −21−20i

67. 2

69. 20

71. 12−136i

73. 2−11i

75. −2−2i3

77. 6+2i15

79. 22

81. 20−9i

83. 12−7i2

85. 3i

87. 541−441i

89. 3+6i

91. −6+2i

93. 72−12i

95. 115−25i

97. 1+8i

99. −12−32i

101. аа2+b2+ba2+b2i

103. −i

105. −611−3311i

107. −i

109. я

111. −2+i

113. 5+6i

115. 0

117. −3

119. −4i2

121. −i2

123. −4аби

125. Доказательство

127. Доказательство

129. Доказательство

131. Ответ может отличаться

133. Ответ может отличаться

Как выполнять операции с комплексными числами

Авторы: Ян Куанг и Эллейн Касе и

Обновлено: 26 марта 2016 г. на действительных и мнимых числах вместе, поэтому вы хотите записать оба числа как комплексные числа, чтобы иметь возможность складывать, вычитать, умножать или делить их.

Рассмотрим следующие три типа комплексных чисел:

• Вещественное число как комплексное: 3 + 0 i

  Обратите внимание, что мнимая часть выражения равна 0.

• Мнимое число как комплексное: 0 + 2 i

  Обратите внимание, что действительная часть выражения равна 0.

• Комплексное число, имеющее как действительную, так и мнимую части: 1 + 4 i

  Это число нельзя описать как исключительно реальное или исключительно воображаемое — отсюда и термин 9.Комплекс 1465.

Вы можете арифметически манипулировать комплексными числами так же, как и действительными числами, для выполнения операций. Вы просто должны быть осторожны, чтобы все и были прямыми. Вы не можете комбинировать действительные части с мнимыми с помощью сложения или вычитания, потому что они не похожи на термины, поэтому вы должны держать их отдельно. Также при умножении комплексных чисел произведение двух мнимых чисел является действительным числом; произведение действительного и мнимого числа остается мнимым; а произведение двух действительных чисел действительно. Многие путаются в этой теме.

В следующем списке представлены возможные операции над комплексными числами.

• Чтобы складывать и вычитать комплексные числа: Просто комбинируйте одинаковые термины. Например, (3 – 2 91 465 i 91 466 ) – (2 – 6 91 465 i 91 466 ) = 3 – 2 91 465 i 91 466 – 2 + 6 91 465 i 91 466 = 1 + 4 91 465 i.

• Чтобы умножить комплексное число, используйте один из трех различных методов в зависимости от ситуации:

  • Чтобы умножить комплексное число на действительное число: Просто распределите действительное число как на действительную, так и на мнимую часть комплексного числа. Например, вот как вы обрабатываете скаляр (константа), умножая комплексное число в скобках: 2(3 + 2 i ) = 6 + 4 i.

  • Чтобы умножить комплексное число на мнимое: Во-первых, поймите, что действительная часть комплексного числа становится мнимой, а мнимая часть становится действительной. Однако, когда вы выражаете свой окончательный ответ, вы по-прежнему сначала выражаете действительную часть, а затем мнимую часть, в форме A + B г.

    Например, вот как 2 i умножается на одно и то же число в скобках: 2 i (3 + 2 i ) = 6 i + 4 i ² . Примечание: Вы определяете и как

    , так что i ² = –1! Таким образом, у вас действительно есть 6 91 465 i 91 466 + 4(–1), поэтому ваш ответ будет равен –4 + 6 91 465 i.

  • Чтобы умножить два комплексных числа: =Просто следуйте процессу FOIL (Первый, Внешний, Внутренний, Последний). Например, (3 – 2 i )(9 + 4 i ) = 27 + 12 i – 18 i – 8 i ² , что равно 27 – 56 i 911. – 8(–1), или 35 – 6 i.

• Для деления комплексных чисел: Умножьте числитель и знаменатель на сопряженную часть знаменателя, ИСКЛЮЧИТЕ числитель и знаменатель отдельно, а затем объедините одинаковые члены. Этот процесс необходим, потому что мнимая часть знаменателя на самом деле представляет собой квадратный корень (из –1, помните?), а знаменатель дроби не должен содержать мнимой части.

Например, вас попросили разделить

Комплексное сопряжение 3 – 4 i равно 3 + 4 i. Выполните следующие действия, чтобы решить проблему:

1. Умножьте числитель и знаменатель на сопряженное.

2. ФОЛЬГА числитель.

   Вы идете с (1 + 2 i )(3 + 4 i ) = 3 + 4 i + 6 i + 8 i ² , что упрощается до (3 – 8) (4 i 91 466 + 6 91 465 i 91 466), или –5 + 10 91 465 i.

3. ФОЛЬГА знаменатель.

   У вас есть (3 – 4 i )(3 + 4 i ), которые превращаются в 9 + 12 i – 12 i – 16 i ² . Поскольку i ² = –1 и 12 i – 12 i = 0, в знаменателе остается действительное число 9 + 16 = 25 (именно поэтому вы умножаете на 3 + 4 ). я в первую очередь).

4. Перепишите числитель и знаменатель.

   Однако этот ответ по-прежнему не соответствует комплексному числу.

5. Разделить и разделить обе части на постоянный знаменатель.

   Обратите внимание, что ответ в конце концов имеет форму A + B i.

Эту статью можно найти в категории:

• Предварительное исчисление,

Операции с комплексными числами: примеры

До сих пор мы имели дело с действительными числами, такими как:

2,13,3,7. 09,…

В этом разделе мы рассмотрим новую концепцию, называемую мнимым числом . Рассмотрим квадратный корень из 2. Мы знаем, что это дает неповторяющееся десятичное число

2=1,414213562…

Итак, чему равен квадратный корень из -2? Вы можете подумать, что квадратный корень из отрицательного числа не имеет решения. Однако это неправда! На самом деле, здесь в игру вступает мнимое число. Понятие мнимого числа происходит от числа 9.0003 мнимая единица , обозначаемая буквой i, и представленная следующим производным:

i2=-1⇔-1=i

Таким образом, квадратный корень из -2 равен просто

-2=- 1×2⇒-2=-12⇒-2=i2⇒-2=1,414i(исправить до 3-х знаков после запятой)

На самом деле, мы можем складывать вместе действительные и мнимые числа. Эта структура чисел приводит нас к идее комплексного числа.

Комплексное число представляет собой алгебраическое выражение, которое включает множитель i = √-1 и записывается в виде z = a + bi.

Стандартная форма комплексных чисел

Стандартная форма комплексных чисел:

z=a+ib

, где

Это также обозначается как

z=Re(z)+Im(z)i=a+ bi

Действительные и мнимые числа

Есть два важных подкласса комплексных чисел: для комплексного числа z = a + bi

• Если Im (z) = 0, то z = a является действительным числом

• Если Re (z) = 0, то z = bi называется чисто мнимым

Почему важны комплексные числа?

Комплексные числа имеют множество применений. Например, они широко используются в области электротехники и квантовой механики . Комплексные числа также помогают нам решать полиномиальные уравнения, которые не имеют реальных решений: взгляните на график и решение квадратных уравнений, где объясняется, как это сделать.

Мы можем выполнять основные арифметические операции с комплексными числами, такие как сложение, вычитание, умножение и деление.

Операции с комплексными числами; Сложение и вычитание

В этом разделе мы объясним наиболее важные операции, которые вы должны уметь выполнять с комплексными числами:

• Сложение и вычитание комплексных чисел
• Скалярное умножение
• Умножение и деление комплексных чисел

Сложение и вычитание комплексных чисел

Чтобы сложить комплексные числа, просто сложите соответствующие действительные и мнимые части . То же правило применяется при вычитании комплексных чисел.

Пусть z ₁ и z ₂ — два комплексных числа, где z ₁ = a + bi и z ₂ = c + di, где a, b, c и d — действительные числа.

Формула сложения комплексных чисел

z1+z2=(a+bi)+(c+di)

Распределяя знак плюс во втором члене (как на действительную, так и на мнимую части) и собирая одинаковые члены, получаем

z1+z2=(a+c)+(b+d)i

Формула вычитания комплексных чисел

z1-z2=(a+bi)-(c+di)

Распределение отрицательного знака в второе слагаемое (как к действительной, так и к мнимой части) и собирая подобные слагаемые, получаем

z1-z2=(a-c)+(b-d)i

Рассчитать α + β

α+β=(3-2i)+(5+7i)⇒α+β=(3+5)+(-2i+7i)⇒α+β=8 +5i

Определить α — β

α-β=(3-2i)-(5+7i)⇒α-β=(3-5)+(-2i-7i)⇒α-β=- 2-9i⇒α-β=-(2+9i)

Скалярное умножение комплексных чисел

Скалярное умножение комплексных чисел — это умножение действительного числа на комплексное число. В этом случае действительное число также называют скаляром .

Чтобы умножить комплексное число на скаляр, просто умножьте действительную и мнимую части на скаляр по отдельности .

Пусть z = a + bi — комплексное число, а c — скаляр, где a , b и c — действительные числа.

Формула скалярного умножения комплексных чисел

c×z=c(a+bi)=ca+cbi

Пусть α = 3 — 2i и β = 5 + 7i — два комплексных числа

Найти 7 α

В этом случае мы умножаем комплексное число α на действительное число 7 (также называемое скаляром ).

7α=7(3-2i)⇒7α=21-14i

Вычислить 2 β

В этом случае мы умножаем комплексное число β на действительное число 2 (также называемое скалярным числом 2 ).

2β=2(5+7i)⇒2β=10+14i

Умножение комплексных чисел

Умножение комплексных чисел точно такое же, как метод биномиального разложения: применяется метод FOIL и комбинируются одинаковые члены.

Формула умножения комплексных чисел

z1×z2=(a+bi)(c+di)=ac-bd+(cb+ad)i

Вот как работает метод FOIL, шаг за шагом.

Пусть z ₁ и z ₂ — два комплексных числа, где z ₁ = a + bi и z ₂ = c + di, где a, b, c и d — действительные числа. Чтобы умножить их

1. Запишите оба в стандартной форме.
2. Выполните биномиальное разложение.
3. Объедините похожие термины.

z1×z2=(a+bi)(c+di)⇒z1×z2=ac+bci+adi+bdi2

Учитывая, что i ² = -1, получаем

z1×z2=ac+bci+adi+bd(-1)⇒z1×z2=ac+bci+adi-bd

Упрощая, получаем

ac-bd+ (cb+ad)i

Пусть α = 3 — 2i и β = 5 + 7i — два комплексных числа.

Найти α x β

)⇒α×β=15+11i+14⇒α×β=29+11i

Деление комплексных чисел

Если у вас есть дробь комплексных чисел, умножьте числитель и знаменатель на комплексное сопряжение знаменателя .

Для комплексного числа z = a + bi комплексно-сопряженное число числа z обозначается как z* = a — bi.

После этого расширить и упростить выражение до стандартной формы комплексных чисел. Результат определяется по следующей формуле:

Формула деления комплексных чисел

z1z2=a+bic+di=ac+bd+(bc-ad)ic2+d2=ac+bdc2+d2+bc-adc2+d2i

При делении комплексных чисел обязательно записывайте окончательный ответ в стандартной форме.

Давайте посмотрим на практике и шаг за шагом, как выполнить деление комплексных чисел. Пусть z ₁ и z ₂ — два комплексных числа, где z ₁ = a + bi и z ₂ = c + di, где a, b, c и d — действительные числа. Разделив z ₁ на z ₂ , мы получим

z1z2=a+bic+di

Комплексное сопряжение знаменателя, z ₂ равно z ₂ * = в — ди.

Теперь, умножив числитель и знаменатель на z ₂ *, мы получим

z1z2=a+bic+di×c-dic-di⇒z1z2=(a+bi)(c-di)(c+di )(c-di)

Разлагая это выражение, получаем

z1z2=ac+bci-adi-bdi2c2+cdi-cdi-d2i2⇒z1z2=ac+bci-adi-bd(-1)c2+cdi-cdi -d2(-1)⇒z1z2=ac+bci-adi+bdc2+d2

Наконец, объединяя подобные члены, мы имеем

z1z2=ac+bd+(bc-ad)ic2+d2

Пусть α = 3 — 2i и β = 5 + 7i — два комплексных числа. Здесь β — знаменатель. Комплексное сопряжение β равно β* = 5 — 7i.

Вычислить α ÷ β

αβ=3-2i5+7i

Здесь β — знаменатель. Комплексное сопряжение β равно β* = 5 — 7i. Таким образом, умножение числителя и знаменателя на β* дает:

αβ=3-2i5+7i×5-7i5-7i⇒αβ=(3-2i)(5-7i)(5+7i)(5-7i)⇒αβ=15-21i-10i+14i225-35i+ 35i-49i2⇒αβ=15-31i+14(-1)25-49(-1)⇒αβ=15-31i-1425+49⇒αβ=1-31i74⇒αβ=174-3174i

Работа с комплексом Числа — ключевые выводы

Операция	Формула
Дополнение	z1+z2=(a+bi)+(c+di)=(a+c)+(b+d)i
Вычитание	z1-z2=(a+bi)-(c+di)=(a-c)+(b-d)i
Скалярное умножение	c×z=c(a+bi)=ca+cbi
Умножение	z1×z2=(a+bi)(c+di)=ac-bd+(cb+ad)i
Отдел	z1z2=a+bic+di=ac+bdc2+d2+bc-adc2+d2i

2.

2: Операции над комплексными числами

1. Последнее обновление

2. Сохранить как PDF

Идентификатор страницы

267

• Исайя Ланкхэм, Бруно Нахтергаэле и Энн Шиллинг

9 Калифорнийский университет, Дэвис

Несмотря на то, что мы формально определили \(\mathbb{C}\) как множество всех упорядоченных пар действительных чисел, тем не менее мы можем расширить обычные арифметические операции над \(\mathbb{R}\), так что они также делают смысл в \(\mathbb{C}\). Мы обсудим такие расширения в этом разделе, наряду с некоторыми другими важными операциями над комплексными числами.

2.2.1 Сложение и вычитание комплексных чисел

Сложение комплексных чисел выполняется покомпонентно, то есть действительная и мнимая части просто объединяются.

Определение 2.2.1. Имея два комплексных числа \((x_{1}, y_{1}), (x_{2}, y_{2}) \in \mathbb{C}\, мы определяем их комплексную сумму как быть

\[ (x_{1}, y_{1}) + (x_{2}, y_{2}) = (x_{1} + x_{2}, y_{1} + y_{2}) . \]

Пример 2.2.2 . \( (3, 2) + (17, -4,5) = (3 + 17, 2 — 4,5) = (20, -2,5).\)

Как и в случае с действительными числами, вычитание определяется как сложение с так -называется аддитивной инверсией , где аддитивная инверсия \(z=(x,y)\) определяется как \(-z=(-x,-y)\).

Пример 2.2.3. \( (\pi, \sqrt{2}) — (\pi/2, \sqrt{19}) = (\pi, \sqrt{2}) + (-\pi/2, -\sqrt{19 }), \)

, где

\[ (\pi, \sqrt{2}) + (-\pi/2, -\sqrt{19}) = (\pi — \pi/2, \sqrt{ 2} — \sqrt{19}) = (\pi/2, \sqrt{2} — \sqrt{19}). \]

Сложение комплексных чисел обладает многими из тех же свойств, что и сложение действительных чисел, включая ассоциативность, коммутативность, существование и уникальность аддитивной идентичности, а также существование и уникальность аддитивных инверсий. Мы резюмируем эти свойства в следующей теореме, которую вы должны доказать на собственном опыте.

Теорема 2.2.4. Пусть \(z_{1}, z_{2}, z_{3} \in \mathbb{C}\) — любые три комплексных числа. Тогда верны следующие утверждения.

1. ( Ассоциативность ) \((z_{1} + z_{2}) + z_{3} = z_{1} + (z_{2} + z_{3})\).
2. ( Коммутативность ) \(z_{1} + z_{2} = z_{2} + z_{1}\).
3. ( Аддитивный идентификатор ) Существует уникальное комплексное число, обозначаемое \(0\), такое, что для любого комплексного числа \(z \in \mathbb{C}\), \(0 + z = z\). Более того, , \(0 = (0, 0)\).
4. ( Аддитивные инверсии ) Для любого комплексного числа \(z \in \mathbb{C}\), существует уникальное комплексное число, обозначаемое \(-z\), такое, что \( z + (-z) = 0\). Более того, если \(z = (x, y)\) с \(x, y \in \mathbb{R}\), , то \(-z = (-x, -y)\ ).

Доказательство этой теоремы простое и опирается исключительно на определение комплексного сложения, а также на знакомые свойства сложения для действительных чисел. Например, чтобы проверить коммутативность, пусть \(z_{1} = (x_{1}, y_{1})\) и \(z_{2} = (x_{2}, y_{2})\) комплексные числа с \(x_{1}, x_{2}, y_{1}, y_{2} \in \mathbb{R}\).
Тогда
\[
z_{1} + z_{2} =
(x_{1} + x_{2}, y_{1} + y_{2}) =
(x_{2} + x_{1} , y_{2} + y_{1}) =
z_{2} + z_{1}.
\]

2.2.2 Умножение и деление комплексных чисел

Определение умножения двух комплексных чисел на первый взгляд несколько менее просто, чем определение сложения.

Определение 2.2.5. Учитывая два комплексных числа \((x_{1}, y_{1}), (x_{2}, y_{2}) \in \mathbb{C}\), мы определяем их комплексных 9{2}
\\
& =
x_{1}x_{2} + x_{1}y_{2}i + x_{2}y_{1}i — y_{1}y_{2}
\\
& =
x_{1}x_{2} — y_{1}y_{2} + (x_{1}y_{2} + x_{2}y_{1})i.
\end{align*}

Как и в случае сложения, основные свойства комплексного умножения достаточно легко доказать с помощью определения. Мы суммируем эти свойства в следующей теореме, которую вам также следует доказать на практике.

Теорема 2.2.6. Пусть \(z_{1}, z_{2}, z_{3} \in \mathbb{C}\) — любые три комплексных числа. Тогда верны следующие утверждения .

1. ( Ассоциативность ) \((z_{1}z_{2})z_{3} = z_{1}(z_{2}z_{3})\).
2. ( Коммутативность ) \(z_{1}z_{2} = z_{2}z_{1}\).
3. ( Мультипликативное тождество ) Существует уникальное комплексное число, обозначаемое \(1\), такое, что для любых \(z \in \mathbb{C}\), \(1 z = z \). Более того, , \(1 = (1, 0)\).
4. ( Распределение умножения по сложению 9{2}}\справа). \]

   Доказательство.

   Уникальность: Комплексное число \(w\) является обратным к \(z\), если \(z w=1\) (по коммутативности комплексного умножения это эквивалентно \(w z=1\) Сначала мы докажем, что если \(w\) и \(v\) — два комплексных числа такие, что \(z w=1\) и \(z v=1\), то мы обязательно имеем \(w=v\ ). Тогда это будет означать, что любой \(z\in\mathbb{C}\) может иметь не более одного обратного. Чтобы увидеть это, мы начнем с \(z v=1\). Умножив обе части на \(w\ ), получаем \(w z v=w 1\). Используя тот факт, что \(1\) является мультипликативной единицей, что произведение коммутативно, и предположение, что \(w\) является обратным, получаем \( z w v=v=w\).9{2}}
   \right)
   =
   \left(
   \frac{3 + 8}{9 + 16}
   ,
   \frac{6 — 4}{9 + 16}
   \right)
   =
   \ влево(
   \frac{11}{25}
   ,
   \frac{2}{25}
   \right).
   \]

   2.2.3 Комплексное сопряжение

   Комплексное сопряжение — это операция над \(\mathbb{C}\), которая окажется очень полезной, поскольку позволяет нам манипулировать только мнимой частью комплексного числа. В частности, в сочетании с понятием модуля (как определено в следующем разделе) это одна из самых фундаментальных операций над \(\mathbb{C}\). Определение и основные свойства комплексного сопряжения следующие. (Как и в предыдущих разделах, вы должны предоставить доказательство теоремы ниже для собственной практики. )

   Определение 2.2.8. Учитывая комплексное число \(z = (x, y) \in \mathbb{C}\) с \(x, y \in \mathbb{R}\), мы определяем ( комплексное ) сопряженное из \(z\) быть комплексным числом

   \[ \bar{z} = (x, -y). \]

   Теорема 2.2.9. Даны два комплексных числа \(z_{1}, z_{2} \in \mathbb{C}\),

   1. \(\overline{z_{1} + z_{2}} = \overline{z_{ 1}} + \overline{z_{2}}\).
   2. \(\overline{z_{1}z_{2}} = \overline{z_{1}}\, \overline{z_{2}}\).
   3. \( \overline{1/z_1} = 1/\overline{z_1}\), для всех \(z_1\neq 0\).
   4. \(\overline{z_{1}} = z_{1}\) тогда и только тогда, когда \(\ImaginaryPart(z_{1}) = 0\).
   5. \(\overline{\overline{z_{1}}} = z_{1}\).
   6. действительная и мнимая части \(z_{1}\) могут быть выражены как

   \[ \mathrm{Re}(z_{1}) = \frac{1}{2}(z_{1} + \overline{z_{1}})
   {\rm \quad и \quad}
   \mathrm{Im}(z_{1}) = \frac{1}{2 i}(z_1 — \overline{z_1} ). \]

   2.2.4 Модуль (он же норма, длина или величина) 9{2}} = \sqrt{9 + 16} = \sqrt{25} = 5. \]

   Чтобы увидеть это геометрически, постройте фигуру на евклидовой плоскости, например

   , и примените теорему Пифагора к полученный прямоугольный треугольник, чтобы найти расстояние от начала координат до точки \((3, 4)\).

   Следующая теорема перечисляет основные свойства модуля, особенно в том, что касается комплексного сопряжения. Вы должны предоставить доказательства для вашей собственной практики.

   Теорема 2.2.12. Даны два комплексных числа \(z_{1}, z_{2} \in \mathbb{C}\),

   1. \(|z_{1}z_{2}| = |z_{1}| \cdot|z_{2}|\).
   2. \({\displaystyle \left|\frac{z_{1}}{z_{2}}\right| = \frac{|z_{1}|}{|z_{2}|}}\), при условии, что \(z_{2} \neq 0\).
   3. \(|\overline{z_{1}}| = |z_{1}|\).
   4. \(|\mathrm{Re}(z_{1})| \leq |z_{1}|\) и \(|\mathrm{Im}(z_{1})| \leq |z_{ 1}|\).
   5. ( Неравенство треугольника 9{2}\), некоторые из операций, определенных в разделе 2. 2, можно непосредственно визуализировать, как если бы они были операциями над векторами .

      Для целей этой главы мы рассматриваем векторы как направленные отрезки, которые начинаются в начале координат и заканчиваются в заданной точке на евклидовой плоскости. Эти отрезки также можно перемещать в пространстве до тех пор, пока сохраняются направление (которое мы будем называть аргументом в разделе 2.3.1 ниже) и длина (также известная как модуль). Таким образом, различие между точками на плоскости и векторами является просто вопросом соглашения, пока мы, по крайней мере, неявно думаем о каждом векторе как о перемещенном, так что он начинается в начале координат.

      Как мы видели в примере 2.2.11 выше, модуль комплексного числа можно рассматривать как длину гипотенузы некоторого прямоугольного треугольника. Сумма и разность двух векторов также могут быть представлены геометрически как длины определенных диагоналей в конкретном параллелограмме, который формируется путем копирования и соответствующего перевода двух объединяемых векторов.

      Пример 2.2.13. Мы изображаем сумму \((3, 2) + (1, 3) = (4, 5)\) как главную штриховую диагональ параллелограмма на крайнем левом рисунке ниже. Разность \((3, 2) — (1, 3) = (2, -1)\) также можно рассматривать как более короткую диагональ того же параллелограмма, хотя мы должны были бы настаивать на том, чтобы эта более короткая диагональ была перенесена так что он начинается в начале координат. Последнее показано на крайнем правом рисунке ниже.

      Авторы

      • Исайя Ланкхэм, математический факультет Калифорнийского университета в Дэвисе
      • Бруно Нахтергаэле, математический факультет Калифорнийского университета в Дэвисе
      • Энн Шиллинг, математический факультет Калифорнийского университета в Дэвисе

      Версии этого учебника в твердом и мягком переплете доступны онлайн на сайте WorldScientific.com.

      ---

      Эта страница под названием 2.2: Операции над комплексными числами распространяется по недекларированной лицензии, ее авторами, ремикшированием и/или кураторами являются Исайя Лэнкхэм, Бруно Нахтергаэле и Энн Шиллинг.

      1. Наверх
      • Была ли эта статья полезной?

      1. Тип изделия

         Раздел или Страница

         Автор

         Исайя Ланкхэм, Бруно Нахтергаэле и Энн Шиллинг

         Показать страницу TOC

         №

      2. Метки

         1. автортег:шиллинг

      Комплексные числа — основные операции

      Определение комплексных чисел Комплексное сопряжение Добавление комплексных чисел Вычитание комплексных чисел Умножение комплексных чисел Разделить два комплексных числа Равенство двух комплексных чисел Определение комплексных чисел Комплексное число z — это число вида г = а + б я где a и b — действительные числа, а i — мнимая единица, определяемая формулой \(я = \sqrt{-1} \) a называется действительной частью z, а b — мнимой частью z. Обратите внимание, что набор R всех действительных чисел является подмножеством комплексного числа C , поскольку любое действительное число может рассматриваться как имеющее мнимую часть, равную нулю. Комплексное сопряжение Сопряженным комплексным числом a + b i называется комплексное число, равное a — b i Примеры: Найдите сопряжение следующих комплексных чисел. а) 2 — i , б) -3 + 4i , в) 5 , г) -5i Решение вышеприведенного примера а) 2 + i б) -3 — 4и в) 5 д) 5и Добавление комплексных чисел Сложение двух комплексных чисел a + b i и c + d i определяется следующим образом. (а + Ь я) + (с + d я) = (а + с) + (б + d) я Это похоже на группировку подобных терминов: действительные части добавляются к действительным частям, а мнимые части добавляются к мнимым частям. Пример: Выразите в виде комплексного числа a + b i. (2 + 3i) + (-4 + 5i) (3и) + (-5 + 6и) (2) + (-2 + 9i) Решение приведенного выше примера. (2 + 3i) + (-4 + 5i) = (2 — 4) + (3 + 5) i = — 2 + 8 i (3i) + (-5 + 6i) = (0 — 5) + (3 + 6) i = -5 + 9я (2) + (-2 + 9i) = (2 — 2) + (9) i = 9i Добавление может быть сделано путем группировки подобных терминов. (2 + 3i) + (-4 + 5i) = 2 + 3i — 4 + 5i = -2 + 8i Доступен калькулятор для сложения комплексных чисел. Вычитание комплексных чисел Вычитание двух комплексных чисел a + b i и c + d i определяется следующим образом. (а + б i) — (с + d i) = (а — b) + (b — d) я Пример: Выразите в виде комплексного числа a + b i. (2 — 5и) — (-4 — 5и) (-7и) — (-5 — 6и) (2) — (2 + 6и) Решение приведенного выше примера (2 — 5i) — (-4 — 5i) = (2 — (-4)) + (-5 — (-5)) i = 6 (-7i) — (-5 — 6i) = (0 — (-5)) + (-7 — (-6)) i = 5 — i (2) — (2 + 6i) = (2 — 2) — 6i = -6i Примечание: вычитание можно выполнить следующим образом: (a + b i) — (c + d i) = (a + bi) + (- c — d i), а затем сгруппируйте подобные термины Пример: (2 — 5i) — (-4 — 5i) = 2 — 5 i + 4 + 5 i = 6 Умножение комплексных чисел Умножение двух комплексных чисел a + b i и c + d i определяется следующим образом. (a + b i)(c + d i) = (a c — b d) + (a d + b c) i Однако вам не нужно запоминать приведенное выше определение, так как умножение может быть выполнено с использованием свойств, аналогичных свойствам действительных чисел, и дополнительного свойства i 2 = -1. (см. пример ниже) Пример: Выразите в виде комплексного числа a + b i. (3 + 2 я) (3 — 3 я) Решение вышеприведенного примера (3 + 2 i)(3 — 3i) Используя распределительный закон, (3 + 2 i)(3 — 3 i) можно записать как (3 + 2 i)(3 — 3 i) = (3 + 2 i)(3) + (3 + 2 i)(-3 i) = 9 + 6 i — 9 i -6 i 2 Сгруппируйте похожие термины и используйте i 2 = -1, чтобы упростить (3 + 2 i)(3 — 3 i) (3 + 2 я) (3 — 3 я) = 15 — 3 я Доступен калькулятор для умножения комплексных чисел. Разделить два комплексных числа Мы используем свойство умножения комплексного числа и его сопряженного числа, чтобы разделить два комплексных числа. Пример: Выразите в виде комплексного числа a + b i. \( \dfrac{8 + 4 i}{1-i} \) Сначала умножаем числитель и знаменатель на комплексно-сопряженное число знаменателя \( \dfrac{(8 + 4 i)\color{red}{(1+i)}}{(1-i)\color{red}{(1+i)}} \) Умножать и группировать подобные термины \( = \dfrac{8 + 4 я + 8 я + 4 я ^ 2} {1 — я + я — я ^ 2} = \dfrac{4 + 12i}{2} \) \(= 2 + 6 я \) Доступен калькулятор для деления комплексных чисел. No related posts. Добавить комментарий Отменить ответ Ваш адрес email не будет опубликован. Обязательные поля помечены * Комментарий * Имя * Email * Сайт