Системы двух уравнений с двумя неизвестными
Похожие презентации:
Системы двух уравнений с двумя неизвестными. 7 класс
Уравнение с двумя переменными
Системы двух линейных уравнений с двумя неизвестными
Системы линейных уравнений с двумя неизвестными
Уравнения первой степени с двумя неизвестными. 7 класс
Решение систем линейных уравнений с двумя переменными. Способ подстановки
Система двух уравнений с двумя неизвестными. Способ подстановки
Системы линейных уравнений с двумя переменными
Системы двух линейных уравнений с двумя неизвестными
Системы двух уравнений первой степени с двумя неизвестными
1. Системы двух уравнений с двумя неизвестными
2. Урок 1 Уравнения первой степени с двумя неизвестными. Системы уравнений
Цели: ввести понятие линейного уравнения сдвумя неизвестными, системы линейных
уравнений с двумя неизвестными;
способствовать усвоению определения решения
системы уравнений с двумя неизвестными.

Уравнение и его свойства
Определение
• Уравнение – это равенство, содержащее одну или несколько
переменных
ax=b
Коэффициенты
ax+by=c
а x + b y = c,
где а, b, c – заданные
числа.
Линейное уравнение с
одной переменной
Свободный член
Линейное
уравнение с
двумя
переменными
4. Из истории уравнений
• Уравнение с двумя неизвестнымивыражает зависимость между
двумя величинами , имеет
бесчисленное множество реше ний и является неопределенным.
• Решением таких уравнений
занимались в древности китайцы,
греки и индийцы.
• В «Арифметике» Диофанта
приведено много задач, решаемых
им с помощью неопределенных
уравнений.
Диофант из
Александрии
( 3 век )
Свойства уравнений
если в уравнении перенести слагаемое из одной части в другую, изменив его
знак, то получится уравнение, равносильное данному
12х – 5у = 7
12х – 7 = 5у
если обе части уравнения умножить или разделить на одно и то же отличное
от нуля число, то получится уравнение, равносильное данному
9х + 15у = 3 Ι 🙁 — 3 )
-3х — 5у = — 1
6.
 Задание 1.1.1. Из линейного
Задание 1.1.1. Из линейногоуравнения с двумя
неизвестными
2х – 8у = — 10
выразите
переменную х:
2х = 8у – 10 Ι : 2,
Х = 4у — 5
1.2. Из линейного
уравнения с двумя
неизвестными
3х – 2у = 5 выразите
переменную у:
3х – 5 = 2у Ι : 2
3х — 5
=у
2
7. Решением уравнения с двумя неизвестными х и у называется упорядоченная пара чисел ( х ; у ), при подстановке которых в это уравнение получает
Решением уравнения с двумянеизвестными
х
и
у
называется упорядоченная пара
чисел ( х ; у ), при подстановке
которых в это уравнение
получается верное числовое
равенство.
8. Задание 2 Найдите все пары ( х ; у ) натуральных чисел, которые являются решениями уравнения.
• 2.1.13х + 4у =55
• 2.2.
5х + 7у =59
Ответ: ( 3 ; 4) Ответ: (2 ; 7)
(9 ; 2)
Система уравнений и её решение
Определение
Системой двух линейных уравнений с двумя неизвестными
называются два уравнения, объединенные фигурной скобкой.

Фигурная скобка означает, что эти уравнения должны быть
решены одновременно.
В общем виде систему двух линейных уравнений с
двумя неизвестными записывают так :
а1 х + b1 y = c1,
а2 х + b2 y = c2;
где
а , b , c а2 , b2 , c2
1
1
1,
10. Из истории систем уравнений
• Задачи на составление ирешение систем уравнений
встречаются в вавилонских
и египетских текстах II тысячелетия до н. э., в трудах
древнегреческих, китайских
и индийских ученых.
• Нижние индексы при буквах
Лейбниц
впервые употребил в 1675 г.
Готфрид Вильгельм
немецкий математик Лейбниц
( 1646 – 1716 )
11. Например, в системе а1 = 1, b1 = -1, с1 = 2; а2 = 3, b2 = -2, с2 = 9.
Например, в системех – у = 2,
3х – 2у = 9.
а1 = 1, b1 = -1, с1 = 2; а2 = 3, b2 = -2, с2 = 9.
Задание 3. (Устно.)
Проверьте, являются ли числа х = 4 , у = 3
решениями системы
2,5х – 3у = 1,
Решение:
5х – 6у = 2.
2,5 ·4 – 3 · 3 =1,
5·4 – 6 · 3 = 2.

Ответ: числа х = 4 , у = 3 являются решениями
системы
12. Решением системы уравнений с двумя переменными называется пара значений переменных, обращающая каждое уравнение системы в верное равенст
Решением системы уравнений сдвумя переменными называется
пара значений переменных,
обращающая каждое уравнение
системы в верное равенство
Решить систему уравнений это значит найти все её
решения или установить, что
их нет
13. Задание 4. Если в системе уравнений
2х – 7у = 3,3х + у = 2.
уравнять модули коэффициентов при х , то
система примет вид
РЕШЕНИЕ
2х – 7у = 3 Ι· 3,
3х + у = 2 Ι · 2.
2 · 3х – 7 · 3у = 3 · 3,
3 · 2х + 2у = 2 · 2;
6х
6х –– 21
21 уу == 9,
9,
6х
6х ++ 2у
2у == 4.
4.
14. Домашнее задание
1. Учебник «Алгебра 7»,авторы Ш.А.Алимов и др. § 33
№ 615(1), 616(1), 617(1), 619(1).
2. Рабочая тетрадь по алгебре, 7,
авторы Ю.М.Колягин и др.

§ 33, № 3, 4(1), 5(1), 14(1).
«Алгебра 7», авторы М.В.Ткачева и др.
§ 33 ( стр. 90) № 4(1), 7.
English Русский Правила
1
Первый слайд презентации
Алгебра 8 класс «Решение систем двух линейных уравнений с двумя неизвестными»
Изображение слайда
2
Слайд 2
Определите, какая из пар чисел (1; 2) (-1; 2) (-8/7;-7) (1; -2) является решением системы уравнений: 7х – 3у = 13, 2х + 5у = -8.
Изображение слайда
3
Слайд 3
Определи ть, какая из пар чисел
( 1 ; 2 ) (-1; 2) (-8/7;-7) (1; -2)
является решением системы уравнений. Решение:
7 1 – 3 2 = 13,
2 1 + 5 2 = -8
.
.
.
.
7 (-1) – 3 2 = 13,
2 (-1) + 5 2 = -8
.
.
.
.
(ложь)
(ложь)
Образец оформления решения:
Решение:
7 1 – 3 2 = 13,
2 1 + 5 2 = -8
.
.
.
.
7 (-1) – 3 2 = 13,
2 (-1) + 5 2 = -8
.
.
.
.
(ложь)
(ложь)
Образец оформления решения:
Изображение слайда
4
Слайд 4
Решите систему графически: у – 3х = 0, 3х + у = -6.
Изображение слайда
5
Слайд 5
Реши ть систему графически: у – 3х = 0, 3х + у = -6. Образец оформления решения: Решение: Даны линейные уравнения. Их графиками являются прямые. Для построения прямых необходимо знать координаты двух точек, принадлежащих каждой прямой. Построим таблицу значений для каждой прямой: х 0 1 у 0 3 х 0 -2 у -6 0
Изображение слайда
6
Слайд 6
Решить систему графически:
у – 3х = 0,
3х + у = -6. Образец оформления решения:
Решение:
х
0
1
у
0
3
х
0
-2
у
-6
0
1
3
-6
-1
-2
у – 3х = 0
3х + у = -6
Р (-1; -3)
Ответ: (-1; -3)
Образец оформления решения:
Решение:
х
0
1
у
0
3
х
0
-2
у
-6
0
1
3
-6
-1
-2
у – 3х = 0
3х + у = -6
Р (-1; -3)
Ответ: (-1; -3)
Изображение слайда
7
Слайд 7
Решите систему методом подстановки: у – 3х = 8, 3х + 2у = 7.
Изображение слайда8
Слайд 8
Реши ть систему методом подстановки: у – 3х = 8, 3х + 2у = 7. Образец оформления решения: Решение: у – 3х = 8, 3х + 2у = 7; = > у = 8 + 3х, 3х + 2у = 7; = > у = 8+3x, 3х + 2 (8+3x) = 7; = > у = 8+3x, 3х + 16+6x = 7;
Изображение слайда
9
Слайд 9
Решить систему методом подстановки:
у – 3х = 8,
3х + 2у = 7. Образец оформления решения:
Решение:
у – 3х = 8,
3х + 2у = 7;
= >
у = 8 + 3х,
3х + 2у = 7;
= >
у = 8+3x,
3х + 2 (8+3x) = 7;
= >
у = 8+3x,
3х + 16+6x = 7;
= >
у = 8+3x,
9 х = 7 -16 ;
= >
у = 8+3x,
9 х = -9 ;
= >
у = 8+3 (-1),
х = -1 ;
.
Образец оформления решения:
Решение:
у – 3х = 8,
3х + 2у = 7;
= >
у = 8 + 3х,
3х + 2у = 7;
= >
у = 8+3x,
3х + 2 (8+3x) = 7;
= >
у = 8+3x,
3х + 16+6x = 7;
= >
у = 8+3x,
9 х = 7 -16 ;
= >
у = 8+3x,
9 х = -9 ;
= >
у = 8+3 (-1),
х = -1 ;
.
Изображение слайда
10
Слайд 10
Решить систему методом подстановки: у – 3х = 8, 3х + 2у = 7. Образец оформления решения: Решение: у – 3х = 8, 3х + 2у = 7; = > = > у = 5, х = -1. … Ответ: (-1; 5 ) у = 8+3 (-1), х = -1 ; . = >
Изображение слайда
11
Слайд 11
Решите систему методом алгебраического сложения: 3х + 2у = 6, 5х + 3у = 11.
Изображение слайда
12
Слайд 12
Реши ть систему методом
алгебраического сложения:
3х + 2у = 6,
5х + 3у = 11;
Образец оформления решения:
Решение:
= >
9 х + 6 у = 18,
-10 х +( -6 у) = -22 ;
х 3
х (-2)
= >
9х + 6у = 18,
— х = — 4 ;
= >
9х+ 6у = 18,
х = 4 ;
= >
9 4 + 6у = 18,
х = 4 ;
. = >
6у = 18 — 36,
х = 4;
= >
у = -3,
х = 4.
Ответ: (4; -3)
= >
6у = 18 — 36,
х = 4;
= >
у = -3,
х = 4.
Ответ: (4; -3)
Изображение слайда
13
Слайд 13
Прямая у= kx+m проходит через точки А(2;-1) и В ( 3;4). Найдите уравнение прямой.
Изображение слайда
14
Слайд 14
Най ти уравнение прямой, проходящей через точки А(2;-1) и В ( 3;4). -1=2k+m, 4=3k+m. Образец оформления решения: Решение: Запишем уравнение всех прямых, проходящих через точку А (2;-1): -1 = 2 k + m Запишем уравнение всех прямых, проходящих через точку В (3;4): 4 = 3 k + m Уравнение искомой прямой удовлетворяет обоим равенствам. Составим и решим систему уравнений:
Изображение слайда
15
Последний слайд презентации: Алгебра 8 класс «Решение систем двух линейных уравнений с двумя неизвестными»
Най ти уравнение прямой, проходящей
через точки А(2;-1) и В ( 3;4). -1=2k+m,
4=3k+m ;
Образец оформления решения:
Решение:
= >
х (-1)
-1=2k+m,
— 4= — 3k — m ;
= >
-1=2k+m,
-5 = — k ;
= >
-1= 10 +m,
k = 5 ;
= >
m= -11,
k = 5.
Ответ: y= 5 x -11
-1=2k+m,
4=3k+m ;
Образец оформления решения:
Решение:
= >
х (-1)
-1=2k+m,
— 4= — 3k — m ;
= >
-1=2k+m,
-5 = — k ;
= >
-1= 10 +m,
k = 5 ;
= >
m= -11,
k = 5.
Ответ: y= 5 x -11
Изображение слайда
Внеклассный урок — Система уравнений с двумя переменными. Системы уравнений с двумя переменными. Способы решения.
Система уравнений с двумя переменными. Уравнения первой степени. Способы решенияУравнение может содержать не одну, а две переменных. Понятно, что такие уравнения называются уравнениями с двумя переменными.
Система уравнений – это два и более уравнений, которыми можно манипулировать для нахождения общих решений. Система из двух уравнений вкючает в себя две переменных, значения которых являются общими для обоих уравнений. С помощью одного уравнения системы решается другое, а в итоге решаются оба уравнения системы.
Способы решения системы уравнений первой степени.
1. Решение методом подстановки.
Суть в том, что в системе уравнений выбираете наиболее простое, в котором одну переменную выражаете через другую. Результат подставляете во второе уравнение, благодаря чему преобразуете его в более простое уравнение с одной переменной. Вычисляете это уравнение и получаете значение одной из переменных. Подставляется его в первое уравнение и получаете значение второй переменной. Так вы решаете всю систему уравнений.
Пример: Решим систему уравнений
│x + y = 1
│2x – y = 2
Решение:
Первое уравнение системы проще второго – его и используем.
Выразим в нем x через у:
x = 1 – y
Подставляем это значение x в наше второе уравнение и находим значение y:
2(1 – y) – y = 2
2 – 2y – y = 2
2 – 3y = 2
3y = 2 – 2
3y = 0
y = 0.
Мы получили значение y. Подставляем его в наше первое уравнение и находим теперь уже значение x:
x + 0 = 1
x = 1
Мы нашли значения обеих переменных.
Ответ:
│x = 1
│y = 0
2. Решение методом сложения.
Этот метод целесообразно применять, если при сложении одно из неизвестных пропадает.
Пример 1: Решим систему уравнений
│x + y = 5
│x – y = 1
Решение.
Сложим (вычтем) почленно оба уравнения системы:
│(x + y) + (x – y) = 5 + 1
│(x + y) – (x – y) = 5 – 1
Раскрываем скобки в обоих уравнениях и сводим подобные члены. В результате в первом уравнении пропадает у, во втором х. Мы получаем уравнения с одной переменной, которые проще решать:
│ x + y + x – y = 6
│ x + y – x + y = 4
↓
│2x = 6
│2y = 4
↓
│x = 6 : 2
│y = 4 : 2
↓
│x = 3
│y = 2
Пример решен.
Необязательно производить взаимное сложение и вычитание двух уравнений системы. Часто достаточно бывает произвести одно из двух действий, чтобы вычислить значение одной из двух переменных. А зная одну переменную, мы уже легко сможем найти и вторую.
Пример 2. Решить систему уравнений
│2х + 4у = 26
│8х + 4у = 44
В обоих уравнениях есть число 4у. Значит, можем применить метод сложения. При этом произвести не взаимное сложение, а совершить лишь одно действие: вычесть из первого уравнения второе, чтобы 4у исчезло и чтобы в результате мы получили уравнение с одной переменной:
2х + 4у – 8х – 4у = 26 – 44.
-6х = -18
х = -18 : (-6)
х = 3
Теперь можем найти и значение у, подставив значение х в любое из двух уравнений системы:
2 · 3 + 4у = 26
6 + 4у = 26
4у = 20
у = 20 : 4
у = 5
Ответ: х = 3, у = 5.
Однако рассмотрим еще один пример.
Пример 3: Решим систему уравнений
│3х + 5у = 21
│8х – 3у = 7
Здесь нет переменных с одинаковыми коэффициентами, чтобы при вычитании они исчезли. Что делать в этом случае? Для таких случаев придумано оригинальное решение: умножим почленно первое уравнение на 3, а второе на 5. От этого истина не пострадает, потому что мы просто получим равносильные уравнения. Зато благодаря этому приему у нас появятся одинаковые переменные 15у:
От этого истина не пострадает, потому что мы просто получим равносильные уравнения. Зато благодаря этому приему у нас появятся одинаковые переменные 15у:
│(3х + 5у = 21) · 3
│(8х – 3у = 7) · 5
↓
│3 · 3х + 3 · 5у = 3 · 21
│5 · 8х – 5 · 3у = 5 · 7
↓
│9х + 15у = 63
│40х – 15у = 35
Итак, у нас появились одинаковые переменные и мы можем сложить два уравнения, чтобы прийти к уравнению с одной переменной:
9х + 15у + 40х – 15у = 63 + 35
49х = 98
х = 2
Осталось найти значение второй переменной, подставив значение х, например, в первое уравнение системы:
3 · 2 + 5у = 21
6 + 5у = 21
5у = 21 – 6
5у = 15
у = 3.
Ответ: х = 2; у = 3.
Опять же не всегда нужно преобразовывать оба уравнения системы так, как было в предыдущем примере. Бывает и так, что достаточно изменить лишь одно из уравнений.
Пример 4. Решим систему уравнений:
│3х – 4у = 7
│х + 3у = 11
Здесь достаточно второе уравнение умножить на –3. Тогда мы получим число –3х, а при сложении двух уравнений придем к уравнению с одной переменной.
Тогда мы получим число –3х, а при сложении двух уравнений придем к уравнению с одной переменной.
Итак, умножаем второе уравнение на –3:
(х + 3у = 11) · (–3)
–3х – 9у = –33
Теперь складываем два уравнения, приходим к уравнению с одной переменной у и решаем его:
3х – 4у –3х – 9у = 7 – 33
–13у = –26
у = 2.
И находим значение х. Это проще сделать во втором уравнении:
х + 3 · 2 = 11
х + 6 = 11
х = 5.
Ответ: х = 5; у = 2.
3. Решение методом введения новой переменной.
Пример. Решить систему уравнений
│ 2 3
│———— + ———— = 2
│ х – 3у 2х + у
│
│ 8 9
│———— – ———— = 1
│ х – 3у 2х + у
Перед нами система сложных уравнений, осложненных дробными числами. Наша задача – упростить их, чтобы потом решить. Если применить какой-нибудь из первых двух методов, получатся еще более сложные уравнения. Зато хорошо подходит метод введения новой переменной, благодаря которому мы целую дробь можем заменить одной переменной. Как это сделать?
Зато хорошо подходит метод введения новой переменной, благодаря которому мы целую дробь можем заменить одной переменной. Как это сделать?
Обратите внимание: у первых чисел обоих уравнений одинаковые знаменатели х – 3у, при этом их числители делятся на 2. У вторых чисел тоже одинаковые знаменатели 2х + у, а их числители делятся на 3. Этим и воспользуемся.
1) Выпишем снова нашу систему уравнений, разложив на множители числители второго уравнения и вынеся их за дробь:
│ 2 3
│———— + ———— = 2
│ х – 3у 2х + у
│
│ 2 3
│4 · ———— – 3 · ———— = 1
│ х – 3у 2х + у
Теперь в обоих уравнениях у нас абсолютно одинаковые первые дроби и абсолютно одинаковые вторые дроби.
2) Заменим эти дроби новыми переменными a и b следующим образом:
2 3
———— = а, ———— = b.
х – 3у 2х + у
Так мы существенно упрощаем уравнения, которые обретают совсем иной вид:
│ а + b = 2
│4а – 3b = 1
3) Применяем уже известный нам метод подстановки.
Первое уравнение проще, поэтому сначала выражаем в нем а через b:
а = 2 – b.
Подставляем полученное значение а во второе уравнение, раскрываем скобки, приводим подобные члены и вычисляем численное значение b:
4 · (2 – b) – 3b = 1
8 – 4b – 3b = 1
8 – 7b = 1
7b = 8 – 1
7b = 7
b = 1
Раз нам известно численное значение b, то мы легко можем найти и численное значение а. Это проще сделать с помощью первого уравнения:
а + b = 2
а + 1 = 2
а = 2 – 1
а = 1.
Итак:
а = 1, b = 1.
Вписываем в дроби эти значения а и b:
│ 2
│———— = 1
│ х – 3у
│
│ 3
│———— = 1
│ 2х + у
4) Преобразуем эти уравнения по известному вам правилу: неизвестные влево, известные вправо:
│ х – 3у = 2 : 1
│2х + у = 3 : 1
↓
│ х – 3у = 2
│2х + у = 3
5) Решаем эту систему уравнений снова с помощью метода подстановки. Для этого в первом уравнении х выражаем через у:
Для этого в первом уравнении х выражаем через у:
х = 2 + 3у.
Подставляем во второе уравнение и находим у:
2 · (2 + 3у) + у = 3
4 + 6у + у = 3
7у = 3 – 4
7у = –1
у = –1/7
И с помощью первого уравнения находим х:
х – 3у = 2
х – 3 · (–1/7) = 2
х + 3/17 = 2
х = 2 – 3/7
х = 11/7.
Мы нашли значения х и у в нашей исходной системе уравнений – а значит, решили ее.
Ответ: х = 11/7, у = –1/7
ПРИМЕЧАНИЕ.
Как видно из этого примера, нередки случаи, когда при решении системы уравнений надо последовательно применить сразу несколько методов.
Решение системы линейных уравнений с двумя неизвестными
Решить {$ main.types[data.type] $}
Введите уравнение* x +=
Введите уравнение* x2 +* x +=
Введите уравнения* x +* y +=
* x +* y +=
Введите уравнения* x +* y +* z =
* x +* y +* z =
* x +* y +* z =
{$ error $}!
Результаты расчёта
- x = {$ result.x|number $}
- y = {$ result.y|number $}
- z = {$ result.z|number $}
Результаты расчёта
- x1 = {$ main.FormatResult(result.x1) $} x2″>x2 = {$ main.FormatResult(result.x2) $}
- x3 = {$ main.FormatResult(result.x3) $}
- x4 = {$ main.FormatResult(result.x4) $}
Значение дискриминанта: b2 − 4 * a * c = {$ result.d|number $}
Система линейных уравнений — это объединение нескольких линейных равенств, каждое из которых содержит по 2 неизвестных. Решением системы уравнений называется процесс поиска таких значений неизвестных, при которых выражение превращается в верное числовое равенство.
Линейные уравнения
Линейное уравнение с двумя переменными — это выражение вида:
ax + by + c = 0,
где x и y — неизвестные корни.
Это общий вид равенства, позволяющий идентифицировать его как линейное, так как очевидно, что неизвестные икс и игрек стоят в первой степени. Если переменные имеют отличную от единицы степень или сами являются показателями степеней, то такие равенства считаются нелинейными. Система двух линейных уравнений — это классический математический объект, с которым мы впервые встречаемся в шестом классе школы.
Система двух линейных уравнений — это классический математический объект, с которым мы впервые встречаемся в шестом классе школы.
Система линейных уравнений
Система линейных алгебраических уравнений или СЛАУ — это совокупность n-ного количества равенств, содержащих k-ое количество неизвестных. В школьной алгебре существует негласное правило, что количество уравнений равно количеству неизвестных, то есть СЛАУ с двумя переменными всегда состоят из двух равенств. Высшая математика может преподносить и другие варианты, однако в школьных примерах это правило действует неукоснительно, и наш калькулятор построен по этому принципу: 2 уравнения и 2 переменных. Выглядит это следующим образом:
- ax + by + c = 0
- dx + fy + g = 0
Под буквами a, b, c, d, f, g скрываются коэффициенты уравнения. Именно их следует вбивать в ячейки калькулятора для решения СЛАУ при помощи нашей программы. Важно учесть, что школьные уравнения обычно представляются в виде:
ax + by = с,
поэтому для корректного ввода данных требуется перенести свободный коэффициент в левую часть равенства с заменой знака на противоположный. Итак, у нас есть СЛАУ с двумя неизвестными. Пусть это будет:
Итак, у нас есть СЛАУ с двумя неизвестными. Пусть это будет:
- 3x − y = 14
- 5x + y = 10
Требуется найти такие значения икса и игрека, при которых уравнения превратятся в числовые тождества. При решении системы равенств возможны три варианта развития событий:
- СЛАУ совместна, определена и имеет всего 1 решение;
- система несовместна и решений нет;
- СЛАУ совместна, но неопределена, поэтому существует бесконечное множество решений.
Существует 3 простых способа поиска корней СЛАУ.
Метод подстановки
Это всем известный школьный метод, согласно которому мы выражаем одну переменную через другую, после чего заменяем вторую переменную в другом уравнении и получаем банальное линейное равенство. Посмотрим на второе уравнение нашей СЛАУ:
5x + y = 10
Мы можем спокойно перенести иксы вправо с заменой знака и выразить игрек через икс:
y = 10 − 5x
Теперь подставим это значение игрека в наше первое уравнение и решим его:
- 3x − (10 − 5x) = 14
- 3x + 5x = 14 + 10
- 8x = 24
- x = 3
Теперь вернемся ко второму уравнению и подставим числовое значение икса.
- 5x + y = 10;
- 5 × 3 + y = 10;
- y = 10 − 15;
- y = −5.
Таким образом, x = 3, y = −5 — это корни системы уравнений.
Метод сложения
Данный способ предлагает умножить обе части выражений на такие коэффициенты, чтобы при сложении двух уравнений произошло взаимное уничтожение одной из переменных. После чего метод повторяет алгоритм школьного способа подстановки. Посмотрим на нашу систему:
- 3x − y = 14
- 5x + y = 10
Очевидно, что игреки имеют разные знаки, поэтому при сложении двух уравнений они взаимно уничтожатся, а в результате получим:
- 8x = 24
- x = 3
Далее алгоритм полностью повторяет школьный метод. Нам повезло, что в условии игреки изначально имели коэффициент 1 с противоположными знаками. Рассмотрим пример, когда это не так. Для этого обратим внимание на иксы и попробуем от них избавиться.
- 3x — y = 14
- 5x + y = 10
Для ликвидации иксов нам потребуется найти наименьшее общее кратное коэффициентов при иксах — НОК (3,5) = 15. Следовательно, нам потребуется умножить первое уравнение на 5, а второе на минус 3. Тогда в каждом равенстве мы получим коэффициент при иксе равный 15, но с разными знаками.
Следовательно, нам потребуется умножить первое уравнение на 5, а второе на минус 3. Тогда в каждом равенстве мы получим коэффициент при иксе равный 15, но с разными знаками.
- 15x − 5y = 70,
- −15x − 3y = −30.
Теперь сложим эти уравнения и решим полученное равенство:
- −8y = 40;
- y = −5.
Как видим, результат идентичен полученным корням при расчете школьным методом.
Графический метод
Суть данного способа заключается в построении графиков функции уравнений на декартовой плоскости. Так как уравнения линейны, то график их функций − это всегда прямая линия. Точка пересечения прямых и будет решением СЛАУ. Если система несовместна и не имеет корней, то прямые уравнений будут параллельны, а если СЛАУ обладает бесконечным множеством решений, то графики будут совпадать и сливаться в одну прямую.
Использование СЛАУ
Системы линейных уравнений находят широкое применение во многих науках. Такие объекты встречаются в физике, экономике, электротехнике, метрологии, компьютерных играх или криптографии — везде, где используется математический аппарат. И если говорить о математике, то системы линейных уравнений используются для определения кривой регрессии в методе наименьших квадратов, в расчете собственных векторов матриц, сингулярном разложении или методе главных компонент.
И если говорить о математике, то системы линейных уравнений используются для определения кривой регрессии в методе наименьших квадратов, в расчете собственных векторов матриц, сингулярном разложении или методе главных компонент.
Калькулятор решения СЛАУ
Наша программа решает системы линейных уравнений графическим способом. Калькулятор отрисовывает прямые, заданные линейными функциями и отыскивает их точку пересечения. Координаты этой точки вида (x; y) и есть корни системы уравнений. Для решений СЛАУ вам потребуется только ввести коэффициенты равенств в соответствующие ячейки.
Заключение
Системы линейных уравнений — наборы равенств, которые широко используются во всех областях науки. Для развязывания СЛАУ используйте наш калькулятор, который наглядно представит графическое решение системы уравнений.
Конспект урока 7 класс » «РЕШЕНИЕ СИСТЕМЫ ЛИНЕЙНЫХ УРАВНЕНИЙ С ДВУМЯ НЕИЗВЕСТНЫМИ МЕТОДОМ ПОДСТАНОВКИ» | Методическая разработка по алгебре (7 класс) на тему:
УРОК «РЕШЕНИЕ СИСТЕМЫ ЛИНЕЙНЫХ УРАВНЕНИЙ С ДВУМЯ НЕИЗВЕСТНЫМИ МЕТОДОМ ПОДСТАНОВКИ»
Три пути ведут к знанию: путь размышления – это путь самый благородный, путь подражания – это путь самый легкий и путь опыта- это путь самый горький.
Конфуций
«Деятельность – единственный путь к знанию»
Дж. Бернард Шоу
Цели урока: создать условия для формирования умения учащихся использовать способ подстановки для решения систем уравнений, воспитывать умение контролировать внимание на всех этапах урока.
Ожидаемые учебные результаты:
Предметные:
- подвести их к составлению алгоритма решения системы двух линейных уравнений методом подстановки;
- сформировать умение учащихся решать системы уравнений методом подстановки;
- продолжить формирование умений упрощать выражения, решать линейные уравнения с одной переменной.
Личностные: умение вести диалог на основе равноправных отношений и взаимного уважения и принятия; умение конструктивно разрешать конфликты;
Метапредметные:
Регулятивные УУД
- целеполагание, включая постановку новых целей, преобразование практической задачи в познавательную;
- умение самостоятельно контролировать своё время и управлять им;
- адекватно самостоятельно оценивать правильность выполнения действия и вносить необходимые коррективы в исполнение, как в конце действия, так и по ходу его реализации;
- умение прогнозировать развитие процесса.

Коммуникативные универсальные учебные действия
- формулировать и аргументировать собственное мнение и позицию
- устанавливать и сравнивать разные точки зрения, прежде чем принимать решения и делать выбор;
- аргументировать свою точку зрения, спорить и отстаивать свою позицию не враждебным для оппонентов образом;
- адекватно использовать речевые средства для решения различных коммуникативных задач; владеть устной и письменной речью;
- организовывать и планировать учебное сотрудничество с учителем и сверстниками, определять цели и функции участников, способы взаимодействия; планировать общие способы работы;
- осуществлять контроль, коррекцию, оценку действий партнёра, уметь убеждать;
Познавательные универсальные учебные действия
- создавать и преобразовывать модели и схемы для решения задач;
- осуществлять выбор наиболее эффективных способов решения задач в зависимости от конкретных условий;
- устанавливать причинно-следственные связи;
- строить логическое рассуждение, включающее установление причинно-следственных связей
Длительность урока: 1 академический час (45 мин)
Место проведения урока: кабинет математики
Оснащение урока: презентация и информационно-технологические материалы; учебник математики, ПК.
Тип и вид урока: Урок изучения нового материала.
①Мотивация учебной деятельности . Постановка учащимися целей и задач урока . | Прочитайте слова , которые выбраны девизом урока. Как вы их понимаете. Почему именно их я выбрала в качестве девиза? Нам предстоит разобраться Каким путём пойти и какой для каждого более удобен
| ||||||||||||||||||||||||||||||||||||||||||||
②Актуализация знаний
| Что мы умеем в математике — наш ОПЫТ Устный счет Задания:
Возможные варианты ответов
2) Решите уравнения
3.) Не выполняя построений найдите точки пересечения прямых а) y=-х+3 и y=2х б) y=3х-8 и y=-2х+7 в) y=-5х и y=3х-16 Возможные варианты ответов (1;2) (3;1) (2;-10) Помощь
На прошлых уроках мы с вами познакомились с новой математической моделью. Эта математическая модель представляет собой систему двух линейных уравнений с двумя переменными. Перед нами стояла задача найти такие пары значений (х; у), которые одновременно удовлетворяют и первому, и второму уравнению.
-Кто может мне сказать: Что называется решением системы двух линейных уравнений с двумя переменными — Каким методом мы пользовались определяя решение системы? …… — Вспомните этапы алгоритма решения системы уравнений графическим методом….. — Есть ли у этого метода недостатки?….. Обоснуйте ответ Домашняя практическая работа: решить систему уравнений графическим способом.
IV. Проверка практической работы:
Возможные выводы учащихся: Вывод1: для решения данных уравнений графический способ не удобен: в варианте 1 решением являются дробные числа, определить которые по графику трудно Вывод2: в варианте 2 решением являются большие числа, для определения которых не достаточно страницы тетради. Итог : Для решения данных систем необходим другой способ решения. | ||||||||||||||||||||||||||||||||||||||||||||
③Изучение нового материала. | Итак, у нас есть опыт и мы убедились, что графический метод решения выручает нас не всегда. Значит, нам нужно располагать надежным алгебраическим методом, который нас не подведет в случае с большими или дробными значениями координат точки.
Этим мы и займемся сегодня на уроке. -В тетрадях запишите, пожалуйста, число, Классная работа. Тема урока: «Метод подстановки». Как вы думаете, какова цель нашего урока? Попробуем решить систему, которою решал на доске ….(ученик, вызванный ранее) другим способом: (учитель начинает рассуждение, затем продолжают ученики)
какова цель ? (1. найти общее решение уравнений;
не строя графики ) — Как тогда можно сформулировать задание( обсудите в парах если необходимо) : Найдите координаты точки пересечения графиков уравнений ) 2х-у = 8 и х-у = -13 не выполняя построения. Кто может пойти к доске и выполнить это задание? (К доске…) Преобразуем уравнения (выразим в каждом значение у) у = 2х-8 и у = х+13 -Нас интересует такое значение х, при которых: 2х-8 = х+13 х=21 , тогда у=34 Ответ(21;34) -Чем эти рассуждения отличались от тех, которые применял ….(имя ученика) при решении этой системы графическим методом? -Откройте, пожалуйста, учебник на странице 65 и, прочитав текст, ответьте мне на этот вопрос. -Как же мы рассуждали? — выразили — подставили — решили -нашли -записали ответ — У меня на доске, а у вас на столах листочки с этапами алгоритма, восстановите его последовательность (напечатано на цветных листах):
— Проанализируйте и сопоставьте алгоритм и решение которое мы получили. Сделайте выводы….. — Ели бы вы решали бы сейчас систему с чего бы вы начали …. Что делали бы дальше …. ( обсуждение в парах ), выводы учащихся. Сравните свои рассуждения с предложенными
Выводы учащихся…… — Давайте вернемся ко второй системе, которая осталась без ответа и решим ее способом подстановки (вызвать к доске…. => => =>=> => => => => Ответ : () Еще раз проговорим этапы алгоритма: (проговорить этапы, слайд мультимедиа) | ||||||||||||||||||||||||||||||||||||||||||||
( предварительные итоги) | Опираясь на опыт, рассуждая мы с вами получили алгоритм решения системы уравнений методом подстановки и решили две «домашние» системы . Давайте ещё раз вспомним : 1) Что называют решением системы уравнений с двумя переменными? Что значит решить систему уравнений? 2) Назови методы решения систем линейных уравнений с двумя переменными. 3) Сформулируйте алгоритм решения по каждому способу решения в нескольких словах, назвав самое главное. Как вы думаете , а есть ли пример применениям систем и в частности метода подстановки в жизни? Метод подстановки, когда одно условие подставляется в другое, мы часто используем в обычной жизни. ПРИМЕР «Поиск в социальных сетях» Представьте такую ситуацию. Вот что вы знаете: 1. Она подруга Пети 2. Она тоже учится в 7 классе, хоть и в другой школе 3. Зовут Женя 4. Живет тоже в Москве Каждое из этих условий имеет очень много решений по отдельности. Друзей у Пети много, 7-классниц огромное количество, девочек с именем Женя тоже и так далее. Но так как все эти условия относятся к одному человеку, то это система: , а решением системы является такой человек, который соответствует сразу всем условиям. И решаем эту систему мы методом подстановки. Выбираем одно условие, потом туда подставляем другое и так далее. Итак: Открываете страничку Пети и выбираете список всех его друзей. Это решения первого условия. Их 256. (См. Рис. 1.) Рис. 1. Решение первого условия системы Подставляем сюда второе условие. Раз в 7 классе, то ее возраст от 12 до 14 лет. Количество решений уменьшилось до 132. Рис. 2. Выполнение первых двух условий системы Добавляем условие, которое мы изначально забыли, но нам его подсказала сеть – пол. Женский. Осталось 54. (См. Рис. 3.) Рис. 3. Еще одно условие Город Москва. Осталось 37 человек (См. Рис. 4.) Рис. 4. Выполнение еще одного условия Имя Женя. Осталось два человека. (См. Рис. 5.) Рис. 5. Итог после выполнения всех условий Итак, система имеет 2 решения, из них несложно выбрать нужного нам человека. Мы последовательно в одно условие подставляли другое и так 4 раза, то есть решили задачу методом подстановки. | ||||||||||||||||||||||||||||||||||||||||||||
⑤Рефлексия : | Каким же путём мы сегодня двигались к знаниям
Найдите своё место на горе. Учащимся предлагается рисунок, на котором нужно отметить свое место положение для данного урока, т.е.: Если мало чего понятного и придется разбираться ещё раз с этим материалом, то вы у подножья горы; Если все предельно понятно, но вы не уверены в своих силах, то вы на пути к вершине; Если нет ни каких вопросов, и вы чувствуете , что полностью владеете данной темой, то вы на пике. | ||||||||||||||||||||||||||||||||||||||||||||
⑥ Итог урока и постановка домашнего задания Творческие задания. | Домашнее задание: параграф 12, знать алгоритм, разобрать самостоятельно примеры 1, 3, № 12.2-12.4 (б) При каких значениях параметра a решением системы уравнений будет неотрицательная пара чисел? №11.21 -Сегодня мы познакомились с вами с еще одним способом решения систем двух линейных уравнений с двумя переменными. Сформулировали алгоритм этого метода. На следующих уроках мы отработаем этот алгоритм на более сложных системах и познакомимся с еще одним очень интересным способом решения. Оценки сегодня получили… Спасибо за урок. До свидания. | ||||||||||||||||||||||||||||||||||||||||||||
Литература:
Учебник А.Г. Мордковича Алгебра 7. Издательство «Мнемозина» 2007.
Интернет ресурсы
- https://kopilkaurokov.ru/matematika/uroki/rieshieniie-sistiem-linieinykh-uravnienii-mietod-podstanovki
- http://festival.1september.ru/articles/530529/
- http://interneturok.ru/algebra/7-klass/glava-3-sistema-dvuh-lineynyh-uravneniy-s-dvumya-peremennymi/osnovnye-ponyatiya-metod-podstanovki
- https://www.youtube.com/watch?v=eIua9gLfh4o
- https://infourok.ru/konspekt_uroka_po_matematike_na_temu_metod_podstanovki_7_klass-383419.htm
Приложение
Устный счёт
1) Выразить х через у или у через х
2) Решите уравнения
3. а) y=-х+3 и y=2х б) y=3х-8 и y=-2х+7 в) y=-5х и y=3х-16 |
Задания:
- Возможные варианты ответов
х= — 3у + 10; х= 3у — 10; х= — 3у — 10 |
у =5 х — 2; у =-5 х +2 у =-5 х-2 |
х =- 3у +4 х =- 3у -4 х =3у +4 |
|
3.) Не выполняя построений найдите точки пересечения прямых
а) y=-х+3 и y=2х б) y=3х-8 и y=-2х+7
в) y=-5х и y=3х-16
Возможные варианты ответов
(1;2) (3;1) (2;-10)
Помощь
а) -х+3 =2х 3 =2х+х 3 =3х x=1 y =2 | б) 3х-8 = -2х+7 3х+2х = 8+7 5х = 15 х = 3 у=1 | в) -5х =3х-16 -5х -3х=-16 -8х =-16 х =2 у=10 |
Приложение 1
Алгоритм решения системы уравнений методом подстановки | |
Выбрать переменную (выбираем желательно хорошую переменную: хорошо, когда перед переменной коэффициент 1 или -1) и выразить одну переменную из любого уравнения через другую . | |
Подставить полученное выражение во второе уравнение | |
Решить уравнение с одной переменной. | |
Найденное значение переменной подставить в первое уравнение и найти значение второй переменной. |
Записать ответ |
Приложение 2
Приложение к уроку
I вариант Практическая работа: решить систему уравнений графическим способом. | II вариант Практическая работа: решить систему уравнений графическим способом. |
|
|
I вариант Практическая работа: решить систему уравнений графическим способом. | II вариант Практическая работа: решить систему уравнений графическим способом. |
|
|
I вариант Практическая работа: решить систему уравнений графическим способом. | II вариант Практическая работа: решить систему уравнений графическим способом. |
|
|
I вариант Практическая работа: решить систему уравнений графическим способом. | II вариант Практическая работа: решить систему уравнений графическим способом. |
|
|
I вариант Практическая работа: решить систему уравнений графическим способом. | II вариант Практическая работа: решить систему уравнений графическим способом. |
|
|
Приложение 3
Алгоритм решения системы уравнений методом подстановки
1 этап
Выбрать переменнную (выбираем желательно хорошую переменную: хорошо когда перед переменной коэффициент 1 или -1) и выразить одну (любую) переменную из любого уравнения. |
Выбрать переменнную (выбираем желательно хорошую переменную: хорошо когда перед переменной коэффициент 1 или -1) и выразить одну (любую) переменную из любого уравнения. |
Выбрать переменнную (выбираем желательно хорошую переменную: хорошо когда перед переменной коэффициент 1 или -1) и выразить одну (любую) переменную из любого уравнения. . |
Выбрать переменнную (выбираем желательно хорошую переменную: хорошо когда перед переменной коэффициент 1 или -1) и выразить одну (любую) переменную из любого уравнения. |
Выбрать переменнную (выбираем желательно хорошую переменную: хорошо когда перед переменной коэффициент 1 или -1) и выразить одну (любую) переменную из любого уравнения. |
Выбрать переменнную (выбираем желательно хорошую переменную: хорошо когда перед переменной коэффициент 1 или -1) и выразить одну (любую) переменную из любого уравнения. |
Выбрать переменнную (выбираем желательно хорошую переменную: хорошо когда перед переменной коэффициент 1 или -1) и выразить одну (любую) переменную из любого уравнения. |
2 этап
Подставить полученное выражение во второе уравнение |
Подставить полученное выражение во второе уравнение |
Подставить полученное выражение во второе уравнение |
Подставить полученное выражение во второе уравнение |
Подставить полученное выражение во второе уравнение |
Подставить полученное выражение во второе уравнение |
Подставить полученное выражение во второе уравнение |
Подставить полученное выражение во второе уравнение |
3 этап
Решить уравнение с одной переменной. |
Решить уравнение с одной переменной. |
Решить уравнение с одной переменной. |
Решить уравнение с одной переменной. |
Решить уравнение с одной переменной. |
Решить уравнение с одной переменной. |
Решить уравнение с одной переменной. |
Решить уравнение с одной переменной. |
4 этап
Найденное значение переменной подставить в одно из первых уравнений и найти значение второй переменной. |
Найденное значение переменной подставить в первое уравнение и найти значение второй переменной. |
Найденное значение переменной подставить в первое уравнение и найти значение второй переменной. |
Найденное значение переменной подставить в первое уравнение и найти значение второй переменной. |
Найденное значение переменной подставить в первое уравнение и найти значение второй переменной. |
Найденное значение переменной подставить в первое уравнение и найти значение второй переменной. |
Найденное значение переменной подставить в первое уравнение и найти значение второй переменной. |
5 этап
Записать ответ |
Записать ответ |
Записать ответ |
Записать ответ |
Записать ответ |
Записать ответ |
Записать ответ |
Записать ответ |
Приложение 4
Рефлексия
Приложение 5
«Рабочий лист»
Ф. И______________________________________________
И______________________________________________
Тема урока:_________________________________________________________________
Знаю | Хочу узнать | Узнал | ||||||||
Задание | Кол-во баллов | |||||||||
Устный счет | ||||||||||
1. Выразить х через у или у через х | ||||||||||
2. Преобразуйте линейное уравнение с двумя переменными к виду линейной функции y=kx+m | ||||||||||
3. | ||||||||||
Алгоритм | ||||||||||
Решение систем линейных уравнений | ||||||||||
Общее количество баллов | ||||||||||
Оценка «2»:менее 3 баллов «3»: от 3 до 5 баллов «4»: от 6 до 8 баллов «5»: от 9 до 11 баллов | ||||||||||
Решить систему уравнений методом подстановки | ||
1 вариант рассуждений | 2 вариант рассуждений |
|
| ||
2у-26-у=8 у=34 | х-2х+8=-13 -х=-21 х=21 |
|
х-34=-13 х=21 | 21-у=-13 -у=-34 у=34 |
|
Ответ : (21;34) | Ответ : (21;34) |
|
Решить систему уравнений методом подстановки | ||
1 вариант рассуждений | 2 вариант рассуждений |
|
| ||
2у-26-у=8 у=34 | х-2х+8=-13 -х=-21 х=21 |
|
х-34=-13 х=21 | 21-у=-13 -у=-34 у=34 |
|
Ответ : (21;34) | Ответ : (21;34) |
|
Два уравнения с тремя неизвестными — Сборка-Доработка
2. 2.1. Определение. Пусть даны линейные уравнения
2.1. Определение. Пусть даны линейные уравнения
a1x+b1y+c1z=d1,(2.2.1)
a2x+b2y+c2z
Если требуется найти общее решение уравнений (2.2.1) и (2.2.2), то говорят, что они образуют систему. Система, состоящая из уравнений (2.2.1) и (2.2.2), обозначается следующим образом:
(2.2.3)
Общее решение уравнений, составляющих систему, называется решением системы. Решить систему (2.2.3) ¾ это значит либо найти множество всех его решений, либо доказать, что их нет.
Ниже мы сформулируем условия, при которых система (2.2.3) имеет более одного решения и не имеет ни одного решения (теорема 2.2.4).
2.2.2. Определение. Пусть дана система (2.2.3) линейных уравнений. Матрица
называется (основной) матрицей системы. Матрица называется расширенной матрицей системы.
Определения равносильных систем, элементарных преобразований систем вводятся аналогично, как и для систем из двух уравнений с двумя неизвестными. Кроме того, напоминаем, что при элементарных преобразованиях системы получается система, равносильная данной.
Это обстоятельство позволяет легко решить систему (2.2.3) с помощью элементарных преобразований.
2.2.3. Пример. Решить системы уравнений:
а)
б) в)
г)
д) е)
Неизвестная z может принимать любое числовое значение a. Тогда x=21-23a и y=12-12a. Таким образом, множество решений системы: <(21-23a; 12-12a; a)|aÎR>.
Тогда x=21-23a и y=12-12a. Таким образом, множество решений системы: <(21-23a; 12-12a; a)|aÎR>.
á(1) Поменяли местами уравнения (преобразование 3-го типа).
(2) Первое уравнение, умноженное на 4, вычли из второго (преобразование 2-го типа).
(3) Перенесли из левых уравнений в правую члены с неизвестной z (поменяв знаки на противоположные)
(4) В первое уравнение вместо y подставили его выражение через z: y=12-12z.ñ
Замечание. Вместо z в правые части мы могли перенести y, и тогда множество решений записалось бы в виде <(-2+
b; b; 1- b)|bÎR>. Естественно, множества <(21-23a; 12-12a; a)|aÎR> и <(-2+ b; b; 1- b)|bÎR> совпадают.
Естественно, множества <(21-23a; 12-12a; a)|aÎR> и <(-2+ b; b; 1- b)|bÎR> совпадают.
б) Разделим первое уравнение на 5. Тогда приходим к системе
которая равносильна уравнению x-2y—z= -3. Она равносильна уравнению x= -3+2y+z, где неизвестные y и z могут принимать любые значения y=a и z=b. Таким образом, множество всех решений системы ¾ следующее: <(-3+2a+b; a; b)|a, bÎR>.
в) Разделим первое уравнение на 5 и вычтем из последнего. Придём к равносильной системе
второе уравнение которой является противоречивым. Следовательно, система решений не имеет.
Ответ: а) (21-23a; 12-12a; a), aÎR;
б) <(-3+2a+b; a; b)|a, bÎR>;
в) Система решений не имеет.
Из предыдущих примеров видно, что система из двух уравнений с тремя неизвестными может иметь бесконечное множество решений, а может вообще их не иметь.
2.2.4. Теорема. Пусть дана система (3.2.3), d1=
, d2= , d3= , D1= , D2= и D3= . Тогда:
Тогда:
1) Если хотя бы один из определителей d1, d2или d3не равен нулю, то система имеет бесконечное множество решений, зависящих от одного параметра.
2) Если d1=d2=d3=0 и хотя бы один из определителей D1, D2или D3не равен нулю, то система решений не имеет.
3) Если d1=d2=d3=D1=D2=D3=0, то система имеет бесконечное множество решений, зависящих от двух параметров.
Замечание. Условие D1=0 равносильно D2=0 или D3=0; так что некоторые из этих условий в формулировке теоремы 3.2.4 излишние.
2.2.5. Упражнение. Решить системы, предварительно исследовав их на наличие решений:
а)
б) в)
г)
д) е)
Решение. а) Так как d1=
а) Так как d1=
=0, d2= =0, d3= =0, D1= =0, D2= =0, D3= =0, то система имеет бесконечное множество решений, зависящих от двух параметров. Найдем их. Эта система равносильна уравнению -3x+2y+z= -9 (второе уравнение получается из этого умножением на -3). Положив y=a и z=b, получаем x=3+ . Тогда (3+ , a, b) ¾ решение системы, a, bÎR.
б) С одной стороны, d1=
=0, d2= =0, d3= =0, с другой, D1= =21¹0. Поэтому система решений не имеет.
в) Так как d1=
=-8¹0, то система имеет бесконечное множество решений, зависящих от одного параметра. Найдём их:
Полагая z=a, получаем множество всех решений системы: <(
, , a) | aÎR>.
Не нашли то, что искали? Воспользуйтесь поиском:
Любые системы уравнений
Этот онлайн калькулятор в два шага:
- Добавить нужное кол-во уравнений
- Ввести уравнения
Решение системы линейных уравнений методом Крамера
Это он-лайн сервис в два шага:
- Ввести количество уравнений в системе
- Ввести коэффициенты при неизвестных слагаемых
Методом Гаусса
Этот онлайн калькулятор в три шага:
- Ввести количество уравнений в системе
- Ввести количество незвестных
- Ввести коэффициенты при неизвестных слагаемых
© Контрольная работа РУ — калькуляторы онлайн
Ответ
Давайте выразим х из первого уравнения и подставим во второе:
Подставим обратно в выражение для х:
Итак, мы нашли х (х = 2), значит, мы можем преобразовать нашу систему до системы с двумя переменными:
Видно, что второе уравнение получено из первого путём умножения на 2. Следовательно, z может быть любым, тогда y = 9 — 1,5z
Следовательно, z может быть любым, тогда y = 9 — 1,5z
Ответ:
x = 2
z — любое
y = 9 — 1,5z
Как решить 2 уравнения с 2 неизвестными в Excel (2 примера)
Excel — мощный инструмент, широко известный благодаря анализу данных и выполнению больших вычислений. В некоторых математических задачах и вычислениях нам нужно решить 2 уравнения с 2 неизвестными. Excel очень удобен в этом отношении. Если вы ищете способы сделать это, вы попали в идеальное место. В этой статье я покажу вам два эффективных метода для решения 2 уравнений с 2 неизвестными в Excel.
Скачать практическую рабочую тетрадь
2 метода решения 2 уравнений с 2 неизвестными в Excel
1. Объедините функции MMULT и MINVERSE.
2. Использование надстройки «Поиск решения» в Excel
Вывод
Статьи по Теме
Скачать рабочую тетрадь
Вы можете скачать нашу рабочую тетрадь отсюда бесплатно!
2 метода решения 2 уравнений с 2 неизвестными в Excel
Допустим, у вас есть 2 уравнения с двумя неизвестными x и y. Уравнения следующие:
Уравнения следующие:
2х + у = 8
3х – 2у = 5
Теперь вы можете решить эти уравнения любым из двух способов, приведенных ниже.
1. Объединить функции ММУЛЬТ и МИНВЕРС
Самый эффективный и быстрый метод решения двух уравнений с двумя неизвестными — это комбинация функций МУЛЬТИМЕДЛ и МИНВЕРС . Чтобы сделать это, выполните следующие действия.
📌 Шаги:
- В первую очередь выберите ячейки D13 и D14 .
- Затем вставьте приведенную ниже формулу, чтобы решить уравнения.
=МНОЖ(МИНВЕРС(B8:C9),E8:E9)
- Затем нажмите Ctrl + Shift + Enter , чтобы получить желаемый результат.
Таким образом, ваши уравнения с двумя неизвестными будут решены и вы получите решения в ячейках D13 и D14. Например, вывод должен выглядеть так.
Например, вывод должен выглядеть так.
Примечание:
Здесь вы должны нажать Ctrl + Shift + Enter , чтобы получить желаемый результат. Потому что это формула массива. Если вы нажмете только Enter, формула не будет работать должным образом, и вы не получите правильный результат.
Подробнее: Как решить для x в Excel (2 простых способа)
Аналогичные показания
- Как решить полиномиальное уравнение в Excel (5 простых методов)
- Решение экспоненциального уравнения в Excel (4 подходящих примера)
- Как решить дифференциальное уравнение в Excel (с помощью простых шагов)
2. Использование надстройки «Поиск решения» в Excel
Еще один разумный способ решить 2 уравнения с 2 неизвестными — использовать надстройку Excel Solver. Выполните следующие шаги, чтобы выполнить это.
📌 Шаг 1. Установка надстройки Solver
- Как правило, Решатель изначально не остается ни на одной вкладке. Скорее, вам нужно добавить его из раздела надстроек Excel.
- Для этого сначала нужно перейти на вкладку File .
- После этого выберите параметр Параметры на расширенной вкладке Файл .
- В это время появится окно Параметры Excel .
- Теперь перейдите на вкладку Надстройки из окна >> выберите опцию Solver Add-in >> нажмите кнопку Перейти… .
- В результате теперь появится окно Add-ins .
- Затем отметьте опцию Solver Add-in в окне и нажмите кнопку OK .
Таким образом, инструмент Solver будет добавлен на вкладку Data .
📌 Шаг 2. Подготовка набора данных в правильном формате для решения функций
Теперь для расчета с помощью Solver , сначала вам нужно будет принять значения неизвестных и вычислить значения функций.
- Для этого мы устанавливаем значения X и Y равными 1 и 1. В результате значения функций будут равны 3 и 1 соответственно. Но нужные значения 8 и 5.
- Теперь запишите эти предполагаемые значения и вычисленные значения функций, а также требуемые значения функций в файле Excel.
📌 Шаг 3: Использование Решателя для получения результатов
Теперь вы, наконец, можете получить значения двух неизвестных.
- Сначала перейдите на вкладку Данные >> Инструмент Solver .
- В результате появится окно Solver Parameters .

- Теперь в текстовом поле Установить цель: обратитесь к ячейке C12 .
- После этого в списке опций To: поставьте переключатель на опцию Value Of: и напишите 8 в текстовом поле рядом с этой опцией.
- Далее в текстовом поле путем изменения ячеек переменных: обратитесь к ячейкам C8:C9 .
- Затем для установки ограничений нажмите кнопку Добавить в группе С учетом ограничений: .
- В результате появится диалоговое окно Добавить ограничение .
- В текстовом поле Cell Reference см. C12 9ячейка 0004.
- Затем выберите знак равенства (=) из раскрывающегося списка и обратитесь к ячейке D12 в текстовом поле Constraint: .
- И последнее, но не менее важное: нажмите кнопку OK .

- Повторите предыдущие 5 шагов, чтобы добавить еще одно ограничение уравнения.
- После этого окно Solver Parameters будет выглядеть следующим образом.
- Здесь выберите Simplex LP вариант из Выберите метод решения: вариантов.
- Затем нажмите кнопку Решить .
- В результате появится окно Solver Results с сообщением о том, что найдено решение.
- Здесь установите переключатель на опцию Keep Solver Solution и нажмите кнопку OK .
Следовательно, ваши уравнения с двумя неизвестными будут решены, и следующие результаты будут показаны в C8:C9клетки. Например, результат будет выглядеть так.
Подробнее: Как решить уравнение для X, если Y задан в Excel
Заключение
В заключение в этой статье я показал вам 2 эффективных метода решения двух уравнений с двумя неизвестными в Excel. Я предлагаю вам внимательно прочитать всю статью и применить полученные знания для своих нужд. Вы также можете скачать нашу бесплатную рабочую тетрадь для практики. Я надеюсь, что вы найдете эту статью полезной и информативной. Если у вас есть какие-либо дополнительные вопросы или рекомендации, пожалуйста, не стесняйтесь комментировать здесь. И посетите ExcelDemy для многих других статей, подобных этой.
Я предлагаю вам внимательно прочитать всю статью и применить полученные знания для своих нужд. Вы также можете скачать нашу бесплатную рабочую тетрадь для практики. Я надеюсь, что вы найдете эту статью полезной и информативной. Если у вас есть какие-либо дополнительные вопросы или рекомендации, пожалуйста, не стесняйтесь комментировать здесь. И посетите ExcelDemy для многих других статей, подобных этой.
Связанные статьи
- Решение квадратного уравнения в Excel VBA (с быстрыми шагами)
- Как решить уравнение Коулбрука в Excel (3 простых способа)
- Решение алгебраических уравнений с несколькими переменными (3 способа)
- Решение кубического уравнения в Excel (2 способа)
Линейные системы с двумя неизвестными — Криста Кинг Математика
Что такое линейная система?
В линейной алгебре нам будет очень интересно решать системы линейных уравнений или линейные системы.
Линейная система — это система уравнений, определенная для набора неизвестных переменных, где каждая из переменных является линейной (переменные первой степени или возведены в степень ???1???).
Привет! Я Криста.
Я создаю онлайн-курсы, чтобы помочь вам в учебе по математике. Читать далее.
Позже мы узнаем о матрицах и о том, как их использовать для решения линейных систем. Итак, чтобы получить базовое представление о том, что мы делаем, когда решаем системы, мы хотим использовать этот урок для обзора других основных методов решения систем.
На вводном уроке по алгебре мы должны были изучить три способа решения систем линейных уравнений: подстановка, исключение и построение графика. Давайте рассмотрим шаги для каждого из этих методов.
Метод замены
Получить переменную саму по себе в одном из уравнений.
Возьмите выражение, полученное для переменной на шаге 1, и подставьте его (заменив скобками) в другое уравнение.

Решите уравнение шага 2 для оставшейся переменной.
Используйте результат шага 3 и подставьте его в уравнение шага 1.
Как решить систему двух линейных уравнений с двумя неизвестными
Пройти курс
Хотите узнать больше о линейной алгебре? У меня есть пошаговый курс для этого. 🙂
Есть три способа решения системы линейных уравнений
Пример
Найдите единственное решение системы уравнений.
???y=x+3???
???2x-3y=10???
Решим систему методом подстановки. С ???г??? уже решено для в первом уравнении, шаг 1 завершен, и мы перейдем к шагу 2, подставив ???x+3??? для тебя??? в другом уравнении.
???2x-3y=10???
???2x-3(x+3)=10???
Найдите ???x???. Начните с распространения ???-3???.
???2x-3x-9=10???
Объедините похожие термины.
???-x-9=10???
Добавить ???9??? в обе стороны.
???-x-9+9=10+9???
???-x=19???
Умножить обе стороны на ???-1???.
???-х(-1)=19(-1)???
???х=-19???
Чтобы найти ???y???, подключим ???-19??? для ???х??? в первом уравнении.
???y=x+3???
???y=-19+3???
???y=-16???
Единственное решение ???(-19,-16)???.
Мы бы узнали три способа решения систем линейных уравнений: замена, исключение и построение графика.
Метод исключения
При необходимости переставьте оба уравнения так, чтобы сначала были члены ???x???, затем ???y???-члены, знак равенства и константа срок (в таком порядке). Если уравнение не имеет постоянного члена, это означает, что постоянный член равен ???0???.
Умножить одно (или оба) уравнения на константу, которая позволит отменить либо ???x???-члены, либо ???y???-члены при сложении или вычитании уравнений (когда их левая и правая части складываются отдельно или когда их левая и правая части вычитаются отдельно).

Сложите или вычтите уравнения.
Найдите оставшуюся переменную.
Подставьте результат шага 4 в одно из исходных уравнений и найдите другую переменную.
Пример
Найдите единственное решение системы уравнений.
???y=3x-4???
???-x+2y=12???
Сначала мы перестроим первое уравнение так, чтобы его отдельные части оказались в правильных местах для исключения. Вычесть ???3x??? с обеих сторон.
???y=3x-4???
???-3x+y=3x-3x-4???
???-3x+y=-4???
Затем умножьте полученный результат на ???2??? так что ???y???-члены сокращаются, когда мы вычитаем уравнения.
???2(-3x+y)=2(-4)???
???-6x+2y=-8???
Теперь вычтем уравнения.
???-6x+2y-(-x+2y)=-8-(12)???
???-6x+2y+x-2y=-8-12???
Объедините похожие термины.
???-6x+x+2y-2y=-20???
???-5x+0=-20???
???-5x=-20???
Разделите обе стороны на ???-5???.
???\frac{-5x}{-5}=\frac{-20}{-5}???
???х=4???
Чтобы найти ???y???, подставим ???4??? для ???х??? в исходном первом уравнении.
???y=3x-4???
???y=3(4)-4???
???y=12-4???
???y=8???
Единственное решение ???(4,8)???.
Графический метод
Решить для ???y??? в каждом уравнении.
Постройте график обоих уравнений в одной и той же декартовой системе координат.
Найдите точку пересечения линий (точку пересечения линий).
Давайте рассмотрим пример с использованием графического метода.
Пример
Нарисуйте оба уравнения, чтобы найти решение системы.
???x+3y=12???
???2x-y=5???
Чтобы изобразить эти уравнения в виде графика, давайте представим их оба в форме пересечения наклона. Начните с первого уравнения системы. Получаем
???x+3y=12???
Вычесть ???x??? с обеих сторон.
???х-х+3у=-х+12???
???3y=-x+12???
Разделите обе части на ???3???.
???\frac{3y}{3}=-\frac{x}{3}+\frac{12}{3}???
???y=-\frac13x+4???
Теперь возьмем второе уравнение.
???2x-y=5???
Вычесть ???2x??? с обеих сторон.
???2x-2x-y=-2x+5???
???-y=-2x+5???
Умножить обе части на ???(-1)???.
???(-y)(-1)=(-2x+5)(-1)???
???y=2x-5???
Строка ???y=-(1/3)x+4??? пересекает ось ???y??? в точке ???4???, а затем имеет наклон ???-1/3???, поэтому его график равен
Строка ???y=2x-5??? пересекает ось ???y??? в точке ???-5???, а затем имеет наклон ???2???, поэтому, если добавить его график к графику ???y= -(1/3)x+4???, получится
Глядя на точку пересечения, кажется, что решение приблизительно равно ???(3.75,2.75)???. На самом деле решение ???(27/7,19/7)\приблизительно(3,86,2,71)???, поэтому наша визуальная оценка ???(3,75,2,75)??? был не так далек.
Получить доступ к полному курсу линейной алгебры
Learn mathКриста Кинг математика, выучить онлайн, онлайн курс, онлайн математика, линейная алгебра, линейные системы, решение линейных систем, системы уравнений, системы линейных уравнений, одновременные уравнения, решение систем с подстановкой, решение систем с исключением, решение систем с графическим построением, графическое устранение замены
0 лайков2 уравнения и 2 неизвестных
залогодержатель
Известный член
- #1
На этой доске кто-то разместил способ решить 3 уравнения и 3 неизвестных, используя функцию под названием minverse. Я пытался заставить его делать 2 уравнения и 2 неизвестных, но я только что получил #ЧИСЛА. Кто-нибудь знает метод excel для быстрого выполнения этого? (Я проверяю HW моей дочери, и я не хочу делать это все)
Я пытался заставить его делать 2 уравнения и 2 неизвестных, но я только что получил #ЧИСЛА. Кто-нибудь знает метод excel для быстрого выполнения этого? (Я проверяю HW моей дочери, и я не хочу делать это все)
Джин, «Ипотечный человек», Кляйн
Знаете ли вы, что Excel предлагает фильтр по выбору?
Нажмите здесь, чтобы открыть ответ
Добавьте значок автофильтра на панель быстрого доступа. Выберите ячейку, содержащую Apple, нажмите «Автофильтр», и вы получите все строки с Apple
.pgc01
MrExcel MVP
- #2
Hi Gene
Например,
2x + 5y = 8
4x + 7y = 13
Запишите параметры в A1:C2, как показано на рисунке
Выберите F1:F2 (Оба одновременно) и введите в строке формул
=МУМНОЖ(МИНВЕРС(A1:B2),C1:C2)
Это формула массива, поэтому ДОЛЖЕН быть введен с помощью CTRL+SHIFT+ENTER, а не просто ENTER.
Это даст вам оба результата.
Hope it’s clear
PGC
| Book1 | ||||||||
|---|---|---|---|---|---|---|---|---|
| A | B | C | D | E | F | G | H | |
| 1 | 2 | 5 | 8 | x | 1.5 | |||
| 2 | 4 | 7 | 13 | y | 1 | |||
| 3 | ||||||||
| 4 | ||||||||
| 5 | ||||||||
Sheet3 | ||||||||
DrSki
Новый член
- #3
убедитесь, что последняя строка вашей матрицы 3×3 равна 0 0 1, а последний столбец равен
0
0
1
что касается правой части последнего уравнения, не имеет значения, что вы вводите, хотя 0 было бы красиво и чисто…
Например, если система
x + 3y = 7
3x- y = 1,
, введите ее, как если бы она была
x + 3y + 0z = 7
3x — y + 0z = 1
0x + 0y+ 1z= 0
Это фактически присваивает z нулевое значение, а затем математика концентрируется на поиске значений x и y.
Для этого примера вы должны получить (x,y,z)= (1,2,0),( но вы можете игнорировать z=0).
Я думаю, что вы, возможно, пытались вставить все нули в последнюю строку, и это означает, что z может быть чем угодно, и это только запутывает вещи и приводит к ситуациям в матричном мире, похожим на попытку деления на ноль с обычными числами.
Надеюсь, это поможет.
залогодержатель
Известный член
- #4
Очень ясно. Работал отлично. Спасибо
Джин, «Ипотечный человек», Кляйн
Вы должны войти или зарегистрироваться, чтобы ответить здесь.
Решить полиномиальное уравнение 6-го порядка в Excel
- кевлонго
- Вопросы Excel
- Ответы
- 4
- просмотров
- 5К
joeu2004
Один или несколько модулей для каждого сабвуфера
- Авария
- Вопросы Excel
- Ответы
- 0
- просмотров
- 277
CrashOD
Первый проект VBA — есть ли лучший способ написать этот код?
- акшай27
- Excel Вопросы
- Ответы
- 0
- просмотров
- 578
akshay27
Сохранение файла в текущей папке
- rossross
- Вопросы Excel
- Ответы
- 7
- просмотров
- 506
Micron
Связывание двух электронных таблиц и автоматический перенос предварительно выбранных данных на лист 2
- bustosjuan
- Вопросы Excel
- Ответы
- 0
- просмотров
- 341
bustosjuan
Делиться:
Фейсбук Твиттер Реддит Пинтерест Тамблер WhatsApp Эл. адрес Делиться Ссылка на сайт
Решение одновременных уравнений с несколькими неизвестными
01 февраля 2018 г.
Это третья статья в нашей серии кратких статей, в которых обсуждаются важные темы, касающиеся техников-электронщиков и электромехаников, а также студентов-технарей, готовящихся к работе в современных условиях. В этой серии мы обсудим некоторые повседневные навыки и темы для практикующих техников, а также некоторые области, которые наши студенты-технари определили как «трудные для понимания» при выполнении общего анализа цепей. Темы обсуждения будут включать в себя методы сокращения схемы, переходные характеристики, а также области сложности при работе с линейными теоремами сети постоянного тока.
В этой серии мы обсудим некоторые повседневные навыки и темы для практикующих техников, а также некоторые области, которые наши студенты-технари определили как «трудные для понимания» при выполнении общего анализа цепей. Темы обсуждения будут включать в себя методы сокращения схемы, переходные характеристики, а также области сложности при работе с линейными теоремами сети постоянного тока.
Как решать одновременные уравнения с несколькими неизвестными
Многие техники сталкиваются с трудностями при решении уравнений узлов или контуров, содержащих несколько неизвестных величин. В этой третьей части серии «Техники-практики» мы рассмотрим способы решения таких уравнений для получения контурных токов или узловых напряжений при выполнении линейного анализа сети постоянного тока. Двумя методами технического уровня для решения одновременных уравнений с несколькими неизвестными, используемыми при работе с двумя или тремя уравнениями, являются «подстановка» и «исключение». Чтобы решить для заданного числа неизвестных, мы требуем, чтобы такое же количество уравнений было предоставлено. Например, нам потребуется два уравнения для решения двух неизвестных величин. Нам потребовались бы три уравнения для решения трех неизвестных величин и так далее.
Чтобы решить для заданного числа неизвестных, мы требуем, чтобы такое же количество уравнений было предоставлено. Например, нам потребуется два уравнения для решения двух неизвестных величин. Нам потребовались бы три уравнения для решения трех неизвестных величин и так далее.
Решите для x и y, учитывая эти два уравнения, содержащие две неизвестные величины.
Уравнение 1 3x + 2 = 2y
Уравнение 2 8x – 4 = 4y
Мы хотим выделить член y в одном уравнении. Под этим мы подразумеваем, что нам нужно уравнение, которое выражает значение одного y через x.
| Уравнение 1 | 3x + 2 = 2y |
| у = (3х + 2) / 2 |
Поскольку теперь у нас есть выражение для значения y через x, мы заменим член y в уравнении 2 этим новым выражением, которое мы получили выше. Это оставит нам только одну неизвестную величину, x, для решения уравнения 2 вместо двух неизвестных, которые у нас были раньше.
| Уравнение 2 | 8х – 4 = 4у |
| 8х – 4 = 4(3х + 2) / 2 | |
| 8х – 4 = (12х + 8) / 2 | |
| 8х – 4 = 6х + 4 | |
| 8х = 6х + 4 + 4 | |
| 8х – 6х = 4 + 4 | |
| 2x = 8 | |
| х = 8/2 | |
| х = 4 |
Имея значение x, мы можем использовать его в уравнении 1 или уравнении 2, чтобы найти значение y. (Используя уравнение 1)
3 (4) + 2 = 2y
12 + 2 = 2y
14 = 2y
y = 14/2
y = 7
использовать для решения двух неизвестных в тех же двух уравнениях.
Уравнение 1 3x + 2 = 2y
Уравнение 2 8x – 4 = 4y
На этот раз наша цель – найти множитель для умножения одного из уравнений, на который мы сможем суммировать два уравнения и исключить одно из неизвестных. Если мы умножим обе части уравнения 1 на коэффициент -2, а затем просуммируем два уравнения, у нас останется выражение, содержащее только одно неизвестное. Мы выбрали -2 в качестве коэффициента для умножения уравнения 1, так что правая часть уравнения 1 при добавлении к правой части уравнения 2 приведет к исключению члена y из результирующего уравнения.
Если мы умножим обе части уравнения 1 на коэффициент -2, а затем просуммируем два уравнения, у нас останется выражение, содержащее только одно неизвестное. Мы выбрали -2 в качестве коэффициента для умножения уравнения 1, так что правая часть уравнения 1 при добавлении к правой части уравнения 2 приведет к исключению члена y из результирующего уравнения.
| Уравнение 1 | 3x + 2 = 2y |
| -2 (3x + 2) = -2 (2y) | |
| -6х – 4 = — 4у |
Теперь мы суммируем это новое выражение для уравнения 1 с нашим исходным уравнением 2. Добавление -4y из правой части нашего нового выражения для уравнения 1 к 4y в правой части уравнения 2 приведет к 0y, что эффективно исключает член y из результирующего уравнения.
Уравнение 1 -6x – 4 = — 4y (уравнение 1 изменено с коэффициентом -2)
Уравнение 2 8x – 4 = 4y
Чтобы просуммировать эти уравнения, добавьте члены из левой части каждого уравнения вместе, и сложите члены из правой части уравнений вместе следующим образом…. .
.
(-6x – 4) + (8x – 4) = (-4y) + (4y)
2x – 8 = 0
2x = 8
x = 8/2
x = 4
Теперь мы будем использовать значение 4 для x в любом из двух исходных уравнений, чтобы найти значение y. (Используя уравнение 2)
8(4) – 4 = 4y
32 – 4 = 4y
28 = 4y
y = 28/4
y = 7
легко узнаваемый способ сведения уравнения к одному неизвестному. Вместо этого мы могли бы исключить переменную x, оставив уравнение с y в качестве единственной неизвестной величины.
Уравнение 1 3x + 2 = 2y
Уравнение 2 8x – 4 = 4y
Чтобы убрать члены x из приведенных выше уравнений, необходимо применить коэффициент к обоим уравнениям, чтобы создать ситуацию мы желаем. Если мы умножим Eq.1 на 8 и Eq.2 на -3, члены x станут 24x и -24x соответственно. Они компенсируют друг друга при суммировании двух уравнений.
Уравнение 1 8(3x + 2) = 8(2y)
Уравнение 1 24x + 16 = 16y
Уравнение 2 -3(8x – 4) = -3(4y)
Уравнение 2 -24x + 12 = -12y
Теперь мы суммируем наши два новых уравнения, чтобы получить уравнение с одной переменной. Если мы напишем уравнения одно поверх другого, мы можем просто просуммировать по вертикали, чтобы получить наше уравнение с одной переменной.
Если мы напишем уравнения одно поверх другого, мы можем просто просуммировать по вертикали, чтобы получить наше уравнение с одной переменной.
| Уравнение 1 | 24x + 16 = 16y |
| Уравнение 2 | -24х + 12 = -12у |
| ———————— | |
| 0x + 28 = 4y | |
| 4г = 28 | |
| г = 28/4 | |
| у = 7 |
Теперь мы будем использовать это известное значение y в одном из исходных уравнений, чтобы найти значение x. (Используйте уравнение 1)
3x + 2 = 2(7)
3x + 2 = 14
3x = 14 – 2
3x = 12
x = 12/3
x = 4
Практический пример того, как применяются эти методы, представлен в видеоролике, посвященном анализу петель ниже. В этом примере используются методы замены и исключения для решения одновременных уравнений цикла KVL, и он проиллюстрирован шаг за шагом.
Мы надеемся, что это было полезно для вас как практикующего или студента-техника. Если вам понравился этот пост, ознакомьтесь с нашей предыдущей статьей из серии «Практикующий техник»;
Использование функции Natural Log или «ln» при анализе цепей.
Как создать правильный закон Ома Уравнения ответвления KCL для узлового анализа
Мы ищем другие идеи для этой продолжающейся серии для практикующих техников. Пожалуйста, дайте нам знать, о чем вы хотели бы, чтобы мы написали, отправив нам свои мысли и вопросы по адресу [email protected].
систем уравнений с двумя переменными | безграничная алгебра |
Введение в системы уравнений
Система уравнений состоит из двух или более уравнений с двумя или более переменными, где любое решение должно удовлетворять всем уравнениям системы одновременно.
Цели обучения
Объясните, какие системы уравнений могут быть представлены
Основные выводы
Ключевые моменты
- Система линейных уравнений состоит из двух или более линейных уравнений, состоящих из двух или более переменных, так что все уравнения в системе рассматриваются одновременно.

- Чтобы найти единственное решение системы линейных уравнений, мы должны найти числовое значение для каждой переменной в системе, которое будет удовлетворять всем уравнениям в системе одновременно.
- Чтобы линейная система имела единственное решение, в ней должно быть как минимум столько уравнений, сколько переменных.
- Решением системы линейных уравнений с двумя переменными является любая упорядоченная пара
(x,y)(x, y)(x,y)
, удовлетворяющая каждому уравнению независимо. Графически решения представляют собой точки, в которых пересекаются прямые.
Основные термины
Система линейных уравнений состоит из двух или более линейных уравнений, составленных из двух или более переменных, так что все уравнения в системе рассматриваются одновременно. Чтобы найти единственное решение системы линейных уравнений, мы должны найти числовое значение для каждой переменной в системе, которое будет удовлетворять всем уравнениям системы одновременно. Некоторые линейные системы могут не иметь решения, а другие могут иметь бесконечное число решений. Чтобы линейная система имела единственное решение, в ней должно быть не меньше уравнений, чем переменных. Тем не менее, это не гарантирует уникальности решения.
Некоторые линейные системы могут не иметь решения, а другие могут иметь бесконечное число решений. Чтобы линейная система имела единственное решение, в ней должно быть не меньше уравнений, чем переменных. Тем не менее, это не гарантирует уникальности решения.
В этом разделе мы сосредоточимся главным образом на системах линейных уравнений, которые состоят из двух уравнений, содержащих две различные переменные. Например, рассмотрим следующую систему линейных уравнений с двумя переменными:
2x+y=153x−y=52x + y = 15 \\ 3x — y = 52x+y=153x−y=5
Решением системы линейных уравнений с двумя переменными является любая упорядоченная пара, удовлетворяющая каждому уравнению независимо. В этом примере упорядоченная пара (4, 7) является решением системы линейных уравнений. Мы можем проверить решение, подставив значения в каждое уравнение, чтобы увидеть, удовлетворяет ли упорядоченная пара обоим уравнениям.
2(4)+7=153(4)−7=52(4) + 7 = 15 \\ 3(4) — 7 = 52(4)+7=153(4)−7=5
Оба утверждения верны, поэтому
(4,7)(4, 7)(4,7)
действительно является решением системы уравнений.
Обратите внимание, что система линейных уравнений может содержать более двух уравнений и более двух переменных. Например,
3x+2y-z=12x-2y+4z=-2-x+12y-z=03x + 2y — z = 12 \\ х — 2у + 4з = -2\ -x + 12y -z = 0 3x+2y−z=12x−2y+4z=−2−x+12y−z=0
представляет собой систему трех уравнений с тремя переменными
х, у, zx, у, zx, у, z
. Решение приведенной выше системы дается выражением
x=1y=-2z=-2x = 1 \\ y = -2 \\ z = — 2x=1y=-2z=-2
, так как оно составляет все три уравнения действительный.
Типы линейных систем и их решения
В общем, линейная система может вести себя одним из трех возможных способов:
- Система имеет единственное уникальное решение.
- Система не имеет решения .
- В системе бесконечно много решений .
Каждая из этих возможностей представляет определенный тип системы линейных уравнений с двумя переменными. Каждый из них может быть отображен графически, как показано ниже. Обратите внимание, что решением системы линейных уравнений является любая точка, в которой пересекаются прямые.
Каждый из них может быть отображен графически, как показано ниже. Обратите внимание, что решением системы линейных уравнений является любая точка, в которой пересекаются прямые.
Системы линейных уравнений: Графическое представление трех типов систем.
Независимая система имеет ровно одну пару решений
(x,y)(x, y)(x,y)
. Точка пересечения двух прямых является единственным решением. Несовместная система не имеет решений. Обратите внимание, что две линии параллельны и никогда не пересекаются.
Зависимая система имеет бесконечно много решений. Линии совершенно одинаковы, поэтому каждая пара координат на линии является решением обоих уравнений.
Решающие системы графически
Простой способ решить систему уравнений — найти точку или точки пересечения уравнений. Это графический метод.
Цели обучения
Графическое решение системы уравнений с двумя переменными
Ключевые выводы
Ключевые моменты
- Чтобы решить систему уравнений графически, нарисуйте уравнения и определите точки пересечения в качестве решений.
 Система уравнений может иметь более одного решения.
Система уравнений может иметь более одного решения. - Система линейных уравнений будет иметь одну точку пересечения или одно решение.
- Чтобы построить график системы уравнений, записанной в стандартной форме, вы должны переписать уравнения в форме наклона и точки пересечения.
Ключевые термины
- система уравнений : Набор уравнений с несколькими переменными, которые можно решить, используя определенный набор значений.
- Графический метод : Способ визуального нахождения набора значений, который решает систему уравнений.
Система уравнений (также известная как одновременные уравнения) представляет собой набор уравнений с несколькими переменными, решаемый, когда значения всех переменных одновременно удовлетворяют всем уравнениям. Наиболее распространенные способы решения системы уравнений:
- Графический метод
- Метод замены
- Метод устранения
Здесь мы обратимся к графическому методу.
Решающие системы графически
Некоторые системы имеют только один набор правильных ответов, в то время как другие имеют несколько наборов, удовлетворяющих всем уравнениям. Как показано графически, набор уравнений, решенных только с одним набором ответов, будет иметь только одну точку пересечения, как показано ниже. Эта точка считается решением системы уравнений. В наборе линейных уравнений (например, на изображении ниже) есть только одно решение.
Система линейных уравнений с двумя переменными : На этом графике показана система уравнений с двумя переменными и только один набор ответов, который удовлетворяет обоим уравнениям.
Система с двумя наборами ответов, удовлетворяющих обоим уравнениям, имеет две точки пересечения (таким образом, два решения системы), как показано на изображении ниже.
Система уравнений с несколькими ответами: Это пример системы уравнений, показанной графически, которая имеет два набора ответов, удовлетворяющих обоим уравнениям системы.
Преобразование в форму пересечения уклонов
Прежде чем успешно решить систему графически, нужно понять, как изобразить уравнения, записанные в стандартной форме, или
Ax+By=CAx+By=CAx+By=C
. Вы всегда можете использовать графический калькулятор для графического представления уравнений, но полезно знать, как формулировать такие уравнения самостоятельно.
Для этого необходимо преобразовать уравнения в форму наклон-пересечение, или
y=mx+by=mx+by=mx+b
, где 91 314 м = уклон и b = точка пересечения с осью Y.
Лучший способ преобразовать уравнение в форму с пересечением наклона — сначала выделить переменную y , а затем разделить правую часть на B , как показано ниже.
Ax+By=CBy=-Ax+Cy=-Ax+CBy=-ABx+CB\begin{align} \displaystyle Ax+By&=C \\By&=-Ax+C \\y&=\frac{-Ax+C}{B} \\y&=-\frac{A}{B}x+\frac{C}{B} \end{align}Ax+ByByyy=C=-Ax+C=B-Ax+C=-BAx+BC
Сейчас
−AB\displaystyle -\frac{A}{B}−BA
это уклон м, и
CB\displaystyle \frac{C}{B}BC
это точка пересечения с координатой Y б .
Поиск решений на графике
После того, как вы преобразовали уравнения в форму пересечения наклона, вы можете построить уравнения. Чтобы определить решения системы уравнений, определите точки пересечения графических уравнений. Упорядоченная пара, представляющая пересечение (пересечения), представляет собой решение (я) системы уравнений.
Метод замены
Метод подстановки — это способ решения системы уравнений путем выражения уравнений только с одной переменной.
Цели обучения
Решите системы уравнений с двумя переменными с помощью подстановки
Ключевые выводы
Ключевые моменты
- Система уравнений — это набор уравнений, которые можно решить, используя определенный набор значений.
- Метод подстановки работает, выражая одну из переменных через другую, затем подставляя ее обратно в исходное уравнение и упрощая ее.

- Очень важно проверить свою работу после того, как вы нашли набор значений для переменных. Сделайте это, подставив найденные значения обратно в исходные уравнения.
- Решение системы уравнений можно записать в виде упорядоченной пары ( x , y ).
Ключевые термины
- метод подстановки : метод решения системы уравнений путем представления уравнения только с одной переменной
- система уравнений : Набор уравнений с несколькими переменными, которые можно решить, используя определенный набор значений.
Метод подстановки для решения систем уравнений — это способ упростить систему уравнений, выражая одну переменную через другую, таким образом удаляя одну переменную из уравнения. Когда полученное упрощенное уравнение имеет только одну переменную для работы, уравнение становится разрешимым.
Метод замены состоит из следующих шагов:
- В первом уравнении найдите одну из переменных через другие.

- Подставьте это выражение в остальные уравнения.
- Продолжайте, пока не сведете систему к одному линейному уравнению.
- Решите это уравнение, а затем подставьте обратно, пока решение не будет найдено.
Решение методом подстановки
Давайте попрактикуемся, решив следующую систему уравнений:
x−y=−1x-y=-1x−y=−1
x+2y=-4x+2y=-4x+2y=-4
Начнем с решения первого уравнения, чтобы выразить x через y .
x−y=−1x=y−1\begin{align} \displaystyle х-у&=-1 \\х&=у-1 \end{align}x−yx=−1=y−1
Затем мы подставим наше новое определение x во второе уравнение:
x+2y=−4(y−1) +2y=−4\displaystyle \begin{выравнивание} x+2y&=-4 \\(у-1)+2у&=-4 \end{align}x+2y(y−1)+2y=−4=−4
Обратите внимание, что теперь это уравнение имеет только одну переменную (y). Затем мы можем упростить это уравнение и решить для г :
(y−1)+2y=−43y−1=−43y=−3y=−1\displaystyle \begin{выравнивание} (y-1)+2y&=-4 \\3y-1&=-4 \\3y&=-3 \\у&=-1 \end{align}(y−1)+2y3y−13yy=−4=−4=−3=−1
Теперь, когда мы знаем значение y , мы можем использовать его, чтобы найти значение другой переменной, x. Для этого подставьте значение y в первое уравнение и найдите x .
Для этого подставьте значение y в первое уравнение и найдите x .
x−y=−1x−(−1)=−1x+1=−1x=−1−1x=−2\displaystyle \begin{выравнивание} x-y&=-1 \\х-(-1)&=-1 \\х+1&=-1 \\х&=-1-1 \\х&=-2 \end{align}x−yx−(−1)x+1xx=−1=−1=−1=−1−1=−2
Таким образом, решение системы:
(-2,-1)(-2, -1)(-2,-1)
, что является точкой графического пересечения двух функций. Проверьте решение, подставив значения в одно из уравнений.
x−y=−1(−2)−(−1)=−1−2+1=−1−1=−1\displaystyle \begin{выравнивание} x-y&=-1 \\(-2)-(-1)&=-1 \\-2+1&=-1 \\-1&=-1 \end{align}x−y(−2)−(−1)−2+1−1=−1=−1=−1=−1
Метод исключения
Метод исключения используется для исключения переменной, чтобы упростить решение оставшейся переменной (переменных) в системе уравнений.
Цели обучения
Решение систем уравнений с двумя переменными с помощью исключения
Основные выводы
Ключевые моменты
- Этапы метода исключения: (1) составить уравнения так, чтобы переменные совпадали, (2) изменить одно уравнение, чтобы оба уравнения разделить непротиворечивую переменную, которую можно исключить, (3) сложить уравнения вместе, чтобы исключить переменную, (4) решить и (5) выполнить обратную замену, чтобы найти другую переменную.

- Всегда проверяйте ответ. Это делается путем подстановки обоих значений в одно или оба исходных уравнения.
Ключевые термины
- метод исключения : Процесс решения системы уравнений путем исключения одной переменной для более простого решения для оставшейся переменной.
- система уравнений : Набор уравнений с несколькими переменными, которые можно решить, используя определенный набор значений.
Метод исключения для решения систем уравнений, также известный как исключение путем сложения , представляет собой способ исключить одну из переменных в системе, чтобы более просто оценить оставшуюся переменную. Как только значения оставшихся переменных были успешно найдены, они подставляются в исходное уравнение, чтобы найти правильное значение для другой переменной.
Метод исключения состоит из следующих шагов:
- Перепишите уравнения так, чтобы переменные выровнялись.

- Измените одно уравнение, чтобы в обоих уравнениях была переменная, которая самоуничтожается при сложении уравнений.
- Добавьте уравнения и исключите переменную.
- Найдите оставшуюся переменную.
- Обратно подставить и найти другую переменную.
Решение методом исключения
Метод исключения можно продемонстрировать на простом примере:
4x+y=82y+x=9\displaystyle 4х+у=8 \\ 2у+х=94x+y=82y+x=9
Сначала выровняйте переменные, чтобы уравнения можно было легко сложить на следующем шаге:
4x+y=8x+2y=9\displaystyle \begin{выравнивание} 4x+y&=8 \\х+2у&=9 \end{align}4x+yx+2y=8=9
Затем посмотрите, не настроены ли уже какие-либо переменные таким образом, что их сложение аннулирует их из системы. Если нет, умножьте одно уравнение на число, позволяющее сократить переменные. В этом примере переменная y можно исключить, если умножить первое уравнение на
−2-2−2
, а затем сложить уравнения вместе.
Шаг умножения:
−2(4x+y=8)x+2y=9\displaystyle \begin{выравнивание} -2(4x+y&=8) \\х+2у&=9 \end{align}−2(4x+yx+2y=8)=9
Результат:
−8x−2y=−16x+2y=9\displaystyle \begin{выравнивание} -8x-2y&=-16 \\х+2у&=9 \end{align}−8x−2yx+2y=−16=9
Теперь добавьте уравнения, чтобы исключить переменную y .
−8x+x−2y+2y=−16+9−7x=−7\displaystyle \begin{выравнивание} -8x+x-2y+2y&=-16+9 \\-7x&=-7 \end{align}−8x+x−2y+2y−7x=−16+9=−7
Наконец, найдите переменную x .
−7x=−7x=−7−7x=1\displaystyle \begin{выравнивание} -7x&=-7 \\x&=\frac{-7}{-7} \\х&=1 \end{align}−7xxx=−7=−7−7=1
Затем вернитесь к одному из исходных уравнений и подставьте найденное значение вместо x . Легче всего выбрать самое простое уравнение, но любое уравнение будет работать.
4x+y=84(1)+y=84+y=8y=4\displaystyle \begin{выравнивание} 4x+y&=8 \\4(1)+у&=8 \\4+у&=8 \\у&=4 \end{align}4x+y4(1)+y4+yy=8=8=8=4
Таким образом, решением уравнения является (1,4). Всегда важно проверить ответ, подставив оба этих значения вместо соответствующих переменных в одно из уравнений.
Всегда важно проверить ответ, подставив оба этих значения вместо соответствующих переменных в одно из уравнений.
4x+y=84(1)+4=84+4=88=8\displaystyle \begin{выравнивание} 4x+y&=8 \\4(1)+4&=8 \\4+4&=8 \\8&=8 \end{align}4x+y4(1)+44+48=8=8=8=8
Несогласованные и зависимые системы с двумя переменными
Для линейных уравнений с двумя переменными несовместные системы не имеют решений, а зависимые системы имеют бесконечно много решений.
Цели обучения
Объясните, когда системы уравнений с двумя переменными несовместимы или зависимы как графически, так и алгебраически.
Ключевые выводы
Ключевые моменты
- Графически уравнения в зависимой системе представляют одну и ту же линию. Уравнения в несовместной системе представляют собой параллельные линии, которые никогда не пересекаются.
- Мы можем использовать методы решения систем уравнений для идентификации зависимых и несовместных систем: Зависимые системы имеют бесконечное число решений.
 Применение методов решения систем уравнений приведет к истинному тождеству, такому как
Применение методов решения систем уравнений приведет к истинному тождеству, такому как0=00 = 00=0
. Несовместные системы не имеют решений. Применение методов решения систем уравнений приведет к противоречию, например, к утверждению0=10 = 10=1
.
Основные термины
Напомним, что линейная система может вести себя одним из трех возможных способов:
- Система имеет единственное уникальное решение.
- Система не имеет решения.
- Система имеет бесконечно много решений.
Напомним также, что каждая из этих возможностей соответствует типу системы линейных уравнений с двумя переменными. Независимая система уравнений имеет ровно одно решение
(x,y)(x,y)(x,y)
. Несовместная система не имеет решений, а зависимая система имеет бесконечное число решений.
В предыдущих модулях обсуждалось, как найти решение для независимой системы уравнений. Теперь мы сосредоточимся на выявлении зависимых и несовместных систем линейных уравнений.
Теперь мы сосредоточимся на выявлении зависимых и несовместных систем линейных уравнений.
Зависимые системы
Уравнения линейной системы являются независимыми , если ни одно из уравнений не может быть алгебраически выведено из других. Когда уравнения независимы, каждое уравнение содержит новую информацию о переменных, и удаление любого из уравнений увеличивает размер набора решений. Системы, которые не являются независимыми, по определению зависимый . Уравнения в зависимой системе могут быть получены одно из другого; они описывают одну и ту же линию. Они не добавляют новой информации о переменных, а потеря уравнения из зависимой системы не меняет размер множества решений.
Мы можем применять методы замены или исключения для решения систем уравнений для идентификации зависимых систем. Зависимые системы имеют бесконечное число решений, потому что все точки на одной прямой находятся также и на другой прямой. После использования замены или сложения результирующее уравнение будет тождеством, например
0=00 = 00=0
.
Например, рассмотрим два уравнения
3x+2y=66x+4y=123x+2y = 6 \\ 6x+4y = 123x+2y=66x+4y=12
Мы можем применить метод исключения для оценки этих . Если бы мы умножили первое уравнение на коэффициент
−2-2−2
, мы бы получили:
−2(3x+2y=6)−6x−4y=−12\displaystyle \begin{выравнивание} -2(3x+2y&=6) \\-6x-4y&=-12 \end{align}−2(3x+2y−6x−4y=6)=−12
Добавление этого ко второму уравнению даст
0=00=00=0
. Таким образом, две линии являются зависимыми. Также обратите внимание, что это одно и то же уравнение, увеличенное в два раза; другими словами, второе уравнение может быть получено из первого.
На графике два уравнения дают одинаковые линии, как показано ниже.
Зависимая система : Уравнения
3x+2y=63x + 2y = 63x+2y=6 при построении графика производят ту же линию.
Заметим, что существует бесконечное число решений зависимой системы, и эти решения попадают на общую прямую.
Несовместимые системы
Линейная система совместна, если она имеет решение, и несовместна в противном случае. Напомним, что графическое представление несовместной системы состоит из параллельных линий, которые имеют одинаковый наклон, но разные
yyy
-пересечения. Они никогда не пересекутся.
Мы также можем применять методы решения систем уравнений для выявления несовместных систем. Когда система несовместна, из уравнений можно вывести противоречие, например утверждение
0=10 = 10=1
.
Рассмотрим следующие два уравнения:
3x+2y=63x+2y=123x+2y = 6 \\ 3x+2y = 123x+2y=63x+2y=12
Мы можем применить метод исключения, чтобы попытаться решить эта система. Вычитая первое уравнение из второго, обе переменные исключаются, и мы получаем
0=60 = 60=6
. Это противоречие, и мы можем определить, что это противоречивая система. Графики этих уравнений на
Графики этих уравнений на
xyxyxy
-плоскость представляет собой пару параллельных прямых.
Несовместная система: Уравнения
3x+2y=63x + 2y = 63x+2y=6
и
3x+2y=123x + 2y = 123x+2y=12
7 несовместимы.В общем случае несоответствия возникают, если левые части уравнений в системе линейно зависимы, а постоянные члены не удовлетворяют соотношению зависимости. Система уравнений, левые части которой линейно независимы, всегда совместна.
Применение систем уравнений
Системы уравнений можно использовать для решения многих реальных задач, в которых используется несколько ограничений для одних и тех же переменных.
Цели обучения
Применение систем уравнений с двумя переменными к примерам из реальной жизни
Основные выводы
Ключевые моменты
- Если у вас есть проблема, включающая несколько переменных, вы можете решить ее, составив систему уравнений.

- После определения переменных определите отношения между ними и запишите их в виде уравнений.
Ключевые термины
- система уравнений : Набор уравнений с несколькими переменными, которые можно решить, используя определенный набор значений.
Системы уравнений реального мира
Система уравнений, также известная как одновременные уравнения, представляет собой набор уравнений с несколькими переменными. Ответом на систему уравнений является набор значений, который удовлетворяет всем уравнениям в системе, и таких ответов для любой данной системы может быть много. Ответы обычно записываются в виде упорядоченной пары:
(х,у)\влево(х,у\вправо)(х,у)
. Подходы к решению системы уравнений включают замену и исключение, а также графические методы.
Существует несколько практических применений систем уравнений. Они подробно показаны ниже.
Планирование мероприятия
Систему уравнений можно использовать для решения задачи планирования, где необходимо учитывать несколько ограничений:
Эмили устраивает крупную вечеринку после школы. Директор наложил два ограничения. Во-первых, общее количество присутствующих (учителей и учеников вместе взятых) должно быть 9 человек.0007
565656
. Во-вторых, на каждые семь учеников должен приходиться один учитель. Итак, сколько учеников и сколько учителей приглашено на вечеринку?
Во-первых, нам нужно идентифицировать и назвать наши переменные. В данном случае нашими переменными являются учителя и ученики. Количество учителей будет
ТТТ
, а количество учеников будет
SSS
.
Теперь нам нужно составить уравнения. Существует ограничение, ограничивающее общее количество присутствующих до 9 человек. 0007
0007
565656
, поэтому:
T+S=56T+S=56T+S=56
На каждые семь учеников должен быть один учитель, поэтому:
S7=T\frac{S}{7 }=T7S=T
Теперь у нас есть система уравнений, которую можно решить подстановкой, исключением или графически. Решение системы:
S=49S=49S=49
и
T=7T=7T=7
.
Поиск неизвестных количеств
Следующий пример иллюстрирует, как системы уравнений используются для нахождения величин.
Группа из
757575
студентов и преподавателей собирает сладкий картофель для нуждающихся в поле. Кейси собирает в три раза больше сладкого картофеля, чем Дэвис, а затем, возвращаясь к машине, собирает еще пять! Глядя на ее недавно увеличенную кучу, Дэвис замечает: «Вау, у тебя на
292929
картошки больше, чем у меня!» Сколько бататов собрали Кейси и Дэвис?
Чтобы решить, мы сначала определяем наши переменные. Количество бататов, которые выбрала Кейси, равно 9.0007
Количество бататов, которые выбрала Кейси, равно 9.0007
KKK
, а количество сладкого картофеля, которое выбирает Дэвис, равно
DDD
.
Теперь мы можем написать уравнения исходя из ситуации:
K−5=3DK-5 = 3DK−5=3D
D+29=KD+29 = KD+29=K
Отсюда замена, исключение , или график покажет, что
K=41K=41K=41
и
D=12D=12D=12
.
Важно всегда проверять свои ответы. Хороший способ проверить решения системы уравнений — посмотреть на функции графически, а затем посмотреть, где графики пересекаются. Или вы можете подставить свои ответы в каждое уравнение и убедиться, что они приводят к точным решениям.
Другие приложения
Существует множество других приложений для систем уравнений, таких как выяснение того, какой ландшафтный дизайнер предлагает лучшее предложение, сколько разные операторы сотовой связи взимают в минуту или сравнение информации о питании в рецептах.
Лицензии и атрибуции
Контент под лицензией CC, совместно используемый ранее
- Курирование и доработка. Автор : Boundless.com. Лицензия : Общественное достояние: Авторские права неизвестны
Лицензионный контент CC, конкретное указание авторства
- Система линейных уравнений. Предоставлено : Википедия. Лицензия : CC BY-SA: Attribution-ShareAlike
- Системы линейных уравнений: две переменные. Предоставлено : OpenStax. Расположен по адресу : https://cnx.org/contents/[email protected]. Лицензия : CC BY: Attribution
- Системы линейных уравнений: две переменные. Предоставлено : OpenStax. Лицензия : CC BY: Attribution
- Системы уравнений. Предоставлено : Википедия. Лицензия : CC BY-SA: Attribution-ShareAlike
- Линейное уравнение.
 Предоставлено : Википедия. Лицензия : CC BY-SA: Attribution-ShareAlike
Предоставлено : Википедия. Лицензия : CC BY-SA: Attribution-ShareAlike - Безгранично. Предоставлено : Безграничное обучение. Лицензия : CC BY-SA: Attribution-ShareAlike
- Бескрайний. Предоставлено : Безграничное обучение. Лицензия : CC BY-SA: Attribution-ShareAlike
- Системы линейных уравнений: две переменные. Предоставлено : OpenStax. Расположен по адресу : https://cnx.org/contents/[email protected]. Лицензия : CC BY: Attribution
- Метод добавления двух линейных уравнений. Предоставлено : Wikibooks. Расположен по адресу : https://en.wikibooks.org/wiki/File:Two_linear_equation_add_method.PNG. Лицензия : CC BY-SA: Attribution-ShareAlike
- Пример одновременных уравнений 1.
 Предоставлено : Wikipedia. Расположен по адресу : https://en.wikipedia.org/wiki/File:Simultaneous_equations_example_1.svg. Лицензия : CC BY-SA: Attribution-ShareAlike
Предоставлено : Wikipedia. Расположен по адресу : https://en.wikipedia.org/wiki/File:Simultaneous_equations_example_1.svg. Лицензия : CC BY-SA: Attribution-ShareAlike - Системы уравнений. Предоставлено : Википедия. Лицензия : CC BY-SA: Attribution-ShareAlike
- Безгранично. Предоставлено : Безграничное обучение. Лицензия : CC BY-SA: Attribution-ShareAlike
- Безгранично. Предоставлено : Безграничное обучение. Лицензия : CC BY-SA: Attribution-ShareAlike
- Безгранично. Предоставлено : Безграничное обучение. Лицензия : CC BY-SA: Attribution-ShareAlike
- Системы линейных уравнений: две переменные. Предоставлено : OpenStax. Расположен по адресу : https://cnx.
 org/contents/[email protected]. Лицензия : CC BY: Attribution
org/contents/[email protected]. Лицензия : CC BY: Attribution - Метод добавления двух линейных уравнений. Предоставлено : Wikibooks. Расположен по адресу : https://en.wikibooks.org/wiki/File:Two_linear_equation_add_method.PNG. Лицензия : CC BY-SA: Attribution-ShareAlike
- Пример одновременных уравнений 1. Предоставлено : Wikipedia. Лицензия : CC BY-SA: Attribution-ShareAlike
- Алгебра/системы уравнений. Предоставлено : Wikibooks. Лицензия : CC BY-SA: Attribution-ShareAlike
- Системы уравнений. Предоставлено : Википедия. Лицензия : CC BY-SA: Attribution-ShareAlike
- Безгранично. Предоставлено : Безграничное обучение. Лицензия : CC BY-SA: Attribution-ShareAlike
- Безгранично.
 Предоставлено : Безграничное обучение. Лицензия : CC BY-SA: Attribution-ShareAlike
Предоставлено : Безграничное обучение. Лицензия : CC BY-SA: Attribution-ShareAlike - Системы линейных уравнений: две переменные. Предоставлено : OpenStax. Расположен по адресу : https://cnx.org/contents/[email protected]. Лицензия : CC BY: Attribution
- Метод добавления двух линейных уравнений. Предоставлено : Wikibooks. Расположен по адресу : https://en.wikibooks.org/wiki/File:Two_linear_equation_add_method.PNG. Лицензия : CC BY-SA: Attribution-ShareAlike
- Пример одновременных уравнений 1. Предоставлено : Википедия. Лицензия : CC BY-SA: Attribution-ShareAlike
- Системы линейных уравнений: две переменные.. Предоставлено : OpenStax. Расположен по адресу : https://cnx.org/contents/[email protected].
 Лицензия : CC BY: Attribution
Лицензия : CC BY: Attribution - Система линейных уравнений. Предоставлено : Википедия. Лицензия : CC BY-SA: Attribution-ShareAlike
- Системы линейных уравнений: две переменные. Предоставлено : OpenStax. Расположен по адресу : https://cnx.org/contents/[email protected]. Лицензия : CC BY: Attribution
- Метод добавления двух линейных уравнений. Предоставлено : Wikibooks. Лицензия : CC BY-SA: Attribution-ShareAlike
- Пример одновременных уравнений 1. Предоставлено : Wikipedia. Лицензия : CC BY-SA: Attribution-ShareAlike
- Параллельные линии. Предоставлено : Википедия. Лицензия : Общественное достояние: неизвестно Авторское право
- Оригинальная фигура Бриттани Мередит.
 Лицензия CC BY-SA 4.0. Предоставлено : Бриттани Мередит. Лицензия : CC BY-SA: Attribution-ShareAlike
Лицензия CC BY-SA 4.0. Предоставлено : Бриттани Мередит. Лицензия : CC BY-SA: Attribution-ShareAlike - Система уравнений. Предоставлено : Википедия. Лицензия : CC BY-SA: ограничение Attribution-ShareAlike
- . Предоставлено : Викисловарь. Лицензия : CC BY-SA: Attribution-ShareAlike
- Безграничный. Предоставлено : Безграничное обучение. Лицензия : CC BY-SA: Attribution-ShareAlike
- Системы линейных уравнений: две переменные. Предоставлено : OpenStax. Расположен по адресу : https://cnx.org/contents/[email protected]. Лицензия : CC BY: Attribution
- Метод добавления двух линейных уравнений. Предоставлено : Wikibooks. Расположен по адресу : https://en.wikibooks.
 org/wiki/Файл:Two_linear_equation_add_method.PNG. Лицензия : CC BY-SA: Attribution-ShareAlike
org/wiki/Файл:Two_linear_equation_add_method.PNG. Лицензия : CC BY-SA: Attribution-ShareAlike - Пример одновременных уравнений 1. Предоставлено : Wikipedia. Лицензия : CC BY-SA: Attribution-ShareAlike
- Параллельные линии. Предоставлено : Википедия. Лицензия : Общественное достояние: неизвестно Авторское право
- Оригинальная фигура Бриттани Мередит. Лицензия CC BY-SA 4.0. Предоставлено : Бриттани Мередит. Лицензия : CC BY-SA: Attribution-ShareAlike
| This Lesson (Геометрическая интерпретация линейной системы двух уравнений с двумя неизвестными) был создан пользователем ikleyn(45816) : Просмотр исходного кода, Показать Геометрическая интерпретация линейной системы двух уравнений с двумя неизвестными — это геометрическое представление двух прямых, соответствующих линейным функциям
В таблице ниже перечислены в упорядоченном виде свойства линейной системы двух уравнений с двумя неизвестными, а также соответствующие свойства их
Другие мои уроки по решению линейной системы двух уравнений с двумя неизвестными на этом сайте: — Словесные задачи, приводящие к простой системе из двух уравнений с двумя неизвестными |


 х + 3у = 10 ; 3. 2х + 6у -8=0 ;
х + 3у = 10 ; 3. 2х + 6у -8=0 ;




 )
) Вы в гостях у своего друга Пети познакомились с девочкой Женей и, уже вернувшись домой, решили найти ее в социальной сети.
Вы в гостях у своего друга Пети познакомились с девочкой Женей и, уже вернувшись домой, решили найти ее в социальной сети. (См. Рис. 2.)
(См. Рис. 2.)

 ) Не выполняя построений найдите точки пересечения прямых
) Не выполняя построений найдите точки пересечения прямых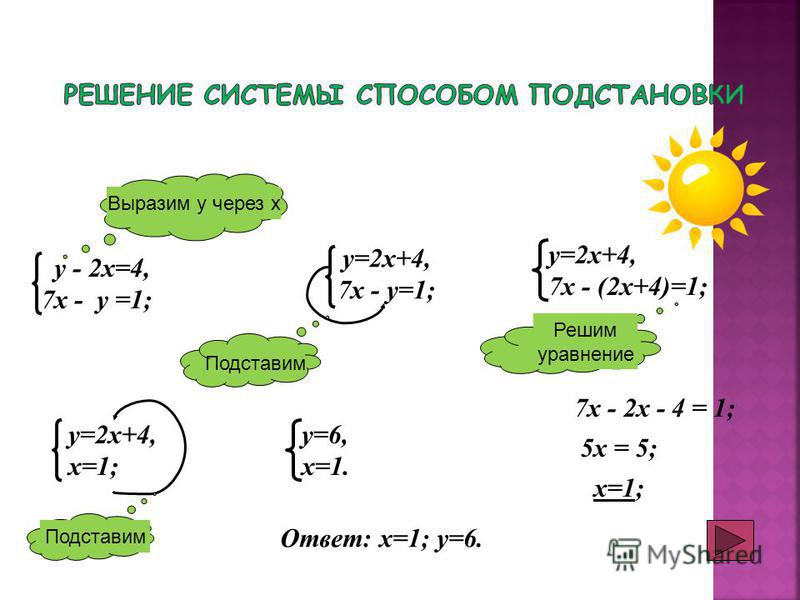




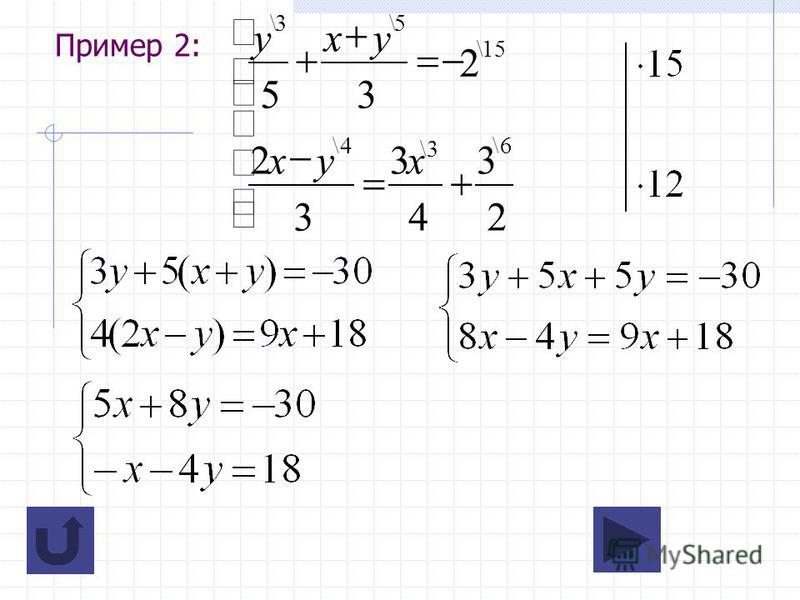
 Не выполняя построений найдите точки пересечения прямых.
Не выполняя построений найдите точки пересечения прямых.






 Система уравнений может иметь более одного решения.
Система уравнений может иметь более одного решения.



 Применение методов решения систем уравнений приведет к истинному тождеству, такому как
Применение методов решения систем уравнений приведет к истинному тождеству, такому как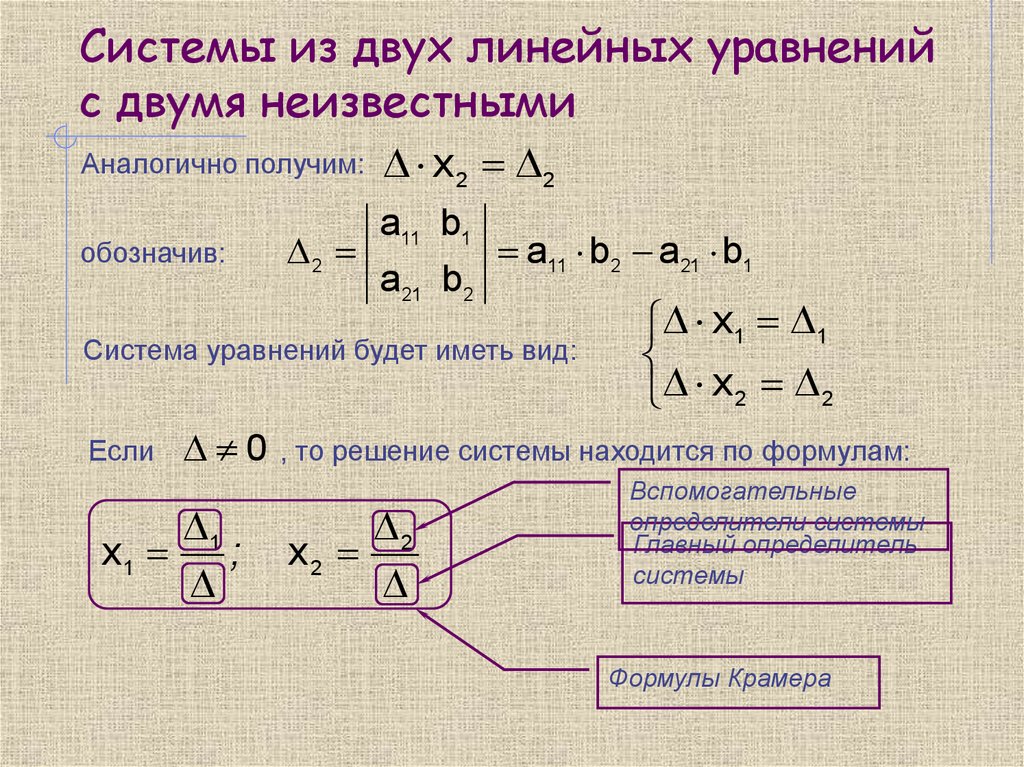
 Предоставлено : Википедия. Лицензия : CC BY-SA: Attribution-ShareAlike
Предоставлено : Википедия. Лицензия : CC BY-SA: Attribution-ShareAlike  Предоставлено : Wikipedia. Расположен по адресу : https://en.wikipedia.org/wiki/File:Simultaneous_equations_example_1.svg. Лицензия : CC BY-SA: Attribution-ShareAlike
Предоставлено : Wikipedia. Расположен по адресу : https://en.wikipedia.org/wiki/File:Simultaneous_equations_example_1.svg. Лицензия : CC BY-SA: Attribution-ShareAlike  org/contents/[email protected]. Лицензия : CC BY: Attribution
org/contents/[email protected]. Лицензия : CC BY: Attribution  Предоставлено : Безграничное обучение. Лицензия : CC BY-SA: Attribution-ShareAlike
Предоставлено : Безграничное обучение. Лицензия : CC BY-SA: Attribution-ShareAlike  Лицензия : CC BY: Attribution
Лицензия : CC BY: Attribution 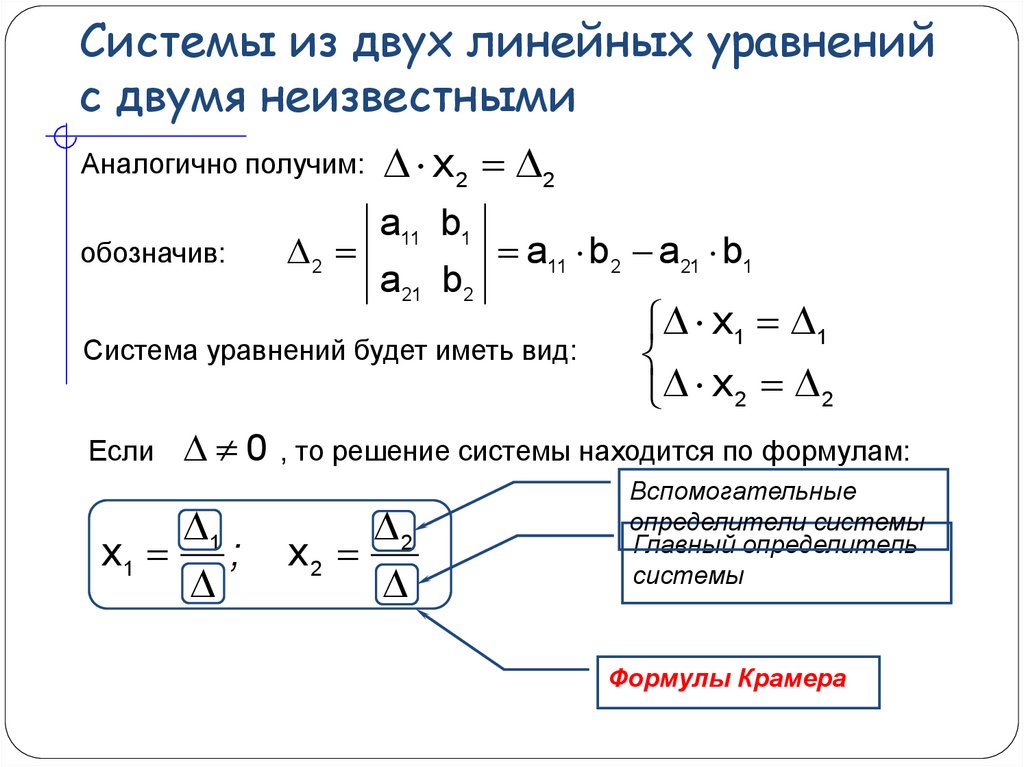 Лицензия CC BY-SA 4.0. Предоставлено : Бриттани Мередит. Лицензия : CC BY-SA: Attribution-ShareAlike
Лицензия CC BY-SA 4.0. Предоставлено : Бриттани Мередит. Лицензия : CC BY-SA: Attribution-ShareAlike  org/wiki/Файл:Two_linear_equation_add_method.PNG. Лицензия : CC BY-SA: Attribution-ShareAlike
org/wiki/Файл:Two_linear_equation_add_method.PNG. Лицензия : CC BY-SA: Attribution-ShareAlike  Это дает вам визуальное изображение, показывающее, является ли данная линейная система последовательной или противоречивой; являются ли уравнения зависимыми
Это дает вам визуальное изображение, показывающее, является ли данная линейная система последовательной или противоречивой; являются ли уравнения зависимыми  уроки, упомянутые выше).
уроки, упомянутые выше).  Геометрическое представление
Геометрическое представление 


