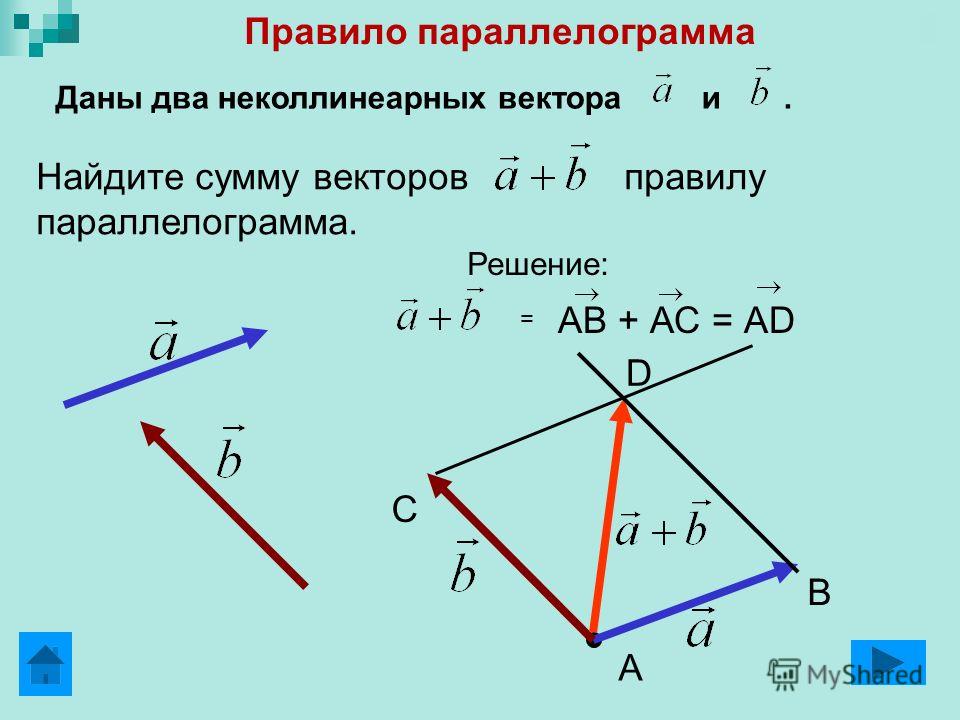
алгебраическое сложение векторов
алгебраическое сложение векторовВы искали алгебраическое сложение векторов? На нашем сайте вы можете получить ответ на любой математический вопрос здесь. Подробное решение с описанием и пояснениями поможет вам разобраться даже с самой сложной задачей и вектор правило треугольника, не исключение. Мы поможем вам подготовиться к домашним работам, контрольным, олимпиадам, а так же к поступлению в вуз. И какой бы пример, какой бы запрос по математике вы не ввели — у нас уже есть решение. Например, «алгебраическое сложение векторов».
Применение различных математических задач, калькуляторов, уравнений и функций широко распространено в нашей
жизни. Они используются во многих расчетах, строительстве сооружений и даже спорте. Математику человек
использовал еще в древности и с тех пор их применение только возрастает. Однако сейчас наука не стоит на
месте и мы можем наслаждаться плодами ее деятельности, такими, например, как онлайн-калькулятор, который
может решить задачи, такие, как алгебраическое сложение векторов,вектор правило треугольника,вектор суммы,вектор суммы двух векторов,вектор формулы,вектора вычитание,вектора вычитание и сложение,вектора правило треугольника,вектора сложение,вектора сумма,векторная сумма,векторное сложение,векторное сложение векторов,векторов формула,векторы вычитание,векторы вычитание и сложение,векторы по правилу треугольника,векторы правила треугольника,векторы правило треугольника,векторы сложение,векторы сложение правило треугольника,выполните сложение векторов а и б,вычитание вектора,вычитание векторов,вычитание векторов примеры,вычитание двух векторов,вычитание сонаправленных векторов,вычитания векторов,вычитания векторов примеры,геометрия сложение векторов,геометрия формулы векторов,для того чтобы сложить два вектора нужно,задачи на вычитание и сложение векторов,задачи на сложение векторов,задачи сложение векторов,как производится вычитание векторов,как складывать вектора в геометрии,как сложить 3 вектора,как сложить вектора по координатам,как сложить векторы по координатам,как сложить векторы по правилу треугольника,как сложить три вектора,какие правила сложения векторов вы знаете,какие правила сложения двух и нескольких векторов вы знаете,когда сумма векторов равна 0,когда сумма векторов равна нулю,методы сложения векторов,на рисунке даны векторы а и б какой из векторов c равен сумме этих векторов,определение сложение векторов,определение сумма векторов,определение суммы векторов,по каким правилам можно выполнять сложение векторов,построить сумму векторов,правила вычитания векторов,правила сложения векторов,правила сложения векторов в геометрии,правила треугольника векторы,правило вектора треугольника,правило разности векторов,правило сложение векторов правило треугольника,правило сложения векторов по правилу треугольника,правило сложения векторов треугольника,правило сумма векторов,правило треугольника вектор,правило треугольника векторы,правило треугольника векторы определение,правило треугольника для векторов,примеры вычитание векторов,примеры вычитания векторов,примеры сложение векторов,разница векторов,разность векторов формула,решение векторов сложение и вычитание векторов,складывание векторов,сложение 3 векторов,сложение вектора,сложение векторов,сложение векторов геометрия,сложение векторов задачи,сложение векторов из одной точки,сложение векторов координат,сложение векторов координаты,сложение векторов методом треугольника,сложение векторов определение,сложение векторов параллельных,сложение векторов по координатам формула,сложение векторов по правилу,сложение векторов по правилу треугольника,сложение векторов правило,сложение векторов правило треугольника,сложение векторов примеры,сложение векторов противоположно направленных,сложение векторов треугольником,сложение векторов формула,сложение векторов это,сложение векторы,сложение двух векторов,сложение и вычитание векторов примеры,сложение и вычитание векторов примеры с решением,сложение и вычитание коллинеарных векторов,сложение нескольких векторов,сложение параллельных векторов,сложение противоположно направленных векторов,сложение противоположных векторов,сложение сонаправленных векторов,сложение трех векторов,сложения векторов,способы сложения векторов,сумма 2 векторов,сумма 3 векторов,сумма вектора,сумма векторов,сумма векторов алгебраическая,сумма векторов определение,сумма векторов по правилу треугольника,сумма векторов правило,сумма векторов правило треугольника,сумма векторов треугольника,сумма векторов формула,сумма векторов формула по координатам,сумма векторов формула через координаты,сумма векторов что такое,сумма векторов это,сумма векторов это определение,сумма двух векторов,сумма и вычитание векторов,сумма противоположных векторов,суммы векторов,суммы векторов определение,суммы векторов формула,формула сложения векторов,формула сумма векторов,формула суммы векторов,формулы сложения векторов,чему равна сумма векторов,чему равна сумма противоположных векторов,что такое сумма векторов.
Решить задачу алгебраическое сложение векторов вы можете на нашем сайте https://pocketteacher.ru. Бесплатный онлайн решатель позволит решить онлайн задачу любой сложности за считанные секунды. Все, что вам необходимо сделать — это просто ввести свои данные в решателе. Так же вы можете посмотреть видео инструкцию и узнать, как правильно ввести вашу задачу на нашем сайте. А если у вас остались вопросы, то вы можете задать их в чате снизу слева на странице калькулятора.
Действия с векторами презентация, доклад, проект
Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Презентация на тему Презентация на тему Действия с векторами из раздела Математика.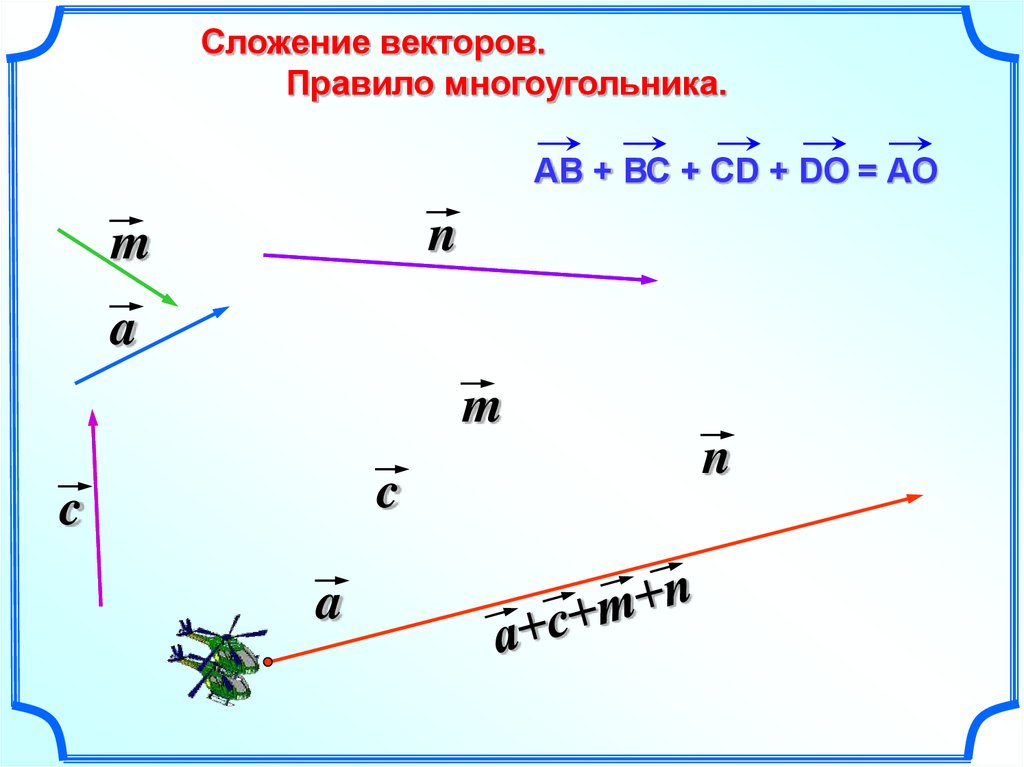
Доклад-презентацию можно скачать по ссылке внизу страницы. Эта презентация для класса содержит 19 слайдов. Для просмотра воспользуйтесь удобным проигрывателем, если материал оказался полезным для Вас — поделитесь им с друзьями с помощью социальных кнопок и добавьте наш сайт презентаций TheSlide.ru в закладки!
ПОВТОРЕНИЕ
MNPQ — трапеция.
Назовите все векторы, изображенные на рисунке.
Среди изображенных на рисунке векторов укажите:
а) коллинеарные;
б) сонаправленные;
в) противоположно направленные;
г) равные;
д) равные по модулю;
е) векторы, сонаправленные вектору
О
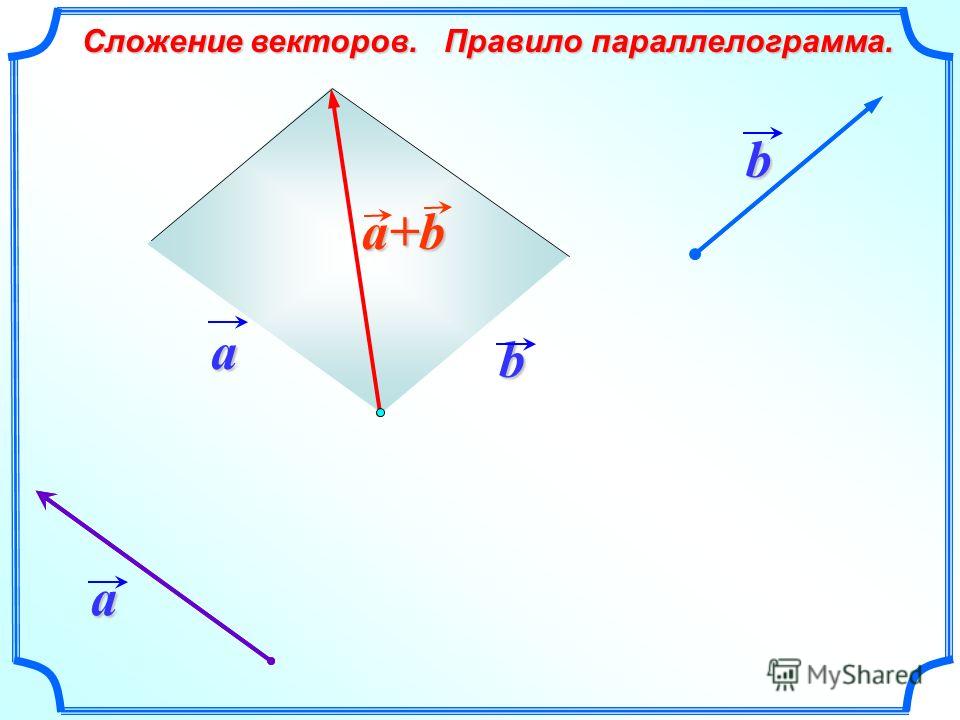
Сложение векторов по правилу треугольника
Построение:
Укажите правильные варианты сложения
1
4
3
2
а
b
c
c
b
а
b
c
b
c
а
Сложение векторов по правилу параллелограмма
Построение:
Вычитание векторов по правилу параллелограмма
А
В
С
ВЕКТОРЫ И
ПРОТИВОПОЛОЖНЫЕ ВЕКТОРЫ
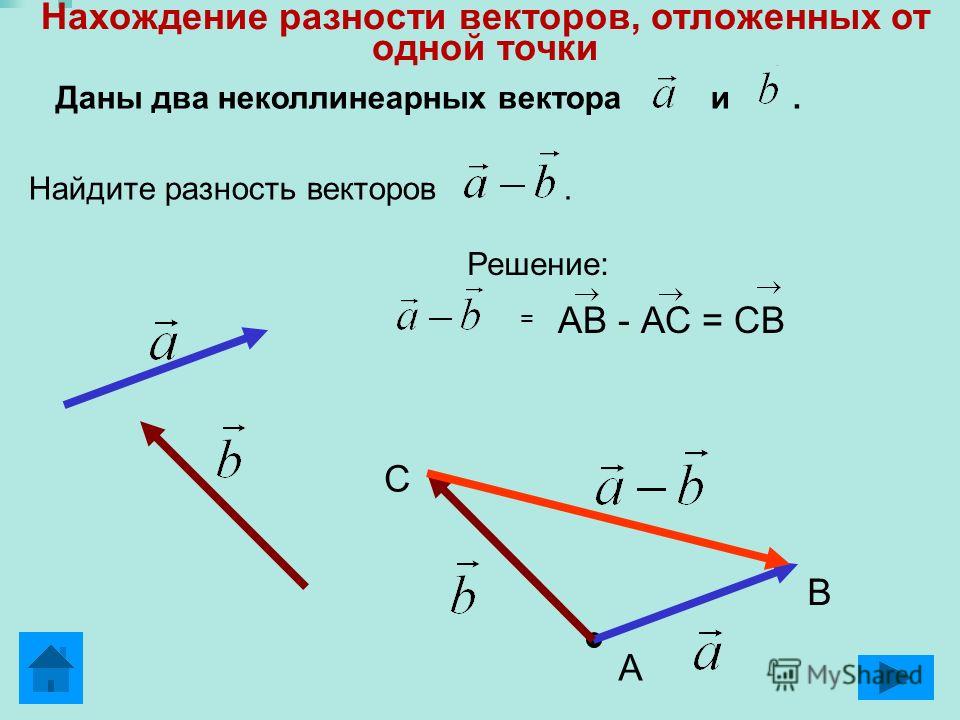
Вычитание векторов по правилу треугольника
А
В
С
Выполните вычитание векторов
A
B
C
D
A
B
C
D
A
B
C
D
A
B
C
D
O
O
Правило многоугольника
A
B
B
C
C
D
D
E
E
F
A
B
C
D
E
F
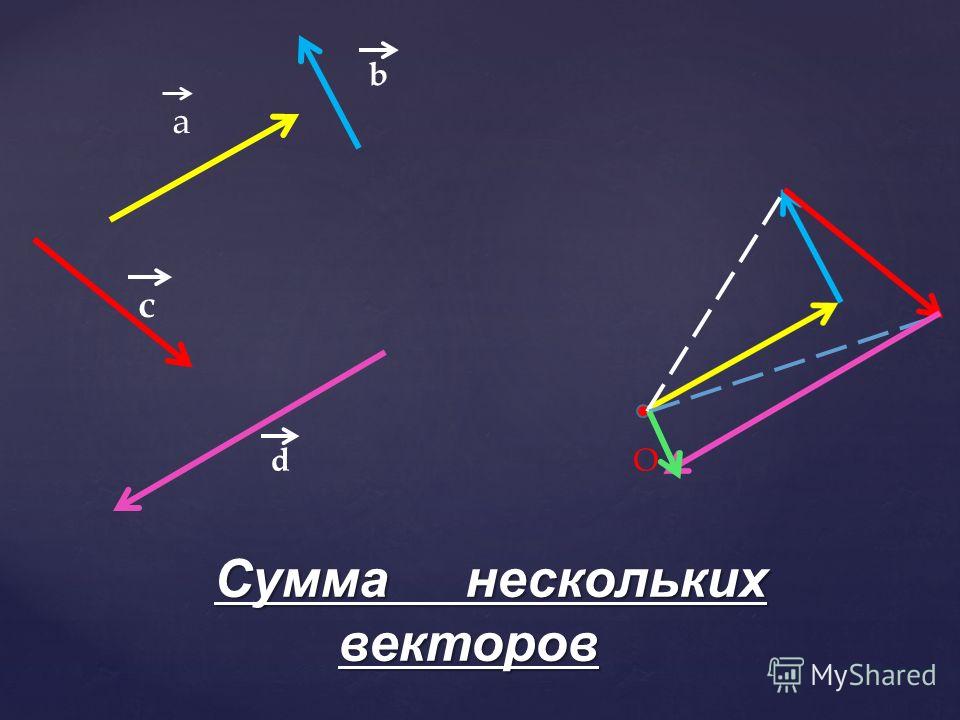
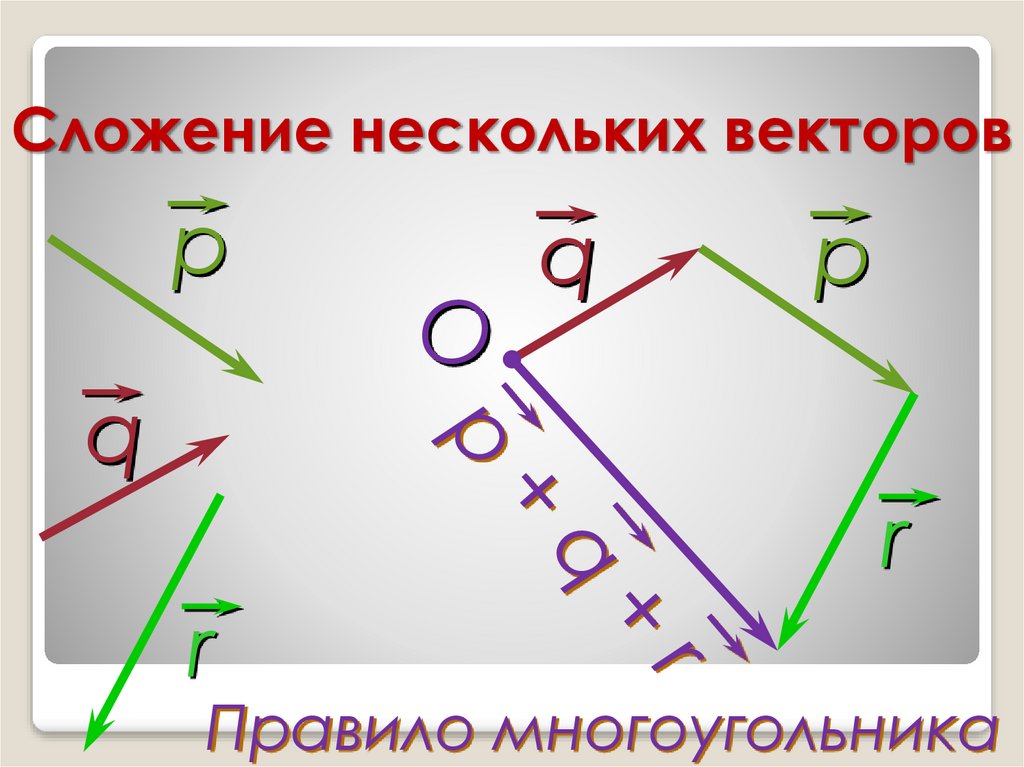
AB + BC + CD + DE + EF =AF
А
В
С
D
?
Найдите сумму векторов
Дано: АВСD – параллелограмм
А
В
С
?
О
Найдите сумму векторов
Дано: АВС – треугольник
А
В
С
D
?
Найдите сумму векторов
Дано: АВСD – параллелограмм
А
В
С
D
?
О
Найдите сумму векторов
Дано: АВСD – прямоугольник
А
В
С
D
?
Найдите сумму векторов
Дано: АВСD – параллелограмм
А
В
С
D
?
О
Найдите сумму векторов
Дано: АВСD – прямоугольник
Упростите выражения:
?
?
?
?
Умножение вектора на число.
Определение:
В тетрадях:
Определение:
В тетрадях:
Основные свойства умножения вектора на число
Свойства действий над векторами позволяют в выражениях, содержащих суммы, разности векторов и произведения векторов на числа, выполнять преобразования по тем же правилам, что и в числовых выражениях. Например,
Скачать презентацию
Обратная связь
Если не удалось найти и скачать доклад-презентацию, Вы можете заказать его на нашем сайте. Мы постараемся найти нужный Вам материал и отправим по электронной почте. Не стесняйтесь обращаться к нам, если у вас возникли вопросы или пожелания:
Email: Нажмите что бы посмотреть
Что такое TheSlide.ru?
Это сайт презентации, докладов, проектов в PowerPoint. Здесь удобно хранить и делиться своими презентациями с другими пользователями.
Для правообладателей
1
Первый слайд презентации: Векторы в пространстве
Изображение слайда
2
Слайд 2: Содержание
I. Понятие вектора в пространстве II. Коллинеарные векторы III. Компланарные векторы IV. Действия с векторами
Изображение слайда
3
Слайд 3: Понятие вектора в пространстве
Вектор(направленный отрезок) –
отрезок, для которого указано какой из его концов считается началом, а какой – концом.
Длина вектора – длина отрезка AB.
А
В
M
Изображение слайда
4
Слайд 4: Коллинеарные векторы
Два ненулевых вектора называются коллинеарными, если они лежат на одной прямой или параллельных прямых. Среди коллинеарных различают: Сонаправленные векторы Противоположно направленные векторы
Изображение слайда
5
Слайд 5: Сонаправленные векторы
Сонаправленные векторы — векторы, лежащие по одну сторону от прямой, проходящей через их начала. Нулевой вектор считается сонаправленным с любым вектором. Равные векторы
Изображение слайда
6
Слайд 6: Равные векторы
Равные векторы — сонаправленные векторы,
длины которых равны.
От любой точки можно отложить вектор,
равный данному, и притом только один.
Изображение слайда
7
Слайд 7: Противоположно направленные векторы
Противоположно направленные векторы – векторы, лежащие по разные стороны от прямой, проходящей через их начала. Противоположные векторы
Изображение слайда
8
Слайд 8: Противоположные векторы
Противоположные векторы – противоположно направленные векторы, длины которых равны. Вектором, противоположным нулевому, считается нулевой вектор.
Изображение слайда
9
Слайд 9: Признак коллинеарности
Изображение слайда
10
Слайд 10: Определение компланарных векторов
Компланарные векторы – векторы, при откладывании которых от одной и той же точки пространства, они будут лежать в одной плоскости.
Пример:
B
А
C
D
A 1
B 1
C 1
D 1
Изображение слайда
11
Слайд 11: О компланарных векторах
Любые два вектора всегда компланарны. Три вектора, среди которых имеются два коллинеарных, компланарны. α если
Изображение слайда
12
Слайд 12: Признак компланарности
Изображение слайда
13
Слайд 13: Свойство компланарных векторов
Изображение слайда
14
Слайд 14: Действия с векторами
Сложение Вычитание Умножение вектора на число Скалярное произведение
Изображение слайда
15
Слайд 15: Сложение векторов
Правило треугольника Правило параллелограмма Правило многоугольника Правило параллелепипеда Свойства сложения
Изображение слайда
16
Слайд 16: Правило треугольника
А B C
Изображение слайда
17
Слайд 17: Правило треугольника
А B C Для любых трех точек А, В и С справедливо равенство:
Изображение слайда
18
Слайд 18: Правило параллелограмма
А B C
Изображение слайда
19
Слайд 19: Свойства сложения
Изображение слайда
20
Слайд 20: Правило многоугольника
Сумма векторов равна вектору, проведенному
из начала первого в конец последнего(при последовательном откладывании).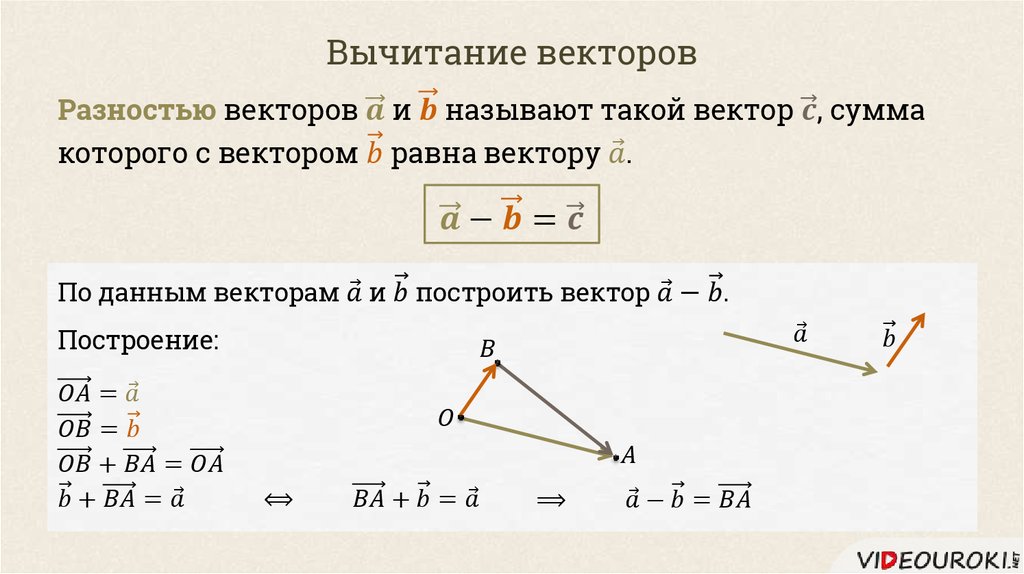
B
A
C
D
E
Пример
Изображение слайда
21
Слайд 21: Пример
C A B D A 1 B 1 C 1 D 1
Изображение слайда
22
Слайд 22: Правило параллелепипеда
B А C D A 1 B 1 C 1 D 1 Вектор, лежащий на диагонали параллелепипеда, равен сумме векторов, проведенных из той же точки и лежащих на трех измерениях параллелепипеда.
Изображение слайда
23
Слайд 23: Свойства
B А C D A 1 B 1 C 1 D 1
Изображение слайда
24
Слайд 24: Вычитание векторов
Вычитание Сложение с противоположным вектором
Изображение слайда
25
Слайд 25: Вычитание
Разностью векторов и называется такой
вектор, сумма которого с вектором равна
вектору.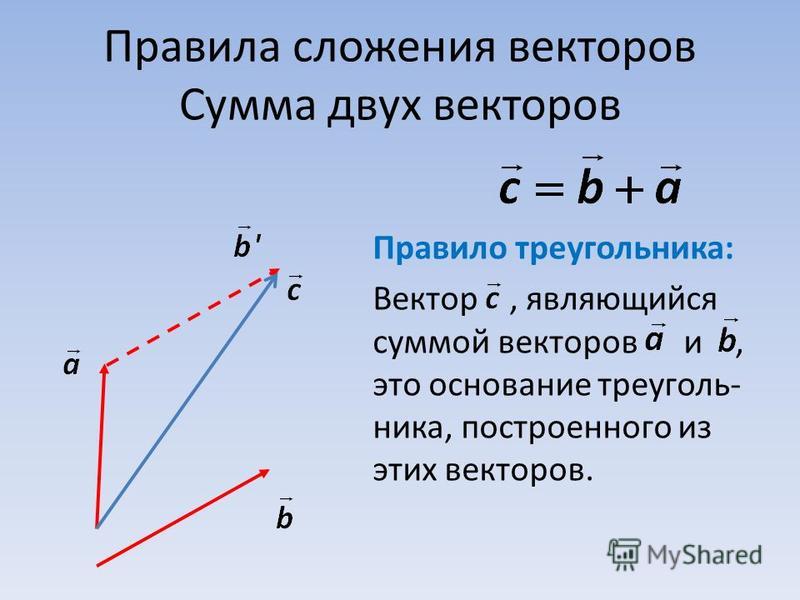
Изображение слайда
26
Слайд 26: Вычитание
B A Правило трех точек C
Изображение слайда
27
Слайд 27: Сложение с противоположным
Разность векторов и можно представить как сумму вектора и вектора, противоположного вектору. А B O
Изображение слайда
28
Слайд 28: Умножение вектора на число
Изображение слайда
29
Слайд 29: Свойства
Произведением нулевого вектора на любое число считается нулевой вектор.
Произведение любого вектора на число нуль есть нулевой вектор.
Изображение слайда
30
Слайд 30: Свойства
Изображение слайда
31
Слайд 31: Проверь себя
Устные вопросы Задачи. Сложение и вычитание векторов
Изображение слайда
32
Слайд 32: Устные вопросы
Справедливо ли утверждение: а) любые два противоположно направленных вектора коллинеарны? б) любые два коллинеарных вектора сонаправлены? в) любые два равных вектора коллинеарны? г) любые два сонаправленных вектора равны? д) е) существуют векторы, и такие, что и не коллинеарны, и не коллинеарны, а и коллинеарны?
Изображение слайда
33
Последний слайд презентации: Векторы в пространстве: Задача 3.
Сложение и вычитание
Выполните действия над векторами (рисунок): а) б) в) г) д) Выберите соответственные точки в пространстве
Изображение слайда
Как складывать и вычитать векторы (с диаграммами)
Вектор – это величина, с которой связаны как величина, так и направление. Это отличается от скалярной величины , которая соответствует только величине. Скорость является примером векторной величины. У него есть как величина (насколько быстро что-то движется), так и направление (направление, в котором оно движется).
Векторы часто рисуются в виде стрелок. Длина стрелки соответствует величине вектора, а острие стрелки указывает направление.
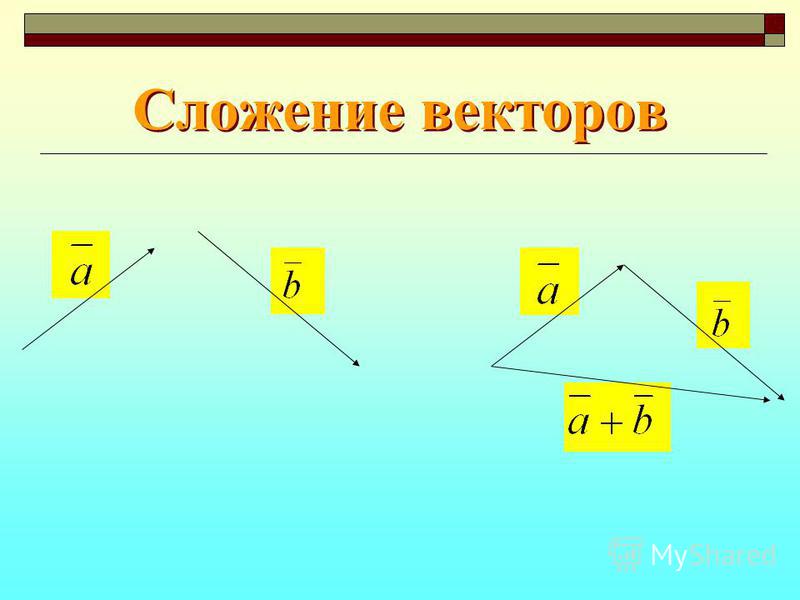
Существует два способа работы со сложением и вычитанием векторов. Первый — графически, манипулируя стрелочными диаграммами самих векторов. Второй — математический, дающий точные результаты.
Графическое сложение и вычитание векторов в одном измерении
При сложении двух векторов хвост второго вектора помещается на вершину первого вектора, сохраняя ориентацию вектора.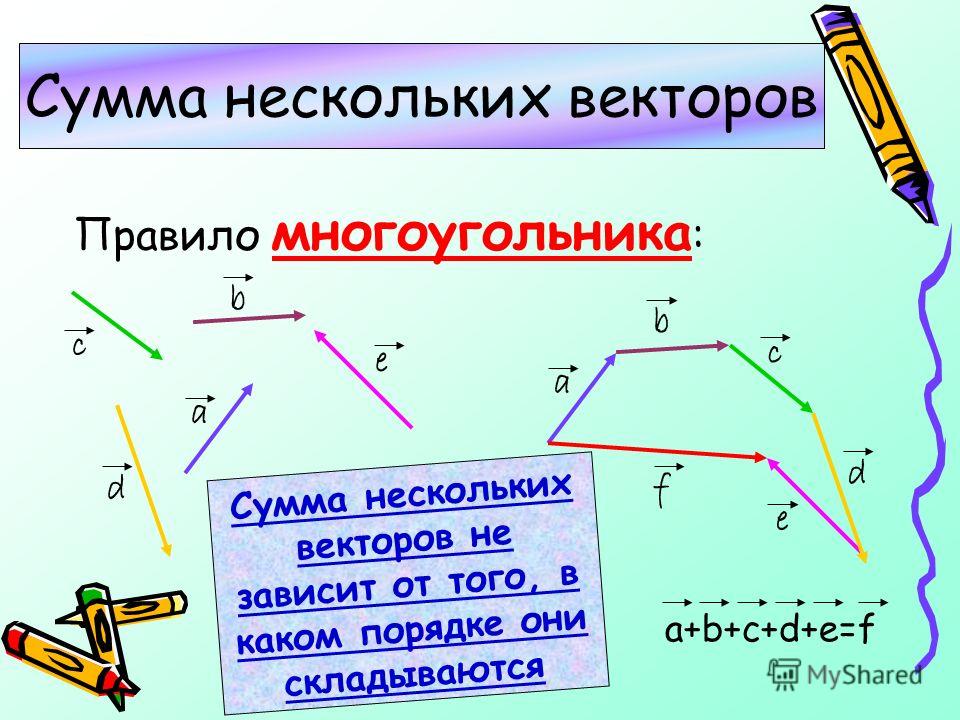
Результирующий вектор – это вектор, который начинается в конце первого вектора и направлен по прямой к вершине второго вектора.
Например, рассмотрим добавление векторов A и B , которые указывают в одном направлении вдоль линии. Мы размещаем их «кончиком к хвосту», и результирующий вектор C указывает в одном направлении и имеет длину, которая является суммой длин A и B .
Вычитание векторов в одном измерении по существу аналогично сложению, за исключением того, что вы «переворачиваете» второй вектор. Это следует непосредственно из того факта, что вычитание — это то же самое, что добавление отрицания.
Математическое сложение и вычитание векторов в одном измерении
При работе в одном измерении направление вектора может быть указано знаком. Мы выбираем одно направление как положительное (обычно «вверх» или «вправо» выбираются как положительные) и назначаем любой вектор, указывающий в этом направлении, как положительную величину.
Любой вектор, указывающий в отрицательном направлении, является отрицательной величиной. При добавлении или вычитании векторов добавляйте или вычитайте их величины с соответствующими знаками.
Предположим, что в предыдущем разделе вектор A имел величину 3, а вектор B имел величину 5. Тогда результирующий вектор C = A + B = 8, вектор величина 8 указывает в положительном направлении, а результирующий вектор D = A — B = -2, вектор величины 2 указывает в отрицательном направлении. Обратите внимание, что это согласуется с графическими результатами, полученными ранее.
Совет: Будьте осторожны, добавляйте векторы только одного типа: скорость + скорость, сила + сила и так далее. Как и во всей математике в физике, единицы измерения должны совпадать!
Графическое сложение и вычитание векторов в двух измерениях
Если первый вектор и второй вектор не лежат на одной прямой в декартовом пространстве, вы можете использовать один и тот же метод «кончик к хвосту», чтобы сложить или вычесть их.
Чтобы добавить два вектора, просто представьте, что вы поднимаете второй и кладете его хвост на кончик первого, сохраняя при этом его ориентацию, как показано. Результирующий вектор представляет собой стрелку, начинающуюся с хвоста первого вектора и заканчивающуюся вершиной второго вектора:
Как и в одном измерении, вычитание одного вектора из другого эквивалентно переворачиванию и сложению. Графически это выглядит следующим образом:
••• Дана Чен | Science
Примечание. Иногда сложение векторов изображают графически, соединяя хвосты двух векторов слагаемых вместе и создавая параллелограмм. Результирующий вектор является диагональю этого параллелограмма.
Математическое сложение и вычитание векторов в двух измерениях
Для математического сложения и вычитания двухмерных векторов выполните следующие действия:
Разложите каждый вектор на компонент x , иногда называемый горизонтальным компонентом, и компонент y , иногда называемый вертикальная составляющая, используя тригонометрию.
(Обратите внимание, что компоненты могут быть отрицательными или положительными в зависимости от того, в каком направлении указывает вектор)0003 y -компоненты обоих векторов вместе. Этот результат дает вам компоненты результирующего вектора x и y .
Величина результирующего вектора может быть найдена с помощью теоремы Пифагора.
Направление результирующего вектора можно найти с помощью тригонометрии, используя функцию арктангенса. Это направление обычно задается как угол относительно положительной оси x .
Тригонометрия в векторном сложении 92
Снарядное движение дает классические примеры того, как мы можем использовать эти отношения как для разложения вектора, так и для определения окончательной величины и направления вектора.
Предположим, двое играют в мяч. Предположим, вам сказали, что мяч брошен с высоты 1,3 м со скоростью 16 м/с под углом 50 градусов к горизонту.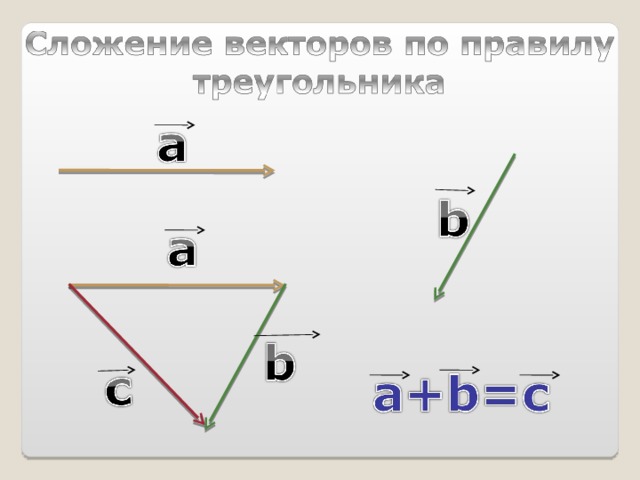
Чтобы приступить к анализу этой задачи, вам нужно будет разложить этот начальный вектор скорости на x и y компоненты, как показано:
v_{xi}=v_i\cos(\theta)=16\times\cos(50)=10,3 \text{ м/с}\\ v_{yi}=v_i\sin(\ theta)=16\times\sin(50)=12.3\text{ м/с}
Если кэтчер промахнется по мячу и он упадет на землю, с какой конечной скоростью он ударится?
Используя кинематические уравнения, мы можем определить, что конечные компоненты скорости мяча равны:
v_{xf}=10,3 \text{ м/с}\\ v_{yf}=-13,3\text{ м/ s}
Теорема Пифагора позволяет найти величину: 9{-1}\Big(\frac{-13.3}{10.3}\Big)=-52.2\степень
Пример сложения и вычитания векторов
Предположим, что автомобиль поворачивает за угол. Предположим, что v i для автомобиля находится в x- направлении с магнитудой 10 м/с, а v f находится под углом 45 градусов с положительным x -ось со скоростью 10 м/с.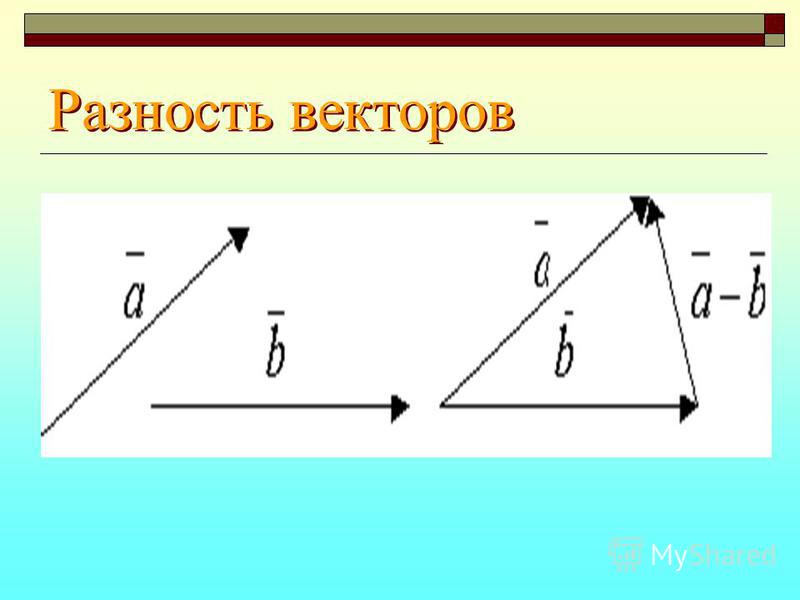
Если это изменение движения происходит за 3 секунды, какова величина и направление ускорения автомобиля при повороте?
Напомним, что ускорение a является векторной величиной, определяемой как: — конечная и начальная скорости соответственно (и, следовательно, тоже векторные величины).
Чтобы вычислить разность векторов v f - v i , , мы должны сначала разложить начальный и конечный векторы скорости:
v_{xi}=10\text{ м/с}\\ v_{yi}=0\text{ м/с}\\ v_{xf}=10\cos(45)=7.07\text{ м/с s}\\ v_{yf}=10\sin(45)=7.07\text{ м/с}
Затем мы вычитаем конечные x и y компоненты из исходных x И Y Компоненты для получения компонентов V F — V I :
Затем мы вычислим x и Y компоненты:
(v_f-v_i)_x=v_{xf}-v_{xi}=7.
07-10=-2.9{-1}\Big(\frac{2.36}{-0.977}\Big)=113\grade
основных векторных операций
основных векторных операций| Для векторной величины должны быть указаны как величина, так и направление, в отличие от скалярной величины, которую можно количественно определить только числом. Любое количество векторных величин одного типа (т. е. одинаковых единиц измерения) может быть объединено с помощью основных векторных операций. | Индекс Математика векторов | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Сложение и вычитание векторов: графические методы | Физика |Векторы в двух измеренияхВектор — это величина, которая имеет величину и направление. Например, перемещение, скорость, ускорение и сила — все это векторы. В одномерном или прямолинейном движении направление вектора может быть задано просто знаком плюс или минус. Однако в двух измерениях (2-d) мы указываем направление вектора относительно некоторой системы отсчета (т. е. системы координат), используя стрелку, длина которой пропорциональна величине вектора и указывает направление вектора. На рисунке 2 показано такое графическое представление вектора на примере полного перемещения человека, идущего по городу, которое рассматривается в книге «Кинематика в двух измерениях: введение». В этом тексте мы будем представлять вектор переменной, выделенной жирным шрифтом. Например, мы представим количественную силу вектором F , который имеет как величину, так и направление. Величина вектора будет представлена переменной, выделенной курсивом, например, F , а направление переменной будет задано углом θ . Рисунок 2. Человек проходит 9 кварталов на восток и 5 кварталов на север. Смещение 10,3 блока под углом 29,1º к северу от востока. Рисунок 3. Чтобы графически описать результирующий вектор для человека, идущего по городу, показанному на рисунке 2, нарисуйте стрелку, представляющую вектор полного перемещения Д . Сложение векторов: метод «голова к хвосту»Метод «голова к хвосту» — это графический способ добавления векторов, описанный на рисунке 4 ниже и в следующих шагах. хвост вектора является начальной точкой вектора, а начало (или кончик) вектора является конечным заостренным концом стрелки. Рис. 4. Метод «голова к хвосту». Метод графического сложения векторов «голова к хвосту» проиллюстрирован для двух перемещений человека, идущего по городу, показанного на рисунке 2. (a) Нарисуйте вектор, представляющий перемещение на восток. (b) Нарисуйте вектор, представляющий смещение на север. Шаг 1. Нарисуйте стрелку, представляющую первый вектор (9 блоков на восток), используя линейку и транспортир . Рисунок 5 Шаг 2. Теперь нарисуйте стрелку, обозначающую второй вектор (5 кварталов на север). Поместите конец второго вектора в начало первого вектора . Рисунок 6 Шаг 3. Шаг 4. Проведите стрелку от хвоста первого вектора к началу последнего вектора . Это равнодействующее или сумма других векторов. Рисунок 7 Шаг 5. Чтобы получить величину равнодействующей, измерьте ее длину линейкой. (Обратите внимание, что в большинстве вычислений мы будем использовать теорему Пифагора для определения этой длины.) Шаг 6. Чтобы получить направление равнодействующей, измерьте угол, который она образует с системой отсчета, используя транспортир. (Обратите внимание, что в большинстве расчетов мы будем использовать тригонометрические отношения для определения этого угла. Пример 1. Графическое добавление векторов с использованием метода «голова к хвосту»: женщина прогуливаетсяИспользуйте графический метод сложения векторов, чтобы найти полное перемещение человека, который проходит следующие три пути (перемещения) по плоскому полю. Сначала она проходит 25,0 м в направлении 49..0º к северу от востока. Затем она проходит 23,0 м в направлении 15,0º к северо-востоку. Наконец, она поворачивается и проходит 32,0 м в направлении 68,0° к югу от востока. Стратегия Представьте каждый вектор смещения графически со стрелкой, обозначив первый A , второй B и третий C , делая длины пропорциональными расстоянию и направлениям, указанным относительно линии восток-запад. (1) Нарисуйте три вектора смещения. Рис. 8. (2) Разместите векторы от начала до конца, сохранив их первоначальную величину и направление. Рис. 9. (3) Нарисуйте результирующий вектор R . Рис. 10. (4) Используйте линейку для измерения величины R и транспортир для измерения направления R . Хотя направление вектора можно указать разными способами, проще всего измерить угол между вектором и ближайшей горизонтальной или вертикальной осью. Поскольку результирующий вектор находится к югу от оси, направленной на восток, мы переворачиваем транспортир вверх ногами и измеряем угол между осью, направленной на восток, и вектором. Рисунок 11 В этом случае видно, что полное смещение R имеет величину 50,0 м и направлено на 7,0º к югу от востока. Используя его величину и направление, этот вектор можно выразить как R = 50,0 м и θ = 7,0º к югу от востока. ОбсуждениеГрафический метод сложения векторов «голова к хвосту» работает для любого количества векторов. Также важно отметить, что результирующая не зависит от порядка добавления векторов. Таким образом, мы можем добавлять векторы в любом порядке, как показано на рисунке 12, и все равно получим то же решение. Рисунок 12. Здесь мы видим, что при добавлении одних и тех же векторов в другом порядке результат будет таким же. Эта характеристика верна в любом случае и является важной характеристикой векторов. Сложение векторов коммутативно . А + В = В + А. (Это верно и для сложения обычных чисел — вы получите один и тот же результат, сложите ли вы, например, 2 + 3 или 3 + 2 ). Это видео можно использовать для просмотра. Он включает в себя основы работы с векторами — рисование векторов/добавление векторов. Вы узнаете об основном понятии вектора, о том, как графически складывать векторы, а также о том, что графически означает умножение вектора на скаляр. Вычитание векторов Вычитание векторов — это прямое расширение сложения векторов. Чтобы определить вычитание (скажем, мы хотим вычесть B из A, записанного A – B), мы должны сначала определить, что мы подразумеваем под вычитанием.0003 отрицательный вектора B определяется как –B; то есть графически отрицательный вектор любого вектора имеет ту же величину, но противоположное направление , как показано на рисунке 13. Рис. 13. Отрицательное значение вектора — это просто другой вектор той же величины, но направленный в противоположном направлении. Таким образом, B является минусом 9.0168 –В ; он имеет ту же длину, но противоположное направление. Затем вычитание вектора B из вектора A просто определяется как сложение –B с A . Обратите внимание, что вычитание вектора — это добавление отрицательного вектора. Порядок вычитания не влияет на результат. А — В = А + (-В) Это аналогично вычитанию скаляров (где, например, 5 – 2 = 5 + (–2)). Опять же, результат не зависит от порядка, в котором производится вычитание. Пример 2. Графическое вычитание векторов: женщина, плывущая на лодкеЖенщина, плывущая на лодке ночью, следует указаниям к пристани. Инструкции гласили: сначала пройти 27,5 м в направлении 66,0º к северу от востока от ее текущего местоположения, а затем пройти 30,0 м в направлении 112º к северу от востока (или 22,0º к западу от севера). Если женщина совершит ошибку и поедет в направлении против на второй этап поездки, где она окажется? Сравните это место с расположением дока. Рисунок 14. Стратегия Мы можем представить первый этап поездки вектором A , а второй этап поездки вектором B . Док находится по адресу A+B . Если женщина по ошибке едет в направлении , противоположном , для второго отрезка пути, она проедет расстояние B (30,0 м) в направлении 180º–112º=68º к югу от востока. Рисунок 15 Выполним сложение векторов, чтобы сравнить положение причала A + B с местом, куда по ошибке прибыла женщина, A + (-B) . Раствор(1) Чтобы определить место, куда случайно попала женщина, нарисуйте векторы А и –В . (2) Разместите векторы лицом к хвосту. (3) Нарисуйте результирующий вектор R . (4) С помощью линейки и транспортира измерьте величину и направление R . Рисунок 16 В этом случае R = 23 . 0 м и θ = 7 . (5) Для определения местоположения дока повторяем этот метод, добавляя векторы A и B . Получаем результирующий вектор R’ : Рисунок 17 В этом случае R = 52,9 м и θ = 90,1° к северу от востока. Мы видим, что женщина окажется на значительном расстоянии от причала, если она отправится в противоположном направлении на второй этап поездки. ОбсуждениеПоскольку вычитание вектора — это то же самое, что сложение вектора с противоположным направлением, графический метод вычитания векторов работает так же, как и сложение. Умножение векторов и скаляров Если бы мы решили пройти в три раза большее расстояние на первом этапе пути, рассматриваемого в предыдущем примере, то мы бы прошли 3 × 27,5 м, или 82,5 м, в направлении 66,0º к северу от востока. Если скаляр отрицательный, то умножение вектора на него изменяет величину вектора и дает новому вектору в противоположном направлении . Например, если умножить на -2, величина удвоится, но изменится направление. Мы можем обобщить эти правила следующим образом: когда вектор A умножается на скаляр c ,
В нашем случае c = 3 и A = 27,5 м. Векторы умножаются на скаляры во многих ситуациях. Обратите внимание, что деление является обратным умножению. Например, деление на 2 равносильно умножению на значение (1/2). Разложение вектора на компонентыВ приведенных выше примерах мы добавляли векторы для определения результирующего вектора. Однако во многих случаях нам нужно будет сделать обратное. Нам нужно будет взять один вектор и найти, какие другие векторы, сложенные вместе, дают его. В большинстве случаев это связано с определением перпендикуляра компоненты одного вектора, например компоненты x — и y , или компоненты север-юг и восток-запад. Например, мы можем знать, что общее перемещение человека, идущего по городу, составляет 10,3 квартала в направлении 29,0º к северу от востока, и мы хотим узнать, сколько кварталов ему пришлось пройти на восток и север. Этот метод называется нахождением компонентов (или частей) смещения в восточном и северном направлениях, и он является обратным процессу, применяемому для нахождения полного смещения. Исследования PhET: Игра в лабиринтУзнайте о положении, скорости и ускорении на «Арене боли». Используйте зеленую стрелку, чтобы переместить мяч. Добавьте больше стен на арену, чтобы усложнить игру. Постарайтесь достичь цели как можно быстрее. Нажмите, чтобы скачать. Запуск с использованием Java. Резюме
Концептуальные вопросы1. Что из перечисленного является вектором: рост человека, высота на Эвересте, возраст Земли, температура кипения воды, стоимость этой книги, население Земли, ускорение свободного падения? 2. Приведите конкретный пример вектора, указав его величину, единицы измерения и направление. 3. Что общего между векторами и скалярами? Чем они отличаются? 4. Два отдыхающих в национальном парке отправляются из своей хижины в одно и то же место на озере, каждый по своему пути, как показано ниже. Общее расстояние, пройденное по Пути 1, составляет 7,5 км, а по Пути 2 — 8,2 км. Каково конечное перемещение каждого туриста? Рис. 5. Если пилоту самолета велят пролететь 123 км по прямой, чтобы добраться из Сан-Франциско в Сакраменто, объясните, почему он может оказаться в любом месте круга, показанного на рисунке 19. Какая еще информация ему потребуется, чтобы добраться до Сакраменто. ? Рисунок 19. 6. Предположим, вы делаете два шага A и B (то есть два ненулевых перемещения). При каких обстоятельствах вы можете оказаться в исходной точке? В более общем смысле, при каких обстоятельствах два ненулевых вектора могут сложиться, чтобы получить ноль? Максимальное расстояние, на котором вы можете оказаться от начальной точки A + B сумма длин двух шагов? 7. Объясните, почему нельзя добавить скаляр к вектору. 8. Если вы сделаете два шага разной длины, сможете ли вы оказаться в исходной точке? В более общем смысле, могут ли два вектора с разными величинами дать в сумме ноль? Можно три или больше? Задачи и упражнения Используйте графические методы для решения этих задач. 1. Найдите следующее для пути А на рис. 20: (а) общее пройденное расстояние и (б) величину и направление смещения от начала до конца. Рисунок 20. Различные линии обозначают пути, по которым идут разные люди, идущие по городу. Все блоки со стороной 120 м. 2. Найдите следующее для пути B на рисунке 20: (a) общее пройденное расстояние и (b) величину и направление смещения от начала до конца. 3. Найдите северную и восточную составляющие смещения для туристов, показанных на Рисунок 20. 4. Предположим, вы идете 18,0 м прямо на запад, а затем 25,0 м прямо на север. Как далеко вы находитесь от своей начальной точки и каково направление по компасу линии, соединяющей вашу начальную точку с вашим конечным положением? (Если вы представляете два этапа ходьбы как векторные смещения A и B , как на рисунке 21, то эта задача требует от вас найти их сумму R = A + B . Рисунок 21. Два смещение A и B добавить, чтобы получить общее смещение R с величиной R и направлением θ . 5. Предположим, вы сначала прошли 12,0 м в направлении 20° к западу от севера, а затем 20,0 м в направлении 40,0° к югу от запада. Как далеко вы находитесь от своей начальной точки и каково направление по компасу линии, соединяющей вашу начальную точку с вашим конечным положением? (Если вы представите два этапа прогулки как векторные смещения A и B , как на рисунке 22, то эта задача найдет их сумму R = A + B .) Рис. 22. 6. Повторите задачу, описанную выше, но в обратном порядке для двух этапов ходьбы; показать, что вы получаете тот же конечный результат. То есть вы сначала проходите участок B , который составляет 20,0 м в направлении точно на 40º к югу от запада, а затем участок A , который составляет 12,0 м в направлении, точно на 12,0 к западу от севера. 7. (a) Повторите задачу двумя предыдущими задачами, но на втором этапе вы пройдете 20,0 м в направлении 40° к северу от востока (что эквивалентно вычесть B от A — то есть до нахождения R’ = A — B ). (b) Повторите задачу двумя предыдущими задачами, но теперь вы сначала пройдете 20,0 м в направлении на 40º к югу от запада, а затем 12,0 м в направлении на 20º к востоку от юга (что эквивалентно вычитанию A из B — это R» = B — A = R’ Покажите, что это так. 8. Покажите, что порядок сложения трех векторов не влияет на их сумму. Покажите это свойство с помощью выбор любых трех векторов A , B , C и C\mathbf{C}C , все они имеют разную длину и направление. |
Представляя векторы стрелками, нарисованными в масштабе, начало вектора B помещается в конец вектора A. Сумма векторов R может быть изображена как вектор от начала до конечной точки.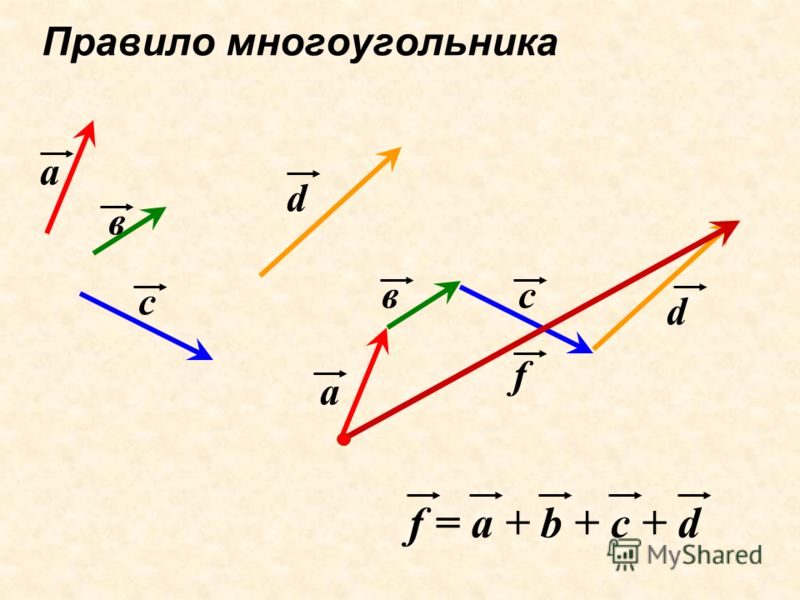
Вы можете изменить длину или угол полярной формы вектора, и компоненты будут рассчитаны ниже.
Существуют некоторые комбинации углов и значений, например, когда ожидается точно нулевой результат или угол ровно 90 градусов, когда процедура Javascript нестабильна и выдает ошибочные значения. Обычно вы можете попробовать значения, очень близкие к таким условиям, чтобы проверить точность.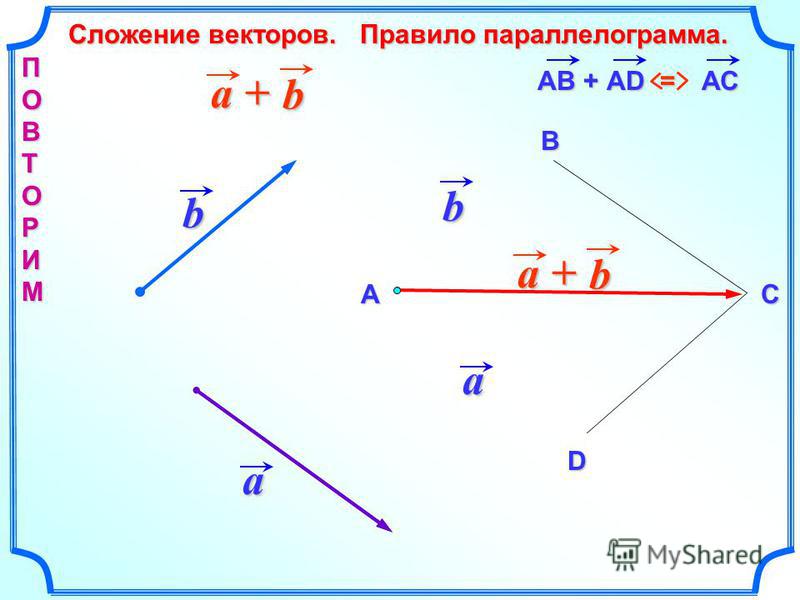
Мы будем использовать обозначение, что жирный символ, такой как D , обозначает вектор. Его величина представлена курсивным символом D , а его направление — θ .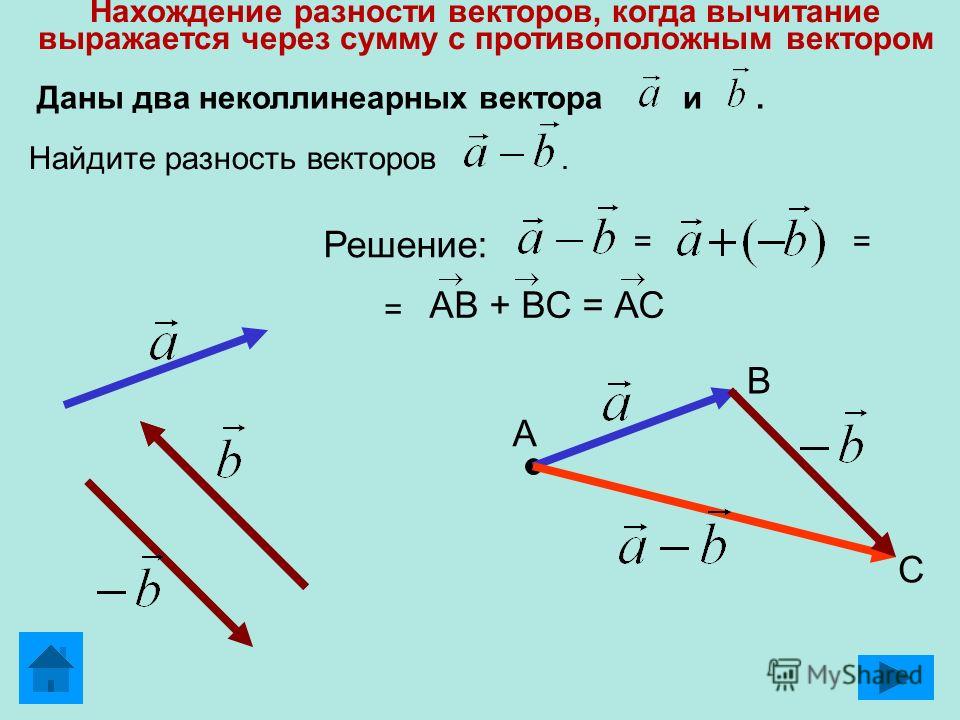
Используя транспортир, нарисуйте линию под углом θ относительно оси восток-запад. Длина D стрелки пропорциональна модулю вектора и измеряется вдоль линии с помощью линейки. В этом примере величина D вектора составляет 10,3 единицы, а направление θ составляет 29,1º к северу от востока.
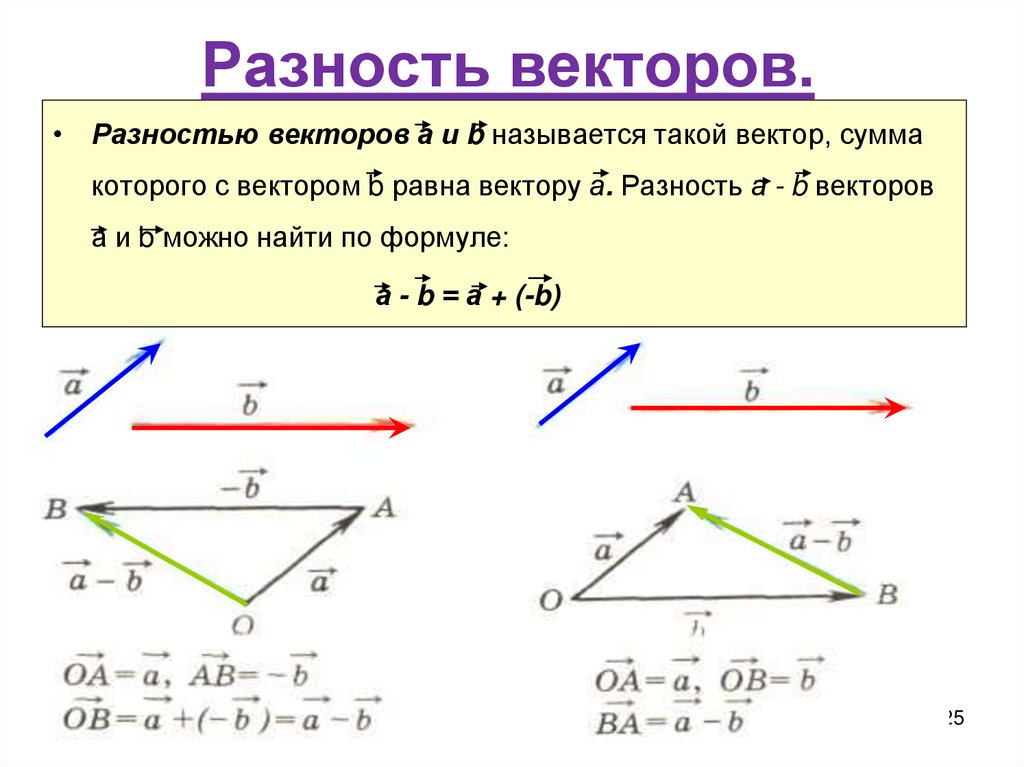Хвост этого вектора должен исходить из головы первого вектора, указывающего на восток. (c) Проведите линию от хвоста вектора, указывающего на восток, до начала вектора, указывающего на север, чтобы получить сумму или результирующий вектор D . Длина стрелки D пропорциональна модулю вектора и составляет 10,3 единицы. Его направление, описываемое как угол относительно востока (или горизонтальной оси) θ, измеренное с помощью транспортира, равно 29,1º.
Если имеется более двух векторов, продолжайте этот процесс для каждого добавляемого вектора. Обратите внимание, что в нашем примере у нас есть только два вектора, поэтому мы закончили размещать стрелки от начала до конца .
) Точность графического сложения векторов ограничена только точностью, с которой могут быть выполнены чертежи, и точностью измерительных инструментов. Это справедливо для любого количества векторов.
Описанный выше метод «голова к хвосту» позволит определить величину и направление результирующего смещения, обозначенного цифрой 9.0168 Р .
Векторы можно добавлять в любом порядке.
Другими словами, B имеет ту же длину, что и -B, но указывает в противоположном направлении. По сути, мы просто переворачиваем вектор так, чтобы он указывал в противоположном направлении.
Когда векторы вычитаются графически, используются описанные выше методы, как показано в следующем примере.
Мы представляем это как –B , как показано ниже. Вектор –B имеет ту же величину, что и B, но направлен в противоположном направлении. Таким образом, она окажется в локации A + (–B) или A – B .
5º к югу от востока.
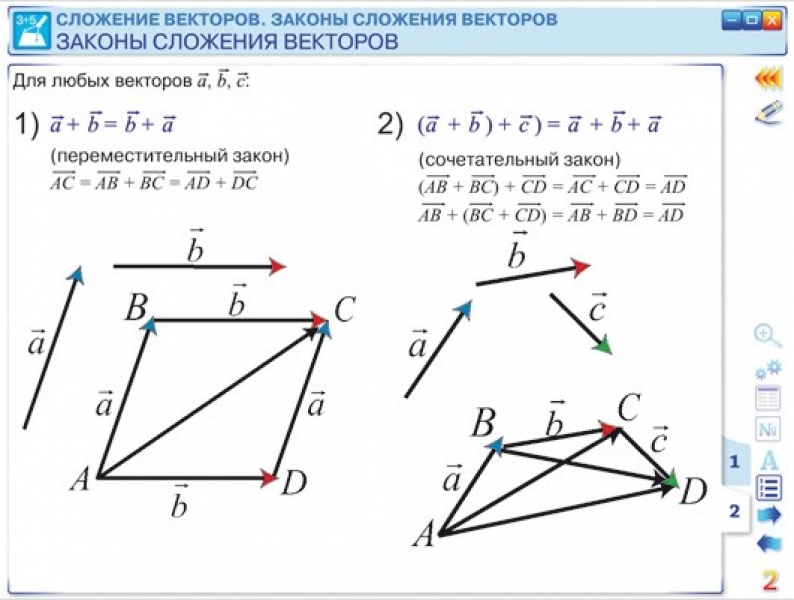Это пример умножения вектора на положительный скаляр . Обратите внимание, что величина меняется, но направление остается прежним.
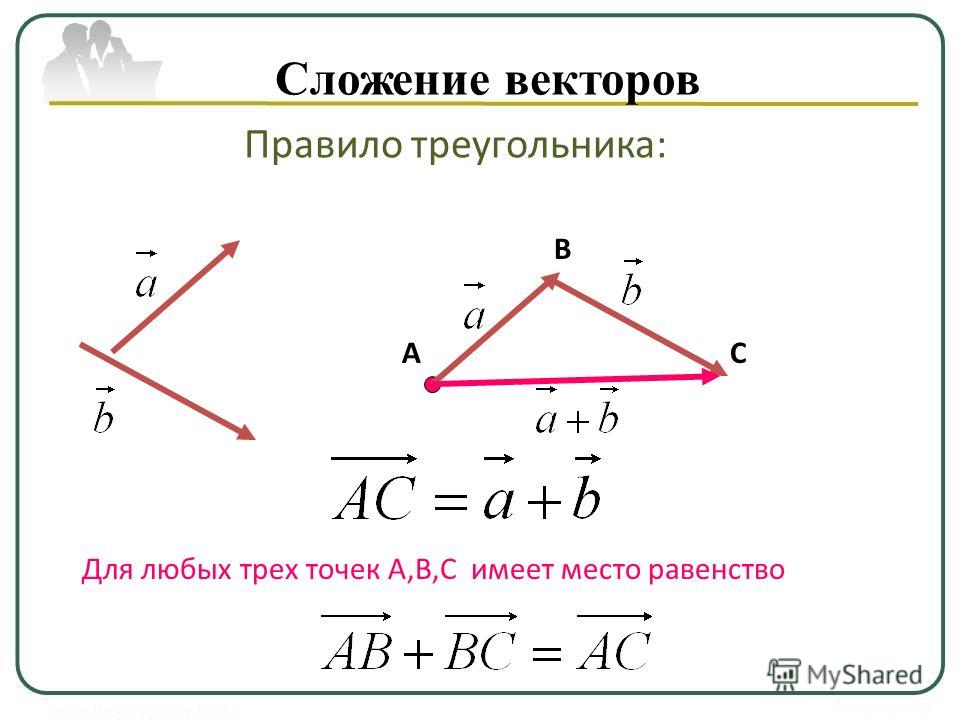Правила умножения векторов на скаляры такие же, как и при делении; просто рассматривайте делитель как скаляр от 0 до 1.
Это один из примеров нахождения компонентов вектора. В физике есть много приложений, где это может оказаться полезным. Мы скоро увидим это в Projectile Motion и многое другое, когда рассмотрим заставляет в динамике: законы движения Ньютона. Большинство из них включают поиск компонентов вдоль перпендикулярных осей (например, север и восток), так что задействованы прямоугольные треугольники. Аналитические методы, представленные в разделе «Сложение и вычитание векторов: аналитические методы», идеально подходят для поиска компонентов вектора.
Результирующий вектор R определяется таким образом, что A + B = R . Величина и направление R затем определяются с помощью линейки и транспортира соответственно.
Если c положителен, направление произведения указывает на то же направление, что и A ; если c отрицательно, направление произведения указывает на направление, противоположное A .
18.
Вы можете предположить, что данные, взятые из графиков, имеют точность до трех цифр. 
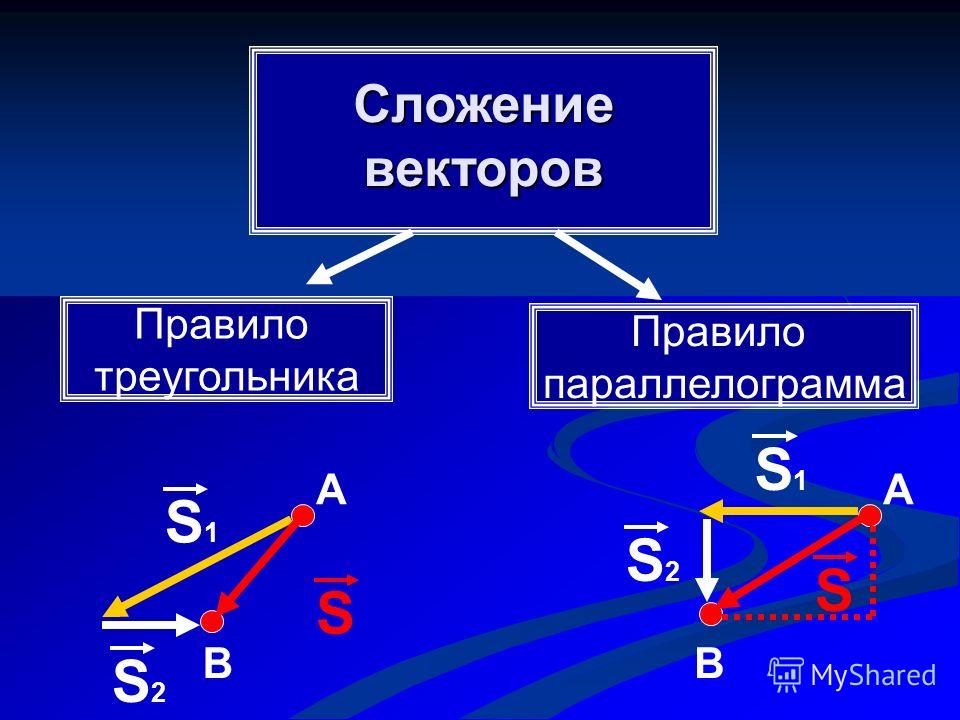
(Эта задача показывает, что A + B = B + A .)