Выразить log16 3 через логарифм по основанию 2: Выразить log16 3 через логарифм по основанию 2…

Содержание

Выразим логарифм…Упр 305 параграф 17 Алгебра Алимов 10-11 класс – Рамблер/класс

Интересные вопросы

Школа

Подскажите, как бороться с грубым отношением одноклассников к моему ребенку?

Новости

Поделитесь, сколько вы потратили на подготовку ребенка к учебному году?

Школа

Объясните, это правда, что родители теперь будут информироваться о снижении успеваемости в школе?

Школа

Когда в 2018 году намечено проведение основного периода ЕГЭ?

Новости

Будет ли как-то улучшаться система проверки и организации итоговых сочинений?

Вузы

Подскажите, почему закрыли прием в Московский институт телевидения и радиовещания «Останкино»?

Привееет! Поможете с заданием?
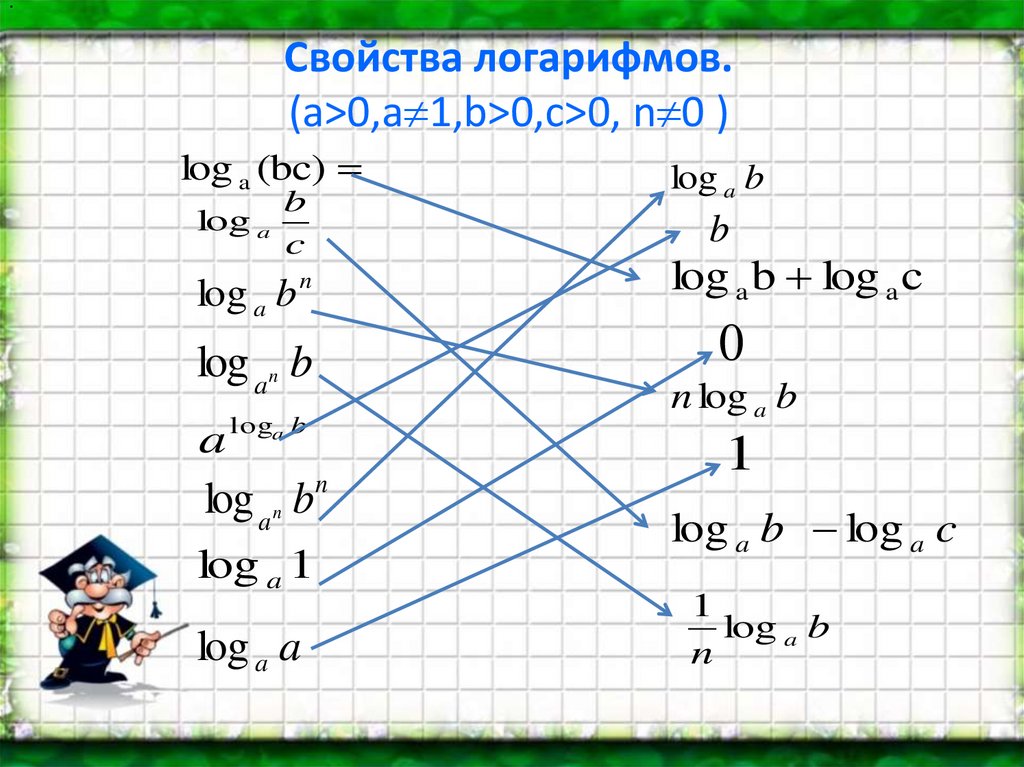
Выразить данный логарифм через логарифм с основанием 7:

1) log5 3;
2) lg 6;
3) log2 7;

5) lg 7;
6) log3 7.

ответы

Конечно помогу! Тут так делается:

ваш ответ

Можно ввести 4000 cимволов

отправить

дежурный

Нажимая кнопку «отправить», вы принимаете условия пользовательского соглашения

похожие темы

ЕГЭ

9 класс

11 класс

Химия

похожие вопросы 5

Алгебра. 9 класс. Алимов Ш. А. Параграф 9. Упражнение №116. Провсти доказательство

Даровчики. Помощь нужна с алгеброй…никак решить не могу(((
Доказать, что —
(Подробнее…)

ГДЗАлгебраАлимов Ш.А.Школа9 класс

Когда скорость изменения функции будет наибольшей или наименьшей? Алгебра 10-11 класс Колмогоров Упр 308

Совсем я в точных науках не сильна) Кто поможет?) Найдите значения аргумента из промежутка [-2; 5], при которых скорость изменения (Подробнее. ..)

ГДЗ11 классКолмогоров А.Н.Алгебра

Почему сейчас школьники такие агрессивные ?

Читали новость про 10 классника который растрелял ? как вы к этому относитесь

Новости10 классБезопасность

11. Выпишите слово, в котором на месте пропуска пишется буква Е. Русский язык ЕГЭ-2017 Цыбулько И. П. ГДЗ. Вариант 12.

11.
Выпишите слово, в котором на месте пропуска пишется буква Е.
произнос., шь (Подробнее…)

ГДЗЕГЭРусский языкЦыбулько И.П.

ЕГЭ-2017 Цыбулько И. П. Русский язык ГДЗ. Вариант 12. 18. Расставьте все знаки препинания: укажите цифру(-ы), на месте которой(-ых)…

18.
Расставьте все знаки препинания: укажите цифру(-ы), на месте которой(-ых)

в предложении должна(-ы) стоять запятая(-ые). (Подробнее…)

ГДЗЕГЭРусский языкЦыбулько И.П.

3-8 9 Оценить квадратный корень из 12 10 Оценить квадратный корень из 20 11 Оценить квадратный корень из 50 94 18 Оценить квадратный корень из 45 19 Оценить квадратный корень из 32

20 Оценить квадратный корень из 18 92

Логарифм и экспоненциальные функции

логарифм по основанию 10 (log)

натуральный логарифм (ln)

экспоненциальная функция (exp or e ^x )

Логарифмическая функция по основанию 10

Фон: Каждое положительное число, и , можно представить в виде 10, возведенного в степень сила, х .

Эта связь описывается уравнением

y = 10 ^х ,

и описывается этим графиком:

Например, число 16 можно представить как 10 ^1,2. Это черная точка на графике. Мы определяем функцию, называемую логарифмом по основанию 10 , которая принимает число вроде 16. в качестве входных данных вычисляет, что это может быть выражено как 10 ^1,2 , и возвращает показатель степени 1.2 в качестве выходного значения:

Вот формальное определение функции логарифма по основанию 10.

Определение: Логарифм по основанию 10 — это функция, которая принимает любое положительное число x в качестве входных данных и возвращает степень, до которой нужно возвести основание 10, чтобы получить x . Обозначается log( x ).

Пример 1: Оценить журнал ( 1000 ).

Аргумент логарифмическая функция (т.е. количество в скобках, 1000), легко выражается как 10 возводится в степень 3. Затем функция логарифмирования возвращает показатель степени.

log ( 1000 ) = log ( 10 ³ ) = 3

Пример 2: Вычислить log ( 10 ^5,7 ).

Аргумент уже выражен как 10, возведенное в степень, поэтому функция логарифмирования просто возвращает показатель степени.

log ( 10 ^5,7 ) = 5,7

Пример 3: Вычислите log ( 16 ).

Согласно графику 16 = 10 ^1,2 . Функция логарифмирования возвращает показатель степени 1,2.

log ( 16 ) = log ( 10 ^1,2 ) = 1,2

График: х ). Обратите внимание, что для любых положительных x это одно значение и для любого отрицательного x это не определено.

Если сравнить этот график с графиком из y = 10 ^x выше тогда вы видите, что одно можно получить из другого путем замены оси x и y .

Для сравнения: красная кривая представляет собой график функции натурального логарифма ( y = ln( x ), рассмотренный в следующем разделе). График натурального логарифма имеет точно такую же форму как график логарифма по основанию 10; он всего в 2,3 раза выше.

Важной особенностью логарифмических функций (независимо от основания) является то, что они очень медленно возрастают. так как x становится очень большим. Они прекрасно описывают, как человек ухо воспринимает громкость и так, как человеческий глаз воспринимает яркость.

Домен и диапазон: Область определения функции логарифма по основанию 10 — это все положительные действительные числа, а диапазон равен все действительные числа.

Функцию логарифмирования по основанию 10 можно распространяется на комплексные числа, в этом случае доменом являются все комплексные числа, кроме нуля.

Логарифм нуля по основанию 10 всегда не определен.

Некоторые специальные значения функции логарифма по основанию 10

Решение уравнения 10 с помощью функции логарифмирования по основанию 10

Предположим, что x неизвестно, но 10 ^x равно известное значение c . Тогда нахождение x требует решения следующее уравнение для x .

10 ^х = с

Решение

x = логарифм ( c )

Это связано с тем, что найти log ( c ) означает выразить c как 10 в степени, а затем возвращает эту степень. Но исходное уравнение говорит, что этот показатель равен x . Обратите внимание, что если c отрицательно, то действительного решения нет. Однако есть комплексное решение. Кроме того, если c = 0, то решения вообще нет.

log ( x ) и 10 ^x являются обратными функциями. 10 ^x , например:
Функция логарифмирования по основанию 10 определена так, чтобы делать прямо противоположное, а именно:
Следовательно, это обратные функции.
Обратите внимание на следующее:
Поскольку функция 10 ^x является обратной Функция логарифма по основанию 10 иногда называется функцией антилогарифма .
Выше мы видели, что решение 10 ^х = у x = логарифм ( y ). Мы должны посмотреть на эти два уравнения как выражение того же отношения между
х и х , но с разных точек зрения. Первое уравнение представляет собой соотношение, решенное для y , а второе — это отношение, решенное для x . (Аналогия состоит в том, что утверждение « Том — брат Джейн » эквивалентно утверждению, что « Джейн — сестра Тома ». )
В предыдущем пункте мы видели, что два уравнения, 10 ^х = y и x = log ( y ), сказал то же самое. Если мы заменим x в первом уравнении на x второго уравнения мы получаем это тождество:
10 ^{log( y )} = y
и если мы заменим на во втором уравнении на y первого уравнения мы получаем это тождество:
x = логарифм (10 ^x )
Эти тождества полезны для демонстрации того, как логарифм и антилогарифм компенсируют друг друга.
Если сравнить график от y = log ( x ) к график из y = 10 ^x тогда вы видите, что одно можно получить из другого путем замены оси x и y . Это всегда происходит с обратными функциями.

Как использовать функцию логарифмирования по основанию 10 в программе Algebra Coach
Введите log(x) в текстовое поле, где x — аргумент. Аргумент должен быть заключен в скобки.
Установите соответствующие параметры:
Установите параметр точная / с плавающей запятой. В режиме с плавающей запятой вычисляется логарифм по основанию 10 от любого числа . В точном режиме логарифм числа 9 по основанию 100924 целое число не оценивается, потому что это приведет к приблизительному числу.
Включите комплексные числа , если вы хотите иметь возможность оценивать логарифм по основанию 10 отрицательного или комплексного числа.
Нажмите кнопку «Упростить».

Алгоритм для функции логарифма по основанию 10
Нажмите здесь чтобы увидеть алгоритм, который компьютеры используют для вычисления функции логарифма по основанию 10.

Функция натурального логарифма
Предыстория: Возможно, вам будет полезно прочитать предыдущий раздел. о функции логарифма по основанию 10, прежде чем читать этот раздел. Две секции тесно параллельны друг другу.
Вспомните, что функция логарифмирования по основанию 10 принимает число вроде 16 в качестве входных данных вычисляет, что его можно записать как 10 ^1,2 , а затем возвращает показатель степени 1,2 в качестве выходного значения. Но зачем использовать базу 10? Ведь, наверное единственная причина, по которой число 10 важно для людей, заключается в том, что у них 10 пальцев, с помощью которых они впервые научились считать. Может быть, на какой-то другой планете, населенной 8-палыми существами, они используют основание 8!
На самом деле, наверное, самый важный номер в вся математика (нажмите здесь, чтобы понять, почему) это число 2,71828…, которому мы даем имя e , в честь Леонарда Эйлера, который первым открыл его. Будет важно иметь возможность взять любое положительное число, и , и выразить это как e , возведенное в некоторую степень, x . Мы можем записать это соотношение в виде уравнения:
у = е ^х
Например, 5 можно записать как e ^1,6. (показатель приблизительный). Откуда мы знаем, что это правильная мощность и ? Потому что мы получаем это из графика, показанного ниже.
Чтобы построить этот график, мы составили таблицу нескольких очевидных значений y = e ^x как показано ниже слева. Затем мы нанесли значения на график (это красные точки) и начертили плавную кривой через них. Затем мы заметили, что кривая проходит через г = 5 и x = 1,6 (черная точка). Это означает, что 5 = e ^1,6 .

Если сравнить этот график с графиком y = 10 ^x вы видите, что оба имеют одинаковую так называемую форму экспоненциального роста но что этот график растет медленнее.

Затем мы определяем функцию, называемую натуральный логарифм , который принимает число вроде 5 в качестве входных данных вычисляет, что его можно записать как e ^1,6 , и возвращает показатель степени 1,6 в качестве выходного значения. Вот формальное определение.

Определение: Натуральный логарифм — это функция, которая принимает любое положительное число x в качестве входных данных и возвращает показатель степени, до которого нужно возвести основание e , чтобы получить x . Обозначается ln( х ). ( e обозначает число 2,71828…)

Обратите внимание, что во избежание путаницы функция натурального логарифма обозначается ln( x ) и функция по основанию 10 логарифм обозначается как log( x ).
Пример 1: Вычислить ln ( e ^4,7 ).
Аргумент функция натурального логарифма уже выражена поскольку e возведены в степень, функция натурального логарифма просто возвращает показатель степени.
ln ( e ^4,7 ) = 4,7

Пример 2: Вычислить ln ( 5 ).
Согласно графику 5 = e ^1,6 . Функция логарифмирования возвращает показатель степени 1,6.
ln ( 5 ) = 1,6

Пример 3: Вычислить ln ( e ).
Выразите аргумент как e возводится в степень 1 и возвращает показатель степени.
пер ( е ) = пер ( е ¹) = 1

Пример 4: Вычислить ln ( 1 ).
Выразите аргумент как e возводится в степень 0 и возвращает показатель степени.
ln ( 1 ) = ln ( e ⁰ ) = 0

График: х ). Обратите внимание, что для любых положительных x это одно значение и для любого отрицательного x это не определено. Если сравнить этот график с график y = e ^x тогда вы видите, что одно можно получить из другого путем замены оси x и y .
Для сравнения синяя кривая показывает функция логарифма по основанию 10, y = log ( x ). Он имеет точно такую же форму, но только на 43% выше.

Домен и диапазон: Областью определения функции натурального логарифма являются все положительные действительные числа, а диапазон равен все действительные числа.
Функция натурального логарифма может быть распространяется на комплексные числа, в этом случае доменом являются все комплексные числа, кроме нуля. Натуральный логарифм нуля всегда не определен.

Решение уравнения e ^x = c для х с помощью функции натурального логарифма
Предположим, что x неизвестно, но e ^x равно известное значение c . Тогда для нахождения x требуется решить это уравнение для х :
е ^х = с
Решение
x = пер ( c )
потому что нахождение ln ( c ) означает выражение c как e возводится в степень, а затем возвращается в степень. Но исходное уравнение говорит, что этот показатель равен x . Обратите внимание, что если c отрицательно, то действительного решения нет. Однако есть комплексное решение. Более того, если c = 0, то решения вообще нет.

ln ( x ) и e ^x являются обратными функциями
Рассмотрим функцию e ^x , которая принимает x и возвращает e ^x , например:
Функция натурального логарифма определена так, чтобы делать прямо противоположное, а именно:
Следовательно, это обратные функции.
Обратите внимание на следующее:
Выше мы видели, что решение e ^х = y есть x = ln ( y ). Мы должны посмотреть на эти два уравнения как выражение того же отношения между x и y , но с разных точек зрения. Первое уравнение представляет собой соотношение, решенное для y , а второе — это отношение, решенное для x . (Аналогия состоит в том, что утверждение « Том — брат Джейн » эквивалентно утверждению, что « Джейн — сестра Тома 9».0925”.)
В предыдущем пункте мы видели, что два уравнения, e ^x = y и x = ln ( y ), сказал то же самое. Если мы заменим x в первом уравнении на x второго уравнения мы получаем это тождество:
e ^{ln ( y )} = y
а если заменить y во втором уравнении на y первого уравнения мы получаем это тождество:
х = пер ( е ^х )
Эти тождества полезны для демонстрации того, как натуральный логарифм и e ^x функции компенсируют друг друга.
Если сравнить график от y = ln ( x ) к график из года = e ^x тогда вы видите, что одно можно получить из другого путем замены оси x и y . Это всегда происходит с обратными функциями.

Как использовать функцию натурального логарифма в программе Algebra Coach
Введите ln(x) в текстовое поле, где x — аргумент. Аргумент должен быть заключен в скобки.
Установите соответствующие параметры:
Установите параметр точная / с плавающей запятой. В режиме с плавающей запятой вычисляется натуральный логарифм любого числа . В точном режиме натуральный логарифм целого числа не оценивается, потому что это приведет к приблизительному числу.
Установить e делает / не представляет 2,718 … опцию. (Установите это значение на , чтобы представить так что, например, ln(e ³ ) упрощается до 3. )
Включите комплексные числа , если вы хотите иметь возможность оценивать натуральный логарифм отрицательного или комплексного числа.
Нажмите кнопку «Упростить».

Алгоритм для функции натурального логарифма
Нажмите здесь чтобы увидеть алгоритм, который компьютеры используют для вычисления функции натурального логарифма.

Показательная функция (с основанием
e , функция e ^x) Предыстория: Возможно, вам будет полезно прочитать предыдущий раздел. на функции натурального логарифма, прежде чем читать этот раздел. Там мы увидели, что можно использовать номер e . (что примерно равно 2,71828…) в качестве базы и поднять ее до любой мощности, x и получить любое положительное число и . Мы можем записать это соотношение в виде уравнения:
y = e ^x
Вот график y = e ^x (синяя кривая). Для сравнения мы также показываем графики y = 2 ^x и y = 4 ^x . Потому что число e находится между 2 и 4 кривая y = e ^x лежит между кривыми y = 2 ^x и y = 4 ^x .
Все три кривые называются экспоненциальными функциями, потому что независимая переменная x находится в показателе степени. Все три имеют свойство что чем выше вы поднимаетесь по кривой, тем круче они становятся. Однако y = e ^x обладает особым свойством, состоящим в том, что в каждый точки на кривой наклон равен высоте . Это свойство склонов делает его очень важной функцией в исчисление.
Примечание: В этом разделе, когда мы говорим «показательная функция», мы имеем в виду функцию с основанием e .

Определение: Мы определяем функцию, называемую экспоненциальной функцией (обозначается exp), которая принимает аргумент x . и возвращает значение e в степени x :

Вы можете думать о exp( x ) просто как об альтернативной (функциональной) нотации для выражение e ^x . Так что, конечно, функциональная форма exp( x ) имеет все свойства, которыми обладает экспоненциальная форма e ^x . У тренера по алгебре есть опция, позволяющая использовать ту или иную форму. Вот таблица, сравнивающая «внешний вид» различных свойств в двух формах:
Функциональная форма Экспоненциальная форма
информация об этом объекте
информация об этом объекте
информация об этом объекте
информация об этом объекте
информация об этом объекте
информация об этом объекте
информация об этом объекте
информация об этом объекте
График: Синяя кривая — это график y = e ^x (т. е. экспоненциальной функции). Он обладает тем свойством, что его наклон везде равен его высоте. Красные пунктирные линии показывают наклон кривой в различных точках вдоль Кривая. Обратите внимание, что наклон равен 5, когда высота равна 5, и так далее.
Если сравнить этот график экспоненциальной функции с график функции натурального логарифма тогда вы видите, что одно можно получить из другого путем замены оси x и y .
Домен и диапазон: Область определения экспоненциальной функции — все действительные числа, а диапазон все положительные действительные числа.
Экспоненциальная функция может быть распространяется на комплексные числа, в этом случае домен и диапазон — все комплексные числа.

Решение уравнения ln ( x ) = c для c с помощью экспоненциальной функции
Предположим, что x неизвестно, но ln ( x ) равно известное значение c . Тогда для нахождения x требуется решить это уравнение для х :
ln ( x ) = c .
Решение:
х = е ^с , или же x = ехр ( c ).
Это было объяснено в предыдущем разделе о функции натурального логарифма.

ln ( x ) и e ^x являются обратными функциями
Это было объяснено в предыдущем разделе о функции натурального логарифма.

Как использовать показательную функцию в программе Algebra Coach
Введите exp(x) в текстовое поле, где x — аргумент. Аргумент должен быть заключен в скобки.
Установите соответствующие параметры:
Установите параметр экспоненциальной функции следующим образом:
Установите параметр точная / с плавающей запятой. В режиме с плавающей запятой exp( r ) для оценивается любое число r . В точном режиме exp( i ) для любого целого числа i не оценивается, потому что это приведет к приблизительному числу.
No related posts.