6.9.3. Решение систем линейных уравнений методом сложения.
Главная » 6 класс. Математика. » 6.9.3. Решение систем линейных уравнений методом сложения.
Автор Татьяна Андрющенко На чтение 3 мин. Просмотров 22.7k. Опубликовано
Чтобы решить систему линейных уравнений с двумя переменными методом сложения, надо:
1) умножить левую и правую части одного или обоих уравнений на некоторое число так, чтобы коэффициенты при одной из переменных в уравнениях стали противоположными числами;
2) сложить почленно полученные уравнения и найти значение одной из переменных;
3) подставить найденное значение одной переменной в одно из данных уравнений и найти значение второй переменной.
Если в данной системе коэффициенты при одной переменной являются противоположными числами, то решение системы начнём сразу с пункта 2).
Примеры. Решить систему линейных уравнений с двумя переменными методом сложения.
Решить систему линейных уравнений с двумя переменными методом сложения.
Так как коэффициенты при у являются противоположными числами (-1 и 1), то решение начинаем с пункта 2). Складываем уравнения почленно и получим уравнение 8х = 24. Вторым уравнением системы можно записать любое уравнение исходной системы.
Найдём х и подставим его значение во 2-ое уравнение.
Решаем 2–ое уравнение: 9-у = 14, отсюда у = -5.
Сделаем проверку. Подставим значения х = 3 и у = -5 в первоначальную систему уравнений.
Примечание. Проверку можно сделать устно и не записывать, если наличие проверки не оговорено в условии.
Ответ: (3; -5).
Если мы умножим 1-ое уравнение на (-2), то коэффициенты при переменной х станут противоположными числами:
Сложим эти равенства почленно.
Мы получим равносильную систему уравнений, в которой 1-ое уравнение есть сумма двух уравнений прежней системы, а 2-м уравнением системы мы запишем 1-ое уравнение исходной системы (обычно записывают уравнение с меньшими коэффициентами):
Находим у из 1-го уравнения и полученное значение подставляем во 2-ое.
Решаем последнее уравнение системы и получаем х = -2.
Ответ: (-2; 1).
Сделаем коэффициенты при переменной у противоположными числами. Для этого все члены 1-го уравнения умножим на 5, а все члены 2-го уравнения на 2.
Подставим значение х=4 во 2-ое уравнение.
3 · 4 — 5у = 27. Упростим: 12 — 5у = 27, отсюда -5у = 15, а у = -3.
Ответ: (4; -3).
дана система уравнений 3х-у=14 и 5х+у=10 математика-6 системы математика-повторение решения систем линейных уравнений решить систему 6 класс решить систему методом сложения системы методом сложения
( 7 оценок, среднее 4.14 из 5 )
Примеры решения систем линейных уравнений способом сложения
Рассмотрим конкретные примеры решения систем линейных уравнений способом сложения.
Ищем наибольший общий делитель коэффициентов при каждой из переменных (коэффициенты берем со знаком «+»).
Наименьшее общее кратное коэффициентов при x — НОК(5;2)=10, при y — НОК(3;3)=3.
Проще работать с y, поскольку для получения перед y противоположных чисел достаточно умножить любое из уравнений на -1. Проще умножить на -1 второе уравнение системы (в этом случае после сложения уравнений коэффициент при x — положительное число).
Теперь подставим x=3 в любое из уравнений системы, например, во второе:
Решаем это уравнение:
6-3y=21
-3y=21-6
-3y=15
y= -5.
Ответ записываем в круглых скобках через точку с запятой в алфавитном порядке.
Ответ: (3; -5).
НОК(6; 4)=12, НОК(13; 5)=65. Проще работать с коэффициентами перед x.
Чтобы получить перед иксами противоположные числа, первую систему умножим на -2, вторую — на 3
и сложим почленно левые и правые части уравнений:
Подставляем y= -1 в первое уравнение системы и находим x:
Ответ: (-2; -1).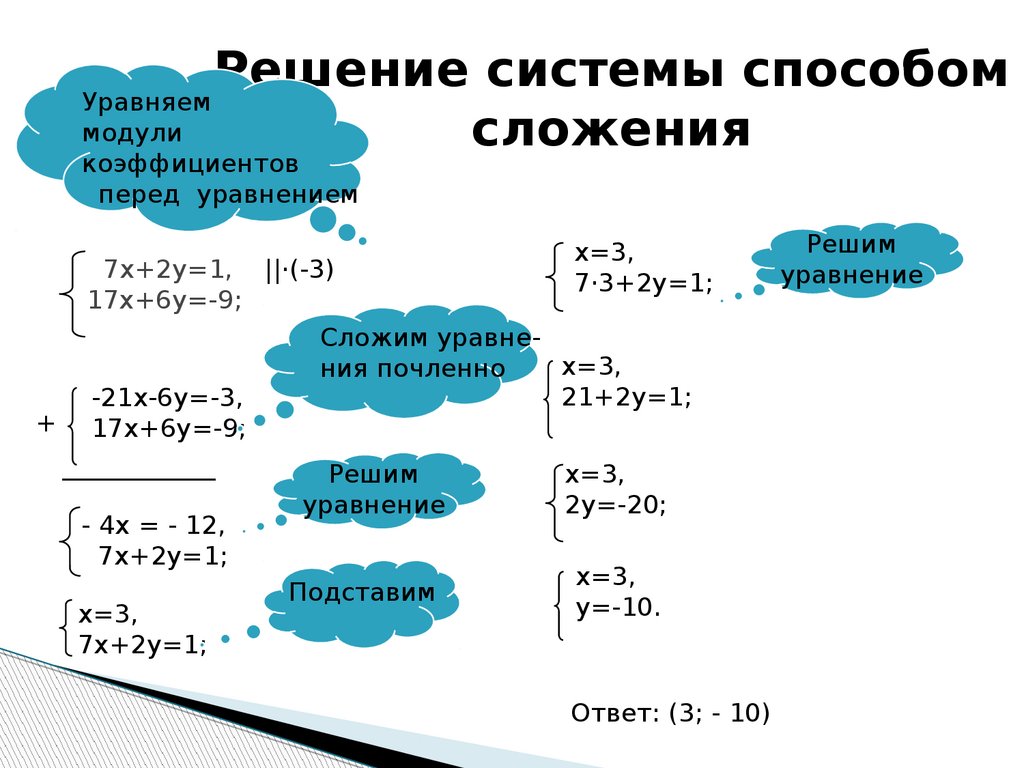
НОК(3; 5)=15, НОК(5; 7)=35. Проще получить противоположные числа перед x.
Для этого умножим первое уравнение системы на 5, второе — на -3:
и сложим почленное левые и правые части полученных уравнений:
Подставляем y=2 в первое уравнение системы и находим x:
Ответ: (-7; 2).
Прежде чем применить способ сложения, данную систему следует упростить. Умножим первое уравнение на наименьший общий знаменатель дробей, во втором раскроем скобки:
Получили систему линейных уравнений с двумя переменными. Для решения её способом сложения достаточно умножить второе уравнение на -1 и сложить почленно левые и правые части уравнений:
Подставляем найденное значение b в первое уравнение системы (линейных уравнений):
Ответ: (-3; 10).
Систему линейных уравнений с тремя переменными можно решить, сначала исключив одно из неизвестных, а затем — другое.
В данной системе проще всего исключить переменную z.
К первому уравнению прибавим третье, умноженное на -3:
Ко второму уравнению прибавим третье, умноженное на 2:
Получили систему линейных уравнений с двумя переменными:
НОК(8;10)=40, НОК(13; 7)=91. Проще работать с x:
Подставив полученные значение y во второе уравнение системы с двумя переменными, найдём x:
Подставив значения y и x в третье уравнение системы с тремя переменными, найдём z:
Ответ: (2; 0; -1).
Системы уравнений: Решение систем линейных уравнений сложением/вычитанием
Решение систем линейных уравнений с помощью сложения и вычитания
Одним из недостатков решения систем с использованием подстановки является то, что выделение переменной часто связано с нечеткими дробями. Существует еще один метод решения систем уравнений: метод сложения/вычитания.
В методе сложения/вычитания два уравнения в системе складываются или вычитаются для создания нового уравнения только с одной переменной. Чтобы в новом уравнении была только одна переменная, другая переменная должна сокращаться. Другими словами, мы должны сначала выполнять операции над каждым уравнением, пока один член не будет иметь равный и противоположный коэффициент, как соответствующий член в другом уравнении.
Мы можем получить равные и противоположные коэффициенты, просто умножая каждое уравнение на целое число. Соблюдайте:
Пример 1 : Сложите и вычтите, чтобы создать новое уравнение только с одной переменной:
| 2 x + 4 y 7 | 22 =|||
| х + 3 у | = | 13 |
Здесь мы можем умножить второе уравнение на -2:
| 2 х + 4 у | = | 4 | |
| -2 х — 6 у | = | -26 |
Добавление этих двух уравнений — 2 y = — 22.
Пример 2 : добавить и вычитать новое уравнение только с одной переменной:
| 4 x –2 г | = | 16 | |
| 7 х + 3 у | = | 15 |
Здесь мы можем умножить первое уравнение на 3, а второе уравнение на 2:
| 12 x — 6 Y | = | 48 | = | 48 | 7 | |
| 14 х + 6 у | = | 30 |
Мы можем складывать и вычитать уравнения с помощью свойства равенства сложения — поскольку две части одного уравнения эквивалентны, мы можем складывать одну часть в одну часть второго уравнения, а другую — в другую.
Вот шаги решения систем уравнений методом сложения/вычитания:
- Переставьте каждое уравнение так, чтобы переменные стояли с одной стороны (в том же порядке), а константа — с другой.
- Умножьте одно или оба уравнения на целое число так, чтобы один член имел равные и противоположные коэффициенты в двух уравнениях.
- Добавьте уравнения, чтобы получить одно уравнение с одной переменной.
- Найдите переменную.
- Подставьте переменную обратно в одно из уравнений и найдите другую переменную.
- Проверьте решение — оно должно удовлетворять обоим уравнениям.
Пример 1 : Решите следующую систему уравнений:
| 2 у — 3 x | = | 7 | |
| 5 x | = | 4 у — 12 |
- Переставьте каждое уравнение:
-3 x + 2 y = 7
5 х — 4 у = — 12 - Умножьте первое уравнение на 2:
-6 x + 4 y = 14
5 х — 4 у = — 12 - Сложите уравнения:
— x = 2 - Решите для переменной:
x = — 2 - Подставьте x = — 2 в одно из уравнений и найдите y :
-3(- 2) + 2 y = 7
6 + 2 у = 7
2 у = 1
y =
Таким образом, решением системы уравнений является (- 2,).
- Проверить:
2() — 3(- 2) = 7 ? Да.
5(- 2) = 4() — 12 ? Да.
Метод сложения — Джеймс Бреннан
Вся проблема с решением системы уравнений заключается в том, что вы не можете решить уравнение, в котором есть два неизвестных. Вам нужно уравнение только с одной переменной, чтобы вы могли изолировать переменную на одной стороне уравнения. Оба метода, которые мы рассмотрим, являются методами исключения одной из переменных, чтобы получить уравнение только с одним неизвестным, которое затем можно решить обычными методами.
Первым методом решения систем линейных уравнений является метод сложения, при котором два уравнения складываются вместе для исключения одной из переменных.
Сложение уравнений означает, что мы складываем вместе левые части двух уравнений и складываем вместе правые части. Это законно из-за принципа сложения, который гласит, что мы можем добавить одну и ту же сумму к обеим частям
уравнения. Поскольку левая и правая части любого уравнения равны друг другу, мы действительно прибавляем одну и ту же сумму к обеим частям уравнения.
Рассмотрим этот простой пример:
Пример:
Если мы добавим эти уравнения вместе, термины, содержащие y , будут добавлены до нуля (2 Y Plus –2 Y Y y y y y y y y y y y y y y y y y y y y y
или
5 x = 5
x = 1
Однако мы еще не закончены — мы знаем x , но мы все еще не надоняем ‘ не знаю г . Мы можем найти х , подставив теперь известное значение х в любое из наших исходных уравнений. Это даст уравнение, которое можно решить для y :
Теперь, когда мы знаем как x , так и y , мы можем сказать, что решением системы является пара (1, 1/ 2).
Этот последний пример было легко увидеть из-за удачного присутствия как положительного, так и отрицательного 2 y . Не всегда так везет. Рассмотрим
Не всегда так везет. Рассмотрим
Пример:
Теперь нет ничего столь очевидного, но мы все же можем кое-что сделать. Если мы умножим первое уравнение на -3, мы получим
(не забудьте умножить каждый член уравнения по обе стороны от знака равенства). Теперь, если мы сложим их вместе, члены, содержащие x , сократятся:
или
Как и в предыдущем примере, теперь, когда мы знаем y мы можем решить для x , подставив в любое исходное уравнение. Первое уравнение кажется самым простым для решения для x , поэтому мы будем использовать его:
Таким образом, точка решения равна (–4, 7/2).
Теперь рассмотрим еще менее очевидный пример:
Пример:
Здесь нет ничего особенно привлекательного в том, чтобы идти после x или 9.0011 и . В любом случае оба уравнения должны быть умножены на некоторый коэффициент, чтобы получить общий коэффициент.

