Высота произвольного треугольника: Как найти высоту в треугольнике abc: формулы, примеры задач

Как построить высоту треугольника | Треугольники

Рассмотрим, как построить высоту треугольника с помощью чертежного угольника.

Чтобы построить высоту остроугольного треугольника, надо приложить угольник так, чтобы одна сторона прямого угла проходила через вершину треугольника, а вторая — через противоположную этой вершине сторону.

AK⊥BC.

AK — высота треугольника ABC, проведённая из вершины A к противолежащей стороне BC.

 

BF⊥AC.

BF — высота треугольника ABC, опущенная из вершины B на сторону AC.

 

CH⊥AB.

CH — высота треугольника ABC, проведённая из вершины C к стороне AB.

 

Все высоты треугольника пересекаются в одной точке.

В остроугольном треугольнике точка пересечения высот лежит внутри треугольника.

Если требуется построить все высоты треугольника, достаточно построить две, а третью провести из вершины треугольника через точку пересечения двух высот.

 

В прямоугольном треугольнике две стороны (катеты) являются также его высотами. Остаётся построить третью высоту.

Угольник прикладываем прямым углом так, чтобы одна сторона проходила через гипотенузу, а другая — через прямой угол.

CD⊥AB.

CD — высота прямоугольного треугольника ABC, проведённая из вершины прямого угла C к гипотенузе AB.

Точка пересечения высот прямоугольного треугольника — вершина прямого угла.

Высоты AC, BC и CD прямоугольного треугольника ABC пересекаются в точке C, ∠C=90°.

 

 

В тупоугольном треугольнике проще всего построить высоту, выходящую из вершины тупого угла.

Прикладываем угольник прямым углом так, чтобы одна его сторона проходила через наибольшую сторону треугольника, а другая — через тупой угол.

AP⊥BC.

AP — высота тупоугольного треугольника ABC, проведённая из вершины тупого угла A к стороне BC.

Только высота, проведённая из вершины тупого угла, лежит внутри треугольника. Две другие высоты находятся вне него.

Высоты тупоугольного треугольника, выходящие из вершин острых углов, проведены не к противолежащим сторонам, а к прямым, содержащим эти стороны.

Чтобы построить высоту, продлеваем противолежащую сторону и прикладываем угольник прямым углом таким образом, чтобы одна сторона угольника проходила через построенную прямую, а другая — через вершину острого угла.

BM⊥AC,

BM — высота тупоугольного треугольника ABC, проведённая из вершины острого угла B к прямой, содержащей противолежащую сторону AC.

 

 

CN⊥AB,

CN — высота тупоугольного треугольника ABC, проведённая из вершины острого угла С к прямой, содержащей противолежащую сторону AB.

 

 

Точка пересечения высот тупоугольного треугольника лежит вне него, за тупым углом, напротив наибольшей стороны.

Чтобы построить точку пересечения высот треугольника ABC, продлим прямые BM, CN и AP до пересечения.

Мы рассмотрели, как строить высоты треугольника с помощью угольника.

Построение высот с помощью циркуля и линейки будем рассматривать в теме «Задачи на построение».

8 класс. Геометрия. Площадь.

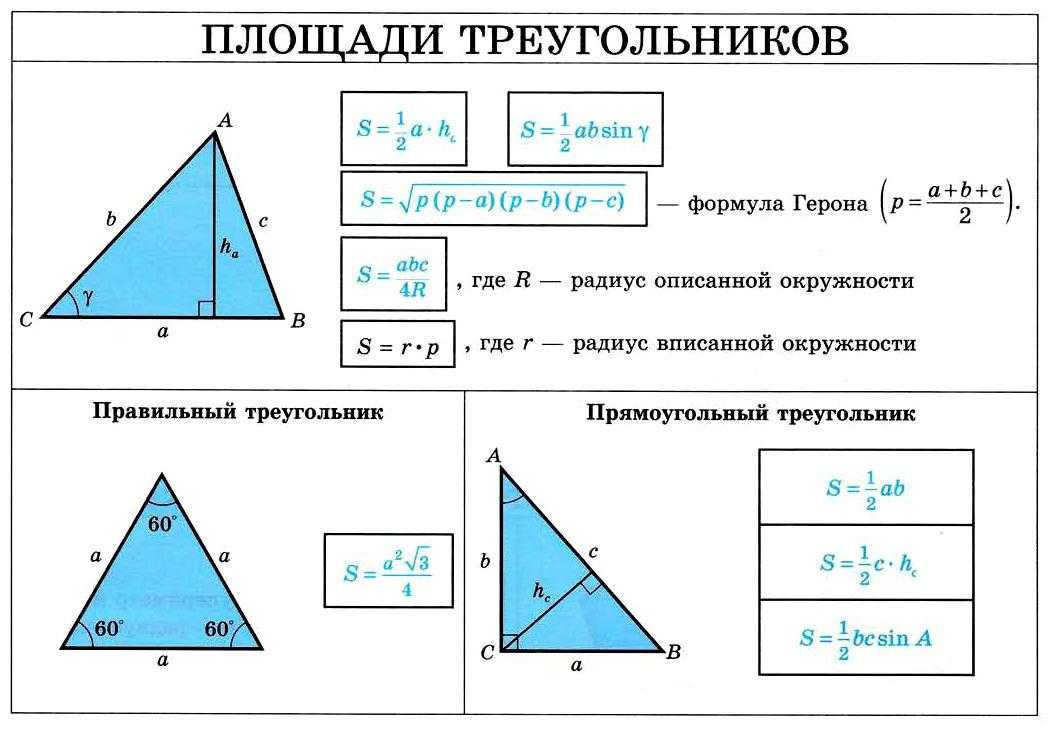Площадь треугольника и трапеции. — Формула Герона для нахождения площади треугольника.

Комментарии преподавателя

История формулы Герона

На данном уроке мы изучим формулу Герона, позволяющую вычислять площадь треугольника по его сторонам.

До этого мы умели вычислять площадь треугольника, зная его основание и высоту:  и катеты (для прямоугольного треугольника): . Формула Герона – это новая формула, которая связывает площадь треугольника и длины всех трёх его сторон.

Открыта эта формула была, по всей видимости, ещё Архимедом в  веке до н.э., но его доказательство не дошло до наших дней. А вот в «Метрике» Герона Александрийского ( век до н.э.) она есть.

Герона (см. Рис. 1) интересовали треугольники с целочисленными сторонами, площадь которых также является целым числом. Такие треугольники в его честь называют героновыми.

Простейший геронов треугольник – так называемый египетский треугольник (со сторонами 3, 4 и 5).

Рис. 1. Герон Александрийский (Источник)

Теорема

Площадь произвольного треугольника можно вычислить по формуле: , где  – полупериметр,  – длины сторон треугольника.

Доказательство

Рассмотрим призвольный треугольник  (пусть  – острые, напомним, что в треугольнике всегда есть хотя бы два острых угла). Обозначим в нём: . Проведём высоту , а также обозначим:  (см. Рис. 2.).

Рис. 2. Иллюстрация к теореме

Воспользуемся следствием из теоремы Пифагора для прямоугольных треугольников :  (1), :  (2).

Приравняв правые части в формулах (1) и (2), получаем:

, откуда: . Так как  (3), то получаем:  (4).

 Сложим формулы (3) и (4):

.

Теперь вернёмся к формуле (1) и подставим в неё полученное выражение для :

.

Теперь вспомним, что полупериметр выражается формулой: . Отсюда: . Тогда преобразуем полученную формулу:

.

Отсюда высота равна: .

Запишем известную нам формулу для площади треугольника: .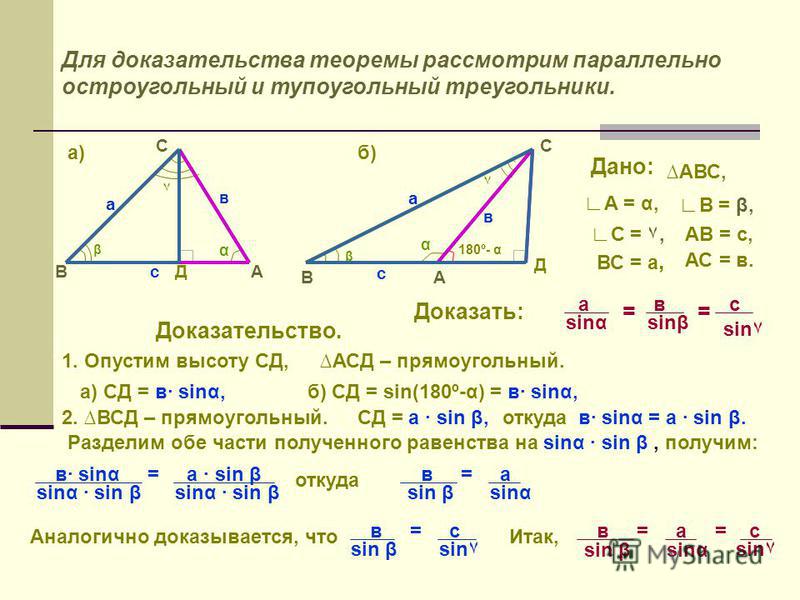

Доказано.

Задача 1

Стороны треугольника равны . Найти высоты этого треугольника.

Доказательство

Рассмотрим треугольник . Проведём в нём высоты . Напомним, что все высоты треугольника пересекаются в одной точке.

Рис. 3. Иллюстрация к задаче

Формула Герона и её доказательство

Вычислим площадь треугольника с помощью формулы Герона.

.

Тогда площадь треугольника:

.

Теперь запишем формулу для площади треугольника через высоту:

.

Аналогично находим остальные высоты: , .

Ответ:.

Задачи на применение формулы Герона

Задача 2

Дан , его основание , боковые стороны  и  соответственно . Точка , лежащая внутри треугольника, находится на расстоянии  от стороны  и  от стороны . Найти расстояние от точки  до стороны  (см. Рис. 4).

Решение

Рис. 4. Иллюстрация к задаче

Рассмотрим треугольник : в нём – высота. Обозначим: . Тогда: .

Найдём площадь треугольника .

Для начала найдём площадь треугольника  через формулу Герона:

.

Теперь вычислим площадь треугольника : .

Площадь треугольника: : .

Теперь, учитывая следующее соотношение: , получаем: .

Теперь найдём расстояние от точки  до стороны : .

Ответ: .

ИСТОЧНИК

http://x-uni.com/geometriya/8-klass/video/formula-gerona-dlya-nahozhdeniya-ploschadi-treugolnika

http://www.youtube.com/watch?v=zp82OIuz93g

http://v.5klass.net/zip/823d1fb40b3ed49403a117ef8517c666.zip

http://kak-kak2.ru/img/605c9fb504028311913e985a5ea8d1e1.jpg

http://hijos.ru/2012/10/03/formula-gerona/

http://www.calc.ru/Formula-Gerona.html

 

 

Высота (треугольник) | Математика Вики

в: Треугольники, Геометрия треугольника

Просмотреть источник

Три высоты, пересекающиеся в ортоцентре

Высота – это перпендикулярный отрезок, проведенный из вершины к ее противоположной стороне. В геометрии высота треугольника представляет собой прямую линию, проходящую через вершину и перпендикулярную (то есть образующую прямой угол с) линией, содержащей основание (противоположная сторона треугольника). Эта линия, содержащая противоположную сторону, называется продолженным основанием высоты. Пересечение между расширенным основанием и высотой называется футов высоты. Длина высоты, которую часто называют просто высотой, представляет собой расстояние между основанием и вершиной. Процесс рисования высоты от вершины до подножия известен как с отбрасыванием высоты этой вершины. Это частный случай ортогональной проекции.

Высоты можно использовать для вычисления площади треугольника: половина произведения длины высоты и длины его основания равна площади треугольника. Таким образом, наибольшая высота перпендикулярна наименьшей стороне треугольника. Высоты также связаны со сторонами треугольника через тригонометрические функции.

В равнобедренном треугольнике (треугольник с двумя конгруэнтными сторонами) высота, имеющая неконгруэнтную сторону в качестве основания, будет иметь середину этой стороны в качестве основания. Также высота, имеющая неконгруэнтную сторону в качестве основания, образует биссектрису угла вершины.

Высота обычно обозначается буквой h (как в высота ), часто подстрочной с названием стороны, с которой исходит высота.

В прямоугольном треугольнике высота с гипотенузой c в качестве основания делит гипотенузу на две длины

p и q . Если мы обозначим длину высоты через h _c , мы получим соотношение

  (теорема о среднем геометрическом)

Содержание

• 1 Ортоцентр
• 2 Ортогональный треугольник
• 3 Некоторые дополнительные теоремы о высоте
  • 3.1 Высота по сторонам
  • 3.2 Теоремы Inradius
  • 3.3 Теорема о радиусе окружности
  • 3.4 Теорема площади
  • 3.5 Специальные треугольники
    • 3.5.1 Равносторонний треугольник
    • 3.5.2 Прямоугольный треугольник

Ортоцентр

Три высоты пересекаются в одной точке, называемой ортоцентром треугольника. Ортоцентр лежит внутри треугольника тогда и только тогда, когда треугольник остроугольный (т. Е. Не имеет угла, большего или равного прямому углу). См. также ортоцентрическую систему. Если один угол прямой, то ортоцентр совпадает с вершиной прямого угла. Таким образом, для остроугольных и прямоугольных треугольников все основания высот попадают на внутреннюю часть или ребро треугольника.

Ортоцентр, центр тяжести, центр описанной окружности и центр девятиконечной окружности лежат на одной линии, известной как линия Эйлера. Центр окружности с девятью точками находится в средней точке между ортоцентром и центром описанной окружности, а расстояние между центром тяжести и центром описанной окружности составляет половину расстояния между центром тяжести и ортоцентром.

Изогональное сопряжение, а также дополнение к ортоцентру является центром описанной окружности.

Четыре точки на плоскости, одна из которых является ортоцентром треугольника, образованного тремя другими, называются ортоцентрической системой или ортоцентрическим четырехугольником.

Пусть A , B , C обозначают углы опорного треугольника, и пусть a = | до н.э. |, б = | СА |, с = | АВ | быть боковыми сторонами. Ортоцентр имеет трилинейные координаты sec A : sec B : sec C и барицентрические координаты

Обозначим вершины треугольника как A , B и C и ортоцентр как H , и пусть D , E и F обозначают основания высот от A , B и C 90 соответственно. Затем:

• Сумма отношений по трем высотам расстояния ортоцентра от основания к длине высоты равна 1:

• Сумма отношений по трем высотам расстояния ортоцентра от вершины до длины высоты 2:

• Произведение длин отрезков, на которые ортоцентр делит высоту, одинаково для всех трех высот: чтобы пересечь описанную окружность в точке P , так что AP является хордой описанной окружности, тогда основание D делит пополам отрезок HP :

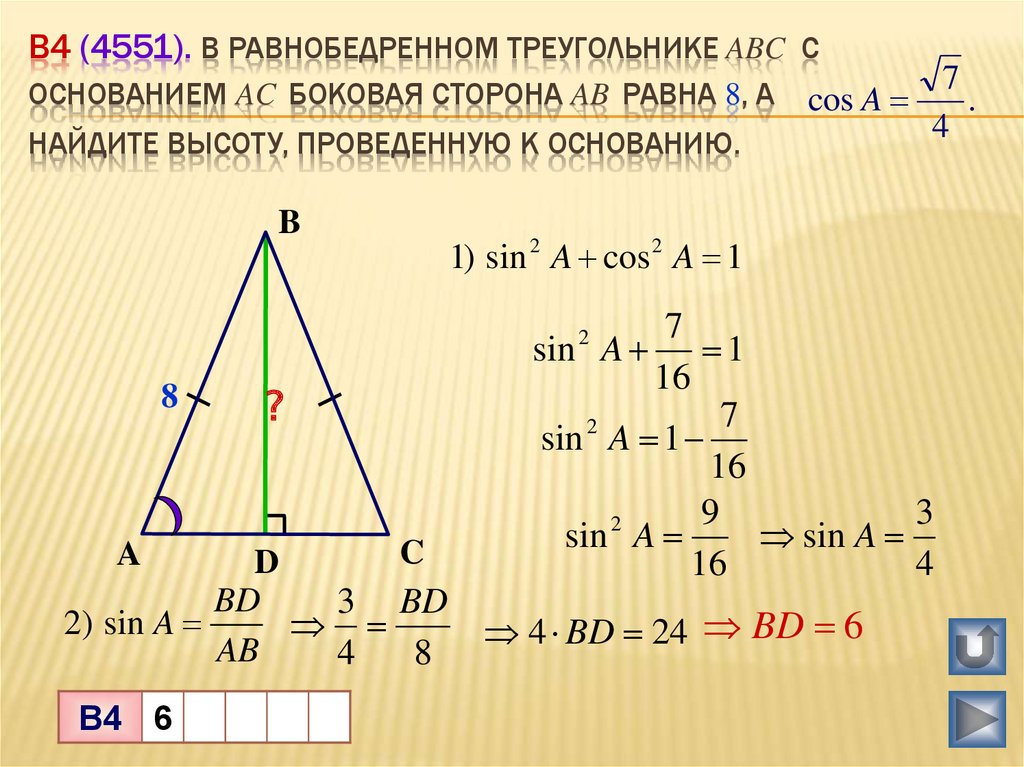Обозначаем ортоцентр треугольника0011 ABC как H , длины сторон обозначаются как a , b и c , а радиус описанной окружности треугольника обозначается как R . затем

In addition, denoting r as the radius of the triangle’s incircle, r _a , r _b , and r _c as the радиусов, если его вписанные окружности, и R снова как радиус описанной окружности, следующие соотношения имеют место относительно расстояний ортоцентра от вершин:

Ортотреугольник

Треугольник abc является ортотреугольником треугольника ABC

Если треугольник ABC косой (не прямоугольный), точки пересечения сторон с высотами треугольника образуют другой треугольник, A’B’C’, называемый орто-треугольником или высотным треугольником . Это педальный треугольник ортоцентра исходного треугольника. Кроме того, центр вписанной окружности (то есть центр вписанной окружности) ортогонального треугольника является ортоцентром исходного треугольника.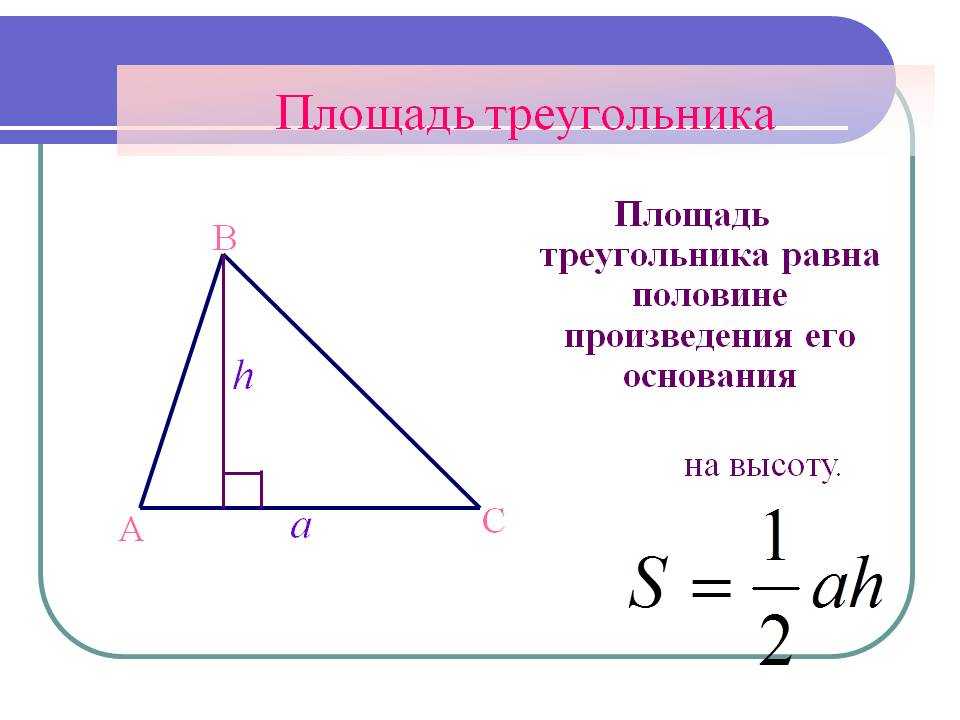

Ортотреугольник тесно связан с касательным треугольником , построенным следующим образом: пусть L _A будет линией, касательной к описанной окружности треугольника ABC в вершине A 1, 9001 определяем _B и L _C

аналогично. Пусть А» = L _B ∩ L _C , B» = L _C  ∩  L _A , C» = L _C  ∩  L _A . Тангенциальный треугольник A»B»C» гомотетичен ортотреугольнику.

Ортогональный треугольник обеспечивает решение задачи Фаньяно, поставленной в 1775 г., о нахождении треугольника с минимальным периметром, вписанного в данный остроугольный треугольник.

Ортотреугольник остроугольного треугольника дает треугольный световой маршрут.

Трилинейные координаты вершин прямоугольного треугольника задаются формулой

• A’ = 0 : сек B : сек C
• B’ = сек A : 0 : сек C
• C’ = sec A : sec B : 0

Трилинейные координаты вершин касательного треугольника задаются формулой

• А» = — а
  : б : с
• B» = a : − b : c
• С» = A : B : — C

.

a+b+c ) / 2, высота со стороны a определяется выражением

Это следует из сочетания формулы Герона для площади треугольника по сторонам с формулой площади (1/2)×основание×высота, где основание принимается за сторону — , а высота — это высота от до .

Теоремы Inradius

Рассмотрим произвольный треугольник со сторонами a, b, c и с соответствующими высоты h _a , h _b , и h _c . Высоты и радиус вписанной окружности r связаны соотношением

Теорема о радиусе окружности

Обозначение высоты с одной стороны треугольника как h _a , две другие стороны как b и c , а радиус описанной окружности треугольника (радиус описанной окружности треугольника) как R , высота определяется по формуле:

Теорема о площади

90 высоты любого треугольника со сторон a , b и c соответственно как , , и , и обозначая полусумму обратных величин высот, как мы имеем

Специальные треугольники

Равносторонний треугольник

Для любой точки P внутри равностороннего треугольника сумма перпендикуляров к трем сторонам равна высоте треугольника. Это теорема Вивиани.

Right triangle

In a right triangle the three altitudes h _a , h _b , and h _c (the first two of which equal the leg lengths б и и соответственно) связаны согласно

Контент сообщества доступен по лицензии CC-BY-SA, если не указано иное.

Произвольный треугольник онлайн-расчет, Онлайн-вычисления, онлайн-калькулятор, калькулятор онлайн-расчет

Категория: Геометрический

Помогите изменить

Край а:

Край б:

Край с:

Градус A：

Градус радианмил знаксекунда минута гон

Градус B：

Градус радианмил знаксекунда минута гон

Градус C：

Градус радианмил знаксекунда минута гон

Площадь:

Периметр:

Радиус окружности：

Радиус касательной окружности：

a Высота края:

b Высота края:

c Высота ребра:

a Биссектриса угла:

b Биссектриса угла:

c Биссектриса угла:

a Боковая срединная линия:

b Боковая срединная линия:

c Боковая срединная линия：

---

Когда известны три координаты треугольника, введите три координаты:

Описание приложения

График замкнутого графа (включая его внутреннюю область) состоящая из трех точек, не лежащих на одной прямой на плоскости и отрезки, которые соединяются через каждые две точки называется треугольником. Составной треугольник

каждый отрезок называется ребром треугольника. Общее концы на соседних сторонах называются вершины треугольника. Угол между двумя соседними стороны называется внутренним углом треугольника, упоминается как три

угловой угол. Угол между продолжением одной стороны треугольник и его сосед называется внешним угол треугольника. Треугольник с вершинами А, В и С записывается как: △ABC.

Фигура, заключенная тремя прямыми линиями на плоскости или тремя дугами на сферическая поверхность. Фигура прилагается тремя прямыми называется плоским треугольником; фигура в окружении тремя дугами называется

Сферический треугольник, также называемый треугольником. △Азбука..

Пример использования

Край A: 5

Край B: 5

Край C:

градуса A ： 90

градус B ： 45

градус C ：

Нажмите «Рассчитайте

Площадь：6.25；Периметр：12.0711；

Радиус окружности：2.5; Окружной радиус：1.0355a;

a Высота края: 2,5; b Высота края: 3,5355;

c Высота края: 3,5355; Биссектриса угла: 2,5;

b Биссектриса угла: 4,6194; c Биссектриса угла: 4,6194;

a Боковая срединная линия：3,5355; b Боковая срединная линия: 5,5902; b Боковая срединная линия: 5,5902;

Когда известны трехточечные координаты треугольника, введите трехточечные координаты:

X Y

A: 5 8

B: 4 3

C: 2 6

Примечание

В известных условиях введите три условия, нажмите рассчитать вычислить результат, и координаты будут рассчитаны, но известные условия не могут быть всеми угловыми условиями.