Высота треугольника геометрия: Что такое высота треугольника? Ответ на webmath.ru

Медиана, биссектриса и высота треугольника.

Дата: 20.11.2020

предмет: геометрия класс: 7 а,б,в

Тема: Медиана, биссектриса и высота треугольника.

Цели урока:

Общеобразовательные: ввести понятие перпендикуляра к прямой, медианы, биссектрисы и высоты треугольника; сформировать умение строить медианы, биссектрисы и высоты треугольника.

Развивающие: формирование мировоззрения учащихся, развитие мышления, пространственного воображения, навыков саморегуляции, развитие устойчивого познавательного интереса к изучению геометрии.

Воспитательные: воспитание активности, ответственности, культуры общения; воспитание эстетической культуры, воспитание графической культуры школьников.

Тип урока: урок изучения нового материала.

Формы организации учебной деятельности: коллективная, индивидуальная, групповая

Ход урока:

1. Организационный момент. Здравствуйте ребята! Приготовились. Садитесь.

2. Эмоционально-психологический настрой.

4. Сообщение темы урока. Целеполагание. Постановка проблемных вопросов.

-Ребята, пожалуйста, посмотрите на рисунок и скажите, что изображено на нем?

-Предположите, какая у нас сегодня будет тема урока?

— Молодцы, ребята! Сегодня мы будем изучать треугольник. Тема сегодняшнего урока: «Медиана, биссектриса и высота треугольника».

-Зная тему урока, определите ее цель.

-Молодцы, правильно, цель урока: «Узнать какие понятия называются: высотой, медианой и биссектрисой треугольника, выполнять их построение».

-Ребята, а что называется высотой треугольника? Периметр???

-Что называется медианой треугольника?

-Что называется биссектрисой треугоника?

Учащиеся выдвигают свои гипотезы.

— А правильно вы ответили или нет, вы узнаете, изучив новый материал урока. Но для начала давайте вспомним все, что мы знаем о треугольнике.

5. Актуализация знаний.

а) «Мозговой штурм»

-А что называется треугольником? (Треугольником называется геометрическая фигура, состоящая из трёх точек, не лежащих на одной прямой и соединённых попарно отрезками).

-Назовите элементы треугольника. (Три стороны и три угла).

-Назовите виды треугольника (по сторонам) (разносторонний, равнобедренный, равносторонний).

-Назовите виды треугольника (по углам) (прямоугольный, тупоугольный, остроугоный).

6. Изучение нового материала.

1. Самостоятельное изучение материала, каждая группа получает задание:

1 группа «Медиана треугольника»,

2 группа: «Высота треугольника»,

3 группа: «Биссектриса треугольника».

Работу осуществить по следующему алгоритму:

1. Изучить материал задания с помощью учебника

2. Обсуждение.

3. Создать чертеж по данной теме.

4. Выбрать спикера, для презентации продукта.

7. Физкультминутка.

8. Закрепление.

1 . Медиана. Слайд 6

Начертите треугольник АВС и найдите середину стороны ВС – точку К.

-Что называется серединой отрезка?

Соедините точку К с вершиной А.

— Как называется отрезок АК?

— Что называется медианой треугольника?

-Сколько вершин у треугольника? (3).

-Сколько у него сторон? (3).

-Сколько медиан можно провести в треугольнике?(3).

“Проведите” три медианы в треугольнике.

Какое свойство медиан вы заметили? (В любом треугольнике все медианы пересекаются в одной точке).

Эта точка называется центром тяжести треугольника. Запишите в тетрадях:

АК – медиана, ВК = КС

ВТ– медиана, АТ = ТС

СР– медиана, АР = РВ

О – точка пересечения медиан

2. Высота. Слайд 7

Начертите треугольник АВС

С помощью чертёжного угольника из вершины В проведём перпендикуляр ВН к прямой АС.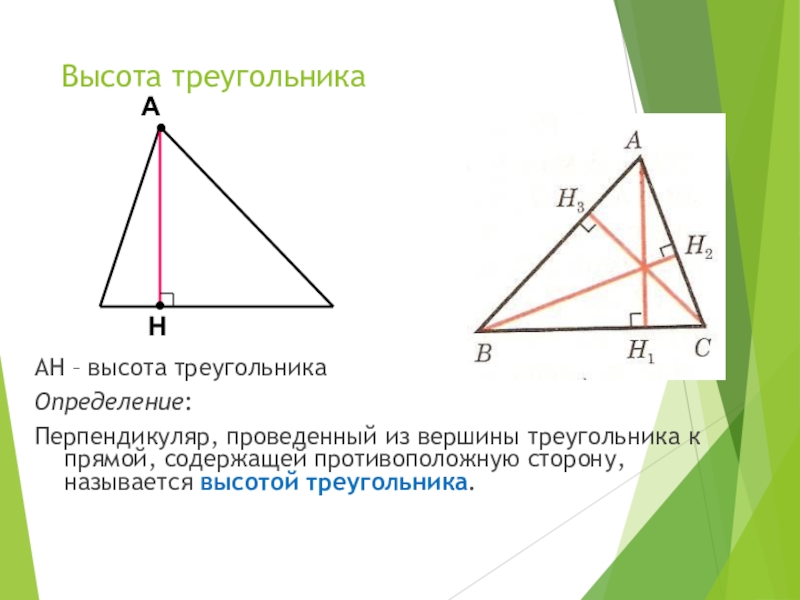

-Как называется данный перпедикуляр?

Запись на доске: ВН  АС, Н  АС.

-Сколько высот имеет треугольник? (3).

-“Постройте” все три высоты в треугольнике.

-Обладают ли высоты аналогичным свойством, что и медианы? (Да).

-А если треугольник тупоугольный, то как построить высоты? (Провести дополнительные полупрямые)

-Как вы думаете, что является высотой в прямоугольном треугольнике? (катеты)

3. Биссектриса. Слайд 8

-Постройте еще один треугольник АВС

-Теперь постройте биссектрису ВК угла В с помощью транспортира. Она пересечёт отрезок АС в точке К.

— Как называется отрезок ВК?

Запись на доске:

AF- биссектриса, ‹ CАF = ‹ FАB

BK — биссектриса, ‹ CBK = ‹ АBK

CS — биссектриса, ‹ АCS = ‹ BCS

О — точка пересечения биссектрис.

Постройте все три биссектрисы в вашем треугольнике.

9. Как запомнить новые понятия.

Запомнить новые математические понятия можно с помощью шутливых стихотворений:

С лайд 9

Высота похожа на кота,
Который, выгнув спину,
И под прямым углом
Соединит вершину
И сторону хвостом.

С лайд 10

Медиана-обезьяна,
У которой зоркий глаз,
Прыгнет точно в середину
Стороны против вершины,
Где находится сейчас.

Слайд 11

Биссектриса – это крыса,
Которая бегает по углам
И делит угол пополам.

10. Контроль знаний.

1) Работаем самостоятельно. Затем каждый проверяет , работу соседа

Задание на определение изученных понятий на чертеже треугольника – геометрия в чертежах. Ответы на доске

2) №139 – 1 человек возле доски

3) Математический диктант.

Заполните пропуски в формулировках элементов треугольника и свойств геометрических фигур.

а) Отрезок, соединяющий вершину треугольника с серединой ______________, называется ___________ треугольника.

(Отрезок, соединяющий вершину треугольника с серединой противоположной стороны, называется медианой треугольника).

б) Из точки, не лежащей на прямой, можно провести перпендикуляр к этой прямой, и притом _____________.

(Из точки, не лежащей на прямой, можно провести перпендикуляр к этой прямой, и притом единственный).

Верны ли следующие утверждения?

в) В любом треугольнике можно провести три медианы. (Да).
г) Точка пересечения высот любого треугольника лежит внутри треугольника. (Не всегда).
д) Все биссектрисы треугольника пересекаются в одной точке. (Да).

+ взаимооценивание.

С какими новыми геометрическими понятиями вы сегодня познакомились? (Медиана, биссектриса, высота).

11. Подведение итогов урока. Оценивание.

12. Домашнее задание.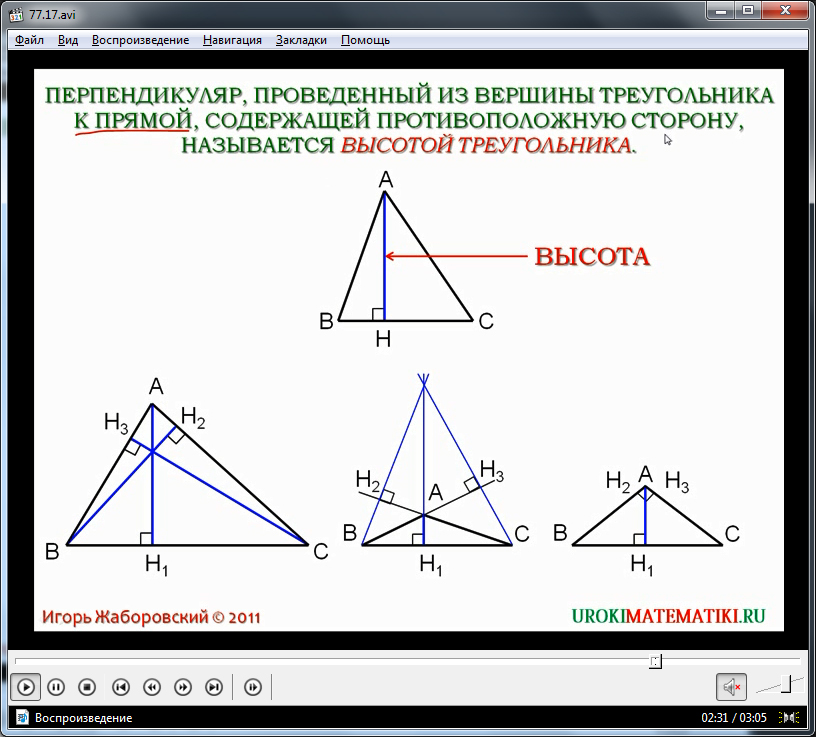 138, дополнительно146

13. Рефлексия, обратная связь

Стратегия «Незаконченные предложения»

— Сегодня на уроке я узнал……..

— Сегодня я на уроке был………..

— Мне больше всего запомнилось……..

— Мне больше всего понравилось…….

— Самым трудным сегодня было…………

— У меня лучше всего получилось……….

— Когда приду домой, то скажу своим родителям, что сегодня на уроке я….

Поставьте себе оценку на полях.

— Спасибо, ребята! На этом урок окончен, можете идти!

Высота (треугольник)

В геометрии высота треугольника — это отрезок прямой, проходящий через вершину и перпендикулярный ( то есть образующий прямой угол с) линией, содержащей основание ( сторону, противоположную вершине). Эта линия, содержащая противоположную сторону, называется продолженным основанием высоты. Пересечение расширенного основания и высоты называется подножием .высоты. Длина высоты, часто называемая просто «высотой», представляет собой расстояние между расширенным основанием и вершиной. Процесс рисования высоты от вершины к подножию известен как опускание высоты в этой вершине. Это частный случай ортогональной проекции .

Высоты можно использовать при вычислении площади треугольника : половина произведения длины высоты и длины его основания равна площади треугольника. Таким образом, наибольшая высота перпендикулярна наименьшей стороне треугольника. Высоты также связаны со сторонами треугольника через тригонометрические функции .

В равнобедренном треугольнике (треугольник с двумя конгруэнтными сторонами) высота, имеющая неконгруэнтную сторону в качестве основания, будет иметь середину этой стороны в качестве основания. Также высота, имеющая неконгруэнтную сторону в качестве основания, будет биссектрисой угла при вершине.

Обычно высота обозначается буквой h (как высота ), часто подстрочной с названием стороны, к которой обращена высота.

В прямоугольном треугольнике высота, проведенная к гипотенузе c , делит гипотенузу на два отрезка длины p и q . Если мы обозначим длину высоты через h _c , то мы имеем соотношение

Для остроугольных треугольников все основания высот падают на стороны треугольника (не вытянутые). В тупоугольном треугольнике (с тупым углом ) основание высоты к тупоугольной вершине попадает внутрь противоположной стороны, а основания высот к остроугольным вершинам падают на противоположную расширенную сторону . , вне треугольника. Это показано на соседней диаграмме: в этом тупоугольном треугольнике высота, опущенная перпендикулярно из верхней вершины, имеющей острый угол, пересекает расширенную горизонтальную сторону вне треугольника.

---

Три высоты треугольника пересекаются в ортоцентре, который для остроугольного треугольника находится внутри треугольника.

Высота прямоугольного треугольника от его прямого угла до гипотенузы — это среднее геометрическое длин отрезков, на которые делится гипотенуза. {2}\;\поэтому h\!=\!{\sqrt {pq}} \\\конец{выровнено}}}

В прямоугольном треугольнике высота каждого острого угла совпадает с катетом и пересекает противоположную сторону в (имеет основание) в прямоугольной вершине, которая является ортоцентром.

Высоты каждого из острых углов тупоугольного треугольника полностью лежат вне треугольника, как и ортоцентр H .

Три высоты, пересекающиеся в ортоцентре

Треугольник △ abc (соответственно △ DEF в тексте) является ортотреугольником треугольника △ ABC.

Сравнение обратной теоремы Пифагора с теоремой Пифагора

Высота треугольника – определение, формула, примеры

Определение

Высота или высота треугольника – это перпендикулярная линия, проведенная из вершины треугольника к его противоположной стороне. Он образует прямой угол с основанием треугольника.

Высота треугольника

Каждый треугольник имеет три возможные высоты. Разные треугольники имеют разные типы высот. Они могут находиться либо внутри треугольника (как в остроугольных треугольниках), либо снаружи (как в тупоугольных треугольниках), либо могут быть одной из трех сторон (как в прямоугольных треугольниках).

Свойства

Свойства высоты треугольника

1. Имеет 3 высоты, по одной из каждой вершины; в △ABC, AE, BQ и CP — три высоты
2. 3 высоты встречаются в общей точке, называемой ортоцентром треугольника; в △ABC точка ‘O’ является ортоцентром
3. Каждая высота является кратчайшим расстоянием от вершины до ее противоположной стороны; например, AE — кратчайшее расстояние от ∠A до стороны BC

Формулы

Как найти высоту треугольника

Высоту треугольника можно рассчитать по приведенной ниже формуле:

Высота треугольника Формула

Вывод

Формула для расчета высоты треугольника может быть получена из стандартной формулы площади треугольника как показано ниже:

Как мы знаем,

Площадь (A) = ½ (b x h), здесь b = основание, h = высота

=> 2A = b x h

=> h = 2A/b

Следовательно, математически , высота треугольника также может быть определена как удвоенная площадь, деленная на основание треугольника.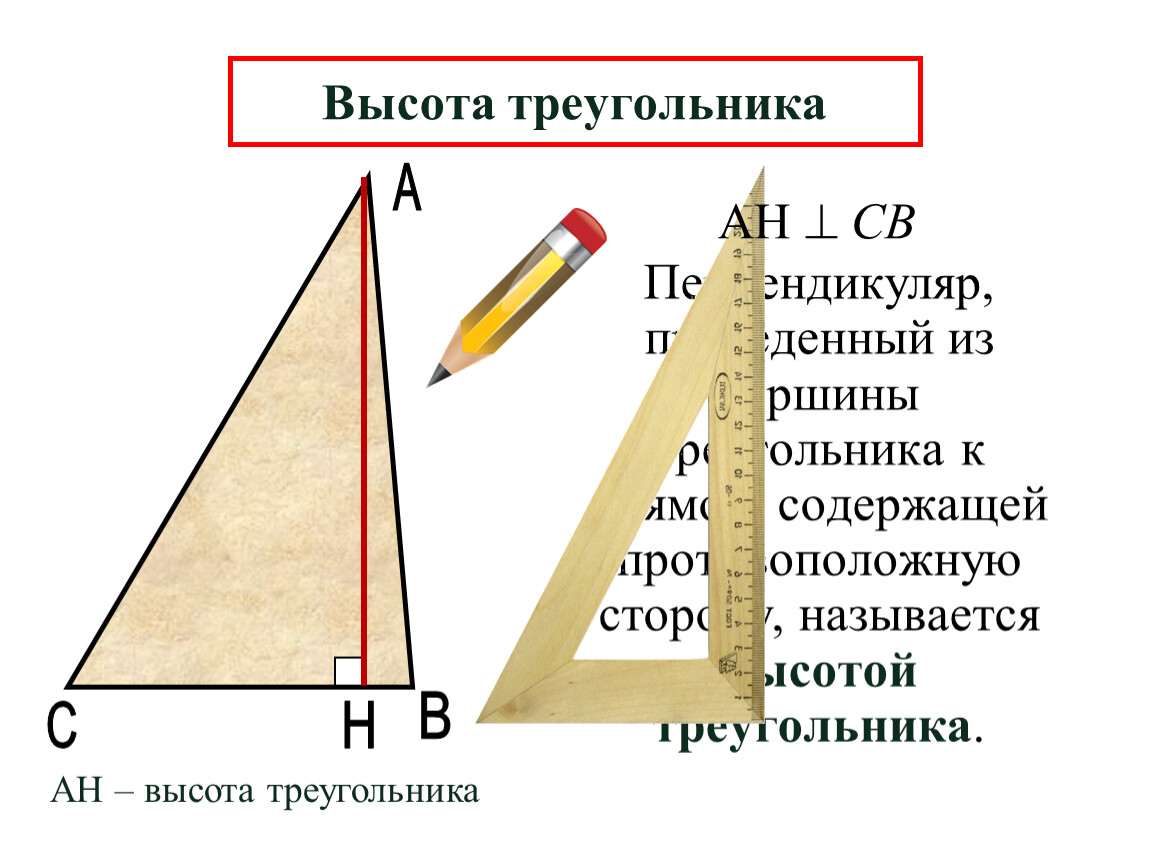

Хотя мы можем использовать приведенную выше формулу для определения высоты для всех типов треугольников, некоторые определенные треугольники, такие как равносторонний треугольник, равнобедренный треугольник и прямоугольный треугольник, имеют специальные формулы для определения их высоты.

Высота равностороннего треугольника

Высота равностороннего треугольника может быть определена с помощью приведенной ниже формулы:

Высота равностороннего треугольника Формула

Вывод

Чтобы вывести формулу высоты равностороннего треугольника, используются два разных метода. может быть использован. Они приведены ниже:

Использование тригонометрической функции

В данном △ABC AB = BC = AC, а AE — это высота, которая делит основание BC поровну на BE и EC.

в △ ABC,

SIN60 ° = перпендикуляр/гипотенуза

√3/2 = h/a [∵ sin60 = √3/2]

H = √3/2a

Использование Формы Херона 64 .

Мы также можем найти высоту равностороннего треугольника, используя формулу Герона для нахождения площади треугольника:

Площадь (A) = √s(s–a)(s–b)(s–c), здесь полупериметр(s) = ½(a+b+c)

В равностороннем треугольнике все три стороны равны, таким образом, s = 3a/2

Подставляя значение s в стандартную формулу h = 2A/b, получаем

h = 2√s(s–a)(s–b)(s –c)/b …..(1)

Поскольку в равностороннем треугольнике a = b

Уравнение ⁿ (1) можно записать как

h = 2√s(s–a)(s– b)(s–c)/a …..(2)

Подставляя значение s в (2), получаем

h = 2/a√3a/2(3a/2 – a) (3a/2 – a) (3a/2 – a)

h = 2/a√3a/2x a/2xa/2xa/2

h = 2/axa ² √3/4

h = a√3/2

Высота разностороннего треугольника

Высота разностороннего треугольника может быть определена по формуле, приведенной ниже:

Высота Формула разностороннего треугольника

Вывод

Чтобы вывести формулу высоты разностороннего треугольника, мы используем формулу Герона для нахождения площади треугольника:

Площадь (A) = √s(s–a)(s–b)(s–c) ……(1), здесь полупериметр(ы) = ½ (a+b+c)

Теперь общие формула площади треугольника имеет вид:

Площадь (A) = ½ (b x h) …… (2), здесь b = основание, h = высота

Приравнивая (1) и (2) получаем,

½ (b x h) = √s(s–a)(s–b)(s–c)

h = 2√s(s–a)(s–b)(s–c)/b

Высота Равнобедренный треугольник

Высоту равнобедренного треугольника можно определить по формуле, приведенной ниже:

Высота равнобедренного треугольника Формула

Происхождение

Высота равнобедренного треугольника делит его основание пополам. Это свойство используется для управления формулой вычисления высоты равнобедренного треугольника.

Используйте наше изображение равнобедренного треугольника и см. приложение

По теореме Пифагора в △AEB, мы получаем

AE ² = AB ² – BE ² …..(1)

стороны BC, делящей BC поровну на BE и EC

Таким образом,

БЭ = ½ X БК (б)…… (2)

Подставляя значение БЭ в уравнение (1) получаем,

АЭ ² = АБ ² – БЭ ²

7 ч 2 9

= a ² – (1/2 x b) ²

h = √a ² – 1/4b ²

Высота прямоугольного треугольника

3 9000 Высота прямоугольного треугольника используя приведенную ниже формулу:

Высота прямоугольного треугольника Формула

Вывод

Высота прямоугольного треугольника делит существующий треугольник на два подобных треугольника. Чтобы вывести формулу высоты прямоугольного треугольника, мы используем «теорему о высоте прямоугольного треугольника», которая гласит: «мера высоты, проведенная от вершины к ее гипотенузе, есть среднее геометрическое измерения двух сегментов, образованных, когда высота делит гипотенузу».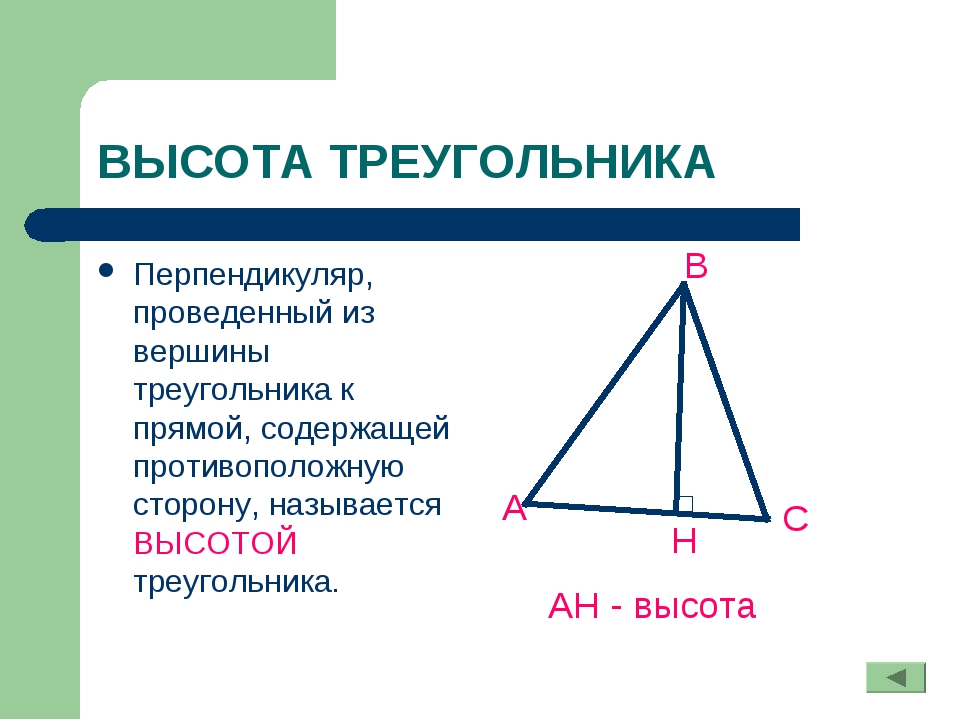

Если два треугольника подобны, то

i) Соответствующие углы равны

ii) Соответствующие стороны равны

Как найти высоту прямоугольного треугольника

На данном рисунке высота AE проведена из вершины A к гипотенузе BC, образуя два подобных треугольника △BEA и △CEA

∠ BEA = ∠CEA = 90°

Поскольку △ABC прямой угол в точке A

∠A = α + β = 90° …… (1)

In △BEA,

∠ABE + ∠EAB + ∠ABE = 180° (свойство суммы углов)

∠ABE = 180° – (90° + β) = 90° – β = α (из уравнения ⁿ 1)

Аналогично,

In △CEA,

∠CEA + ∠EAC + ∠ACE = 180° (Свойство суммы углов)

∠ACE = 180° – (90° + α) = 90° – α = β ( Из уравнения ^N 1)

по теореме сходства,

△ Bea ≅ △ CEA

AE/CE = BE/AE

H/Y = X/H

H ² = XY

H = √xy

Высота тупоугольного треугольника

В тупоугольном треугольнике высота лежит вне треугольника. Основание удлинено, а высота проведена от противоположной вершины к его основанию.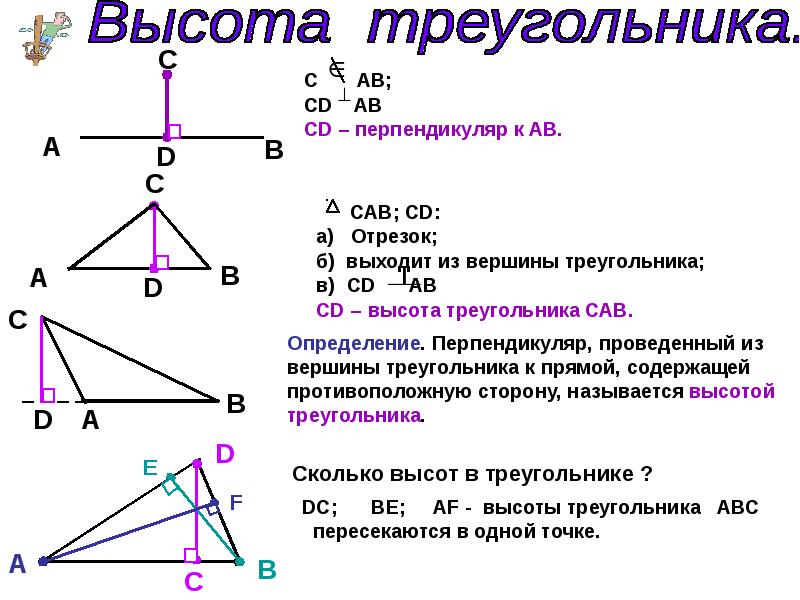 Высоту тупоугольного треугольника можно определить по формуле, приведенной ниже:

Формула высоты тупоугольного треугольника

Решенные примеры

Чтобы найти высоту треугольника, нам сначала нужно определить тип треугольника. После идентификации типа мы используем конкретные формулы, приведенные выше для каждого типа, чтобы найти значение высоты.

Давайте решим несколько примеров, чтобы лучше понять концепции.

Найдите высоту равностороннего треугольника со стороной 6 см.

Решение:

Как известно,
h = √3/2a, здесь a = 6 см
= √3/2 x 6
= 3√3 [∵√3 ~ 1,732]
= 5,196 Высота разностороннего треугольника со сторонами 5 см, 6 см и 7 см.

Решение:

Как известно,
h = 2√s(s–a)(s–b)(s–c)/b, здесь a = 5 см, b = 6 см, c = 7 см
В данном треугольнике
s = (5+6+7)/2 = 9 см
Таким образом,
h = 2√9(9-5)(9-6)(9-7)/6
= 2√216/6
= 2√36
=2√6 х 6
= 12 см

Найдите высоту равнобедренного треугольника со сторонами 6 см, 4 см и 6 см.

Решение:

Как известно,
h = √a ² – 1/4b ² , здесь a = 6 см, b = 4 см
= √6 ^{8 – 900 2
= 3 см}

Найдите высоту прямоугольного треугольника, который делит его основание 12 см на 8 см и 4 см.

Решение:

Как известно,
h = √xy, здесь x = 8 см, y = 4 см
= √8 x 4
= 5,65 см

стороны 4 м, 5 м и 6 м.

Решение:

Как известно,
h = 2√s(s–a)(s–b)(s–c)/b, здесь a = 4 см, b = 5 см, c = 6 см
В данном треугольнике
s = (4+5+6)/2 = 7,5 см
Таким образом,
h = 2√7,5(7,5-4)(7,5-5)(7,5-6)/5
= 2√(7,5 х 3,5 х 2,5 х 1,5)/5
= 2√19,68
= 8,87 см

Высота и медиана треугольника

Высота — это расстояние по перпендикуляру от основания до противоположной вершины. Его можно найти как снаружи, так и внутри треугольника. Напротив, медиана треугольника — это отрезок, проведенный от вершины к противоположной стороне, который делит треугольник на две равные части. Медиана делит пополам треугольник, образованный вершиной, из которой он проведен, и основанием треугольника. Он всегда лежит внутри треугольника.

Высота и медиана треугольника

аналитическая геометрия — Найти высоту треугольника

Задавать вопрос

спросил 6 лет, 7 месяцев назад

Изменено 6 лет, 7 месяцев назад

Просмотрено 381 раз

$\begingroup$

Нам дано уравнение следующих прямых: $$AB: x — 2y + 3 = 0$$ $$АС: 2х — у — 3 = 0$$ $$BC: 3x + 2y + 1 = 0$$

Найдите уравнение высоты, соответствующее $BC$ треугольника $ABC$.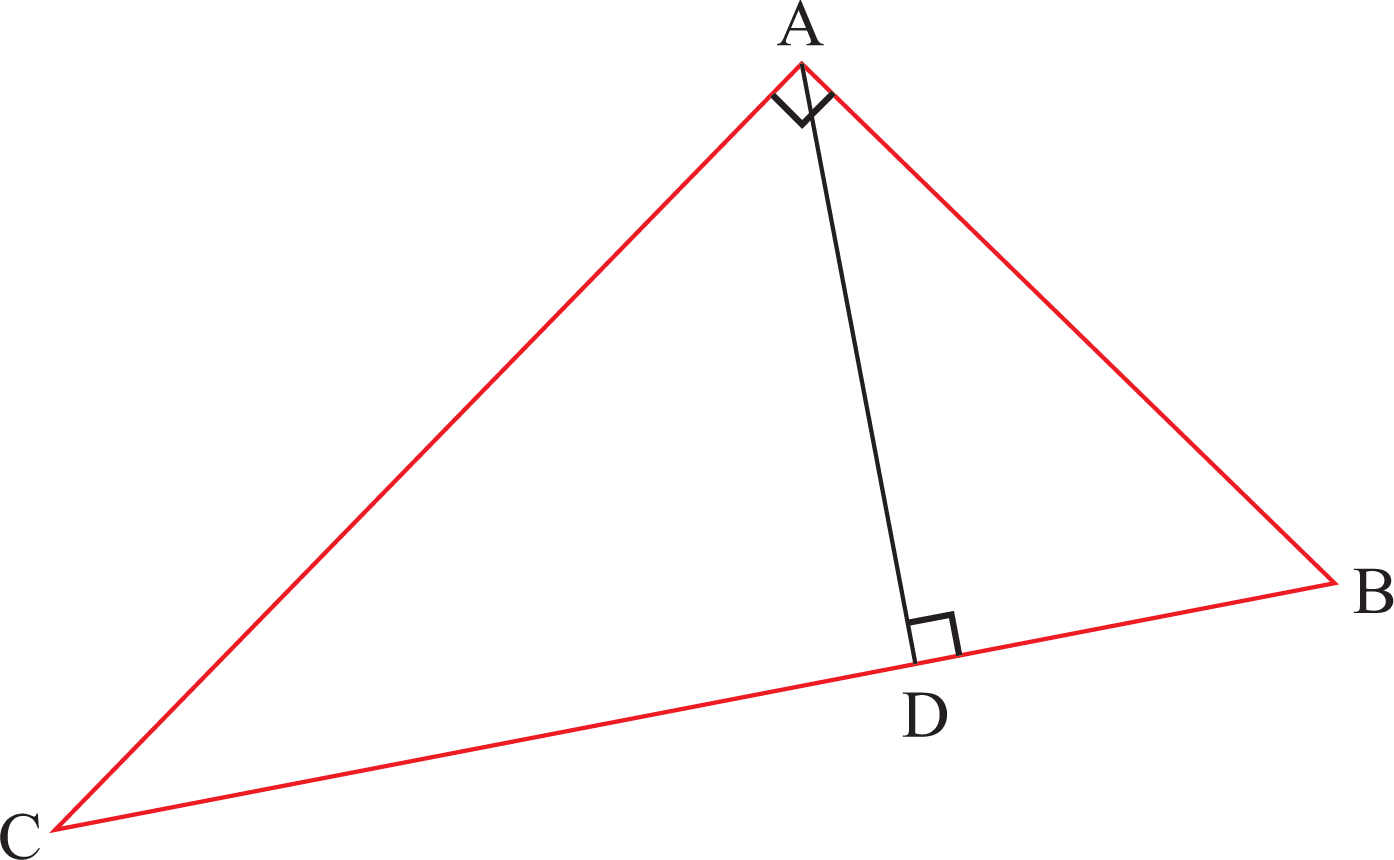

Вот что я сделал до сих пор:

Пусть $h: ax + by +c = 0$ будет уравнением высоты, соответствующим $BC$. Поскольку $h$ и $BC$ перпендикулярны, произведение их наклонов равно $-1$. Я получил $3a = -2b$.

Теперь $h$ содержит точку $A(3, 3)$, поэтому $3a + 3b +c = 0$. Подставив $3a = -2b$, я получил $c = -b$.

На данный момент я понятия не имею, что делать дальше.

Итак, если вы знаете, пожалуйста, помогите мне!

Спасибо!

• аналитическая геометрия
• треугольники

$\endgroup$

$\begingroup$

Предположим, что высота $h_{BC}$, соответствующая $BC$ треугольника $ABC$, имеет уравнение $y=kx+n$.

Поскольку она перпендикулярна прямой $BC$, мы знаем, что $$(k,-1)(3,2)=0,$$, откуда получаем $$k=\frac{2}{3}.$ $ Итак, высота, соответствующая $BC$, имеет уравнение $y=\frac{2}{3}x+n$.

Из условия $A\in h_{BC}$ получаем $$3=\frac{2}{3}3+n=2+n$$ и $$n=1. $$

Высота $h_ {BC}$ имеет уравнение $$-2x+3y-3=0.$$

$\endgroup$

$\begingroup$

У вас есть уравнение вашей «высотной линии» (2 уравнения с 3 неизвестными $a,b,c$, но это не имеет значения, такие уравнения все равно определены только с точностью до постоянного множителя).

Найдите пересечение между вашей «высотной линией» и базой $BC$, назовите ее $X$.

Найдите точку пересечения $AB$ и $AC$, т.е. положение точки $A$.

Высота равна расстоянию $|A-X|$

$\endgroup$

$\begingroup$

Из полученных уравнений $3a=-2b$ и $c=-b$ уже получено уравнение $$h:\frac{-2}{3}bx+by-b=0.$$ Вы можете указать любое ненулевое значение $b$, которое вы хотите, и уравнение по существу будет тем же самым, то есть уравнение представляет одну и ту же линию независимо от того, какое ненулевое значение $b$ вы введете.

No related posts.