10+ советов по написанию быстрого кода в Mathematica / Хабр
Перевод поста Джона Маклуна (Jon McLoone) «10 Tips for Writing Fast Mathematica Code».
Выражаю огромную благодарность Кириллу Гузенко KirillGuzenko за помощь в переводе.
Пост Джона Маклуна рассказывает о распространенных приемах ускорения кода, написанного на языке Wolfram Language. Для тех, кто заинтересуется этим вопросом мы рекомендуем ознакомиться с видео «Оптимизация кода в Wolfram Mathematica», из которого вы подробно и на множестве интересных примеров узнаете о приемах оптимизации кода, как рассмотренных в статье (но более детально), так и других.
Когда люди говорят мне, что Mathematica недостаточно быстро работает, обычно я прошу посмотреть код и часто обнаруживаю, что проблема не в производительности Mathematica, а в её не оптимальном использовании. Я хотел бы поделиться списком тех вещей, на которые я обращаю внимание в первую очередь при попытке оптимизировать код в
1. Используйте числа с плавающей точкой, и переходите к ним на как можно более ранней стадии.
Самая распространённая ошибка, которую я замечаю, когда разбираюсь с медленным кодом — задание слишком высокой точности для данной задачи. Да, неуместное использование точной символьной арифметики — самый распространенный случай.
У большинства вычислительных программных систем нет такого понятия, как точная арифметика — для них 1/3 это то же самое, что и 0,33333333333333. Это различие может играть большую роль, когда вы сталкиваетесь со сложными и неустойчивыми задачами, однако для большинства задач числа с плавающей точкой вполне удовлетворяют нуждам, и что важно — вычисления с ними проходят значительно быстрее. В Mathematica любое число с точкой и с менее чем 16 цифрами автоматически обрабатывается с машинной точностью, потому всегда следует использовать десятичную точку, если в данной задаче скорость важнее точности (например, ввести треть как 1.
То же самое можно сказать и для символьных вычислений. Если для вас не принципиальна символьная форма ответа и устойчивость в этой задаче не играет особой роли, то постарайтесь как можно раньше перейти к форме числа с плавающей точкой. Например, решая это полиномиальное уравнение в символьном виде, перед тем, как подставить значения, Mathematica строит промежуточное символьное решение на пять страниц.
Но если сперва выполнить подстановку, то Solve будет использовать значительно более быстрые численные методы.
При работе со списками данных следует быть последовательным в использовании действительных чисел. Всего лишь одно точное значение в наборе данных переведёт его в более гибкую, но менее эффективную форму.
2. Используйте
Compile…Функция Compile принимает код Mathematica и позволяет предварительно задавать типы (действительный, комплексный и т. д.) и структуры (значение, список, матрица и т. д.) входных аргументов. Это лишает части гибкости языка Mathematica, но освобождает от необходимости беспокоиться о том, «Что же делать, если аргумент в символьной форме?» и других подобных вещах. Mathematica может оптимизировать программу и создать байт-код для его запуска на своей виртуальной машине (возможна также компиляция в C — см. ниже). Не всё можно скомпилировать, и очень простой код может и не получить никаких преимуществ, однако сложный и низкоуровневый вычислительный код может получить действительно большое ускорение.
Вот пример:
Использование Compile вместо Function даёт ускорение более чем в 80 раз.
Но мы можем пойти дальше, сообщая Compile о возможности распараллеливания этого кода, получая ещё лучший результат.
На моей двухъядерной машине я получил результат в 150 раз быстрее, чем в изначальном случае; прирост скорости будет ещё заметнее с большим количеством ядер.
Однако следует помнить, что многие функции в Mathematica, такие как Table, Plot, NIntegrate и ещё некоторые автоматически компилируют свои аргументы, так что вы не увидите каких-либо улучшений при использовании Compile для вашего кода.
2.5.… и используйте
Compile для генерации кода на C.Кроме того, если ваш код компилируется, то вы также можете использовать опцию
3. Используйте встроенные функции.
Mathematica содержит много функций. Больше, чем обычный человек сможет выучить за один присест (последняя версия Mathematica 10.2 содержит уже более 5000 функций). Так что не удивительно, что я часто вижу код, где кто-то реализовывает какие-то операции, не зная, что Mathematica уже умеет их осуществлять. И это не только пустая трата времени на изобретение велосипеда; наши ребята основательно потрудились, создав и наиболее эффективно реализовав лучшие алгоритмы для различных типов входных данных, так что встроенные функции работают действительно быстро.
Если вы найдете что-то похожее, но не совсем то, то вам следует проверить параметры и необязательные аргументы — часто они обобщают функции и охватывают многие специальные и более отдалённые приложения.
Вот пример. Если у меня есть список из миллиона матриц 2х2, который я хочу превратить в список из миллиона одномерных списков из 4 элементов, то по идее самый простой способ будет использовать Map на функцию Flatten, применённую к списку.
Но Flatten знает, как самой решить эту задачу, если вы укажете, что уровни 2 и 3 структуры данных должны быть объединены, а уровень 1 чтобы не затрагивался. Указание подобных деталей может быть несколько неудобным, однако используя только одну Flatten, наш код будет выполнен в 4 раза быстрее, чем в случае, когда мы будем заново изобретать встроенные в функцию возможности.
Так что не забывайте заглянуть в справку перед тем, как вводить какой-то свой функционал.
4. Используйте Wolfram
Workbench.Mathematica прощает некоторые виды ошибок в коде, и всё будет спокойно работать, если вы вдруг забыли инициализировать переменную в нужный момент, и не нужно заботиться о рекурсии или неожиданных типах данных. И это здорово, когда вам нужно просто по-быстрому получить ответ. Однако подобный код с ошибками не позволит вам получить оптимальное решение.
Workbench помогает сразу несколькими способами.
Во-первых, он позволяет лучше отлаживать и организовывать крупные проекты, а когда всё ясно и организованно, то значительно проще писать хороший код. Но ключевой особенностью в данном контексте является профайлер, который позволяет увидеть, какие строки кода используется в определённые моменты времени, сколько раз они были вызваны.
Рассмотрим в качестве примера подобный, ужасно неоптимальный (с точки зрения вычислений) способ получения чисел Фибоначчи. Если вы не задумывались о последствиях двойной рекурсии, то, вероятно, несколько удивитесь 22-м секундам для оценки fib[35] (примерно столько же времени потребуется встроенной функции для расчета всех 208 987 639 цифр Fibonacci[1000000000] [см. пункт 3]).
Выполнение кода в Profiler показывает причину. Главное правило вызывается 9 227 464 раз, а значение fib[1] запрашивается 18 454 929 раз.
Увидеть код таким, каким он является в действительности — может стать настоящим откровением.
5. Запоминайте значения, которые вам понадобятся в дальнейшем.
Это хороший совет для программирования на любом языке. Вот как это можно реализовать в Mathematica:
Она сохраняет результат вызова f для любого аргумента, так что если функция будет вызвана для уже вызванного ранее аргумента, то Mathematica не потребуется вычислять его снова. Тут мы отдаем память, взамен получая скорость, и, конечно, если количество возможных аргументов функции огромно, а вероятность повторного вызова функции с тем же аргументом весьма мала, то так делать не стоит. Но если множество возможных аргументов невелико, то это действительно может помочь. Вот этот код спасает программу, которую я использовал для иллюстрации совета 3. Нужно заменить первое правило на это:
И код начинает работать несравнимо быстро, и для вычисления fib [35] главное правило должно быть вызвано лишь 33 раза. Запоминание предыдущих результатов предотвращает необходимость неоднократно рекурсивно спускаться к fib[1].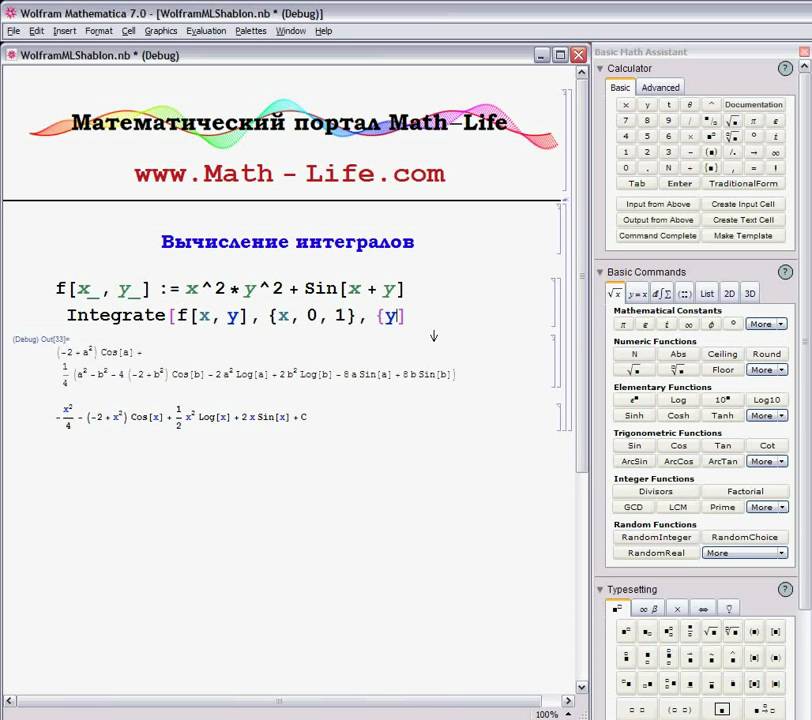
6. Распараллеливайте код.
Всё большее число операций в Mathematica автоматически распаралливаются на локальные ядра (особенно задачи линейной алгебры, обработки изображений, статистики), и, как мы уже видели, по запросу могут быть реализованы через Compile
Для этого есть набор инструментов, однако в случае принципиально монопоточных задач использование одних лишь ParallelTable, ParallelMap и ParallelTry может увеличить время вычислений. Каждая из функций автоматически решает задачи коммуникации, управления и сбора результатов. Существует некоторые дополнительные издержки в отправке задачи и получении результата, то есть получая выигрыш во времени в одном, мы теряем время в другом. Mathematica поставляется с определенным максимальным количеством доступных вычислительных ядер (зависит от лицензии), и вы можете масштабировать их с gridMathematica, если у вас есть доступ к дополнительным ядрам.
В этом примере ParallelTable дает мне двойную производительность, поскольку выполняется на моей двухъядерной машине. Большее количество процессоров дадут больший прирост.
Всё, что может сделать Mathematica, может быть распараллелено. Например, вы можете отправить наборы параллельных задач удалённым устройствам, каждое из которых компилирует и работает в C или на GPU.
6.5. Подумайте об использовании
CUDALink и OpenCLLink.С помощью GPU некоторые задачи могут в параллельном режиме решаться значительно быстрее. Не считая случая, когда для решения ваших задач требуются уже оптимизированные под CUDA функции, вам потребуется проделать небольшую работу, однако инструменты CUDALink и OpenCLLink автоматизируют для вас большое количество всякой рутины.
7. Используйте
Sow и Reap для накопления больших объемов данных (но не AppendTo).
Из-за гибкости структур данных в Mathematica,AppendTo не может знать, что вы будете добавлять число, потому что вы можете точно так же добавлять документ, звук или изображение.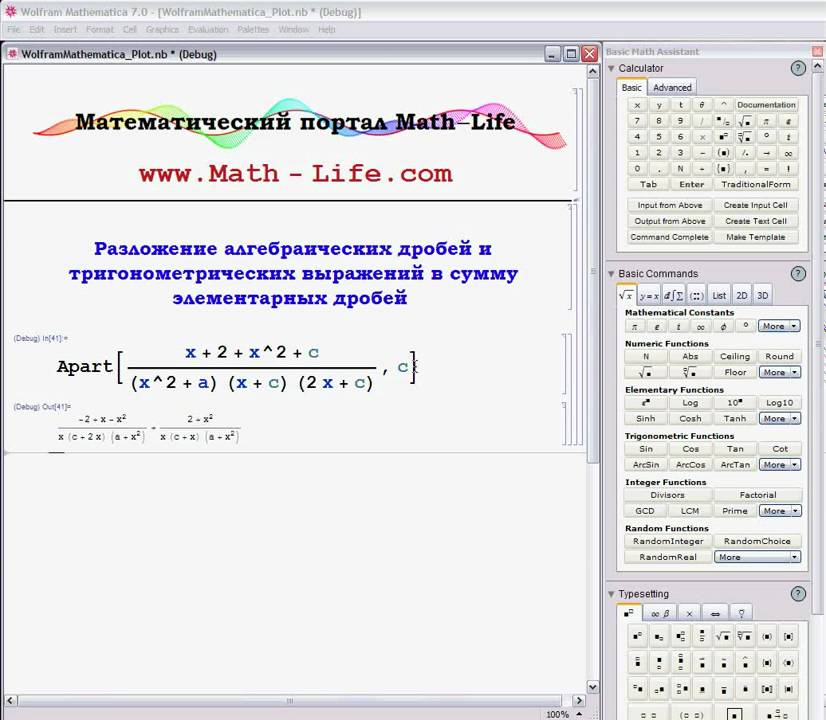
Вместо этого используйте Sow и Reap. Sow передаёт значения, которые вы хотите собрать, а Reap собирает их и создаёт объект данных в конце. Следующие примеры эквивалентны:
8. Используйте
Block и With вместо Module.Block (локализация значения переменной), With (замена переменных во фрагменте кода на их конкретные значения с последующим вычислением всего кода) и Module (локализация имен переменных) представляют собой ограничивающие конструкции, которые имеют несколько различные свойства. По моему опыту, Block и Module взаимозаменяемы, по крайней мере в 95% случаев, с которыми я сталкиваюсь, но Block, как правило, работает быстрее, а в некоторых случаях With (фактически Block с переменными, доступными лишь для чтения) ещё быстрее.
9. Не перебарщивайте с шаблонами.
Шаблонные выражения — это здорово. Многие задачи с их помощью легко решаются. Однако шаблоны — это не всегда быстро, особенно такие нечёткие, как BlankNullSequence (обычно записывается как «___»), которые могут долго и упорно осуществлять поиск шаблонов в данных, которых там явно не может быть. Если скорость выполнения принципиальна, используйте чёткие модели, или вообще откажитесь от шаблонов.
В качестве примера приведу изящный способ осуществить сортировку пузырьком в одну строчку кода через шаблоны:
В теории всё аккуратно, но слишком медленно по сравнению с процедурным подходом, который я изучал, когда только начинал программировать:
Конечно, в этом случае следует использовать встроенную функцию Sort (см. совет 3), которая работает наиболее быстро.
10. Используйте разные подходы.
Одна из самых сильных сторон Mathematica — возможность решать задачи по-разному.
Это позволяет писать код так, как вы мыслите, а не переосмысливать проблему под стиль языка программирования. Тем не менее, концептуальная простота не всегда есть то же, что и вычислительная эффективность. Иногда простая для понимания идея порождает больше работы, чем это необходимо.
Но другой момент заключается в том, что из-за всяких специальных оптимизаций и умных алгоритмов, которые автоматически применяются в Mathematica, часто трудно становится предсказать, какой из путей следует выбрать. Например, вот два способа расчёта факториала, но второй более чем в 10 раз быстрее.
Почему? Вы могли бы предположить, что Do медленнее прокручивает циклы, или все эти присваивания Set к temp занимают время, или ещё что-то не так с первой реализацией, но настоящая причина, вероятно, окажется довольно неожиданной. Times (оператор умножения) знает хитрый трюк с бинарным разбиением, который может использоваться, когда у вас есть большое количество целочисленных аргументов.
Рекурсивное разделение аргументов на два меньших произведения (1 * 2 *… * 32767) * (32768 *… * 65536) работает быстрее, чем обработка всех аргументов — от первого до последнего. Количество умножений получается таким же, однако однако меньшее количество из них включают большие числа, потому в среднем алгоритм осуществляется быстрее. Есть много другого скрытого волшебства в Mathematica, и с каждой версией его всё больше.
Конечно лучший вариант в данном случае — использовать встроенную функцию (опять-таки совет 3):
Mathematica способна обеспечить превосходную вычислительную производительность, а также высокую скорость и точность, но не всегда одновременно. Надеюсь, что эти советы помогут вам сбалансировать зачастую противоречивые требования быстрого программирования, быстрого исполнения и точных результатов.
Все тайминги приводятся для 7 64-разрядной Windows PC, с 2,66 ГГц Intel Core 2 Duo и 6 Гб оперативной памяти.
Помимо этого краткого поста Джона Маклуна, мы рекомендуем вам ознакомиться с двумя видео, приведенными ниже.
Разработка больших приложений в Mathematica
Распространенные ошибки и заблуждения начинающих пользователей Mathematica
НОУ ИНТУИТ | Лекция | Системы компьютерной алгебры
< Лекция 7 || Лекция 8: 12345678910 || Лекция 9 >
Аннотация: В данной лекции рассматриваются программы Mathematica и Maxima, позволяющие проводить обработку как числовой, так и символьной информации, а также осуществлять вычисления с большой степенью точности и оперировать огромными числами.
Ключевые слова: программные средства, тождество, выражение, программа, Windows, компьютерная алгебра, GNU, интерфейс, первообразная, значение, функция, MathCAD, mapl, описание системы, фирма, место, машинно-независимость, ядро, пользователь, вычисление, правильный ответ, algebraic, calculus, geometry, statistics, подпакет, сумма ряда, соответствие шаблону, аннулирование, simplify, expandability, polys, многочлен, plotting, HSB, hue, saturation, brightness, thickness, ‘dashed, tick, automatic, график функции, список переменных, equation, мнимая единица, бесконечное множество, натуральный логарифмы, приближенное решение уравнения, infinity, предел функции, аналитические функции, Series, производная функции, дифференцирование, вторая производная, определенный интеграл, матричная форма, определитель, inverse, transpose, транспонирование, линейное уравнение, умножение матриц, импликация, упрощение логического выражения, GPL, shell, меню, сеанс, оболочка, информация, метка, вывод, Command, регистр, запись, присваивание, kill, параметр, прерывание, DESCRIBE, имя функции, иррациональное число, non-numerical, COTS, ACO, divide-by-zero, gcd, обыкновенное дифференциальное уравнение, кратность, неопределенный интеграл, интеграл, divergent, determine, определитель матрицы, invertible, Алгебраическим дополнением, система линейных уравнений, коэффициентами системы, свободными членами, Единичная матрица, batch
intuit.ru/2010/edi»>В этой главе будут рассмотрены программные средства, позволяющие проводить обработку как числовой, так и символьной информации, а также осуществлять вычисления с большой степенью точности и оперировать огромными числами.Большинство компьютерных программ, предназначенных для вычислений, работают только с числовыми выражениями. Как правило их результаты бывают приближенными, ведь при операциях с вещественными числами происходит их округление. В последнее время все большее распространение приобретают системы для научных и инженерных расчетов, избавленные от подобных недостатков. Они способны использовать в процессе вычислений математические теоремы и факты. Так, широко известное тригонометрическое тождество гласит, что sin2x+cos2x=1 для любого x. Ни один калькулятор не способен применить это тождество в процессе преобразований, в то время как такие программы, как Mathematica или Maxima, предназначенные для символьных вычислений, легко справляются с подобными задачами.
Там, где необходимо выполнить вычисления точно, либо осуществить аналитическое преобразование, например, упростить сложное математическое выражение, вычислить в символьном виде производную или первообразную заданной функции, разложить ее в ряд Тейлора, найти корни уравнения, заданного в достаточно общем виде и т. д., применяются так называемые системы компьютерной алгебры (системы символьных вычислений). Отметим также особую роль подобных систем в техническом и математическом образовании. Они позволяют проверить результаты громоздких математических расчетов и наглядно представить сложные математические объекты.
Мировым лидером среди подобного рода систем справедливо считается программа Mathematica. Ее версии доступны пользователям различных операционных систем, в том числе Windows и Linux. Следует отметить, что эта программа, заслуженно пользующаяся популярностью, стоит достаточно дорого.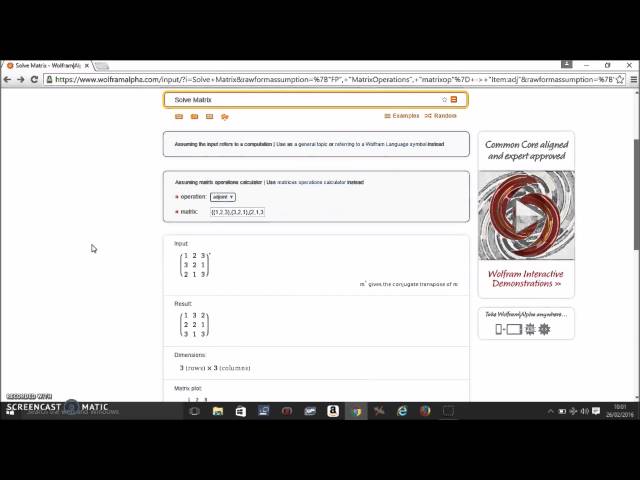
Другой системой компьютерной алгебры, рассматриваемой в этом курсе, является Maxima. Эта программа распространяется под лицензией GNU, что позволяет рекомендовать ее широкому кругу пользователей. У каждой из этих двух программ есть свои сильные и слабые стороны. Удобный графический интерфейс является несомненным достоинством программы Mathematica, в то время как Maxima зачастую дает более корректные ответы. Так, например, при вычислении первообразной функции xn Maxima просит уточнить значение n, так как при n = -1 результатом является функция ln x, а при других n первообразная равна xn+1/(n+1). Программа Mathematica для такой функции всегда в качестве первообразной выдает значение xn+1/(n+1), хотя если в качестве функции задать 1/x, то получим верный результат — ln x. Другими представителями систем такого рода являются программы Mathcad и Maple, но в данном курсе они рассмaтриваться не будут.
Mathematica
intuit.ru/2010/edi»>Этот раздел посвящен описанию системы компьютерной алгебры Mathematica. Многие считают ее мировым лидером среди систем подобного класса. Разработкой этой программы занимается компьютерная фирма Wolfram Research, Inc. Число легальных пользователей программы Mathematica во всем мире превысило миллион человек. К сожалению, достаточно высокая для индивидуального пользователя нашей страны цена этой программы делает практически невозможным ее легальное использование в России.Центральное место в системе Mathematica занимает машинно-независимое ядро математических операций Kernel. Оно гарантирует идентичность результатов, полученных при одних и тех же вычислениях в системах Mathematica, установленных на разных платформах. В дальнейшем изложении мы будем рассматривать процесс работы с этой программой в ОС Linux.
Работа с системой происходит в диалоговом режиме: пользователь задает вопрос и получает на него ответ.
Mathematica допускает вычисление и по заранее подготовленным программам, но в этом учебном пособии вопросы, связанные с программированием в системе Mathematica, не затрагиваются.
Следует отметить, что Mathematica позволяет решать корректно поставленные математические задачи, но вся ответственность за их формулировку и перевод на язык этой системы лежит на пользователе. Не понимая постановки задачи, невозможно получить правильный ответ.
Работа с выражениями
Для запуска программы наберите команду mathematica в командном окне, либо в стартовом меню выберите пункт Mathematica.
При старте открывается рабочее окно, в котором отображаются ввод и вывод программы. В верхней его части находится меню, позволяющее выполнять различные действия, в том числе сохранение текущей сессии в файле с расширением nb. Кроме основного окна в работе участвуют так называемые палитры.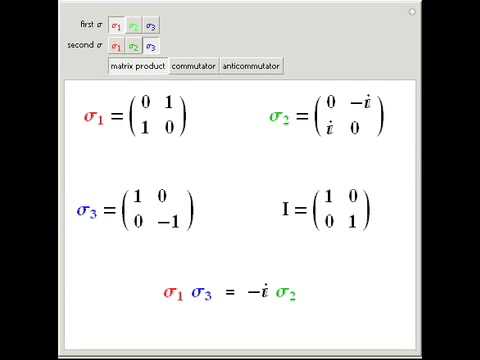
Если они не появились при старте, то для их открытия можно воспользоваться пунктом Palettes из меню File. Палитра Basic Input предоставляет набор кнопок для ввода наиболее употребительных символов, таких как корни, дроби, интегралы, буквы греческого алфавита и т. д. Палитра Basic Calculations содержит шаблоны для вычисления основных алгебраических функций.
Чтобы инициировать процесс вычисления после набора команды нужно одновременно нажать клавиши Shift и Enter (либо клавишу Enter на числовой клавиатуре справа). После завершения расчета программа присваивает имена вида In[1] и Out[1] исходному выражению и результату. Можно отменить показ имен, отключив в меню Kernel пункт Show In/Out Names.
Mathematica в качестве имен функций почти всегда использует их английские названия. Исключениями являются несколько наиболее употребимых функций: кроме N для определения численного значения, символ D используется для нахождения производной.
Дополнительную информацию о назначении той или иной функции в ходе работы с системой можно получить, используя следующие команды:
? Name — помощь по заданному слову Name;
?? Name — расширенная помощь по заданному слову Name.
Большинство функций программы Mathematica являются встроенными, т. е. становятся доступными сразу после загрузки системы. Кроме того, имеется набор так называемых пакетов расширения, содержащих специализированные функции для работы в той или иной области. Среди них Algebra, Calculus, DiscreteMath, Geometry, LinearAlgebra, Miscellaneous, Graphics, NumberTheory, NumericalMath, Statistics и некоторые другие. Каждый из пакетов содержит набор подпакетов, например, в пакет Algebra входят такие подпакеты, как InequalitySolve для решения неравенств, SymbolicSum для вычисления сумм рядов, Trigonometry для работы с тригонометрическими выражениями и другие.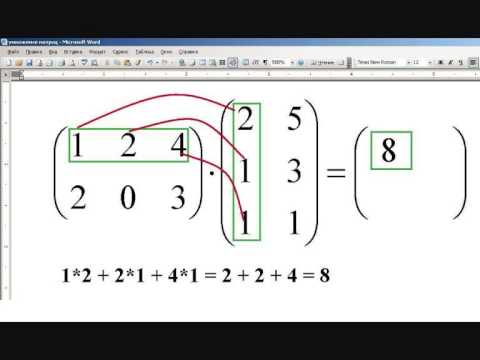
Для того чтобы сделать доступными функции, входящие в состав специализированных пакетов, следует их подключить командой типа
Needs[«Algebra`Trigonometry`»]
или
<<Algebra`Trigonometry`
обратите внимание на использование обратных апострофов). Если загружаемый подпакет содержит несколько функций, то их перечень выводится на экран. При наличии в пакете только одной функции ее имя совпадает с именем пакета.
Mathematica всегда старается упростить введенное выражение. Если вы попробуете вычислить корень квадратный из двадцати, для чего после ввода соответствующего выражения нажмете Shift+Enter, то результатом окажется выражение, равное двум корням из пяти. Программа упростит выражение, оставив его в символьном виде. Для того чтобы получить численное значение выражения expr, следует использовать функцию N[expr] или N[expr, n], где n задает точность вычислений.
По умолчанию выводится значение выражения с пятью знаками после запятой.
Для ввода выражений удобно пользоваться палитрой Basic Input, которая содержит шаблоны для ввода степеней, дробей, радикалов, греческих букв и т. п. При выборе соответствующего шаблона появляется возможность ввести нужные значения (место для ввода значений выглядит как небольшой квадратик).
Отметим некоторые особенности синтаксиса системы, используемого при записи арифметических выражений:
- знак умножения может быть заменен пробелом;
- имена встроенных функций начинаются с большой буквы;
- параметры функций задаются в квадратных скобках, например Sin[2] ;
- круглые скобки используются для того, чтобы выделить части выражений и изменить порядок выполнения операций;
intuit.ru/2010/edi»>фигурные скобки используются при задании списков, например, при перечислении уравнений, входящих в систему.Дальше >>
< Лекция 7 || Лекция 8: 12345678910 || Лекция 9 >
Раздел MMA Mathematica
Раздел MMA Mathematica Предупреждение: jsMath
требует JavaScript для обработки математики на этой странице.
Если ваш браузер поддерживает JavaScript, убедитесь, что он включен.
Раздел ММА Mathematica
Из первого курса линейной алгебры
Версия 2.23
© 2004.
Лицензия GNU Free Documentation License.
http://linear.ups.edu/
Примечание к вычислениям ME.MMA: матричная запись
Матрицы вводятся как списки списков, так как список является базовой структурой данных в системе Mathematica.
Матрица представляет собой список строк, каждая из которых вводится как список. Mathematica использует фигурные скобки
((\ влево \{\ вправо .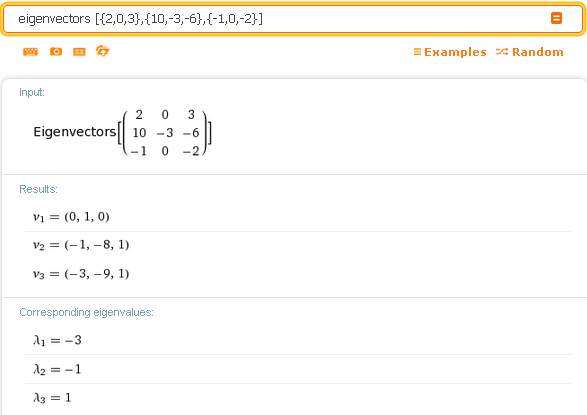
, \ влево .\право \}))
для разграничения списков. Итак, ввод
а = \{\{1, 2, 3, 4\},\{5, 6, 7, 8\},\{9, 10, 11, 12\}\} |
создаст 3 × 4 матрица с именем a, равная
\влево [\массив{ 1 и 2 и 3 и 4\кр 5 и 6 и 7 и 8 \кр 9&10&11&12 } \right ] |
Чтобы отобразить матрицу с именем «красиво» в Mathematica, введите MatrixForm[a] , и вывод будет отображаться со строками и столбцами. Если вы просто наберете , то вы получите список списков, например, как вы вводите матрицу в первом место.
Примечание к вычислениям RR.MMA: уменьшение строки
Если a — это имя матрицы в системе Mathematica, то команда RowReduce[a] выведет уменьшенную ступенчатую форму матрицы.
Примечание к вычислениям LS.MMA: Linear Solve
Mathematica решит линейную систему уравнений, используя LinearSolve[]
команда.
Входные данные представляют собой матрицу с коэффициентами переменных (но не
столбец констант) и список, содержащий постоянные термины каждого
уравнение. Это будет выглядеть немного странно, так как списки в матрице являются строками, а
столбец констант также вводится как список и поэтому выглядит как строка, а не как
столбец. Результатом будет единственное решение (даже если их бесконечно много),
сообщается в виде списка или утверждения об отсутствии решения. Когда есть
бесконечно много, сообщаемое единственное решение — это именно то решение, которое использовалось в
доказательство теоремы RCLS, где все свободные переменные равны нулю, а
зависимые переменные идут вместе со значениями из последнего столбца таблицы
матрица с уменьшенной строкой.
Например, архетип A
\eqalignno{ {x}_{1} – {x}_{2} + 2{x}_{3} & = 1 & & \кр 2{x}_{1} + {x}_{2} + {x}_{3} & = 8 & & \кр {x}_{1} + {x}_{2} & = 5 & & }
Чтобы запросить у Mathematica решение, введите
LinearSolve[\ \{\{1,\kern 1. |
95872pt — 1,\kern 1.95872pt 2\},\{2,\kern 1.95872pt 1,\kern 1.95872pt 1\},\{1,\kern 1.95872 pt 1,\kern 1.95872pt 0\}\},\ \{1,\kern 1.95872pt 8,\kern 1.95872pt 5\}\ ]и вы получите единое решение
\{3,\kern 1.95872pt 2,\kern 1.95872pt 0\} |
Позже мы увидим, как уговорить Mathematica дать нам бесконечно много решения для этой системы (Расчет ВФСС.ММА).
Примечание к вычислениям VLC.MMA: векторные линейные комбинации
Предоставлено Robert Beezer
Векторы в Mathematica представлены в виде списков, записываются и отображаются
горизонтально. Например, вектор
v = \слева [\массив{ 1\кр 2 \кр 3\кр 4 } \right ] |
будет введено и названо с помощью команды
v = \{1,\kern 1. |
95872pt 2,\kern 1.95872pt 3,\kern 1.95872pt 4\}Сложение векторов и скалярное умножение тогда очень естественны. Если и и v два списка одинаковой длины, тогда
2u + (−3)v |
вычислит правильный вектор и вернет его в виде списка. Если у и v есть разного размера, то Mathematica будет жаловаться на «объекты неравных размеров». длина.»
Примечание к вычислениям NS.MMA: Null Space
Учитывая матрицу A, Mathematica вычислит набор векторов-столбцов, диапазон которых является нулевым пространством матрица с помощью команды NullSpace[]. Возможно, не случайно этот набор точно \ влево \ {\ влево . {z} _ {j} \ вправо \ vert 1 ≤ j ≤ n — r \ вправо \}. Однако Mathematica предпочитает выводить векторы в обратном порядке. тот, который мы выбрали. Вот небольшой пример. 9{\text{RREF}} &B & = \left [\array{ \text{1}&0& 3 &−2\cr 0&\текст{1} &−2 & 1 \кр 0&0& 0 & 0 } \right ] & & & & & & & }
Мы можем извлечь записи из B
для построения векторов {z}_{1}
и {z}_{2} согласно
Теорема SSNS и описание N\kern -1.
95872pt \left (A\right )
как промежуток множества \left \{{z}_{1},\kern 1.95872pt {z}_{2}\право\}.
Вместо этого, если
был установлен на А,
затем выполнение команды NullSpace[a] дает список списков (столбец
векторы),
\eqalignno{ \{\{2,−1, 0, 1\},\{ — 3, 2, 1, 0\}\} & & }
Обратите внимание, как наш {z}_{1}
является вторым в списке. Чтобы «исправить» это, мы можем использовать команду обработки списка из
Mathematica, Reverse[] следующим образом:
9{м}
является вектор-столбцом. Мы могли бы захотеть найти все решения линейной системы
ℒS\kern -1.95872pt\left (A,\kern 1.95872pt b\right ).
LinearSolve[A, b] Mathematica вернет не более одного
решение (Расчет LS.MMA). Однако, когда система
непротиворечивым, то это единственное решение, о котором сообщается, является в точности вектором
в,
описано в формулировке теоремы VFSLS.
Векторы {u}_{j}, 1 ≤ j ≤ n − r из Теорема VFSLS – это в точности результат Mathematica NullSpace[] команда, хотя Mathematica перечисляет их в обратном порядке из выбранного нами порядка. Это те же векторы, что и {г}_{к}, 1 ≤ j ≤ n − r в теореме SSNS. С с производится с помощью команды LinearSolve[], а {и}_{к} исходя из команды NullSpace[], мы можем использовать символический код Mathematica. команды манипулирования для создания выражения, описывающего все решения.
Начните с системы ℒS\kern -1.95872pt\left (A,\kern 1.95872pt b\right ). Ряд-уменьшить A (вычисление RR.MMA) и определите свободные переменные, определив неосновной столбцы. Предположим, ради аргумента, что у нас есть три свободных переменных {х}_{3}, {x}_{7} и {х}_{8}. Затем следующая команда создаст выражение для произвольного решение:
\eqalignno{ \text{ LinearSolve[A,b]+\{x8,x7,x3\}.NullSpace[A] } & & }
Не забудьте поставить точку прямо перед командой NullSpace[] — она
эффект создания линейной комбинации векторов в нулевом пространстве с использованием
скаляры, которые являются символами, напоминающими переменные.
Здесь поможет конкретный пример. Предположим, мы хотим набор решений для линейной системы с матрицей коэффициентов А и вектор констант b,
\eqalignno{ А & = \влево [\массив{ 1&2&3&−5& 1 &−1& 2\cr 2&4 &0 & 8 &-4 & 1 &-8 \кр 3&6&4& 0 &−2& 5 & 7 } \right ] &b & = \left [\array{ 8\кр 1 \кр −5 } \справа ] & & & & }
Если бы мы применяли теорему VFSLS, мы бы извлекли компоненты с и {u}_{j} из сокращенная по строкам версия расширенной матрицы системы (полученная с Mathematica, вычисления RR.MMA),
\влево [\массив{ \text{1}&2&0& 4 &−2&0&−5& 2\cr 0&0 &\text{1} &−3 &1 &0 &3 &1 \кр 0&0&0& 0 & 0 &\text{1}& 2 &−3 } \right ] |
Вместо этого мы будем использовать эту расширенную матрицу в сокращенной ступенчатой форме только для определите свободные переменные. В этом примере мы находим несводные столбцы и видим что {x}_{2}, {х}_{4}, {x}_{5} и {x}_{7} бесплатны. Если мы имеем установить a на коэффициент матрица и б к вектору констант, то выполняем команду Mathematica,
\eqalignno{
\text{ LinearSolve[a, b]+\{x7, x5, x4, x2\}.
NullSpace[a] } & &
}
На выходе получаем вектор-столбец (список),
\eqalignno{ \слева [\массив{ 2 — 2\текст{х2}- 4\текст{х4} + 2\текст{х5} + 5\текст{х7}\кр \текст{х2} \кр 1 + 3\текст{х4}-\текст{х5}- 3\текст{х7}\кр \текст{x4} \кр \текст{x5}\cr −3 − 2\текст{x7} \кр \text{ x7 } } \right ] & & }
Расчетная записка GSP.MMA: Процедура Грама-Шмидта
Mathematica имеет встроенную процедуру, которая выполняет тест Грама-Шмидта.
процедура (теорема GSP). На вход подается набор векторов, который должен
быть линейно независимым. Записывается в виде списка, содержащего списки, которые
являются векторами. Пусть a будет таким списком списков, содержащих векторы
{в}_{я},
1 ≤ i ≤ p из
утверждение теоремы. Вам нужно будет сначала загрузить правильный пакет Mathematica
— выполните <
Затем
выполнить GramSchmidt[a] . На выходе будет другой список списков, содержащих
векторы {u}_{i},
1 ≤ i ≤ p из
утверждение теоремы. Mathematica пожалуется, если вы не предоставите
линейно независимый набор в качестве входных данных (попробуйте!).
Пример. Предположим, что наш линейно независимый набор (проверьте это!) равен
\eqalignno{ S знак равно \ влево \ {\ влево [\ массив { −1\кр 4 \кр 1\кр 0 \кр 3 } \right ],\kern 1.95872pt \left [\array{ 0\кр 3 \кр 0\кр 3 \кр −3 } \right ],\kern 1.95872pt \left [\array{ −1\кр 2 \кр 0\кр −1 \кр −2 } \справа ],\керн 1.95872pt \влево [\массив{ −1\кр −2 \кр −3\кр 1 \кр 4 } \right ],\kern 1.95872pt \left [\array{ 1\кр 6 \кр −1\кр 4 \кр 6 } \справа ]\справа \} & & }
Выводом команды GramSchmidt[] будет набор,
\eqalignno{
Т знак равно \ влево \ {\ влево [\ массив {
− {1\более
3\квадрат{3}}
\кр
{4\более
3\квадрат{3}}
\кр
{1\более
3\квадрат{3}}
\кр
0
\кр
{1\более
\sqrt{3}} } \right ],\kern 1.
95872pt \left [\array{
{1\более
12\кв{15}}
\кр
{23\более
12\кв{15}}
\кр
− {1\более
12\кв{15}}
\кр
{3\sqrt{{3\более
5}}\более
4}
\кр
−{\ sqrt {{5 \ более
3}}\более
2} } \справа ],\керн 1.95872pt \влево [\массив{
− {37\более
4\кв{685}}
\кр
{29\более
4\кв{685}}
\кр
− {3\более
4\кв{685}}
\кр
− {79\более
4\кв{685}}
\кр
−{5\sqrt{ {5\более
137}}\более
2} } \right ],\kern 1.95872pt \left [\array{
− {337\более
2\кв{120423}}
\кр
− {37\более
6\кв{120423}}
\кр
− {1763\более
6\кв{120423}}
\кр
{337\более
6\кв{120423}}
\кр
{50\более
\sqrt{120423}} } \right ],\kern 1.95872pt \влево [\массив{
{23\более
\sqrt{879}}
\кр
{26\более
3\кв{879}}
\кр
− {44\более
3\кв{879}}
\кр
− {23\более
3\кв{879}}
\кр
{1\более
\sqrt{879}} } \right ]\right \} & &
}
Некрасиво, но факт. На этом этапе вам также может быть предложено подумать о
Процедура Грама-Шмидта как вычислительный черный ящик, линейно независимое множество
в, ортогональные, сохраняющие пролет изложены.
Чтобы убедиться, что выходной набор ортогонален, мы можем легко проверить ортогональность отдельных пар векторов. Предположим, что выход был установлен равным b (скажем, через b=GramSchmidt[a] ). Мы можем извлечь отдельные векторы c как «parts» с синтаксисом вроде c[[3]] , который вернет третий вектор в наборе. Когда наши векторы содержат только вещественные числа, мы можем выполнить внутренний продукт с «точкой». Так, например, вы должны обнаружить, что c[[3]].c[[5]] вернет ноль. Попробуйте сами с другой парой векторы.
Примечание к вычислениям TM.MMA: транспонирование матрицы
Предоставлено Robert Beezer
Предположим, что a — это имя матрицы, хранящейся в системе Mathematica. Затем транспонировать [a]
создаст транспонирование файла .
Примечание к вычислениям MM.MMA: умножение матриц
Если А
и Б
являются матрицами, определенными в системе Mathematica, то A.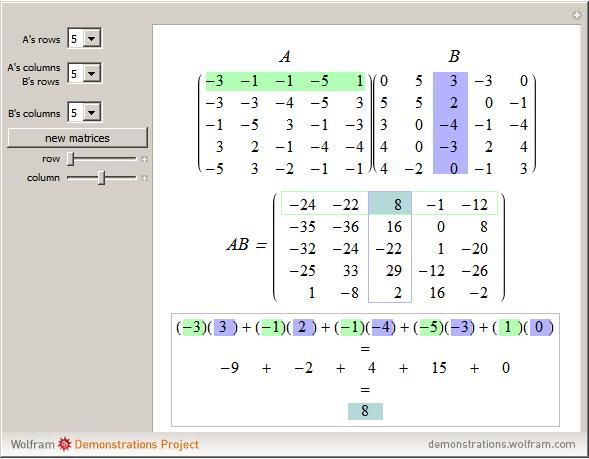
B вернет
произведение двух матриц (обратите внимание на точку между матрицами). Если
А — матрица
и v
является вектором, то A.v вернет вектор, являющийся матрично-векторным произведением
А и
с. В
в каждом случае размеры матриц и векторов должны быть правильными.
Некоторые примеры:
\begin{массив}{cl} \{\{1,\kern 1.95872pt 2\},\kern 1.95872pt \{3,\kern 1.95872pt 4\}\}.\{\{5,\kern 1.95872pt 6,\kern 1.95872pt 7\ },\kern 1.95872pt \{8,\kern 1.95872pt 9,\kern 1.95872pt 10\}\} = \{\{21,\kern 1.95872pt 24,\kern 1.95872pt 27\},\kern 1.95872pt \{47,\kern 1.95872pt 54,\kern 1.95872pt 61\}\}& \\ \{\{1,\kern 1.95872pt 2\},\kern 1.95872pt \{3,\kern 1.95872pt 4\}\}.\{\{5\},\kern 1.95872pt \{6\}\ } = \{\{17\},\kern 1.95872pt \{39\}\} & \\ \{\{1,\керн 1,95872pt 2\},\kern 1.95872pt \{3,\kern 1.95872pt 4\}\}.\{5,\kern 1.95872pt 6\} = \{17,\kern 1.95872pt 39\} & \end{ массив}
Понимание разницы между двумя последними примерами поможет
объясняя, как работают некоторые конструкции Mathematica.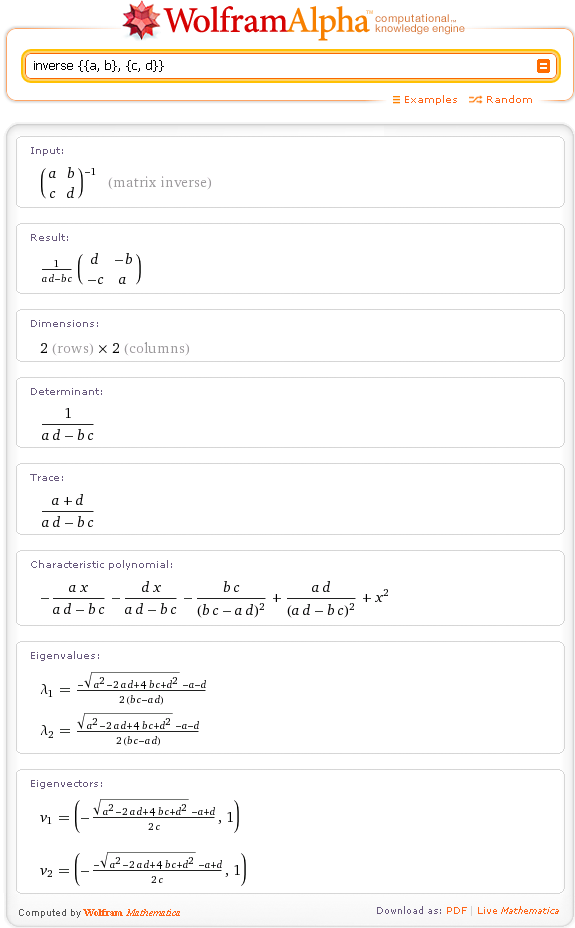
Примечание к вычислениям MI.MMA: Матрица, обратная
Если А — это матрица, определенная в Mathematica, то Inverse[A] вернет обратную матрицу А, если он существует. В случае, когда А не имеет обратной Mathematica скажет вам, что матрица сингулярна (см. Теорема NI).
Как сложить две матрицы в Mathematica?
Как добавить две матрицы в Mathematica? | 8 ответов из научных статейЭкстракция (химия)
Умножение матриц
Обратное преобразование Лапласа
Преобразование Лапласа
Миграция клеток
8 найденных ответов .
Метод распределенной передаточной функции для решения задач теплопроводности в многослойных композитах
11 сентября 2008 г.
• Численный расчет теплопередачи, часть B — основные принципы
12
цитирования
Мы также получили улучшенные алгоритмы для умножения более чем двух разреженных матриц.
Быстрое умножение разреженных матриц
14 сентября 2004 г. •
20
цитирования
Если две такие матрицы различаются хотя бы одним элементом, то они представляют разные векторные подпространства.
Биективные методы в теории конечных векторных пространств
01 июл 1984 • Журнал комбинаторной теории, серия A
21
Цитаты
Однако эти матрицы не позволяют контролировать
3D -миграционные исследования с использованием двухфотонных материалов.
206
цитирования
Этот метод позволяет достичь пределов количественного определения, необходимых для двух матриц.
Экстракция сверхкритической жидкостью в сочетании с иммуноаффинной очисткой для анализа следовых количеств органических загрязнителей в различных матрицах
01 ноября 1997 г. • Хроматография
23
цитирования
Мы показываем, что эти две матрицы определяют друг друга, и устанавливаем между ними несколько полезных взаимосвязей.
Замечание о двух матрицах, встречающихся в решении квазипроцессов рождения и смерти две квадратные нулевые гамильтоновы матрицы.
Каждая симплектическая матрица является продуктом четырех симплектических инволюций для больших матриц.