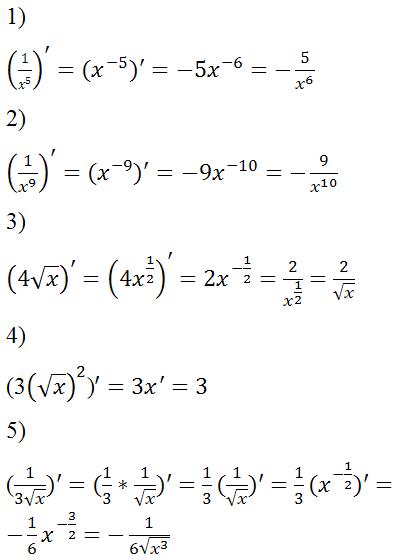X 1 2 производная: Найти производную y’ = f'(x) = (x)^(1/2) ((х) в степени (1 делить на 2))

{2}}$

Полная таблица производных Решение производных онлайн

Читать дальше: производная корня икс, sqrt(x)’.

2

Вопрос

Обновлено: 23.03.2021

MBD ПУБЛИКАЦИЯ-ЛИМИТ И ДИФФЕРЕНЦИАЦИЯ-БАНК ВОПРОСОВ

20 видео

РЕКЛАМА

Текст Решение

Решение 1)2
Затем dyx =2(x−1)

Ответ

Пошаговое решение, разработанное экспертами, чтобы помочь вам в разрешении сомнений и получении отличных оценок на экзаменах.

Ab Padhai каро бина объявления ке

Khareedo DN Pro и дехо сари видео бина киси объявление ки rukaavat ке! 93):}

648502873

Text Solution

World Web Math: производные полиномов

World Web Math: производные полиномов Предлагаемые предпосылки: Значение дифференциация,

Полиномы — одни из самых простых функций, которые мы используем. Мы должны знать производные многочленов, таких как х ⁴ +3 х , 8 x ² +3x+6 и 2.

Начнем с самая простая из них, функция г = f ( x )= c , где c — любая константа, например 2, 15,4 или один миллион четыре. (10 ⁶ +4). Оказывается, производная любой постоянной функция равна нулю. Это имеет смысл, если вы думаете о производной как наклон касательной. Чтобы использовать определение производная, с f ( x ) = c ,

Для полноты рассмотрим теперь у = f ( х ) = х . Это уравнение прямой линии с наклоном 1, и мы ожидаем найти это из определения производной. Мы не разочарованы:

Две вещи, которые следует отметить в вышеизложенном:

• Может возникнуть соблазн «отменить» термин « dx » в промежуточный шаг. Это верно, но только в этом простом случае.
• Никогда больше не будет так просто, хотя и не намного Сильнее.
  Прежде чем перейти к самому общему случае, рассмотреть y = f ( x ) = x ² . Как показано, это самая простая парабола. производная от f ( x ) все еще можно найти из базовой алгебры:

  Это говорит нам именно то, что мы ожидаем; производная равна нулю в x = 0, имеет тот же знак, что и x , и становится круче (более отрицательное или положительное) по мере того, как x становится более отрицательным или положительный.

  Интересный результат нахождения эта производная состоит в том, что наклон секущей равен наклону функция в середине отрезка. Конкретно,

  (На приведенном рисунке 90 107 x 90 108  = -1 и ч  = 3, поэтому ( x + ч /2) = +1/2.
  Обратите внимание, что параболические функции являются функциями

  и только . (кроме линейных или постоянных функций), для которых это всегда истинный.

  Отсюда можно и нужно считать y = f ( x ) = x ⁿ для любое положительное целое число n . Есть много способов сделать это, с разной степенью официальности.

  Для начала рассмотрим, что для n положительное целое число биномиальная теорема позволяет нам выразить f ( x +h) как

  (В приведенном выше всегда будет не более n +1 ненулевые члены.) Затем алгебра снова дает нам

  Видно, что эта очень удобная форма воспроизводит приведенные выше результаты для n =1, n =2 и даже n =0, т.е. случай с =1.
  

  Приведенный выше результат можно получить из индуктивного процесса, используя правило произведения, но индуктивный шаг подобен тому, который позволяет распространение биномиальной теоремы на все положительные целые числа и добавляет немного для этой презентации.

  Расширение от f ( x )= x ⁿ произвольным полиномам (здесь будет рассматриваться только конечный порядок) нужны только два простых, возможно, даже очевидных результата:

  • Производная суммы двух функций есть сумма производные.

    No related posts.