Филиппов § 5. Линейные уравнения первого порядка
Бесплатные решения из сборника задач по дифференциальным уравнениям А.Ф. Филиппова. Решения дифференциальных уравнений в данном разделе доступны в режиме онлайн без регистрации.
§ 5. Линейные уравнения первого порядка
136. Решить уравнение: xy’ — 2y = 2×4.
137. Решить уравнение: (2x + 1)y’ = 4x + 2y.
138. Решить уравнение: y’ + y tg x = sec x.
139. Решить уравнение: (xy + ex)dx — x dy = 0.
140. Решить уравнение: x2y’ + xy + 1 = 0.
141. Решить уравнение: y = x(y’ — x cos x).
142. Решить уравнение: 2x(x2 + y)dx = dy.
143. Решить уравнение: (xy’ — 1)ln x = 2y.
144. Решить уравнение: xy’ + (x + 1)y = 3x2e-x.
145. Решить уравнение: (x + y2) dy = y dx.
147. Решить уравнение: (sin2 y + x ctg y)y’ = 1.
148. Решить уравнение: (2x + y)dy = y dx + 4 ln y dy.
149. Решить уравнение: y’ = y/(3x — y2).
150. Решить уравнение: (1 — 2xy)y’ = y(y — 1).
151. Решить уравнение: y’ + 2y = y2ex.
152. Решить уравнение: (x + 1)(y’ + y2) = -y.
153. Решить уравнение: y’ = y4 cos x + y tg x.
154. Решить уравнение: xy2y’ = x2 + y3.
155. Решить уравнение: xy dy = (y2 + x)dx.
156. Решить уравнение: xy’ — 2×2 sqrt(y) = 4y.
157. Решить уравнение: xy’ + 2y + x5y3ex = 0.
158. Решить уравнение: 2y’ — x/y = xy/(x2 — 1).
159. Решить уравнение: y’x3 sin y = xy’ — 2y.
160. Решить уравнение: (2x2y ln y — x)y’ = y.
161. С помощью замены переменных или дифференцирования привести уравнение к линейному и решить его. x dx = (x2 — 2y + 1)dy.
162. С помощью замены переменных или дифференцирования привести уравнение к линейному и решить его. (x + 1)(yy’ — 1) = y2.
163. С помощью замены переменных или дифференцирования привести уравнение к линейному и решить его. x(ey — y’) = 2.
164. С помощью замены переменных или дифференцирования привести уравнение к линейному и решить его. (x2 — 1)y’ sin y + 2x cos y = 2x — 2×3.
165. С помощью замены переменных или дифференцирования привести уравнение к линейному и решить его. y(x) = 0x∫ y(t)dt + x + 1.
166. С помощью замены переменных или дифференцирования привести уравнение к линейному и решить его. 0x∫ (x — t)y(t)dt = 2x + 0x∫ y(t)dt…
167.
Найти путем подбора частное решение, привести данное дифференциальное уравнение Риккати к уравнению Бернулли и решить его.
x2y’ + xy + x2y2 = 4…
168. Найти путем подбора частное решение, привести данное дифференциальное уравнение Риккати к уравнению Бернулли и решить его.
3y’ + y2 + 2/x2 = 0.
169. Найти путем подбора частное решение, привести данное дифференциальное уравнение Риккати к уравнению Бернулли и решить его.
xy’ — (2x + 1)y + y2 = -x2.
170. Найти путем подбора частное решение, привести данное дифференциальное уравнение Риккати к уравнению Бернулли и решить его.
y’ — 2xy + y2 = 5 — x2.
171. Найти путем подбора частное решение, привести данное дифференциальное уравнение Риккати к уравнению Бернулли и решить его.
y’ + 2yex — y2 = e2x…
173. Найти кривые, у которых площадь трапеции, ограниченной осями координат, касательной и ординатой точки касания, есть величина постоянная, равная 3a2.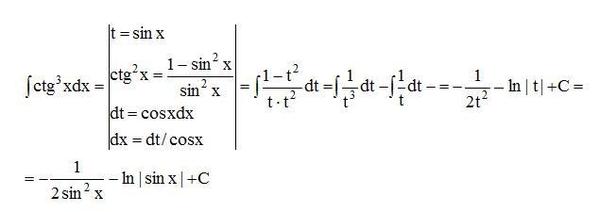
174. Найти кривые, у которых площадь треугольника, ограниченного касательной, осью абсцисс и отрезком от начала координат до точки касания, есть величина постоянная, равная a2…
175. В баке находится 100 л раствора, содержащего 10 кг соли. В бак втекает 5 л воды в минуту, а смесь с той же скоростью переливается в другой 100-литровый бак, первоначально наполненный…
176. За время Δt (где Δt очень мало и выражено в долях года) из каждого грамма радия распадается 0,00044 Δt грамма и образуется 0,00043 Δt грамма радона. Из каждого…
177. Даны два различных решения y1 и y2 линейного уравнения первого порядка. Выразить через них общее решение этого уравнения.
178. Найти то решение дифференциального уравнения y’ sin 2x = 2(y + cos x), которое остается ограниченным при x → π/2.
179. Пусть в уравнении xy’ + ay = f(x) имеем a = const > 0, f(x) → b при х → 0.
Показать, что только одно решение уравнения остается ограниченным при х → 0, и найти предел…
180. Пусть в уравнении предыдущей задачи а = const < 0, f(x) → b при х → 0. Показать, что все решения этого уравнения имеют один и тот же конечный предел при х → 0. Найти…
181. Показать, что уравнение dx/dt + x = f(t), где |f(t)| ≤ M при -∞ < t < +∞, имеет одно решение, ограниченное при -∞ < t < +∞. Найти это решение…
182. Показать, что только одно решение уравнения xy’ — (2×2 + 1)y = x2 стремится к конечному пределу при х → +∞, и найти этот предел. Выразить это решение…
183. Найти периодическое решение уравнения y’ = 2y cos2 x — sin x. Примечание: искомое решение выражается через интеграл с бесконечным пределом.
184. Пусть в уравнении dx/dt + a(t)x = f(t), a(t) ≥ c > 0, f(t) → 0 при t → +∞. Доказать, что каждое решение этого уравнения стремится к нулю при t → +∞.
..
185. Пусть в уравнении предыдущей задачи имеем a(t) ≥ c > 0 и пусть x0(t) — решение с начальным условием x0(0) = b. Показать, что для любого ε > 0.
| 1 | Найти производную — d/dx | бревно натуральное х | |
| 2 | Оценить интеграл | интеграл натурального логарифма x относительно x | |
| 3 | Найти производную — d/dx | 92)||
| 21 | Оценить интеграл | интеграл от 0 до 1 кубического корня из 1+7x относительно x | |
| 22 | Найти производную — d/dx | грех(2x) | |
| 23 | Найти производную — d/dx | 9(3x) по отношению к x||
| 41 | Оценить интеграл | интеграл от cos(2x) относительно x | |
| 42 | Найти производную — d/dx | 1/(корень квадратный из х) | |
| 43 | Оценка интеграла 9бесконечность | ||
| 45 | Найти производную — d/dx | х/2 | |
| 46 | Найти производную — d/dx | -cos(x) | |
| 47 | Найти производную — d/dx | грех(3x) | 92+1|
| 68 | Оценить интеграл | интеграл от sin(x) по x | |
| 69 | Найти производную — d/dx | угловой синус(х) | |
| 70 | Оценить предел | ограничение, когда x приближается к 0 из (sin(x))/x 92 по отношению к х | |
| 85 | Найти производную — d/dx | лог х | |
| 86 | Найти производную — d/dx | арктан(х) | |
| 87 | Найти производную — d/dx | бревно натуральное 5х92 |
Детская кроватка (x)
Детская кроватка (x)| Дом | Учитель | Родители | Глоссарий | О нас | |||||
|
|
у = грех х. то находим du = cos x dx замените du=cos x, u=sin x
= пер |у| + С заменить обратно u=sin x = пер |sin х| + C |
