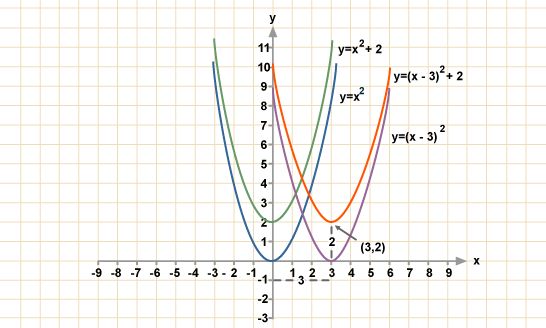
заказ решений на аукционе за минимальную цену с максимальным качеством
Предлагаю идею сайта-аукциона по выполнению домашних заданий. Он будет включать:
- решение задач по математике (сейчас доступен решебник Филиппова), физике, химии, экономике
- написание лабораторных, рефератов и курсовых
- выполнение заданий по литературе, русскому или иностранному языку.
Основное отличие от большинства сайтов, предлагающих выполнение работ на заказ – сайт рассчитан на две категории пользователей: заказчиков и решающих задания. Причем, по желанию (чтобы заработать, увеличить свой рейтинг, получить решение сложной задачи) пользователи могут играть любую из этих ролей.
Объединение сервисов в одну систему
Основой для идеи послужили несколько работающих систем, объединение которых позволит сделать сервис для решения задач на заказ. Эти системы:
- Форум, где посетители обмениваются идеями и помогают друг другу
- Система bugtracking, где обнаруженные проблемы проходят путь от публикации до принятия в исполнение и решения
- Аукцион, где цена за товар или услугу определяется в результате торгов
- Система рейтингов, где участники могут оценивать ответы друг друга.
Причем, чем больше рейтинг пользователя, тем более значимым становится его голос
Причем, чем больше рейтинг пользователя, тем более значимым становится его голосПринцип работы
Для удобства и проведения аналогий с реальной жизнью назовем заказчиков студентами, а решающих задания – репетиторами.
Итак, студенту необходимо решить несколько задач. Он заходит на сайт, выбирает раздел с соответствующей дисциплиной и создает новую тему (аналогия с форумом). Но при создании темы он также указывает стартовую (максимальную) цену, которую он готов заплатить за решение задач и крайний срок исполнения задания. Можно будет назначить и нулевую цену – если студенту нужно только бесплатное решение.
Как только тема создана, все пожелавшие подписаться на раздел репетиторы получают уведомление. Причем, условие получения уведомлений можно настроить. Например, уведомлять только о заказах со стартовой ценой более 500 р. и сроком решения не менее недели.
Заинтересовавшиеся репетиторы делают ставки. Причем студент (автор темы) видит ставки и может посмотреть информацию по каждому репетитору (его решения, рейтинг, дату начала участия в проекте).
Когда студент посчитает нужным, он может остановить аукцион и назначить задание одному из репетиторов, сделавшему ставку (не обязательно самую низкую, т.к. можно учитывать и другие факторы – см. выше).
Деньги блокируются на счете студента, и репетитор начинает решать задание. Он должен представить его к сроку, заданному изначально. Выполненное решение публикуется в свободном доступе и его может оценить как заказчик, так и другие репетиторы. На этих оценках и строится рейтинг. Если к решению нет претензий – деньги окончательно переводятся со счета студента на счет репетитора.
За счет чего будет развиваться сервис
Первое – положительная обратная связь. Чем больше условий задач и решений будет опубликовано на сайте, тем чаще его будут находить пользователи через поисковики, будет больше ссылок на готовые решения. Именно поэтому важно размещать решенные задачи в свободном доступе. Знаю это по опыту своего сайта exir.ru (ex irodov.nm.ru) – большая ссылочная база получена исключительно за счет благодарных пользователей.
Второе – удобный сервис для заказчиков и для желающих заработать на решениях.
Преимущества для заказчиков
Студентам и школьникам не нужно перебирать десятки сайтов для сравнения цен, а потом надеяться, что после оплаты они получат качественное решение (и, вообще, все не закончится перечислением денег). Заказчики создают аукцион на понижение цены и могут смотреть на рейтинги желающих решить задачи и ранее выполненные ими решения. Кроме того, деньги окончательно перечисляются исполнителю только после полного решения.
Преимущества для решающих задания
Не нужно создавать и продвигать свой сайт, размещать множество объявлений во всех доступных источниках информации. Заказчики сами придут к вам. Не нужно решать все присланные задания с целью поддержания репутации – можно выбирать те, которые будут интересны по уровню сложности, цене и срокам решения.
Преимущества для владельца сервиса
Если вы не понимаете, какую выгоду получит делающий вам какое-нибудь предложение – будьте осторожны! 🙂 У меня уже есть большой опыт работы с сайтом, предоставляющим бесплатные решения по физике.
И вариант с получением прибыли от размещения рекламы подходит и для нового сервиса. Кроме того, мне нравится помогать людям и довольно тяжело смотреть, как множество вопросов по задачам остаются на форуме без ответа. Предложенный аукцион решений сможет значительно сократить число вопросов без ответов.
В будущем возможен вариант и с получением некоторого небольшого процента от оплаты заказов. Но процент этот должен быть минимален и на начальном этапе он взиматься точно не будет.
Что необходимо для создания сервиса
- Самым важное сейчас – собрать команду, готовую принять участие в выполнении заданий. Если покупатели заходят в пустой магазин – они надолго забывают в него дорогу.
Поэтому я собираю предварительные заявки от посетителей, готовых заниматься решениями. Не нужно подписания никаких договоров о намерениях. Просто сообщите, на какие темы вы готовы решать задания, какой у вас опыт подобной работы (e-mail: [email protected]). Когда сервис заработает – я пришлю приглашение на регистрацию.
- Выбрать платежную систему.
- Сделать подходящий движок для сайта. Нужно решить – создавать его с нуля или изменить какой-нибудь существующий движок (например, форумный) с открытой лицензией.
- Привлечь посетителей. Учитывая посещаемость exir.ru и число публикуемых на форуме вопросов, думаю, это не будет большой проблемой.
Desertai be cukraus Vilniuje: tortai, pyragaičiai, saldainiai
Ответ: 4. Найдите объем твердого тела…
Задача 1E: Начертите и обозначьте точки A0,-3, B3,-4, C5, 6, D-2,-5 и E-3, 5 .Задача 2E: Дайте координаты каждой точки A, B, C, D и E. Также назовите квадрант, в котором находится каждая точка… Задача 3E: Найдите расстояние между каждой парой точек: a 5, -3 и 5, 1 c 0, 2 и 0, -3 b -3, 4 и 5, 4 d… Задача 4E: Если расстояние между -2, 3 и -2,a равно 5 единицам, найти все возможные значения a.Задача 5E: Если расстояние между b,3 и 7,3 составляет 3,5 единицы, найти все возможные значения b.Задача 6EЗадача 7E: Найти расстояние между каждой парой точек: a 0,-3 и 4, 0 c 3, 2 и 5,-2 b -2, 5 и 4,-3 d.
.. Задача 8E: Найдите расстояние между каждой парой точек: a -3,-7 и 2, 5 c -a,-b и a,b b 0, 0 и -2, 6 d… Задача 9E: Найдите середину отрезка, соединяющего каждую пару точек: a 0, -3 и 4, 0 c 3, 2 и… Задача 10E Задача 11E: Точки A и B имеют симметрию относительно начала координат O. Найдите координаты B, если A является… Задача 12E: Точки A и B имеют симметрию относительно точки C 2,3. Найдите координаты B, если A является… Задача 13E: Точки A и B имеют симметрию относительно точки C. Найдите координаты C для заданной точки: a A… Задача 14E: Точки A и B имеют симметрию относительно оси x. Найдите координаты B, если A является… Задача 15E Задача 16E: Точки A и B имеют симметрию относительно вертикальной линии, где x=2. Найдите координаты A… Задача 17E: Точки A и B имеют симметрию относительно оси y. Найдите координаты A, если B это… Задача 18E Задача 19E: Точки A и B имеют симметрию относительно вертикальной линии x=a или горизонтальной линии y=b. Задайте… Задача 20E: В упражнениях с 20 по 22 примените формулу средней точки.
M 3,-4является серединой AB-, в которой A является… Задача 21EЗадача 22EЗадача 23E: Прямоугольник ABCD имеет три вершины в точках A2,-1,B6,-1 и C6,3. Найдите четвертую вершину и… Задача 24E: Прямоугольник MNPQ имеет три вершины в точках M0, 0, Na, 0 и Q0, b. Найдите четвертую вершину P и… Задача 25E: Используйте формулу расстояния, чтобы определить тип треугольника, который имеет эти вершины: a A0, 0, B4,0,… Задача 26E: Используйте метод из примера 4, чтобы найти уравнение прямой, описывающей все равноудаленные точки… Задача 27E. Воспользуйтесь методом из примера 4, чтобы найти уравнение прямой, описывающей все равноудаленные точки… Задача 28E. Для компланарных точек A, B и C , предположим, что вы использовали формулу расстояния, чтобы показать, что… Задача 29EЗадача 30EЗадача 31EЗадача 32E: На оси абсцисс имеются две точки, расположенные на расстоянии 6 единиц от точек 3,1….Задача 33E: Треугольник с вершинами M-4,0,N3,- 1 и Q2,4 заключены в рамки, как показано. Найдите площадь.
.. Задача 34E: Используйте метод бокса, предложенный в упражнении 33, чтобы найти площадь RST с R-2,4,S-1,-2 и T6,5…. Задача 35E: Определите площадь ABC, если A=2,1,B=5,3, а C является отражением B относительно оси X. Задача 36E: Найдите площадь ABC В упражнении 35, но предположим, что C является отражением B по оси Y. Задача 37E. Найдите точный объем твердого тела, которое получается, когда треугольная область с вершинами находится в точках 0, 0, 5,…. Задача 38E. Найдите точный объем твердого тела, которое получается, когда треугольная область с вершинами 0, 0, 6,… Задача 39E: Найдите точный объем твердого тела, которое получается, когда прямоугольная область с вершинами находится в точках 0, 0,… Задача 40E: Найдите точный объем тела, которое получается, когда область, ограниченная осями в квадранте I… Задача 41E: Найдите точную площадь поперечной поверхности каждого твердого тела в упражнении 40. Найдите точный объем образовавшегося твердого тела… Задача 42E: Найдите объем твердого тела, образовавшегося, когда треугольная область имеет вершины в точках 2, 0, 4, 0.
, и 2,… Задача 43E: По определению, эллипс — это геометрическое место точек, сумма расстояний которых от двух фиксированных точек F1 и… Задача 44E: По определению, гипербола — это геометрическое место точек, положительная разность которых расстояния от двух… Задача 45EЗадача 46E: Используйте формулу расстояния, чтобы показать, что уравнение параболы с фокусом F0,2 и директрисой… Задача 47E: После 90 вращение против часовой стрелки вокруг начала координат, изображение A3, 1 точка B-1, 3. Что… Задача 48E: Рассмотрим точку Ca,b. Каким будет образ C после поворота против часовой стрелки на 90 вокруг… Задача 49E Задача 50E: Графики парабол eith уравнений y=x2 и прямой y=18-x2 пересекаются в двух точках. Найти… Задача 51E format_list_bulleted
Вычислить объем цилиндрических оболочек с помощью интеграции
Предоставил:
В этом разделе мы узнаем:
Как применить метод цилиндрических оболочек для определения объема твердого тела.
1.
6
ЗАЯВКИ ИНТЕГРАЦИИ
2.
ПРИМЕНЕНИЕ ИНТЕГРАЦИИ
6.3
Объемы по
Цилиндрические оболочки
В этом разделе мы узнаем:
для определения объема твердого тела.
3.
ОБЪЕМЫ ПО ЦИЛИНДРИЧЕСКИМ ОБОЛОЧКАМ
Некоторые проблемы с объемом очень
трудно обрабатывать методами
, описанными в разделе 6.2
4.
ОБЪЕМЫ ЦИЛИНДРИЧЕСКИМИ ОБОЛОЧКАМИ
Рассмотрим задачу нахождения
объема твердого тела, полученного вращением вокруг оси y на
области, ограниченной y = 2×2 — x3
и y = 0,
5.
ОБЪЕМЫ ЦИЛИНДРИЧЕСКИМИ ОБОЛОЧКАМИ
Если разрезать перпендикулярно оси у,
получится шайба.
Однако для вычисления внутреннего радиуса и внешнего
радиус шайбы,
нам пришлось бы
решить кубическое
уравнение y = 2×2 — x3
для x через y.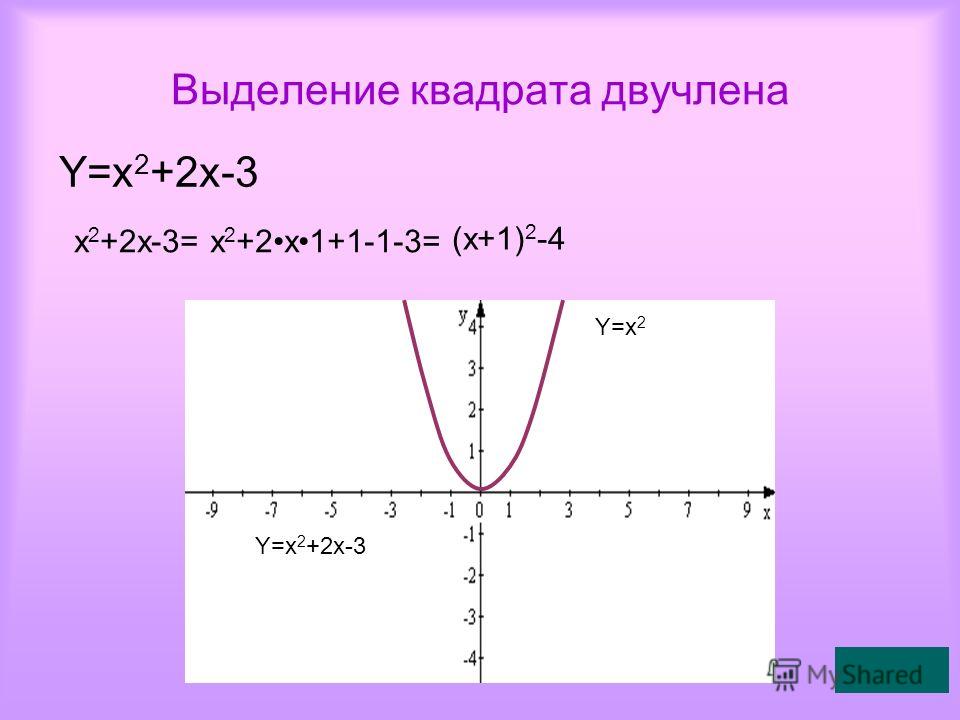
Это непросто.
6.
ОБЪЕМЫ ЦИЛИНДРИЧЕСКИМИ ОБОЛОЧКАМИ
К счастью, есть метод — метод
7.
МЕТОД ЦИЛИНДРИЧЕСКИХ ОБОЛОЧЕК
На рисунке показана цилиндрическая оболочка
с внутренним радиусом r1, внешним радиусом r2,
и высотой h.
8.
МЕТОД ЦИЛИНДРИЧЕСКИХ ОБОЛОЧЕК
Его объем V рассчитывается путем вычитания
объема V1 внутреннего цилиндра из
объема внешнего цилиндра V2.
9.
МЕТОД ЦИЛИНДРИЧЕСКИХ ОБОЛОЧЕК
Таким образом, имеем:
V V2 V1
2 2
r2 h r h 1
2 2
(r2 r )h 1
(r2 r1 )(r2 r1 )h
r2 r1
2 h(r2 r1 )
2
10.
МЕТОД ЦИЛИНДРИЧЕСКИХ ОБОЛОЧЕК Формула 1
Пусть ∆r = r2 – r1 (толщина оболочки) и
r 12 r2 r1
(средний радиус оболочки).
принимает вид:
В 2 rhr
11.
МЕТОД ЦИЛИНДРИЧЕСКИХ ОБОЛОЧЕК
V 2 rhr
Уравнение можно запомнить как:
V = [длина окружности] [высота] [толщина]
12.
МЕТОД ЦИЛИНДРИЧЕСКИХ ОБОЛОЧЕК
Пусть теперь S будет телом
, полученным вращением
вокруг оси y область
, ограниченная
y = f(x) [где f(x) ≥ 0],
y = 0, x = a и x = b,
, где b > a ≥ 0,
13.
МЕТОД ЦИЛИНДРИЧЕСКИХ ОБОЛОЧЕК
Разобьем интервал [a, b] на n подинтервалов
[xi — 1, xi ] одинаковой ширины xi и пусть x
— середина i-го подинтервала.
14.
МЕТОД ЦИЛИНДРИЧЕСКИХ ОБОЛОЧЕК
Прямоугольник с
основанием [xi — 1, xi ] и
высотой f ( xi ) поворачивается на
относительно оси Y.
Результатом является цилиндрическая оболочка
со средним радиусом xi
, высотой f (xi)
.
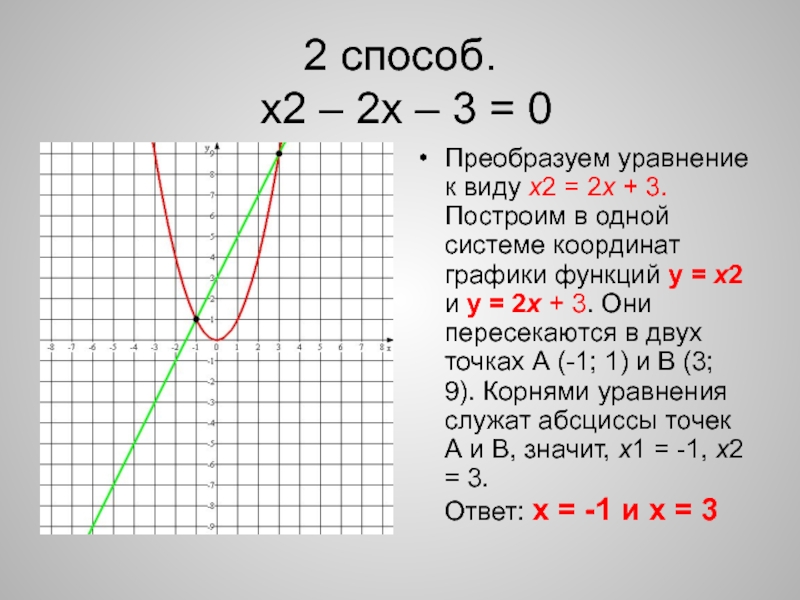
15.
МЕТОД ЦИЛИНДРИЧЕСКИХ ОБОЛОЧЕК
Таким образом, по формуле 1 его объем равен
и рассчитывается следующим образом:
Vi (2 xi )[ f ( xi )]x
16.
МЕТОД ЦИЛИНДРИЧЕСКИХ ОБОЛОЧЕК
Итак, приближение к объему V S
дается суммой объемов
этих оболочек:
n n
В Vi 2 xi f ( xi )x
i 1 i 1
17.
МЕТОД ЦИЛИНДРИЧЕСКИХ ОБОЛОЧЕК
Аппроксимация становится лучше
при n →∞.
Однако из определения интеграла
мы знаем, что:
18.
МЕТОД ЦИЛИНДРИЧЕСКИХ ОБОЛОЧЕК Формула 2
Таким образом, представляется правдоподобным следующее.
Объем твердого тела, полученного при вращении
вокруг оси y область под кривой
y = f(x) от a до b:
b
V 2 xf ( x)dx
, где 0 ≤ a
19.
МЕТОД ЦИЛИНДРИЧЕСКИХ ОБОЛОЧЕК
Рассуждение с использованием цилиндрических оболочек
делает формулу 2 разумной,
но позже мы сможем это доказать.
20.
МЕТОД ЦИЛИНДРИЧЕСКИХ ОБОЛОЧЕК
Вот лучший способ запомнить
формулу.
Представьте типичную раковину,
разрезанную и сплющенную,
с радиусом x,
окружностью 2πx,
высотой f(x) и
толщиной ∆x или dx:
b
2 x f( x)
a dx 9001 1 высота окружности толщина
21.
МЕТОД ЦИЛИНДРИЧЕСКИХ ОБОЛОЧЕК
Этот тип рассуждений будет полезен
в других ситуациях, например, когда мы
вращаемся вокруг линий, отличных от оси у.
22.
МЕТОД ЦИЛИНДРИЧЕСКИХ ОБОЛОЧЕК Пример 1
Найти объем твердого тела, полученного с помощью
вращается вокруг оси y область
, ограниченная y = 2×2 — x3 и y = 0,
23.
МЕТОД ЦИЛИНДРИЧЕСКИХ ОБОЛОЧЕК Пример 1
Мы видим, что типичная оболочка имеет радиус
x, длину окружности 2πx и высоту
f(x) = 2×2 — x3.
24.
МЕТОД ЦИЛИНДРИЧЕСКИХ ОБОЛОЧЕК Пример 1
Итак, по методу оболочек
объем равен: 4
2 х (2 х х )dx
0
4 5 2
2 х х
1
2
1
5 0
2 8 325 165
25.
МЕТОД ЦИЛИНДРИЧЕСКИХ ОБОЛОЧЕК Пример 1
Можно проверить, что метод оболочки
дает тот же ответ, что и разрезание.
На рисунке показано
сгенерированное компьютером
изображение твердого тела
, объем которого мы
вычислили в примере
.
26.
Сравнивая решение примера 1 с
замечаний в начале раздела
мы видим, что метод цилиндрических оболочек
намного проще, чем метод шайбы
для задачи.
Нам не нужно было находить координаты локального максимума
.
Нам не нужно было решать уравнение кривой
относительно x через y.
27.
Однако в других примерах
методы, изученные в Разделе 6.2
, могут быть проще.
28.
МЕТОД ЦИЛИНДРИЧЕСКИХ ОБОЛОЧЕК Пример 2
Найдите объем тела, полученного
вращением вокруг оси y области
между y = x и y = x2.
29.
МЕТОД ЦИЛИНДРИЧЕСКИХ ОБОЛОЧЕК Пример 2
Здесь показаны область и типичная оболочка
.
Мы видим, что оболочка имеет радиус x, длину окружности 2πx,
и высоту x — x2.
30.
МЕТОД ЦИЛИНДРИЧЕСКИХ ОБОЛОЧЕК Пример 2
Таким образом, объем твердого тела равен:
1
V 2 x x x 2 dx
0
1
2 х х dx
2 3
0
3 4 1
х х
2
3 4 0 6
31.
МЕТОД ЦИЛИНДРИЧЕСКИХ ОБОЛОЧЕК
Как показывает следующий пример,
метод оболочек работает так же хорошо,
если мы вращаемся вокруг оси x.
Нам просто нужно нарисовать диаграмму, чтобы определить
радиус и высоту оболочки.
32.
МЕТОД ЦИЛИНДРИЧЕСКИХ ОБОЛОЧЕК Пример 3
Используйте цилиндрические оболочки, чтобы найти объем
твердого тела, полученного вращением вокруг оси x
области под кривой y x от 0 до 1.
Эта задача была решена с использованием дисков в примере 2
в разделе 6.2
33.
МЕТОД ЦИЛИНДРИЧЕСКИХ ОБОЛОЧЕК Пример 3
Чтобы использовать оболочки, мы переобозначили кривую
y x
как x = y2.