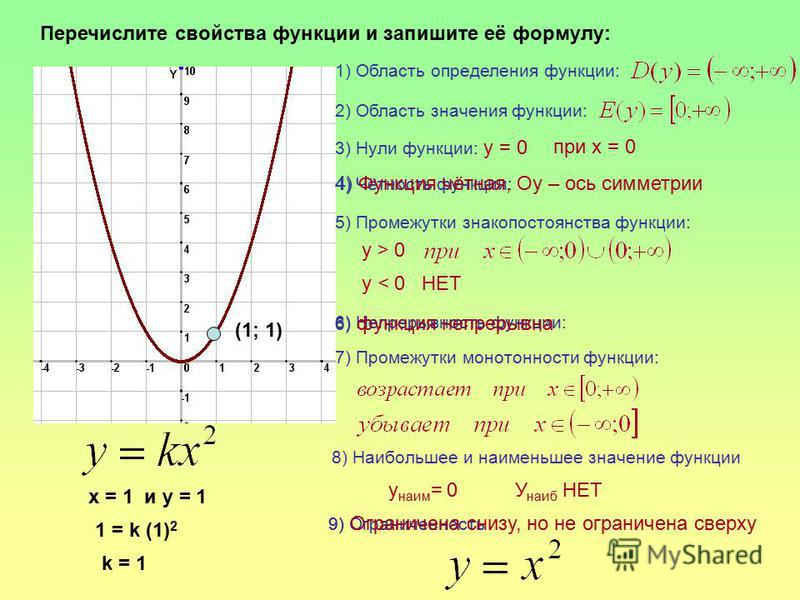
x=\frac{-\left(-15\right)±\sqrt{225-4\times 3\left(-y\right)}}{2\times 3}
Возведите -15 в квадрат.
x=\frac{-\left(-15\right)±\sqrt{225-12\left(-y\right)}}{2\times 3}
Умножьте -4 на 3.
x=\frac{-\left(-15\right)±\sqrt{225+12y}}{2\times 3}
Умножьте -12 на -y.
x=\frac{-\left(-15\right)±\sqrt{12y+225}}{2\times 3}
Прибавьте 225 к 12y.
x=\frac{15±\sqrt{12y+225}}{2\times 3}
Число, противоположное -15, равно 15.
x=\frac{15±\sqrt{12y+225}}{6}
Умножьте 2 на 3.
x=\frac{\sqrt{12y+225}+15}{6}
Решите уравнение x=\frac{15±\sqrt{12y+225}}{6} при условии, что ± — плюс. Прибавьте 15 к \sqrt{225+12y}.
x=\frac{\sqrt{12y+225}}{6}+\frac{5}{2}
Разделите 15+\sqrt{225+12y} на 6.
x=\frac{-\sqrt{12y+225}+15}{6}
Решите уравнение x=\frac{15±\sqrt{12y+225}}{6} при условии, что ± — минус. Вычтите \sqrt{225+12y} из 15.
x=-\frac{\sqrt{12y+225}}{6}+\frac{5}{2}
Разделите 15-\sqrt{225+12y} на 6.
В15 ЕГЭ по математике. Исследование функции
Задача 1. Найдите точку максимума функции
Решение: + показать
Задача 2. Найдите точку минимума функции
Решение: + показать
Задача 3. Найдите наименьшее значение функции на отрезке .
Решение: + показать
Задача 4. Найдите наибольшее значение функции на отрезке
Решение: + показать
Задача 5. Найдите наибольшее значение функции на отрезке
Решение: + показать
Задача 6. Найдите наибольшее значение функции на отрезке
Решение: + показать
Задача 7. Найдите точку максимума функции
Решение: + показать
Задача 8. Найдите наибольшее значение функции на отрезке
Решение: + показать
Задача 9. Найдите точку минимума функции .
Решение: + показать
Задача 10. Найдите наименьшее значение функции на
Решение: + показать
Задача 11.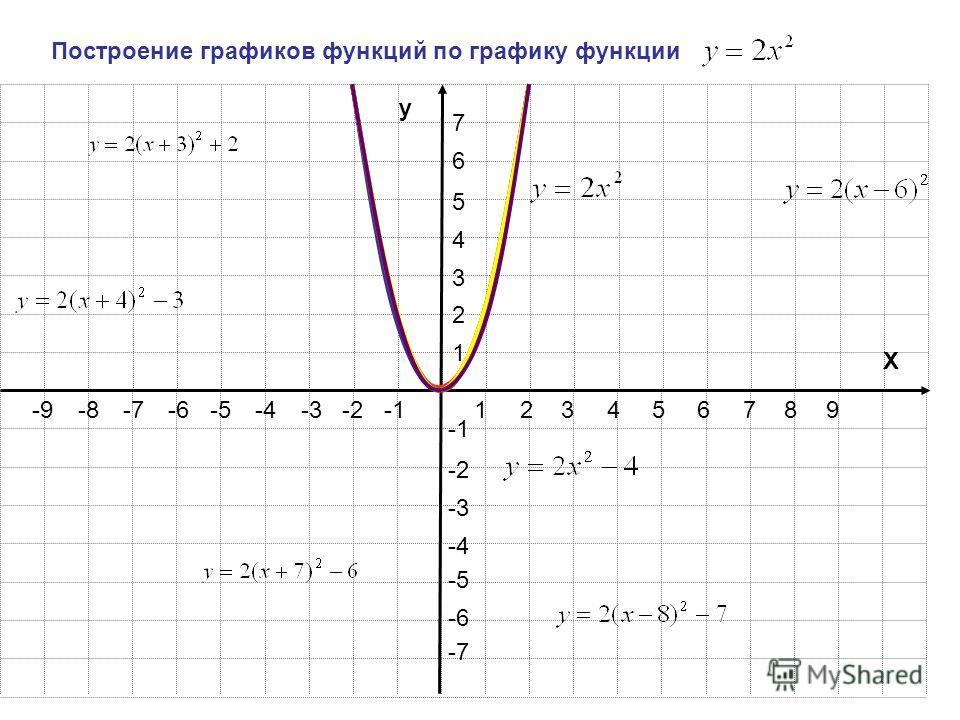
Найдите точку максимума функции
Решение: + показать
Задача 12. Найдите точку минимума функции
Решение: + показать
Задача 13. Найдите точку максимума функции
Решение: + показать
Задача 14. Найдите наименьшее значение функции на отрезке .
Решение: + показать
Задача 15. Найдите наибольшее значение функции на отрезке
Решение: + показать
Задача 16. Найдите наименьшее значение функции на отрезке
Решение: + показать
Задача 17. Найдите наименьшее значение функции на отрезке
Решение: + показать
Задача 18. Найдите наименьшее значение функции на отрезке .
Решение: + показать
Задача 19. Найдите наибольшее значение функции на отрезке
Решение: + показать
Задача 20. Найдите наименьшее значение функции на отрезке
Решение: + показать
Задача 21.
Найдите наибольшее значение функции на отрезке .
Решение: + показать
Задача 22. Найдите наименьшее значение функции на отрезке
Решение: + показать
Задача 23. Найдите наименьшее значение функции на отрезке
Решение: + показать
Задача 24. Найдите точку минимума функции принадлежащую промежутку .
Решение: + показать
* Замечание. Важно!
Не следует считать (могло сложиться такое мнение при разборе примеров выше), что наименьшее (наибольшее) значение функции на отрезке совпадает с минимумом (максимумом) на отрезке!
Например, на рисунке ниже наименьшее значение функции на отрезке достигается на конце отрезка , а именно, в точке .
То есть, вообще говоря, при нахождении наименьшего значения функции на отрезке следует выбрать наименьшую из величин:
1) (их может быть несколько) из рассматриваемого отрезка
2) ,
При нахождении наибольшего значения функции на отрезке следует выбрать большую из величин:
1) (их может быть несколько) из рассматриваемого отрезка
2) ,
Но, если, например, на рассматриваемом отрезке функция имеет только один экстремум – минимум и мы ищем наименьшее значение, то отпадает необходимость находить значения функции на концах отрезка.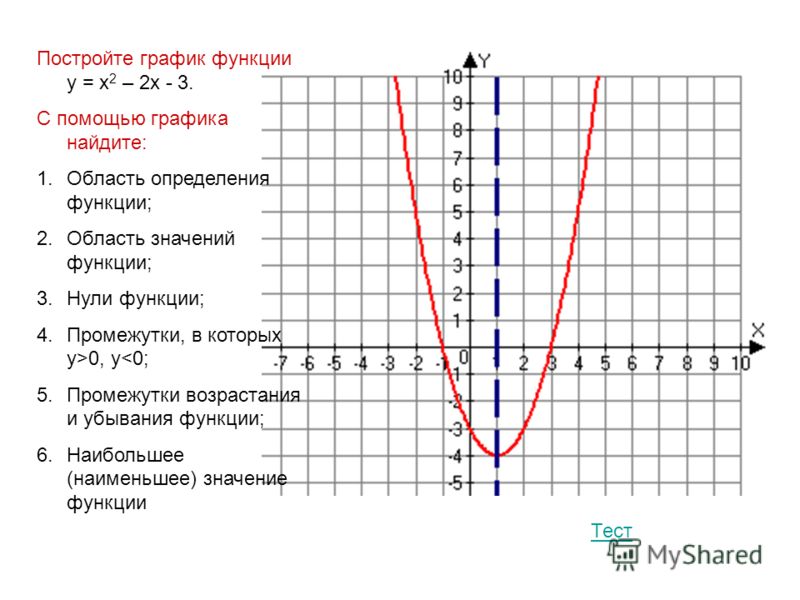
Аналогично в случае с нахождением наибольшего значения функции на отрезке, на котором содержится только один экстремум – максимум.
В случае же, когда на отрезке рассматриваемом функция не имеет экстремумов, то для нахождения наибольшего/наименьшего значений требуется лишь сравнить эти самые значения функции на концах отрезка и взять наибольшее/наименьшее из них.
Вы можете пройти тест “Исследование функции при помощи производной”
{2}-4ac}}{2a}.x=\frac{-\left(-9\right)±\sqrt{81-4\times 3\left(-y\right)}}{2\times 3}
Square -9.
x=\frac{-\left(-9\right)±\sqrt{81-12\left(-y\right)}}{2\times 3}
Умножить -4 раза 3.
x =\frac{-\left(-9\right)±\sqrt{81+12y}}{2\times 3}
Умножить -12 раз -y.
x=\frac{-\left(-9\right)±\sqrt{12y+81}}{2\times 3}
Прибавь 81 к 12y.
x=\frac{9±\sqrt{12y+81}}{2\times 3}
Противоположность -9равно 9.
x=\frac{9±\sqrt{12y+81}}{6}
Умножьте 2 раза на 3.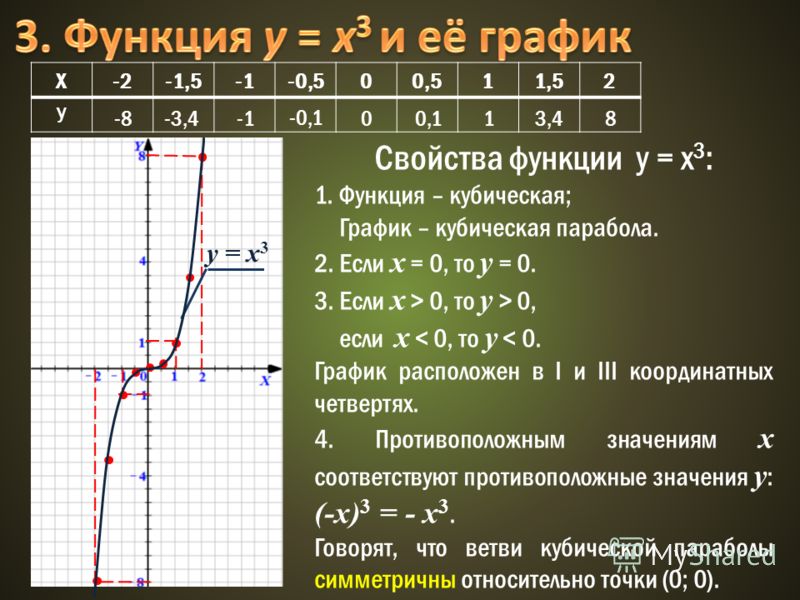
x=\frac{\sqrt{12y+81}+9}{6}
Теперь решите уравнение x=\frac{9±\sqrt{12y+81}}{6}, если ± равно плюсу. Добавьте 9 к \sqrt{81+12y}.
x=\frac{\sqrt{12y+81}}{6}+\frac{3}{2}
Разделите 9+\sqrt{81+12y} на 6.
x=\frac{- \sqrt{12y+81}+9}{6}
Теперь решите уравнение x=\frac{9±\sqrt{12y+81}}{6}, когда ± минус. Вычтите \sqrt{81+12y} из 9.
x=-\frac{\sqrt{12y+81}}{6}+\frac{3}{2} 9{ 2 } — 4 x — 5 = 0
Тригонометрия
4 \sin \theta \cos \theta = 2 \sin \theta
Линейное уравнение
y = 3x + 4
Арифметика 3 0 3 0 9
90Матрица
\left[ \begin{array} { l l } { 2 } & { 3 } \\ { 5 } & { 4 } \end{array} \right] \left[ \begin{array} { l l l } { 2 } & { 0 } & { 3 } \\ { -1 } & { 1 } & { 5 } \end{массив} \right]
Одновременное уравнение
\left. \begin{cases} { 8x+2y = 46 } \\ { 7x+3y = 47 } \end{cases} \right. 9{2}+2 x-3}
Как отразить график по оси x, оси y или исходной точке?
Это письмо недавно пришло от читателя Стюарта:
Можете ли вы объяснить принципы построения графика, включающего y = − f ( x ), являющегося отражением графика y = f ( x ) на оси x и график y = f (− x ) отражение графика y = f ( x ) по оси y-?
Спасибо
Мой ответ
Привет, Стюарт
Давайте посмотрим, что это значит, на примере.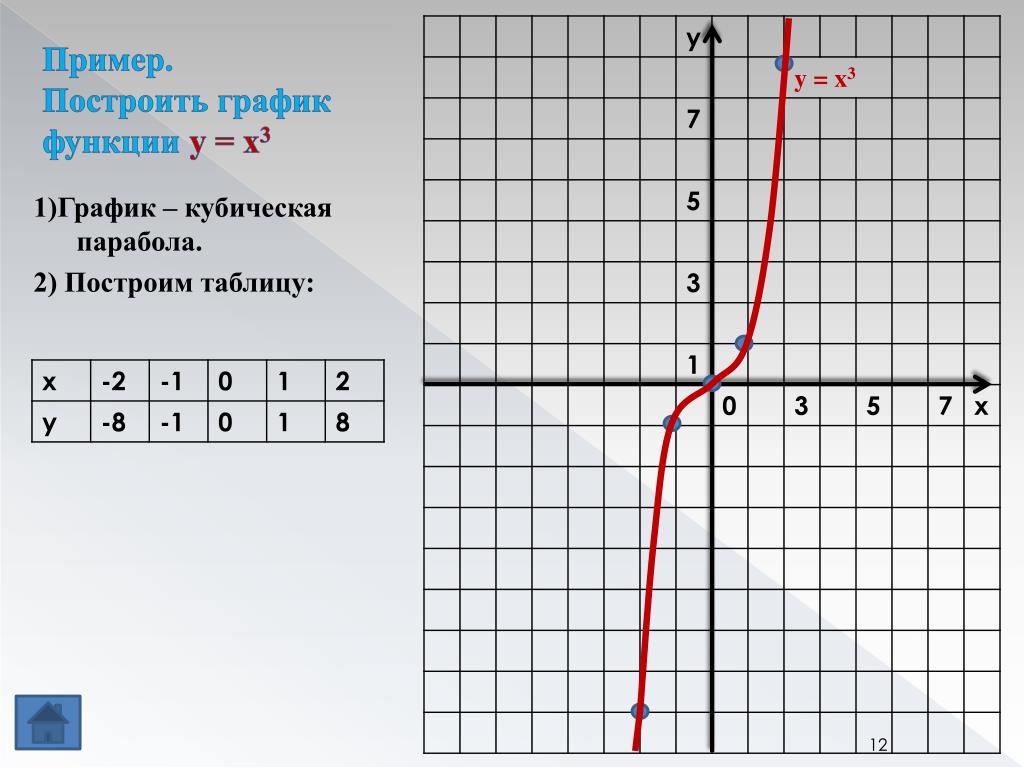
Пусть f ( x ) = 3 x + 2
Если вы не уверены, как это выглядит, вы можете построить график с помощью этого графического средства.
Вы увидите, что это прямая линия, наклон 3 (положительный, т. е. идет в гору слева направо) и y — точка пересечения 2.
Теперь давайте рассмотрим — f ( x ).
Это дает нам
— f ( x ) = -3 x — 2
Наша новая линия имеет отрицательный наклон (она идет вниз при сканировании слева направо) и проходит через — 2 на оси и .
Когда вы откладываете 2 линии на одних и тех же осях, это выглядит так:
Обратите внимание, что если вы отразите синий график ( y = 3 x + 2) в x -ось, вы получите зеленый график ( y = -3 x — 2) (как показано красными стрелками).
Что мы сделали, так это взяли каждое значение и и перевернули их вверх дном (это эффект минус спереди).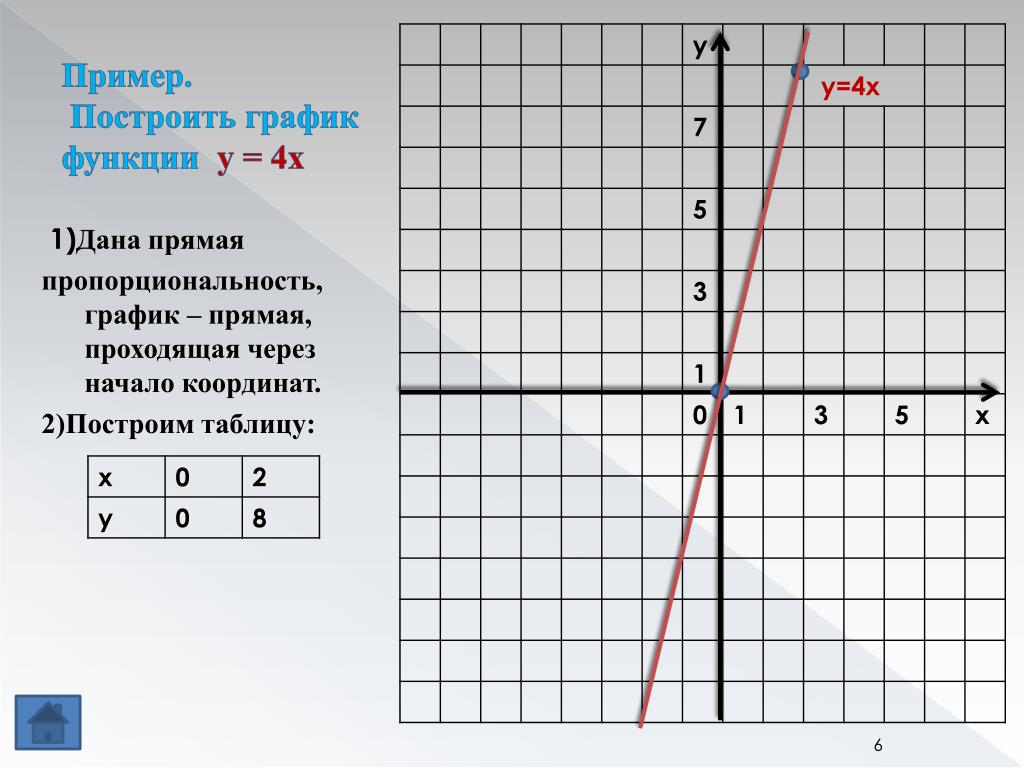
Теперь для
f (− x )Аналогично, f (− x ).
Поскольку f ( x ) = 3 x + 2, тогда
f ( -x ) = -3 x + 2 (замените каждое « x » на « -x «).
Теперь, изобразив их на тех же осях, мы имеем:
Обратите внимание, что эффект «минус» в f ( −x ) должен отражать синюю исходную линию ( y = 3 x + 2) по оси y , и мы получаем зеленую линию, которая равна ( y = −3 x + 2). Зеленая линия также проходит через 2 на y -ось.
Дальнейший пример
Вот пример использования кубического графа.
Синий график: F ( x ) = x 3 -3 x 2 + x -2 2 + x -2 2 + x -2 2 + x -2 2 + x -2 .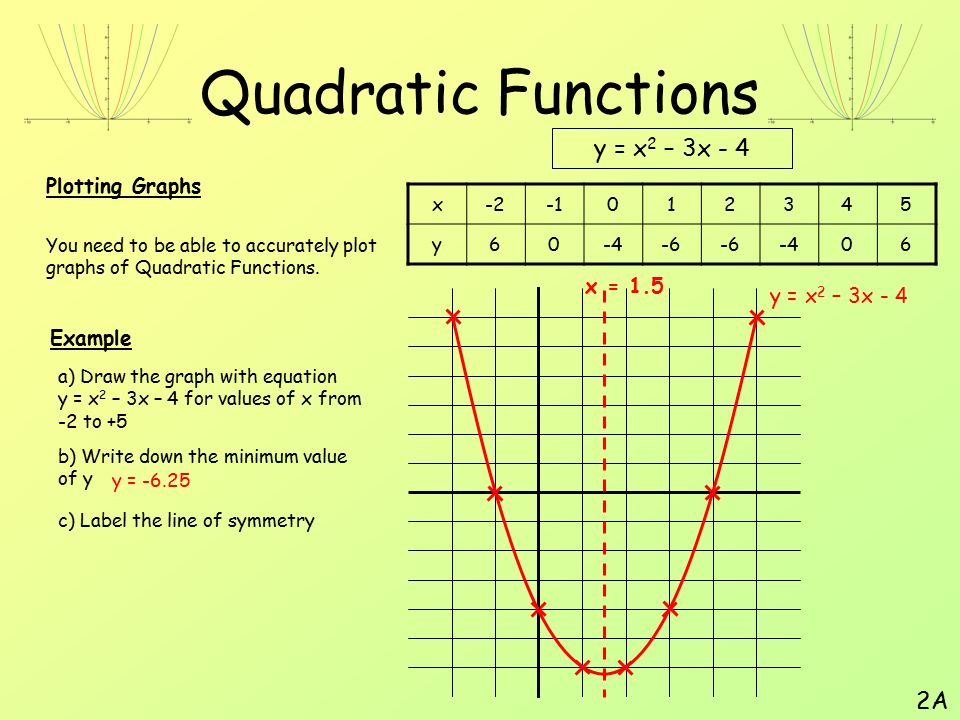
f ( x ) = — x 3 + 3 x 2 — x + 2
y-90 Теперь отразим по оси.
Синий график: F ( x ) = x 3 -3 x 2 + x 2 + x x 2 + x 2 + x 9013. f ( −x ) = −x 3 − 3 x 2 − x − 2
Even and Odd Functions
We really should mention even and odd functions прежде чем покинуть эту тему.
Для каждого из приведенных выше примеров отражения по осям x или y давали график, который отличался на . Но иногда отражение совпадает с исходным графиком. Мы говорим, что отражение «сопоставляется» с оригиналом.
Четные функции
Четная функция обладает свойством f ( − x ) = f ( x ).
То есть, если мы отразим четную функцию в y -оси, он будет выглядеть точно так же, как оригинал.
Примером ровной функции является F ( x ) = x 4 — 29 x 2 + 100
. Выше даже функция. ( x ) = ( x + 5)( x + 2)( x — 2)( x — 5)
Обратите внимание, если мы отразим график по оси 3 y — , мы получаем тот же граф (или можно сказать, что он «отображает» сам себя).
Нечетные функции
Нечетная функция имеет свойство f ( − x ) = − f ( x ).
На этот раз, если мы отразим нашу функцию в как по оси x , так и по оси y , и если она будет выглядеть точно так же, как оригинал, то у нас будет нечетная функция.
Этот тип симметрии называется исходной симметрией . Нечетная функция либо проходит через начало координат (0, 0), либо отражается через начало координат.