| 1 | Найти производную — d/dx | бревно натуральное х | |
| 2 | Оценить интеграл | интеграл натурального логарифма x относительно x | |
| 3 | Найти производную — d/dx | 92)||
| 21 | Оценить интеграл | интеграл от 0 до 1 кубического корня из 1+7x относительно x | |
| 22 | Найти производную — d/dx | грех(2x) | |
| 23 | Найти производную — d/dx | 9(3x) по отношению к x||
| 41 | Оценить интеграл | интеграл от cos(2x) относительно x | |
| 42 | Найти производную — d/dx | 1/(корень квадратный из х) | |
| 43 | Оценка интеграла 9бесконечность | ||
| 45 | Найти производную — d/dx | х/2 | |
| 46 | Найти производную — d/dx | -cos(x) | |
| 47 | Найти производную — d/dx | грех(3x) | 92+1|
| 68 | Оценить интеграл | интеграл от sin(x) по x | |
| 69 | Найти производную — d/dx | угловой синус(х) | |
| 70 | Оценить предел | ограничение, когда x приближается к 0 из (sin(x))/x 92 по отношению к х | |
| 85 | Найти производную — d/dx | лог х | |
| 86 | Найти производную — d/dx | арктан(х) | |
| 87 | Найти производную — d/dx | бревно натуральное 5х92 |
Алгебра, линейная алгебра, геометрия, векторная геометрия, тригонометрия, предварительное исчисление и исчисление с одной переменной
Определение обратных и взаимно однозначных функций
свою первоначальную функцию.
Чтобы определить обратную функцию, сама функция должна быть инъективной или взаимно однозначной, что означает, что она должна иметь только одно значение x для каждого значения y. Если функция не является инъективной или не взаимно однозначной, то область определения должна быть ограничена, прежде чем можно будет определить обратную функцию.Тригонометрические функции, заданные на целой прямой, не являются взаимно однозначными функциями, что делает их необратимыми. Однако можно соответствующим образом ограничить область определения каждой тригонометрической функции, чтобы они стали взаимно однозначной функцией. Обратные тригонометрические функции обратны тригонометрическим функциям с ограниченными областями.
Функция синуса главного значения
Функция синуса главного значения, обозначаемая как Sine или Sin, представляет собой ограничение синуса интервалом [-π/2,π/2].
Синус представляет собой функцию, тождественную обратной функции, называемой арксинусом.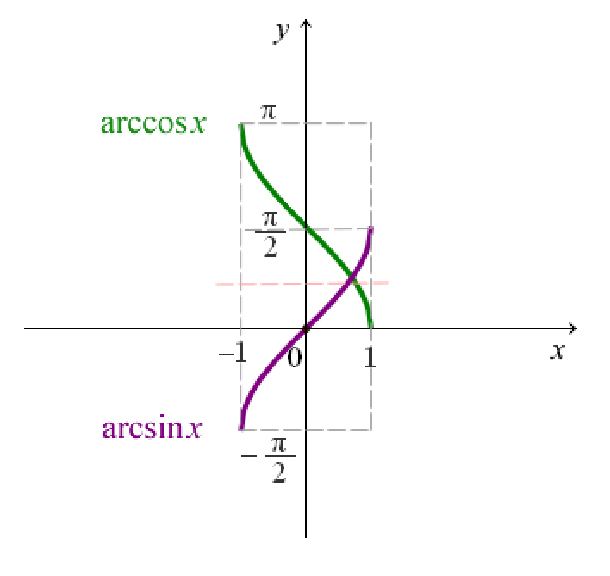
домен Arcsin = [-1,1] = диапазон Sin
диапазон Arcsin = [-π/2,π/2] = домен Sin
График y = Arcsinx является зеркальным отражением графика y = Sinx в строке y = x. Точно так же график x = Siny является зеркальным отражением графика x = Arcsiny на линии y = x. Обратите внимание, что y = Arcsinx равно x = Siny, а x = Arcsiny равно y = Sinx.
Производная Arcsin
Неявное дифференцирование используется для вычисления производной Arcsin.
Так как y = Arcsinx равно x = Siny:
Поскольку на единичной окружности между -π/2 и π/2 значение cosy положительно, то верно следующее:
Поскольку x = siny, тогда:
Таким образом, следующая производная от Arcsin с использованием вышеприведенного и цепного правила:
Неопределенный интеграл от Arcsin
Следующая производная от Arcsin при умножении x на 1/|a| и 1/а (а > 0):
Первая производная дает следующий неопределенный интеграл:
Функция косинуса главного значения
Функция косинуса главного значения, обозначаемая как косинус или Cos, представляет собой ограничение косинуса интервалом [0,π].
Косинус — это функция взаимно однозначного соответствия с обратной функцией, называемой арккосинусом. Арккосинус также обозначается как Arccos или cos⁻¹. Cos является убывающей функцией.
домен Arccos = [-1,1] = диапазон Cos
диапазон Arccos = [0,π] = домен Cos
График y = Arccosx является зеркальным отображением графика y = Cosx на линии y = x. Точно так же график x = Cosy является зеркальным отображением графика x = Arccosy в строке y = x. Обратите внимание, что y = Arccosx равно x = Cosy, а x = Arccosy равно y = Cosx.
Производная Arccos
Неявное дифференцирование используется для вычисления производной Arccos.
Так как y = Arccosx равно x = Cosy:
Поскольку siny положителен на единичной окружности между 0 и π, то верно следующее:
Так как x = cosy, тогда:
Следовательно, следующая производная от Arccos с использованием вышеприведенного и цепного правила:
Неопределенный интеграл от Arccos
Следующая производная от Arccos при умножении x на 1 /|а| и 1/a (a > 0):
Первая производная дает следующий неопределенный интеграл:
Тождества Arcsin и Arccos
Для -1 < x < 1:
Следовательно, Arcsinx + Arccosx равно константе на ( -1,1).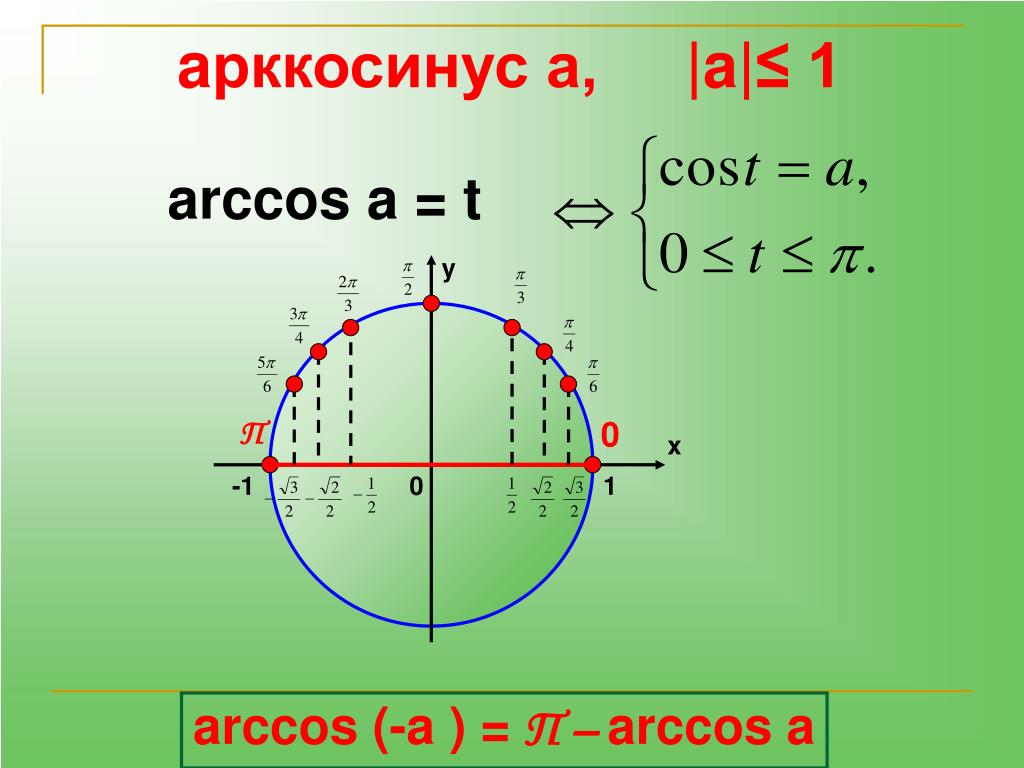
Поскольку Arcsin0 = 0 и Arccos0 = π/2, для любого x в (-1,1):
Arcsinx + Arccosx = π/2
Если -π/2 ≤ x ≤ π/2, то:
Функция тангенса главного значения
Функция тангенса главного значения, обозначаемая как тангенс или тангенс, является ограничением тангенса на интервал (-π/2,π/2).
Тангенс — это функция взаимно однозначного соответствия с обратной функцией, называемой арктангенс. Арктангенс также обозначается как Arctan или tan⁻¹. Тан является возрастающей функцией.
домен Arctan = (-∞,∞) = диапазон Tan
диапазон Arctan = (-π/2,π/2) = домен Tan
График y = Arctanx является зеркальным отображением графика y = Tanx на линии y = x. Точно так же график x = Tany является зеркальным отражением графика x = Arctany в строке y = x. Обратите внимание, что y = Arctanx равно x = Tany, а x = Arctany равно y = Tanx.
Производная от Arctan
Неявное дифференцирование используется для вычисления производной от Arctan.
Так как y = Arctanx равно x = Tany:
Поскольку sec²y положителен, то верно следующее:
Поскольку x = tany, тогда:
Следовательно, следующая производная от Arctan с использованием вышеприведенного и цепного правила:
Неопределенный интеграл от Arctan
Ниже приведена производная от Arctan, если x умножить на 1/a:
Это дает следующие два неопределенных интеграла:
Функция секущей главного значения
Функция секущей главного значения, обозначаемая как Secant или Sec, равна ограничение секанса до ограничения 1/Cosx, которое совпадает с ограничением Cosx [0,π], однако 1/Cosx не определено при x = π/2, поэтому секанс является ограничением секанса на [0,π/2 ) U (π/2,π].
Секанс — это функция взаимно однозначного соответствия с обратной функцией, называемой арксеканс. Арксеканс также обозначается как Arcsec или sec⁻¹.
домен Arcsec = (-∞,-1] U [1,∞) = диапазон Sec
график y = Arcsecx является зеркальным отображением графика y = Secx в линии y = x Аналогично, график x = Secy является зеркальным отображением графика x = Arcsecy в линии y = x. что y = Arcsecx равно x = Secy, а x = Arcsecy равно y = Secx.
Производная Arcsec
Производная Arccos используется для расчета производной Arcsec.
Неопределенный интеграл от Arcsec
Скоро…
Функция косеканса главного значения
Функция косеканса главного значения, обозначаемая как Cosecant или Csc, является ограничением косеканса до ограничения 1/Sinx, что то же самое ограничение как Sinx [-π/2,π/2], однако 1/Sinx не определено при x = 0, поэтому косеканс является ограничением косеканса на [-π/2,0) U (0,π/2].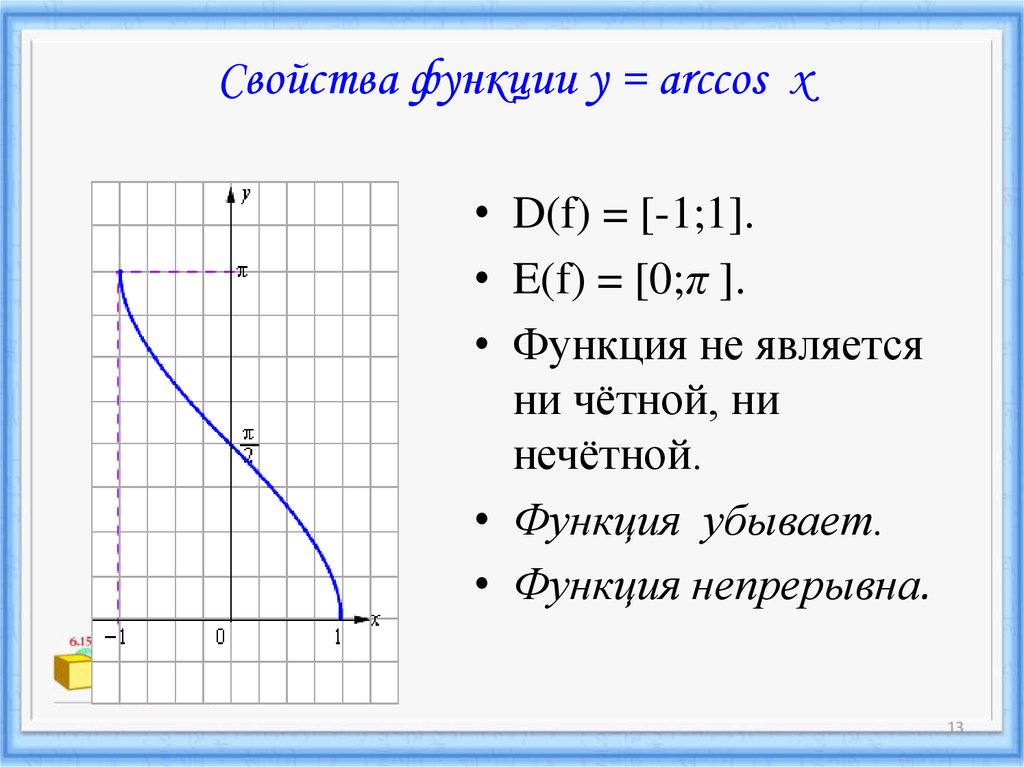
Косеканс — это функция взаимно однозначного соответствия с обратной функцией, называемой арккосеканс. Арккосеканс также обозначается как Arccsc или csc⁻¹.
домен Arccsc = (-∞,-1] U [1,∞) = диапазон Csc
диапазон Arccsc = [-π/2,0) U (0,π/2] = домен Csc
График y = Arccscx является зеркальным отображением графика y = Cscx на линии y = x Аналогично, график x = Cscy является зеркальным отражением графика x = Arccscy на линии y = x. Обратите внимание, что y = Arccscx равно x = Cscy, а x = Arccscy равно y = Cscx.
Производная Arccsc
Производная Arcsin используется для расчета производной Arccsc.
Неопределенный интеграл от Arccsc
Скоро…
Функция котангенса главного значения
Функция котангенса главного значения, обозначаемая как Cot, представляет собой ограничение котангенса тем же интервалом, что и Cosx, который равен [ 0,π], однако Cot не определен при x = 0, π, поэтому котангенс есть ограничение котангенса на (0,π).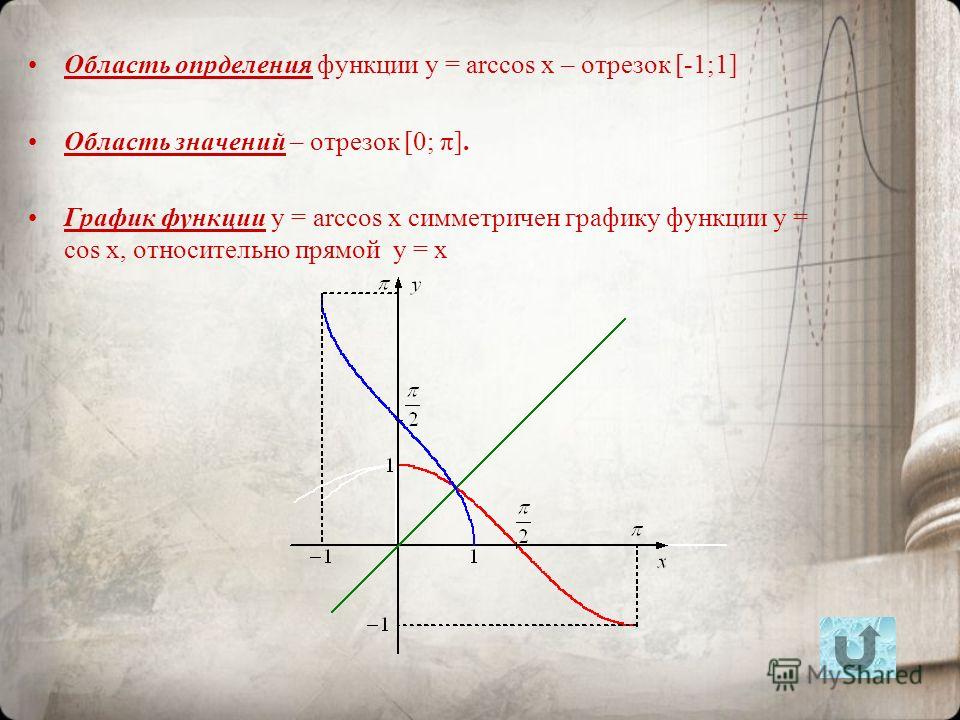
Котангенс — это функция взаимно однозначного соответствия с обратной функцией, называемой арккотангенс. Арккотангенс также обозначается как Arccot или cot⁻¹.
домен Arccot = (-∞,∞) = диапазон Cot
диапазон Arccot = (0,π) = домен Cot
График y = Arccotx является зеркальным отражением графика y = Cotx в линия у = х. Точно так же график x = Coty является зеркальным отражением графика x = Arccoty на линии y = x. Обратите внимание, что y = Arccotx равно x = Coty, а x = Arccoty равно y = Cotx.
Производная Arccot
Производная Arctan используется для расчета производной Arccot.
Indefinite Integral of Arccot
Coming soon…
Evaluate the following expression:
Since Arcsinx = y, Siny = x:
Evaluate the following expression:
Arctan(-1)
Так как Arctanx = y, Tany = x:
Arctan(-1) = y <–> Tany = -1 = -π/4
Обратите внимание на домен Тана на единичном круге.
Оцените следующее выражение:
Вычисление tan(2π/3):
Так как Arctanx = y, Tany = x:
Обратите внимание на домен Тана на единичной окружности.
Оцените следующее выражение:
Пусть t = Arccosx, тогда, если t = Arccosx, x = стоимость.
Оцените следующее:
tanArctan200
Пусть t = Arctanx, тогда, если t = Arctanx, x = tant.
tant = x = 200
Упростите следующее выражение:
cosArccosx
Пусть t = Arccosx, тогда, если t = Arccosx, x = стоимость.
cost = x = x
Упростите следующее выражение:
sinArccosx
Пусть t = Arccosx, тогда, если t = Arccosx, x = стоимость.
Упростите следующее выражение:
tanArccosx
Пусть t = Arccosx, тогда, если t = Arccosx, x = стоимость и sint = √(1 — cos²t) = √(1 — x²).
Упростите следующее выражение:
Arcsinsinx
Ниже приведен график y = Arcsinsinx:
Обратите внимание, что есть интервалы, в которых Arcsinsinx увеличивается и уменьшается.
Следующая формула охватывает все интервалы x, когда Arcsinsinx увеличивается:
Причина, по которой существует 2kπ, заключается в том, что требуется период 2kπ, чтобы перейти от следующего интервала x, когда Arcsinsinx увеличивается.
Причина, по которой π/2 вычитается из левой части, а π/2 прибавляется к правой, заключается в том, что начальный интервал всех интервалов x при увеличении Arcsinsinx равен (-π/2,π/2). Обратите внимание, что для перехода от одного возрастающего интервала к другому требуется период π.
Следующая формула охватывает все интервалы x, когда Arcsinsinx уменьшается:
Причина, по которой существует 2kπ, заключается в том, что требуется период 2kπ, чтобы перейти от следующего интервала x, когда Arcsinsinx уменьшается.
Причина, по которой π/2 добавляется слева, а 3π/2 добавляется справа, заключается в том, что начальный интервал всех интервалов x при уменьшении Arcsinsinx равен (π/2,3π/2), учитывая, что π /2 — конечная точка интервала возрастания Arcsinsinx.
Также обратите внимание, что для перехода от одного убывающего интервала к другому требуется период π.
Поскольку домен Sinx равен [-π/2,π/2]:
Тогда Arcsinsinx = ArcsinsinX = Arcsinsin(x — 2kπ) = x — 2kπ
Тогда Arcsinsinx = ArcsinsinX = Arcsinsin(2kπ + π — x ) = 2kπ + π — x
Обратите внимание, что использовались законы неравенств.
Следовательно, есть два возможных ответа на упрощение Arcsinsinx:
Упрощение следующего выражения:
Arccoscosx
Ниже приведен график y = Arccoscosx:
Обратите внимание, что есть интервалы, в которых Arccoscosx увеличивается и уменьшается.
Следующая формула охватывает все интервалы x, когда Arccoscosx увеличивается:
Причина, по которой существует 2kπ, заключается в том, что требуется период 2kπ, чтобы перейти от следующего интервала x, когда Arccoscosx увеличивается.
Причина, по которой ничего не вычитается из левой части, а π добавляется в правую, заключается в том, что начальный интервал всех интервалов x при увеличении Arccoscosx равен (0,π).
Обратите внимание, что для перехода от одного возрастающего интервала к другому требуется период π.
Следующая формула охватывает все интервалы x, когда Arccoscosx уменьшается:
Причина, по которой существует 2kπ, заключается в том, что требуется период 2kπ, чтобы перейти от следующего интервала x, когда Arccoscosx уменьшается.
Причина, по которой π добавляется слева, а 2π — справа, заключается в том, что начальный интервал всех интервалов x при уменьшении Arccoscosx равен (π, 2π), учитывая, что π является конечной точкой интервала когда Arccoscosx увеличивается. Также обратите внимание, что для перехода от одного убывающего интервала к другому требуется период π.
Так как домен Cosx равен [0,π]:
Тогда Arccoscosx = ArccoscosX = Arccoscos(x — 2kπ) = x — 2kπ
Тогда Arccoscosx = ArccoscosX = Arccoscos(2kπ + 2π — x) = 2kπ + 2π — x
Обратите внимание, что использовались законы неравенств.
Таким образом, есть два возможных ответа на упрощение Arccoscosx:
Нарисуйте следующую функцию:
y = sinArcsinx
Начните с упрощения выражения функции.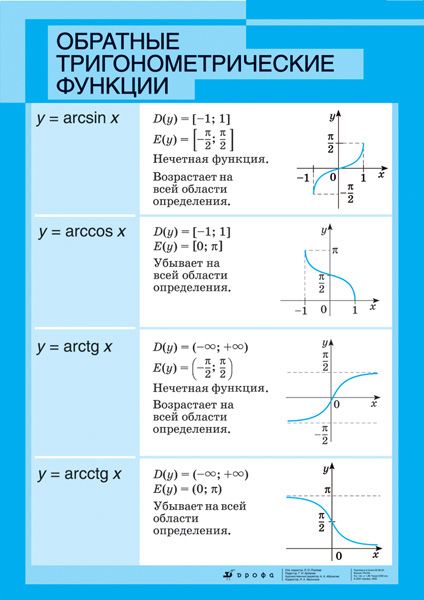
Пусть t = Arcsinx, тогда, если t = Arcsinx, x = sint.
sint = x
Следовательно, график y = sinArcsinx выглядит как y = x, однако домен и диапазон другие.
Область определения внутренней функции Arcsinx равна [-1,1]. Область определения всей упрощенной функции x равна (-∞, ∞). Однако важно учитывать домен внутренней функции, поэтому конечный домен — [-1,1].
Диапазон всей функции равен y(Dt), где Dt — область значений t или Arcsinx. Домен Arcsinx — [-1,1]. Диапазон y(Dt) упрощен по y с доменом t или диапазоном x с доменом Arcsinx, который по-прежнему равен [-1,1].
Следовательно, зная, что sinArcsinx представляет собой форму y = x с областью определения и диапазоном значений [-1,1], следующий график y = sinArcsinx:
Дифференцируем следующую функцию:
y = sinArcsinx
Поскольку sinArcsinx был упрощен до x:
Однако можно провести различие, используя цепное правило и упрощение:
Пусть t = Arcsinx, тогда, если t = Arcsinx, x = sint.
Различают следующую функцию:
Используя цепное правило:
Дифференцируйте следующую функцию:
Используя цепное правило, предполагая, что x является независимой переменной:
Дифференцируйте следующую функцию:
f(0)907
Используя правило произведения и правило цепочки:
Дифференцируйте следующую функцию:
F(x) = (1 + x²)Arctanx
Используя правило произведения и правило цепочки:
Дифференцируйте следующую функцию:
Использование правила Отношения и правила цепи:
Дифференцируйте следующую функцию:
. правило и цепное правило:
Дифференцируйте следующую функцию:
Используя правило вычитания и цепное правило:
Решите следующую задачу с начальными значениями:
Когда его просят решить задачу с начальным значением, он запрашивает исходную функцию y, учитывая начальную точку.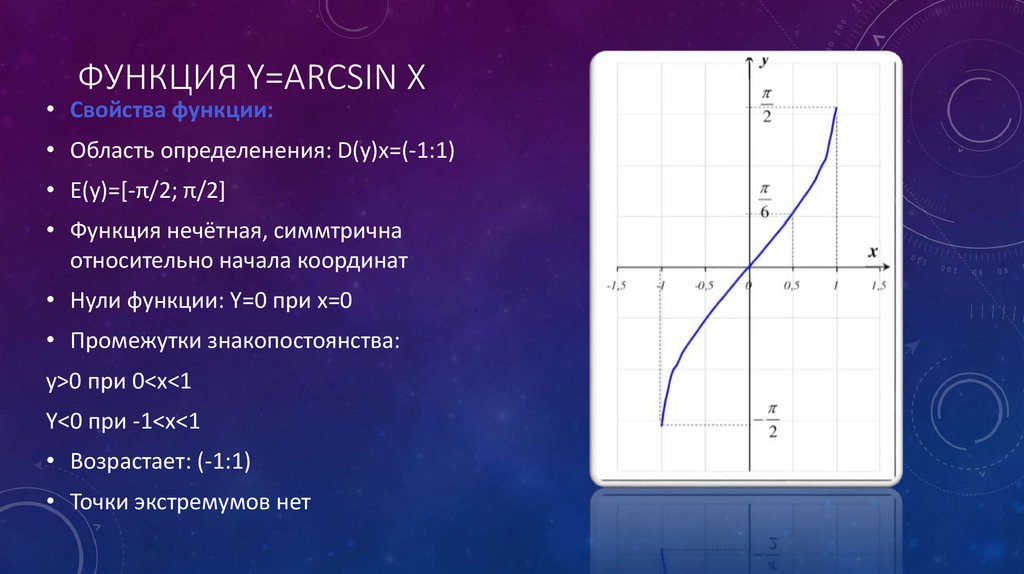
Антидифференцирующий y’:
Нахождение C, когда y(0) = 1:
y = Arctanx + C
1 = Arctan0 + C
1 = 0 + C
C = 1
Следовательно, y = Arctanx + 1
Решите следующую задачу с начальными значениями:
Когда просят решить задачу с начальными значениями, запрашивается исходная функция y при заданной начальной точке.
Антидифференцирующий y’:
Нахождение C, когда y(½) = 1:
y = Arcsinx + C
1 = Arcsin(½) + C
1 = π/6 + C
C = 1 — π/6
Следовательно, y = Arcsinx + 1 — π/6
Упрощение следующего выражения:
cosArctanx
Пусть t = Arctanx, тогда если t = Arctanx, x = tant.
Тождество, относящееся к косинусу и тангенсу, следующее:
Поскольку x = tant:
Следовательно:
Упростите следующее выражение:
sinArctan2x
Пусть t = Arctan2x, тогда, если t = Arctan2x, то 2x = tant.
Нахождение тождества, связанного с синусом и тангенсом:
Нахождение тождества, связанного с косинусом и тангенсом:
Так как 2x = tant:
Следовательно:
Найдите f(x) следующей производной, если f (1) = 0:
Антидифференцирующая f'(x):
Результат C, когда f(1) = 0:
Следовательно:
Оцените следующее выражение:
tanArcsec4
Пусть t = Arcsec4, тогда, если t = Arcsec4, sect = 4.