| 1 | Найти точное значение | sin(30) | |
| 2 | Найти точное значение | sin(45) | |
| 3 | Найти точное значение | sin(30 град. ) | |
| 4 | Найти точное значение | sin(60 град. ) | |
| 5 | Найти точное значение | tan(30 град. ) | |
| 6 | Найти точное значение | arcsin(-1) | |
| 7 | Найти точное значение | sin(pi/6) | |
| 8 | cos(pi/4) | ||
| 9 | Найти точное значение | sin(45 град. ) ) | |
| 10 | Найти точное значение | sin(pi/3) | |
| 11 | Найти точное значение | arctan(-1) | |
| 12 | Найти точное значение | cos(45 град. ) | |
| 13 | Найти точное значение | cos(30 град. ) | |
| 14 | Найти точное значение | tan(60) | |
| 15 | Найти точное значение | csc(45 град. ) | |
| 16 | Найти точное значение | tan(60 град. ) | |
| 17 | Найти точное значение | sec(30 град. ) ) | |
| 18 | Найти точное значение | cos(60 град. ) | |
| 19 | Найти точное значение | cos(150) | |
| 20 | Найти точное значение | sin(60) | |
| 21 | Найти точное значение | cos(pi/2) | |
| 22 | Найти точное значение | tan(45 град. ) | |
| 23 | Найти точное значение | arctan(- квадратный корень из 3) | |
| 24 | Найти точное значение | csc(60 град. ) | |
| 25 | Найти точное значение | sec(45 град. ) ) | |
| 26 | Найти точное значение | csc(30 град. ) | |
| 27 | Найти точное значение | sin(0) | |
| 28 | Найти точное значение | sin(120) | |
| 29 | Найти точное значение | cos(90) | |
| 30 | Преобразовать из радианов в градусы | pi/3 | |
| 31 | Найти точное значение | tan(30) | |
| 32 | Преобразовать из градусов в радианы | 45 | |
| 33 | Найти точное значение | cos(45) | |
| 34 | Упростить | sin(theta)^2+cos(theta)^2 | |
| 35 | Преобразовать из радианов в градусы | pi/6 | |
| 36 | Найти точное значение | cot(30 град. ) ) | |
| 37 | Найти точное значение | arccos(-1) | |
| 38 | Найти точное значение | arctan(0) | |
| 39 | Найти точное значение | cot(60 град. ) | |
| 40 | Преобразовать из градусов в радианы | 30 | |
| 41 | Преобразовать из радианов в градусы | (2pi)/3 | |
| 42 | Найти точное значение | sin((5pi)/3) | |
| 43 | Найти точное значение | sin((3pi)/4) | |
| 44 | Найти точное значение | tan(pi/2) | |
| 45 | Найти точное значение | sin(300) | |
| 46 | Найти точное значение | cos(30) | |
| 47 | Найти точное значение | cos(60) | |
| 48 | Найти точное значение | cos(0) | |
| 49 | Найти точное значение | cos(135) | |
| 50 | Найти точное значение | cos((5pi)/3) | |
| 51 | Найти точное значение | cos(210) | |
| 52 | Найти точное значение | sec(60 град. ) ) | |
| 53 | Найти точное значение | sin(300 град. ) | |
| 54 | Преобразовать из градусов в радианы | 135 | |
| 55 | Преобразовать из градусов в радианы | 150 | |
| 56 | Преобразовать из радианов в градусы | (5pi)/6 | |
| 57 | Преобразовать из радианов в градусы | (5pi)/3 | |
| 58 | Преобразовать из градусов в радианы | 89 град. | |
| 59 | Преобразовать из градусов в радианы | 60 | |
| 60 | Найти точное значение | sin(135 град. ) ) | |
| 61 | Найти точное значение | sin(150) | |
| 62 | Найти точное значение | sin(240 град. ) | |
| 63 | Найти точное значение | cot(45 град. ) | |
| 64 | Преобразовать из радианов в градусы | (5pi)/4 | |
| 65 | Найти точное значение | sin(225) | |
| 66 | Найти точное значение | sin(240) | |
| 67 | Найти точное значение | cos(150 град. ) | |
| 68 | Найти точное значение | tan(45) | |
| 69 | Вычислить | sin(30 град. ) ) | |
| 70 | Найти точное значение | sec(0) | |
| 71 | Найти точное значение | cos((5pi)/6) | |
| 72 | Найти точное значение | csc(30) | |
| 73 | Найти точное значение | arcsin(( квадратный корень из 2)/2) | |
| 74 | Найти точное значение | tan((5pi)/3) | |
| 75 | Найти точное значение | tan(0) | |
| 76 | Вычислить | sin(60 град. ) | |
| 77 | Найти точное значение | arctan(-( квадратный корень из 3)/3) | |
| 78 | Преобразовать из радианов в градусы | (3pi)/4 | |
| 79 | Найти точное значение | sin((7pi)/4) | |
| 80 | Найти точное значение | arcsin(-1/2) | |
| 81 | Найти точное значение | sin((4pi)/3) | |
| 82 | Найти точное значение | csc(45) | |
| 83 | Упростить | arctan( квадратный корень из 3) | |
| 84 | Найти точное значение | sin(135) | |
| 85 | Найти точное значение | sin(105) | |
| 86 | Найти точное значение | sin(150 град. ) ) | |
| 87 | Найти точное значение | sin((2pi)/3) | |
| 88 | Найти точное значение | tan((2pi)/3) | |
| 89 | Преобразовать из радианов в градусы | pi/4 | |
| 90 | Найти точное значение | sin(pi/2) | |
| 91 | Найти точное значение | sec(45) | |
| 92 | Найти точное значение | cos((5pi)/4) | |
| 93 | Найти точное значение | cos((7pi)/6) | |
| 94 | Найти точное значение | arcsin(0) | |
| 95 | Найти точное значение | sin(120 град. 2 2 |
Ответы | ||||||||||||||||||||||||||||||||||||||||||||||||||||||
| |||||||||||
|
|
| |||||||||||||||||||||||||||||||||||||||||||||||||||
Посмотреть всех экспертов из раздела Учеба и наука
| Похожие вопросы |
Алла на 6 лет моложе Веры. Сейчас папа в 11 раз старше Аллы и на 24 года старше Веры. Через сколько лет папа будет в 3 раза старше Веры?
Решено
На доске написано натурвльное число b. Про него сказали три утверждения 1. Это число четное, 2. Это число меньше 102, 3. Уравнение х2 + 20х +b=0 имеет хотя бы 1 корень. Какое наибольшее число
Это число меньше 102, 3. Уравнение х2 + 20х +b=0 имеет хотя бы 1 корень. Какое наибольшее число
На экзамене 20 билетов, Андрей не выучил 1 из них. Найдите вероятность того, что ему попадется выученный билет
Решено
Сколько дров надо сжечь в топке паровой машины с КПД=33 %, чтобы получить воду при 14 °С из снега массой 104 кг, взятого при температуре−11 °С.
Билеты в кино стоят 4…
Пользуйтесь нашим приложением
ОБРАТНЫЕ ТРИГОНОМЕТРИЧЕСКИЕ ФУНКЦИИ • Большая российская энциклопедия
ОБРА́ТНЫЕ ТРИГОНОМЕТРИ́ЧЕСКИЕ ФУ́НКЦИИ (аркфункции, круговые функции), функции, обратные тригонометрическим функциям. Значения О. т. ф. являются решением следующей задачи: найти число по заданному значению его тригонометрич. функции. Шести осн. тригонометрич. функциям соответствуют шесть О. {–1}x.$
{–1}x.$
| Таблица 1. Свойства обратных тригонометрических функций | |||
| Функция | Область определения | Множество значений | Монотонность |
| $\arcsin x$ | $-1⩽x⩽1$ | $\big[-\frac{\pi}{2}, \frac{\pi}{2}\big]$ | возрастает |
| $\arccos x$ | $-1⩽x⩽1$ | $[0, \pi]$ | убывает |
| $\arctan x$ | $-\infty \lt x +\infty$ | $\big[-\frac{\pi}{2}, \frac{\pi}{2}\big]$ | возрастает |
| $\textrm {arccot}\,x$ | $-\infty \lt x \lt +\infty$ | $[0, \pi]$ | убывает |
| Таблица 2. Значения обратных тригонометрических функций арксинус и арккосинус | ||
| Аргумент | Функция | |
| $$\arcsin x$$ | $$\arccos x$$ | |
| $$-1$$ | $$-\frac{\pi}{2}$$ | $$\pi$$ |
| $$-\frac{\sqrt3}{2}$$ | $$-\frac{\pi}{3}$$ | $$\frac{5\pi}{6}$$ |
| $$-\frac{\sqrt 2}{2}$$ | $$-\frac{\pi}{4}$$ | $$\frac{3\pi}{4}$$ |
| $$-\frac{1}{2}$$ | $$-\frac{\pi}{6}$$ | $$\frac{2\pi}{3}$$ |
| $$0$$ | $$0$$ | $$\frac{\pi}{2}$$ |
| $$\frac{1}{2}$$ | $$\frac{\pi}{6}$$ | $$\frac{\pi}{3}$$ |
| $$\frac{\sqrt 2}{2}$$ | $$\frac{\pi}{4}$$ | $$\frac{\pi}{4}$$ |
| $$\frac{\sqrt 3}{2}$$ | $$\frac{\pi}{3}$$ | $$\frac{\pi}{6}$$ |
| $$1$$ | $$-\frac{\pi}{2}$$ | $$0$$ |
Таблица 3. 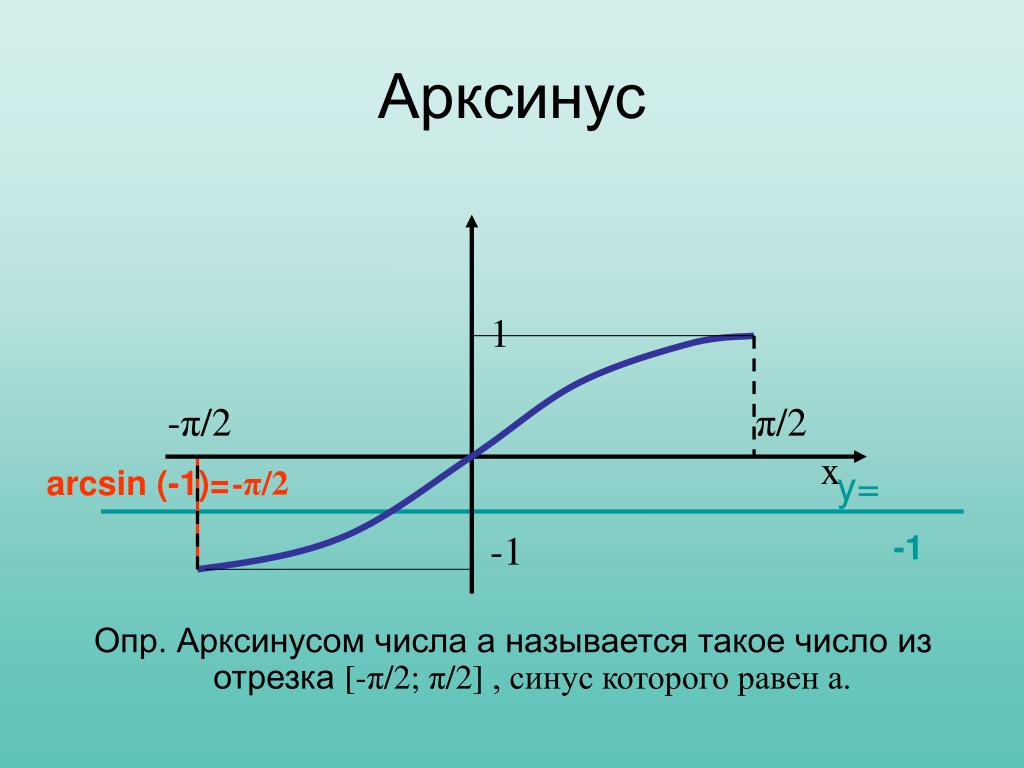 Значения обратных тригонометрических функций арктангенс и арккотангенс Значения обратных тригонометрических функций арктангенс и арккотангенс | ||
Аргумент | Функция | |
| $$\arctan x$$ | $$\textrm{arccot}\,x $$ | |
| $$-\infty$$ | $$-\frac{\pi}{2}$$ | $$\pi$$ |
| $$-\sqrt3$$ | $$-\frac{\pi}{3}$$ | $$\frac{5\pi}{6}$$ |
| $$-1$$ | $$-\frac{\pi}{4}$$ | $$\frac{3\pi}{4}$$ |
| $$-\frac{\sqrt3}{3}$$ | $$-\frac{\pi}{6}$$ | $$\frac{2\pi}{3}$$ |
| $$0$$ | $$0$$ | $$\frac{\pi}{2}$$ |
| $$\frac{\sqrt3}{3}$$ | $$\frac{\pi}{6}$$ | $$\frac{\pi}{3}$$ |
| $$1$$ | $$\frac{\pi}{4}$$ | $$\frac{\pi}{4}$$ |
| $$\sqrt 3$$ | $$\frac{\pi}{3}$$ | $$\frac{\pi}{6}$$ |
| $$+\infty$$ | $$\frac{\pi}{2}$$ | $$0$$ |
Впервые спец. символы для О. т. ф. использовал Д. Бернулли (1729, 1736), совр. обозначения для О. т. ф. ввели в 1772 австр. математик К. Шерфер и Ж. Лагранж.
символы для О. т. ф. использовал Д. Бернулли (1729, 1736), совр. обозначения для О. т. ф. ввели в 1772 австр. математик К. Шерфер и Ж. Лагранж.
Обратные тригонометрические функции действительного переменного $arcsinx, arccosx, arctgx, arcctgx$ определяются как обратные к функциям $\sin x, \cos x, \tan x, \cot x$, заданным соответственно на промежутках $[-π/2, π/2], [0, π], (-π/2, π/2), (0, π)$. Т. о., равенство$$y=\arcsin x$$означает, что $\sin y=x$ и $-π/2 \leqslant y \leqslant π/2:$$$\{ y=\arcsin x \} ⇔ \{ \sin y=x, -π/2 \leqslant y \leqslant π/2 \}.$$
Аналогично,$$\{ y= \arccos x \} ⇔ \{ \cos y=x, 0 \leqslant y \leqslant π \}, \\ \{ y= \arctan x \} ⇔ \{ \tan y=x, -\pi/2 \lt y \lt \pi/2 \}, \\ \{y = \arctan x \} ⇔ \{\cot y=x, 0 \lt y \lt \pi \}.$$ Эти О. т. ф. однозначны, непрерывны и их свойства вытекают из свойств тригонометрич. функций (табл. 1). Значения О. т. ф. для некоторых значений аргумента приведены в таблицах 2 и 3. 2… -reshimne.ru
2… -reshimne.ru
Новые вопросы
Ответы
Похожие вопросы
У=-3х+2 постройте график…
Найти производную функции f(x)=sinx*tgx в точке x0=π/6…
Решить уравнения …13*х+15*х-24*х=60. и .19*(39-2*у) =703…
Петя прочитал 40 страниц. Это состовляет 30% от всей книги. Сколько страниц в книге?…
В столовую привезли 12 одинаковых пакетов с луком и 16 таких же пакетов с морковью.Сколько килограммов моркови привезли в столовую,если лука было привезено 84 кг
. ..
..
Помогите пожалуйста даю 15 баллов! Задание номер 12 сделать столбиком, по действиям….
Математика
Литература
Алгебра
Русский язык
Геометрия
Английский язык
Химия
Физика
Биология
Другие предметы
История
Обществознание
Окружающий мир
География
Українська мова
Українська література
Қазақ тiлi
Беларуская мова
Информатика
Экономика
Музыка
Право
Французский язык
Немецкий язык
МХК
ОБЖ
Психология
Электронный справочник по математике обратные тригонометрические функции арксинус арккосинус арктангенс арккотангенс определение свойства графики значения
| Справочник по математике | Тригонометрия |
ОПРЕДЕЛЕНИЕ 1. Пусть число a удовлетворяет неравенству . Число x называют арксинусом числа a и обозначают x = arcsin a, если выполнены два условия:
Пусть число a удовлетворяет неравенству . Число x называют арксинусом числа a и обозначают x = arcsin a, если выполнены два условия:
ОПРЕДЕЛЕНИЕ 2. Пусть число a удовлетворяет неравенству . Число x называют арккосинусом числа a и обозначают x = arccos a, если выполнены два условия:
ОПРЕДЕЛЕНИЕ 3. Рассмотрим произвольное число a . Число x называют арктангенсом числа a и обозначают x = arctg a, если выполнены два условия:
ОПРЕДЕЛЕНИЕ 4. Рассмотрим произвольное число a . Число x называют арккотангенсом числа a и обозначают x = arcctg a, если выполнены два условия:
Арксинус, арккосинус, арктангенс и арккотангенс удовлетворяют, в частности, следующим соотношениям:
| arcsin (– a) = – arcsin a , |
| arccos (– a) = = π – arccos a , |
| arctg (– a) = – arctg a , |
| arcctg (– a) = = π – arcctg a .  |
Обратными тригонометрическими функциями называют функции:
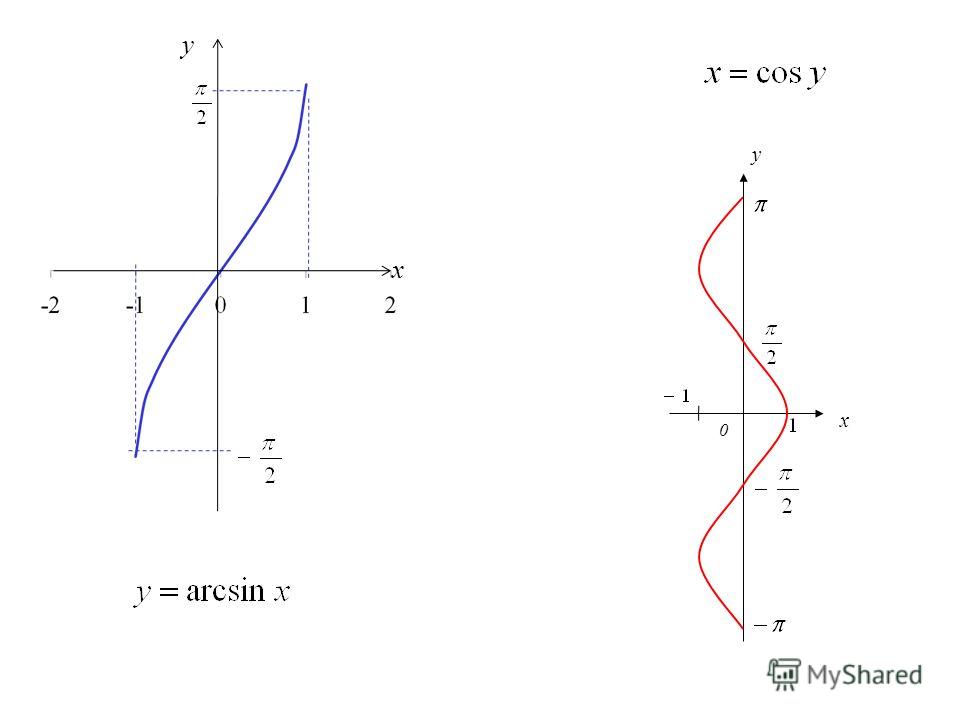
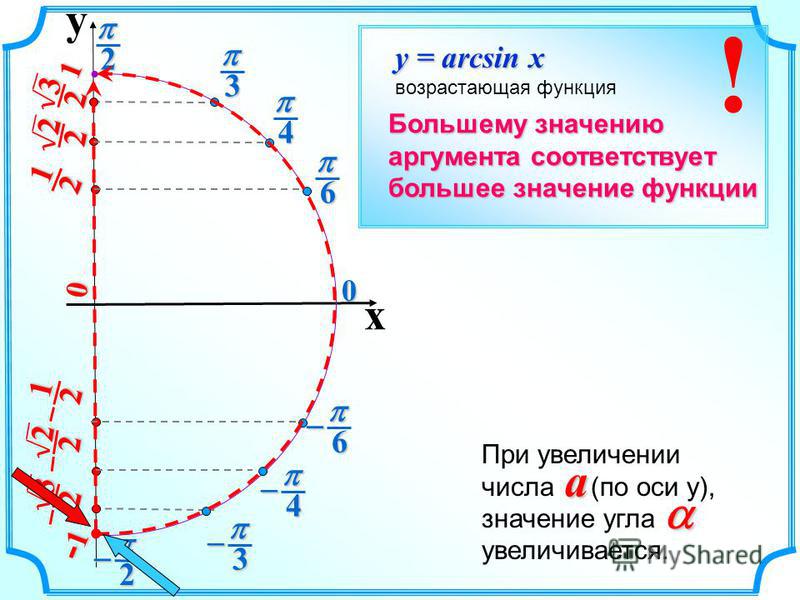
Графики этих функций изображены на рисунках 1, 2, 3, 4.
Рис. 1. График функции y = arcsin x
ТАБЛИЦА ЗНАЧЕНИЙ ФУНКЦИИ y = arcsin x
| x | – 1 | 0 | 1 | ||||||
| y = arcsin x | 0 |
| x | y = arcsin x |
| – 1 | |
| 0 | 0 |
| 1 |
Рис.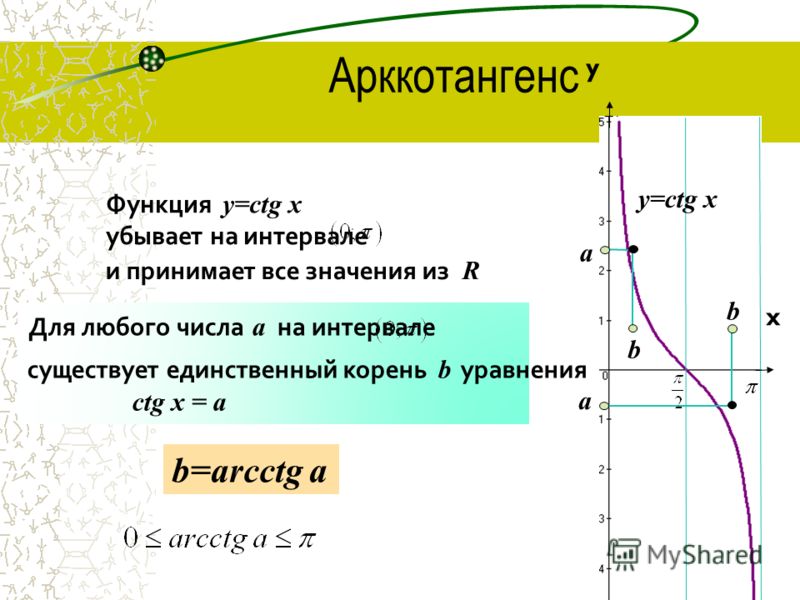 2. График функции y = arccos x
2. График функции y = arccos x
ТАБЛИЦА ЗНАЧЕНИЙ ФУНКЦИИ y = arccos x
| x | – 1 | 0 | 1 | ||||||
| y = arccos x | π | 0 |
| x | y = arccos x |
| – 1 | π |
| 0 | |
| 1 | 0 |
Рис. 3. График функции y = arctg x
ТАБЛИЦА ЗНАЧЕНИЙ ФУНКЦИИ y = arctg x
| x | – 1 | 0 | 1 | ||||
| y = arctg x | 0 |
| x | y = arctg x |
| – 1 | |
| 0 | 0 |
| 1 | |
Рис.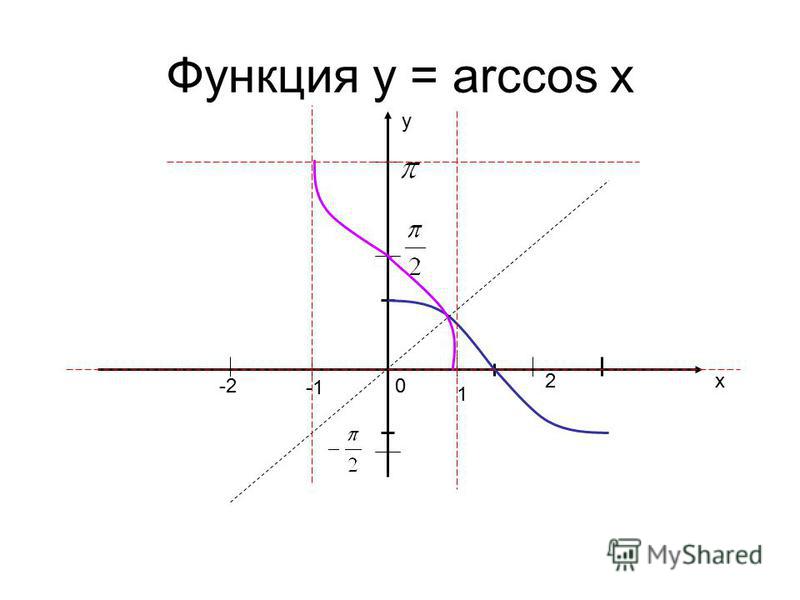 4. График функции y = arcctg x
4. График функции y = arcctg x
ТАБЛИЦА ЗНАЧЕНИЙ ФУНКЦИИ y = arcctg x
| x | – 1 | 0 | 1 | ||||
| y = arcctg x |
| x | y = arcctg x |
| – 1 | |
| 0 | |
| 1 | |
ПРИМЕР. Решить уравнение
2 arcsin 2x = arccos 7x .
РЕШЕНИЕ. Возьмём косинус от обеих частей уравнения. Тогда в левой части уравнения получим:
cos ( 2 arcsin 2x ) = 1 – 2sin2( arcsin 2x ) = 1 – 2 ( 2x )2 = 1 – 8x2 .
cos ( 2 arcsin 2x ) =
= 1 – 2sin2( arcsin 2x ) =
= 1 – 2 ( 2x )2 = 1 – 8x2 .
В правой части уравнения получим:
cos ( arccos 7x ) = 7x.
Следовательно, возникает квадратное уравнение:
В силу того, что область определения обратных тригонометрических функций y = arcsin x и y = arccos x имеет вид: , второй корень должен быть отброшен.
ОТВЕТ:
3-8Решение | Инверсия или нет? | Тригонометрия: треугольники в функции
Взгляните на три графика ниже.
| График А | График Б | График С |
На одном из графиков показано \(y=\arctan(\tan x)\). Другой показывает \(y=\tan (\arctan x)\). Что это за графики и почему?
Поскольку \(\tan x\), \(\sin x\) и \(\cos x\) являются периодическими функциями, существует много значений \(x\), которые дают одно и то же значение \(\tan х\), \(\sin х\) или \(\cos х\). Это означает, что обратные функции, такие как \(\arctan x\) и \(\arcsin x\), должны быть очень тщательно определены. Подробнее об этом можно прочитать в разделе Обратные тригонометрические функции, и эти идеи используются в этом решении.
Глядя на три графика, я замечаю, что график C выглядит как график \(y=x\) для всех действительных значений \(x.\). Напротив, график B выглядит как график \(y=x). x\), но только для \(x\) в интервале \(\left(\frac{-\pi}{2}, \frac{\vphantom{-}\pi}{2}\right)\). Подумав о графике B, я теперь могу думать о графике A как о повторяющейся версии графика B с периодом \(\pi\).
Чтобы увидеть, какие графики показывают функции \(\arctan(\tan x)\) и \(\tan (\arctan x)\), я могу думать о доменах и диапазонах.
При составлении функций \(f(x)\) и \(g(x)\) для формирования \(g(f(x))\) мне нужно подумать об области определения \(f(x) \). Мне нужно проверить, что любой вывод \(f\) находится в домене \(g\) и каковы эти выходы, поэтому диапазон \(g(f(x))\) зависит от домена и диапазона из \(f\), а также диапазон \(g\).
Начиная с внутренней функции в \(\arctan(\tan x)\), я знаю, что \(\tan x\) определено для всех действительных \(x\), за исключением случаев, когда \(x=\frac{( 2n+1)\pi}{2}\). Это домен \(\tan x\). Диапазон — это все действительные числа. Это означает, что входными данными для внешней функции \(\arctan\) являются все действительные числа, поэтому выходными данными для \(\arctan\) является диапазон ее основных значений, который представляет собой интервал \(\left(-\frac{\ pi}{2},\frac{\pi}{2}\right)\). Следовательно, график \(\arctan(\tan x)\) имеет область определения, которая представляет собой всю ось \(x\), за исключением точек, где \(x=\frac{(2n+1)\pi {2}\), а диапазон равен \(\left(-\frac{\pi}{2},\frac{\pi}{2}\right)\), поэтому на графике A показано \(y= \арктан(\тангенс х)\).
Теперь я воспользуюсь тем же мышлением, чтобы выяснить, что является графиком \(y= \tan (\arctan x)\). На этот раз \(\arctan x\) является внутренней функцией. Его доменом являются все действительные числа, но диапазон равен \(\left(-\frac{\pi}{2},\frac{\pi}{2}\right)\).
Этот график показывает \(y= \tan x\) для \(x\) в интервале \(\left(-\frac{\pi}{2},\frac{\pi}{2}\right )\). Можете ли вы использовать его, чтобы объяснить, почему на графике C должно отображаться \(y=\tan (\arctan x)\)?
Сопоставьте эти уравнения с графиками ниже и объясните свои рассуждения.
\[y=\arcsin(\sin x)\]
\[y=\sin(\arcsin x)\]
\[y=\arccos(\cos x)\]
\[y =\cos(\arccos x)\]
| График D | График Е | График F |
| График G | График H | График J |
Я заметил одну вещь: все четыре функции отображают \(0\) в \(0\), поэтому графики должны проходить через начало координат. Это исключает график G.
Это исключает график G.
\[y=\arcsin(\sin x)\]
Домен \(\sin x\) является действительным \(x\) и диапазоном является интервал \([-1,1]\ ). Областью определения \(\arcsin x\) является интервал \([-1,1]\), а диапазон главных значений равен \(\left[-\frac{\pi}{2},\frac{\ pi}{2}\right]\) (дополнительные пояснения см. в разделе «Обратные тригонометрические функции»).
Итак, функция \(\arcsin(\sin x)\) определена для всех вещественных \(x\) и имеет диапазон \(\left[-\frac{\pi}{2},\frac{\pi {2}\справа]\). В пределах домена \(\left[-\frac{\pi}{2},\frac{\pi}{2}\right]\) функция будет отображать \(x\) на себя, поэтому график будет выглядеть как что из \ (у = х \). Так что это должен быть график D.
Обратите внимание, что по мере увеличения \(x\) от \(\frac{\pi}{2}\) до \(\frac{3\pi}{2}\), \(\sin x\) уменьшается от \(1\) до \(-1\) и, таким образом, \(\ arcsin(\sin x)\) уменьшается от \(\frac{\pi}{2}\) до \(-\frac{\pi} {2}\). А затем эта закономерность продолжается, образуя зигзагообразный график.
\[y=\sin(\arcsin x)\]
Областью определения \(\arcsin x\) является интервал \([-1,1]\), и он не определен в других местах. В пределах этой области он имеет диапазон \(\left[-\frac{\pi}{2},\frac{\pi}{2}\right]\), и эти значения являются входными для \(\sin x\) производить значения в диапазоне \([-1,1]\). Таким образом, граф будет выглядеть как \(y=x\), ограниченный доменом \(-1\le x\le1\), который является графом E.
\[y=\arccos(\cos x)\]
\(\cos x\) определяется для всех действительных \(x\) и имеет диапазон \([-1,1]\). \(\arccos x\) определен в домене \([-1,1]\) и его основной диапазон значений равен \([0,\pi]\). Таким образом, областью определения этой композиции являются все действительные числа, а ее диапазон равен \([0,\pi]\). Этому соответствует только график J.
Для проверки, когда \(x\) увеличивается от \(0\) до \(\pi\), значение \(\cos x\) уменьшается от \(1\) до \(-1\) и, таким образом, \(\arccos(\cos x)\) увеличивается от \(0\) до \(\pi\). В этой области граф выглядит как \(y=x\). По мере дальнейшего увеличения \(x\) от \(\pi\) до \(2\pi\), \(\cos x\) увеличивается от \(-1\) до \(1\) и \(\arccos (\cos x)\) уменьшается от \(\pi\) до \(0\). Таким образом, мы получаем зигзагообразный узор.
В этой области граф выглядит как \(y=x\). По мере дальнейшего увеличения \(x\) от \(\pi\) до \(2\pi\), \(\cos x\) увеличивается от \(-1\) до \(1\) и \(\arccos (\cos x)\) уменьшается от \(\pi\) до \(0\). Таким образом, мы получаем зигзагообразный узор.
\[y=\cos(\arccos x)\]
\(\arccos x\) определяется только для \(x\) в интервале \([-1,1]\). Его диапазон равен \([0,\pi]\), а \(\cos\) этих значений имеет диапазон \([-1,1]\). Таким образом, наш график будет выглядеть как \(y=x\), ограниченный областью \([-1,1]\), и это должен быть график E, такой же, как для уравнения (2).
Интересно отметить, что функции \(\cos x\) и \(\arccos x\) на этих интервалах являются убывающими функциями, но композиция функций возрастает. Так ли это на любая пара убывающих функций?
Для каких значений \(x\) является \(\tan(\arctan x)=x\)? А как насчет \(\arctan(\tan x)=x\)?
Что вы можете сказать о решениях подобных уравнений, таких как \(\sin(\arcsin x)=x\) или \(\arccos(\cos x)=x\)?
Поскольку график C представляет собой \(y=\tan(\arctan x)\), он должен быть равен \(\tan(\arctan x)=x\) для всех действительных \(x\).
График A показывает \(y=\arctan(\tan x)\), поэтому \(\arctan(\tan x)=x\) только для \(x\) в интервале \(\left(-\ tfrac{\pi}{2},\tfrac{\pi}{2}\right)\), так как это единственная часть графика, для которой \(y=x\) совпадает с графиком \(y=\ арктан(\тангенс х)\).
Чтобы проиллюстрировать, что происходит, если \(x\) находится за пределами этого интервала, давайте попробуем \(x=\tfrac{4\pi}{3}\). Я знаю \(\tan \tfrac{4\pi}{3} = \sqrt{3}\), но \(\arctan \sqrt{3}= \tfrac{\pi}{3}\). Поэтому \(\arctan\left(\tan \tfrac{4\pi}{3}\right)= \arctan \sqrt{3}=\tfrac{\pi}{3}\). Обобщая этот пример, я вижу, что если \(x\) находится вне интервала \(\left(-\tfrac{\pi}{2},\tfrac{\pi}{2}\right)\) и \(\tan x\) определен, то \(\arctan(\tan x)\) переводит \(x\) в соответствующее значение внутри интервала \(\left(-\tfrac{\pi}{2} ,\tfrac{\pi}{2}\right)\).
Мы можем сделать соответствующие выводы для композиций \(\sin\) и \(\cos\), взглянув на графики D, E и J. не путать с ), является функцией обратного синуса. Синус имеет обратный только в ограниченной области ≤x≤. На рисунке ниже часть графика, выделенная красным цветом, показывает часть графика sin(x), которая имеет обратную сторону.
Синус имеет обратный только в ограниченной области ≤x≤. На рисунке ниже часть графика, выделенная красным цветом, показывает часть графика sin(x), которая имеет обратную сторону.
Домен должен быть ограничен, потому что для того, чтобы у функции была обратная функция, она должна быть взаимно однозначной, а это означает, что никакая горизонтальная линия не может пересекать график функции более одного раза. Поскольку синус является периодической функцией, без ограничения области определения горизонтальная линия будет периодически пересекать функцию бесконечно много раз.
Одно из свойств обратных функций состоит в том, что если точка (a, b) находится на графике функции f, то точка (b, a) находится на графике обратной функции. Это фактически означает, что график обратной функции является отражением графика функции через прямую y = x.
График y = arcsin(x) показан ниже.
Как видно из рисунка, y = arcsin(x) является отражением sin(x) при ограниченной области ≤x≤ через прямую y = x.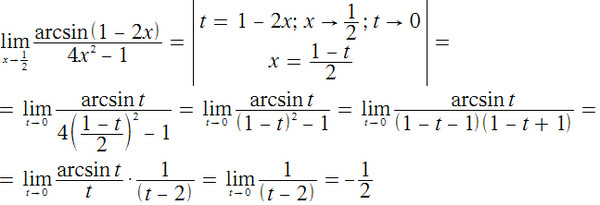 Домен arcsin(x), -1≤x≤1, является диапазоном sin(x), а его диапазон ≤y≤ является доменом sin(x).
Домен arcsin(x), -1≤x≤1, является диапазоном sin(x), а его диапазон ≤y≤ является доменом sin(x).
Калькулятор арксинуса
Ниже приведен калькулятор для определения либо значения арккоса числа от -1 до 1, либо значения косинуса угла.
| угловой синус | = | деградировать | ||
Использование специальных углов для нахождения арксинуса
Хотя мы можем найти значение арксинуса для любого значения x в интервале [-1, 1], существуют определенные углы, которые часто используются в тригонометрии (0°, 30°, 45°, 60°, 90°, их кратные и эквиваленты в радианах), значения синуса и арксинуса которых стоит запомнить. Ниже приведена таблица, показывающая эти углы (θ) как в радианах, так и в градусах, а также их соответствующие значения синусов, sin(θ).
| θ | -90° | -60° | -45° | -30° | 0° | 30° | 45° | 60° | 90° |
| sin(θ) | -1 | 0 | 1 |
Один из методов, который может помочь в запоминании этих значений, состоит в том, чтобы выразить все значения sin(θ) в виде дробей, содержащих квадратный корень.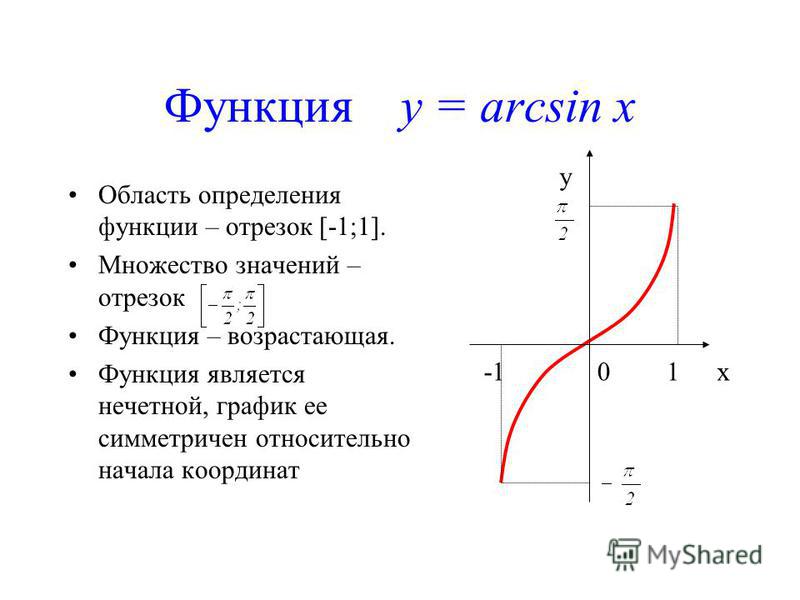 Начиная с 0° и заканчивая 90°, sin(0°) = 0 = . Последующие значения sin(30°), sin(45°), sin(60°) и sin(90°) следуют шаблону, так что используя значение sin(0°) в качестве эталона, чтобы найти значения синуса для последующих углов, мы просто увеличиваем число под знаком радикала в числителе на 1, как показано ниже.
Начиная с 0° и заканчивая 90°, sin(0°) = 0 = . Последующие значения sin(30°), sin(45°), sin(60°) и sin(90°) следуют шаблону, так что используя значение sin(0°) в качестве эталона, чтобы найти значения синуса для последующих углов, мы просто увеличиваем число под знаком радикала в числителе на 1, как показано ниже.
| θ | 0° | 30° | 45° | 60° | 90° |
| sin(θ) |
Значения синуса от 0° до -90° следуют той же схеме, за исключением того, что значения отрицательные, а не положительные, поскольку синус отрицателен в квадранте IV. Этот шаблон периодически повторяется для соответствующих угловых измерений, и мы можем определить значения sin(θ) на основе положения θ в единичной окружности, принимая во внимание знак синуса: синус положительный в квадрантах I и II и отрицательный в квадрантах III и IV.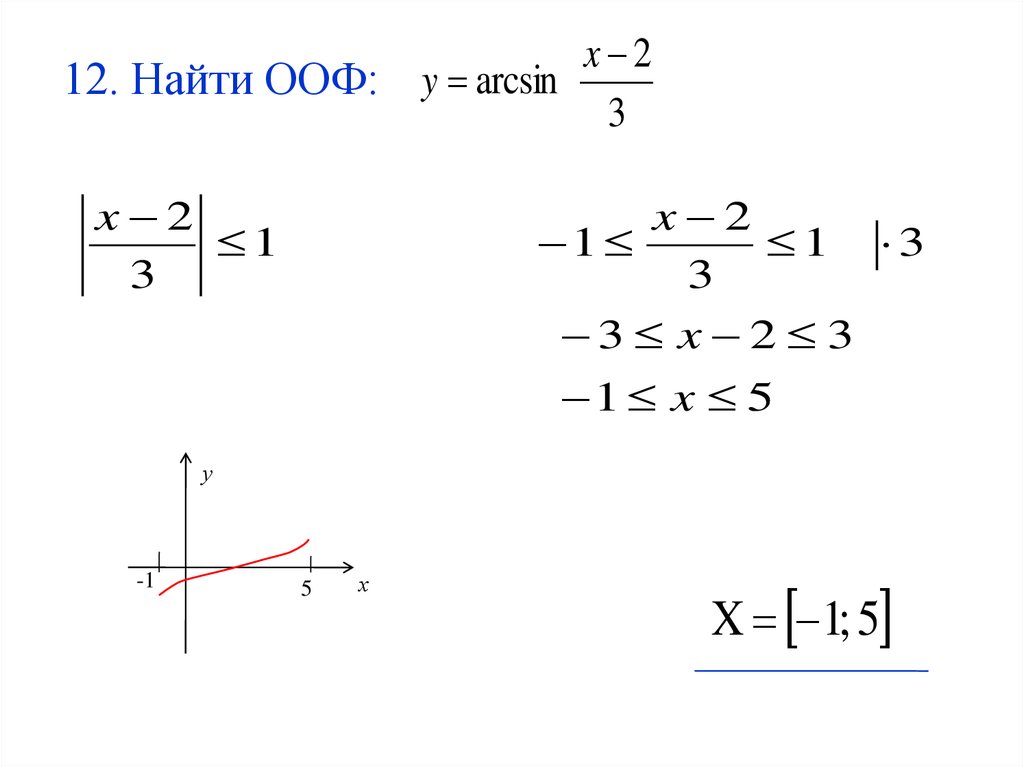
После того, как мы запомнили значения, или если у нас есть какая-то ссылка, становится относительно просто распознавать и определять значения синуса или арксинуса для специальных углов.
Пример:
Найти arcsin(), arcsin() и arcsin(3) в радианах.
, .
, .
arcsin(3) не определено, потому что 3 не находится в интервале -1≤arcsin(θ)≤1, области определения arcsin(x).
Обратные свойства
Как правило, функции и их обратные свойства демонстрируют соотношение
f(f -1 (x)) = x и f -1 (f(x)) = x
при условии, что x находится в области определения функции. То же самое верно для sin(x) и arcsin(x) в пределах их соответствующих ограниченных доменов:
sin(arcsin(x)) = x для всех x в [-1, 1]
и
arcsin(sin (x)) = x, для всех x в [ ]
Эти свойства позволяют нам оценить композицию тригонометрических функций.
Композиция арксинуса и синуса
Если x находится в области определения, оценка композиции арксинуса и синуса относительно проста.
Примеры:
1.
2.
Если x не входит в область значений, нам необходимо определить опорный угол, а также соответствующий квадрант. Учитывая arcsin(sin() ), мы не можем оценить это, как мы сделали выше, потому что x не находится внутри [ ], поэтому решение не может быть . Чтобы оценить это, нам сначала нужно определить sin() перед использованием arcsin:
3.
В приведенном выше примере опорный угол равен , а sin() равен . Однако находится в квадранте III, где sin отрицателен, поэтому sin() = , и единственный угол в области определения arcsin(x), синус которого равен .
Композиция других тригонометрических функций
Мы также можем составить композиции, используя все другие тригонометрические функции: косинус, тангенс, косеканс, секанс и котангенс.
Пример:
Найти cos(arcsin()).
Так как не является одним из отношений для специальных углов, мы можем использовать прямоугольный треугольник, чтобы найти значение этой композиции. Учитывая arcsin()=θ, мы можем найти, что sin(θ)=. Прямоугольный треугольник ниже показывает θ и отношение его противоположной стороны к гипотенузе треугольника.
Учитывая arcsin()=θ, мы можем найти, что sin(θ)=. Прямоугольный треугольник ниже показывает θ и отношение его противоположной стороны к гипотенузе треугольника.
Чтобы найти косинус, нам нужно найти прилежащую сторону, так как cos(θ)=. Пусть b длина смежной стороны. Используя теорему Pythagorean,
3 2 + B 2 = 5 2
9 + B 2 = 25
B 2 = 16
B = 4 909.909.
B 2 = 16
B . () = θ, поэтому мы можем переписать задачу и найти cos(θ), используя треугольник, который мы построили выше, и тот факт, что cos(θ)=:
cos(arcsin()) = cos(θ) =
Тот же процесс можно использовать с переменным выражением.
Пример:
Найти tan(arcsin(2x)).
Учитывая arcsin(2x) = θ, мы можем найти, что sin(θ) = и построить следующий треугольник:
Чтобы найти касательную, нам нужно найти смежную сторону, поскольку tan(θ)=.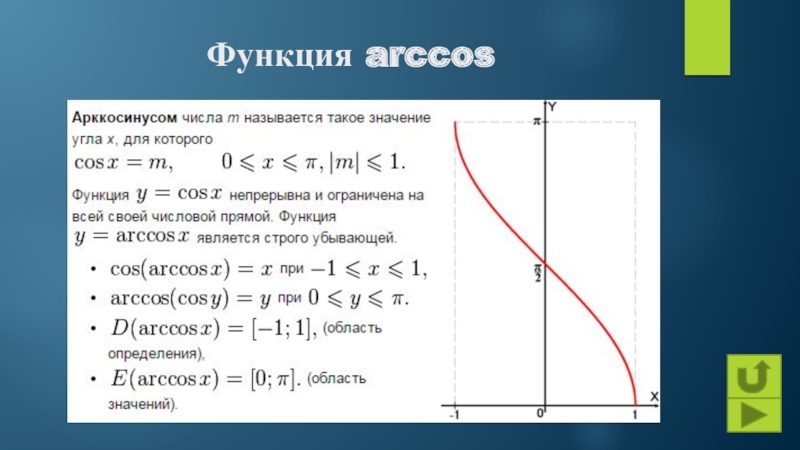 Пусть b длина смежной стороны. Используя теорему Пифагора,
Пусть b длина смежной стороны. Используя теорему Пифагора,
(2x) 2 + b 2 = 1 2
4x 2 + b 2 = 1
b 2 = 1 — 4x 2
b =
и
tan(arcsin(2x)) = tan(θ) = , где Арксинус также можно использовать для решения тригонометрических уравнений, включающих функцию синуса. Примеры: Решите следующие тригонометрические уравнения относительно x, где 0≤x<2π. 1. 2sin(x) = 2sin(x) = sin(x) = Синус положителен в двух квадрантах, квадрантах I и квадрантах II, поэтому есть два решения: x= и x=. Это единственные два угла в пределах 0≤x. 2. 2sin 2 (x) + 5sin(x) — 3 = 0 2sin 2 (x) + 5sin(x) — 3 = 0 (2sin(x) — 1)(sin (x) + 3) = 0 2sin(x) — 1 = 0 или sin(x) + 3 = 0 sin(x) = или sin (x) = -3 x = arcsin() или x = arcsin(-3) Решение для x = arcsin(), x= или : Мы не можем решить для x = arcsin(-3), потому что оно не определено, поэтому x= или являются единственными решениями. 1. На интервале [-/2,
/2], у=синх
растет. С этим ограниченным доменом y=sinx имеет обратный
функция, известная как функция обратного синуса. Это
записывается как y= arcsin x или y= sin –1 x. Это функции
диапазон [-1,1], а его диапазон [-/2,
/2]. Функция обратного синуса определяется как y= arcsin x
только если siny = x, где -1
Икс
1 и -/2
г/2.
домен [-1,1], а диапазон [-/2,
/2]. Из этого вы можете построить график y=arcsinx. Его диапазон от
[-/2,
/2].
график ниже — это весь график y=arcsinx. Потому что
это должна быть функция, ее домен и диапазон были
сдвинуты так, чтобы для каждого значения x существовало
только одно значение y. ∞ Определение обратных и взаимно однозначных функций Тригонометрические функции, заданные на целой прямой, не являются взаимно однозначными функциями, что делает их необратимыми. Однако можно соответствующим образом ограничить область определения каждой тригонометрической функции, чтобы они стали взаимно однозначной функцией. Обратные тригонометрические функции обратны тригонометрическим функциям с ограниченными областями. Функция синуса главного значения Синус представляет собой функцию, тождественную обратной функции, называемой арксинусом. домен Arcsin = [-1,1] = диапазон Sin График y = Arcsinx является зеркальным отражением графика y = Sinx в строке y = x. Точно так же график x = Siny является зеркальным отражением графика x = Arcsiny на линии y = x. Обратите внимание, что y = Arcsinx равно x = Siny, а x = Arcsiny равно y = Sinx. Производная Arcsin Так как y = Arcsinx равно x = Siny: Так как уют положителен на единичной окружности между -π/2 и π/2, то верно следующее: Поскольку x = siny, тогда: Следовательно, следующая производная от Arcsin с использованием вышеприведенного и цепного правила: Неопределенный интеграл от Arcsin Первая производная дает следующий неопределенный интеграл: Функция косинуса главного значения Косинус — это функция взаимно однозначного соответствия с обратной функцией, называемой арккосинусом. Арккосинус также обозначается как Arccos или cos⁻¹. Cos является убывающей функцией. домен Arccos = [-1,1] = диапазон Cos График y = Arccosx является зеркальным отображением графика y = Cosx на линии y = x. Точно так же график x = Cosy является зеркальным отражением графика x = Arccosy в строке y = x. Обратите внимание, что y = Arccosx равно x = Cosy, а x = Arccosy равно y = Cosx. Производная Arccos Так как y = Arccosx равно x = Cosy: Поскольку siny положителен на единичной окружности между 0 и π, то верно следующее: Так как x = cosy, тогда: Следовательно, следующая производная от Arccos с использованием вышеприведенного и цепного правила: Неопределенный интеграл от Arccos Первая производная дает следующий неопределенный интеграл: Arcsin и Arccos Тождества Следовательно, Arcsinx + Arccosx равно константе на ( -1,1). Поскольку Arcsin0 = 0 и Arccos0 = π/2, для любого x в (-1,1): Если -π/2 ≤ x ≤ π/2, то: Функция тангенса главного значения Тангенс — это функция взаимно однозначного соответствия с обратной функцией, называемой арктангенс. Арктангенс также обозначается как Arctan или tan⁻¹. Тан является возрастающей функцией. домен Arctan = (-∞,∞) = диапазон Tan График y = Arctanx является зеркальным отображением графика y = Tanx в строке y = x. Точно так же график x = Tany является зеркальным отражением графика x = Arctany в строке y = x. Обратите внимание, что y = Arctanx равно x = Tany, а x = Arctany равно y = Tanx. Производная от Arctan Так как y = Arctanx равно x = Tany: Поскольку sec²y положительно, то верно следующее: Поскольку x = tany, тогда: цепное правило: Неопределенный интеграл от арктангенса Это дает следующие два неопределенных интеграла: Функция секанса главного значения Секанс является взаимно однозначной функцией с обратной функцией, называемой аркссеканс. Аркссеканс также обозначается как Arcsec или сек⁻¹. домен Arcsec = (-∞,-1] U [1,∞) = диапазон Sec График y = Arcsecx является зеркальным отображением графика y = Secx на линии y = x. Производная Arcsec Неопределенный интеграл от Arcsec Функция косеканса главного значения Косеканс является однозначной функцией с обратной функцией, называемой арккосеканс. также обозначается как Arccsc или csc⁻¹. домен Arccsc = (-∞,-1] U [1,∞) = диапазон Csc График y = Arccscx является зеркальным отображением графика y = Cscx на линии y = x Точно так же график x = Cscy является зеркальным отображением графика x = Arccscy в строке y = x. Производная Arccsc Неопределенный интеграл от Arccsc Функция котангенса главного значения Котангенс — это функция взаимно однозначного соответствия с обратной функцией, называемой арккотангенсом. Арккотангенс также обозначается как Arccot или cot⁻¹. домен Arccot = (-∞,∞) = диапазон Cot График y = Arccotx является зеркальным отображением графика y = Cotx на линии y = x. Точно так же график x = Coty является зеркальным отражением графика x = Arccoty на линии y = x. Производная Arccot Неопределенный интеграл от Arccot Оценить следующее выражение: Со времени Arcsinx = y, Siny = x: Оцените следующее выражение: (-1) (-1) (-1) (-1) (-1). Tany = x: Arctan(-1) = y <–> Tany = -1 = -π/4 Примечание. Область Тана на единичной окружности. Вычислите следующее выражение: Вычисление tan(2π/3): Так как Arctanx = y, Tany = x: Обратите внимание на область Тана на единичной окружности. Оцените следующее выражение: Пусть t = Arccosx, тогда, если t = Arccosx, x = стоимость. Оцените следующее: tanArctan200 Пусть t = Arctanx, тогда, если t = Arctanx, x = tant. tant = x = 200 Упростите следующее выражение: cosArccosx Пусть t = Arccosx, тогда, если t = Arccosx, x = стоимость. cost = x = x Упростите следующее выражение: sinArccosx Пусть t = Arccosx, тогда, если t = Arccosx, x = стоимость. Упростите следующее выражение: tanArccosx Пусть t = Arccosx, тогда, если t = Arccosx, x = стоимость и sint = √(1 — cos²t) = √(1 — x²). Упростите следующее выражение: Arcsinsinx Ниже приведен график y = Arcsinsinx: Обратите внимание, что есть интервалы, в которых Arcsinsinx увеличивается и уменьшается. Следующая формула охватывает все интервалы x, когда Arcsinsinx увеличивается: Причина, по которой существует 2kπ, заключается в том, что требуется период 2kπ, чтобы перейти от следующего интервала x, когда Arcsinsinx увеличивается. Следующая формула охватывает все интервалы x, когда Arcsinsinx уменьшается: Причина, по которой существует 2kπ, заключается в том, что требуется период 2kπ, чтобы перейти от следующего интервала x, когда Arcsinsinx уменьшается. Поскольку домен Sinx равен [-π/2,π/2]: Тогда Arcsinsinx = ArcsinsinX = Arcsinsin(x — 2kπ) = x — 2kπ Тогда Arcsinsinx = ArcsinsinX = Arcsinsin(2kπ + π — x ) = 2kπ + π — x Следовательно, существует два возможных ответа на упрощение Arcsinsinx: Упрощение следующего выражения: Arccoscosx Ниже приведен график y = Arccoscosx: Обратите внимание, что есть интервалы, в которых Arccoscosx увеличивается и уменьшается. Следующая формула покрывает все интервалы x при увеличении Arccoscosx: Причина, по которой существует 2kπ, заключается в том, что требуется период 2kπ, чтобы перейти от следующего интервала x при увеличении Arccoscosx. Следующая формула охватывает все интервалы x, когда Arccoscosx уменьшается: Причина, по которой существует 2kπ, заключается в том, что требуется период 2kπ, чтобы перейти от следующего интервала x, когда Arccoscosx уменьшается. Поскольку домен Cosx равен [0,π]: Тогда Arccossx = ArccoscosX = Arccoscos(x — 2kπ) = x — 2kπ — x Следовательно, есть два возможных ответа на упрощение Arccoscosx: Нарисуйте следующую функцию: y = sinArcsinx Начните с упрощения выражения функции. Пусть t = Arcsinx, тогда, если t = Arcsinx, x = sint. sint = x Следовательно, график y = sinArcsinx выглядит как y = x, однако домен и диапазон другие. Область определения внутренней функции Arcsinx равна [-1,1]. Область определения всей упрощенной функции x равна (-∞, ∞). Однако важно учитывать домен внутренней функции, поэтому конечный домен — [-1,1]. Диапазон всей функции равен y(Dt), где Dt — область значений t или Arcsinx. Домен Arcsinx — [-1,1]. Диапазон y(Dt) упрощен по y с доменом t или диапазоном x с доменом Arcsinx, который по-прежнему равен [-1,1]. Следовательно, зная, что sinArcsinx является формой y = x с областью определения и диапазоном [-1,1], график y = sinArcsinx выглядит следующим образом: Дифференцируем следующую функцию: y = sinArcsinx Поскольку sinArcsinx был упрощен до x: Однако можно провести различие, используя цепное правило и упрощение: Пусть t = Arcsinx, тогда, если t = Arcsinx, x = sint. Различают следующую функцию: Используя цепное правило: Дифференцируйте следующую функцию: Используя цепное правило, предполагая, что x является независимой переменной: Дифференцируйте следующую функцию: Используя правило произведения и правило цепочки: Дифференцируйте следующую функцию: F(x) = (1 + x²)Arctanx Используя правило произведения и правило цепочки: Дифференцировать следующую функцию: Использование правила коэффициента и правило цепи: Дифференцируйте следующую функцию: Использование цепочки: . Дифференцируйте следующую функцию: Используя правило вычитания и цепное правило: Решите следующую задачу с начальными значениями: Когда его просят решить задачу с начальным значением, он запрашивает исходную функцию y для заданной начальной точки. Антидифференцирующий y’: Нахождение C, когда y(0) = 1: Следовательно, y = Arctanx + 1 Решите следующую задачу с начальными значениями: Когда просят решить задачу с начальными значениями, запрашивается исходная функция y при заданной начальной точке. Антидифференцирующий y’: Нахождение C, когда y(½) = 1: Следовательно, y = Arcsinx + 1 — π/6 Упрощение следующего выражения: cosArctanx Пусть t = Arctanx, тогда, если t = Arctanx, x = tant. Тождество, относящееся к косинусу и тангенсу, следующее: Поскольку x = tant: Следовательно: Упростите следующее выражение: sinArctan2x Пусть t = Arctan2x, тогда, если t = Arctan2x, то 2x = tant. Нахождение тождества, связанного с синусом и тангенсом: Нахождение тождества, связанного с косинусом и тангенсом: Поскольку 2x = tant: Следовательно: Найдите f(x) следующей производной, если f (1) = 0: Антидифференцирующая f'(x): Нахождение C, когда f(1) = 0: Следовательно: Оцените следующее выражение: tanArcsec4 Пусть t = Arcsec4, тогда, если t = Arcsec4, sect = 4. = 4 и x = 1. По теореме Пифагора y = √15. Следовательно: tanArcsec4 = tant = sint/cost = (√15/4)/(¼) = √15 Вычислить следующее выражение: sin(2Arcsin(4/18)) 901 Пусть t = Arcsin(3/5), тогда, если t = Arcsin(3/5), sint = 3/5. Предположим, что y = 3 и r = 5. По теореме Пифагора x = 4. Отсюда: sin(2Arcsin(3/5)) = sin2t = 2sintcost = 2(3/5)(4/5 ) = 6/5 Оцените следующее выражение: Arccossin(6π/5) Во-первых, точка sin(6π/5) должна быть найдена до того, как угол Arccossin(5π/6) найденный. Поскольку угол 6π/5 неизвестен, он будет нарисован с помощью логических рассуждений. Поскольку π + π/5 = 6π/5, 6π/5 больше π и создает угол π/5 между π и конечным плечом 6π/5. Это создает прямоугольный треугольник, где вертикальная сторона помечена t из-за необходимости найти значение синуса, а горизонтальная сторона помечена результирующим значением x, найденным при использовании y = t и r = 1 в теореме Пифагора. Если y = -t, x = -√(1 — t²) и r = 1, то sin(6π/5) = y/r = -t/1 = -t. Тогда Arccossin(6π/5) = Arccos(-t) = некоторый угол θ, следовательно: cosθ = -t квадрант III перемещается в квадрант II. Кроме того, sin(6π/5) изначально был равен -t, но теперь необходимо найти значение cosθ, поэтому значения x и y также изменяются в перемещенном треугольнике. Следовательно: Arccossin(6π/5) Вы изучили, как
тригонометрические функции
грех
(
Икс
)
,
потому что
(
Икс
)
, а также
загар
(
Икс
)
можно использовать для нахождения неизвестной длины стороны прямоугольного треугольника, если известна длина одной стороны и мера угла. обратные тригонометрические функции грех
−
1
(
Икс
)
,
потому что
−
1
(
Икс
)
, а также
загар
−
1
(
Икс
)
, используются для нахождения неизвестной меры угла прямоугольного треугольника, когда известны длины двух сторон. Пример 1: Основание лестницы размещено
3
футах от
10
высотой в фут, так, чтобы верх лестницы совпадал с верхом стены. Чему равен угол, образованный лестницей и землей? Здесь у нас есть прямоугольный треугольник, в котором мы знаем длины двух катетов, то есть сторон, противоположных и примыкающих к углу. Итак, мы используем функцию арктангенса. Если вы введете это в калькулятор, установленный в режим «градус», вы получите загар
−
1
(
10
3
)
≈
73,3
° Если у вас установлен калькулятор в радианном режиме, вы получите загар
−
1
(
10
3
)
≈
1,28 Если вы запомнили соотношения длин сторон, встречающиеся в
45
−
45
−
90
а также
30
−
60
−
90
треугольников, возможно, вы сможете найти некоторые значения обратных тригонометрических функций без использования калькулятора. Пример 2: Находить
потому что
−
1
(
3
2
)
. Вы можете вспомнить, что в
30
−
60
−
90
треугольник, если гипотенуза имеет длину
1
, то длинная нога имеет длину
3
2
. Поскольку косинус — это отношение прилежащего катета к гипотенузе, значение арккосинуса равно
30
°
, или около
0,52
радианы. потому что
−
1
(
3
2
)
знак равно
30
° Все тригонометрические функции
периодические функции
. Таким образом, графики ни одного из них не проходят
Горизонтальная линия
Тест и так не
1
−
к
−
1
. Поскольку графики периодические, если мы выберем соответствующую область, мы можем использовать все значения
диапазон
. Если мы ограничим домен
ф
(
Икс
)
знак равно
грех
(
Икс
)
к
[
−
π
2
,
π
2
]
мы сделали функцию
1
−
к
−
1
. Диапазон
[
−
1
,
1
]
. (Хотя есть много способов ограничить домен для получения
1
−
к
−
1
функция это согласованный используемый интервал.) Мы обозначаем
обратная функция
в качестве
у
знак равно
грех
−
1
(
Икс
)
. Чтобы построить график функции, обратной синусоиде, помните, что график представляет собой отражение линии.
у
знак равно
Икс
функции синуса. Обратите внимание, что домен теперь является диапазоном, а диапазон теперь является доменом. Поскольку домен ограничен, все положительные значения дадут
1
ул.
угол квадранта и все отрицательные значения дадут
4
й
квадрантный угол. Точно так же мы можем ограничить области значений функций косинуса и тангенса, чтобы сделать их
1
−
к
−
1
. Область определения функции арккосинуса
[
−
1
,
1
]
и диапазон
[
0
,
π
]
. Это означает, что положительное значение даст
1
ул.
угол квадранта и отрицательное значение даст
2
й
квадрантный угол. Область определения функции арктангенса равна
(
−
∞
,
∞
)
и диапазон
(
−
π
2
,
π
2
)
. Функция, обратная касательной, даст значения в
1
ул.
а также
4
й
квадранты. Тот же процесс используется для нахождения обратных функций для остальных тригонометрических функций — котангенса, секанса и косеканса.
Тригнет
Чтобы функция имела обратную, она должна
пройти тест горизонтальной линии. Y=sinx не проходит это
test, потому что разные значения x дают одно и то же значение y.
Однако, если вы возьмете только сегмент, ограничив
домен на интервал [-/2
х/2]
свойства теста сохраняются для этого сегмента. 
2. На интервале [-/2,
/2], у=синх
принимает полный диапазон значений от –1 до 1
3. На интервале [-/2,
/2], у=синх
проходит тест горизонтальной линии
Другие обратные функции Арксинус:
По определению, y=arcsinx и siny=x равны
равный. Поэтому оба графика одинаковы. Из siny=x
вы можете назначить значения для создания таблицы значений для y=arcsinx. Арккосинус
Функция косинуса убывает на
интервал 0
Икс .  График
y=cosx показывает этот интервал. Этот интервал имеет обратную
функция, обозначаемая как y=arcos x или y= cos –1 x.
значения этих двух функций одинаковы, и
значения:
График
y=cosx показывает этот интервал. Этот интервал имеет обратную
функция, обозначаемая как y=arcos x или y= cos –1 x.
значения этих двух функций одинаковы, и
значения:
Арктангенс Подобно арксинусу и арккосинусу, вы можете найти обратную
касательная функция, ограничивающая область определения y=tanx до
интервал (-/2,
/2). Определения обратных функций
Y=arcsin x, только если siny=x. Домен= -1×1.
Диапазон = -/2
г/2.
Домен= -1×1.
Диапазон = -/2
г/2.
Y=arccos x, только если cosy=x. Домен= -1×1.
Диапазон = 0
у .
Y=arctan, только если tany=x. Домен= —
Икс .
Диапазон = -/2
г/2.
Продолжить… Алгебра, линейная алгебра, геометрия, векторная геометрия, тригонометрия, предварительное исчисление и исчисление с одной переменной
Обратные тригонометрические функции
9 функция — это определенная функция, которая находится с использованием исходной функции.  Чтобы определить обратную функцию, сама функция должна быть инъективной или взаимно однозначной, что означает, что она должна иметь только одно значение x для каждого значения y. Если функция не является инъективной или не взаимно однозначной, то область определения должна быть ограничена, прежде чем можно будет определить обратную функцию.
Чтобы определить обратную функцию, сама функция должна быть инъективной или взаимно однозначной, что означает, что она должна иметь только одно значение x для каждого значения y. Если функция не является инъективной или не взаимно однозначной, то область определения должна быть ограничена, прежде чем можно будет определить обратную функцию.
Функция синуса главного значения, обозначаемая как Sine или Sin, представляет собой ограничение синуса интервалом [-π/2,π/2].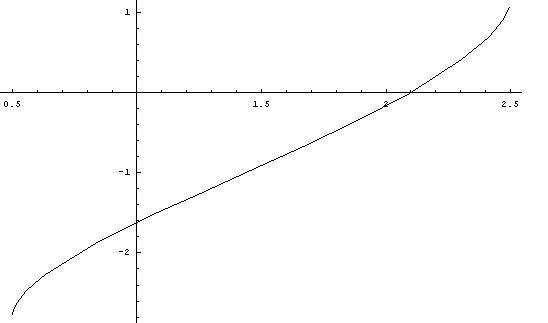 Арксинус также обозначается как арксинус или грех⁻¹. Грех – это возрастающая функция.
Арксинус также обозначается как арксинус или грех⁻¹. Грех – это возрастающая функция.
диапазон Arcsin = [-π/2,π/2] = домен Sin
Неявное дифференцирование используется для вычисления производной Arcsin.
Следующая производная от Arcsin при умножении x на 1/|a| и 1/а (а > 0):
Функция косинуса главного значения, обозначаемая как косинус или Cos, представляет собой ограничение косинуса интервалом [0,π].
диапазон Arccos = [0,π] = домен Cos
Неявное дифференцирование используется для вычисления производной Arccos.
Следующая производная от Arccos при умножении x на 1 /|а| и 1/a (a > 0):
Для -1 < x < 1: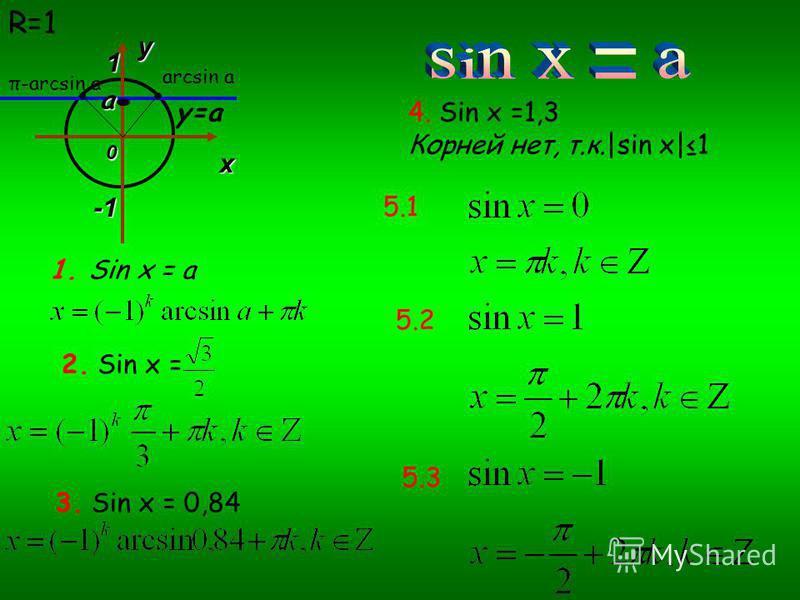
Arcsinx + Arccosx = π/2
Функция тангенса главного значения, обозначаемая как Tangent или Tan, является ограничением тангенса на интервал (-π/2,π/2).
диапазон Arctan = (-π/2,π/2) = домен Tan
Неявное дифференцирование используется для вычисления производной от Arctan.
Ниже приведена производная от арктангенса, если x умножить на 1/a:
Функция секанса главного значения, обозначаемая как Secant или Sec, является ограничением секанса до ограничения 1/Cosx, которое является тем же ограничением, что и Cosx [0,π], однако 1/Cosx не определено при x = π/ 2, поэтому секанс является ограничением секанса на [0,π/2) U (π/2,π].
диапазон Arcsec = [0,π/2) U (π/2,π] = домен раздела Точно так же график x = Secy является зеркальным отображением графика x = Arcsecy на линии y = x. Обратите внимание, что y = Arcsecx равно x = Secy, а x = Arcsecy равно y = Secx.
Точно так же график x = Secy является зеркальным отображением графика x = Arcsecy на линии y = x. Обратите внимание, что y = Arcsecx равно x = Secy, а x = Arcsecy равно y = Secx.
Производная Arccos используется для расчета производной Arcsec.
Скоро…
Функция косеканса главного значения, обозначаемая как Cosecant или Csc, является ограничением косеканса до ограничения 1/Sinx, которое является тем же ограничением, что и Sinx [-π/2,π/2], однако 1/Sinx не определено при x = 0, поэтому косеканс является ограничением косеканса на [-π/2,0) U (0,π/2].
диапазон Arccsc = [-π/2,0) U (0,π/2] = область значений Csc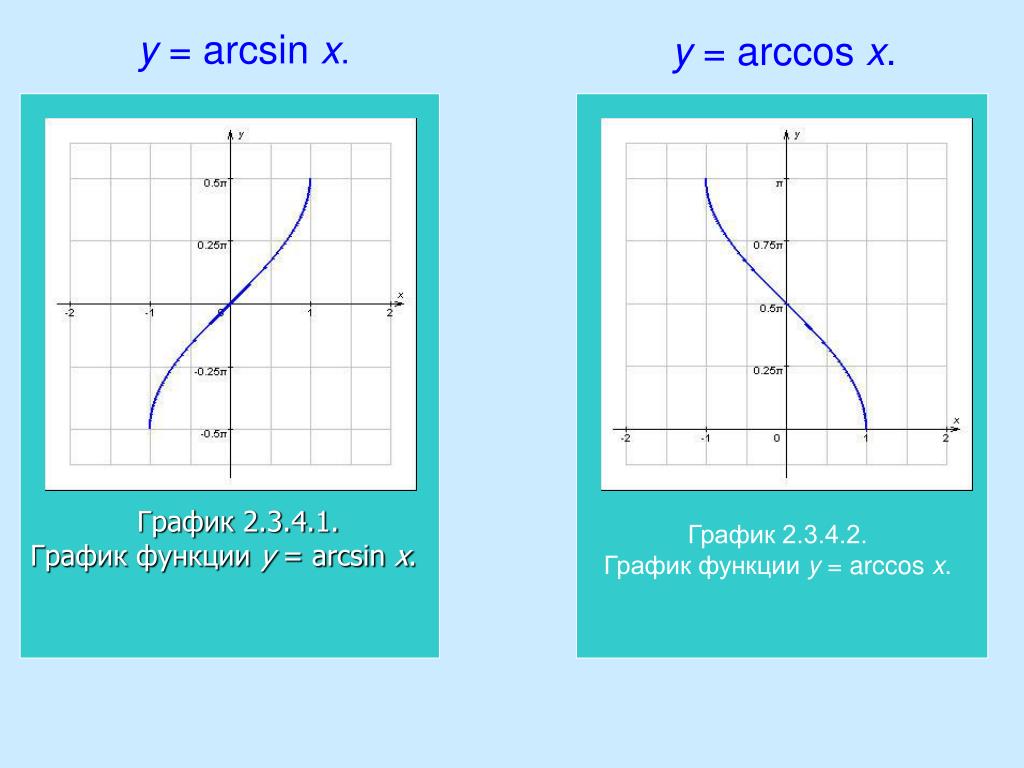 Обратите внимание, что y = Arccscx равно x = Cscy, а x = Arccscy равно y = Cscx.
Обратите внимание, что y = Arccscx равно x = Cscy, а x = Arccscy равно y = Cscx.
Производная Arcsin используется для вычисления производной Arccsc
Скоро будет…
Функция котангенса главного значения, обозначаемая как Котангенс или Cot, представляет собой ограничение котангенса на тот же интервал, что и Cosx, который равен [0,π], однако Cot не определен, когда x = 0, π, поэтому котангенс — это ограничение котангенса на (0, π).
диапазон Arccot = (0,π) = домен Cot Обратите внимание, что y = Arccotx равно x = Coty, а x = Arccoty равно y = Cotx.
Обратите внимание, что y = Arccotx равно x = Coty, а x = Arccoty равно y = Cotx.
Производная Arctan используется для расчета производной Arccot.
Скоро…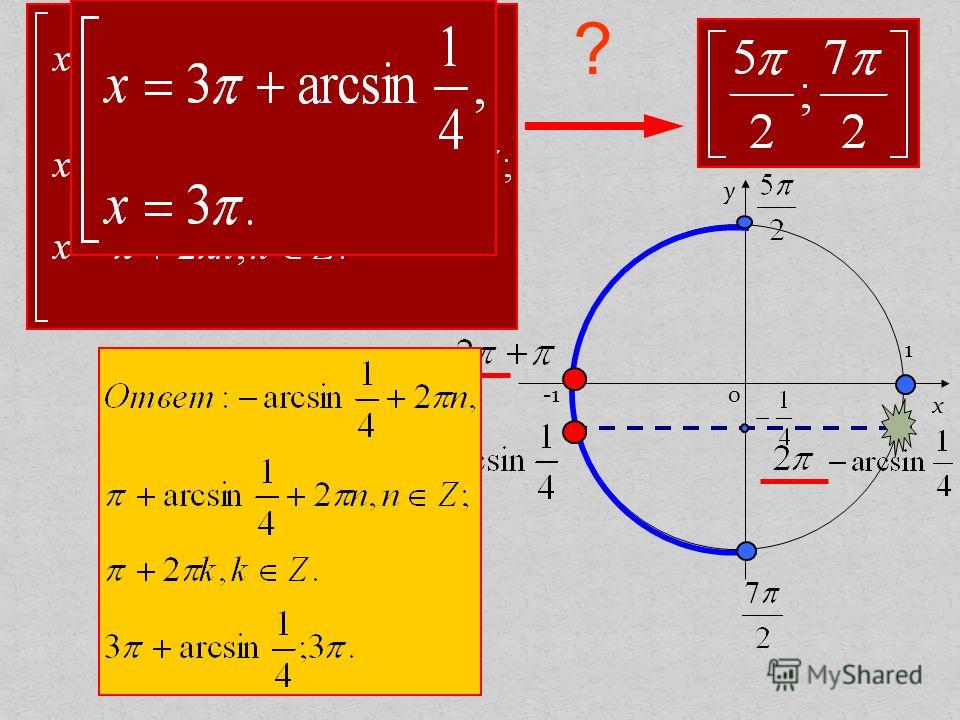
Причина, по которой π/2 вычитается из левой части, а π/2 прибавляется к правой, заключается в том, что начальный интервал всех интервалов x при увеличении Arcsinsinx равен (-π/2,π/2). Обратите внимание, что для перехода от одного возрастающего интервала к другому требуется период π.
Обратите внимание, что для перехода от одного возрастающего интервала к другому требуется период π.
Причина, по которой π/2 добавляется слева, а 3π/2 добавляется справа, заключается в том, что начальный интервал всех интервалов x при уменьшении Arcsinsinx равен (π/2,3π/2), учитывая, что π /2 — конечная точка интервала возрастания Arcsinsinx. Также обратите внимание, что для перехода от одного убывающего интервала к другому требуется период π.
Обратите внимание, что использовались законы неравенств.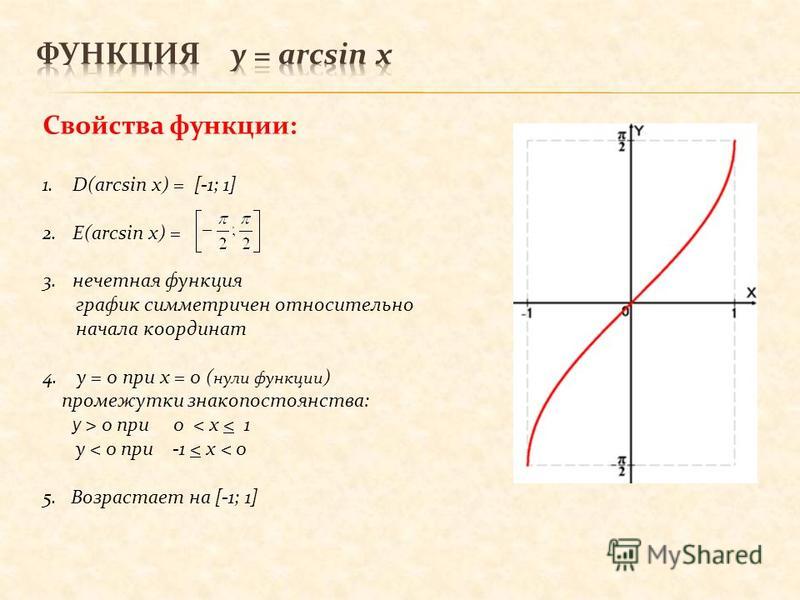
Причина, по которой ничего не вычитается из левой части, а π добавляется в правую, заключается в том, что начальный интервал всех интервалов x при увеличении Arccoscosx равен (0,π). Обратите внимание, что для перехода от одного возрастающего интервала к другому требуется период π.
Причина, по которой π добавляется слева, а 2π — справа, заключается в том, что начальный интервал всех интервалов x при уменьшении Arccoscosx равен (π, 2π), учитывая, что π является конечной точкой интервала когда Arccoscosx увеличивается. Также обратите внимание, что для перехода от одного убывающего интервала к другому требуется период π.
Также обратите внимание, что для перехода от одного убывающего интервала к другому требуется период π.
Обратите внимание, что использовались законы неравенств.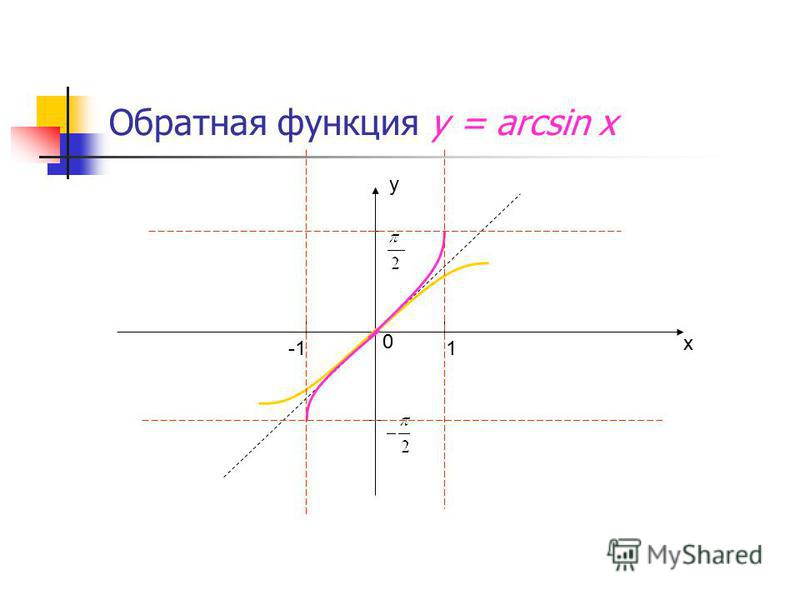
 правило и цепное правило:
правило и цепное правило:
y = Arctanx + C
1 = Arctan0 + C
1 = 0 + C
C = 1
y = Arcsinx + C
1 = Arcsin(½) + C
1 = π/6 + C
C = 1 — π/6

—> cosθ = -t
—> θ = π/2 + π/5 = 7π/10 Обратные тригонометрические функции

Графики обратных тригонометрических функций
 Это означает, что ни один из них не имеет обратного, если только
домен
каждого ограничено, чтобы сделать каждый из них
1
−
к
−
1
.
Это означает, что ни один из них не имеет обратного, если только
домен
каждого ограничено, чтобы сделать каждый из них
1
−
к
−
1
. это читается
у
является обратным синусу
Икс
и означает
у
— это действительный числовой угол, значение синуса которого равно
Икс
. Будьте осторожны с используемыми обозначениями. Верхний индекс «
−
1
” НЕ показатель степени. Чтобы избежать этого обозначения, в некоторых книгах используется обозначение
у
знак равно
арксин
(
Икс
)
вместо.
это читается
у
является обратным синусу
Икс
и означает
у
— это действительный числовой угол, значение синуса которого равно
Икс
. Будьте осторожны с используемыми обозначениями. Верхний индекс «
−
1
” НЕ показатель степени. Чтобы избежать этого обозначения, в некоторых книгах используется обозначение
у
знак равно
арксин
(
Икс
)
вместо.
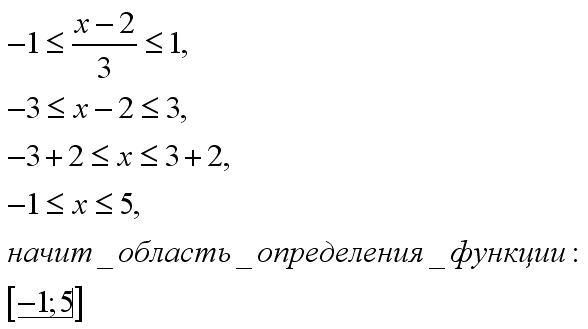

 12.17
12.17
