«Почему 0!=1?» — Яндекс Кью
ПопулярноеСообщества
Стать экспертом Кью
Математика
Иннокентий Луганский
·
53,4 K
На Кью задали 1 похожий вопросОтветить2УточнитьСергей Чабовский
Математика
429
Инженер-радиофизик, преподаватель физической культуры и спорта · 21 авг
n! = n(n-1)!, ⇒ (n-1)! = n!/n, при n = 1 ⇒ 0! = 1, ЧТД.
Сергей Чабовский
23 августа
Ой! Кому это что-то не так? Известный Частный предприниматель, математик-заочник, — это ж надо же!
Комментировать ответ…Комментировать…
Maxim Vyalkov
Математика
1,1 K
Интересующие темы: история математики, история христианства, библеистика. (infty) 1/i! или 1/0!+1/1!+1/2!+…, откуда 1=1/0!, или 0!=1
(infty) 1/i! или 1/0!+1/1!+1/2!+…, откуда 1=1/0!, или 0!=1
Вот
1 эксперт согласен
Комментировать ответ…Комментировать…
Леонид Коганов
125
Член ММО — Московского математического Общества. Кстати, старейшего в мире. Л.М. Коганов. · 18 мая
Мы хотим сохранить при n = 0 определяющую при n ≥ 1 рекуррентность, а именно: ( n + 1)! = ( n! ) • ( n + 1 ). Подставив значение n = 0 в обе части рекуррентности, что — чуть выше, получим последовательно: 1! = ( 0 ! ) • 1, и, поскольку 1! = 1 по определению (по соглашению = конвенции), то, стало быть, отсюда необходимо, чтобы ( 0! ) = 1. Что и требовалось установить Л.К. Читать далее
1 эксперт согласен
Комментировать ответ…Комментировать…
Pavel Vilenkin
224
Программирование, машинное обучение, анализ данных, статистика, теория вероятностей · 9 дек 2017
Это соглашение, с которым многие формулы с факториалом становятся проще. k определяется как n!/(k!*(n-k)!) для всех k от 0 до n. Если бы соглашения про 0! не было, то случаи k=0 и k=n пришлось бы рассматривать отдельно
k определяется как n!/(k!*(n-k)!) для всех k от 0 до n. Если бы соглашения про 0! не было, то случаи k=0 и k=n пришлось бы рассматривать отдельно
Леонид Коганов
18 мая
П.А., приветствую!
Откомментируюсь тоже.
Л.К.
Комментировать ответ…Комментировать…
Георгий Ф.
493
Студент НИЯУ МИФИ · 15 дек 2017
Простые способы показать равенство 0! = 1 были уже разобраны. Давайте немного помучаем себя и докажем это строго! Способ сложный — не для школы точно) Вспомним замечательную гамма-функцию Γ(z). Вообще говоря, это функция комлексного переменного, иными словами: z ∈ ℂ. Но так как ℝ ⊂ ℂ (то есть все действительные числа — комплексные тоже), мы можем подставлять и действител… Читать далее
Игорь Нахал
16 декабря 2017
Отлично!
Комментировать ответ…Комментировать…
Игорь Нахал
20
Магрибинец · 13 дек 2017
Это очень просто доказать. Смотрите:
5!=1*2*3*4*5
4!=1*2*3*4 или 5!/5
3!=1*2*3 или 4!/4
2!=1*2=3!/3
1!=1=2!/2
А значит мы получаем, что:
0!=1!/1 =1 Читать далее
Смотрите:
5!=1*2*3*4*5
4!=1*2*3*4 или 5!/5
3!=1*2*3 или 4!/4
2!=1*2=3!/3
1!=1=2!/2
А значит мы получаем, что:
0!=1!/1 =1 Читать далее
Алексей Амелькин
13 декабря 2017
Из вашего доказательства вывод 0!=1 напрямую не следует, так как из самого определения факториала следует, что… Читать дальше
Комментировать ответ…Комментировать…
Денис Г.
11
23 апр 2020
Давайте сначала посчитаем, чему равняется X!. 1 — 1 0.9 — 0.961765832 0.8 — 0.931383771 0.7 — 0.908638733 0.6 — 893515349 0.5 — 0.886226925 0.4 — 0.887263818 0.3 — 0.897470696 0.2 — 0.918168742 0.1 — 0.95135077 Как вы видите, при уменьшении до 0.5, факториал X действительно уменьшается и стремится к нулю. Однако, потом факториал начинает расти, поэтому логично… Читать далее
1 эксперт не согласен
Иван Демидов
возражает
10 октября 2020
Первое — факториал не определен вне натуральных чисел с нулём. Пытаться называть значения «факториала» для дробных… Читать дальше
Пытаться называть значения «факториала» для дробных… Читать дальше
Вы знаете ответ на этот вопрос?
Поделитесь своим опытом и знаниями
Войти и ответить на вопрос
1 ответ скрыто(Почему?)
Ответы на похожие вопросы
Почему 0!=1? — 2 ответа, заданСергей Чабовский
Математика
429
Инженер-радиофизик, преподаватель физической культуры и спорта · 21 авг
n! = n(n-1)!, ⇒ (n-1)! = n!/n, при n = 1 ⇒ 0! = 1, ЧТД.
Комментировать ответ…Комментировать…
Почему факториал нуля равен единице?
Термин «факториал» ввел в математику в 1800 году французский математик Луи Франсуа Антуан Арбогаст. В математике факториалом называют произведение всех натуральных чисел, включая указанное.
5! = 1 х 2 х 3 х 4 х 5 = 120
Официальную версию вхождения факториала в математику я тревожить не стал, поскольку и сам прекрасно догадываюсь, как же было на самом деле. А дело было так…
Завершив все выкладки по теории и практике факториальных исчислений, Арбогаст понес свое творение на суд Святой Математической Инквизиции. Функции надзора за математиками от имени Святой Математической Инквизиции в данной местности выполняли Святые Ученые Немощи. Ответственность на них лежала огромная, работы было не початый край, точнее, делать было вообще нечего, поэтому Святые Ученые Немощи самозабвенно ковырялись в носу. За этим занятием Их и застал Арбогаст.
Оформленная по всем правилам бюрократического искусства, папка с теорией факториалов легла пред светлы очи Святых Ученых Немощей. Немощи вынули палец из недоковырянной ноздри, брезгливо поморщились и начали этим же пальцем листать папку, проверяя её соответствие «Закону об оформлении бумаг, подаваемых на рассмотрение Святой Математической Инквизиции».
Тщательно сверив всё, написанное рукой Арбогана, с «Толковым словарем для бестолковых Бюрократов. Правила написания Слов и Букв» (сей шедевр прятался от глаз посетителей под грифом «Для служебного пользования»), Святые Ученые Немощи изрекли:
— Ваши материалы будут рассмотрены в установленный Законом срок.
Руководящий палец погрузился в ту же ноздрю, продолжая прерванную работу, что должно было означать конец аудиенции.
По прошествии положенного по закону времени, Аргобан снова стоял перед Святыми Учеными Немощами. Немощи недовольно поморщились, почесали свой затылок, питаясь вспомнить о чем идет речь, потом достали папку с факториалом и углубились в изучение. Ответ нужно было дать сегодня, поскольку отведенное на бюрократическую волокиту время уже закончилось. Немощи поерзали задом, проверяя, достаточно ли крепко держится под ними Руководящее Кресло. Руководящее Кресло предательски скрипнуло.
Ответ нужно было дать сегодня, поскольку отведенное на бюрократическую волокиту время уже закончилось. Немощи поерзали задом, проверяя, достаточно ли крепко держится под ними Руководящее Кресло. Руководящее Кресло предательски скрипнуло.
– А известно ли уважаемому Аргобану, что ноль является натуральным числом? – изрекли Немощи, облегченно вздохнув, – Все ваши факториалы по определению будут равняться нулю.
Напомню читателям, что дело происходило на диком западе, где и сегодня ноль считается натуральным числом.
– Но ваша работа очень интересна и будет действительно жаль, если она останется никому не известной – продолжали Немощи – Я бы мог посодействовать публикации вашей работы, если вы добавите меня в соавторы.
Это очень распространенный в науке прием, при помощи которого бездари карабкаются по служебной лестнице. Предложение нисколько не удивило Аргобана, и он ответил:
– Я сочту за великую честь быть в соавторах такого выдающегося ученого, как вы. Но как же быть с нулем?
– Как ученый, я не вижу особых проблем, – от принятого предложения Немощи начали излучать самодовольство и величие, – В Святом Математическом Писании сказано, что любое число, умноженное на ноль, равняется нулю. Но в этом Писании нет ни слова о факториале нуля. Я приложу к вашей работе свое прошение к Святой Математической Инквизиции о внесении изменений в текст Святого Математического Писания. Пусть допишут, что факториал нуля равен единице.
Но в этом Писании нет ни слова о факториале нуля. Я приложу к вашей работе свое прошение к Святой Математической Инквизиции о внесении изменений в текст Святого Математического Писания. Пусть допишут, что факториал нуля равен единице.
На том и порешили. Аргобан тут же вписал в свою работу соавтора. Святые Ученые Немощи нашкалябали прошение. Все это творение немедленно было отправлено на рассмотрение вышестоящего научного начальства.
Вышестоящее научное начальство прекрасно знало все правила бюрократических игр. Имя Аргобана никто не трогал, а вот имя своего подчиненного каждый вышестоящий начальник сошкрябывал и вписывал себя, любимого, на место соавтора. В итоге дошкрябались до того, что в соавторах Аргобана оказалась дырка.
С тех самых пор в Святом Математическом Писании присутствует шедевр научной мысли: Евангелие от Правил Умножения гласит, что ноль, умноженный на единицу, будет равен нулю
0 х 1 = 0
Евангелие от Факториала утверждает, что ноль, умноженный на единицу, равен единице
0 х 1 = 1
Вот так математика превращается в маразм.
_______________
Это было литературное произведение. А теперь суровая проза жизни. Правила бюрократических игр в науку остались неизменными. И сегодня, для того, что бы получить право откусить свой кусок от научного пирога, нужно представить пред светлы очи Святой Научной Инквизиции список своих научных заглуг. Единицей измерения заслуг в научном мире являются научные публикации. Одним из журналов, предоставляющих такую возможность, является журнал «Молодой учёный». Этот журнал получил свой «одобрямс» у Святой Научной Инквизиции и публикации в этом журнале засчитываются в качестве научных публикаций при восхождении на научный Олимп. Правила оформления статей довольно демократичны, по зубам даже блондинкам. Так что, если у вас есть научная мыслЯ, можете поделиться ею с человечеством (благодарным или не благодарным — это уж как у вас получится).
Факториал — Математика для всех
Что такое факториал
Чтобы найти факториал числа, нужно умножить все целые числа от 1 до этого числа.
Рассчитать онлайн факториал любого числа можно на этом онлайн калькуляторе.
Факториал обозначается символом «!»
Примеры:
4! = 1 · 2 · 3 · 4 = 24
5! = 1 · 2 · 3 · 4 · 5 = 120
Выражение 5! = 120 читается так: «пять факториал равно 120» или «факториал пяти равен 120»
Расчет факториала от предыдущего значения
Мы можем легко вычислить факториал из факториала предыдущего числа.
Небольшая таблица для понимания
| Число | Факториал числа | Другое разложение | Значение факториала |
| 1 | 1 | 1 | 1 |
| 2 | 1 · 2 | 1! · 2 | 2 |
| 3 | 1 · 2 · 3 | 2! · 3 | 6 |
| 4 | 1 · 2 · 3 · 4 | 3! · 4 | 24 |
| 5 | 1 · 2 · 3 · 4 · 5 | 4! · 5 | 120 |
. . . . . | и т. д. |
- Чтобы получить 6!, умножьте 6 на 5! или на 120, чтобы получить 720
- Чтобы получить 7!, умножьте 7 на 6! или на 720, чтобы получить 5040
- И так далее
Пример:
9! равняется 362880. Попробуйте посчитать 10!
10! = 10 × 9!
10! = 10 × 362880 = 3 628 800
Итак, правило такое:
п! = n × (n − 1)!
которое говорит :
«Чтобы получить факториал любого числа, нужно это число, умножить на факториал предыдущего числа »
Итак, 10! = 10 × 9!, … и 125! = 125 × 124!, и т. д.
д.
Факториал нуля
А существует ли факториал нуля?
Принято считать, что 0! = 1. Таким образом, факториал нуля равен единице. Почему именно так, можно узнать, посетив страницу Факториалы.
Где используется факториал
Одна из областей, в которой факториал часто используется — это раздел математики, который называется комбинаторика, где нужно посчитать количество перестановок, размещений или сочетаний.
Пример:
Сколько существует способов расположить буквы а,б,в,г без повторений.
Для одной буквы — это один способ — а (или 1! способов)
Для двух букв — два способа — аб, ба. (или 2! способов)
Для трех букв — шесть способов — абв, авб, бав, бва, ваб, вба (или 3! способов).
Для четырех букв — 24 или 4! способов (комбинации попробуйте сами)
Факториалы отрицательных чисел
Могут ли быть факториалы для чисел типа -1, -2 и т. д.?
д.?
Нет. Факториалы отрицательных целых чисел не определены. Если вам интересно, почему нельзя получить факториалы чисел, меньших нуля, посмотрите Почему нет факториалов отрицательных чисел.
Интересные факты о факториале
Шесть недель — ровно 10! секунд (= 3 628 800)
Есть 52! способа перемешать колоду карт.
Это 8,0658175 … × 10 67 способов
В наблюдаемой вселенной около 60! атомов.
60! составляет около 8,320987 … × 10 81, а текущие оценки числа атомов составляют от 10 78до 10 82 .
Что означает Факториал? — Ваша онлайн-энциклопедия
Содержание
- — Чему равен 1 Факториал?
- — Как выразить Факториал?
- — Для чего используется Факториал?
- — Что означает знак двойного факториала?
- — Сколько будет 200 Факториал?
- — Почему Факториал 0 равен 1?
- — Как расписать N Факториал?
- — Как работает двойной факториал?
- — Чему равно n факториал?
- — В каком классе проходят Факториал?
- — Сколько будет 50 Факториал?
- — Что означает Факториал числа?
- — Что возрастает быстрее степень или Факториал?
- — Чему равен Факториал бесконечности?
Факториал числа n — это произведение натуральных чисел от 1 до n. Обозначается n, произносится «эн-факториал». Факториал определен для целых неотрицательных чисел.
Обозначается n, произносится «эн-факториал». Факториал определен для целых неотрицательных чисел.
Чему равен 1 Факториал?
Определяется она следующим образом: F (0) = F (1) = 1; F (n) = n * F (n-1). По общепринятой договоренности 0! = 1 (факториал нуля равен единице). приблизительно равен 2.28803779534.
Как выразить Факториал?
Факториал числа — это произведение натуральных чисел от 1 до самого числа (включая данное число). Обозначается факториал восклицательным знаком «!». Примеры: 3!
Для чего используется Факториал?
Факториал очень активно используется в различных разделах математики, особенно там, где заходит речь о различных вариантах, перестановках, комбинациях и т. п. Он применяется в комбинаторике, теории чисел, математическом анализе и других областях.
Что означает знак двойного факториала?
Двойной факториал числа n обозначается n‼ и определяется как произведение всех натуральных чисел в отрезке [1,n], имеющих ту же чётность, что и n. Связь между двойными факториалами двух соседних целых неотрицательных чисел и обычным факториалом одного из них.
Связь между двойными факториалами двух соседних целых неотрицательных чисел и обычным факториалом одного из них.
Сколько будет 200 Факториал?
Точная и приблизительная таблицы факториалов (1-255)
| Факториал | Значение |
|---|---|
| 121! | 8,09*10200 |
| 122! | 9,88*10202 |
| 123! | 1,21*10205 |
| 124! | 1,51*10207 |
Почему Факториал 0 равен 1?
i=0! Факториал это частный случай гамма-функции для натуральных n. Ноль не является натуральным числом, поэтому определение факториала для него бессмыслено, однако гамма-функция имеет значение в точке ноль, поэтому факториалу «приписали» значение от нуля.
Как расписать N Факториал?
По определению факториал n! можно записать как n * (n-1)! . Другими словами, factorial(n) можно получить как n умноженное на результат factorial(n-1) .
Другими словами, factorial(n) можно получить как n умноженное на результат factorial(n-1) .
Как работает двойной факториал?
Двойной факториал Для четного целого числа n двойной факториал является произведением всех четных положительных целых чисел, меньших или равных n. Для нечетного целого числа p двойной факториал является произведением всех нечетных положительных целых чисел, меньших или равных p.
Чему равно n факториал?
Факториал натурального числа n (обозначение – “n! “) равен произведению всех натуральных чисел от 1 до n включительно.
В каком классе проходят Факториал?
Факториал — урок. Алгебра, 9 класс.
Сколько будет 50 Факториал?
В таблице приведены значения факториалов для чисел от 0 до 50.
| число | факториал числа |
|---|---|
| 48! | 12413915592536072670862289047373375038521486354677760000000000 |
| 49! | 608281864034267560872252163321295376887552831379210240000000000 |
| 50! | 30414093201713378043612608166064768844377641568960512000000000000 |
Что означает Факториал числа?
Факториал: определение
Факториал числа n — это произведение натуральных чисел от 1 до n. Обозначается n, произносится «эн-факториал». Факториал определен для целых неотрицательных чисел.
Обозначается n, произносится «эн-факториал». Факториал определен для целых неотрицательных чисел.
Что возрастает быстрее степень или Факториал?
Известно что экспонента растет быстрее любого конечного полинома. Экспонента за единицу времени увеличивается в константу раз, а факториал — во все возрастающее число раз. следовательно факториал растет быстрее любого конечного полинома.
Чему равен Факториал бесконечности?
При всех вышеперечисленных условиях, больше одной их быть не может. Отсюда легко вычисляем факториал её бесконечности, как одного целого числа. Он будет равен единице. Кстати, факториал нуля, как это не парадоксально, тоже равен единице.
Интересные материалы:
Сколько калорий в конфетах кис кис?
Сколько калорий в конфете коровка Рот Фронт?
Сколько калорий в куриной Самсе с курицей?
Сколько калорий в молочных сосисках?
Сколько калорий в натуральном кофе без сахара?
Сколько калорий в одной арахисовой Вафле?
Сколько калорий в одном кусочке цельнозернового хлеба?
Сколько калорий в семечках без шелухи?
Сколько калорий в сливочной конфете коровка?
Сколько калорий в сухариках Флинт?
Факториал — frwiki.
 wiki
wikiВ математике , то факториал из натурального целого числа п является продукт строго положительных целых чисел меньше или равно п .
Эта операция с отмечено восклицательным , п !, Который считывает либо «факториал п », или «факториала п» или «п факториала» (последнее выражение является наименее используется). Это обозначение было введено в 1808 году Кристианом Крампом .
Например, факториал 10 выражает количество возможных комбинаций размещения 10 гостей вокруг стола (мы говорим перестановку гостей). Первый гость сидит на одном из 10 мест, имеющихся в его распоряжении. Каждое из 10 мест размещения открывает 9 новых возможностей для второго гостя, эти 8 — для третьего и так далее.
Факториал играет важную роль в комбинаторной алгебре, потому что существует n ! разные способы перестановки n объектов. Он появляется во многих математических формулах, таких как биномиальная формула и формула Тейлора .
Резюме
- 1 Определение
- 1.
 1 Значение 0!
1 Значение 0!
- 1.
- 2 свойства
- 3 Обобщение
- 4 приближение
- 5 Примеры приложений
- 6 Теория чисел
- 7 вариантов
- 8 Алгоритм
- 9 Примечания и ссылки
- 10 См. Также
- 10.1 Статьи по теме
- 10.2 Внешние ссылки
Определение
| нет | п ! |
|---|---|
| 0 | 1 |
| 1 | 1 |
| 2 | 2 |
| 3 | 6 |
| 4 | 24 |
| 5 | 120 |
| 6 | 720 |
| 7 | 5 040 |
| 8 | 40 320 |
| 9 | 362 880 |
| 10 | 3 628 800 |
| 11 | 39 916 800 |
| 12 | 479 001 600 |
| 13 | 6 227 020 800 |
| 14 | 87 178 291 200 |
| 15 | 1 307 674 368 000 |
| 16 | 20 922 789 888 000 |
| 17 | 355 687 428 096 000 |
| 18 | 6 402 373 705 728 000 |
| 19 | 121 645 100 408 832 000 |
| 20 | 2 432 902 008 176 640 000 |
. .. .. | … |
| 25 | 1,551 121 004 333 098 598 4 × 10 25 |
Заметки:
| |
Пусть n — натуральное число. Его факториал формально определяется следующим образом:
- нет!знак равно∏1⩽я⩽нетязнак равно1×2×3×…×(нет-1)×нет.{\ displaystyle n! = \ prod _ {1 \ leqslant i \ leqslant n} i = 1 \ times 2 \ times 3 \ times \ ldots \ times (n-1) \ times n.}
Таблица справа дает первые факториалы; например, у нас есть
- 1! = 1
- 2! = 1 × 2 = 2
- 3! = 1 × 2 × 3 = 6
- 4! = 1 × 2 × 3 × 4 = 24
- 10! = 1 × 2 × 3 × 4 × 5 × 6 × 7 × 8 × 9 × 10 = 3 628 800
Значение 0!
Это определение также дает
- 0! = 1
поскольку по соглашению пустой продукт равен нейтральному элементу умножения. {- t} {\ rm {d}} t = \ Gamma (n + 1) .}
{- t} {\ rm {d}} t = \ Gamma (n + 1) .}
Более того, функция z ↦ Γ ( z + 1) удовлетворяет тому же рекуррентному соотношению, что и факториал:
- ∀z∈ПРОТИВ∖(-НЕТ),Γ(z+1)знак равноzΓ(z).{\ Displaystyle \ forall z \ in \ mathbb {C} \ setminus (- \ mathbb {N}), \ quad \ Gamma (z + 1) = z \ Gamma (z).}
Такое видение (переведенной) гамма-функции как привилегированного расширения факториала оправдано следующими причинами:
- две функции имеют одно и то же повторяющееся определение;
- гамма-функция обычно используется в контексте, аналогичном (хотя и более общему) факториалу;
- гамма-функция — единственная функция, которая удовлетворяет этому определению индукции по комплексным числам, которая является голоморфной и чей логарифм ограничения на положительные действительные числа выпуклый ( теорема Бора-Моллерупа ).
Однако есть и другие расширения с «хорошими свойствами», такие как « Гамма-функция Адамара (in) », которая заполнена . {n}}.
{n}}.
где число e обозначает основание экспоненты .
Выведем приближение логарифма от п ! :
Примеры приложений
В комбинаторике существует n ! различные способы расположения n различных объектов (т.е. n ! перестановок ). А количество способов выбрать k элементов из набора n определяется биномиальным коэффициентом :
- (нетk)знак равнонет!k!(нет-k)!.{\ displaystyle {n \ select k} = {n! \ over k! (nk)!}.}
Факториалы также появляются в анализе . Например, теорема Тейлора , которая выражает значение в x функции ƒ как целочисленный ряд , включает факториал n ! для члена, соответствующего n- й производной в точке x .
Объем гиперсферы в даже н измерения может быть выражен:
- Vнетзнак равноπнет2рнет(нет2)!.{\ displaystyle \ mathrm {V} _ {n} = {\ frac {\ pi ^ {\ frac {n} {2}} \ mathrm {R} ^ {n}} {\ left ({\ frac {n} {2}} \ right)!}}.
 }
}
Факториалы широко используются в теории вероятностей .
Факториалы часто используются в качестве примера — с последовательностью Фибоначчи — для изучения рекурсии в информатике из-за их простого повторяющегося определения.
Теория чисел
Факториалы имеют множество приложений в теории чисел .
Например, теорема Вильсона показывает, что целое число n > 1 является простым тогда и только тогда, когда ( n — 1)! ≡ –1 (mod n ).
В частности, если n простое, то оно не делит ( n — 1) !, что, кроме того, можно вывести непосредственно из леммы Евклида ; обратное почти верно: если п является составным числом , кроме 4, то ( п — 1)! ≡ 0 (mod n ).
Доказательство последнего утверждения использований , что произведение P из K последовательных целых чисел всегда делится на к (так как один из K факторов ). Фактически, P делится даже на k ! мы можем доказать это, выразив P / k ! как биномиальный коэффициент , либо путь сравнения, для любого простого числа р , то кратность р в простых факторах разложения в Р и к !, благодаря формуле Лежандра .
Единственный факториал, который также является простым числом, — это 2, но есть простые числа вида n ! ± 1, называемые факториальными простыми числами .
Варианты
Многие авторы определили похожие функции, которые растут еще быстрее, а также продукты, ограниченные только определенными целыми числами. Таким образом, в литературе мы находим первичные , многофакторные, надфакториальные, гиперфакториальные и т. Д. Функции. Но не похоже, что, в отличие от факториала, вездесущего в большинстве разделов математики, эти другие функции имели много применений помимо развлекательных , за исключением примориалов; Что касается их использования для обозначения очень больших чисел , обозначения Кнута и Конвея оказались более управляемыми и гораздо более эффективными.
Алгоритм
Вычисление факториала можно перевести с помощью следующего рекурсивного алгоритма , написанного в псевдокоде :
Fonction factorielle (n: entier): entier
Début
Si n > 1
Retourner n * factorielle(n - 1)
Sinon
Retourner 1
Fin si
Fin
Примечания и ссылки
(fr) Эта статья частично или полностью взята из английской статьи в Википедии под названием « Факториал » ( см. список авторов ) .
список авторов ) .
- ↑ Жан Дьедонне , Во имя человеческого духа: математика сегодня , Hachette ,, 316 с. ( ISBN 978-2-01-014000-6 , OCLC 20000703 ) , стр. 102.
- ↑ (in) Х.М. Шривастава и Джунесанг Чой, Зета- и q-дзета-функции и связанные ряды и интегралы , Elsevier,( читать онлайн ) , стр. 124.
- ↑ Гаусс , Арифметические исследования , § 127 .
- ↑ « Это одно и то же доказательство? » , В блоге Гауэрса ,.
- ↑ Особенно в OEIS .

Смотрите также
Статьи по Теме
- Экспоненциальный факториал
- Формула Стирлинга
- Дигамма функция
- Простое факториальное число
- Первобытный
- Альтернативные серии факториалов
- Аналоги факториала
Внешние ссылки
- факториал n! на сайте factorielle.free.fr
- (ru) Питер Лушни, « Быстрые факторные функции »
Большие числа целые | |
|---|---|
| Последовательности от 1000 до 9999 | Числа от 1000 до 1999 · числа от 2000 до 2999 · числа от 3000 до 3999 · числа от 4000 до 4999 · числа от 5000 до 5999 · числа от 6000 до 6999 · числа от 7000 до 7999 · числа от 8000 до 8999 · числа от 9000 до 9999 |
| Последовательности от 10,000 до 9,999,999,999 | Номера 10 000-99 999 · номера 100 000 999 999 · Номера 1 000 000–9 999 999 • номера 10 000 000–99 999 999 • номера от 100 000 000 до 999 999 999 • Номера 1 000 000 000–9 999 999 999 |
| Большие замечательные числа | 142 857 ( циклическое число и число Капрекара ) · 144 000 (1 бактун — длинный счет майя ) · 1048576 ( 20- я степень двойки ) · 4294967296 ( 32- я степень двойки ) · 4294967297 ( число Ферма ) · 107 928 278 317 (см. тройная теорема Пифагора и Грина-Тао ) тройная теорема Пифагора и Грина-Тао ) |
| Общие представления о больших числах | Быстрый рост иерархии · Бесконечность · большое количество имен · рейтинговые стрелки, прикованные цепью Конвей · итерация подсчета очков Кнут · Величина · Парадоксальные интересные числа · Индийский счет |
Числовое понятие | ||
|---|---|---|
| Обычные наборы | Целое число ( ) НЕТ{\ Displaystyle \ scriptstyle \ mathbb {N}} · относительно Целого числа ( ) Z{\ Displaystyle \ scriptstyle \ mathbb {Z}} · Десятичного числа ( ) D{\ Displaystyle \ scriptstyle \ mathbb {D}} · рационального числа ( ) Q{\ Displaystyle \ scriptstyle \ mathbb {Q}} · Фактического ( ) р{\ Displaystyle \ scriptstyle \ mathbb {R}} · Комплексного числа ( )ПРОТИВ{\ Displaystyle \ scriptstyle \ mathbb {C}} | |
| Расширения | Кватерниона ( ) ЧАС{\ Displaystyle \ scriptstyle \ mathbb {H}} · октонионы ( ) О{\ Displaystyle \ scriptstyle \ mathbb {O}} · седенионы ( ) S{\ Displaystyle \ scriptstyle \ mathbb {S}} · Комплексного число развернет · Tessarine · Количество бикомплекс ( ) ПРОТИВ2{\ Displaystyle \ scriptstyle \ mathbb {C} _ {2}} · Числа мультикомплекс ( ПРОТИВнет{\ displaystyle \ scriptstyle \ mathbb {C} _ {n}} · ) · бикватернионных · расщепленные кватернионы · гиперболических кватернионы · октонионы развернуты · Число hypercomplexe · Число р-адический ( ) · Число гиперреальное · Число superréel · Число двойственное · законченное действительное Справа · Число Кардинал · Порядковое число · Число сюрреалистическое · Число псевдореальноеMПРОТИВнет{\ Displaystyle \ scriptstyle {\ mathcal {M}} \ mathbb {C} _ {n}} Qп{\ Displaystyle \ scriptstyle \ mathbb {Q} _ {p}} | |
| Особые свойства | Четность · Номер первое · Номер состоит · Количества фигурного · Номер идеально · Количество положительного · Количество отрицательна · доли диадического · Число иррациональное · Алгебраического Количество · Количество трансцендентный · Количество чисто мнимое · Количество Лиувилля · Период · Количество Нормального · Номер вселенная · Номер здание · Актуально вычислимое · число трансфини · бесконечно малое | |
| Примеры | Пи ( π ) · квадратный корень из двух ( ) · Число золота (φ) · Ноль (0) · Мнимая единица ( i ) · Константа Непер ( e ) · Алеф-ноль (ℵ 0 ) · Табличные математические константы2{\ displaystyle \ scriptstyle {\ sqrt {2}}} | |
| Статьи по Теме | Продажи · Количество · Дробь · Операция · Вычисление · Алгебра · Арифметика · Следующее целое число · бесконечность ( ∞ ) · Значащая цифра | |
<img src=»//fr. wikipedia.org/wiki/Special:CentralAutoLogin/start?type=1×1″ alt=»» title=»»>
wikipedia.org/wiki/Special:CentralAutoLogin/start?type=1×1″ alt=»» title=»»>
Python Factorial | Программа Python для факториала числа
Автор оригинала: Team Python Pool.
Что такое факториал?
В Python, любом другом языке программирования или в общем термине факториал числа является произведением всех целых чисел от одного до этого числа. Математически формула для факториала выглядит следующим образом. Если n-целое число, большее или равное единице, то факториал n равен,
*2*3*4....*n
Кроме того, факторное значение ноль равно один и факторные значения для отрицательных целых чисел не определены.
Примеры:
- 4! × 3 ×
- 7! × 6 × 5 × 4 × 3 ×
- а факториал one – это one
Вычисление По Предыдущему значению
Мы можем легко вычислить <сильный>факториал из предыдущего:
В виде таблицы:
| 1 | 1 | 1 | 1 |
| 2 | 2 × × | ||
| 3 | 3 × 2 × × | ||
| 4 | 4 × 3 × 2 × × | ||
| 5 | 5 × 4 × 3 × 2 × × | ||
| 6 | и т. д. д. | и т.д. |
- Чтобы отработать 7! умножьте 7 на 720, чтобы получить 5040
- И так далее
Пример: 8! равно 40320. Попробуйте посчитать 9!
9! × 8!
9! × 40320 = 3,62880
Итак, правило таково:
n! × (n−1)!
Что говорит
“факториал любого числа это число умноженное на факториал (это число минус один)”
Поиск факториала числа в Python с помощью итерации
(i) Факториал числа с использованием цикла for
Программа
(input("enter>Выход
Enter the Number :7 Factorial of 7 is 5040
В этой программе python сначала мы принимаем ввод с клавиатуры с помощью функции input() , а затем у нас есть условный оператор для отрицательных входов, так как факториал отрицательного числа не существует.
Тогда у нас есть цикл for в диапазоне от 1 до самого числа внутри цикла, мы просто перебираем переменную цикла i и умножаем ее на переменную fact, определенную выше. В конце концов, мы просто распечатываем результат, используя форматирование строк.
(ii) Факториал числа с использованием цикла While
def factorialUsingWhileLoop(n):
while(n>1):
*n
- 1
print('Factorial is %d'%(fact))
if:
factorialUsingWhileLoop(4)Подобно приведенной выше программе , мы можем использовать один цикл ‘ while ‘, чтобы узнать факториал . Процесс тот же. Единственная разница заключается в том, что мы используем один цикл «while «вместо цикла» for loop».
Метод’ factorialUsingWhileLoop ‘ используется для определения факториала с помощью цикла while. Как и в приведенной выше программе, переменная ‘fuck’ используется для хранения конечного факторного значения. Цикл while будет выполняться до тех пор, пока значение ‘n’ не станет больше ‘one’. На каждой итерации цикла мы уменьшаем значение ‘n’ на ‘один’. Этот цикл завершится, когда значение ‘n’ будет равно ‘0’. Мы печатаем факторное значение, когда оно заканчивается.
Подробнее: Что такое Null в Python
Поиск факториала числа в Python с помощью рекурсии
Рекурсия означает метод, вызывающий себя до тех пор, пока не будет выполнено некоторое условие. Метод, который вызывает сам себя, называется рекурсивным методом. A href=»https://en.wikipedia.org/wiki/Recursion»>рекурсивный метод должен иметь условие, которое должно заставить его вернуться, иначе он будет продолжать вызывать себя бесконечно, что приведет к переполнению памяти.Вычисление факториала числа с помощью рекурсивного метода должно работать по следующему алгоритму. *. Создайте метод, который принимает один аргумент. Проверьте, является ли значение аргумента one, а затем верните one из этого метода. Это будет конечным условием рекурсивного метода. Возвращает произведение аргумента и возвращаемого значения этого метода (argument – one). href=»https://en.wikipedia.org/wiki/Recursion»>рекурсивный метод должен иметь условие, которое должно заставить его вернуться, иначе он будет продолжать вызывать себя бесконечно, что приведет к переполнению памяти.Вычисление факториала числа с помощью рекурсивного метода должно работать по следующему алгоритму.*. Создайте метод, который принимает один аргумент. Проверьте, является ли значение аргумента one, а затем верните one из этого метода. Это будет конечным условием рекурсивного метода. Возвращает произведение аргумента и возвращаемого значения этого метода (argument – one).
*. Создайте метод, который принимает один аргумент. Проверьте, является ли значение аргумента one, а затем верните one из этого метода. Это будет конечным условием рекурсивного метода. Возвращает произведение аргумента и возвращаемого значения этого метода (argument – one). href=»https://en.wikipedia.org/wiki/Recursion»>рекурсивный метод должен иметь условие, которое должно заставить его вернуться, иначе он будет продолжать вызывать себя бесконечно, что приведет к переполнению памяти.Вычисление факториала числа с помощью рекурсивного метода должно работать по следующему алгоритму.*. Создайте метод, который принимает один аргумент. Проверьте, является ли значение аргумента one, а затем верните one из этого метода. Это будет конечным условием рекурсивного метода. Возвращает произведение аргумента и возвращаемого значения этого метода (argument – one).
Код следует
# recursive method which returns the factorial of a number
def factorial_recursion(number):
# check if number is 1
if number:
# return 1 from the method
return 1
return number * factorial_recursion(number-1)
#(5)
# read number from keyboard(input("Enter a number\n"))
# find factorial(number)
print("Factorial is "+str(factorial))Метод будет продолжать вызывать себя и возвращать продукт предоставленного ему аргумента с одним меньше, чем аргумент. Если значение аргумента равно one, он вернет one. Таким образом, рекурсивный метод вернет произведение всех чисел, начиная с аргумента до одного.
Если значение аргумента равно one, он вернет one. Таким образом, рекурсивный метод вернет произведение всех чисел, начиная с аргумента до одного.
Введите число6Факториал равен 720
Python Программа для поиска факториала числа с помощью функций
Эта python factorial программа такая же, как и в первом примере. Однако мы разделили логику с помощью Функции
# Python Program to find Factorial of a Number
def factorial(num):
for i in range(1, num + 1):
* i
return fact
(input(" Please enter any Number to find factorial : "))
(number)
print("The factorial of %d = %d" %(number, facto))Выход:
Please enter any Number to find factorial : 6 The factorial of
Встроенное решение для вычисления факториала числа в Python
from math import factorial
(input("Enter the Number :"))
(num)
if num < 0:
print("Factorial of negative number is not defined")
else:
print("Factorial of {} is {}". format(num, fact))
format(num, fact))Выход:
Enter the Number :5 Factorial of 5 is 120
Вывод:
В этом уроке мы узнали, как узнать факториал числа в python. Мы научились вычислять факториал с помощью четырех различных методов. Попробуйте выполнить примеры, показанные выше, и опустите один комментарий ниже, если у вас есть какие-либо запросы.
Нулевой факториал | Lunatic Laboratories
Перестановки, комбинации и математика, о боже! Сегодня я делаю домашнюю работу по статистике и вспомнил о странном кварке в математике, нулевом факториале. Это не очень интуитивно понятно, и я очень люблю странную математику, поэтому я решил поделиться своим весельем. Я никогда не говорил, что я нормальный… В любом случае, сегодня мы рассмотрим, почему 0! (нулевой факториал) это так интересно!
Я никогда не говорил, что я нормальный… В любом случае, сегодня мы рассмотрим, почему 0! (нулевой факториал) это так интересно!
Что ж, я решил отвлечься от разговоров о написании грантов, вам все равно это надоело… да? Для тех, кто пропустил веселье и только находит меня, я учусь на третьем курсе доктора наук в области нейроинженерии. Я изучаю, как травма спинного мозга меняет связь с мозгом, и способы использования этого изменения в целях реабилитации. В последнее время я писал несколько грантов (подробнее здесь), потому что мне нужно финансирование, чтобы закончить свою работу, чтобы я мог получить высшее образование и перейти к более крупным вещам (в идеале). Сегодня мы говорим о математике, потому что мне нужен перерыв, и я уверен, что мои подписчики устали слышать одно и то же о написании грантов (это ужасно, я не рекомендую это). После введения давайте поговорим о 0!
Во-первых, для тех из вас, кто не знаком с факториалами, мы пишем их так: n ! где n любое целое число и например 3! выписано выглядит так
3! = 3*2*1
Теперь мы можем написать формулу для этого, но сначала мы должны поговорить о нулевом факториале или 0! используя приведенную выше формулу, вы можете подумать, что ответ будет выглядеть так:
0! = 0… но это не так!
На самом деле 0! решает быть…
0! = 1
Верно, когда мы возьмем факториал нуля, мы получим единицу! Разве это не странно!? Это все равно, что пытаться положить ноль долларов в банк, и они дают вам один доллар за каждый вложенный ноль. Это просто не имеет никакого смысла! Но не волнуйтесь, мы действительно можем понять, почему это так, просто не в хорошем смысле (не вся математика удовлетворяет детей). Начнем с полностью развернутой формы общей формулы факториала. Пусть n — любое положительное целое число (целое число 1, 2, 3, … и т. д.), тогда формула принимает вид 9.0003
Это просто не имеет никакого смысла! Но не волнуйтесь, мы действительно можем понять, почему это так, просто не в хорошем смысле (не вся математика удовлетворяет детей). Начнем с полностью развернутой формы общей формулы факториала. Пусть n — любое положительное целое число (целое число 1, 2, 3, … и т. д.), тогда формула принимает вид 9.0003
н! = n * (n-1) * (n-2) * … * 3 * 2 * 1
, где эти последние биты уже решены, так как мы достигли точки, где y в n – y будет равно n . Хитрость заключается в том, чтобы посмотреть на частично развернутую форму, которую немного удобнее писать, и я думаю, что она интуитивно понятнее, чем полностью развернутая версия, которая выглядит так…
n! = п * (п-1)!
Она частично расширена, потому что мы используем фаториал для определения формулы, но именно поэтому мы определили, как она работает выше, так что эта форма должна иметь смысл для вас сейчас, и вы знаете, что она расширяется до чего-то похожего на полностью развернутую форма. Теперь, когда это не так, давайте поговорим о том, как мы получаем 0! = 1 из всего этого, это дико.
Теперь, когда это не так, давайте поговорим о том, как мы получаем 0! = 1 из всего этого, это дико.
Допустим, мы хотим найти 1! поэтому мы подставляем это в нашу формулу, мы знаем, что
1! = 1
Мы это знаем точно, это довольно интуитивно понятно, ничего другого быть не должно… верно? Вот где происходит волшебство, давайте решим 1! используя частично расширенную форму n!, которая выглядит так
н! = п * (п-1)!
1! = 1 * (1-1)!
1! = 1 * (0)!
1! = 1 * 0!
Видите, что только что произошло? Мы заканчиваем с 0! в нашем уравнении. Мы знаем, что уравнение правильное, и мы точно знаем, что 1! = 1, поэтому это доказательство того, что
0! = 1
Теперь немного мелкого шрифта… вы можете взять факториал отрицательных чисел, математика работает, но для практических целей n! живет в натуральных числах (включая ноль). Если вы большой заядлый математический гений — зачем бы вам было читать это, если бы вы не были… — вы можете прочитать здесь больше, чем когда-либо хотели бы знать о факториалах действительных отрицательных и мнимых чисел.
Одно замечание на прощание. Вы можете думать о факториале как о скольких различных способах что-то упорядочить. Если у меня есть 3 объекта, я могу расположить их 6 разными способами:
1,2,3
1,3,2
3,2,1
2,3,1
2,1,3
3,1,2
Вы заметите, что 1,2,3 и 3,2,1 имеют тот же порядок, но в обратном порядке. Это потому, что, когда мы используем факториал, порядок имеет значение, вроде слов. Если я напишу слово «word», это не то же самое, что написать «odrw», даже если в нем будут использоваться те же буквы. Когда порядок имеет значение, это называется перестановкой. Когда порядок не имеет значения, это называется комбинацией, и это другая формула, которая выглядит так:
n!/(r!(n-r)!)
Извините за форматирование, wordpress не любит математику (это я все равно могу найти). В данном случае в этой формуле n есть количество вещей на выбор, и мы выбираем r из них, без повторений, порядок не имеет значения. По сути, если бы у нас был мешок с 20 шариками разных цветов, формула позволила бы нам найти все комбинации (порядок здесь не имеет значения!), которые мы могли бы нарисовать r шариков из мешка до r = n или 20 в примере с шариками. По этой причине, говоря о формуле, мы обычно говорим n выбрать r .
По сути, если бы у нас был мешок с 20 шариками разных цветов, формула позволила бы нам найти все комбинации (порядок здесь не имеет значения!), которые мы могли бы нарисовать r шариков из мешка до r = n или 20 в примере с шариками. По этой причине, говоря о формуле, мы обычно говорим n выбрать r .
Но теперь мы спускаемся в кроличью нору комбинаций/перестановок, когда на самом деле я просто хотел поделиться своим волнением по поводу 0! что, скажем прямо, довольно интересно. Я упоминаю о различиях, потому что в факториале важен порядок, и это разные способы, которыми мы можем что-то упорядочить, поэтому формула говорит о том, что 0! = 1, потому что есть только один способ ничего не выбирать.
Одно замечание на прощание: поскольку при работе с перестановками (факториалом) важен порядок, очень легко запомнить разницу между перестановками и комбинациями. Самый простой способ — просто помнить, что кодовый замок на самом деле следует называть замком перестановки. По крайней мере, это то, что засело у меня в голове, ваш пробег может отличаться.
Самый простой способ — просто помнить, что кодовый замок на самом деле следует называть замком перестановки. По крайней мере, это то, что засело у меня в голове, ваш пробег может отличаться.
Нравится:
Нравится Загрузка…
Эта запись была опубликована 7 февраля 2021 г. пользователем The Lunatic. Он был подан под рубрикой 365 Days of Academia — Year two, Math и был помечен как академические круги, комбинации, ежедневное ведение блога, образование, факториал, математика, перестановки, PhD, postaday, школа, наука, студент.
→
←
%d блоггеров нравится это:
не волнующий номер. – Occupy Math
Факториал числа – это то, что вы получаете, когда перемножаете это число и меньшие его (до единицы) вместе. Это означает, что пятифакториал равен 5x4x3x2x1=120. В математическом обозначении факториала используется восклицательный знак: 5!=120. Occupy Math преподавал курс, в котором для подсчета вещей использовались факториалы, и один из самых сообразительных студентов продолжал решать задачи неправильно. Occupy Math написала на доске «5» и спросила: «Какое это число?» Ученик ответил «пять». Occupy Math добавил восклицательный знак, чтобы получить «5!» и снова спросил студента, что это за число. Студент ответил: «ПЯТЬ!» Это был студент третьего курса университета — отсюда и эта воспитательная должность. На этой неделе Occupy Math расскажет, что делают факториалы (например, они считают вещи). Факториалы также дают пример чего-то, что растет быстрее , чем экспоненциально.
Occupy Math написала на доске «5» и спросила: «Какое это число?» Ученик ответил «пять». Occupy Math добавил восклицательный знак, чтобы получить «5!» и снова спросил студента, что это за число. Студент ответил: «ПЯТЬ!» Это был студент третьего курса университета — отсюда и эта воспитательная должность. На этой неделе Occupy Math расскажет, что делают факториалы (например, они считают вещи). Факториалы также дают пример чего-то, что растет быстрее , чем экспоненциально.
Факториал определен только для положительных целых чисел и нуля. Значение нулевого факториала равно единице (ниже в Occupy Math объясняется, почему). Начнем с вопроса «Сколькими способами можно выстроить 4 учеников?» Occupy Math даст этим учащимся довольно лаконичные имена A, B, C и D и просто перечислит все возможные строки. Это дает нам:
Убедитесь сами, что больше нет способов выстроить этих учеников в очередь. Occupy Math представила эти 24 способа объединить четырех учеников в четыре группы по шесть человек. Каждая группа начинается с одной буквы, а после этого остальная часть группы из шести содержит все способы выстроить трех оставшихся учеников. Другой интересный факт заключается в том, что 4!=24. На самом деле факториалы точно подсчитывают количество различных способов выстроить людей в ряд.
Каждая группа начинается с одной буквы, а после этого остальная часть группы из шести содержит все способы выстроить трех оставшихся учеников. Другой интересный факт заключается в том, что 4!=24. На самом деле факториалы точно подсчитывают количество различных способов выстроить людей в ряд.
Конечно, Occupy Math — это всего лишь , утверждающая, что верна, основываясь на одном, возможно, случайном примере. При внимательном рассмотрении этого примера 3!=6, поэтому идея «выбрать одного ученика, а затем выстроить оставшихся трех учеников всеми возможными способами» — это второй пример, который согласуется с утверждением Occupy Math. В общем случае алгоритм поиска всех способов выстроить учеников в очередь такой. Выберите первого ученика — затем будет группа линий, где этот ученик стоит во главе. Внутри этой группы перечислите все способы выстроить оставшихся учеников в очередь. Если есть n студентов, то общее количество очередей равно n (количество различных вариантов выбора для первого учащегося), умноженное на количество способов выстроить остальных студентов. Если вы выстраиваете всех учеников, это означает, что вы умножаете количество учеников на это число минус один, затем на это число минус два и так далее. Вы останавливаетесь на одном, потому что есть (очевидно) только один способ выстроить одного ученика.
Если вы выстраиваете всех учеников, это означает, что вы умножаете количество учеников на это число минус один, затем на это число минус два и так далее. Вы останавливаетесь на одном, потому что есть (очевидно) только один способ выстроить одного ученика.
Это дает нам математическое определение n! следующим образом:
Давайте вычислим пять факториалов таким образом — помните, что «!» является математическим символом, а не знаком препинания. «5!» это «5×4!» это «5x4x3!» это «5x4x3x2!» это «5x4x3x2x1!» это «5x4x3x2x1» это «120». Это пример рекурсивного определения, которое что-то объясняет в терминах самого себя, но самого себя в меньшем размере. Если вы дойдете до первого случая, 1!=1, то это совершенно хорошее определение. Он выглядит круглым, но это не так, потому что размер экземпляра того, над чем вы работаете, уменьшается. Важно знать, где заканчивается это самосокращающееся определение, т.е. в «один факториал один».
Как можно расти быстрее экспоненциального?
Когда у нас есть экспоненциальная функция, она выглядит как 2 5 = 2x2x2x2x2. В английском языке от двух до пятых — это два раза пять раз. Пять факториалов, по сравнению с двумя в пятой, составляют 1x2x3x4x5. Это также пять чисел, умноженных вместе, но они не все равны 2. Три из них больше, чем два. В этом вся хитрость. Если бы мы смотрели на восемь в степени n , то мы бы умножили 8 на 9.0166 п раз. Если n намного больше восьми, то n! 90 167 вычисляется путем умножения семи элементов меньше восьми, одного элемента, равного восьми, и множества элементов больше восьми. Неважно, какое число вы возьмете в качестве базовой константы экспоненты — факториал в конечном итоге начнет расти быстрее, чем основание экспоненты, и преимущество членов, умноженных для получения факториала, только увеличивается по мере увеличения n .
В английском языке от двух до пятых — это два раза пять раз. Пять факториалов, по сравнению с двумя в пятой, составляют 1x2x3x4x5. Это также пять чисел, умноженных вместе, но они не все равны 2. Три из них больше, чем два. В этом вся хитрость. Если бы мы смотрели на восемь в степени n , то мы бы умножили 8 на 9.0166 п раз. Если n намного больше восьми, то n! 90 167 вычисляется путем умножения семи элементов меньше восьми, одного элемента, равного восьми, и множества элементов больше восьми. Неважно, какое число вы возьмете в качестве базовой константы экспоненты — факториал в конечном итоге начнет расти быстрее, чем основание экспоненты, и преимущество членов, умноженных для получения факториала, только увеличивается по мере увеличения n .
Что учитывают факториалы?
Мы уже знаем, что факториалы подсчитывают количество способов, которыми ученики могут быть выстроены в очередь. Порядок набора объектов называется перестановкой объектов. Перефразируя результат «выстраивания»: количество перестановок набора из n объектов равно n! Это уже интересно, но давайте продолжим.
Перефразируя результат «выстраивания»: количество перестановок набора из n объектов равно n! Это уже интересно, но давайте продолжим.
Предположим, у вас есть клуб из десяти членов. Сколько существует способов выбрать президента, вице-президента и казначея? Есть десять вариантов для президента, девять оставшихся вариантов для вице-президента, и после того, как эти два будут выбраны, останется восемь вариантов для казначея. Всего 10х9×8=720 вариантов. Это первая часть факториала. На самом деле 10x9x8=10!/7! Что происходит, так это то, что вы разделяете (не относящийся к делу) способ заказа семи человек, не выбранных для офиса. Такую задачу подсчета также называют перестановкой, но неполной.
А если факториал нуля равен единице?
Предположим, мы складываем список чисел. Мы можем сделать это, начав с нуля, а затем добавляя числа в списке по одному к промежуточной сумме. Начинать с нуля кажется немного эксцентричным, за исключением того, что это говорит нам о том, что произойдет, если мы добавим список вообще без чисел: мы получим ноль. Лавка с лимонадом без продаж принесла ноль денег, поэтому есть реальный пример, который показывает, что это имеет смысл. Теперь предположим, что мы умножаем список чисел аналогичным образом. Если мы начнем с нуля, мы останемся там: начав с единицы, мы получим правильный результат. Вот почему произведение пустого списка чисел равно единице (что и является нулевым факториалом). Почему ноль и единица для сложения и умножения? Ноль — это число, которое вы можете добавить к другому числу, не изменяя его; единица — это число, которое можно умножить на другое число, не изменяя его. Есть еще один способ увидеть, что 0!=1. Помните, что факториалы подсчитывают количество заказов, в которые вы можете поместить группу? Ну, есть один способ заказать группу, в которой никого нет.
Лавка с лимонадом без продаж принесла ноль денег, поэтому есть реальный пример, который показывает, что это имеет смысл. Теперь предположим, что мы умножаем список чисел аналогичным образом. Если мы начнем с нуля, мы останемся там: начав с единицы, мы получим правильный результат. Вот почему произведение пустого списка чисел равно единице (что и является нулевым факториалом). Почему ноль и единица для сложения и умножения? Ноль — это число, которое вы можете добавить к другому числу, не изменяя его; единица — это число, которое можно умножить на другое число, не изменяя его. Есть еще один способ увидеть, что 0!=1. Помните, что факториалы подсчитывают количество заказов, в которые вы можете поместить группу? Ну, есть один способ заказать группу, в которой никого нет.
Occupy Math довольно глубоко погрузился в океан математики в этом посте — отчасти в надежде, что будущий студент не будет смеяться над своими сверстниками, когда он скажет «ПЯТЬ!» вместо «сто двадцать». Еще один важный момент заключается в том, что существует множество различных задач, которые начинаются со слов «сколько…», и факториалы являются ключом к решению многих из этих проблем. Область математики, связанная с такого рода подсчетами, называется перечислительной комбинаторикой , и Occupy Math преподавала как университетские, так и аспирантские курсы по этому предмету. Результаты могут быть действительно странными. Теперь Occupy Math потроллит вас странным примером: количество случаев, когда турнир может иметь совершенно однозначный результат (нет A побеждает B, B побеждает C, C побеждает A), равно количеству способов присвоить отрицательным единицам цвета. команды так, чтобы никакие две команды, играющие друг с другом, не были одного цвета. Самое сложное в этом — найти ситуацию, в которой «отрицательный цвет» имеет смысл. Occupy Math обещает, что такая ситуация существует, и мы рассмотрим ее в следующем посте.
Область математики, связанная с такого рода подсчетами, называется перечислительной комбинаторикой , и Occupy Math преподавала как университетские, так и аспирантские курсы по этому предмету. Результаты могут быть действительно странными. Теперь Occupy Math потроллит вас странным примером: количество случаев, когда турнир может иметь совершенно однозначный результат (нет A побеждает B, B побеждает C, C побеждает A), равно количеству способов присвоить отрицательным единицам цвета. команды так, чтобы никакие две команды, играющие друг с другом, не были одного цвета. Самое сложное в этом — найти ситуацию, в которой «отрицательный цвет» имеет смысл. Occupy Math обещает, что такая ситуация существует, и мы рассмотрим ее в следующем посте.
Другим важным моментом является то, что когда вы работаете с вероятностью, способ вычислить шансы того, что что-то произойдет, состоит в том, чтобы сначала вычислить количество способов, которыми может произойти то, что вас интересует, а затем разделить на количество случаев, когда что-либо вообще произойдет. может случиться. Дисциплина счета вещей (перечислительная комбинаторика) является одной из основ вероятности. Даже в этой абстрактной сфере присутствуют вещи, возникающие в мире. У вас есть тема, чтобы предложить? Пожалуйста, прокомментируйте или твитните!
может случиться. Дисциплина счета вещей (перечислительная комбинаторика) является одной из основ вероятности. Даже в этой абстрактной сфере присутствуют вещи, возникающие в мире. У вас есть тема, чтобы предложить? Пожалуйста, прокомментируйте или твитните!
Надеюсь увидеть вас здесь снова,
Дэниел Эшлок,
Университет Гвельфа,
Факультет математики и статистики
Нравится:
Нравится Загрузка…
Что такое Zero Factorial – от Numberphile (Youtube)
Компьютерные науки, математика, программирование, Python, Udacity
Джонни
Проницательное видео на YouTube, объясняющее идею факториала, нулевого факториала и промежуточного факториала.
ИнформатикаFactorialIn-between FactorialMathematicsUdacityYoutubeZero FactorialJohnny Chan
Консультант, аналитик данных, разработчик.
Персональные ссылки
Просмотреть полный профиль →
вихрь — Программирование на R — Урок 9 — Функции
OpenCV-Python — Как установить пакет OpenCV-Python в Anaconda (Windows)
swirl — Программирование R — Индексная страница журнала консоли
Упражнение NumPy — Argsort и необычное индексирование
вихрь — Программирование на R — Урок 12 — Анализ данных
вихрь — Программирование на R — Урок 15 — Базовая графика
swirl — Программирование на R — Урок 1 — Основные строительные блоки
swirl — Урок программирования на R 14 — Даты и время
swirl — Программирование на R — Урок 2 — Рабочая область и файлы
вихрь — Программирование на R — Урок 8 — Логика
- 3,5 года спустя… 140 000 посетителей из 180+ стран. Отражение на конец 2017 года
9 января 2018 г.

- atlas7.gitib.io 24 ноября 2017 г.
- JavaScript — Bind Intuition — Дьявол берет верх над Джимом 3 ноября 2017 г.
- Как настроить ноутбук Tensorflow Jupyter на кластере Intel Nervana AI Cluster (Colfax) для глубокого обучения 25 сентября 2017 г.
- Как настроить ноутбук PyTorch Jupyter на кластере Intel Nervana AI Cluster (Colfax) для глубокого обучения 25 сентября 2017 г.
- Инициализация массивов Numpy с помощью метода распаковки кортежей — примеры np.random.rand и np.zeros 13 сентября 2017 г.
- Высокопроизводительные вычисления (HPC) под управлением Intel Xeon Phi: пример моделирования N-body 7 сентября 2017 г.
- Кластер Intel Colfax — ориентирован на определенный набор инструкций / архитектуру процессоров Intel 22 августа 2017 г.
- Кластер Intel Colfax — оценка теоретических пиковых значений FLOPS для процессоров Intel Xeon Phi 21 августа 2017 г.
- Кластер Intel Colfax — оптимизация реализации числовой интеграции с помощью параллельного программирования и распределенных вычислений
17 августа 2017 г.

Ускоренный C++ ИИ С++ Колфакс Колфакс Исследования Информатика Описательная статистика бриллианты Распределенных вычислений ЭДА Упражнения Исследовательский анализ данных ggplot2 гистограмма HPC проверка гипотезы Выведенный статистика Интел JavaScript линукс Машинное обучение Математика Современный код пустышка ООП Оптимизация Параллельное программирование Программирование питон р Рекурсия Рубин на рельсах выборочное распределение Научное программирование Простое решение небольшие проекты Решения Статистика Водоворот Удасити неконтролируемое обучение Веб-разработка Вордпресс ксеон Ксеон Фи
- О
- Ускоренные решения C++
- Разработка Alexa — Примечания
- Книги
- Глубокое обучение в кластере Intel Nervana AI (он же Colfax HPC Cluster)
- Разведочный анализ данных – Алмазы
- Проекты Google Earth Engine
- Высокопроизводительные вычисления (HPC) с Intel Xeon Phi, параллельное программирование и распределенные вычисления
- Учебные пособия Intel Edison Workshop
- Специалист по машинному обучению — план обучения и основные этапы
- Полный стек проекта
- Небольшой проект — Распределение выборки — Средний балл в кости
- Малые проекты — Введение
- Малые проекты – Список проектов
- swirl — Программирование R — Индексная страница журнала консоли
- Шпаргалка по командам Ubuntu / Linux
- Udacity — Аутентификация и авторизация — OAuth — Примечания
- Udacity — Настройка веб-серверов Linux — Примечания
- Udacity — Анализ данных с помощью R — Примечания
- Udacity – Основы полного стека
- Udacity — введение в AJAX
- Udacity — Введение в алгоритм — Примечания
- Udacity — Введение в искусственный интеллект — Примечания
- Udacity – Введение в информатику – Учебные заметки
- Udacity — Введение в науку о данных — Примечания
- Udacity – Введение в описательную статистику – Учебные заметки
- Udacity — Введение в HTML и CSS — Примечания
- Udacity – Введение в логическую статистику – Учебные заметки
- Udacity — Введение в реляционные базы данных — Примечания
- Udacity — Основы JavaScript — Примечания
- Udacity — основы команд Linux
- Udacity — основы программирования на Python — примечания
- Udacity — Веб-разработка — Примечания
- Полезные ресурсы
- Проект отслеживания видео — с OpenCV
- Искусственный интеллект (14)
- Ведение блога (4)
- шпаргалка (1)
- Колфакс (16)
- Информатика (40)
- CUDA (1)
- Наука о данных (3)
- Глубокое обучение (2)
- докер (1)
- Исследовательский анализ данных (EDA) (22)
- ggplot2 — бриллианты (17)
- Гитхаб (1)
- Суть (1)
- Надлежащая практика (1)
- Хакатон (2)
- HPC (1)
- Интел Эдисон (2)
- IPython (1)
- JavaScript (9)
- каггле (1)
- Mac (2)
- Машинное обучение (7)
- Математика (8)
- OpenCV (4)
- OpenCV-Питон (2)
- Другое (1)
- Программирование (216)
- С++ (93)
- ООП (8)
- Питон (80)
- cv2 (4)
- число (10)
- Р (35)
- Рубин (2)
- Ruby-on-Rails (5)
- САС (2)
- Разработка программного обеспечения (2)
- Электронная таблица (2)
- SQL (2)
- Статистика (19)
- Описательная статистика (12)
- Логическая статистика (10)
- Удасити (120)
- Без рубрики (10)
- Полезные инструменты (10)
- Блокнот IPython (1)
- Возвышенный текст (3)
- Проект отслеживания видео (1)
- Видео (2)
- Визуализация (3)
- Веб-разработка (7)
- Окна (1)
- Вордпресс (4)
- Январь 2018 (1)
- ноябрь 2017 г.
 (2)
(2) - сентябрь 2017 г. (4)
- август 2017 г. (18)
- июль 2017 г. (2)
- июнь 2017 г. (1)
- май 2017 г. (9)
- Апрель 2017 г. (3)
- Октябрь 2016 г. (2)
- Сентябрь 2016 г. (1)
- Май 2016 (1)
- Апрель 2016 г. (1)
- март 2016 г. (3)
- Февраль 2016 г. (4)
- Январь 2016 (12)
- Декабрь 2015 г. (3)
- Октябрь 2015 г. (3)
- Сентябрь 2015 г. (4)
- август 2015 г. (1)
- июль 2015 г. (8)
- июнь 2015 г. (6)
- Май 2015 (12)
- апрель 2015 г. (54)
- март 2015 г. (52)
- Февраль 2015 г. (4)
- Октябрь 2014 г. (4)
- Сентябрь 2014 (30)
- август 2014 (18)
- июль 2014 (24)
- июнь 2014 г. (22)
Определение, нулевой факториал, использование, примеры
Значение факториала широко используется в теории чисел, а также для приближений. Факториалы обозначаются восклицательным знаком (!). В этой статье мы узнаем о свойствах факториалов с их определением, способах расширения, случае факториала нуля, факториалов мнимых и отрицательных чисел с решенными примерами.
В этой статье мы узнаем о свойствах факториалов с их определением, способах расширения, случае факториала нуля, факториалов мнимых и отрицательных чисел с решенными примерами.
Что такое факториал?
Использование ! был начат Кристианом Крампом в 1808 году. В математике факториал неотрицательного целого числа n, обозначаемый n! является произведением всех положительных целых чисел, меньших или равных n. Где n может быть любым натуральным числом. Факториал n. 9nn……………….n\geq0\)
Выражение n! читается как «n факториал».
Это определение расширено до числа 0 с помощью соглашения:
0! = 1
Также читайте о статистике здесь.
Два способа разложения факториала переменной n Записывается как n!
Есть два способа расширить факториал переменной n. Вы можете использовать восходящий или нисходящий порядок. Оба эти метода показаны ниже.
По убыванию
Факториал числа n или n! можно записать следующим образом в порядке убывания
n! = n x (n-1) x (n-2) x (n-3) x … x 3 x 2 x 1
По возрастанию
Факториал числа n или n! можно записать следующим образом в порядке возрастания
n! = 1 x 2 x 3 x … x (n-3) x (n-2) x (n-3)
Использование факториалов
Факториалы используются в следующих приложениях
- В теории вероятностей существует множество сценарии, в которых мы должны вычислить все возможные расположения данного набора.
 В теории вероятностей факториалы широко используются для оценки перестановок и комбинаций.
В теории вероятностей факториалы широко используются для оценки перестановок и комбинаций.
Например, если мы подбросим монету 20 раз, каков будет размер выборки.
Или, если мы хотим выбрать команду из 10 учеников из класса из 50 человек, сколько различных команд мы можем создать? Факториал — это математическая операция, которая помогает нам вычислять такие схемы и, следовательно, играет важную роль в теории вероятностей.
- Правило факториала упрощает вычисления сложных выражений, содержащих факториалы.
- Мы можем использовать факториал в рекурсивном определении числа.
- Распределения вероятностей, такие как биномиальное распределение, включают использование факториала для определения вероятности события.
- Значения факториала широко используются в теории чисел, а также для приближений.
Факториалы от 1 до 20
Факториалы первых 20 натуральных чисел:
Другие темы по математике смотрите здесь.
Решенные примеры
- Чему равен факториал числа 5?
Числа меньше или равные 5 — это 5, 4,3,2,1. Следовательно,
5! = 5 × 4 × 3 × 2 × 1 = 120.
- Вычислить \({7!\over{4!}}\)
7! = 7 × 6 × 5 × 4 × 3 × 2 × 1
4! = 4 × 3 × 2 × 1
Следовательно, \({7!\over{4!}}\)= \({ 7 × 6 × 5 × 4 × 3 × 2 × 1 \over{4 × 3 × 2 × 1}}\)
= (7 × 6 × 5)
= 210
- Вычислить \({6!\over{3\times4!}}\)
Используя правило факториала, мы можем написать
6
3 ! = 6 × 5 x 4 x 3 x 2 x 1
Однако у нас их 4! в знаменателе, поэтому мы снова применяем правило факториала, чтобы получить
6! = 6 × 5 × 4!. Соответственно,
\({6!\over{3\times4!}}\) = \({6\times5\times4!\over{3\times4!}}\) = \({6\times5\over {3}}\) = 10.
- Вычислить \({11!\over{5!\times8!}}\)
11! = 11×10×9×8!
Следовательно,
\({11!\более{5!\times8!}}\) = \({11\times10\times9\times8!\over{5!\times8!}}\) = \( {11\times10\times9\over{5!}}\) = \({990\over{120}}\) = 8,25
Факториалы Свойства нуля
Определение факториала гласит, что значение 0! = 1. Факториал — это произведение всех целых чисел, равных или меньших по значению исходному числу. Факториал — это количество возможных комбинаций с числами, меньшими или равными этому числу. Ноль не имеет чисел меньше него, но все же сам по себе является числом.
Факториал — это произведение всех целых чисел, равных или меньших по значению исходному числу. Факториал — это количество возможных комбинаций с числами, меньшими или равными этому числу. Ноль не имеет чисел меньше него, но все же сам по себе является числом.
Если мы хотим, чтобы 1 подчинялась правилу факториала, то из формулы факториала очевидно, что 1! = 1.
Однако по правилу факториала
1! = 1 × 0!
1 = 1 × 0!
Это означает, что 0!=1. Факториал не определен для отрицательных целых чисел, поэтому правило факториала нельзя применить к 0.
Следовательно, по определению факториал нуля равен 1.
Также читайте о дифференциальных уравнениях здесь.
Факториалы Свойства 9{−t}}dt Это известно как гамма-функция Эйлера. Это связано с функцией Пи как \(\)\prod(x)=\gamma(x+1)=x!\)
Факториалы Свойства мнимого числа
Факториалы Свойства мнимого числа задаются следующими формула
- \(i!=\gamma(1+i)=i\gamma(i)≈0,498−0,155i\)
- \((−i)!=\gamma(1−i)=−i \gamma(−i)≈0,498+0,155i\)
- \((−1+i)!=\gamma(i)≈−1549−0,498i\)
- \(|\gamma(ix)|= \sqrt{\pi{xsinh}(\pi{x})}\), где x — действительное число.
 {-n-1}\over{-n-1!}}\text{для}n<0\)
{-n-1}\over{-n-1!}}\text{для}n<0\)
, где латинская буква ⌊n⌉ определяется как n для n ≠ 0 и 1 для n = 0.
Надеюсь, что эта статья о свойствах факториалов была информативной. Попрактикуйтесь в том же в нашем бесплатном приложении Testbook. Скачать сейчас!
Часто задаваемые вопросы о свойствах факториалов
В.1 Каковы свойства факториалов?
Ответ 1 В математике факториал неотрицательного целого числа n, обозначаемый n! является произведением всех положительных целых чисел, меньших или равных n. Где n может быть любым натуральным числом. Факториал n.
н! = n x (n-1) x (n-2) x (n-3) x … x 3 x 2 x 1
Q.2 Что такое нулевой факториал?
Ответ 2 Определение факториала гласит, что значение 0! = 1. Факториал — это произведение всех целых чисел, равных или меньших по значению исходному числу. Факториал — это количество возможных комбинаций с числами, меньшими или равными этому числу. Ноль не имеет чисел меньше него, но все же сам по себе является числом.
Ноль не имеет чисел меньше него, но все же сам по себе является числом.
Q.3 Что такое факториал 1?
Ответ 3 Если мы хотим, чтобы 1 следовала правилу факториала, то из формулы факториала очевидно, что 1! = 1.
Однако по правилу факториала
1! = 1 × 0!
1 = 1 × 0!
В.4 Почему используется факториал?
Ответ 4 В теории вероятностей существует множество сценариев, в которых мы должны вычислить все возможные варианты расположения заданного множества. В теории вероятностей факториалы широко используются для оценки перестановок и комбинаций. Например, если мы подбросим монету 20 раз, каков будет размер выборки. Или, если мы хотим выбрать команду из 10 учеников из класса из 50 человек, сколько различных команд мы можем создать? Факториал — это математическая операция, которая помогает нам вычислять такие схемы и, следовательно, играет важную роль в теории вероятностей.
Q.5 Кто изобрел факториал?
Ответ 5 Использование ! был начат Кристианом Крампом в 1808 году. Распределения вероятностей, такие как биномиальное распределение, включают использование факториала для определения вероятности события.
Скачать публикацию в формате PDF
| Формула суммы арифметической прогрессии: Знайте формулу, используя решенные примеры! |
| Центр масс и центр тяжести |
| Collisions, Newton’s Second Law for System of Particles with Examples |
| States of Matter and Characteristics of Solid, Liquid, Gas, Plasma |
| Discovery of Electron, Proton and Neutron |
Why zero факториал один?
Автор вопроса: Джованни Рат
Оценка: 5/5 (28 голосов)
Факториал числа в математике — это произведение всех положительных чисел, меньших или равных числу. Но нет положительных значений меньше нуля, поэтому набор данных не может быть организован, что считается возможной комбинацией того, как данные могут быть организованы (не может). Таким образом, 0! = 1.
Но нет положительных значений меньше нуля, поэтому набор данных не может быть организован, что считается возможной комбинацией того, как данные могут быть организованы (не может). Таким образом, 0! = 1.
Есть ли у нуля факториал?
Нулевой факториал — это математическое выражение количества способов упорядочить набор данных без значений в нем, что равно единице. … Определение факториала гласит, что 0! = 1 .
Какой ответ для 0 факториала?
Идея факториала (просто говоря) используется для вычисления количества перестановок (комбинаций) упорядочивания набора из n чисел. Можно сказать, что пустой набор можно заказать только в одну сторону, поэтому 0! = 1 .
Почему что-то в нулевой степени 1?
Короче говоря, 0 — это единственное число, такое что для любого числа х х + 0 = х. … Итак, причина того, что любое число в нулевой степени равно единице, заключается в том, что любое число в нулевой степени является просто произведением вообще ни одного числа , что является мультипликативным тождеством, 1. Ответ 2: Мне интересно, что вы задали этот вопрос.
Ответ 2: Мне интересно, что вы задали этот вопрос.
Чему равен факториал N?
Говоря более математически, факториал числа (n!) равен и равен n(n-1) . Например, если вы хотите вычислить факториал для четырех, вы должны написать: 4!
Почему 0! = 1?
Найдено 29 связанных вопросов
Сколько стоит 5 бесконечностей?
Обычно любое число, деленное на 0, равно бесконечности. Возьмем 1, разделенное на 0. Теперь давайте разделим 5 на бесконечность. Следовательно, 5 разделить на бесконечность равно нулю .
Определен ли 0 в степени 0?
Нуль в степени нуля, обозначаемый 0 0 , представляет собой математическое выражение без согласованного значения . Наиболее распространенные возможности: 1 или оставить выражение неопределенным, с обоснованиями, существующими для каждого, в зависимости от контекста.
Наиболее распространенные возможности: 1 или оставить выражение неопределенным, с обоснованиями, существующими для каждого, в зависимости от контекста.
Почему степень 0 в 0 не определена?
Ни одно значение не может быть присвоено 0 в степени 0 без возникновения противоречий. Таким образом, 0 в степени 0 не определено!
N равно нулю?
Мы знаем, что произведение любых двух чисел равно 0, если одно или оба числа равны 0. Поскольку другое число не равно нулю, мы можем определенно сказать, что n равно 0 .
Кто изобрел 0?
Первый современный эквивалент цифры ноль происходит от индуистский астроном и математик Брахмагупта в 628 году. Его символом для обозначения числа была точка под числом.
Что такое нулевой факториал?
Определение 1: В математике нулевой факториал — это выражение, означающее упорядочивание данных, не содержащих значений . Факториал используется для определения возможных наборов данных в последовательности, также известной как перестановка.
Является ли 0 действительным числом?
На самом деле действительные числа — это практически любые числа, которые только можно придумать. … Действительные числа могут быть положительными или отрицательными, и включает число ноль . Их называют действительными числами, потому что они не мнимые, а это другая система чисел.
Что такое 0 в математике?
Ноль — это целое число, обозначенное 0, которое при использовании в качестве счетного числа означает отсутствие объектов . Это единственное целое (и, по сути, единственное действительное число), которое не является ни отрицательным, ни положительным. Число, отличное от нуля, называется отличным от нуля. Корень функции также иногда называют «нулем».
Можно ли разделить ноль на 1?
Ответ: Ноль разделить на 1 равно 0 .
Что такое ноль в любой степени?
В соответствии с правилом нулевого экспонента или нулевым свойством экспонент, любое число, возведенное в степень нуля, всегда равно 1 . Кроме того, мы можем сказать, что если показатель степени равен нулю, то результат всегда равен 1.
Кроме того, мы можем сказать, что если показатель степени равен нулю, то результат всегда равен 1.
Каково значение 0 на 0?
Ответ: 0 разделить на 0 не определено .
Любая дробь с нулем в числителе дает только нулевое десятичное значение.
Что происходит, когда ограничение равно 0 0?
Как правило, ноль в знаменателе означает, что это не определено . … При простом вычислении уравнения 0/0 не определено. Однако, принимая предел, если мы получаем 0/0, мы можем получить множество ответов, и единственный способ узнать, какой из них правильный, — это фактически вычислить предел.
Что такое факториал бесконечности?
что такое ! бесконечности? (факториал) Если вы интерпретируете этот вопрос как «каков предел n!, когда n стремится к бесконечности?», ответ будет бесконечность .
Сколько будет 2 в степени бесконечности?
1/2power бесконечности будет очень мало. стремится к 0 поэтому ответ 0. .
.
Что такое факториал 20?
Ответ: Факториал числа 20 равен 24328176640000 .
Что такое факториал 100?
Ответ: Приблизительное значение 100! 9.3326215443944E+157 . Количество конечных нулей в 100! равно 24. Количество цифр в факториале 100 равно 158.
Какой самый большой факториал когда-либо вычислялся?
Самый большой из когда-либо вычисленных факториалов равен 170 .
Похожие вопросы
- 31Является ли нуль рациональным числом?
- 24Убьет ли вас абсолютный ноль?
- 45Нулевой допуск?
- 21Происходит ли диффузия при абсолютном нуле?
- 41Когда ре ноль сезон 2 часть 2?
- 27Почему машинки для стрижки с нулевым зазором?
Реклама
Популярные вопросы
- 16Что означает в Библии превремя?
- 32Выдержит ли Эйфелева башня землетрясение?
- 15Чувствуют ли себя нарциссы неудачниками?
- 24Кто обладает законодательной властью в уездном правительстве?
- 29На кого похоже имплантационное кровотечение?
- 18Насколько богат илон маск?
- 39Будет ли материализован смысл?
- 30Как сделать деионизированную воду?
- 32Зачем использовать дефлекторы окон?
- 36Можно ли играть в Townscaper на телефоне?
нулевой факториал | Поиск в TikTok
TikTokЗагрузить
Для вас
Читать
math_enjoyer
Math_Enjoyer
Zero factorial #math #maths #mathematics #information #learn #education #study #edit #edits #fyp #meme #познавательный #интересный #факты #школа #ноги #вирусный #числофил #пи0002 709,1 тыс. лайков, 6,3 тыс. комментариев. Видео TikTok от Math_Enjoyer (@math_enjoyer): «Нулевой факториал #математика #математика #математика #информация #учиться #образование #учиться #редактировать #редактировать #fyp #мем #образовательный #интересное #факты #школа #ноги #вирусный #нумерофил #пи «. оригинальный звук.
лайков, 6,3 тыс. комментариев. Видео TikTok от Math_Enjoyer (@math_enjoyer): «Нулевой факториал #математика #математика #математика #информация #учиться #образование #учиться #редактировать #редактировать #fyp #мем #образовательный #интересное #факты #школа #ноги #вирусный #нумерофил #пи «. оригинальный звук.
3,9 млн просмотров|
оригинальный звук — Math_Enjoyer
calculuscious
mathycathy
Полное видео: Zero Factorial от Numberphile ☺️ #mathtok #math #maths
768 лайков, 24 комментария. Видео TikTok от mathycathy (@calculuscious): «Полное видео: «Zero Factorial» от Numberphile ☺️ #mathtok #math #maths». 0! = 1 | Мое любимое объяснение этого от Numberphile: | Доктор Джеймс Грайм 🥰 | …. оригинальный звук.
7399 просмотров|
оригинальный звук — математика
смысл
смысл
Факториал нуля >>> vid cred : Numberphille @math_enjoyer #fyp #the_meaning #mathedit #math #education #edit #themeaning #mathenjoyer #infinity #alephnull #educationedit #omega # foryoupage
30,1 тыс. лайков, 251 комментарий. Видео TikTok со значением (@the.meaning): «Нулевой факториал >>> vid cred : Numberphille @math_enjoyer #fyp #the_meaning #mathedit #math #education #edit #themeaning #mathenjoyer #infinity #alephnull #educationedit #omega #foryoupage «. оригинальный звук.
лайков, 251 комментарий. Видео TikTok со значением (@the.meaning): «Нулевой факториал >>> vid cred : Numberphille @math_enjoyer #fyp #the_meaning #mathedit #math #education #edit #themeaning #mathenjoyer #infinity #alephnull #educationedit #omega #foryoupage «. оригинальный звук.
241,9 тыс. просмотров|
оригинальный звук — смысл
andymath.com
AndyMath.com
Zero factorial fun #math #maths
960 лайков, 43 комментария. Видео TikTok от AndyMath.com (@andymath.com): «Нулевой факториал веселья #математика #математика». Песня Мерцания.
14,9 тыс. просмотров| 0! = 1 🤔⁉️ #математика #Factorial #zeroFactorial #Factorials #Mathematics #Math
Видео Tiktok от Thequirky-ishtutor (@thequirkyishtutor): «Как 0! факториалы #математика #математика». оригинальный звук.
оригинальный звук.
510 просмотров|
оригинальный звук — TheQuirky-ishTutor
conwherrett
Connor Wherrett
#stitch with @your.bummy.math.tutor вот почему 0! (нулевой факториал) равен 1, несмотря на то, что это кажется незаконным #maths #math #mathematics
4,1 тыс. лайков, 88 комментариев. Видео TikTok от Коннора Уэрретта (@conwherrett): «#стежка с @your.bummy.math.tutor, вот почему 0! (нулевой факториал) равен 1, несмотря на то, что это кажется незаконным #математика #математика #математика» . 0! = 1 | Что такое факториал? | Так почему же 0!=1? | …. оригинальный звук.
32,4 тыс. просмотров|
original sound — Connor Wherrett
kitty.grrl
matt
Reply to @vickyssecrets99 #greenscreen part 2❤️ #math #mathematics #zerofactorial #mathjokes #calc #calculus #calculator #calculusjokes
1,3 тыс. отметок «Нравится», 22 комментария. Видео TikTok от Мэтта (@kitty.grrl): «Ответить @vickyssecrets99 #greenscreen часть 2❤️ #math #mathematics #zerofactorial #mathjokes #calc #calculus #calculator #calculusjokes». оригинальный звук.
отметок «Нравится», 22 комментария. Видео TikTok от Мэтта (@kitty.grrl): «Ответить @vickyssecrets99 #greenscreen часть 2❤️ #math #mathematics #zerofactorial #mathjokes #calc #calculus #calculator #calculusjokes». оригинальный звук.
13,6 тыс. просмотров|
оригинальный звук — 🌟
wallacestem
wallaceSTEM: Тренды Mathtok!
Ответ на @mitchellmahlum Не на самом деле доказательство… но шаблон проверяет… #mathtok #0 #Factorial #Math #Maths #zero #zerofactorial #mathtersoft.
798 лайков, 56 комментариев. Видео TikTok от WallaceSTEM: тренды Mathtok! (@wallacestem): «Ответ @mitchellmahlum на самом деле не является доказательством… но шаблон подтверждается… #mathtok #0 #factorial #math #maths #zero #zerofactorial #mathteachersoftiktok».

 1 Значение 0!
1 Значение 0! }
}
 format(num, fact))
format(num, fact))
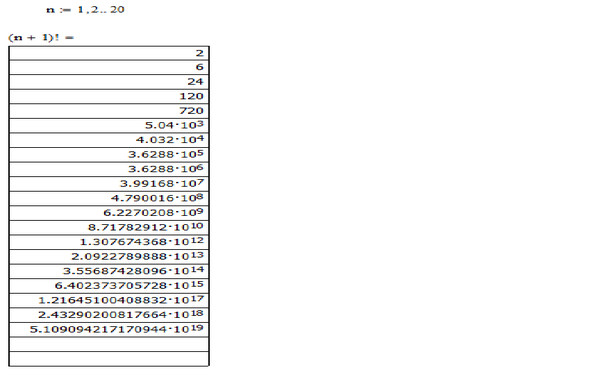
 (2)
(2) В теории вероятностей факториалы широко используются для оценки перестановок и комбинаций.
В теории вероятностей факториалы широко используются для оценки перестановок и комбинаций. {-n-1}\over{-n-1!}}\text{для}n<0\)
{-n-1}\over{-n-1!}}\text{для}n<0\)