Действие со степенями с одинаковыми основаниями: Свойства степеней, действия со степенями

Содержание

Умножение с разными степенями. Как умножать степени, умножение степеней с разными показателями. Применение степеней и их свойств

Имеют одинаковые степеней, а показатели степеней неодинаковы, 2² * 2³ , то результатом будет основание степени с тем же одинаковым основанием членов произведения степеней, возведённого в показатель степени, равный сумме показателей всех перемножаемых степеней.

2² * 2³ = 2²⁺³ = 2⁵ = 32

Если члены произведения степеней имеют разные основания степеней, а показатели степеней одинаковы, например, 2³ * 5³ , то результатом будет произведение оснований этих степеней, возведённое в показатель степени, равный этому одинаковому показателю степени.

2³ * 5³ = (2*5)³ = 10³ = 1000

Если перемножаемые степени равны между собой, например, 5³ * 5³ , то результатом будет степень с основанием, равного этим одинаковым основаниям степеней, возведённое в показатель степени, равный показателю степеней, умноженного на количество этих одинаковых степеней.

5³ * 5³ = (5³)² = 5³*² = 5⁶ = 15625

Или другой пример с таким же результатом:

5² * 5² * 5² = (5²)³ = 5²*³ = 5⁶ = 15625

Источники:

Что такое степень с натуральным показателем
произведение степеней

Математические действия со степенями можно выполнять только в том случае, когда основания показателей степени одинаковы, и когда между ними стоят знаки умножения или деления. Основание показателя степени – это число, которое возводится в степень.

Инструкция

Если числа делятся друг на друга (см 1), то у (в данном примере – это число 3) появляется степень, которая образуется из вычитания показателей степени. Причем, это действие проводится впрямую: из первого показателя вычитается второй. Пример 1. Введем : (а)в, где в скобках – а — основание, за скобками – в – показатель степени. (6)5: (6)3 = (6)5-3 = (6) 2 = 6*6 = 36.Если в ответе получается число в отрицательной степени, то такое число преобразуется в обыкновенную дробь, в числителе которой стоит единица, а в знаменателе основание с полученным при разности показателем степени, только в положительном виде (со знаком плюс).

Пример 2. (2) 4: (2)6 = (2) 4-6 = (2) -2 = 1/(2)2 = ¼. Деление степеней может быть записано в другом виде, через знак дроби, а не как указано в этом шаге через знак «:». От этого принцип решения не меняется, все производится точно также, только запись будет вестись со знаком горизонтальной (или косой) дроби, вместо двоеточия.Пример 3. (2) 4 /(2)6 = (2) 4-6 = (2) -2 = 1/(2)2 = ¼.

При умножении одинаковых оснований, имеющих степени, производится сложение степеней. Пример 4. (5) 2* (5)3 = (5)2+3 =(5)5 = 3125.Если показатели степеней имеют разные знаки, то их сложение проводится согласно математическим законам.Пример 5. (2)1* (2)-3 = (2) 1+(-3) = (2) -2 = 1/(2)2 = ¼.

Если основания показателей степени различаются, то скорое всего их можно привести к одному и тому же виду, путем математического преобразования. Пример 6. Пусть надо найти значение выражения: (4)2: (2)3. Зная, что число четыре можно представить как два в квадрате, решается данный пример так:(4)2: (2)3 = (2*2)2: (2)3.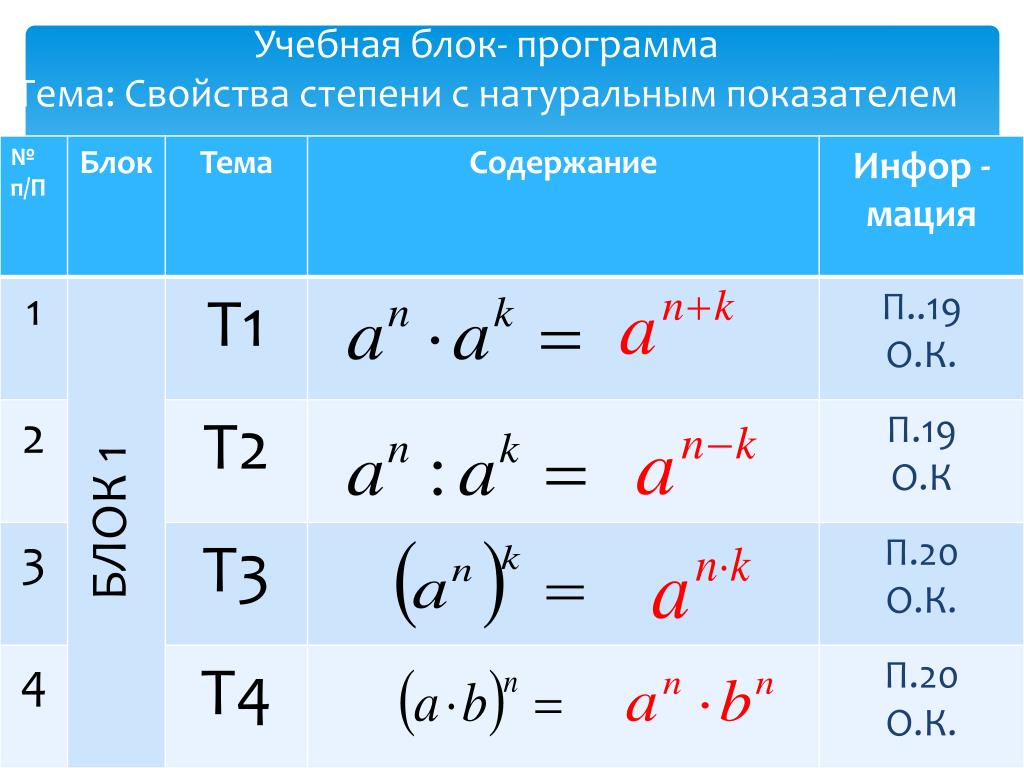

Далее при возведении в степень числа. Уже имеющего степень, показатели степеней умножаются друг на друга: ((2)2)2: (2)3 = (2)4: (2)3 = (2) 4-3 = (2)1 = 2.

Полезный совет

Помните, если данное основание кажется непохожим на второе основание, надо искать математический выход. Просто так разные числа не даются. Разве, что в учебнике наборщиком сделана опечатка.

Степенной формат записи числа — это сокращенная форма записи операции умножения основания на само себя. С числом, представленным в такой форме, можно осуществлять те же операции, что и с любыми другими числами, в том числе и возводить их в степень. Например, можно возвести в произвольную степень квадрат числа и получение результата на современном уровне развития техники не составит какой-либо трудности.

Вам понадобится

Доступ в интернет или калькулятор Windows.

Инструкция

Для возведения квадрата в степень используйте общее правило возведения в степень , уже имеющего степенной показатель. При такой операции показатели перемножаются, а основание остается прежним. Если основание обозначить как x, а исходный и дополнительный показатели — как a и b, записать это правило в общем виде можно так: (xᵃ)ᵇ=xᵃᵇ.

Формулы степеней используют в процессе сокращения и упрощения сложных выражений, в решении уравнений и неравенств.

Число c является n -ной степенью числа a когда:

Операции со степенями.

1. Умножая степени с одинаковым основанием их показатели складываются:

a m ·a n = a m + n .

2. В делении степеней с одинаковым основанием их показатели вычитаются:

3. Степень произведения 2-х либо большего числа множителей равняется произведению степеней этих сомножителей:

(abc…) n = a n · b n · c n …

4. Степень дроби равняется отношению степеней делимого и делителя:

(a/b) n = a n /b n .

5. Возводя степень в степень, показатели степеней перемножают:

(a m) n = a m n .

Каждая вышеприведенная формула верна в направлениях слева направо и наоборот.

Например . (2·3·5/15)² = 2²·3²·5²/15² = 900/225 = 4 .

Операции с корнями.

1. Корень из произведения нескольких сомножителей равняется произведению корней из этих сомножителей:

2. Корень из отношения равен отношению делимого и делителя корней:

3. При возведении корня в степень довольно возвести в эту степень подкоренное число:

4. Если увеличить степень корня в

n раз и в тоже время возвести в n -ую степень подкоренное число, то значение корня не поменяется:

5. Если уменьшить степень корня в n раз и в тоже время извлечь корень n -ой степени из подкоренного числа, то значение корня не поменяется:

Степень с отрицательным показателем. Степень некоторого числа с неположительным (целым) показателем определяют как единицу, деленную на степень того же числа с показателем, равным абсолютной величине неположительного показателя:

Формулу a m :a n =a m — n можно использовать не только при m > n , но и при m n .

Например . a 4:a 7 = a 4 — 7 = a -3 .

Чтобы формула a m :a n =a m — n стала справедливой при m=n , нужно присутствие нулевой степени.

Степень с нулевым показателем.

Степень всякого числа, не равного нулю, с нулевым показателем равняется единице.

Например . 2 0 = 1,(-5) 0 = 1,(-3/5) 0 = 1.

Степень с дробным показателем. Чтобы возвести действительное число а в степень m/n , необходимо извлечь корень n -ой степени из m -ой степени этого числа а .

Сложение и вычитание степеней

Очевидно, что числа со степенями могут слагаться, как другие величины , путем их сложения одно за другим со своими знаками .

Так, сумма a 3 и b 2 есть a 3 + b 2 .
Сумма a 3 — b n и h 5 -d 4 есть a 3 — b n + h 5 — d 4 .

Коэффициенты одинаковых степеней одинаковых переменных могут слагаться или вычитаться.

Так, сумма 2a 2 и 3a 2 равна 5a 2 .

Это так же очевидно, что если взять два квадрата а, или три квадрата а, или пять квадратов а.

Но степени

различных переменных и различные степени одинаковых переменных , должны слагаться их сложением с их знаками.

Так, сумма a 2 и a 3 есть сумма a 2 + a 3 .

Это очевидно, что квадрат числа a, и куб числа a, не равно ни удвоенному квадрату a, но удвоенному кубу a.

Сумма a 3 b n и 3a 5 b 6 есть a 3 b n + 3a 5 b 6 .

Вычитание степеней проводится таким же образом, что и сложение, за исключением того, что знаки вычитаемых должны соответственно быть изменены.

Или:
2a 4 — (-6a 4) = 8a 4
3h 2 b 6 — 4h 2 b 6 = -h 2 b 6
5(a — h) 6 — 2(a — h) 6 = 3(a — h) 6

Умножение степеней

Числа со степенями могут быть умножены, как и другие величины, путем написания их одно за другим, со знаком умножения или без него между ними.

Так, результат умножения a 3 на b 2 равен a 3 b 2 или aaabb.

Или:
x -3 ⋅ a m = a m x -3
3a 6 y 2 ⋅ (-2x) = -6a 6 xy 2
a 2 b 3 y 2 ⋅ a 3 b 2 y = a 2 b 3 y 2 a 3 b 2 y

Результат в последнем примере может быть упорядочен путём сложения одинаковых переменных.
Выражение примет вид: a 5 b 5 y 3 .

Сравнивая несколько чисел(переменных) со степенями, мы можем увидеть, что если любые два из них умножаются, то результат — это число (переменная) со степенью, равной сумме степеней слагаемых.

Так, a 2 .a 3 = aa.aaa = aaaaa = a 5 .

Здесь 5 — это степень результата умножения, равная 2 + 3, сумме степеней слагаемых.

Так, a n .a m = a m+n .

Для a n , a берётся как множитель столько раз, сколько равна степень n;

И a m , берётся как множитель столько раз, сколько равна степень m;

Поэтому, степени с одинаковыми основами могут быть умножены путём сложения показателей степеней.

Так, a 2 .a 6 = a 2+6 = a 8 . И x 3 .x 2 .x = x 3+2+1 = x 6 .

Или:

4a n ⋅ 2a n = 8a 2n
b 2 y 3 ⋅ b 4 y = b 6 y 4
(b + h — y) n ⋅ (b + h — y) = (b + h — y) n+1

Умножьте (x 3 + x 2 y + xy 2 + y 3) ⋅ (x — y).
Ответ: x 4 — y 4 .
Умножьте (x 3 + x — 5) ⋅ (2x 3 + x + 1).

Это правило справедливо и для чисел, показатели степени которых — отрицательные .

1. Так, a -2 .a -3 = a -5 . Это можно записать в виде (1/aa).(1/aaa) = 1/aaaaa.

2. y -n .y -m = y -n-m .

3. a -n .a m = a m-n .

Если a + b умножаются на a — b, результат будет равен a 2 — b 2: то есть

Результат умножения суммы или разницы двух чисел равен сумме или разнице их квадратов.

Если умножается сумма и разница двух чисел, возведённых в квадрат , результат будет равен сумме или разнице этих чисел в четвёртой степени.

Так, (a — y).(a + y) = a 2 — y 2 .
(a 2 — y 2)⋅(a 2 + y 2) = a 4 — y 4 .
(a 4 — y 4)⋅(a 4 + y 4) = a 8 — y 8 .

Деление степеней

Числа со степенями могут быть поделены, как и другие числа, путем отнимая от делимого делителя, или размещением их в форме дроби.

Таким образом a 3 b 2 делённое на b 2 , равно a 3 .

Запись a 5 , делённого на a 3 , выглядит как $\frac $. Но это равно a 2 . В ряде чисел
a +4 , a +3 , a +2 , a +1 , a 0 , a -1 , a -2 , a -3 , a -4 .
любое число может быть поделено на другое, а показатель степени будет равен разнице показателей делимых чисел. 3$

Необходимо очень хорошо усвоить умножение и деление степеней, так как такие операции очень широко применяются в алгебре.

Примеры решения примеров с дробями, содержащими числа со степенями

1. Уменьшите показатели степеней в $\frac $ Ответ: $\frac $.

2. Уменьшите показатели степеней в $\frac $. Ответ: $\frac $ или 2x.

3. Уменьшите показатели степеней a 2 /a 3 и a -3 /a -4 и приведите к общему знаменателю.
a 2 .a -4 есть a -2 первый числитель.
a 3 .a -3 есть a 0 = 1, второй числитель.
a 3 .a -4 есть a -1 , общий числитель.
После упрощения: a -2 /a -1 и 1/a -1 .

4. Уменьшите показатели степеней 2a 4 /5a 3 и 2 /a 4 и приведите к общему знаменателю.
Ответ: 2a 3 /5a 7 и 5a 5 /5a 7 или 2a 3 /5a 2 и 5/5a 2 .

5. Умножьте (a 3 + b)/b 4 на (a — b)/3.

6. Умножьте (a 5 + 1)/x 2 на (b 2 — 1)/(x + a).

7. Умножьте b 4 /a -2 на h -3 /x и a n /y -3 .

8. Разделите a 4 /y 3 на a 3 /y 2 . Ответ: a/y.

Свойства степени

Напоминаем, что в данном уроке разбираются свойства степеней с натуральными показателями и нулём. Степени с рациональными показателями и их свойства будут рассмотрены в уроках для 8 классов.

Степень с натуральным показателем обладает несколькими важными свойствами, которые позволяют упрощать вычисления в примерах со степенями.

Свойство № 1

Произведение степеней

При умножении степеней с одинаковыми основаниями основание остаётся без изменений, а показатели степеней складываются.

a m · a n = a m + n , где « a » — любое число, а « m », « n » — любые натуральные числа.

Данное свойство степеней также действует на произведение трёх и более степеней.

Упростить выражение.
b · b 2 · b 3 · b 4 · b 5 = b 1 + 2 + 3 + 4 + 5 = b 15
Представить в виде степени.
6 15 · 36 = 6 15 · 6 2 = 6 15 · 6 2 = 6 17
Представить в виде степени.
(0,8) 3 · (0,8) 12 = (0,8) 3 + 12 = (0,8) 15

Обратите внимание, что в указанном свойстве речь шла только об умножении степеней с одинаковыми основаниями . Оно не относится к их сложению.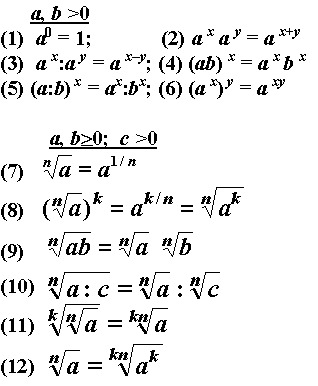

Нельзя заменять сумму (3 3 + 3 2) на 3 5 . Это понятно, если
посчитать (3 3 + 3 2) = (27 + 9) = 36 , а 3 5 = 243

Свойство № 2

При делении степеней с одинаковыми основаниями основание остаётся без изменений, а из показателя степени делимого вычитают показатель степени делителя.

Записать частное в виде степени
(2b) 5: (2b) 3 = (2b) 5 − 3 = (2b) 2
Вычислить.

11 3 − 2 · 4 2 − 1 = 11 · 4 = 44
Пример. Решить уравнение. Используем свойство частного степеней.
3 8: t = 3 4

Ответ: t = 3 4 = 81

Пользуясь свойствами № 1 и № 2, можно легко упрощать выражения и производить вычисления.

Пример. Упростить выражение.
4 5m + 6 · 4 m + 2: 4 4m + 3 = 4 5m + 6 + m + 2: 4 4m + 3 = 4 6m + 8 − 4m − 3 = 4 2m + 5

Пример. Найти значение выражения, используя свойства степени.

2 11 − 5 = 2 6 = 64

Обратите внимание, что в свойстве 2 речь шла только о делении степеней с одинаковыми основаниями.

Нельзя заменять разность (4 3 −4 2) на 4 1 . Это понятно, если посчитать (4 3 −4 2) = (64 − 16) = 48 , а 4 1 = 4

Свойство № 3

Возведение степени в степень

При возведении степени в степень основание степени остаётся без изменения, а показатели степеней перемножаются.

(a n) m = a n · m , где « a » — любое число, а « m », « n » — любые натуральные числа.

Напоминаем, что частное можно представить в виде дроби. Поэтому на теме возведение дроби в степень мы остановимся более подробно на следующей странице.

Как умножать степени

Как умножать степени? Какие степени можно перемножить, а какие — нет? Как число умножить на степень?

В алгебре найти произведение степеней можно в двух случаях:

1) если степени имеют одинаковые основания;

2) если степени имеют одинаковые показатели.

При умножении степеней с одинаковыми основаниями надо основание оставить прежним, а показатели — сложить:

При умножении степеней с одинаковыми показателями общий показатель можно вынести за скобки:

Рассмотрим, как умножать степени, на конкретных примерах.

Единицу в показателе степени не пишут, но при умножении степеней — учитывают:

При умножении количество степеней может быть любое. Следует помнить, что перед буквой знак умножения можно не писать:

В выражениях возведение в степень выполняется в первую очередь.

Если нужно число умножить на степень, сначала следует выполнить возведение в степень, а уже потом — умножение:

Умножение степеней с одинаковыми основаниями

Этот видеоурок доступен по абонементу

У вас уже есть абонемент? Войти

На этом уроке мы изучим умножение степеней с одинаковыми основаниями. Вначале вспомним определение степени и сформулируем теорему о справедливости равенства . Затем приведем примеры ее применения на конкретных числах и докажем ее. Также мы применим теорему для решения различных задач.

Тема: Степень с натуральным показателем и ее свойства

Урок: Умножение степеней с одинаковыми основаниями (формула )

1.

Основные определения

Основные определения:

n — показатель степени,

— n -ая степень числа.

2. Формулировка теоремы 1

Теорема 1. Для любого числа а и любых натуральных n и k справедливо равенство:

По-иному: если а – любое число; n и k натуральные числа, то:

Отсюда правило 1:

3. Разъясняющие задачи

Вывод: частные случаи подтвердили правильность теоремы №1. Докажем ее в общем случае, то есть для любого а и любых натуральных n и k.

4. Доказательство теоремы 1

Дано число а – любое; числа n и k – натуральные. Доказать:

Доказательство основано на определении степени.

5. Решение примеров с помощью теоремы 1

Пример 1: Представьте в виде степени.

Для решения следующих примеров воспользуемся теоремой 1.

ж)

6. Обобщение теоремы 1

Здесь использовано обобщение:

7.

Решение примеров с помощью обобщения теоремы 1

8. Решение различных задач с помощью теоремы 1

Пример 2: Вычислите (можно использовать таблицу основных степеней).

а) (по таблице)

б)

Пример 3: Запишите в виде степени с основанием 2.

а)

Пример 4: Определите знак числа:

, а – отрицательное, так как показатель степени при -13 нечетный.

Пример 5: Замените (·) степенью числа с основанием r:

Имеем , то есть .

9. Подведение итогов

1. Дорофеев Г.В., Суворова С.Б., Бунимович Е.А. и др. Алгебра 7. 6 издание. М.: Просвещение. 2010 г.

1. Школьный помощник (Источник).

1. Представьте в виде степени:

а) б) в) г) д)

3. Запишите в виде степени с основанием 2:

4. Определите знак числа:

а)

5. Замените (·) степенью числа с основанием r:

а) r 4 · (·) = r 15 ; б) (·) · r 5 = r 6

Умножение и деление степеней с одинаковыми показателями

На этом уроке мы изучим умножение степеней с одинаковыми показателями. Сначала вспомним основные определения и теоремы об умножении и делении степеней с одинаковыми основаниями и возведении степень в степень. Затем сформулируем и докажем теоремы об умножении и делении степеней с одинаковыми показателями. А затем с их помощью решим ряд типичных задач.

Напоминание основных определений и теорем

Здесь a — основание степени,

— n -ая степень числа.

Теорема 1. Для любого числа а и любых натуральных n иk справедливо равенство:

При умножении степеней с одинаковыми основаниями показатели складываются, основание остается неизменным.

Теорема 2. Для любого числа а и любых натуральных n и k, таких, что n > k справедливо равенство:

При делении степеней с одинаковыми основаниями показатели отнимаются, а основание остается неизменным.

Теорема 3. Для любого числа а и любых натуральных n иk справедливо равенство:

Все перечисленные теоремы были о степенях с одинаковыми основаниями , на этом уроке будут рассмотрены степени с одинаковыми показателями .

Примеры на умножение степеней с одинаковыми показателями

Рассмотрим следующие примеры:

Распишем выражения по определению степени.

Вывод: из примеров можно заметить, что , но это еще нужно доказать. Сформулируем теорему и докажем ее в общем случае, то есть для любых а и b и любого натурального n.

Формулировка и доказательство теоремы 4

Для любых чисел а и b и любого натурального n справедливо равенство:

Доказательство теоремы 4.

По определению степени:

Итак, мы доказали, что .

Чтобы перемножить степени с одинаковыми показателями, достаточно перемножить основания, а показатель степени оставить неизменным.

Формулировка и доказательство теоремы 5

Сформулируем теорему для деления степеней с одинаковыми показателями.

Для любого числа а и b () и любого натурального n справедливо равенство:

Доказательство теоремы 5.

Распишем и по определению степени:

Формулировка теорем словами

Итак, мы доказали, что .

Чтобы разделить друг на друга степени с одинаковыми показателями, достаточно разделить одно основание на другое, а показатель степени оставить неизменным.

Решение типичных задач с помощью теоремы 4

Пример 1: Представить в виде произведения степеней.

Для решения следующих примеров воспользуемся теоремой 4.

Для решения следующего примера вспомним формулы:

Обобщение теоремы 4

Обобщение теоремы 4:

Решение примеров с помощью обобщенной теоремы 4

Продолжение решения типичных задач

Пример 2: Запишите в виде степени произведения.

Пример 3: Запишите в виде степени с показателем 2.

Примеры на вычисление

Пример 4: Вычислить самым рациональным способом.

2. Мерзляк А.Г., Полонский В.Б., Якир М.С. Алгебра 7. М.: ВЕНТАНА-ГРАФ

3. Колягин Ю. М., Ткачёва М.В., Фёдорова Н.Е. и др. Алгебра 7 .М.: Просвещение. 2006 г.

2. Школьный помощник (Источник).

1. Представить в виде произведения степеней:

а) ; б) ; в) ; г) ;

2. Запишите в виде степени произведения:

3. Запишите в виде степени с показателем 2:

4. Вычислить самым рациональным способом.

Урок математики по теме «Умножение и деление степеней»

Разделы: Математика

Педагогическая цель :

ученик научится различать свойства умножения и деления степеней с натуральным показателем; применять эти свойства в случае с одинаковыми основаниями;

ученик получит возможность уметь выполнять преобразования степеней с разными основаниями и уметь выполнять преобразования в комбинированных заданиях.

Задачи :

организовать работу учащихся посредством повторения ранее изученного материала;

обеспечить уровень воспроизведения посредством выполнения упражнений различного типа;

организовать проверку по самооценке учащихся посредством тестирования.

Деятельностные единицы учения: определение степени с натуральным показателем; компоненты степени; определение частного; сочетательный закон умножения.

I. Организация демонстрации овладение учащимися имеющимися знаниями. (шаг 1)

а) Актуализация знаний:

2) Сформулировать определение степени с натуральным показателем.

a n =a a a a … а (n раз)

b k =b b b b a… b (k раз) Обосновать ответ.

II. Организация самооценивания обучаемого степенью владения актуальным опытом. (шаг 2)

Тест для самопроверки: (индивидуальная работа в двух вариантах.)

А1) Представьте произведение 7 7 7 7 x x x в виде степени:

А2) Представить в виде произведения степень (-3) 3 х 2

A3) Вычислите: -2 3 2 + 4 5 3

Количество заданий в тесте я подбираю в соответствии с подготовкой уровня класса.

К тесту даю ключ для самопроверки. Критерии: зачёт – не зачёт.

III. Учебно-практическая задача (шаг 3) + шаг 4. (сформулируют свойства сами ученики)

вычислите: 2 2 2 3 = ? 3 3 3 2 3 =?

Упростите: а 2 а 20 = ? b 30 b 10 b 15 = ?

В ходе решения задачи 1) и 2) учащиеся предлагают решение, а я, как учитель, организую класс на нахождение способа для упрощения степеней при умножении с одинаковыми основаниями.

Учитель: придумать способ для упрощения степеней при умножении с одинаковыми основаниями.

На кластере появляется запись:

Формулируется тема урока. Умножение степеней.

Учитель: придумайте правило деления степеней с одинаковыми основаниями.

Рассуждения: каким действием проверяется деление? а 5: а 3 = ? что а 2 а 3 = а 5

Возвращаюсь к схеме – кластер и дополняем запись – ..при делении вычитаем и дописываем тему урока. …и деление степеней.

IV. Сообщение учащимся пределов познания (как минимум и как максимум).

Учитель: задачей минимума на сегодняшний урок является научиться применять свойства умножения и деления степеней с одинаковыми основаниями, а максимума: применять умножение и деление совместно.

На доске записываем: а m а n = а m+n ; а m: а n = а m-n

V. Организация изучения нового материала. (шаг 5)

а) По учебнику: №403 (а, в, д) задания с разными формулировками

№404 (а, д, е) самостоятельная работа, затем организую взаимопроверку, даю ключи.

б) При каком значении m справедливо равенство? а 16 а m = а 32 ; х h х 14 = х 28 ; х 8 (*) = х 14

Задание: придумать аналогичные примеры для деления.

в) № 417(а), №418 (а) Ловушки для учеников : х 3 х n = х 3n ; 3 4 3 2 = 9 6 ; а 16: а 8 = а 2 .

VI. Обобщение изученного, проведение диагностической работы (что побуждает учеников, а не учителя изучать данную тему)(шаг 6)

Диагностическая работа.

Тест (ключи поместить на обратной стороне теста).

Варианты заданий: представьте в виде степени частное х 15: х 3 ; представьте в виде степени произведение (-4) 2 (-4) 5 (-4) 7 ; при каком m справедливо равенство а 16 а m = а 32 ; найдите значение выражения h 0: h 2 при h =0,2; вычислите значение выражения (5 2 5 0) : 5 2 .

Итог урока. Рефлексия. Делю класс на две группы.

Найдите аргументы I группа: в пользу знания свойств степени, а II группа – аргументы, которые будут говорить о том, что можно обойтись без свойств. Все ответы выслушиваем, делаем выводы. На последующих уроках можно предложить статистические данные и назвать рубрику «В голове не укладывается!»

Средний человек съедает 32 10 2 кг огурцов в течение жизни.

Оса способна совершить беспосадочный перелёт на 3,2 10 2 км.

Когда стекло трескается, трещина распространяется со скоростью около 5 10 3 км/ч.

Лягушка съедает за свою жизнь более 3 тонн комаров. Используя степень, запишите в кг.

Наиболее плодовитой считается океанская рыба – луна (Моlа mola), которая откладывает за один нерест до 300000000 икринок диаметром около 1,3 мм. Запишите это число, используя степень.

VII. Домашнее задание.

Историческая справка. Какие числа называют числами Ферма.

П.19. №403, №408, №417

Используемая литература:

Учебник «Алгебра-7», авторы Ю.

Н. Макарычев, Н.Г. Миндюк и др.

Дидактический материал для 7 класса, Л.В. Кузнецова, Л.И. Звавич, С.Б. Суворова.

Энциклопедия по математике.

Журнал «Квант».

Свойства степеней, формулировки, доказательства, примеры.

После того как определена степень числа, логично поговорить про свойства степени . В этой статье мы дадим основные свойства степени числа, при этом затронем все возможные показатели степени. Здесь же мы приведем доказательства всех свойств степени, а также покажем, как применяются эти свойства при решении примеров.

Навигация по странице.

Свойства степеней с натуральными показателями

По определению степени с натуральным показателем степень a n представляет собой произведение n множителей, каждый из которых равен a . Отталкиваясь от этого определения, а также используя свойства умножения действительных чисел , можно получить и обосновать следующие свойства степени с натуральным показателем :

основное свойство степени a m ·a n =a m+n , его обобщение a n 1 ·a n 2 ·…·a n k =a n 1 +n 2 +…+n k ;

свойство частного степеней с одинаковыми основаниями a m:a n =a m−n ;

свойство степени произведения (a·b) n =a n ·b n , его расширение (a 1 ·a 2 ·…·a k) n =a 1 n ·a 2 n ·…·a k n ;

свойство частного в натуральной степени (a:b) n =a n:b n ;

возведение степени в степень (a m) n =a m·n , его обобщение (((a n 1) n 2) …) n k =a n 1 ·n 2 ·…·n k ;

сравнение степени с нулем:

если a>0 , то a n >0 для любого натурального n ;
если a=0 , то a n =0 ;
если a 2·m >0 , если a 2·m−1 n ;
если m и n такие натуральные числа, что m>n , то при 0m n , а при a>0 справедливо неравенство a m >a n .

Сразу заметим, что все записанные равенства являются тождественными при соблюдении указанных условий, и их правые и левые части можно поменять местами. Например, основное свойство дроби a m ·a n =a m+n при упрощении выражений часто применяется в виде a m+n =a m ·a n .

Теперь рассмотрим каждое из них подробно.

Начнем со свойства произведения двух степеней с одинаковыми основаниями, которое называют основным свойством степени : для любого действительного числа a и любых натуральных чисел m и n справедливо равенство a m ·a n =a m+n .

Докажем основное свойство степени. По определению степени с натуральным показателем произведение степеней с одинаковыми основаниями вида a m ·a n можно записать как произведение . В силу свойств умножения полученное выражение можно записать как , а это произведение есть степень числа a с натуральным показателем m+n , то есть, a m+n . На этом доказательство завершено.

Приведем пример, подтверждающий основное свойство степени.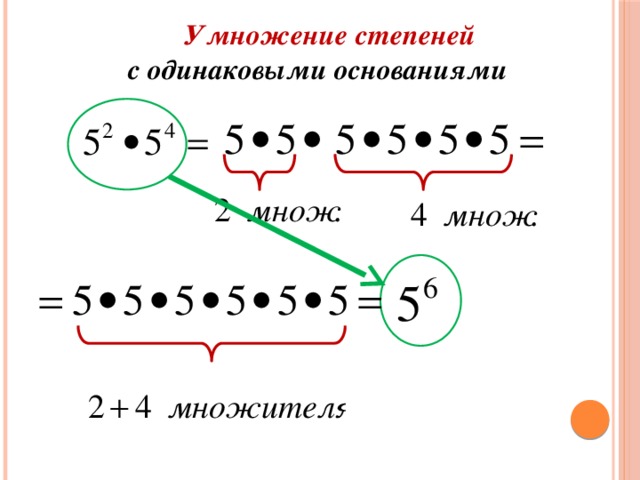 Возьмем степени с одинаковыми основаниями 2 и натуральными степенями 2 и 3 , по основному свойству степени можно записать равенство 2 2 ·2 3 =2 2+3 =2 5 . Проверим его справедливость, для чего вычислим значения выражений 2 2 ·2 3 и 2 5 . Выполняя возведение в степень, имеем 2 2 ·2 3 =(2·2)·(2·2·2)=4·8=32 и 2 5 =2·2·2·2·2=32 , так как получаются равные значения, то равенство 2 2 ·2 3 =2 5 — верное, и оно подтверждает основное свойство степени.

Основное свойство степени на базе свойств умножения можно обобщить на произведение трех и большего числа степеней с одинаковыми основаниями и натуральными показателями. Так для любого количества k натуральных чисел n 1 , n 2 , …, n k справедливо равенство a n 1 ·a n 2 ·…·a n k =a n 1 +n 2 +…+n k .

Например, (2,1) 3 ·(2,1) 3 ·(2,1) 4 ·(2,1) 7 = (2,1) 3+3+4+7 =(2,1) 17 .

Можно переходить к следующему свойству степеней с натуральным показателем – свойству частного степеней с одинаковыми основаниями : для любого отличного от нуля действительного числа a и произвольных натуральных чисел m и n , удовлетворяющих условию m>n , справедливо равенство a m:a n =a m−n .

Прежде чем привести доказательство этого свойства, обговорим смысл дополнительных условий в формулировке. Условие a≠0 необходимо для того, чтобы избежать деления на нуль, так как 0 n =0 , а при знакомстве с делением мы условились, что на нуль делить нельзя. Условие m>n вводится для того, чтобы мы не выходили за рамки натуральных показателей степени. Действительно, при m>n показатель степени a m−n является натуральным числом, в противном случае он будет либо нулем (что происходит при m−n), либо отрицательным числом (что происходит при m m−n ·a n =a (m−n)+n =a m . Из полученного равенства a m−n ·a n =a m и из связи умножения с делением следует, что a m−n является частным степеней a m и a n . Этим доказано свойство частного степеней с одинаковыми основаниями.

Приведем пример. Возьмем две степени с одинаковыми основаниями π и натуральными показателями 5 и 2 , рассмотренному свойству степени отвечает равенство π 5:π 2 =π 5−3 =π 3 .

Теперь рассмотрим свойство степени произведения : натуральная степень n произведения двух любых действительных чисел a и b равна произведению степеней a n и b n , то есть, (a·b) n =a n ·b n .

Действительно, по определению степени с натуральным показателем имеем . Последнее произведение на основании свойств умножения можно переписать как , что равно a n ·b n .

Приведем пример: .

Данное свойство распространяется на степень произведения трех и большего количества множителей. То есть, свойство натуральной степени n произведения k множителей записывается как (a 1 ·a 2 ·…·a k) n =a 1 n ·a 2 n ·…·a k n .

Для наглядности покажем это свойство на примере. Для произведения трех множителей в степени 7 имеем .

Следующее свойство представляет собой свойство частного в натуральной степени : частное действительных чисел a и b , b≠0 в натуральной степени n равно частному степеней a n и b n , то есть, (a:b) n =a n:b n .

Доказательство можно провести, используя предыдущее свойство. Так (a:b) n ·b n =((a:b)·b) n =a n , а из равенства (a:b) n ·b n =a n следует, что (a:b) n является частным от деления a n на b n .

Запишем это свойство на примере конкретных чисел: .

Теперь озвучим свойство возведения степени в степень : для любого действительного числа a и любых натуральных чисел m и n степень a m в степени n равна степени числа a с показателем m·n , то есть, (a m) n =a m·n .

Например, (5 2) 3 =5 2·3 =5 6 .

Доказательством свойства степени в степени является следующая цепочка равенств: .

Рассмотренное свойство можно распространить на степень в степени в степени и т.д. Например, для любых натуральных чисел p , q , r и s справедливо равенство . Для большей ясности приведем пример с конкретными числами: (((5,2) 3) 2) 5 =(5,2) 3+2+5 =(5,2) 10 .

Осталось остановиться на свойствах сравнения степеней с натуральным показателем.

Начнем с доказательства свойства сравнения нуля и степени с натуральным показателем.

Для начала обоснуем, что a n >0 при любом a>0 .

Произведение двух положительных чисел является положительным числом, что следует из определения умножения. Этот факт и свойства умножения позволяют утверждать, что результат умножения любого числа положительных чисел также будет положительным числом. А степень числа a с натуральным показателем n по определению является произведением n множителей, каждый из которых равен a . Эти рассуждения позволяют утверждать, что для любого положительного основания a степень a n есть положительное число. В силу доказанного свойства 3 5 >0 , (0,00201) 2 >0 и .

Достаточно очевидно, что для любого натурального n при a=0 степень a n есть нуль. Действительно, 0 n =0·0·…·0=0 . К примеру, 0 3 =0 и 0 762 =0 .

Переходим к отрицательным основаниям степени.

Начнем со случая, когда показатель степени является четным числом, обозначим его как 2·m , где m — натуральное. Тогда . По правилу умножения отрицательных чисел каждое из произведений вида a·a равно произведению модулей чисел a и a , значит, является положительным числом. Следовательно, положительным будет и произведение и степень a 2·m . Приведем примеры: (−6) 4 >0 , (−2,2) 12 >0 и .

Наконец, когда основание степени a является отрицательным числом, а показатель степени есть нечетное число 2·m−1 , то . Все произведения a·a являются положительными числами, произведение этих положительных чисел также положительно, а его умножение на оставшееся отрицательное число a дает в итоге отрицательное число. В силу этого свойства (−5) 3 17 n n представляет собой произведение левых и правых частей n верных неравенств aсвойств неравенств справедливо и доказываемое неравенство вида a n n . Например, в силу этого свойства справедливы неравенства 3 7 7 и .

Осталось доказать последнее из перечисленных свойств степеней с натуральными показателями. Сформулируем его. Из двух степеней с натуральными показателями и одинаковыми положительными основаниями, меньшими единицы, больше та степень, показатель которой меньше; а из двух степеней с натуральными показателями и одинаковыми основаниями, большими единицы, больше та степень, показатель которой больше. Переходим к доказательству этого свойства.

Докажем, что при m>n и 0m n . Для этого запишем разность a m −a n и сравним ее с нулем. Записанная разность после вынесения a n за скобки примет вид a n ·(a m−n −1) . Полученное произведение отрицательно как произведение положительного числа a n и отрицательного числа a m−n −1 (a n положительна как натуральная степень положительного числа, а разность a m−n −1 отрицательна, так как m−n>0 в силу исходного условия m>n , откуда следует, что при 0m−n меньше единицы). Следовательно, a m −a n m n , что и требовалось доказать. Для примера приведем верное неравенство .

Осталось доказать вторую часть свойства. Докажем, что при m>n и a>1 справедливо a m >a n . Разность a m −a n после вынесения a n за скобки принимает вид a n ·(a m−n −1) . Это произведение положительно, так как при a>1 степень a n есть положительное число, и разность a m−n −1 есть положительное число, так как m−n>0 в силу начального условия, и при a>1 степень a m−n больше единицы. Следовательно, a m −a n >0 и a m >a n , что и требовалось доказать. Иллюстрацией этого свойства служит неравенство 3 7 >3 2 .

Свойства степеней с целыми показателями

Так как целые положительные числа есть натуральные числа, то все свойства степеней с целыми положительными показателями в точности совпадают со свойствами степеней с натуральными показателями, перечисленными и доказанными в предыдущем пункте.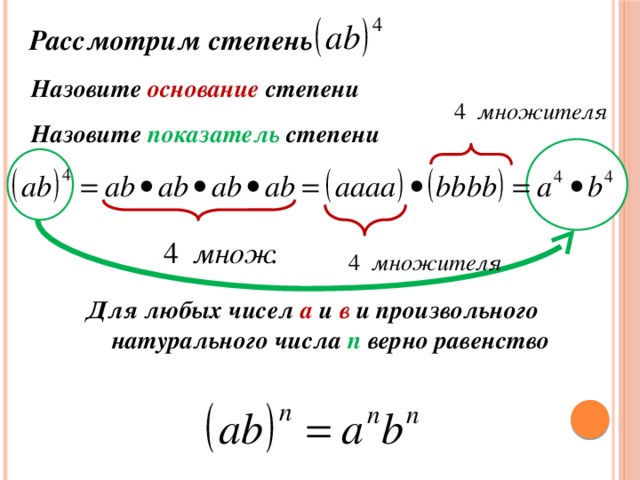

Степень с целым отрицательным показателем, а также степень с нулевым показателем мы определяли так, чтобы оставались справедливыми все свойства степеней с натуральными показателями, выражаемые равенствами. Поэтому, все эти свойства справедливы и для нулевых показателей степени, и для отрицательных показателей, при этом, конечно, основания степеней отличны от нуля.

Итак, для любых действительных и отличных от нуля чисел a и b , а также любых целых чисел m и n справедливы следующие свойства степеней с целыми показателями :

a m ·a n =a m+n ;
a m:a n =a m−n ;
(a·b) n =a n ·b n ;
(a:b) n =a n:b n ;
(a m) n =a m·n ;
если n – целое положительное число, a и b – положительные числа, причем an n и a −n >b −n ;
если m и n – целые числа, причем m>n , то при 0m n , а при a>1 выполняется неравенство a m >a n .

При a=0 степени a m и a n имеют смысл лишь когда и m , и n положительные целые числа, то есть, натуральные числа. Таким образом, только что записанные свойства также справедливы для случаев, когда a=0 , а числа m и n – целые положительные.

Доказать каждое из этих свойств не составляет труда, для этого достаточно использовать определения степени с натуральным и целым показателем, а также свойства действий с действительными числами. Для примера докажем, что свойство степени в степени выполняется как для целых положительных чисел, так и для целых неположительных чисел. Для этого нужно показать, что если p есть нуль или натуральное число и q есть нуль или натуральное число, то справедливы равенства (a p) q =a p·q , (a −p) q =a (−p)·q , (a p) −q =a p·(−q) и (a −p) −q =a (−p)·(−q) . Сделаем это.

Для положительных p и q равенство (a p) q =a p·q доказано в предыдущем пункте. Если p=0 , то имеем (a 0) q =1 q =1 и a 0·q =a 0 =1 , откуда (a 0) q =a 0·q . Аналогично, если q=0 , то (a p) 0 =1 и a p·0 =a 0 =1 , откуда (a p) 0 =a p·0 . Если же и p=0 и q=0 , то (a 0) 0 =1 0 =1 и a 0·0 =a 0 =1 , откуда (a 0) 0 =a 0·0 .

Теперь докажем, что (a −p) q =a (−p)·q . По определению степени с целым отрицательным показателем , тогда . По свойству частного в степени имеем . Так как 1 p =1·1·…·1=1 и , то . Последнее выражение по определению является степенью вида a −(p·q) , которую в силу правил умножения можно записать как a (−p)·q .

Аналогично .

И .

По такому же принципу можно доказать все остальные свойства степени с целым показателем, записанные в виде равенств.

В предпоследнем из записанных свойств стоит остановиться на доказательстве неравенства a −n >b −n , которое справедливо для любого целого отрицательного −n и любых положительных a и b , для которых выполняется условие a. Запишем и преобразуем разность левой и правой частей этого неравенства: . Так как по условию an n , следовательно, b n −a n >0 . Произведение a n ·b n тоже положительно как произведение положительных чисел a n и b n . Тогда полученная дробь положительна как частное положительных чисел b n −a n и a n ·b n . Следовательно, откуда a −n >b −n , что и требовалось доказать.

Последнее свойство степеней с целыми показателями доказывается так же, как аналогичное свойство степеней с натуральными показателями.

Свойства степеней с рациональными показателями

Степень с дробным показателем мы определяли, распространяя на нее свойства степени с целым показателем. Иными словами, степени с дробными показателями обладают теми же свойствами, что и степени с целыми показателями. А именно:

свойство произведения степеней с одинаковыми основаниями при a>0 , а если и , то при a≥0 ;
свойство частного степеней с одинаковыми основаниями при a>0 ;
свойство произведения в дробной степени при a>0 и b>0 , а если и , то при a≥0 и (или) b≥0 ;
свойство частного в дробной степени при a>0 и b>0 , а если , то при a≥0 и b>0 ;
свойство степени в степени при a>0 , а если и , то при a≥0 ;
свойство сравнения степеней с равными рациональными показателями: для любых положительных чисел a и b , a0 справедливо неравенство a p p , а при p p >b p ;
свойство сравнения степеней с рациональными показателями и равными основаниями: для рациональных чисел p и q , p>q при 0p q , а при a>0 – неравенство a p >a q .

Доказательство свойств степеней с дробными показателями базируется на определении степени с дробным показателем, на свойствах арифметического корня n-ой степени и на свойствах степени с целым показателем. Приведем доказательства.

По определению степени с дробным показателем и , тогда . Свойства арифметического корня позволяют нам записать следующие равенства . Дальше, используя свойство степени с целым показателем, получаем , откуда по определению степени с дробным показателем имеем , а показатель полученной степени можно преобразовать так: . На этом доказательство завершено.

Абсолютно аналогично доказывается второе свойство степеней с дробными показателями:

По схожим принципам доказываются и остальные равенства:

Переходим к доказательству следующего свойства. Докажем, что для любых положительных a и b , a0 справедливо неравенство a p p , а при p p >b p . Запишем рациональное число p как m/n , где m – целое число, а n – натуральное. Условиям p 0 в этом случае будут эквивалентны условия m 0 соответственно. При m>0 и am m . Из этого неравенства по свойству корней имеем , а так как a и b – положительные числа, то на основе определения степени с дробным показателем полученное неравенство можно переписать как , то есть, a p p .

Аналогично, при m m >b m , откуда , то есть, и a p >b p .

Осталось доказать последнее из перечисленных свойств. Докажем, что для рациональных чисел p и q , p>q при 0p q , а при a>0 – неравенство a p >a q . Мы всегда можем привести к общему знаменателю рациональные числа p и q , пусть при этом мы получим обыкновенные дроби и , где m 1 и m 2 – целые числа, а n — натуральное. При этом условию p>q будет соответствовать условие m 1 >m 2 , что следует из правила сравнения обыкновенных дробей с одинаковыми знаменателями. Тогда по свойству сравнения степеней с одинаковыми основаниями и натуральными показателями при 0m 1 m 2 , а при a>1 – неравенство a m 1 >a m 2 . Эти неравенства по свойствам корней можно переписать соответственно как и . А определение степени с рациональным показателем позволяет перейти к неравенствам и соответственно. Отсюда делаем окончательный вывод: при p>q и 0p q , а при a>0 – неравенство a p >a q .

Свойства степеней с иррациональными показателями

Из того, как определяется степень с иррациональным показателем, можно заключить, что она обладает всеми свойствами степеней с рациональными показателями. Так для любых a>0 , b>0 и иррациональных чисел p и q справедливы следующие свойства степеней с иррациональными показателями :

a p ·a q =a p+q ;
a p:a q =a p−q ;
(a·b) p =a p ·b p ;
(a:b) p =a p:b p ;
(a p) q =a p·q ;
для любых положительных чисел a и b , a0 справедливо неравенство a p p , а при p p >b p ;
для иррациональных чисел p и q , p>q при 0p q , а при a>0 – неравенство a p >a q .

Отсюда можно сделать вывод, что степени с любыми действительными показателями p и q при a>0 обладают этими же свойствами.

Алгебра – 10 класс. Тригонометрические уравнения Урок и презентация на тему: «Решение простейших тригонометрических уравнений» Дополнительные материалы Уважаемые пользователи, не забывайте оставлять свои комментарии, отзывы, пожелания! Все материалы […]
Открыт конкурс на позицию «ПРОДАВЕЦ — КОНСУЛЬТАНТ»: Обязанности: продажа мобильных телефонов и аксессуаров для мобильной связи сервисное обслуживание абонентов Билайн, Теле2, МТС подключение тарифных планов и услуг Билайн и Теле2, МТС консультирование […]
Параллелепипед формулы Параллелепипед – это многогранник с 6 гранями, каждая из которых является параллелограммом. Прямоугольный параллелепипед – это параллелепипед, каждая грань которого является прямоугольником. Любой параллелепипед характеризуется 3 […]
Принять закон о Родовых поместьях Принять федеральный закон о безвозмездном выделении каждому желающему гражданину Российской Федерации или семье граждан участка земли для обустройства на нем Родового Поместья на следующих условиях: 1. Участок выделяется для […]
Общество защиты прав потребителя астана Для того, что бы получить pin-код для доступа к данному документу на нашем сайте, отправьте sms-сообщение с текстом zan на номер Абоненты GSM-операторов (Activ, Kcell, Beeline, NEO, Tele2) отправив SMS на номер, […]
ИНСПЕКЦИЯ ГОСТЕХНАДЗОРА БРЯНСКОЙ ОБЛАСТИ Квитанция об оплате госпошлины(Скачать-12,2 kb) Заявления на регистрацию для физ.лиц(Скачать-12 kb) Заявления на регистрацию для юр.лиц(Скачать-11,4 kb) 1. При регистрации новой машины: 1.заявление 2.паспорт […]
ПРАВОПИСАНИЕ Н И НН В РАЗНЫХ ЧАСТЯХ РЕЧИ С.Г.ЗЕЛИНСКАЯ ДИДАКТИЧЕСКИЙ МАТЕРИАЛ Теоретическая зарядка 1. Когда в прилагательных пишется нн? 2. Назовите исключения из этих правил. 3. Как отличить отглагольное прилагательное с суффиксом -н- от причастия с […]
Пивоев В.М. Философия и методология науки: учебное пособие для магистров и аспирантов Петрозаводск: Изд-во ПетрГУ, 2013. ― 320 с.ISBN 978-5-821-1647-0 PDF 3 mb Учебное пособие предназначено для студентов старших курсов, магистров и аспирантов социального и […]

Так, сумма a 3 и b 2 есть a 3 + b 2 .
Сумма a 3 — b n и h 5 -d 4 есть a 3 — b n + h 5 — d 4 .

Коэффициенты одинаковых степеней одинаковых переменных могут слагаться или вычитаться.

Так, сумма 2a 2 и 3a 2 равна 5a 2 .

Это так же очевидно, что если взять два квадрата а, или три квадрата а, или пять квадратов а.

Но степени различных переменных и различные степени одинаковых переменных , должны слагаться их сложением с их знаками.

Так, сумма a 2 и a 3 есть сумма a 2 + a 3 .

Это очевидно, что квадрат числа a, и куб числа a, не равно ни удвоенному квадрату a, но удвоенному кубу a.

Сумма a 3 b n и 3a 5 b 6 есть a 3 b n + 3a 5 b 6 .

Или:
2a 4 — (-6a 4) = 8a 4
3h 2 b 6 — 4h 2 b 6 = -h 2 b 6
5(a — h) 6 — 2(a — h) 6 = 3(a — h) 6

Умножение степеней

Так, результат умножения a 3 на b 2 равен a 3 b 2 или aaabb.

Или:
x -3 ⋅ a m = a m x -3
3a 6 y 2 ⋅ (-2x) = -6a 6 xy 2
a 2 b 3 y 2 ⋅ a 3 b 2 y = a 2 b 3 y 2 a 3 b 2 y

Так, a 2 .a 3 = aa.aaa = aaaaa = a 5 .

Здесь 5 — это степень результата умножения, равная 2 + 3, сумме степеней слагаемых.

Так, a n .a m = a m+n .

Для a n , a берётся как множитель столько раз, сколько равна степень n;

И a m , берётся как множитель столько раз, сколько равна степень m;

Поэтому, степени с одинаковыми основами могут быть умножены путём сложения показателей степеней.

Так, a 2 .a 6 = a 2+6 = a 8 . И x 3 .x 2 .x = x 3+2+1 = x 6 .

Или:
4a n ⋅ 2a n = 8a 2n
b 2 y 3 ⋅ b 4 y = b 6 y 4
(b + h — y) n ⋅ (b + h — y) = (b + h — y) n+1

Умножьте (x 3 + x 2 y + xy 2 + y 3) ⋅ (x — y).
Ответ: x 4 — y 4 .
Умножьте (x 3 + x — 5) ⋅ (2x 3 + x + 1).

Это правило справедливо и для чисел, показатели степени которых — отрицательные .

1. Так, a -2 .a -3 = a -5 . Это можно записать в виде (1/aa).(1/aaa) = 1/aaaaa.

2. y -n .y -m = y -n-m .

3. a -n .a m = a m-n .

Если a + b умножаются на a — b, результат будет равен a 2 — b 2: то есть

Результат умножения суммы или разницы двух чисел равен сумме или разнице их квадратов.

Так, (a — y).(a + y) = a 2 — y 2 .
(a 2 — y 2)⋅(a 2 + y 2) = a 4 — y 4 .
(a 4 — y 4)⋅(a 4 + y 4) = a 8 — y 8 .

Деление степеней

Числа со степенями могут быть поделены, как и другие числа, путем отнимая от делимого делителя, или размещением их в форме дроби. 5}$. Ответ: $\frac{2x}{1}$ или 2x.

5. Умножьте (a 3 + b)/b 4 на (a — b)/3.

6. Умножьте (a 5 + 1)/x 2 на (b 2 — 1)/(x + a).

7. Умножьте b 4 /a -2 на h -3 /x и a n /y -3 .

8. Разделите a 4 /y 3 на a 3 /y 2 . Ответ: a/y.

9. Разделите (h 3 — 1)/d 4 на (d n + 1)/h.

Как делить числа с одинаковыми степенями?

Содержание

— Как считать деление со степенями?
— Как сложить числа с одинаковыми основаниями и разными степенями?
— Когда умножаются степени?
— Как сокращение степени при делении?
— Как умножать и делить числа с разными степенями?
— Как перевести дробь в степень?
— Как сложить два числа с одинаковыми знаками?
— Что происходит со степенями при умножении и делении?
— Как решать примеры с отрицательными степенями?
— Как разделить число в отрицательной степени?
— Как умножать числа с разными степенями?
— Как решить число в степени?
— Как можно сокращать степени?
— Как можно сократить дробь?
— Какие бывают степени в математике?

Как считать деление со степенями?

При делении степеней с одинаковыми основаниями основание остаётся без изменений, а из показателя степени делимого вычитают показатель степени делителя. = am − n, где «a» — любое число, не равное нулю, а «m», «n» — любые натуральные числа такие, что «m > n». Примеры. Вычислить.

Как сложить числа с одинаковыми основаниями и разными степенями?

Как складывать числа с одинаковыми степенями

Если степени одинаковые, а основания разные, то нельзя сложить основания и затем эту сумму возводить в степень. Сначала возводим каждое число в степень и затем выполняем сложение.

Когда умножаются степени?

Когда возводим степень в степень, то основание степени остается неизмененным, а показатели степеней умножаются друг на друга.

Как сокращение степени при делении?

Степени и корни

При умножении степеней с одинаковым основанием их показатели складываются:
a m · a n = a m + n .
При делении степеней с одинаковым основанием их показатели вычитаются.
Степень произведения двух или нескольких сомножителей равна произведению степеней этих сомножителей.

Как умножать и делить числа с разными степенями?

При умножении степеней с одинаковыми основаниями показатели складываются, основание остается неизменным. Теорема 2. Для любого числа а и любых натуральных n и k, таких, что n > k справедливо равенство: При делении степеней с одинаковыми основаниями показатели отнимаются, а основание остается неизменным.

Как перевести дробь в степень?

Для того, чтобы возвести дробь в степень, необходимо возвести её числитель и знаменатель в эту же степень. При возведение в степень смешанной дроби, сначала нужно эту дробь преобразовать в неправильную, а затем возвести в степень её числитель и знаменатель.

Как сложить два числа с одинаковыми знаками?

Чтобы сложить два числа одинаковых знаков, надо сложить их модули и поставить перед суммой знак слагаемых. Чтобы сложить числа разных знаков, нужно из большего модуля вычесть меньший и полученную разность взять со знаком того слагаемого, модуль которого больше.

Что происходит со степенями при умножении и делении?

При умножении двух степеней с одинаковым показателем, в произведении показатель степени остаётся таким же, а основания перемножаются друг с другом. Ответ: ac · bc = (a∙b)c. При делении двух степеней с одинаковым показателем, в частном показатель степени остаётся таким же, а основания делятся друг на друга.

Как решать примеры с отрицательными степенями?

Чтобы возвести число в отрицательную степень нужно:

«перевернуть» число. Записать его в виде дроби с единицой наверху (в числителе) и с исходным числом в степени внизу;
заменить отрицательную степень на положительную;
возвести число в положительную степень.

Как разделить число в отрицательной степени?

Степень с отрицательным показателем

При делении степеней с одинаковыми основаниями из показателя степени делимого вычитают показатель степени делителя. Следовательно, если степень делимого будет меньше степени делителя, то в результате получится число с отрицательной степенью: a 5 : a 8 = a5 — 8 = a -3. = x -2.

Как умножать числа с разными степенями?

При умножении степеней с одинаковыми основаниями основание остаётся без изменений, а показатели степеней складываются. a m · a n = a m + n , где « a » — любое число, а « m », « n » — любые натуральные числа. Данное свойство степеней также действует на произведение трёх и более степеней.

Как решить число в степени?

Чтобы вычислить значение степени, нужно выполнить действие умножения, то есть перемножить основания степени указанное число раз. На умении быстро умножать и основано само понятие степени с натуральным показателем.

Как можно сокращать степени?

Степени сокращаем на степень с наименьшим показателем. Сократить дробь — значит, разделить числитель и знаменатель на один и тот же делитель, а при делении степеней показатели вычитаем. a² и a⁷ сокращаем на a².

Как можно сократить дробь?

Сократить дробь — значит разделить ее числитель и знаменатель на общий делитель, положительный и отличный от единицы. В результате такого действия получится дробь с новым числителем и знаменателем, равная исходной дроби.

Какие бывают степени в математике?

Особенности степеней

Отрицательное число, возведенное в четную степень, – число положительное;
Отрицательное число, возведенное в нечетную степень, – число отрицательное;
Положительное число в любой степени – число положительное;
Ноль в любой степени равен 0;
Любое число в нулевой степени равно 1;

Интересные материалы:

Какой пролив в Африке?
Какой процент берет Сбербанк за оплату коммунальных услуг?
Какой процессор для GeForce 1070?
Какой провод плюс черный или белый?
Какой пульс считается брадикардией?
Какой район Ростова на Дону лучше для проживания?
Какой расход топлива у Явы 350?
Какой регион 293?
Какой регион Краснодарский край?
Какой регион на 928?

умножение, сложение и вычитание степеней

В предыдущей статье мы рассказали, что из себя представляют одночлены. В этом материале разберем, как решать примеры и задачи, в которых они применяются. Здесь будут рассмотрены такие действия, как вычитание, сложение, умножение, деление одночленов и возведение их в степень с натуральным показателем. Мы покажем, как определяются такие операции, обозначим основные правила их выполнения и то, что должно получится в результате. Все теоретические положения, как обычно, будут проиллюстрированы примерами задач с описаниями решений.

Удобнее всего работать со стандартной записью одночленов, поэтому все выражения, которые будут использованы в статье, мы приводим в стандартном виде. Если изначально они заданы иначе, рекомендуется сначала привести их к общепринятой форме.

Правила сложения и вычитания одночленов

Наиболее простые действия, которые можно проводить с одночленами – это вычитание и сложение. В общем случае результатом этих действий будет являться многочлен (одночлен возможен в некоторых частных случаях).

Когда мы складываем или вычитаем одночлены, сначала записываем в общепринятой форме соответствующую сумму и разность, после чего упрощаем получившееся выражение. Если есть подобные слагаемые, их нужно привести, скобки – раскрыть. Поясним на примере.

Пример 1

Условие: выполните сложение одночленов −3·x и 2,72·x3·y5·z.

Решение

Запишем сумму исходных выражений. Добавим скобки и поставим между ними плюс. У нас получится следующее:

(−3·x)+(2,72·x3·y5·z)

Когда мы выполним раскрытие скобок, получится -3·x+2,72·x3·y5·z. Это многочлен, записанный в стандартной форме, который и будет результатом сложения данных одночленов.

Ответ: (−3·x)+(2,72·x3·y5·z)=−3·x+2,72·x3·y5·z.

Если у нас задано три, четыре и больше слагаемых, мы осуществляем это действие точно так же.

Пример 2

Условие: проведите в правильном порядке указанные действия с многочленами

3·a2-(-4·a·c)+a2-7·a2+49-223·a·c

Решение

Начнем с раскрытия скобок.

3·a2+4·a·c+a2-7·a2+49-223·a·c

Мы видим, что полученное выражение можно упростить путем приведения подобных слагаемых:

3·a2+4·a·c+a2-7·a2+49-223·a·c==(3·a2+a2-7·a2)+4·a·c-223·a·c+49==-3·a2+113·a·c+49

У нас получился многочлен, который и будет результатом данного действия.

Ответ: 3·a2-(-4·a·c)+a2-7·a2+49-223·a·c=-3·a2+113·a·c+49

В принципе, мы можем выполнить сложение и вычитание двух одночленов с некоторыми ограничениями так, чтобы получить в итоге одночлен. Для этого нужно соблюсти некоторые условия, касающиеся слагаемых и вычитаемых одночленов. О том, как это делается, мы расскажем в отдельной статье.

Правила умножения одночленов

Действие умножения не налагает никаких ограничений на множители. Умножаемые одночлены не должны соответствовать никаким дополнительным условиям, чтобы в результате получится одночлен.

Чтобы выполнить умножение одночленов, нужно выполнить следующие шаги:

Правильно записать произведение.
Раскрыть скобки в полученном выражении.
Сгруппировать по возможности множители с одинаковыми переменными и числовые множители отдельно.
Выполнить необходимые действия с числами и применить к оставшимся множителям свойство умножения степеней с одинаковыми основаниями.

Посмотрим, как это делается на практике.

Пример 3

Условие: выполните умножение одночленов 2·x4·y·z и -716·t2·x2·z11 .

Решение

Начнем с составления произведения.

2·x4·y·z·-716·t2·x2·z11

Раскрываем в нем скобки и получаем следующее:

2·x4·y·z·-716·t2·x2·z11

Далее нам нужно объединить числовые множители в одну группу, а потом сгруппировать множители с одинаковыми переменными:

2·-716·t2·x4·x2·y·z3·z11

Все, что нам осталось сделать – это умножить числа в первых скобках и применить свойство степеней для вторых. В итоге получим следующее:

2·-716·t2·x4·x2·y·z3·z11=-78·t2·x4+2·y·z3+11==-78·t2·x6·y·z14

Ответ: 2·x4·y·z·-716·t2·x2·z11=-78·t2·x6·y·z14 .

Если у нас в условии стоят три многочлена и больше, мы умножаем их по точно такому же алгоритму. Более подробно вопрос умножения одночленов мы рассмотрим в рамках отдельного материала.

Правила возведения одночлена в степень

Мы знаем, что степенью с натуральным показателем называют произведение некоторого числа одинаковых множителей. На их количество указывает число в показателе. Согласно этому определению, возведение одночлена в степень равнозначно умножению указанного числа одинаковых одночленов. Посмотрим, как это делается.

Пример 4

Условие: выполните возведение одночлена −2·a·b4 в степень 3.

Решение

Мы можем заменить возведение в степень на умножение 3-х одночленов −2·a·b4. Запишем и получим нужный ответ:

(−2·a·b4)3=(−2·a·b4)·(−2·a·b4)·(−2·a·b4)==((−2)·(−2)·(−2))·(a· a· a)·(b4·b4·b4)=−8·a3·b12

Ответ: (−2·a·b4)3=−8·a3·b12.

А как быть в том случае, когда степень имеет большой показатель? Записывать большое количество множителей неудобно. Тогда для решения такой задачи нам надо применить свойства степени, а именно свойство степени произведения и свойство степени в степени.

Решим задачу, которую мы привели выше, указанным способом.

Пример 5

Условие: выполните возведение −2·a·b4 в третью степень.

Решение

Зная свойство степени в степени, мы можем перейти к выражению следующего вида:

(−2·a·b4)3=(−2)3·a3·(b4)3.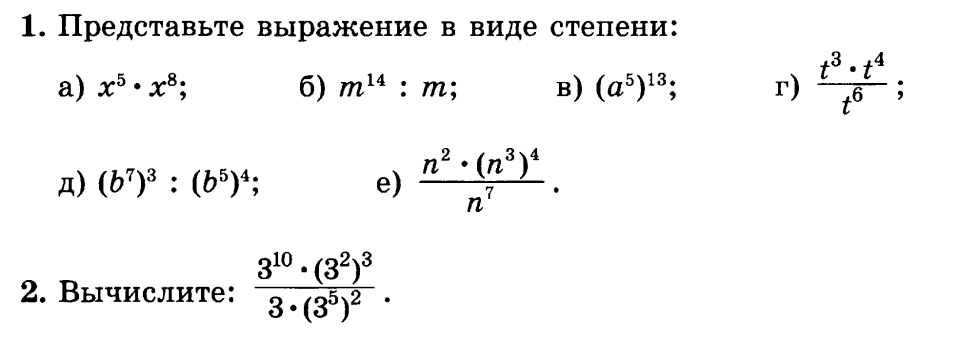

После этого мы возводим в степень -2 и применяем свойство степени в степени:

(−2)3·(a)3·(b4)3=−8·a3·b4·3=−8·a3·b12.

Ответ: −2·a·b4=−8·a3·b12.

Возведению одночлена в степень мы также посвятили отдельную статью.

Правила деления одночленов

Последнее действие с одночленами, которое мы разберем в данном материале, – деление одночлена на одночлен. В результате мы должны получить рациональную (алгебраическую) дробь (в некоторых случаях возможно получение одночлена). Сразу уточним, что деление на нулевой одночлен не определяется, поскольку не определяется деление на 0.

Для выполнения деления нам нужно записать указанные одночлены в форме дроби и сократить ее, если есть такая возможность.

Пример 6

Условие: выполните деление одночлена −9·x4·y3·z7 на −6·p3·t5·x2·y2.

Решение

Начнем с записи одночленов в форме дроби.

-9·x4·y3·z7-6·p3·t5·x2·y2

Эту дробь можно сократить. После выполнения этого действия получим:

3·x2·y·z72·p3·t5

Ответ: -9·x4·y3·z7-6·p3·t5·x2·y2=3·x2·y·z72·p3·t5.

Условия, при которых в результате деления одночленов мы получим одночлен, приводятся в отдельной статье.

Решение задач от 1 дня / от 150 р. Курсовая работа от 5 дней / от 1800 р. Реферат от 1 дня / от 700 р.

Электронная рабочая тетрадь. Алгебра. 7 класс доклад, проект

Слайд 1Текст слайда:

Степени с натуральным показтелем

Определение

Произведение одинаковых сомножителей, умноженных n раз называется ____________________________________________

а – называется _________________
n – называется __________________
an – называется __________________

Если n = 2, например, х2, 52, (a + b)2, то говорят икс в квадрате, пять в квадрате, а плюс b в квадрате.
Если n = 3, например, х3, 53, (a + b)3, то говорят икс в кубе, пять в кубе, а плюс b в кубе.
При других показателях, например, х5, 56, (a + b)4, говорят икс в пятой степени, пять в шестой степени, а плюс b в четвертой степени.

степенью с натуральным показателем

аn

основанием

показателем

степенью

Слайд 2Текст слайда:

Любое число в первой степени равно ____________________________.

Единица в любой степени равна ___________________________.

а1 = _____

Единицу в показателе не пишут.

1n = _____

Нуль в любой степени равен _____________________.

0n = _____

1. В таблицу проставьте номера выражений в четной и нечетной степени:

22;
(-2)3;
0,33;
(½ )6;
(-10)5;
a8;
(4b)3;
(x-y)4;

9) 2,62;
10) (-a)10;
11) (1 ½ )9;
12) (ab )6;
13) (3)2n;
14) a2n +1;
15) (4b) 2k +2;
16) (a +b)4n – 1 ;

Слайд 3Текст слайда:

Таблица основных степеней

Заполните таблицу

Степень чисел, оканчивающихся нулями

2. К результату приписать столько нулей,
сколько их в основании, умноженном на показатель.

1. Возвести в степень число без нулей;

Слайд 4Текст слайда:

Степень десятичной дроби

2. Справа налево отсчитать столько знаков, сколько их в произведении количества знаков после запятой в основании на показатель степени.

1. Возвести в степень число, не взирая на запятую;

Знак степени

Определите знак степени, используя определение степени:

(-2)2 = (-2) (-2) = +
(-2)3=_________________________
(-2)4=_________________________
(-2)5=_________________________
(-2)6=_________________________

Сделайте вывод!
Минус в четной степени будет
__________________________
Минус в нечетной степени будет
__________________________

Слайд 5Текст слайда:

Определите к чему относятся минусы. Определите знак при возведении в степень:
(-2)4 минус у _____________________________ Знак ________
— (2х)4 минус у _____________________________ Знак ________
( — 2/5)3 минус у _____________________________ Знак ________
— (-а)5 минус у _____________________________ Знак ________
— (х -1)2 минус у ______________________________ Знак ________

Выполните примеры. Сначала поставьте знак, потом вычисляйте.
(-2)4 = ______________________
— (2х)4 = _______________________
( — 2/5)3 = _______________________
— (-а)5 = _______________________

Слайд 6Текст слайда:

Свойства степеней

Одинаковые основания

1. Произведение степеней с одинаковыми основаниями

Выполните по примеру

33∙ 32 = _________________________________________
(0,2)2 ∙ (0,2) = ____________________________________
a3 ∙ a3 = _________________________________________
a n ∙ a m =________________________________________

Чтобы перемножить степени с одинаковыми основаниями, надо: основание ___________________________,a показатели _______________________.

Сделайте вывод. Заполните пропуски

основание оставить тем же

сложить

Слайд 7Текст слайда:

Свойства степеней

Одинаковые основания

2. Частное степеней с одинаковыми основаниями

Чтобы разделить степени с одинаковыми основаниями, надо: основание ___________________________,a показатели _______________________.

Сделайте вывод. Заполните пропуски

основание оставить тем же

вычесть

Слайд 8Текст слайда:

Представьте произведение в виде степени:

2) 23·27· 24 = 2

3) 103·102 = 10

5) k3·k7· k4 = k

6) 103·10т = 10

7) 103+2m·10т = 10

Представьте в виде степени. Найдите значение выражения:

1) 23·24 = _______

2) 33·3 = _______

3) 103·102 = _______

4) 0,53·0,5 = _______

5) 16·24 = _______

6) 33·9 = _______

7) 2·103· 3·102 = __________

8) 32·32 = _________

Представьте частное в виде степени:

6) 103:10т = 10

Представьте в виде степени. Найдите значение выражения:

1) 25:24 = _______

= _______

3) 109/106 = _______

4) 0,53:0,5 = _______

5) 32/24 = _______

6) 34/27 = _______

= __________

8) x 6 : x = _________

Любое число кроме ___________ равно _____

3+т

3+3т

28 =256

100000

0,0625

35 =243

600000

210=1024

1+т

3-т

128

1000

2/3·104

х5

нуля

0,0625

Слайд 9Текст слайда:

Свойства степеней

Одинаковые основания

3. Возведение степени в степень

Выполните по примеру

(22) 3 = (2· 2)· (2· 2) · (2· 2) =

{

(33)2 = _________________________________________
(0,22)4 = ________________________________________
(a3 )5 = _________________________________________
(a n) m =________________________________________

Чтобы возвести степень в степень, надо: основание ________________________,a показатели _______________________.

Сделайте вывод. Заполните пропуски

основание оставить тем же

умножить

Слайд 10Текст слайда:

Представьте выражение в виде степени:

2) 23·27 = 2

3) 103·102 = 10

5) (k5) 3= k

6) (103 )т = 10

7) (103+2m )т = 10

Представьте в виде степени. Найдите значение выражения:

1) (-23)4 = _______

2) (-32)2 = _______

3) ((-10)2 )3 = _______

4) (0,54 )2 = _______

Свойства степеней

Одинаковые основания

Показатели ________________

умножение

сложить

дробь

вычесть

Возведение в степень

умножить

Слайд 11Текст слайда:

Действия в выражениях, содержащих степени

Действия с числовыми основаниями

1. Разложение числа на простые множители.

Представьте составное числа в виде произведения степеней с простыми основаниями:

1) 12 = _________

2) 24 = _________

3) 75 = __________

4) 48 = ____________

5) 72 = _________

6) 250 = _________

7) 54 = __________

8) 80 = ____________

Разложите числа на простые множители:

576

540

1296

864

864 =

576 =

540 =

1296 =

22·3

23·3

52·3

24·3

23·32

53·2

33·2

24·5

432

216

108

25·33

26·32

22·33·5

24·34

Слайд 12Текст слайда:

Возведение в степень – действия первой ступени: выполняются раньше других

При наличии числовых оснований – разложите их на простые множители

Представьте в виде произведения степеней с простым основанием:

1) (12)2 = _________

2) 64 = _________

3) (15)3 = __________

4) (48)3 = ____________

5) 722 = _________

6) 84 = _________

7) 27 2= __________

8) (80 )3 = ___________

при с = -3 ответ: _____

при с = ¼ ответ: ________

Слайд 13Текст слайда:

Вычислите:

Разделите степени с основанием 2 и степени с основанием 3

Разложите составные числа на степени с простым основанием. Выполните действия:

Слайд 14Текст слайда:

Свойства степеней

Разные основания

3. Возведение произведения в степень

Выполните по примеру

(2 · 3)3 = 2· 2 · 2 · 3 · 3· 3 = 2 3 · 33 = 108

{

(3 · 4)2 = _________________________________________
(0,2 · 5)4 = ________________________________________
(a ·b )5 = _________________________________________
(a b) m =________________________________________

Чтобы возвести произведение в степень, надо возвести в эту степень _________________________________________________________________.

Сделайте вывод. Заполните пропуски

{

32·42 = 9 · 16 = 144

а5 · b5

аm · bm

каждый множитель

Слайд 15Текст слайда:

Для числовых оснований можно сначала умножить, а потом возвести в степень.

(3 · 4)2 = 122 = 144

Возведите в степень:

1) (3a ) 2 = ________

2) (-2x)4 = ________

3) (ab)3 = ________

4) (-3x 2)3 = ___________

5) (xy4) 2 = ________

6) (-0,5n2) 4 = _______

7) (2 ¼ c) 2 = ________

8) (-2mn2 )3 = _________

Не забывайте!

возводить в степень коэффициент перед буквенной частью с учетом знака.

(-1,1n3 m) 2 = (-1,1)2 n6 m2 = 1,21 n6 m2

Заполните таблицу, используя свойство

Что это?

Как это?

16х4

а3b3

-27х6

х2y8

0,0625n8

81/16c2

-8m3 n6

Произведение степеней с разными основаниями

63 = 216

(ab)3

(ab)n

а2

Слайд 16Текст слайда:

Свойства степеней

Разные основания

4. Возведение дроби в степень

Выполните по примеру

Чтобы возвести дробь в степень, можно возвести в эту степень _________________________________________________________________.

Сделайте вывод. Заполните пропуски

числитель и знаменатель

Слайд 17Текст слайда:

Возведение в степень смешанной дроби

Возведите в степень:

Сделайте вывод. Заполните пропуски:

Чтобы возвести смешанную дробь в степень, надо эту дробь перевести в _______
__________ и _________________________________________.

Возведите
в степень:

Что это?

Как это?

Заполните таблицу, используя свойство

неправильную

возвести в степень числитель и знаменатель

Деление степеней с разными основаниями

Слайд 18Текст слайда:

Свойства степеней

Одинаковые основания

Что это?

Как это?

(a n)m =

a n ∙ a m =

Разные основания

Что это?

Как это?

(ab) n =

a n ∙ b n =

a n + m

a n — m

a n m

сложить

вычесть

умножить

каждый
множитель

основания

числитель и
знаменатель

b
возвести в степень

a n ∙ b n

(ab) n

Слайд 19Текст слайда:

Определите к чему относится минус. Впишите соответствующие выражения в таблицу, определите знак :

(-2)4, -а3, (-3х)4, — 24, (- а)3, — (х+2)2

Выполните :
(-2)4 _=____________ — (2х)4 =_____________ ( — 2/5)3 =______________
— (-а)5 =____________ (- (х -1)2)3 = __________ — 1/3 (- 3b2)3 = __________

Определите на какую цифру оканчивается 22011

Сравните:

Скорость света равна 3·108 м/с, расстояние от Земли до Солнца 1,5·1011 м. За какое время пройдет луч света от Солнца до земли?

Знаки в выражениях

Слайд 20Текст слайда:

Одночлены

Выражения, содержащие действия умножения и степени, называются одночленами

2а2, -28(х3у)4, — х, 7аb2 , ½ с, d, (5n)2, ½ , x/2 …

Одночлены могут иметь числовой множитель и буквенную часть.

2 a2

Числовой множ.

Буквенная часть

Числовой множитель называется коэффициентом.

Коэффициенты 1 и – 1 не записываются.

Определите коэффициенты одночленов:

В стандартном виде коэффициент записывается перед буквенной частью, буквенная часть записываются латинскими прописными буквами по алфавиту.

Знак умножения ( · ) не ставится

Слайд 21Текст слайда:

Произведение одночленов

2. Определить знак; (можно определять сначала)

1. Возвести в степень при наличии;

Выполните примеры

0,2а 3(3b) =
(-2)2(4n2) =
(-1/3 c)(-9c2) =
(-2bc)2( b2c)=

3. Умножить коэффициенты ;

4. Умножить буквенную часть.

Помните!

При умножении степеней с одинаковыми основаниями показатели _______________

Выполните действия:

( — 2а)2 ( — 3ab) =
2) ( — 3a2bc)( — 5ab2c)( — 0,4abc2) =

Слайд 22Текст слайда:

Многочлены

Выражения, содержащие сумму одночленов называются ___________________________

2а2 +3, -7х -2y, х2 +3x -1, 7аb2 + a2b , ½ с – 5, (5n)2 — m, a –b +3, (a + b)2

Приведение подобных слагаемых

Одночлены, имеющие одинаковую буквенную часть называются _______________________________

Чтобы сложить подобные слагаемые, надо: ________________________________
_________________________________________________________________________

Пример:

4 а2 + 8 а – 12 а2 +5 а – 3 = (4 – 12)а2 + ( 8 + 5 )а – 3 = — 8а2 +13а – 3

4 а2 + 8 а – 12 а2 + 5 а – 3 = — 8а2 +13а – 3

2. Повторить с другими слагаемыми. Использовать двойную черту и т. д.

1. Подчеркнуть одной чертой первое слагаемое, подчеркнуть подобные, посчитать, записать;

Слайд 23Текст слайда:

2ху2 – 3х2у + 4 ху2 + 6х2у -8 =
6ху2 + 3х2у — 8

2ху2 – 3х2у + 4 ху2 + 6х2у -8 =

2ху2 – 3х2у + 4 ху2 + 6х2у -8

Усвоим алгоритм действия

2ху2 – 3х2у + 4 ху2 + 6х2у -8 = 6ху2

Слайд 24Текст слайда:

6ab – 2a2b – 8ba + 4a2b + 4

Усвоим алгоритм действия

6ab – 2a2b – 8ba + 4a2b + 4 =

Слайд 25Текст слайда:

Упростите выражение:

11х2 + 4х – х2 – 4х =

Сделайте вывод: одинаковые слагаемые, но с разными знаками можно ____________________

11х2 + 4х – х2 – 4х = 10 х2

Упростите выражения, представьте многочлен в стандартном виде:

3х4 + 7х2 – 8х – 4х4 + 3х =

3ab2 +4 a3 – 5a2b – 3a3 – 9b2a =

12a – 8c – 7 + 3c – 12a=

2(n – 2) + 4m2 + 4 (n – 2)=

Слайд 26Текст слайда:

Умножение одночлена на многочлен

Запишите распределительное свойство умножения:

a(b + c) = ___________

Умножьте: 2а( 6а – 5) = __________________

Заполните пропуски:

Чтобы умножить одночлен на многочлен, надо одночлен умножить на _________________________________________

Выполните умножение. Упростите:

— 4х(х2 + 2х -7) =

(2а2b – 4 a) · (- 1,5 ab)=

7(x – y) – 6(2x + 5y)=

Слайд 27Текст слайда:

Раскрытие скобок

Переход от выражения со скобками к выражению без скобок называется раскрытие скобок

Упростите:

4х — (х2 + 2х -7) =

2(0,1а – d) – (3,2a + 7d) =

— 2y – (y2 +4y – 9) – (y2 + 9) =

Слайд 28Текст слайда:

Произведение многочленов

(a + b)(c + d) = ___________

Заполните пропуски:

Чтобы умножить многочлен на многочлен, надо каждое слагаемое одного многочлена умножить на _____________________________________________________

Выполните умножение. Упростите:

( 2- 4х)(2х -7) =

(а + 3)(а – 2)=

(x – y)(х + y) – (x2 + y2)=

+dc

+bc

+bd

на каждое слагаемое другого

4х – 14 – 8х2 + 28х =

– 8х2 + 32х – 14

а2 – 2а + 3а – 6 =

а2 + а – 6

х2 + ху – ух – у2 – х2 – у2 =

— 2у2

Слайд 29Текст слайда:

Для работы с числовыми основаниями нужно знать таблицу степеней

При выполнении действий со степенями, одночленами, многочленами нужно проговаривать операцию

При выполнении действий с минусом помни о знаке

Если минус перед скобкой, то при раскрытии их тяни минус до конца

Слайд 30Текст слайда:

Самоконтроль

Заполните пропуски:

Упростите:

1) 5a5 – 7 a2b + 4 ab2 – 8 ba2 – 9a5 =

2) (а + 3)- 4(а – 2)= 3) x2 — x(4 – x) =

4) (x – y) — (х +3y)(2х – у) – (2×2 +3y2 – 1)=

( 2- 4х)6 __ = 12у — ____; — 2ab( ___- 3b) = — 12 a2b2 + _____

5) 2ab(a -4) – 4(a2b + 2ab) =

Найдите значение выражения: х2 +2х + 18 — (х +6)(3 – 2х) при х = — 3

Найдите сумму значений многочлена х5 – 1,7х3 + 2,5 при х = 21,7 и х = — 21,7

Слайд 31Текст слайда:

Самоконтроль

Решите уравнение:

Упростите:

1) Выполните умножение у = (х -6)(х +2)

2) 3)

4) Возведите в квадрат (а + b)2 =

( 2- 4х)х – 2(х+4) = 12 – 4х2
(0,5х +2)(7х – 0,21) = 0

5) Умножьте скобки (a – b)(a +b) =

Найдите значение выражения:

Решите уравнения: х2 = 4 2х2 = 18

Слайд 32Текст слайда:

Самоконтроль

Найдите у = 4х2 – 1 , если х = — ½ ; х = -1, х = 0; х = 1; х = ½

Поставьте точки на координатную плоскость, соедините точки плавной кривой

Слайд 33Текст слайда:

Справочный материал

________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________

Слайд 34Текст слайда:

Уравнения

Равенство, выполняемое при некоторых значениях переменной называется _____________________

Корнями уравнения называются значения переменной, при которых уравнение обращается в верное _____________________.

Решить уравнение – значит ____________________________________.

Уравнения, имеющие одни и те же корни называются ______________

Свойства равносильности

Если слагаемое перенести из одной части в другую, поменяв его знак, то получится уравнение ________________________________________

Если обе части уравнения умножить или разделить на одно и то же число, не равное нулю, то получится уравнение ____________________ ________________________________________

Одинаковые слагаемые в обеих частях уравнения можно ____________

Слайд 35Текст слайда:

Линейные уравнения

Уравнение вида kx = b, где k и b любые числа называется __________

k — ___________________________________; b – ____________________________

Решение.
Используя второе свойство равносильности разделим обе части на k , получим

Чтобы найти неизвестное, надо ________________________________________
______________________________________________________________________

Х =

Решите уравнения

kx = b

Слайд 36Текст слайда:

Решение уравнений, сводящихся к линейным

неизвестное ____________________

Что это?

Как это?

Это уравнение, содержащее

Проверяйте: поменяли ли знак при переносе, привели ли подобные

Слайд 37Текст слайда:

х – 6х + 1 = 4х – 24 + 16х

Решите уравнение х-2(3х- ½ ) = 4х-8(3-2х)

-5х – 20х = -24 – 1

-25х = — 25

х = 1

-5х + 1 = 20х -24

Усвоим алгоритм действия

Слайд 38Текст слайда:

Теперь усвойте ключевые слова

1. Неизвестные в одну сторону, свободные члены в другую

2. Свободный член разделить на коэффициент при неизвестном

1. Решите уравнение 8х — 1,5 = 3х — 8,7

Выполните пункты, заполните соответствующие строчки.

Поменяйте знак при переносе

Слайд 39Текст слайда:

Возможные ошибки

Не изменены знаки
при переносе

Ошибка в счете

Ошибка при нахождении х:
Потерян минус;
Разделили k на b

36х-4(6х-2)+38=х+3(4-2х)

Решите уравнения:

0,36х – 0,3(0,4х – 1,2) = 0,6

Слайд 40Текст слайда:

Уравнения вида 0x = b и 0х = 0

Решите уравнения:

1. Коэффициент при неизвестном равен нулю. k = 0, b ≠ 0.
Любое число, умноженное на нуль равно нулю.

0∙ х = b Решений нет.

2. Коэффициент при неизвестном и свободный член равны нулю. k = 0, b = 0.

0∙ х = 0, х – любое действительное число.

6(1,2х – 0,5) – 1,3х = 5,9х – 3

28 – 20х = 2х +25 – 22х – 12

Слайд 41Текст слайда:

Уравнения в виде пропорции

Умножить крест на крест

Решите уравнения:

х = _______

Уравнения с дробями

Любое уравнение с дробями целесообразно привести к целому виду.

1. Умножьте обе части уравнения на НОЗ знаменателей

Теперь легко решить уравнение.

Это действие можно записать и выполнить короче.

Слайд 42Текст слайда:

НОЗ = 6

Решите уравнение

По решению запиши в соответствующие строчки пункты алгоритма

2х – 3(х – 1) = 10х + 3х – 12

Слайд 43Текст слайда:

Решите уравнения

Приведите к целому виду, проговаривая пункты алгоритма

5. Решить уравнение

Слайд 44Текст слайда:

Уравнения вида произведение равно нулю

Произведение равно нулю, если хотя бы один из множителей равен нулю, а другой при этом не теряет смысла.

= 0

или

Решите уравнения:

( х – 3 )(2х +5 ) = 0

12х(х – 5 ) = 0

или

Ответ:

или

Ответ:

Уравнения с модулем

│а│ = а ,если а ≥ 0,

│а│ = — а , если а

а по модулю равно самому а ,если а больше или равно нулю; а по модулю равно противоположному а ( — а), если а меньше нуля.

Под а понимается любое выражение, например 2х -3 или х/2 +7 и т. д.

Слайд 45Текст слайда:

Переход от модуля к выражению без модуля называется раскрытием модуля.

Заметим, что │а│ ≥ 0 при любом а! Модуль всегда больше или равен нулю.

Решим уравнение: │х│ = 5
Так как │х│= х или │х│= -х, получим два уравнения
х = 5 или х = — 5 Ответ: ± 5

Решите уравнения:

| х – 3| = 0

12 |1 – 5x | = 0

или

Ответ:

или

Ответ:

3│5 – 2х│ — 4 = 5

или

Ответ:

Слайд 46Текст слайда:

Разложение на множители

Слайд 47Текст слайда:

Разложение на множители

Что это?

Сумма

______________

Слайд 48Текст слайда:

Вынесение общего множителя за скобку

Что это?

Это способ разложения на множители

______________

_____________

Так как a(b + c)

То ab + ac

= ______________

= ___________

Это

Разложение на множители

Слайд 49Текст слайда:

a(b + c)

ab + ac

= ab + ac

= a(b + c)

Разделить каждое слагаемое на общий множитель

_________________________________
_________________________________

______________________

2х(4 -5х) = __________

8х – 10х2 = ___________

Что это?

Как это?

Умножить каждое слагаемое в скобке на множитель перед скобкой

4а(3 +2а2) = __________

с2 (4 -3с) = ___________

12а + 8а2 = ___________

4с2 – 3с3 = ___________

Слайд 50Текст слайда:

Вынесение общего множителя за скобку

Элементы

Что общего в каждом слагаемом?

Общий множитель —

Слайд 51Текст слайда:

3у

Впиши выражения в соответствующие фигуры и выполни разложение

sinx

Слайд 52Текст слайда:

Определение общих множителей

Вид общего множителя: числовой; буквенный; числовой и буквенный; сложный в скобках.

Слайд 53Текст слайда:

Как найти общий множитель?

Общий множитель среди чисел

1. Разложить числа на простые множители;

2. Выписать одинаковые множители;

3. Найти их произведение.

— это наибольший общий делитель (кратное) данных чисел

Для небольших чисел общий множитель можно найти устно:
подобрать общий делитель так, чтобы он был наибольшим

Слайд 54Текст слайда:

12 и 16

15 и 20

Найдите общий множитель, для чего разложите числа на множители.

27 и 18

3·9 и 2·9

Найдите общий множитель. Вынесите общий множитель за скобку.

12х – 16у = __________________ 3) 15 с2 + 20 = __________________
36ab + 48c = _________________ 4) 54 x + 42a = _________________
5) 15b + 36c = __________________ 6) 36y – 72x = __________________

Слайд 55Текст слайда:

Если устно трудно найти общий множитель,
используйте алгоритм

Для разложения используйте признаки делимости сначала на 2, потом на 3, 5 и т. д.

1. Разложить числа на простые множители;

2. Выписать одинаковые множители;

3. Найти их произведение.

Пример:

Справа пишите делитель

Слева пишите результат деления

Найдите наибольший общий множитель:

1) 140 и 84

НОМ = __________________

2) 180 и 135

НОМ = __________________

Слайд 56Текст слайда:

3) 48, 40 и 196

НОМ = __________________

4) 11, 363 и 55

НОМ = __________________

40 = ______________

55 = ______________

Найдите общий множитель. Вынесите общий множитель за скобку.

140х – 84у = __________________ 4) 11 с2 + 55с — 363 = _______________
180a + 135 = _________________ 5) 4·0,85+8·0,075 = _________________
48b +40c+196 = __________________ 6) 12·0,3 – 8·0,4 = __________________
7) 1372 + 137·63 = ________________ 8) 122 – 288 = _____________________

Вывод

Вычисления производить проще, если можно вынести ОМ за скобку!

Слайд 57Текст слайда:

Общий множитель среди букв

одинаковые буквы

в меньшей степени

Это одинаковая буквенная часть в каждом слагаемом в меньшей степени

х, у

ху

Одинаковые буквы

Меньшая степень

Общий множитель

Слайд 58Текст слайда:

вынесения общего множителя

Слайд 59Текст слайда:

4a2 – 3a3b 6x2y – 3xy3

1. Разложите на множители

Запиши операции в соответствующие строчки

4a2 – 3a3b = ______( ______ — _______ 6x2y – 3xy3 = ______( ______ — _______

Слайд 60Текст слайда:

48a3 b2 – 36a2b3 + 30ab3

1. Разложите на множители

Запиши операции в соответствующие строчки

48a3 b2 – 36a2b3 + 30ab3 = ______( ______ — _______ + _______

Слайд 61Текст слайда:

Разложите на множители

6a3b2 — 7a2b = ___________________________________________________
x3 — 7x2y = ______________________________________________________
6(x – 1)3 — 7(x – 1) = ______________________________________________
6y(x – 1)3 — 7y(x – 1)2 = ____________________________________________
15a6b4 + 9 a2b2 – 6a3bc = ___________________________________________

Хочешь выполнять без ошибок? Проговаривай каждую операцию деления!

Слайд 62Текст слайда:

Ключевые слова

48a3 b2 – 36a2b3 + 30ab3 = 6ab2 ( 8a2 – 6ab + 5b)

общий множитель
скобка

Результат деления

Выполните, проговаривая ключевые слова:

20х2у4 — 12х4у2 + 28х3у3 = _______________________________________
9х(х + 3)2 – 36х2(х + 3) = _______________________________________
4cosx – xcos3x = ______________________________________________

Слайд 63Текст слайда:

—

Разложите на множители:

6(а — 1) + b(1 — а) =

Как это?

Выражение имеет скобки с противоположными выражениями.

Что это?

Нужно получить одинаковые скобки.

b(a – 1)

—

6(а – 1)

Чтобы скобки (а – 1) и (1 – а) преобразовать к одинаковому виду, надо __________
_________________________________________________________________________

Вынесение минуса за скобку

Вынесение минуса за скобку – это вынесение общего множителя, равного _______

Помните! 1 как множитель не пишется.

1. ______________________________________________

2. ______________________________________________

Вывод

При вынесении минуса получается выражение __________________________ данному

Слайд 64Текст слайда:

Противоположные выражения

Выражения называются противоположными, если они __________________, но ______________________ по знакам.

2 и ____

а и ____

a — b и — (_____)

-2 и ____

— а и ____

a — b и b_____

Запишите противоположные выражения:

Вынесите минус из подчеркнутого выражения:

Слайд 65Текст слайда:

Чтобы получить противоположное выражение, надо:

2. Поменять плюсы на минусы

3. Поменять минусы на плюсы

4. Поставить минус перед всем выражением,
заключив его в скобки с противоположными
знаками (Вынести минус за скобку)

Поменять знаки у каждого
слагаемого в скобке

6(а — 1) — b(a — 1) =

_____________________________________________

2) 6(а — 1) — b(1 — а) = _______________________________________________

3) 6(а — 1)2 + b(1 — а) = _______________________________________________

Чтобы не делать ошибок,

проговаривайте операцию деления: в 3) «а минус один в квадрате разделить на а минус один, будет а минус один»…

Разложите на множители :

1) 3(х – у)(х + у) – х + у = ____________________________________________________
2) 3(х – у)(х + у) – (х + у)2 = ___________________________________________________
3) (х – у)2 — 3( у — х) – х + у = __________________________________________________

*Разложите на множители :

Слайд 66Текст слайда:

Разложение способом группировки

Группы с общим множителем

Что это?

Выражение не имеет общего множителя (ОМ), но можно создать группы, в которых будут общие множители, при вынесении которых получатся одинаковые скобки

Например, ab + 2a + 3b + 6

Разделим на две группы

Каждая группа содержит ОМ

При вынесении а получим: а(b + 2)

При вынесении 3 получим: 3(b + 2)

Такие выражения можно разложить на множители: надо общий множитель в виде скобки (b + 2) вынести за скобки.

Как это?

Слайд 67Текст слайда:

Запишите пункты алгоритма:

Разложите на множители, решите уравнение :

Вычислите: 139·15 + 18·139 + 15·261 + 18·261 = ______________________________
_________________________________________________________________________

Слайд 68Текст слайда:

Формулы сокращенного умножения

Квадрат суммы

Выполните действие:

(a + b)2 = (a + b)( a + b) = _______________________________
_____________________________________________________

Расставьте по местам:

Квадрат
первого числа

Квадрат
второго числа

Удвоенное
произведение

(a + 2)2 = ___________________________________________

Возведите в квадрат, проговаривая операцию:

Квадрат суммы двух чисел
равен квадрату первого
числа, плюс удвоенное
произведение первого
на вторе, плюс квадрат
второго числа

Слайд 69Текст слайда:

Квадрат разности

Выполните действие:

(a — b)2 = (a — b)( a — b) = _______________________________
_____________________________________________________

Расставьте по местам:

Квадрат
первого числа

Квадрат
второго числа

Удвоенное
произведение

(a — 2)2 = ___________________________________________

Возведите в квадрат, проговаривая операцию:

Квадрат разности двух чисел
равен квадрату первого
числа, минус удвоенное
произведение первого
на вторе, плюс квадрат
второго числа

Слайд 70Текст слайда:

Квадрат суммы, разности

Квадрат суммы, разности двух чисел равен квадрату первого
числа, плюс, минус удвоенное произведение первого
на вторе, плюс квадрат второго числа

Возведите в квадрат:

Не забывать удвоенное произведение !

х2 – 2ху + у2

9а2 + 12ab + 4b2

х2 – 2х + 1

¼ a2 – 2a + 4

9а4 + 12a2 b4 + b8

4х2y2 – 4хy + 1

Слайд 71Текст слайда:

Выполните действия, сделайте вывод:

Сравните: (а – b)2 = _________________________
(b – a)2 = __________________________

Вывод

(a – b)2=

Сравните: ( — a – b )2 = _______________________
(a + b)2 = __________________________

(- a – b)2=

Примените формулу, раскройте скобки:

Решите уравнение:

*Найдите 1/х2 + х2 , если а) 1/х + х = 4: _____________________________________
_________________________________________________________________________
б) 1/х + х = t: _____________________________________________________________
_________________________________________________________________________

Слайд 72Текст слайда:

Разложение по ФСУ

Квадрат суммы (разности)

Многочлен

Произведение

Разложение квадратного трехчлена на множители

Разложите на множители:

Слайд 73Текст слайда:

Стандартный вид квадратного трехчлена

1. Стандартный вид по местам

1 место: ________________________ ;

2 место: _________________________;

3 место: ________________________;

Квадратный трехчлен

Квадрат
первого числа

Квадрат
второго числа

Удвоенное
произведение

1 место

3 место

2 место

a2 + 4b2 – 4ab = __________________________________

квадрат первого числа

удвоенное произведение

квадрат второго числа

а2

-4аb

+4b2

Слайд 74Текст слайда:

Расставьте слагаемые по местам:

6x – x2 – 9 = ________________________________________________
1 + 4а2 + 4а = _______________________________________________

Стандартный вид квадратного трехчлена

2. Стандартный вид по знакам

+ + +

+ — +

или

Слайд 75Текст слайда:

Приведите в стандартный вид:

Разложение квадратного трехчлена на множители

Разложите на множители x2 — 6х + 9, для чего впишите в квадратики соответствующие элементы: сначала 1-ое число а, потом 2-ое b

Первое число а = _____

Второе число b = _________

Проверьте удвоенное произведение, запишите в виде (а ± b)2

x2 — 6х + 9 = ______________________

(x – 3)2

Слайд 76Текст слайда:

разложения по квадрату суммы или разности

По квадрату первого числа найти число;

По квадрату второго числа найти число;

Записать выражение в виде (a ± b)2.

Проверить удвоенное произведение;

Привести выражение в стандартный вид;

Составьте

Слайд 77Текст слайда:

Используя трафарет, разложите на множители:

2ab

= (a + b)

36m2 – 12mn + n2 = ___________________________________________________
x4 + 16 + 8×2 = _______________________________________________________
— 25a2 + 10ab – b2 = ___________________________________________________
½ y + 1 + ¼ y2 = ______________________________________________________

*Решите уравнения: 16х2 – 8х + 1 = 0 __________________________________
100 + 20х + х2 = 0 _______________________________________________________

*Выведите формулу ( a + b)3: ___________________________________________
______________________________________________________________________

x = ¼

x = — 10

Слайд 78Текст слайда:

Формулы сокращенного умножения

Разность квадратов

= (a — b)(a + b)

разность

сумма

Разность квадратов двух чисел равна произведению разности
чисел на их сумму

Произведение разности чисел на их сумму равно
разности квадратов двух чисел

(a — b)(a + b) =

Слайд 79Текст слайда:

Формулы сокращенного умножения

Разность квадратов

____________________________________________________________

Что это?

Как это?

Выполните умножение:

(х – 1)(х + 1) = ____________________ 6) (x – 1)( -x – 1) =_______________________
(2a – b)(2a + b) = __________________ 7) ( ¼ x + 2)(¼ x – 2)= ____________________
(c2 – d)(c2 + d) = ___________________ 8) 48 · 52 = _____________________________
(n + m)(m – n) = ___________________ 9) 2011 · 1989 = ________________________
(0,2 – a4)(0,2 + a4 ) = ________________ __________________________

Решите уравнения:

(х – 1)(х + 1) = х2 – 2(х – 2) __________________________________________________
____________________________________________________________________________
(3х + 1)(3х + 1) – (3х – 2)(2 + 3х) = 17_________________________________________
____________________________________________________________________________

Слайд 80Текст слайда:

Разложение на множители

Разность квадратов

Разложите на множители:

Как это?

Что это?

___________________________________________________________

____________________________________________________________

Решите уравнения, вычислите:

х2 – 4= 0__________________________________________________________________
9x 2 – 4 = 0 _____________________________________________________________
542 – 442 = ________________________________________________________________
252 – 122 = ________________________________________________________________

Слайд 81Текст слайда:

Сумма, разность кубов

Сумма, разность кубов двух чисел равна произведению суммы,
разности чисел на неполный квадрат разности, суммы

= (a + b)(a — ab + b )

= (a — b)(a + ab + b )

Разложите на множители, умножьте :

Слайд 82Текст слайда:

Общий алгоритм разложения на множители

Виды группровок

а) группировка с общим множителем

14am – 7an + 8bm – 4bn = __________________________________________________

б) группировка с общим множителем и ФСУ

х2 – у2 – 2х – 2у =__________________________________________________________

в) группировка с ФСУ

х2 + 2ху + у2 – 1 =__________________________________________________________

7а(2т – n) + 4b(2m – n) = (2m – n)(7a + 4b)

(x – y)(x + y) – 2(x – y) = (x – y)(x + y – 2)

(x + y)2 – 1 = (x + y – 1)(x + y + 1)

Слайд 83Текст слайда:

Разложите на множители:

3(x2 – 1) = 3(x – 1)(x + 1)

2(a2 – 2ay + y2) = 2(a – y)2

6(x3 + 1) = 6(x + 1)(x2 — 2 + 1)

7m(n2 – 4mn + 4m2) = 7m(n – 2m)2

(5x – 4)2

(3n – 2 – 1)(3n – 2 + 1) = (3n – 3)(3n – 1) = 3(n – 1)(3n – 1)

(a2 – 1)(a2 + 1) = (a – 1)(a + 1)(a2 + 1)

Слайд 84Текст слайда:

Пунктов 1,2 — нет. Группируем: с ОМ – нет; с ФСУ и ОМ – да

да

6(4х2 – 12х + 9 – у2)

ФСУ

= 6((2х – 3)2 – у2) = 6(2х – 3 – у)(2х – 3 + у)

да

= (х – 1 – (х2 +1)( х – 1 + х2 + 2)

= (х – х2 — 2)( х + х2 + 3)

Слайд 85Текст слайда:

да

4х (х – 1)( х — 1 + 2х) = 4х (х – 1)( 3х — 1)

ФСУ

(с – 1)2 — ( d + х)2 = (c – 1 – (d + x))( c — 1 + d + x)

= (c – 1 – d — x)( c — 1 + d + x)

sinx(2sinx – 1)

= x2 – x + 4x – 4

— x

+4 x

= x2 – x + 4x – 4

= x(x – 1) + 4(x – 1)

= (x – 1)(x + 4)

да

Слайд 86Текст слайда:

Алгебраические преобразования

Что это?

Как это?

Применение алгебраических преобразований

Что это?

Как это?

Слайд 87Текст слайда:

Алгебраические преобразования

Алгебраические преобразования применяются для: 1) приведения выражений к более простому виду; 2) разложению на множители 3)приведению уравнений к решаемому виду;

Решение уравнений Уравнение вида произведение равно нулю

Произведение равно нулю, если ___________________________________________
_________________________________________________________________________

Решите уравнения:

Разложите на множители

х2 — х + 1 ≠ 0

Разложите на множители

Можно раскрыть скобки

Слайд 88Текст слайда:

Алгебраические преобразования

Алгебраические преобразования применяются для: 1) приведения выражений к более простому виду; 2) разложению на множители 3)приведению уравнений к решаемому виду; 4) упрощению при вычислениях; 5) сокращения дробей и другое

Вычисления

Вычислите:

Сокращение дробей

Сократите дробь:

Слайд 89Текст слайда:

Самоконтроль

Упростите, раскройте скобки, решите уравнение:

12х (3х2 – 4) – 5 (х3 – 4х) = 0 _________________________________________________
(х – 3)(х +2) – (4 – х)(х + 1) = 0_______________________________________________
____________________________________________________________________________
(х -4)2 + 12х = х2 + 4х _______________________________________________________
____________________________________________________________________________

12 х2у – 180 ху2 – 30 х 3у3 = _________________________________________________
2) 12а(а –b) – 6b(a – b) = _______________________________________________________
3) x2(y – 7) – y2(7 – y) = ________________________________________________________
4) 3(a – 1)2 – 6a(1 – a) = _______________________________________________________

Вынесите общий множитель:

Разложите на множители:

12 х2у – 180 ху2 – 30 х 3у3 = __________________________________________________
2) 12а(а –b) – 6b(a – b) = _______________________________________________________
3) x2(y – 7) – y2(7 – y) = ________________________________________________________
4) 3(a – 1)2 – 6a(1 – a) = _______________________________________________________

Слайд 90Текст слайда:

Решите уравнение:

х2 – 2х + 1 = 0 = ___________________________________________________________
х2 – 64 = 0 ________________________________________________________________
х2 – 6х = 0 ________________________________________________________________
4) (t – 4)2 – 2(t – 4) = 0 ________________________________________________________
5) у4 – 2у3 – у 2 + 2у =0 ________________________________________________________
6) 2х – 3(х2 + х) = 6 – 5х – 3х2 ___________________________________________________________________________

1) 322 – 122 = ______________________________________________________________
2) 7∙ 28 – 19∙ 72 + 28∙ 72 – 7∙ 19 = _______________________________________________
3) 982 = ____________________________________________________________________
___________________________________________________________

Вычислите:

* Сократите дробь:

_________________________________________________________

__________________________________________________________

Самоконтроль

Слайд 91Текст слайда:

Алгебра

7 класс

Учени ____ 7 ____ класса
_______________________________
_______________________________

Часть 1

Слайд 92Текст слайда:

Алгебра

7 класс

Учени ____ 7 ____ класса
_______________________________
_______________________________

Часть 2

Действия со степенями

org/Person»> Салахова Гульнара Мансуровна

Разделы: Математика

Тип урока: урок обобщения и систематизации знаний

Цели:

обучающие – повторить определение степени, правила умножения и деления степеней, возведения степени в степень, закрепить умения решения примеров, содержащих степени,
развивающие – развитие логического мышления учащихся, интереса к изучаемому материалу,
воспитывающие – воспитание ответственного отношения к учебе, культуры общения, чувства коллективизма.

Оборудование: компьютер, мультимедийный проектор, интерактивная доска, презентация “Степени” для устного счета, карточки с заданиями, раздаточный материал.

План урока:

Организационный момент.
Повторение правил
Устный счет.
Историческая справка.
Работа у доски.
Физкультминутка.
Работа на интерактивной доске.
Самостоятельная работа.
Домашнее задание.
Подведение итогов урока.

Ход урока

I. Организационный момент

Сообщение темы и целей урока.

На предыдущих уроках вы открыли для себя удивительный мир степеней, научились умножать и делить степени, возводить их в степень. Сегодня мы должны закрепить полученные знания при решении примеров.

II. Повторение правил (устно)

Дайте определение степени с натуральным показателем? (Степенью числа а с натуральным показателем, большим 1, называется произведение n множителей, каждый из которых равен а.)
Как умножить две степени? (Чтобы умножить степени с одинаковыми основаниями, надо основание оставить тем же, а показатели сложить. )
Как разделить степень на степень? (Чтобы разделить степени с одинаковыми основаниями, надо основание оставить тем же, а показатели вычесть.)
Как возвести произведение в степень? (Чтобы возвести произведение в степень, надо каждый множитель возвести в эту степень)
Как возвести степень в степень? (Чтобы возвести степень в степень, надо основание оставить тем же, а показатели перемножить)

III. Устный счет (по мультимедиа)

IV. Историческая справка

Все задачи из папируса Ахмеса, который записан около 1650 года до н. э. связаны с практикой строительства, размежеванием земельных наделов и т. п. Задачи сгруппированы по тематике. По преимуществу это задачи на нахождение площадей треугольника, четырёхугольников и круга, разнообразные действия с целыми числами и дробями, пропорциональное деление, нахождение отношений, здесь присутствует и возведение в разные степени, решение уравнений первой и второй степени с одним неизвестным.

Полностью отсутствуют какие бы то ни было объяснения или доказательства. Искомый результат либо даётся прямо, либо приводится краткий алгоритм его вычисления. Такой способ изложения, типичный для науки стран древнего Востока, наводит на мысль о том, что математика там развивалась путём обобщений и догадок, не образующих никакой общей теории. Тем не менее, в папирусе есть целый ряд свидетельств того, что египетские математики умели извлекать корни и возводить в степень, решать уравнения, и даже владели зачатками алгебры.

V. Работа у доски

Найдите значение выражения рациональным способом:

Вычислите значение выражения:

VI. Физкультминутка

для глаз
для шеи
для рук
для туловища
для ног

VII. Решение задач (с показом на интерактивной доске)

Является ли корень уравнения положительным числом?

а) 3x + (-0,1)⁷ = (-0,496)⁴ (x > 0)

б) (10,381)⁵ = (-0,012)³ — 2x (x < 0)

VIII. Самостоятельная работа

IX. Домашнее задание

№ 580,581,582

Х. Подведение итогов урока

Анализ результатов, объявление оценок.

Полученные знания о степенях мы будем применять при решении уравнений, задач в старших классах, также они часто встречаются в ЕГЭ.

1.07.2010

Свойства степени с одинаковыми основаниями.

Понятие степени в математике вводится еще в 7 классе на уроке алгебры. И в дальнейшем на протяжении всего курса изучения математики это понятие активно используется в различных своих видах. Степени — достаточно трудная тема, требующая запоминания значений и умения правильно и быстро сосчитать. Для более быстрой и качественной работы со степенями математики придумали свойства степени. Они помогают сократить большие вычисления, преобразовать огромный пример в одно число в какой-либо степени. Свойств не так уж и много, и все они легко запоминаются и применяются на практике. Поэтому в статье рассмотрены основные свойства степени, а также то, где они применяются.

Свойства степени

Мы рассмотрим 12 свойств степени, в том числе и свойства степеней с одинаковыми основаниями, и к каждому свойству приведем пример. Каждое из этих свойств поможет вам быстрее решать задания со степенями, а так же спасет вас от многочисленных вычислительных ошибок.

1-е свойство.

а⁰= 1

Про это свойство многие очень часто забывают, делают ошибки, представляя число в нулевой степени как ноль.

2-е свойство.

а¹ = а

3-е свойство.

аⁿ * a^m = a^(n+m)

Нужно помнить, что это свойство можно применять только при произведении чисел, при сумме оно не работает! И нельзя забывать, что это, и следующее, свойства применяются только к степеням с одинаковыми основаниями.

4-е свойство.

aⁿ/a^m = a^(n-m)

Если в знаменателе число возведено в отрицательную степень, то при вычитании степень знаменателя берется в скобки для правильной замены знака при дальнейших вычислениях.

Свойство работает только при делении, при вычитании не применяется!

5-е свойство.

(aⁿ)^m = a^(n*m)

6-е свойство.

a^-n = 1/aⁿ

Это свойство можно применить и в обратную сторону. Единица деленная на число в какой-то степени есть это число в минусовой степени.

7-е свойство.

(a*b)^m = a^m * b^m

Это свойство нельзя применять к сумме и разности! При возведении в степень суммы или разности используются формулы сокращенного умножения, а не свойства степени.

8-е свойство.

(a/b)ⁿ = aⁿ/bⁿ

9-е свойство.

а^½ = √а

Это свойство работает для любой дробной степени с числителем, равным единице, формула будет та же, только степень корня будет меняться в зависимости от знаменателя степени.

Также это свойство часто используют в обратном порядке. Корень любой степени из числа можно представить, как это число в степени единица деленная на степень корня. Это свойство очень полезно в случаях, если корень из числа не извлекается.

10-е свойство.

(√а)² = а

Это свойство работает не только с квадратным корнем и второй степенью. Если степень корня и степень, в которую возводят этот корень, совпадают, то ответом будет подкоренное выражение.

11-е свойство.

ⁿ √aⁿ = a

Это свойство нужно уметь вовремя увидеть при решении, чтобы избавить себя от огромных вычислений.

12-е свойство.

a^m/n = ⁿ √a^m

Каждое из этих свойств не раз встретится вам в заданиях, оно может быть дано в чистом виде, а может требовать некоторых преобразований и применения других формул. Поэтому для правильного решения мало знать только свойства, нужно практиковаться и подключать остальные математические знания.

Применение степеней и их свойств

Они активно применяются в алгебре и геометрии. Степени в математике имеют отдельное, важное место. С их помощью решаются показательные уравнения и неравенства, а так же степенями часто усложняют уравнения и примеры, относящиеся к другим разделам математики. Степени помогают избежать больших и долгих расчетов, степени легче сокращать и вычислять. Но для работы с большими степенями, либо со степенями больших чисел, нужно знать не только свойства степени, а грамотно работать и с основаниями, уметь их разложить, чтобы облегчить себе задачу. Для удобства следует знать еще и значение чисел, возведенных в степень. Это сократит ваше время при решении, исключив необходимость долгих вычислений.

Особую роль понятие степени играет в логарифмах. Так как логарифм, по сути своей, и есть степень числа.

Формулы сокращенного умножения — еще один пример использования степеней. В них нельзя применять свойства степеней, они раскладываются по особым правилам, но в каждой формуле сокращенного умножения неизменно присутствуют степени.

Так же степени активно используются в физике и информатике. Все переводы в систему СИ производятся с помощью степеней, а в дальнейшем при решении задач применяются свойства степени. В информатике активно используются степени двойки, для удобства счета и упрощения восприятия чисел. Дальнейшие расчеты по переводам единиц измерения или же расчеты задач, так же, как и в физике, происходят с использованием свойств степени.

Еще степени очень полезны в астрономии, там редко можно встретить применение свойств степени, но сами степени активно используются для сокращения записи различных величин и расстояний.

Степени применяют и в обычной жизни, при расчетах площадей, объемов, расстояний.

С помощью степеней записывают очень большие и очень маленькие величины в любых сферах науки.

Показательные уравнения и неравенства

Особое место свойства степени занимают именно в показательных уравнениях и неравенствах. Эти задания очень часто встречаются, как в школьном курсе, так и на экзаменах. Все они решаются за счет применения свойств степени. Неизвестное всегда находится в самой степени, поэтому зная все свойства, решить такое уравнение или неравенство не составит труда.

Справедливость против равенства и других определений расовой справедливости

Обновлено 14 апреля 2021 г. и первоначально опубликовано 24 августа 2020 г. Фондом Энни Э. Кейси

Часто разговоры на тему расы срываются, потому что люди используют одни и те же термины по-разному. Одна из задач эффективного общения о расе состоит в том, чтобы перевести людей от узкого и индивидуального определения расизма к более всеобъемлющему и системному пониманию.

Чтобы осветить расизм, нам нужно «назвать его, сформулировать и объяснить».

Создание общего языка для представления данных, описания условий и результатов и выявления основных причин неравенства выполняет важную функцию. Общий язык создает повествование, которое упрощает передачу приверженности расовому равенству как внутри организации, так и за ее пределами, а также создает платформу для скоординированной работы для достижения справедливых результатов.

Узнайте, как превратить язык в справедливые результаты:

Загрузить Руководство по расовому равенству и интеграции

Ниже приведены определения основных концепций, которые могут помочь группам разработать общий язык для расового равенства и интеграции:

Определения и основные концепции

Справедливость

Справедливость определяется как «состояние, качество или идеал справедливости, беспристрастности и честности». Понятие справедливости является синонимом честности и справедливости. Полезно думать о справедливости не просто как о желаемом положении дел или высокой ценности. Чтобы достичь и поддерживать равенство, его необходимо рассматривать как структурную и системную концепцию.

Справедливость и равенство

Справедливость подразумевает попытки понять и дать людям то, что им нужно для полноценной и здоровой жизни. Равенство, напротив, направлено на то, чтобы все получали одинаковые вещи для полноценной и здоровой жизни. Как и равенство, равенство направлено на продвижение честности и справедливости, но оно может работать только в том случае, если все начинают с одного и того же и нуждаются в одних и тех же вещах.

Системная справедливость

Системная справедливость — это сложная комбинация взаимосвязанных элементов, сознательно разработанных для создания, поддержки и поддержания социальной справедливости. Это динамический процесс, который усиливает и воспроизводит справедливые идеи, власть, ресурсы, стратегии, условия, привычки и результаты.

Например, сообщества со значительной долей заключенных жителей экономически обременены и, следовательно, не имеют ресурсов для надлежащей поддержки семей. Общий приговор предлагает систематические и справедливые предложения для поддержки детей и семей во время и после лишения свободы родителей.

Узнайте, как Фонд Энни Э. Кейси помогает сообществам Саутсайда в Атланте ликвидировать системные барьеры для цветных людей в Изменение шансов: прогресс и обещание в Атланте .

Включение

Включение — это действие или состояние включения или включения в группу или структуру. Инклюзивность подразумевает не просто разнообразие и численное представление, а подлинное и уполномоченное участие, а также подлинное чувство принадлежности.

Узнайте, что нужно для создания культуры инклюзивности на рабочем месте, из Продвижение миссии: инструменты для справедливости, разнообразия и инклюзивности .

Расовая справедливость

Расовая справедливость — это систематическое справедливое обращение с людьми всех рас, результатом которого являются равные возможности и результаты для всех. Все люди могут полностью реализовать свой потенциал в жизни, независимо от расы, этнической принадлежности или сообщества, в котором они живут.

Структура «расовой справедливости» может переместить нас от реактивной позиции к более мощному, упреждающему и даже превентивному подходу. Узнайте о важности развития лидерства для расовой справедливости и о том, как развивать и поддерживать лидеров, которые вносят свой вклад в движение в Лидерство и раса .

Раса

Раса – это социально созданная система классификации людей, в значительной степени основанная на наблюдаемых физических характеристиках (фенотипах), таких как цвет кожи и происхождение. Нет никакой научной основы или заметного различия между расовыми категориями.

Идеология расы укоренилась в нашей идентичности, институтах и культуре и используется как основа для дискриминации и доминирования. Тем, кто поддерживает расовую справедливость, может быть трудно даже начать искренний, подлинный разговор о расе.

Расизм

Понятие расизма широко рассматривается как простое личное предубеждение, но на самом деле это сложная система расовых иерархий и неравенств. На микроуровне расизма, или на индивидуальном уровне, находятся интернализованный и межличностный расизм. На макроуровне расизма мы смотрим не только на отдельных людей, но и на более широкую динамику, включая институциональный и структурный расизм.

Внутренний расизм

Внутренний расизм описывает частные расовые убеждения, которых придерживаются люди и внутри них. То, как мы усваиваем социальные сообщения о расе и принимаем их как личные убеждения, предубеждения и предубеждения, находится в сфере внутреннего расизма.

Для цветных людей внутреннее угнетение может включать веру в негативные сообщения о себе или своей расовой группе. Для белых людей внутренние привилегии могут включать в себя чувство превосходства и права или наличие негативных убеждений в отношении цветных людей.

Межличностный расизм

Межличностный расизм — это то, как наши личные представления о расе становятся достоянием общественности, когда мы взаимодействуем с другими. Когда мы действуем в соответствии со своими предубеждениями или бессознательными предубеждениями — намеренно, явно, вербально или нет — мы вступаем в межличностный расизм. Межличностный расизм также может быть преднамеренным и открытым, принимая форму фанатизма, разжигания ненависти или расового насилия.

Институциональный расизм

Институциональный расизм — это расовое неравенство в институтах и системах власти, таких как места работы, государственные учреждения и социальные службы. Это может принимать форму несправедливой политики и практики, дискриминационного обращения и неравных возможностей и результатов.

Школьная система, в которой цветные люди концентрируются в наиболее переполненных школах с ограниченными ресурсами и наименее квалифицированными учителями по сравнению с образовательными возможностями белых учащихся, является примером институционального расизма.

Структурный расизм

Структурный расизм (или структурная расизация) — это расовые предубеждения в институтах и обществе. В нем описывается кумулятивный и усугубляющий эффект множества факторов, которые систематически отдают предпочтение белым людям и ставят в невыгодное положение цветных.

Поскольку слово «расизм» часто понимается как сознательное убеждение, «расизация» может быть лучшим способом описать процесс, который не требует преднамеренности. Эксперт по расовому равенству Джон А. Пауэлл пишет:

««Расизация» означает процесс, а не статическое событие. Это подчеркивает изменчивый и динамичный характер расы… «Структурная расизация» — это набор процессов, которые могут порождать неравенство или ухудшать результаты жизни без каких-либо расистских акторов».

Узнайте больше о структурном расизме и его значении для построения сообщества и развития молодежи. Вы также можете подписаться на наши информационные бюллетени по изменению сообщества и процветанию по телефону 25 ^® для получения последних данных, отчетов и новостей по этим темам.

Системная расизация

Системная расизация описывает динамическую систему, которая производит и воспроизводит расовые идеологии, идентичности и неравенства. Системная расизация — это хорошо институционализированная модель дискриминации, которая затрагивает основные политические, экономические и социальные организации в обществе.

Общественное внимание к расизму, как правило, сосредоточено на симптомах (таких как расистское оскорбление или преувеличение чернокожих женщин и девочек отдельным лицом или группой), а не на системе расового неравенства.

Расовые привилегии и расовое угнетение

Подобно двум сторонам одной медали, расовые привилегии описывают расовые преимущества и предпочтительное обращение на основе цвета кожи, в то время как расовое угнетение относится к расовым недостаткам, дискриминации и эксплуатации по цвету кожи.

Продолжайте узнавать о расовом равенстве и инклюзивности

Фонд Энни Э. Кейси предлагает различные отчеты и ресурсы, помогающие продвигать расовое равенство и инклюзивность в Америке. Изучите приведенные ниже ресурсы и подпишитесь на наши информационные бюллетени, чтобы узнать больше и помочь продвигать равенство и инклюзивность в вашей жизни:

Изучите 7 шагов по продвижению и внедрению расовой справедливости и инклюзивности в вашей организации в Руководстве по обеспечению расовой справедливости и инклюзивности .
Узнайте об институциональном расизме и о том, как развивать и поддерживать лидерство, которое способствует расовой справедливости, в Лидерство и раса .
Узнайте о детях, живущих в районах с высоким уровнем бедности по всей стране, и о рисках концентрированной бедности для детей в Дети, живущие в районах с высоким уровнем бедности и низкими возможностями .
Узнайте, как требования к работе изменились с течением времени, и какие усилия предпринимаются, чтобы помочь работникам с низким доходом добиться большей экономической стабильности в Принятие мер: позиционирование работников с низким доходом для достижения успеха в изменяющейся экономике .
Узнайте о предубеждении взросления, стереотипах, обычно применяемых к чернокожим женщинам и девочкам, и о том, как к чернокожим ученицам относятся иначе, чем к их белым сверстникам, в Слушая чернокожих женщин и девочек: жизненный опыт предубеждения взросления .

4 вида власти: Над чем власть; власть с; сила и сила внутри?

(Фото: Pixabay)

Когда я впервые начал работать молодежным работником в 1991 году, я работал в центре временного размещения для бездомных молодых людей. Я действительно боролся с властью, так как только что получил степень по социальному обеспечению, в которой особое внимание уделялось «самоопределению клиента». Мне было очень некомфортно в родительской роли, когда я должен был принимать решения о том, что молодые люди могут или не могут делать, где я отвечал за управление поведением и где я должен был быть готов устанавливать ограничения.

У меня была реальная власть, и я чувствовал себя очень неловко по этому поводу, тем более, что я видел множество примеров использования власти довольно принудительным, если не оскорбительным образом. Мне пришлось научиться тому, как быть у власти, что соответствовало бы моей философии и подходу.

У меня была власть над жителями, но мне нужно было понять, что это не определяло отношения в целом, и были и другие виды власти, которые также были важны, и я мог развивать их.

Ряд авторов различают четыре вида мощности ^[1-3] .

Власть над
Мощность с
Мощность до
Мощность в пределах

Власть над

Власть над тем, как чаще всего понимается власть ^{[1, 2]} . Этот тип власти построен на силе, принуждении, господстве и контроле ^{[1, 4]} , и мотивируется в основном страхом ^[4] . Эта форма власти основана на вере в то, что власть — это ограниченный ресурс, которым могут владеть люди, и что у одних она есть, а у других ее нет.

Starhawk ^[4] утверждает, что сила, которая позволяет одному человеку или группе принимать решения, влияющие на других, и брать под свой контроль, в конечном итоге поддерживает власть.

Он может править с помощью физического оружия или путем управления ресурсами, необходимыми нам для жизни: деньгами, едой, медицинской помощью или более тонкими ресурсами: информацией, одобрением, любовью. Мы так привыкли к власти над, так пропитаны ее языком и ее скрытыми угрозами, что часто осознаем ее функционирование только тогда, когда видим ее крайние проявления ^[4] (стр. 9).

Другие формы власти признают, что власть не принадлежит отдельным лицам, а является динамикой, присутствующей во всех отношениях ^[5] . Как предлагает Starhawk (1990):

Власть никогда не бывает статичной, ибо власть — это не то, что мы можем удерживать или хранить, это движение, отношения, баланс, текучесть и переменчивость. Власть, которой один человек может обладать над другим, зависит от множества внешних факторов и тонких соглашений (стр. 268).

Сила с

Сила с — это общая сила, которая вырастает из сотрудничества и отношений. Он основан на уважении, взаимной поддержке, разделении власти, солидарности, влиянии, расширении прав и возможностей и совместном принятии решений ^{[1, 2, 4, 5, 6]} . Власть с связана с «социальной властью, влиянием, которым мы обладаем среди равных» ^[4] (стр. 9). Сила может помочь навести мосты внутри групп (например, семьи, организации, движения за социальные изменения) или через различия (например, пол, культура, класс) ^{[1, 2]} . Вместо господства и контроля власть ведет к коллективным действиям и способности действовать вместе ^[3] .

Power to

Power to относится к «производительному или порождающему потенциалу власти и новым возможностям или действиям, которые могут быть созданы без использования отношений господства» ^[2] (стр. 57). Он построен на «уникальном потенциале каждого человека для формирования своей жизни и мира» ^[1] (стр. 45). Это сила изменить ситуацию, создать что-то новое или достичь цели.

Внутренняя сила

Внутренняя сила связана с «чувством собственного достоинства и самопознанием человека; оно включает в себя способность признавать индивидуальные различия при уважении других» ^[1] (стр. 45). Внутренняя сила включает в себя людей, обладающих чувством собственного достоинства и собственной значимости ^[2] . Сила внутри позволяет людям осознать свою «силу для» и «силу с помощью» и поверить, что они могут изменить ситуацию ^[1] .

Работая с семьями и сообществами, мы хотим взращивать силу в себе, силу и силу внутри, а не действовать с позиции власти над собой. Наша цель должна состоять не в том, чтобы максимизировать нашу власть над другими людьми, а в том, чтобы

Чтобы создать условия для совместного использования энергии. Цель состоит в том, чтобы создать условия, в которых возможность каждого человека осуществлять власть максимально возрастает в контексте более крупного сообщества ^[7] (стр. 21).

Если вам понравился этот пост , пожалуйста, подпишитесь на мой блог , и вы, возможно, захотите посмотреть:

Практика, основанная на мощности и сильных сторонах
Принципы ненасилия
Ненасилие как основа для практики работы с молодежью
Что такое авторитарный, разрешительный, невовлеченный и авторитарный стили воспитания ?
Что такое сильные стороны?
Семь принципов подхода к работе с группами, основанного на сильных сторонах

Если вы обнаружите какие-либо проблемы с блогом (например, неработающие ссылки или опечатки), я буду рад узнать о них. Вы можете либо добавить комментарий ниже, либо связаться со мной через страницу контактов.

Ссылки

Вене Класен, Л., и Миллер, В. (2007). Новое переплетение власти, людей и политики: руководство по защите интересов и участию граждан . Уорикшир: Издательство практических действий. Глава 3 о власти и расширении прав и возможностей доступна по адресу https://justassociates.org/en/resources/new-weave-power-people-politics-action-guide-advocacy-and-citizen-participation
Мэти, А., Кэмерон, Дж., и Гибсон, К. (2017). Развитие на основе активов и под руководством граждан: использование линзы дифрагированной силы для анализа возможностей и проблем. Progress in Development Studies, 17 (1), 1-13. doi: 10.1177/1464993416674302 Доступно по адресу http://journals.sagepub.com/doi/abs/10.1177/1464993416674302
Хунджан, Р., и Кеофилавон, С. (2010). Власть и перемены . Файф: Фонд Карнеги Великобритании. Доступно по адресу https://www.carnegieuktrust.org.uk/publications/power-and-making-change-happen/
Звездный ястреб. (1990). Правда или действие: встреча с силой, властью и тайной . Сан-Франциско: HarperSanFrancisco.
Мейердинг, Дж. (1982). Возвращение к ненасилию: некоторые мысли для женщин-феминисток, которые раньше были ненасильственными, и наоборот. В П. Макалистер (ред.), Переплетение паутины жизни: феминизм и ненасилие . Филадельфия: Издательство Нового Общества.
Бергер, Б.К. (2005). Власть над, власть с и власть над отношениями: критические размышления о связях с общественностью, доминирующей коалиции и активности. Журнал исследований по связям с общественностью, 17 (1), 5-28. doi: 10.1207/s1532754xjprr1701_3 Доступно по адресу https://doi.org/10.1207/s1532754xjprr1701_3
Брюн С. и Рэйман П. (ред.). (1979). Ненасильственные действия и социальные изменения . Нью-Йорк: Irvington Publishers.

Нравится:

Нравится Загрузка…

Эта запись была опубликована в Семья и воспитание детей, Работа с сообществами с метками Для студентов, Ненасилие, Власть, Что такое, Работа с сообществами, Работа с семьями, Работа с группами. Добавьте постоянную ссылку в закладки.

Кодекс поведения сотрудников правоохранительных органов

Статья 1

Должностные лица по поддержанию правопорядка должны всегда выполнять возложенные на них законом обязанности, служа обществу и защищая всех лиц от противоправных действий, в соответствии с высокой степенью ответственности, требуемой их профессией.

Комментарий:

Термин «должностные лица по поддержанию правопорядка» включает всех должностных лиц правоохранительных органов, независимо от того, назначены они или избраны, которые осуществляют полицейские полномочия, особенно полномочия арестовывать или задерживать.
В странах, где полицейские полномочия осуществляются военными властями, независимо от того, одеты они в форму или нет, или силами государственной безопасности, определение должностных лиц по поддержанию правопорядка должно рассматриваться как включающее офицеров таких служб.
Услуги обществу включают в себя, в частности, оказание услуг помощи тем членам общества, которые по причинам личных, экономических, социальных или других чрезвычайных ситуаций нуждаются в немедленной помощи.
Это положение предназначено для охвата не только всех насильственных, хищнических и вредоносных действий, но и распространяется на весь спектр запретов в соответствии с уголовными законами. Он распространяется на поведение лиц, не способных нести уголовную ответственность.

Статья 2

При исполнении своих обязанностей сотрудники правоохранительных органов уважают и защищают человеческое достоинство, а также поддерживают и защищают права человека всех лиц.

Комментарий:

Указанные права человека определены и защищены национальным и международным законодательством. К числу соответствующих международных документов относятся Всеобщая декларация прав человека, Международный пакт о гражданских и политических правах, Декларация о защите всех лиц от пыток и других жестоких, бесчеловечных или унижающих достоинство видов обращения и наказания, Декларация Организации Объединенных Наций о ликвидации всех форм расовой дискриминации, Международной конвенции о ликвидации всех форм расовой дискриминации, Международной конвенции о борьбе с преступлением апартеида и наказании за него, Конвенции о предупреждении преступления геноцида и наказании за него, Минимальные стандартные правила обращения с заключенными и Венская конвенция о консульских сношениях.
Национальные комментарии к этому положению должны указывать региональные или национальные положения, определяющие и защищающие эти права.

Статья 3

Должностные лица по поддержанию правопорядка могут применять силу только в случае крайней необходимости и в объеме, необходимом для выполнения их обязанностей.

Комментарий:

В этом положении подчеркивается, что применение силы сотрудниками правоохранительных органов должно носить исключительный характер; хотя это подразумевает, что должностные лица по поддержанию правопорядка могут быть уполномочены применять силу, если это разумно необходимо в данных обстоятельствах для предотвращения преступления или для осуществления или оказания помощи в законном аресте правонарушителей или подозреваемых правонарушителей, применение силы, выходящей за рамки этого, не допускается.
Национальное законодательство обычно ограничивает применение силы сотрудниками правоохранительных органов в соответствии с принципом соразмерности. Следует понимать, что такие национальные принципы пропорциональности должны соблюдаться при толковании этого положения. Ни в коем случае это положение не должно толковаться как санкционирующее применение силы, несоразмерной преследуемой законной цели.
Применение огнестрельного оружия считается крайней мерой. Следует приложить все усилия, чтобы исключить применение огнестрельного оружия, особенно в отношении детей. Как правило, огнестрельное оружие не должно применяться, за исключением случаев, когда подозреваемый преступник оказывает вооруженное сопротивление или иным образом подвергает опасности жизнь других лиц, а менее крайние меры недостаточны для сдерживания или задержания подозреваемого преступника. В каждом случае выстрела из огнестрельного оружия следует незамедлительно сообщать в компетентные органы.

Статья 4

Информация конфиденциального характера, находящаяся в распоряжении сотрудников правоохранительных органов, должна храниться в тайне, если исполнение служебных обязанностей или нужды правосудия строго не требуют иного.

Комментарий :

По роду своих обязанностей сотрудники правоохранительных органов получают информацию, которая может иметь отношение к частной жизни или потенциально наносить ущерб интересам и особенно репутации других лиц. Следует проявлять большую осторожность при сохранении и использовании такой информации, которая должна раскрываться только при исполнении служебных обязанностей или для нужд правосудия. Любое раскрытие такой информации для других целей является совершенно неправомерным.

Статья 5

Ни одно должностное лицо по поддержанию правопорядка не может применять, подстрекать или допускать какие-либо акты пыток или других жестоких, бесчеловечных или унижающих достоинство видов обращения или наказания, равно как и любое должностное лицо по поддержанию правопорядка не может ссылаться на приказы вышестоящих лиц или исключительные обстоятельства, такие как состояние войны или угроза войны, угроза национальной безопасности, внутренняя политическая нестабильность или любое другое чрезвычайное положение в качестве оправдания пыток или другого жестокого, бесчеловечного или унижающего достоинство обращения или наказания.

Комментарий:

а. Этот запрет вытекает из Декларации о защите всех лиц от пыток и других жестоких, бесчеловечных или унижающих достоинство видов обращения и наказания, принятой Генеральной Ассамблеей, согласно которой:

«[Такие действие является] оскорблением человеческого достоинства и подлежит осуждению как отказ от целей Устава Организации Объединенных Наций и как нарушение прав человека и основных свобод, провозглашенных во Всеобщей декларации прав человека [и других документы о правах].

b. В Декларации пытка определяется следующим образом:

«…пытка означает любое действие, посредством которого сильная боль или страдание, физическое или моральное, умышленно причиняются или по подстрекательству государственного должностного лица лицу за такое целей, как получение от него или третьего лица информации или признания, наказание его за деяние, совершенное им или в совершении которого он подозревается, или запугивание его или других лиц. к законным санкциям в той мере, в какой это соответствует Минимальным стандартным правилам обращения с заключенными».

c.Термин «жестокое, бесчеловечное или унижающее достоинство обращение или наказание» не был определен Генеральной Ассамблеей, но его следует толковать таким образом, чтобы расширить максимально возможную защиту от злоупотреблений, физических или психических.

Статья 6

Должностные лица по поддержанию правопорядка должны обеспечить полную охрану здоровья лиц, находящихся под их стражей, и, в частности, должны принимать немедленные меры для обеспечения медицинской помощи, когда это необходимо.

Комментарий :

«Медицинская помощь», которая относится к услугам, оказываемым любым медицинским персоналом, включая сертифицированных практикующих врачей и фельдшеров, должна быть обеспечена по мере необходимости или по запросу.
В то время как медицинский персонал, вероятно, будет прикомандирован к правоохранительным органам, сотрудники правоохранительных органов должны принимать во внимание мнение такого персонала, когда они рекомендуют предоставить лицу, находящемуся под стражей, надлежащее лечение с помощью или в консультации с медицинским персоналом извне. правоохранительная операция.
Предполагается, что сотрудники правоохранительных органов также должны обеспечить медицинскую помощь жертвам нарушений закона или несчастных случаев, произошедших в ходе нарушений закона.

Статья 7

Должностные лица правоохранительных органов не должны совершать никаких коррупционных действий. Они также будут решительно противодействовать всем таким актам и бороться с ними.

Комментарий :

Любой коррупционный акт, как и любое другое злоупотребление властью, несовместим с профессией сотрудника правоохранительных органов. Закон должен применяться в полной мере в отношении любого должностного лица правоохранительных органов, совершившего коррупционный акт, поскольку правительства не могут рассчитывать на обеспечение соблюдения закона среди своих граждан, если они не могут или не хотят применять закон в отношении своих собственных агентов и в своих агентствах. .
Хотя определение коррупции должно регулироваться национальным законодательством, его следует понимать как охватывающее совершение или бездействие действия при исполнении или в связи с выполнением своих обязанностей, в ответ на подарки, обещания или поощрения, запрошенные или принятые, или их неправомерное получение после совершения или бездействия деяния.
Упомянутое выше выражение «акт коррупции» следует понимать как охватывающее попытку коррупции.

Статья 8

Должностные лица по поддержанию правопорядка уважают закон и настоящий Кодекс. Они также в меру своих возможностей предотвращают любые их нарушения и решительно противодействуют им.

Должностные лица по поддержанию правопорядка, у которых есть основания полагать, что нарушение настоящего Кодекса имело место или может произойти, должны сообщить об этом вышестоящим органам и, при необходимости, другим соответствующим органам или органам, наделенным полномочиями по рассмотрению или устранению нарушений.

Комментарий:

Настоящий Кодекс следует соблюдать всякий раз, когда он включен в национальное законодательство или практику. Если законодательство или практика содержат более строгие положения, чем положения настоящего Кодекса, эти более строгие положения должны соблюдаться.
Статья направлена на сохранение баланса между необходимостью внутренней дисциплины ведомства, от которой во многом зависит общественная безопасность, с одной стороны, и необходимостью борьбы с нарушениями основных прав человека, с другой. Должностные лица по поддержанию правопорядка должны сообщать о нарушениях в рамках цепочки подчинения и предпринимать другие законные действия за пределами цепочки подчинения только тогда, когда другие средства правовой защиты недоступны или эффективны. При этом понимается, что должностные лица правоохранительных органов не подлежат административному или иному наказанию за то, что они сообщили о нарушении настоящего Кодекса или о том, что оно может произойти.
Термин «соответствующие органы или органы, наделенные полномочиями по пересмотру или исправлению положения», относится к любому органу или органу, существующему в соответствии с национальным законодательством, будь то внутренним по отношению к правоохранительному органу или независимым от него, с установленными законом, обычными или иными полномочиями рассматривать возникающие жалобы и жалобы. из-за нарушений, подпадающих под действие настоящего Кодекса.
В некоторых странах можно считать, что средства массовой информации выполняют функции по рассмотрению жалоб, аналогичные тем, которые описаны в подпункте (c) выше. Поэтому должностные лица по поддержанию правопорядка могут быть оправданы, если в качестве крайней меры и в соответствии с законами и обычаями своей страны и положениями статьи 4 настоящего Кодекса они доводят нарушения до сведения общественности посредством СМИ.
Сотрудники правоохранительных органов, которые соблюдают положения настоящего Кодекса, заслуживают уважения, полной поддержки и сотрудничества со стороны общества и правоохранительных органов, в которых они служат, а также сотрудников правоохранительных органов.

Фуко: власть повсюду | Понимание силы социальных изменений | powercube.net

Мишель Фуко, французский постмодернист, оказал огромное влияние на формирование понимания власти, уводя от анализа акторов, использующих власть как инструмент принуждения, и даже от дискретных структур, в которых действуют эти акторы. , к идее, что «власть повсюду», рассеянной и воплощенной в дискурсе, знании и «режимах истины» (Фуко 19).91; Рабинов 1991). Власть для Фуко — это то, что делает нас тем, что мы есть, работая на уровне, совершенно отличном от других теорий:

«Его работа знаменует собой радикальный отход от предыдущих способов понимания власти и не может быть легко интегрирована с предыдущими идеями, поскольку власть скорее рассеяна. чем концентрированный, воплощенный и разыгранный, а не одержимый, дискурсивный, а не чисто принудительный, и конституирует агентов, а не развертывается ими» (Gaventa 2003: 1)

Фуко бросает вызов идее о том, что власть принадлежит людям или группам посредством « эпизодические» или «суверенные» акты господства или принуждения, рассматривая их вместо этого как рассредоточенные и всеобъемлющие. «Власть повсюду» и «приходит отовсюду», так что в этом смысле она не является ни агентством, ни структурой (Фуко 19).98: 63). Наоборот, это своего рода «метавласть» или «режим истины», пронизывающий общество и находящийся в постоянном движении и обсуждении. Фуко использует термин «власть/знание», чтобы обозначить, что власть конституируется посредством общепринятых форм знания, научного понимания и «истины»:

«Истина есть вещь этого мира: она создается только благодаря множеству форм принуждения». . И это вызывает регулярные эффекты власти. Каждое общество имеет свой режим истины, свою «общую политику» истины: то есть типы дискурса, которые оно принимает и заставляет функционировать как истинные; механизмы и случаи, позволяющие различать истинные и ложные утверждения, средства, с помощью которых каждое из них санкционируется; методы и процедуры, придающие значение в обретении истины; статус тех, кого обвиняют в том, что они говорят то, что считается правдой» (Фуко, в Rabinow 1991).

Эти «общая политика» и «режимы истины» являются результатом научного дискурса и институтов и постоянно подкрепляются (и переопределяются) системой образования, средствами массовой информации и потоком политических и экономических идеологий. В этом смысле «битва за истину» ведется не за какую-то абсолютную истину, которую можно обнаружить и принять, а является битвой за «правила, согласно которым истина и ложь отделяются и к истине прикрепляются специфические эффекты силы». «… битва за «статус истины и ту экономическую и политическую роль, которую она играет» (Фуко, в Rabinow 19).91). Это вдохновило Хейворда на сосредоточение внимания на власти как на границах, которые позволяют и ограничивают возможности для действия, а также на относительных способностях людей знать и формировать эти границы (Hayward 1998).

Фуко — один из немногих писателей о власти, которые признают, что власть — это не просто негативная, принудительная или репрессивная вещь, которая заставляет нас делать что-то вопреки нашей воле, но также может быть необходимой, продуктивной и позитивной силой в обществе (Гавента 2003: 2):

«Мы должны раз и навсегда перестать описывать эффекты власти в отрицательных терминах: она «исключает», «подавляет», «цензурирует», «абстрагирует», «маскирует», это «скрывает». На самом деле сила производит; он производит реальность; он производит области объектов и ритуалы истины. Индивидуум и знание, которое может быть о нем получено, принадлежат этому произведению» (Фуко 19).91: 194).

Власть также является важным источником социальной дисциплины и подчинения. Отвлекая внимание от «суверенной» и «эпизодической» реализации власти, традиционно сосредоточенной в феодальных государствах для принуждения своих подданных, Фуко указал на новый вид «дисциплинарной власти», которую можно было наблюдать в административных системах и социальных службах, которые были созданы в Европе 18 века, такие как тюрьмы, школы и психиатрические больницы. Их системы наблюдения и оценки больше не требовали силы или насилия, поскольку люди научились дисциплинировать себя и вести себя ожидаемым образом.

Фуко был очарован механизмами наблюдения за тюрьмами, школьной дисциплиной, системами управления и контроля над населением, а также продвижением норм телесного поведения, включая секс. Он изучал психологию, медицину и криминологию, а также их роль как совокупности знаний, определяющих нормы поведения и отклонения. Физические тела подчиняются и заставляют вести себя определенным образом, как микрокосм социального контроля над более широким населением, посредством того, что он назвал «биовластью». Дисциплина и биовласть создают «дискурсивную практику» или совокупность знаний и поведения, которые определяют, что является нормальным, приемлемым, девиантным и т. д., — но это дискурсивная практика, которая, тем не менее, находится в постоянном движении (Фуко 19).91).

Ключевым моментом подхода Фуко к власти является то, что он выходит за рамки политики и рассматривает власть как повседневное, социализированное и воплощенное явление. Вот почему государственноцентричная борьба за власть, включая революции, не всегда приводит к изменению общественного порядка. Некоторым концепция власти Фуко кажется настолько неуловимой и оторванной от агентности или структуры, что кажется, что практических действий практически не остается. Но он оказал огромное влияние, указав на то, как нормы могут быть внедрены настолько, что выходят за пределы нашего восприятия, заставляя нас дисциплинировать себя без какого-либо преднамеренного принуждения со стороны других.

Вопреки многим интерпретациям, Фуко верил в возможность действия и сопротивления. Он был активным социальным и политическим комментатором, который видел роль «органического интеллектуала». Его представления о действиях, как и у Хейворда, были связаны с нашей способностью распознавать и подвергать сомнению социальные нормы и ограничения. Бросить вызов власти — это не поиск какой-то «абсолютной истины» (которая в любом случае является властью, произведенной обществом), а «отделение власти истины от форм гегемонии, социальной, экономической и культурной, в рамках которых она действует и в настоящее время» (Фуко, у Рабинова 1991: 75). Дискурс может быть местом как власти, так и сопротивления, с возможностью «уклонения, подрыва или оспаривания стратегий власти» (Gaventa 2003: 3):

«Дискурсы не раз и навсегда подчинены власти или восстают против нее… Мы должны учитывать сложный и неустойчивый процесс, при котором дискурс может быть как инструментом и следствием власти, так и помехой, точкой преткновения сопротивления и отправной точкой для противоположной стратегии. Дискурс передает и производит власть; оно укрепляет его, но также подрывает и обнажает, делает его хрупким и позволяет мешать» (Фуко 19).98: 100-1).

Силовой куб нелегко совместим с фукоанским пониманием власти, но есть возможности для критического анализа и стратегических действий на уровне оспаривания или формирования дискурса – например, использование психологического/культурного значения «невидимой силы» и «гегемонии». как линза, с помощью которой можно смотреть на целое. Подход Фуко широко использовался для критики мышления и парадигм развития, а также способов, которыми дискурсы развития наполняются силой (Gaventa 2003, цитируя работы Эскобара, Кастельса и других критиков «пост-развития»).

На уровне практики активисты и практики используют методы анализа дискурса для определения языка нормативной помощи, который требует более тщательного изучения, и для формирования альтернативных фреймов. Пример очень практичного инструмента для этого включен в сборник IIED Power Tools под названием «Письменный инструмент», а на семинарах НПО мы использовали простой метод анализа дискурса для изучения заявлений о миссии и целей программы.

Спасибо Джонатану Гавенте (2003) за его вклад в этот раздел.

Ссылки для дальнейшего чтения

Foucault, M. (1991). Дисциплина и наказание: рождение тюрьмы. Лондон, Пингвин.

Фуко, Мишель (1998) История сексуальности: воля к знанию , Лондон, Пингвин.

Гавента, Джон (2003) Власть после Луки: обзор литературы , Брайтон: Институт исследований развития.

Хейворд, Кларисса Райл (1998) «Власть без лица», Polity 31(1).

Рабинов, Пол (редактор) (1991) The Foulcault Reader: введение в мысли Фоулко, London, Penguin.

Автоматизация Обзор | Airtable Support

Смотрите тренировку! Усильте свой рабочий процесс

Обзор

Автоматизация позволяет настраивать настраиваемые рабочие процессы с триггерным действием непосредственно в базе Airtable. Это позволит вам и вашей команде сэкономить время за счет автоматизации повторяющихся задач, повышения эффективности коммуникации и снижения общей погрешности.

Автоматизация ограничена отдельными базами и может быть найдена рядом с кнопкой «Поделиться» в базе в настольных/браузерных версиях Airtable. Автоматизация в наших приложениях для iOS и Android в настоящее время недоступна.

Автоматизация может создаваться/редактироваться только лицами с разрешениями Owner или Creator . Соавторы с разрешениями уровня Editor и ниже смогут просматривать, но не редактировать автоматизации.

Триггеры

Триггер A — это определенное событие, которое инициирует автоматизацию. Доступные триггеры включают:

Когда запись входит в представление ( Примечание : записи, которые покидают представление и повторно входят в него, срабатывают снова)
Когда создается запись
Когда запись обновляется
Когда запись соответствует условию
При отправке формы
В назначенное время триггер автоматизации
Триггер новой строки для Google Sheets
Триггер нового ответа для Google Forms
Триггеры событий для Календаря Google
Триггеры автоматизации Outlook
Триггеры входящих веб-перехватчиков

ПРИМЕЧАНИЕ

Существующие записи в вашей базе не будут запускать вновь созданную автоматизацию. Только после , когда вы включили автоматизацию, любая запись, соответствующая новому условию триггера, вызовет запуск автоматизации. Для внесения больших обновлений в несколько существующих записей в вашей базе мы рекомендуем проверить расширение пакетного обновления.

Действия

Действие — это шаг, который выполняет такую задачу, как отправка электронной почты. Когда срабатывает триггер и завершаются последующие действия, говорят, что автоматизация выполнена.

В настоящее время доступно множество действий:

Отправить электронное письмо
Создать запись
Обновить запись
Найти записи
Отправить сообщение Slack
Отправить сообщение Microsoft Teams 9 действий

Действия G Suite (Отправка электронной почты из учетной записи Gmail, Создание новой строки в Google Sheet, Создание ответа на форму Google и Создание события Google Calendar)
Создать задачу в Jira Cloud
Создать действие публикации для страниц Facebook
Создать твит в Твиттере
Hootsuite: Запланировать публикацию

Salesforce: Создать новую запись можно включить автоматику.

В инициирует шаг автоматизации, тестовая запись может быть выбрана для использования на протяжении всего остального процесса настройки автоматизации. После того, как вы установили свойства, нажмите кнопку «Выбрать запись для тестирования». Это откроет всплывающее окно со всеми записями, которые соответствуют конфигурации вашей конфигурации триггера. Вы сможете выполнить поиск или прокрутить до записи и выбрать ту, которую хотите использовать в качестве тестовой записи.

Это полезно, потому что если что-то пойдет не так, как планировалось позже в процессе настройки автоматизации, вы можете скорректировать данные в выбранной вами тестовой записи. Вы также можете вернуться к настройке триггера и выбрать другую тестовую запись. Всегда не забывайте повторно тестировать любые ранее проверенные шаги в вашей автоматизации, чтобы убедиться, что была захвачена самая последняя версия вашей базы.

ПРИМЕЧАНИЕ

Выбор тестовых записей недоступен ни для каких действий в автоматизации. Однако повторное тестирование и выбор новой тестовой записи на этапе триггера обычно приводит к появлению другой тестовой записи на более поздних этапах действия. Подробнее о тестовых записях в этой статье.

Эта функция также работает с триггерами рабочей области Google, за исключением триггера Google Forms. Например, если вы используете триггер «Календарь Google: когда событие создано», вы сможете выбрать предстоящее событие или событие, произошедшее за последние 3 месяца, для использования в качестве тестового события.

Советы по правильной настройке

Создание представления для конкретной автоматизации

Перед созданием автоматизации рекомендуется создать представление исключительно для этой автоматизации или набора автоматизаций. Воспользуйтесь преимуществами условий фильтрации здесь.

Блокировка представления для предотвращения непредвиденных запусков

Рассмотрите возможность блокировки представления и добавления примечания о том, что изменение условий фильтрации представления может привести к запуску непреднамеренных автоматизаций.

Рассмотрите триггер перед созданием автоматизации e

Подумайте, когда вы хотите, чтобы срабатывал триггер записи и последующее действие. Это когда создается запись, изменяется статус или когда все поля в записи заполнены и запись считается «завершенной»? Некоторые идеи включают в себя:

Поле состояния изменено на «Готово к отправке электронной почты» или на другую подходящую фразу для конкретного действия.
Поле «Создано», использующее тип поля времени создания. Установите условия фильтрации представления, чтобы включать только записи до сегодняшнего дня. Это создаст задержку при отправке записей.
Используйте форму. При использовании только формы для создания новых записей все поля добавляются одновременно при отправке. Идеально подходит для автоматизации, которая срабатывает при создании записи.
Для простого способа пометить запись как завершенную добавьте поле флажка.

Узнайте о тестовых записях

Убедитесь, что выбранная вами тестовая запись имеет значение в каждом из полей, необходимых для вашей автоматизации. На данный момент используемые поля получаются из результата проверки триггера. Если тестовое поле пустое, оно не будет отображаться в настройках. Подробнее о тестовых записях здесь.

Узнайте об идентификаторах записей

Четкое представление об идентификаторах записей в Airtable может быть очень полезным для автоматизации, особенно при использовании действия обновления записи.

Разрешения и автоматизация

Если в вашей базе есть какие-либо разрешения на редактирование полей или таблиц, которые ограничивают редактирование только определенными пользователями, вы можете добавить разрешения для автоматизации на внесение изменений с помощью этого переключателя:

Помощь в устранении неполадок

Ознакомьтесь с нашей статьей об автоматизации устранение неполадок, если вы застряли, обнаружили ошибку в своей автоматизации или получили уведомления о неудачном запуске.

ПРИМЕЧАНИЕ

Отдельный пользователь, который включает автоматизацию, получает уведомления о неудачном запуске автоматизации.

Ограничения по току

При желании вы можете добавить до 50 автоматов в базу. Важно отметить, что автоматизаций, которые отключены (неактивны), по-прежнему учитываются при этом ограничении в 50 автоматизаций .

Дополнительно можно создать до 25 действий в одной автоматизации. Добавление до 25 действий в одну автоматизацию может помочь, если вы обнаружите, что приближаетесь к общему лимиту в 50 автоматизаций. Там, где это применимо, действие может использовать выходные данные предыдущих действий в той же автоматизации.

Run limits

. действие сценария» недоступно

Workspace Plan	Automation runs (per month, per workspace)	Automation run history	Notes
Enterprise	500,000 ¹	3 years
Pro	50,000 ¹	1 year
плюс	5000 ¹	6 месяцев	«Отправить электронное письмо». Действие может по электронной почте только сотрудники по электронной почте на базе, не Arbitrary Addales
БЕСПЛАТНО	100 60

ПРИМЕЧАНИЕ

Пределы запуска автоматизации сбрасываются в первого числа каждого месяца .

¹ Наша система подсчитывает «запуск» автоматизации каждый раз, когда вызывается триггер. Это означает, что как неудачные, так и успешные попытки автоматизации будут учитываться при расчете ежемесячной нормы запуска рабочей области.

URL-адреса автоматизации

Начиная с 25 января 2022 года Airtable внесла изменение в форматирование URL-адресов в триггерах и действиях автоматизации. Теперь базовый идентификатор (appXXXXXXXXXXXXXXX) будет отображаться в начале пути URL. Это изменение совпадает с недавним изменением, предусматривающим включение базовых идентификаторов в URL-адреса Airtable во всей остальной части продукта. Изменение формата URL-адреса записи произойдет в следующих местах:

Свойство url записи, выводимой триггером/действием.
Свойство url модели Table или View, полученное действием Run Script.

Это может быть критическим изменением , если ваша автоматизация делает жесткие предположения о формате свойства URL-адреса (например, путем деконструкции возвращенного URL-адреса на его составные части или аналогичного). Никаких действий не требуется, если ваша автоматизация использует URL-адрес только для целей навигации. Навигация в браузере будет по-прежнему работать для URL-адресов Airtable в старом стиле через перенаправления, хотя эти перенаправления могут не поддерживаться бесконечно в будущем. Если ваша автоматизация создает URL-адреса Airtable с нуля, мы рекомендуем обновить логику построения, чтобы также включить базовый идентификатор (приложения).

Часто задаваемые вопросы

Общие

Будет ли автоматика работать, даже если ни у кого нет открытой базы?

Да. Поскольку автоматизация находится на стороне сервера, она будет работать, даже если ни у кого нет открытой базы.

Кто может создавать/редактировать автоматизацию?

Автоматизация может создаваться или редактироваться только пользователями с правами «Создатель» (или «Владелец»).

Перестанет ли работать автоматика, если создателя автоматики удалить из базы?

Они должны продолжать работать — автоматизация не зависит от учетных данных Airtable какого-либо конкретного пользователя для запуска. Поэтому он должен продолжать работать, даже если владелец подключенного аккаунта удален из базы.

Запускаются ли автоматы задним числом?

Только вперед. Например, если есть условный триггер, настроенный на «когда поле не пусто», а затем эта автоматизация включена, автоматизация не будет запускаться для предыдущих записей со значением в указанном поле. Однако создание записи, которая не соответствует условиям, а затем снова соответствует им, вызовет автоматизацию.

Можно ли просмотреть журнал/историю изменений того, какие пользователи редактировали автоматизацию?

В настоящее время эта функция недоступна.

Можно ли увеличить месячный лимит запуска автоматизации?

С каждым планом выставления счетов связан месячный лимит запуска автоматизации. Единственный стандартный способ увеличить лимит — перейти на более высокий тарифный план.

Есть ли способ найти/узнать, какие автоматы вы создали в определенной базе или рабочей области?

В настоящее время эта функция недоступна.

Триггеры

Работают ли триггеры автоматизации с полями формул?

Да, они работают. Они срабатывают примерно каждые 5 минут, пока загружается база из-за интерактивности пользователя, и раз в час в противном случае.

Почему триггеры «При создании записи» и «При обновлении записи» срабатывают до того, как я закончу редактирование полей?

Эти триггеры срабатывают, как только пользователь вводит первые несколько символов. Мы понимаем, что это не идеально, и мы должны решить эту проблему.

Можно ли сделать так, чтобы триггер «При обновлении записи» срабатывал при добавлении комментария?

Комментарии к записям считаются метаданными и не могут запускать автоматизацию.

Как выбирается тестовая запись при тестировании шага?

Поиск записей: Все совпадающие записи
Когда запись соответствует условию: Первая совпадающая запись
Когда запись создана: Первая запись в таблице/представлении
Когда запись обновляется: Первая запись в таблице/представлении
Когда запись входит в представление: Первая запись в таблице/представлении
Создана строка в листах Google: Последняя строка в листе
Новый ответ Триггер формы Google: Последний ответ/строка в таблице, на которую отправлен ответ

Действия

Должны ли получатели «Отправить электронное письмо» быть соавторами?

Бесплатно/Плюс: Да, все получатели должны быть подтверждены соавторами.
Pro: Может отправлять сообщения на 100 уникальных адресов электронной почты, не являющихся соавторами, в день.
Предприятие: Нет ограничений на количество несотрудников, которым вы можете отправлять электронные письма в день.

Вы можете увидеть ограничение своего рабочего пространства, если создадите действие «Отправить электронное письмо» для автоматизации.

Можно ли в дайджесте отображать дату в локализованном часовом поясе вместо UTC?

Непосредственно в автоматизации, но это можно сделать, используя поле формулы, как описано в этой статье поддержки.

Можно ли применить пользовательское форматирование к сетке или списку записей в электронном письме?

К сожалению, нет. Вы можете использовать «Найти записи по представлению», чтобы применить ту же сортировку, которая применяется в представлении, и вы можете выбрать, хотите ли вы усекать или не усекать длинные значения поля, но мы не предоставляем дополнительные возможности настройки на данный момент.

Связанный видеоконтент

Была ли эта статья полезной?

Супер сила — Аниме — MyAnimeList.net

2886232 8,51 20151005 Человек с одним ударом

ТВ, 2015 Завершено 12 эп., 24 мин

Действие Комедия

У кажущегося невпечатляющим Сайтамы есть довольно уникальное хобби: быть героем. Чтобы осуществить свою детскую мечту, Сайтама неустанно тренировался в течение трех лет, потеряв в процессе все свои волосы. Теперь Сайтама настолько силен, что может победить любого врага всего одним ударом. Однако отсутствие никого, способного сравниться с ним в силе, привело Сайтаму к неожиданной проблеме: он больше не может получать удовольствие от битвы, и ему стало очень скучно. Однажды Сайтама привлекает внимание 19-летний киборг Генос, который видит свою силу и желает стать учеником Сайтамы. Генос предлагает двоим присоединиться к Ассоциации героев, чтобы стать сертифицированными героями, которые будут признаны за их положительный вклад в общество. Сайтама, шокированный тем, что никто не знает, кто он такой, быстро соглашается. Встречая новых союзников и сражаясь с новыми врагами, Сайтама отправляется в новое путешествие в качестве члена Ассоциации героев, чтобы испытать азарт битвы, который он когда-то испытывал. [Написано MAL Rewrite]

StudioMadhouse

SourceWeb manga

ThemesParodySuper Power

DemographicSeinen

My Hero Academia

2714765 7,92 20160403 Академия Боку но Герой

ТВ, 2016Готово 13 эп., 24 мин.

Действие

Появление «причуд», недавно обнаруженных сверхспособностей, неуклонно растет с годами, и 80 процентов человечества обладают различными способностями от управления элементами до изменения формы. Это оставляет остальную часть мира совершенно бессильной, и Изуку Мидория является одним из таких людей. С самого детства амбициозный школьник не хотел ничего, кроме как быть героем. Несправедливая судьба Изуку заставляет его восхищаться героями и делать о них заметки всякий раз, когда он может. Но, похоже, его настойчивость принесла свои плоды: Изуку встречает героя номер один и своего личного кумира Всемогущего. Причуда Всемогущего — уникальная способность, которую можно передать по наследству, и он выбрал Изуку своим преемником! Выдержав многие месяцы изнурительных тренировок, Изуку поступает в UA High, престижную среднюю школу, известную своей превосходной программой подготовки героев, и первокурсники этого года выглядят особенно многообещающе. Со своими причудливыми, но талантливыми одноклассниками и надвигающейся угрозой злодейской организации Изуку скоро узнает, что на самом деле значит быть героем. [Написано MAL Rewrite]

StudioBones

SourceManga

ThemesSchoolSuper Power

DemographicShounen

My Hero Academia Season 2

2273646 8.14 20170401 Boku no Hero Academia 2-й сезон

ТВ, 2017Готово 25 эп. , 23 мин.

Действия

В UA Academy даже жестокое нападение не может сорвать их самое престижное мероприятие: школьный спортивный фестиваль. Этот фестиваль, известный во всей Японии, дает начинающим героям возможность продемонстрировать свои способности как публике, так и потенциальным рекрутерам. Однако путь к славе никогда не бывает легким, особенно для Изуку Мидории, чья причуда обладает огромной грубой силой, но при этом крайне неэффективна. Противостоя своим талантливым одноклассникам, таким как Шото Тодороки, владеющему огнем и льдом, Изуку должен использовать свой острый ум и управлять своим окружением, чтобы добиться победы и доказать миру свою ценность. [Написано MAL Rewrite]

StudioBones

SourceManga

ThemesSchoolSuper Power

Демографические Shounen

Code Geass: Lelouch of the Rebellion

2045109 8,70 20061006 Код Гиас: Ханъяку но Лелуш

ТВ, 2006 г. Завершен 25 эп., 24 мин.

Действие Драма Sci-Fi

В 2010 году Священная империя Британии становится доминирующей военной державой, начиная с завоевания Японии. Япония, переименованная в Зону 11 после своего быстрого поражения, столкнулась с серьезным сопротивлением этим тиранам в попытке восстановить независимость. Лелуш Ламперуж, британский студент, к сожалению, оказывается под перекрестным огнем между британскими и повстанческими силами Зоны 11. Однако ему удается сбежать благодаря своевременному появлению загадочной девушки по имени СиСи, которая наделяет его Гиасом, «Силой королей». Осознав огромный потенциал своей новообретенной «силы абсолютного послушания», Лелуш отправляется в опасное путешествие в роли линчевателя в маске, известного как Зеро, возглавляя безжалостную атаку на Британию, чтобы отомстить раз и навсегда. [Написано MAL Rewrite]

StudioSunrise

SourceOriginal

ThemesMechaMilitarySchoolSuper Power

My Hero Academia Season 3

1956747 8. 07 20180407 Boku no Hero Academia 3-й сезон

ТВ, 2018Готово 25 эп., 23 мин.

Действие

Когда для студентов UA Academy наступает лето, каждый из этих супергероев-стажеров делает все возможное, чтобы стать известными героями. Они отправляются в лесной тренировочный лагерь, управляемый профессиональными героями UA, где студенты сталкиваются друг с другом в битвах и проходят опасные испытания, улучшая свои способности и преодолевая свои пределы. Однако их школьная поездка внезапно переворачивается с ног на голову, когда прибывает Лига злодеев, вторгаясь в лагерь с миссией по захвату одного из учеников. 3-й сезон Boku no Hero Academia следует за Изуку «Деку» Мидорией, амбициозным учеником, который тренируется, чтобы осуществить свою мечту стать героем, подобным его образцу для подражания — Всемогущему. Будучи одним из учеников, оказавшихся в центре хаоса нападения злодеев, Деку должен встать на сторону своих одноклассников и бороться за их выживание. [Написано MAL Rewrite]

StudioBones

SourceManga

ThemesSchoolSuper Power

DemographicShounen

1895255 7,47 20140707 Убийца Акаме!

ТВ, 2014 г. Завершено 24 эп., 23 мин.

Действие Fantasy

«Ночной рейд» — тайное подразделение Революционной армии, занимающееся убийствами, восстание, собравшееся для свержения премьер-министра Честного, чья жадность и жажда власти заставили его воспользоваться неопытностью ребенка-императора. Без сильного и доброжелательного лидера остальная часть нации будет тонуть в нищете, раздорах и разорении. Хотя все члены «Ночного рейда» — опытные убийцы, они понимают, что отнимать жизни далеко не похвально и что они, скорее всего, столкнутся с возмездием, поскольку безжалостно уничтожают всех, кто стоит на пути революции. Новейшим членом этой веселой банды убийц является Тацуми, наивный мальчик из отдаленной деревни, который отправился в путешествие, чтобы помочь своему обедневшему родному городу, и был покорен не только идеалами Night Raid, но и их решимостью. Убийца Акаме! следует за Тацуми, когда он сражается с Империей и сталкивается лицом к лицу с мощным оружием, вражескими убийцами, вызовами его собственной морали и ценностям и, в конечном счете, с тем, что на самом деле означает быть убийцей со своим делом. [Написано MAL Rewrite]

StudioWhite Fox

SourceManga

ThemesGoreSuper Power

DemographicShounen

1801145 8,48 20160711 Моб Психо 100

ТВ, 2016Готово 12 эп., 24 мин.

Действие Комедия Сверхъестественное

Восьмиклассник Шигео Кагеяма по прозвищу «Моб» в юном возрасте воспользовался своим внутренним источником экстрасенсорных способностей. Но сила быстро оказывается помехой, когда он осознает потенциальную опасность своих навыков. Решив подавить свою силу, Моб в настоящее время использует свои способности только для того, чтобы произвести впечатление на свою давнюю любовь Цубоми, которой вскоре надоедают одни и те же уловки. Чтобы контролировать свои навыки, Моб вступает под крыло Аратаки Рейгена, мошенника, утверждающего, что он экстрасенс, который использует силы Моба для получения мелочи. Теперь изгнание злых духов по команде стало частью повседневной монотонной жизни Моба. Однако психическая энергия, которую он излучает, — это лишь верхушка айсберга; если его огромный потенциал и необузданные эмоции выйдут из-под контроля, произойдет катастрофическое событие, которое сделает его совершенно неузнаваемым. Движение к взрыву Моба нарастает, и попытки его остановить бесполезны. [Написано MAL Rewrite]

StudioBones

Манга SourceWeb

ThemeSuper Power

Code Geass: Lelouch of the Rebellion R2

1613276 8,91 20080406 Код Гиас: Ханъяку но Лелуш R2

ТВ, 2008 г. Завершен 25 эп., 24 мин.

Действие Драма Sci-Fi

Прошел год после Черного Восстания, неудавшегося восстания против Священной Британской Империи, возглавляемого мстителем Зеро в маске, который сейчас пропал без вести. В растерянности без своего революционного лидера группа сопротивления Зоны 11 — Черные рыцари — оказываются слишком бессильными, чтобы противостоять жестокости, нанесенной Одиннадцати Британией, которая значительно усилилась, чтобы подавить любую надежду на будущее восстание. Лелуш Ламперуж, потерявший все воспоминания о своей двойной жизни, мирно живет со своими друзьями, будучи учеником старшей школы в Академии Эшфорд. Его бывшая партнерша СиСи, не в силах смириться с таким поворотом событий, берет на себя ответственность напомнить ему о его прошлой цели, надеясь, что вдохновитель Зеро снова поднимется, чтобы закончить то, что он начал, в этом захватывающем завершении сериала. [Написано MAL Rewrite]

StudioSunrise

SourceOriginal

ThemesMechaMilitarySuper Power

1588097 8.04 20131004 Убей ла убей

ТВ, 2013 г. Завершено 24 эп., 24 мин.

Действие Комедия Ecchi

После убийства своего отца Рюуко Матой бродит по стране в поисках убийцы. Следуя своей единственной наводке — недостающей половине его изобретения, Лезвию-ножницам, — она поступает в престижную Академию Хоннодзи, среднюю школу, не похожую ни на одну другую. Академией правит импозантный и хладнокровный президент студенческого совета Сацуки Кирюин вместе со своими могущественными подчиненными, Элитной четверкой. В жесткой конкурентной иерархии школы Сацуки награждает тех, кто находится на вершине, специальной одеждой, называемой «Униформа Гоку», которая наделяет владельца уникальными сверхчеловеческими способностями. Тщательно побежденная в бою с одним из учеников в форме, Рюуко отступает в свой разрушенный дом, где натыкается на Сенкетсу, редкого и разумного «Камуи», или Одежду Бога. Вступив в контакт с кровью Рюуко, Сенкецу просыпается, цепляется за нее и наделяет ее огромной силой. Теперь, вооружившись Сенкецу и Лезвием-ножницами, Рюуко противостоит Элитной четверке, надеясь добраться до Сацуки и раз и навсегда раскрыть виновного в убийстве ее отца. [Написано MAL Rewrite]

StudioTrigger

SourceOriginal

ThemesSchoolSuper Power

My Hero Academia Сезон 4

1511173 7,93 201

Boku no Hero Academia 4-й сезон

ТВ, 2019Готово 25 эп. , 24 мин.

Действие

После успешной сдачи экзамена на временную лицензию героя Изуку «Деку» Мидория ищет внеклассную стажировку в профессиональном агентстве героев. По рекомендации своего наставника Всемогущего Мидория получает место под руководством бывшего помощника Всемогущего, сэра Ночноглаза, ныне известного героя. В то время как одноклассники Мидории совершенствуют свои способности посредством различных стажировок, подающий надежды злодей Кай Чисаки использует свои ужасающие способности, чтобы снискать расположение в преступном мире. Амбиции Чисаки, известного под прозвищем Капитальный ремонт, сталкиваются с Лигой злодеев и ее лидером Томурой Шигараки. Работая с сэром Ночным Глазом, Мидория обнаруживает преступный синдикат Чисаки и враждебные отношения злодея с загадочной молодой девушкой по имени Эри. Опасаясь за безопасность ребенка, Мидория и его старшеклассник Мирио Тоогата должны работать вместе, чтобы положить конец террору Чисаки. [Написано MAL Rewrite]

StudioBones

SourceManga

ThemesSchoolSuper Power

DemographicShounen

One Punch Man Season 2

1475821 7,48 201

Ванпанчмен 2 сезон

ТВ, 2019Готово 12 эп. , 23 мин.

Действие Комедия

После победы над Боросом и его могучей армией Сайтама вернулся к своей ничем не примечательной повседневной жизни в Z-City. Однако, без его ведома, количество появляющихся монстров все еще постоянно растет, что создает нагрузку на ресурсы Ассоциации героев. Их высшие руководители решаются на смелый шаг по вербовке хулиганов, чтобы помочь в их битве. Но во время первой встречи с этими потенциальными пришельцами появляется таинственный человек, называющий себя Гару. Называя себя монстром, он начинает безжалостно атаковать толпу. Таинственный Гару продолжает свою ярость против Ассоциации Героев, сокрушая каждого героя, с которым он сталкивается. Он оказывается лучшим бывшим учеником легендарного мастера боевых искусств Серебряного Клыка и, кажется, руководствуется неизвестными мотивами. Как бы то ни было, этого зверя-человека кажется неудержимым. Заинтригованный этим загадочным новым врагом и ненасытной жаждой денег, Сайтама решает воспользоваться возможностью и присоединяется к интересному соревнованию по боевым искусствам. Когда турнир начинается, а Гару продолжает буйствовать, появляется новая великая угроза, угрожающая всему человеческому миру. Могло ли это, наконец, быть той катастрофой, которая была предсказана великой провидицей мадам Сибабава? [Написано MAL Rewrite]

StudioJ.C.Staff

SourceWeb manga

ThemesParodySuper Power

DemographicSeinen

1450480 7,75 20150705 Шарлотта

ТВ, 2015 Завершено 13 эп., 24 мин.

Если бы не его способность завладевать разумом и телом людей, Юу Отосака был бы обычным старшеклассником. Хотя это длится всего пять секунд за раз, таинственная сила Юу позволила ему обманным путем добраться до вершины своего класса и поступить в престижную среднюю школу, где он продолжает свои нечестные действия. Его махинации в конце концов останавливает Нао Томори — упрямый президент студенческого совета Академии Хосиноуми, который видит его обман насквозь. По принуждению Нао убеждает Юу перейти в Хошиноуми и присоединиться к студенческому совету. Академия Хосиноуми — это тайное учреждение, созданное для подростков, обладающих сверхъестественными способностями, а студенческий совет служит средством обнаружения тех, кто злоупотребляет своими способностями. Поскольку Юу неохотно помогает в делах совета, группа намеревается найти и защитить новых пользователей способностей от вреда. Однако по мере того, как они продолжают исследовать способности, их открытия запутывают их в гораздо более сложных вещах, чем они могли себе представить. [Написано MAL Rewrite]

Студия П.А. Работы

ИсточникОригинал

ТемыШколаСуперсила

1297373 8,81 201

ТВ, 2019Готово 13 эп., 24 мин.

Действие Комедия Сверхъестественное

Шигео «Моб» Кагеяма сейчас взрослеет и понимает свою роль сверхъестественного экстрасенса, способного радикально влиять на жизнь других людей. Он и его наставник Рейген Аратака продолжают выполнять сверхъестественные запросы клиентов, будь то изгнание злых духов или решение городских легенд, преследующих горожан. Хотя рабочий процесс остается прежним, Моб больше не просто слепо следует за Рейгеном. Со всем его опытом как невероятно сильного экстрасенса сверхъестественные приключения Моба теперь имеют для них большее значение. Вещи приобретают серьезный и мрачный тон, поскольку опасности, с которыми сталкиваются Моб и Рейген, гораздо более ощутимы и тревожны, чем когда-либо прежде. [Написано MAL Rewrite]

StudioBones

SourceWeb манга

ThemeSuper Power

Bungo Stray Dogs

1189887 7,82 20160407 Банго Бродячие псы

ТВ, 2016Готово 12 эп., 23 мин.

Действие Комедия Тайна Сверхъестественное

Вот уже несколько недель приют Ацуши Накадзимы терзает мистический тигр, о котором, похоже, не знает только он. Подозреваемый в причастности к странным происшествиям, 18-летнего подростка внезапно выгоняют из приюта, и он остается голодным, бездомным и скитается по городу. Голодая на берегу реки, Ацуши спасает от утопления довольно эксцентричного человека по имени Осаму Дазай. Причудливый энтузиаст самоубийства и сверхъестественный детектив, Дазай расследует дело того же тигра, который терроризировал мальчика. Вместе с партнером Дазая Доппо Куникидой они разгадывают тайну, но ее разрешение ставит Ацуши в затруднительное положение. По мере того, как происходят различные странные события, Ацуши вынужден присоединиться к их фирме сверхъестественных следователей, берущихся за необычные дела, с которыми полиция не может справиться, вместе со своими многочисленными загадочными коллегами. [Написано MAL Rewrite]

StudioBones

SourceManga

ThemeSuper Power

DemographicSeinen

1139700 7,43 20111014 Виновная корона

ТВ, 2011 г. Завершен 22 эп., 24 мин.

Действие Драма Sci-Fi

24 декабря 2029 года — день, в просторечии известный как «Потерянное Рождество», — вирус Апокалипсиса распространился по Японии, неся смерть ее гражданам и погрузив страну в полнейший хаос. Стремясь навести порядок, Организация Объединенных Наций отправляет штаб для оказания помощи в кризисе, сдерживая вспышку, лишая при этом всякой политической автономии. Спустя десятилетие страна все еще живет под их контролем, не в силах вырваться из-под их драконовского правления. Разочарованная состоянием нации, группа сопротивления под названием «Похоронное бюро» стремится освободить Японию от штаб-квартиры. Во главе с харизматичным Гаем Цуцугами группа замышляет украсть флакон с «геномом пустоты» для достижения своих целей. Флакон попадает в руки интернет-вокалистки Инори Юзурихи, за которой в конечном итоге охотятся силы Anti-Bodies штаб-квартиры. Ей некуда идти, она ищет убежища на складе, где встречает Шуу Ому — социально неуклюжего старшеклассника, который является большим поклонником ее музыки. Шу оказывается втянутым в конфликт в тот момент, когда он спасает Инори, и геном Пустоты разбивается в его руке, наделяя его «Силой королей». Изучая, как контролировать свою новую великую способность, Шуу теперь должен сражаться, чтобы освободить Японию от ее жестоких угнетателей. [Написано MAL Rewrite]

StudioProduction I.G

SourceOriginal

ThemesMechaRomantic SubtextSuper Power

1122347 8.15 198

ТВ, 1989 г. Готово 291 эп., 24 мин.

Действие Приключение Комедия Fantasy

Спустя пять лет после победы на Всемирном турнире по боевым искусствам Гоку живет мирной жизнью со своей женой и сыном. Однако это меняется с появлением таинственного врага по имени Радиц, который представляется давно потерянным братом Гокуу. Он показывает, что Гокуу — воин из когда-то могущественной, но теперь практически вымершей расы Сайян, чей родной мир был полностью уничтожен. Когда его отправили на Землю младенцем, единственной целью Гоку было завоевать и уничтожить планету; но после того, как он перенес амнезию из-за травмы головы, его жестокий и дикий характер изменился, и вместо этого он вырос добрым и воспитанным мальчиком, который теперь борется, чтобы защитить других. С его неудачной попыткой насильно завербовать Гокуу в качестве союзника, Радиц предупреждает друзей Гокуу о новой угрозе, которая быстро приближается к Земле — угрозе, которая может ввергнуть Землю в межгалактический конфликт и заставить содрогаться сами небеса. Война будет вестись за семь мистических шаров дракона, и только сильнейшие выживут в Dragon Ball Z. [Написано MAL Rewrite]

СтудияToei Animation

ИсточникМанга

ТемыБоевые искусстваСуперсила

ДемографияСёнен

Моя геройская академия 5 сезон

962265 7,42 20210327 Boku no Hero Academia 5-й сезон

ТВ, 2021 Завершено 25 эп. , 23 мин.

Действие

Класс 1-A Академии UA был в центре внимания общественности из-за многочисленных нападений злодеев, с которыми они столкнулись за последний учебный год. Это внимание сильно огорчило соперников класса 1-A, класса 1-B. Желая доказать свои навыки, они с нетерпением ждут предоставленной им возможности: серии тренировочных сражений между учениками каждого класса. Классы разделены на отряды по четыре человека, каждому из которых поручено захватить других членов группы. Побеждает та группа, которая первой обезопасит всю команду соперника. Хотя это звучит просто, в дело вмешивается студентка общего курса Хитоши Шинсо, которая хочет перейти на курс героев. Несмотря на то, что он использовал свое обучение с классным руководителем класса 1-A Сёта «Голова-ластик» Айзава, чтобы доказать, что он способен быть настоящим героем, он все еще сильно отстает от других из-за отсутствия у него опыта. Однако Шинсо полон решимости преодолеть эту проблему. Так начинается ожесточенное соревнование между классами 1-A и 1-B, каждый из которых пытается доказать свое превосходство над другим. [Написано MAL Rewrite]

StudioBones

SourceManga

ThemesSchoolSuper Power

DemographicShounen

936873 7,96 19860226 Жемчуг дракона

ТВ, 1986 г. Готово 153 эп., 24 мин

Приключение Комедия Fantasy

Гокуу Сон — мальчик, который живет в лесу в полном одиночестве, пока девочка по имени Булма не сталкивается с ним в поисках набора волшебных предметов, называемых «Жемчуг дракона». Поскольку артефакты, как говорят, исполняют одно желание того, кто соберет все семь, Булма надеется собрать их и пожелать идеального парня. У Гоку оказывается шар дракона, но, к сожалению для Булмы, он отказывается расстаться с ним, поэтому она заключает с ним сделку: он может присоединиться к ней в ее путешествии, если он позволит ей позаимствовать силу шара дракона. С этим они вдвоем отправились в путешествие всей жизни. Они не отправляются в путешествие в одиночку. По пути они встречают старого Мутен-Роси и подражателя Куририна, с которым Гокуу тренируется, чтобы стать более сильным мастером боевых искусств для предстоящего Всемирного турнира по боевым искусствам. Однако это еще не все развлечения и игры; способность воплотить любое желание в реальность — это мощная способность, и есть другие, которые поступили бы намного хуже, чем просто желали бы парня. Чтобы остановить тех, кто попытается злоупотребить легендарной силой, они тренируются, чтобы стать более сильными бойцами, используя свою новообретенную силу, чтобы помогать окружающим их людям на этом пути. [Написано MAL Rewrite]

СтудияToei Animation

ИсточникМанга

ТемыБоевые искусстваСуперсила

ДемографияСёнен

Темнее черного

880151 8.07 20070406 Темнее черного: Куро-но Кейякуся

ТВ, 2007 г. Завершен 25 эп., 24 мин.

Действие Тайна Sci-Fi

Прошло 10 лет с тех пор, как «Врата рая» появились в Южной Америке, а «Врата ада» — в Японии, завесив когда-то знакомое ночное небо гнетущим пейзажем. Их цели неизвестны, эти Врата представляют собой пространства, в которых игнорируются сами законы физики. С появлением Врат появились Подрядчики, которым в обмен на их человечность были дарованы сверхъестественные способности. В японском городе, окружающем Врата Ада, начальник Секции 4 Мисаки Кирихара сталкивается с печально известным подрядчиком под кодовым именем Хей. Прозванный «Черным жнецом» в подземном мире, Хей, как и его соратники, выполняет миссии таинственного и безжалостного Синдиката, медленно сдирая темные слои, скрывающие гнусный заговор, который угрожает самому существованию Подрядчиков. Научно-фантастический триллер Тенсая Окамура представляет собой тонкое разоблачение войны, в которой политические позиции и справедливость не имеют значения, — войны, которая ведется исключительно в тени. [Написано MAL Rewrite]

StudioBones

SourceOriginal

ThemeSuper Power

Blood Blockade Battlefront

795006 7,61 20150405 Кеккай Сенсен

ТВ, 2015 Завершено 12 эп. , 26 мин

Действие Комедия Фантазия Сверхъестественное

Сверхзвуковые обезьяны, вампиры, говорящие рыболюди и всевозможные сверхъестественные монстры, живущие рядом с людьми — это уже некоторое время является частью повседневной жизни в Уделе Хеллсалема, ранее известном как Нью-Йорк. Когда три года назад открылись ворота между Землей и Запредельным, жители Нью-Йорка и существа из другого измерения оказались в ловушке непроницаемого пузыря и были вынуждены жить вместе. Весы — это секретная организация, состоящая из чудаков и сверхлюдей, которым поручено поддерживать порядок в городе и следить за тем, чтобы хаос не распространился на остальной мир. Занимаясь фотографией в качестве хобби, Леонардо Уотч живет обычной жизнью со своими родителями и сестрой. Но когда он получает «Всевидящее око богов» за счет зрения своей сестры, он отправляется в Удел Хеллсалема, чтобы помочь ей, найдя ответы о таинственных силах, которые он получил. Вскоре он сталкивается с Весами, и когда Лео неожиданно присоединяется к их рядам, он получает больше, чем рассчитывал. Кеккай Сенсен следует за злоключениями Лео в самом странном месте на Земле с его такими же странными товарищами, когда обычный мальчик невольно видит, как его жизнь превращается в нечто экстраординарное. [Написано MAL Rewrite]

StudioBones

SourceManga

ThemesSuper PowerVampire

Демографический Shounen

A Certain Magical Index

756890 7,37 20081005 Тоару Мадзюцу без индекса

ТВ, 2008 г. Завершен 24 эп., 23 мин.

Действие Sci-Fi

Академгород, Япония, находится на переднем крае науки. Помимо того, что он на 30 лет опережает мир в технологическом отношении, более трех четвертей населения этого своеобразного города составляют студенты, развивающие свои экстрасенсорные способности в качестве эсперов в различных учреждениях. Среди этих учеников Тома Камидзё, старшеклассник с самым низким психическим рангом, равным нулю, но обладающий таинственной силой, которую не может понять ни один ученый: «Разрушитель воображения», которая позволяет ему сводить на нет другие сверхъестественные способности. Это, однако, нисколько не влияет на жизнь Камидзё, поскольку он играет роль обычного подростка; то есть до тех пор, пока он не встречает странную Index Librorum Prohibitorum, молодую девушку, которая выучила наизусть все запрещенные гримуары, и теперь за Индекс охотится опасная организация. С несколькими магами, стремящимися навредить девушке, Камидзё будет защищать своего нового компаньона любой ценой, поскольку он открывает странное новое царство сверхъестественного. [Написано MAL Rewrite]

StudioJ.C.Staff

Роман SourceLight

ThemeSuper Power

740117 7,42 20150705 Жемчуг дракона Супер

ТВ, 2015 Завершено 131 эп. , 23 мин.

Действие Приключение комедия Fantasy

Через семь лет после событий Dragon Ball Z на Земле воцарился мир, и ее жители живут вдали от любых опасностей, таящихся во вселенной. Однако этот мир недолговечен; спящее зло пробуждается в темных уголках галактики: Берус, безжалостный Бог Разрушения. Обеспокоенный пророчеством о том, что он будет побежден «Супер Сайянским Богом», Берус и его ангельский помощник Вис начинают искать во вселенной это таинственное существо. Вскоре они достигают Земли, где встречают Гоку Сона, одного из самых могущественных воинов планеты, и его таких же могущественных друзей. [Написано MAL Rewrite]

СтудияToei Animation

ИсточникМанга

ТемыБоевые искусстваСуперсила

ДемографияСёнен

Bungo Stray Dogs 2

732602 8.20 20161006 Бродячие псы Бунгу 2-й сезон

ТВ, 2016Готово 12 эп. , 23 мин.

Действие Тайна Сверхъестественное

Несмотря на различия в положении, трое мужчин — самый молодой руководитель портовой мафии Осаму Дазай; участник с самым низким рейтингом, Сакуносукэ Ода; и агент разведки Анго Сакагути — собираются в баре «Люпин» в конце дня, чтобы расслабиться и насладиться компанией друзей. Однако однажды ночью Анго исчезает. Фотография, сделанная в баре, — это все, что осталось от троих вместе. Перенесемся в настоящее: Дазай теперь член Вооруженного детективного агентства. Гильдия, американская одаренная организация, вступила в бой и намерена получить разрешение на работу от Агентства. Теперь они должны разделить свое внимание между двумя группами, Гильдией и Портовой мафией, которые выступают против самого их существования. [Написано MAL Rewrite]

StudioBones

SourceManga

ThemeSuper Power

DemographicSeinen

714845 7,44 20121005 К

ТВ, 2012 г. Завершен 13 эп., 24 мин.

Действие Тайна Сверхъестественное

«Короли» — это люди, которые были наделены невероятными сверхъестественными способностями и получили возможность вербовать других в свои кланы. Защита жизни и чести членов своего клана — неотъемлемая часть обязанностей королей. После того, как видео, изображающее гнусное убийство члена Красного клана, стало вирусным, скромный студент Яширо Исана обвиняется в убийстве. Теперь за его головой ведется розыск, в результате чего он сталкивается с печально известным «Черным псом» Куро Ятогами — опытным фехтовальщиком и мастером боевых искусств, решившим следовать желаниям своего покойного хозяина, Седьмого короля. Между тем, нынешний Красный Король, Микото Суо, сталкивается с неминуемой кончиной, поскольку поиски Яширо сужаются. Но пока Яширо пытается доказать свою невиновность, за кулисами раскрывается еще больший заговор; В его памяти начинают появляться тучи, а близкие друзья начинают сомневаться в самом его существовании. То, что началось как простое убийство, теперь ведет к полномасштабной войне между королями, в которой на карту поставлена сама судьба мира. [Написано MAL Rewrite]

StudioGoHands

SourceOriginal

ThemeSuper Power

My Hero Academia: Two Heroes

666728 7,57 20180803 Boku no Hero Academia Фильм 1: Futari no Hero

Фильм, 2018Завершен 1 эп, 96 мин.

Действие

U.A. Учащиеся средней школы 1-А класса отправились на летние каникулы. Изуку Мидория сопровождает своего наставника Всемогущего на праздничный фестиваль супергероев на Ай-Айленде, изолированном участке земли, посвященном изучению причуд и всему остальному, что связано с бизнесом героев. Мидории предоставляется возможность встретиться с другом Всемогущего Дэйвом и дочерью Дэйва Мелиссой, двумя талантливыми инженерами-героями. Он также встречает своих одноклассников, большинству из которых была предоставлена возможность провести часть летних каникул на фестивале. Однако таинственный отряд злодеев проникает на Ай-Айленд, и Мидория и его друзья должны противостоять им, используя свои развивающиеся причуды, чтобы отбиться от нового врага и раскрыть коварный заговор. [Написано MAL Rewrite]

StudioBones

SourceManga

ThemeSuper Power

Демографический Shounen

652085 8.02 20061003 Д. Грей-мэн

ТВ, 2006 г. Завершен 103 эп., 23 мин.

Действие Приключение Комедия

Потеря любимого человека настолько болезненна, что иногда хочется иметь возможность воскресить его — слабость, которую использует загадочный Миллениум Граф. Чтобы сделать свое механическое оружие известным как «Акума», он использует души мертвых, которых призывают обратно. Как только душа помещается в Акума, она оказывается в ловушке навсегда, и единственный способ спасти их — изгнать их из их сосуда с помощью оружия Анти-Акумы «Невинность». Проведя три года в качестве ученика генерала Кросса, Аллен Уокер отправляется в Черный Орден — организацию, состоящую из тех, кто готов сразиться с Акумой и Графом Тысячелетия, — чтобы стать официальным экзорцистом. С рукой как его Невинностью и проклятым глазом, который может видеть страдающие души внутри Акума, Аллен и его товарищи-экзорцисты должны остановить окончательный заговор Тысячелетнего графа: тот, который может привести к разрушению мира. [Написано MAL Rewrite]

StudioTMS Entertainment

ИсточникМанга

ТемыМифологияСуперсила

ДемографияСёнен

627756 7,75 20070404 Клеймор

ТВ, 2007 г. Завершен 26 эп., 23 мин.

Действие Приключение Фантазия Сверхъестественное

Когда демон-оборотень, жаждущий человеческой плоти, известный как «йома», прибывает в деревню Раки, одинокая женщина с серебряными глазами входит в город с мечом за спиной. Она «Клеймор», существо, созданное как получеловек-полуйома специально для истребления этих монстров. После того, как семья Раки убита, Клеймор спасает ему жизнь, но впоследствии его изгоняют из дома. Поскольку больше некуда идти, Раки находит Клеймор, известную как Клэр, и решает следовать за ней в ее путешествиях. По мере того, как пара путешествует из города в город, по пути побеждая йома, выясняется больше об организации Клэр и ее товарищах-воинах. С каждым очищенным городом и уничтоженным демоном они приближаются к йома, которым Клэр стремилась отомстить с тех пор, как она решила стать Клеймором. [Написано MAL Rewrite]

StudioMadhouse

ИсточникМанга

ТемыГорМифологияСуперсила

ДемографияСёнен

582021 6,47 19960207 Жемчуг дракона GT

ТВ, 1996 г. Завершен 64 эп., 24 мин.

Действие Приключение Комедия Фантазия Sci-Fi

После долгих лет поисков император Плов наконец-то заполучил шары дракона Черной звезды, которые, как говорят, в два раза мощнее обычных земных. Плов собирается загадать желание мирового господства, когда его прерывает Гоку Сон. В результате Плов проваливает свое желание и случайно превращает Гоку обратно в ребенка. После того, как желание исполняется, Шары Дракона Черной Звезды разлетаются по галактике. Однако Гокуу обнаруживает, что они заставят Землю взорваться, если их всех не вернут в течение года. Объединившись со своей внучкой Пан и молодым взрослым Стволом, Гокуу отправляется в приключение по вселенной, чтобы найти Шары Дракона Черной Звезды и спасти свою планету от разрушения. [Написано MAL Rewrite]

StudioToei Animation

SourceManga

ThemeSuper Power

Демография Shounen

A Certain Scientific Railgun

566134 7,68 200

ТВ, 2009 г. Завершен 24 эп., 24 мин.

Действие Sci-Fi

Академгород, полный студентов, находится в авангарде научного прогресса и является домом для программы развития эсперов. Семь эсперов «Уровня 5» являются самыми могущественными в Академгороде, а третье место среди них занимает Микото Мисака, ученица средней школы, манипулятор электричеством, известный как «Рейлган». Когда по всему городу начинают происходить странные инциденты, она обнаруживает, что каждое преступление связано с неуловимым «Верхним уровнем», легендарным устройством, которое якобы повышает уровень эспера своего пользователя. По мере обострения ситуации становится очевидным, что на Верхнем уровне есть нечто большее, чем кажется на первый взгляд, и что Академгород может быть гораздо более запутанным местом, чем гламурная утопия, которой он кажется. Toaru Kagaku no Railgun сосредотачивается на Микото и ее друзьях, а также на опасных ситуациях, в которых они оказываются, когда они оказываются втянутыми в дела Верхнего уровня. Как говорит Микото: «В этом городе никогда не бывает скучно». [Написано MAL Rewrite]

StudioJ.C.Staff

SourceManga

ThemeSuper Power

Reborn!

527861 8. 14 20061007 Katekyo Hitman возрождается!

ТВ, 2006 г. Завершен 203 эп., 24 мин.

Действие Комедия

Нет ничего проще — Цунаёси Савада никуда не годится. Он неуклюжий, бездарный и отчаянно влюблен в школьного кумира Кёко Сасагаву, девушку, которая совершенно ему не подходит. Одноклассники прозвали его «Неудачник Тсуна», он кажется олицетворением неудачи в образе ученика средней школы. Скучная жизнь Тсуны принимает неожиданный оборот, когда он встречает таинственного Возрожденного, который оказывается наемным убийцей… и, что шокирует, младенцем! Посланный из самой сильной мафиозной семьи в Италии, Реборн получил сложную миссию по подготовке скучного школьника к тому, чтобы он стал преемником девятого босса пресловутой семьи Вонгола, который находится на грани выхода на пенсию. У скучного мальчика впереди изнурительный путь, но с помощью его новых преступных сообщников и своеобразного домашнего наставника, возможно, даже Неудачник Тсуна сможет достичь величия. [Написано MAL Rewrite]

СтудияArtland

ИсточникМанга

ТемыОрганизованная преступностьСуперсила

ДемографияСёнен

Bungo Stray Dogs 3

519942 8.22 201

ТВ, 2019Готово 12 эп., 23 мин.

Действие Тайна Сверхъестественное

После завершения трехсторонней организационной войны правительственный чиновник Анго Сакагучи вспоминает событие, которое произошло много лет назад, после смерти бывшего босса портовой мафии. Осаму Дазаю, в то время еще новичку, было поручено расследовать слухи, связанные с таинственным взрывом, уничтожившим часть города много лет назад, и его связью с предполагаемым новым появлением бывшего босса. По независящим от него обстоятельствам он становится партнером Чуи Накахара, одаренного, но импульсивного лидера соперничающего клана, известного как «Овцы», чтобы раскрыть правду, стоящую за этим делом, и пролить свет на миф об Арахабаки. бог огня, который мог бы привести Дазая к разгадке дела. Между тем, в настоящее время для Вооруженного детективного агентства все идет как обычно. Однако их мирный разрыв продлится недолго, поскольку старые и новые враги собираются с силами и готовятся к новому противостоянию. [Написано MAL Rewrite]

StudioBones

SourceManga

ThemeSuper Power

DemographicSeinen

My Hero Academia: Heroes Rising

489585 8.01 201

Boku no Hero Academia Фильм 2: Герои: Восход

Фильм, 2019Завершен 1 эп, 104 мин.

Действие

Изуку «Деку» Мидория и его сокурсники в классе 1-A курса героев UA High были выбраны для участия в программе безопасности на острове Набу. Чтобы еще больше улучшить свои навыки и получить опыт в более Обычная героика, студенты помогают добрым гражданам мелкими услугами и повседневными делами.При низком уровне преступности в тихом сообществе все вроде бы хорошо, но появление нового злодея грозит испытать мужество студентов и бросить вызов своим способностям героев. Безжалостный злодей по имени Девятый ищет некую «причуду», необходимую для выполнения его дьявольского плана — создания общества, в котором безраздельно правят только те, у кого самые сильные причуды. Поскольку его нападение на остров Набу ставит под угрозу жизни жителей, обеспечение безопасности граждан становится первоочередной задачей для класса 1-A; также необходимо победить Девятого вместе с его злыми сообщниками. Простая стратегия формулируется до тех пор, пока мальчику по имени Кацума Шимано, с которым подружился Деку, внезапно не требуется особая защита. Обеспокоенные благополучием мальчика, Деку и его одноклассники теперь должны разработать план, чтобы любой ценой обеспечить безопасность Кацумы. С Девятым, сеющим хаос, чтобы найти катализатор его злонамеренных планов, и героями, отчаянно пытающимися защитить Кацуму от зла, смогут ли Деку и его друзья выйти победителями, или они окажутся не в состоянии выбраться из безнадежной ситуации? [Написано MAL Rewrite]

StudioBones

SourceManga

ThemeSuper Power

Демографический Shounen

482074 7,25 20200104 Игра Дарвина

ТВ, 2020Завершено 11 эп. , 26 мин

Действие Тайна Sci-Fi

Старшеклассник Канаме Судо получает от одноклассника приглашение сыграть в Darwin’s Game, мобильную игру, о которой он никогда не слышал. Однако, как только он открывает приложение, с экрана его телефона внезапно выскакивает зеленая змея и кусает его за шею, оставляя его без сознания. Очнувшись в лазарете без каких-либо признаков укуса змеи, школа приказала ему взять выходной до конца дня. Хотя он озадачен тем, что произошло, он отвергает сюрреалистический опыт как галлюцинацию и садится на поезд домой. К сожалению, его любопытство берет верх над ним, и он снова использует приложение. Поскольку приложение похоже на любую другую боевую игру, Канаме вздохнул с облегчением и решил начать свой первый матч. Однако приятное удивление недолговечно, так как его игровой противник неожиданно появляется прямо перед ним и пытается выследить его с ножом. Отчаянно спасаясь бегством, Канаме складывает два и два и понимает, что Игра Дарвина — это не обычная игра, а жестокая борьба за выживание. [Написано MAL Rewrite]

StudioNexus

SourceManga

ThemesHigh Stakes GameSuper PowerSurvival

Демографические Shounen

A Certain Magical Index II

432271 7,54 20101008 Тоару Мадзюцу но Индекс II

ТВ, 2010 г. Завершен 24 эп., 23 мин.

Действие Sci-Fi

Поскольку напряженность между миром магии и Академгородом продолжает расти, Тома Камидзё и его рука отрицания должны противостоять как эсперу, так и магу, чтобы защитить жизни окружающих. Конечно, он не одинок в своей борьбе; будь то рядом с ним или вне поля зрения, союзники и враги, как старые, так и новые, вступят в бой, чтобы помочь ему. Toaru Majutsu no Index II продолжает историю боевика и комедии, поскольку масштаб битвы Томы и его союзников становится все больше. На горизонте медленно назревает конфликт, и магия и наука снова пересекутся в грядущей войне. [Написано MAL Rewrite]

StudioJ.C.Staff

Роман SourceLight

ThemeSuper Power

423594 7.03 20140413 Мекакусити Актеры

ТВ, 2014 г. Завершено 12 эп., 23 мин

Комедия Научная фантастика Сверхъестественное

Жарким летним днем 14 августа Синтаро Кисараги впервые за два года вынужден покинуть свою комнату. Во время спора с кибер-девушкой Эне, которая живет в его компьютере, Синтаро Кисараги случайно проливает газировку на клавиатуру. Хотя они пытаются найти замену в Интернете, большинство магазинов закрыты из-за фестиваля Обон, и у них нет другого выбора, кроме как посетить местный универмаг. Выход на улицу очень беспокоит Шинтаро, но мысль о жизни без компьютера еще хуже. Ему просто повезло, что в тот день, когда он наконец вышел, он попал в ужасающую ситуацию с заложниками. К счастью, группа подростков с таинственными способностями глаз, которые называют себя «Мекакуси Дан», помогают Шинтаро разрешить ситуацию. В результате он вынужден присоединиться к их группе вместе с Эне. Их способности кажутся кусочками головоломки, соединяющими друг друга, и по мере того, как раскрывается прошлое каждого члена, секрет, который связывает их вместе, медленно раскрывается. [Написано MAL Rewrite]

StudioShaft

SourceMusic

ThemeSuper Power

Blood Blockade Battlefront & Beyond

394818 7,80 20171008 Кеккай Сенсен и не только

ТВ, 2017Готово 12 эп., 24 мин.

Действие Комедия Фантазия Сверхъестественное

Три года назад в Нью-Йорке открылись врата между Землей и Потусторонним миром, заманив в непроницаемый пузырь как инопланетных существ, так и людей. После восстановления города монстры, магия и безумие стали обычным явлением в районе, ныне известном как Удел Хеллсалема. Леонардо Уотч, молодой фотограф, невольно получивший «Всевидящее око богов» в обмен на зрение своей сестры, приехал в этот паранормальный город, чтобы найти ответы на таинственную силу, которой он обладает. Позже он обнаруживает, что его жизнь резко изменилась, когда он присоединяется к Весам, секретной организации людей со сверхъестественными способностями, призванной поддерживать порядок в повседневном хаосе Уделы Хеллсалема. Однако это только начало неожиданного путешествия Леонардо вперед. Несмотря на постоянную угрозу со стороны потусторонних врагов, он полон решимости раскрыть секреты своей силы и найти способ вернуть сестре зрение. Kekkai Sensen & Beyond следует за Леонардо, который вместе со своими товарищами отправляется в новые безумные приключения, борясь за мир и порядок. [Написано MAL Rewrite]

StudioBones

SourceManga

ThemesSuper PowerVampire

Демографические Shounen

Darker than Black: Gemini of the Meteor

392619 7,44 200

ТВ, 2009 г. Завершен 12 эп., 24 мин.

Действие Тайна Sci-Fi

Однажды ночью, когда метеоры проносятся по звездному небу, Шион Павличенко становится подрядчиком. Несмотря на трансформацию своего брата, сестра-близнец Шион Суо продолжает жить довольно обычной жизнью, посещая среднюю школу со своими друзьями и попадая в неловкость взросления. Однако все меняется, когда в ее дом вторгается человек в маске, одетый в черное, разрушая любое чувство нормальности, которое у нее когда-то было. Выяснилось, что она обладает собственными скрытыми способностями Подрядчика, Суо оказывается зажатой между семьей, друзьями и собственным чувством цели, когда она отправляется в безжалостный мир головорезов и шпионажа, который Подрядчики называют своим домом. Тем временем в Токио ведется расследование внезапного обрушения Врат Ада, и пророческие признаки гибели указывают на седовласую куклу. [Написано MAL Rewrite]

StudioBones

SourceOriginal

ThemeSuper Power

Aesthetica of a Rogue Hero

389907 6,76 20120706 Хагуре Юуша но Эстетика

ТВ, 2012 г. Завершен 12 эп., 24 мин.

Действие Фантазия Ecchi

С момента открытия «Синдрома Самона» 30 лет назад тысячи молодых людей отправились в фантастические миры, и немногим вернувшимся удалось сохранить особые способности, приобретенные ими в этих параллельных вселенных. Акацуки Усава, известный как «Герой-разбойник», отказывается от своей мирной жизни в фантастическом мире Алайзард, чтобы столкнуться с новыми проблемами по возвращении на Землю. Он возвращается с Миу, дочерью Короля Демонов, которого он победил, и теперь вынужден скрывать свою истинную личность, изображая из себя его младшую сестру. Вскоре они присоединяются к Вавилону, специальной школе, предназначенной для тех, кто приобрел особые способности и магические силы во время путешествия в мир фантазий. Казалось бы, Вавилон был основан для обучения молодых межпространственных путешественников и «наведения их на правильный путь ради человечества и самих себя», но его истинная цель остается неясной для псевдобратьев и сестер. Смогут ли Акацуки и Миу одолеть враждебный, могущественный студенческий совет и раскрыть силы, действующие за кулисами? [Написано MAL Rewrite]

StudioArms

ИсточникЛегкий роман

ТемыIsekaiSuper Power

381735 7.06 20080702 Секирей

ТВ, 2008 г. Завершен 12 эп., 23 мин.

Действие Комедия Ecchi

Борющийся, но блестящий 19-летний Минато Сахаши во второй раз провалил вступительные экзамены в колледж, в результате чего окружающие считают его бесполезным. Однако ход его, казалось бы, безрадостного будущего резко меняется, когда с неба в его жизнь падает красивая, сверхъестественная женщина. Эта женщина, Мусуби, уникальное существо, известное как «Сэкирей», гуманоидный инопланетянин с экстраординарными способностями. Эти инопланетяне известны тем, что целуют людей, несущих ген Асикаби, чтобы пробудить дополнительные скрытые силы глубоко внутри. Признавая потенциал в, казалось бы, незначительном юноше, Мусуби целует сбитого с толку Минато, инициируя связь между ними двумя. Это затягивает его в мир высоких ставок Сэкирей, где он и его новый партнер должны соревноваться с другими в битве за выживание, называемой «План Сэкирей». Однако, без ведома участников, существует гораздо больший риск, чем то, что первоначально влекло за собой соревнование. [Написано MAL Rewrite]

StudioSeven Arcs

SourceManga

ThemesHaremSuper Power

A Certain Scientific Railgun S

361001 8.03 20130412 Тоару Кагаку но Рейлган S

ТВ, 2013 г. Завершено 24 эп., 24 мин.

Действие Sci-Fi

Микото Мисака и ее друзья вернулись, расследуя слухи в Академгороде. Вскоре Микото обнаруживает нечто ужасающее: по всему городу проходят ужасающие эксперименты, связанные с убийством тысяч эсперов. Причем эти эсперы далеко не простые люди: это клоны самой Микото. Чувствуя ответственность за их лечение, она отправляется положить конец экспериментам; однако силы, противостоящие ей, намного опаснее, чем она ожидала, и Микото сталкивается с одними из самых могущественных эсперов, которых только можно себе представить. Toaru Kagaku no Railgun S продолжает историю Рейлгана, поскольку она отчаянно борется за то, чтобы положить конец бесчеловечным экспериментам, которые, по ее мнению, она помогла провести, и в процессе ее жизнь погрузилась в глубокое отчаяние. В Академгороде никогда не бывает скучно, но никто и не говорил, что все они будут приятными. [Написано MAL Rewrite]

StudioJ.C.Staff

SourceManga

ThemeSuper Power

Baka & Test – Summon the Beasts 2

354233 7,70 20110708 Бака для тестирования Шоукандзю Ни!

ТВ, 2011 г. Завершен 13 эп., 24 мин

Комедия Романтика

Болваны класса F возвращаются с новыми злоключениями! Вместо того, чтобы отчаянно конкурировать с элитными учениками класса А за лучшие условия, у них есть другие проблемы. В то время как девочки постоянно борются за внимание мальчиков, Акихиса Ёсии и Юдзи Сакамото подвергаются шантажу преследователя, который угрожает раскрыть их самые неловкие секреты всей школе. Более того, у всех аватарка начинает вести себя странно. Наполненные кровью из носа и глазами, мальчики класса F должны работать вместе, чтобы раскрыть личность сталкера и справиться с несчастьями, которые приходят с любовью среди дураков. [Написано MAL Rewrite]

StudioSILVER LINK.

SourceЛегкий роман

ТемыLove PolygonSchoolSuper Power

Dragon Ball Z Kai

350763 7,72 200

Жемчуг дракона Кай

ТВ, 2009 г. Завершен 97 эп., 23 мин.

Действие Приключение Комедия Fantasy

Спустя пять лет после событий Dragon Ball эксперт по боевым искусствам Гоку уже взрослый мужчина, женатый на своей жене Чи-Чи, у которого есть четырехлетний сын по имени Гохан. Во время встречи на Черепашьем острове со своими старыми друзьями Мастером Роши, Криллином, Булмой и другими празднества прерываются, когда гуманоидный инопланетянин по имени Радиц не только раскрывает правду о прошлом Гокуу, но и похищает Гохана. Поскольку Радиц демонстрирует силу, превосходящую все, что Гокуу видел раньше, он вынужден объединиться со своим старым врагом Пикколо, чтобы спасти своего сына. Но когда Гокуу и Пикколо раскрывают секрет семи мистических шаров дракона, исполняющих желания, Радитцу, он сообщает дуэту, что есть еще представители его расы, сайяны, и они не упустят возможности захватить силу дракона. Шары дракона для себя. Эти события начинают сагу Dragon Ball Kai, историю, в которой Гокуу, его друзья и семья постоянно защищают галактику от все более мощных угроз. Причудливые, комичные, трогательные и угрожающие персонажи собираются вместе в серии сражений, в которых силы и способности Гокуу и его друзей выходят за пределы всего, что они когда-либо испытывали.

СтудияToei Animation

ИсточникМанга

ТемыБоевые искусстваСуперсила

ДемографияСёнен

344725 7,76 20010704 Король-шаман

ТВ, 2001 г. Завершено 64 эп., 23 мин.

Действие Приключение Комедия Сверхъестественное

В Токио вот-вот начнется битва: битва шаманов, турнир, проводимый каждые пятьсот лет, где шаманы — те, кто может управлять духами — противостоят друг другу в бою. Победитель этого состязания становится Королем-шаманом и единственным, кто может контактировать с Великим Духом и управлять им, позволяя ему изменять мир по своему усмотрению благодаря его огромной силе. Во время поздней ночной прогулки Манта Оямада сталкивается со своим одноклассником, беззаботным Ю Асакурой, который приглашает его понаблюдать за звездами с друзьями, которые, к ужасу Манты, оказываются призраками с местного кладбища! Однако знание, которым обладает Манта — редкое шестое чувство, позволяющее Манте видеть этих духов — вызывает у мальчика симпатию к Вам. Поэтому, когда Ю узнает, что его нового товарища избила местная банда, он решает отомстить за него с помощью Амидамару, призрака-самурая, чью могилу разбил главарь банды. Вскоре Манта узнает больше о мире духов, в том числе о битве шаманов, в которой его новый друг Ю стремится одержать победу. [Написано MAL Rewrite]

StudioXebec

SourceManga

ThemeSuper Power

Демографический Shounen

Black Rock Shooter

337157 6,81 20120203 Черный ★ рок-шутер (ТВ)

ТВ, 2012 г. Завершен 8 эп., 23 мин.

Действие Драма

В первый день средней школы Мато Курои случайно сталкивается с Ёми Таканаси, застенчивой, замкнутой девушкой, которой сразу же проявляет интерес. Мато изо всех сил старается завязать разговор с Ёми, желая подружиться с ней. Сначала ее избегают, но лед трескается, когда Йоми случайно замечает декоративную синюю птицу, прикрепленную к телефону Мато, из книги «Маленькие птички в игре». Обнаружив, что у них есть общие интересы, между ними завязывается крепкая дружба. В альтернативной вселенной молодые девушки существуют как параллельные существа, Мато как Стрелок с Черной Скалы, а Йоми как Мертвый Мастер. Каким-то образом то, что происходит в одном мире, кажется, влияет на другой, и, не подозревая об этом, девушки неосознанно запутываются в нитях судьбы. [Написано MAL Rewrite]

StudiosOrdetSANZIGEN

SourceOther

ThemesMahou ShoujoSuper Power

336874 8.14 20181214 Жемчуг дракона Супер: Броли

Фильм, 2018Завершен 1 эп, 100 мин

Действие Приключение Fantasy

Сорок один год назад на планете Вегета, родине печально известной расы воинов Сайян, король Вегета заметил младенца по имени Броли, чья скрытая сила превосходила силу его собственного сына. Полагая, что сила Броли однажды превзойдет силу его ребенка, Вегеты, король отправляет Броли на пустынную планету Вампа. Отец Броли Парагус следует за ним, намереваясь спасти своего сына. Однако его корабль повреждается, в результате чего двое проводят годы в ловушке в бесплодном мире, не подозревая о спасении, которое однажды придет от неожиданного союзника. Спустя годы на Земле Гокуу Сон и принц Вегета, которые считаются последними выжившими из расы сайян, тренируются на отдаленном острове. Но их спарринг прерывается, когда появление их старого врага Фризы заставляет их искать последний из исполняющих желания Шаров Дракона на замерзшем континенте. Оказавшись там, Фриза хвастается своими новыми союзниками: Парагусом и теперь чрезвычайно могущественным Броли. Легендарная битва, которая сотрясает основу мира, начинается, когда Гокуу и Вегета противостоят Броли, воину, которому нет равных, чья ярость только и ждет, чтобы вырваться на свободу. [Написано MAL Rewrite]

StudioToei Animation

ИсточникМанга

ТемыБоевые искусстваСуперсила

ДемографияShounen

BNA: Brand New Animal

324049 7,36 20200409 БНА

ТВ, 2020Завершено 12 эп. , 22 мин.

Действие Fantasy

На протяжении всей истории люди враждовали со зверолюдами — расой, способной менять форму благодаря своему генетическому «фактору зверя». Из-за этого конфликта зверолюди были вынуждены скрываться. Анима Сити служит убежищем для этих угнетенных людей, где они могут жить без человеческого вмешательства. Во время фестиваля, посвященного 10-летию города, Мичиру Кагемори, человек, внезапно превратившийся в тануки, обнаруживает, что Анима Сити далек от рая. Увидев взрыв на площади, она сталкивается с Широ Огами, несокрушимым волком и поклявшимся защитником всех зверолюдей. Преследуя преступников, стоящих за взрывом, они обнаруживают, что Мичиру совсем не обычный зверолюд, и пытаются исследовать ее таинственное прошлое и сверхъестественные способности. Может ли она оказаться недостающим звеном между людьми и зверолюдами? [Написано MAL Rewrite]

StudioTrigger

SourceOriginal

ThemesAnthropomorphicSuper Power

310324 7,57 20151003 К: Возвращение королей

ТВ, 2015 Завершено 13 эп. , 24 мин.

Действие Сверхъестественное

Напряженность между кланами накаляется, поскольку Зеленый Король начинает предпринимать шаги, которые угрожают ввергнуть мир в столпотворение. После смерти Золотого короля безопасность Дрезденского сланца, источника власти королей, оказалась под угрозой. Нагаре Хисуи, хитрый и загадочный лидер джунглей Зеленого клана, полон решимости любыми возможными способами заполучить могущественный сланец. Прямо на его пути стоит Скипетр 4, Синий клан, возглавляемый их непреклонным королем Рейси Мунаката. Однако мрачный вид его рушащегося Дамоклова меча ставит под угрозу стабильность его клана и всей Японии. Тем временем, все еще оправляясь от своих трагических потерь, Анна Кушина и ее агрессивный клан ХОМРА оказываются втянутыми в игры Зеленого Короля. Среди хаоса Куро Ятогами и Неко остаются уязвимыми, а их любимый друг Яширо Исана, Серебряный Король, пропал без вести. K: Return of Kings рассказывает о борьбе оставшихся кланов против грозных сил Зеленого Короля, когда появляется последний король. [Написано MAL Rewrite]

StudioGoHands

SourceOriginal

ThemeSuper Power

310060 6,73 20121007 Взломщик кода

ТВ, 2012 г. Завершен 13 эп., 24 мин.

Действие Комедия Сверхъестественное

Хотя Сакура Сакуракодзи жизнерадостная и деликатная, она является искусным мастером боевых искусств с чувством справедливости, которое никогда не колеблется — независимо от ситуации. Увидев, как люди горят синим пламенем по дороге домой на автобусе, она звонит в полицию, чтобы привлечь их убийцу к ответственности, но обнаруживает, что улик не осталось. Однако все ее сомнения относительно того, что она увидела, исчезают, когда на следующий день к ее классу присоединяется новая переводная ученица Рей Оогами; он тот самый мальчик, на глазах которого она хладнокровно совершает убийство. Рей добрая, милая и быстро становится популярной, что противоречит обвинениям Сакуры. Достаточно скоро она узнает его истинную природу: взломщик кодов или «тот, кого не существует». К шоку Сакуры, Рей, вооруженная таинственными способностями, стремится восстановить справедливость по принципу «око за око». Решив направить Рей на правильный путь, Сакура держится рядом с ним в надежде избавить его от его путей, прежде чем другие пострадают. [Написано MAL Rewrite]

StudioKinema Citrus

ИсточникМанга

ТемыШколаСуперсила

ДемографияСёнен

Квасер стигматов

306774 6,36 20100110 Seikon не Qwaser

ТВ, 2010 г. Завершен 24 эп., 24 мин.

Действие Сверхъестественное Ecchi

Когда отец Томо Яманобе, бывший директор Академии Святого Михайлова, исчез, он не оставил после себя ничего, кроме произведения искусства под названием «икона». Вскоре после его исчезновения стали распространяться слухи о серийном убийце, нападавшем на студенток академии. Когда Томо и ее сестра Мафую Орибэ возвращаются домой после мучений в школе, Томо спотыкается о раненого седовласого мальчика, который внезапно исчезает, пока за ним ухаживают. Мафую отправляется на его поиски, но обнаруживает, что церковь с иконой горит. Когда она пытается спасти картину, серийный убийца, по слухам, внезапно нападает на нее с таинственной способностью контролировать магний. Появившийся из ниоткуда седовласый мальчик, владеющий железом, спасает Мафую. Мафую узнает, что мальчик по имени Александр Николаевич «Саша» Хелл является «квасером» — существом, способным управлять стихией с помощью силы «сомы», полученной в результате грудного вскармливания. Сбитая с толку испытанием, Мафую безуспешно пытается пройти мимо него, поскольку на следующий день Саша переходит в ее класс. Что станет с обычной школьной жизнью Томо и Мафуйу, если рядом с ними нависла опасность других квасеров? [Написано MAL Rewrite]

StudioHoods Entertainment

SourceManga

ThemeSuper Power

DemographicSeinen

299717 7,70 20151204 Ванпанчмен: Дорога к герою

OVA, 2015 г. Завершено 1 эп, 24 мин.

Действие Комедия

До того, как Сайтама стал тем, кем он является сегодня, он бесконечно тренировался и сражался, чтобы стать героем. В то время как каждая драка оставляет его спортивный костюм в лохмотьях, он всегда чинит его бесплатно благодаря своему местному портному. Однако однажды портной сообщает ему, что он должен закрыть магазин из-за давления со стороны местной банды. Сайтама решает помочь ему и в процессе получает кое-что незаменимое. [Написано MAL Rewrite]

StudioMadhouse

SourceWeb manga

ThemesParodySuper Power

DemographicSeinen

Специальное предложение, 2015 г. Завершено 6 эп., 12 мин.

Действие Комедия

Специальные предложения, включенные в выпуски Blu-ray и DVD One Punch Man.

StudioMadhouse

ИсточникВеб-манга

ТемыПародияSuper Power

DemographicSeinen

[C] CONTROL — Деньги и Душа Возможностей

289155 7.19 20110415 C: Деньги души и контроль возможностей

ТВ, 2011 г. Завершен 11 эп., 22 мин.

Действие Тайна Suspense

Деньги — это сила, и без них жизнь бессмысленна. В стране, экономика которой находится в упадке, студент второго курса экономического университета Кимимаро Йога слишком хорошо понимает этот факт, поскольку он окружен относительно роскошной жизнью своих сверстников и изо всех сил пытается свести концы с концами. Однако его мир переворачивается с ног на голову, когда однажды поздно ночью к его двери приходит незнакомец в цилиндре. Под именем Масакаки посетитель просит Йогу приехать в Восточный финансовый район, место, где деньги текут в изобилии, если кто-то предлагает свое «будущее» в качестве залога. Несмотря на сопротивление, жадность побеждает разум, и Йога принимает предложение; таким образом, принимая мантию «Entre». Но без его ведома земля богатства, в которую он вошел, представляет собой альтернативное царство, построенное по подобию его собственного, где Энтрес вынуждены участвовать в еженедельных дуэлях под названием «Сделки», где на карту поставлен их залог. Столкнувшись со своими соотечественниками и судьбой, Йога должен быстро адаптироваться в этом новом мире, если он надеется защитить свое состояние и будущее и узнать, сколько на самом деле стоят деньги. [Написано MAL Rewrite]

StudioTatsunoko Production

SourceOriginal

ThemeSuper Power

287084 7,26 20140108 Хаматора Анимация

ТВ, 2014 г. Завершено 12 эп., 24 мин

Комедия Драма Тайна

Способность творить чудеса — это не просто сверхъестественное явление; это дар, который проявляется у ограниченного числа людей. «Минимум» или маленькие чудеса — это особые силы, которыми обладают только избранные люди, называемые «Держатели минимума». Детективное агентство Yokohama Troubleshooting, или сокращенно Hamatora, состоит из «минимального держателя PI Duo», Найс и Мурасаки. Их офис — одинокий столик в Cafe Nowhere, где пара и их коллеги ждут новых клиентов. Внезапно работа, которую они начинают получать, кажется, имеет странную связь с серийным убийцей, которого ищет их друг Арт, полицейский. Жертвы убийства имеют одно общее сходство: все они имеют минимальные держатели. Найс и Мурасаки, как сами холдеры, вовлечены в это дело, но какая именно связь между Ниццей и тем, кто все это организует? [Написано MAL Rewrite]

StudioNAZ

SourceMixed media

ThemeSuper Power

Code Geass: Lelouch of the Re;surrection

285614 7,92 201 Код Гиас: Фуккацу но Лелуш

Фильм, 2019Завершен 1 эп, 112 мин

Действие Драма Sci-Fi

С тех пор, как год назад умер человек, считавшийся самым злобным императором Британии, под руководством Организации Объединенных Наций в мире воцарился беспрецедентный мир. Однако это хрупкое спокойствие нарушается, когда вооруженные боевики успешно похищают бывшую принцессу Нанналли ви Британия и Судзаку Куруруги, главного советника Черных рыцарей, что вызывает международный кризис. Могущественное и ненадежное Королевство Зилхстан обвиняется в организации их захвата. Для расследования мировые власти отправляют Каллен Штадтфельд и ее сообщников для секретной операции в страну. Там они встречают бессмертную ведьму Си-Си, которая должна завершить воскрешение человека, ответственного за величайшую революцию в истории, — легенды, которая восстанет, возьмет на себя командование и снова спасет мир от опасности. [Написано MAL Rewrite]

StudioSunrise

SourceOriginal

ThemesMechaMilitarySuper Power

Talentless Nana

281966 7.19 20201004 Муноу на Нана

ТВ, 2020Завершено 13 эп., 23 мин

Сверхъестественное Suspense

Пятьдесят лет назад ужасные существа, прозванные «врагами человечества», внезапно появились по всему миру. Чтобы противостоять этим угрозам, подростки, одаренные сверхъестественными способностями, называемыми «талантами», такими как пирокинез и путешествия во времени, оттачивают свои способности в академии на уединенном острове. Однако Нанао Накадзима сильно отличается от других на острове: у него нет Таланта. Вокруг него много «талантливых» подростков, Нанао часто становится мишенью для издевательств, но даже в этом случае он все еще стремится завершить свое обучение. Вскоре к классу присоединяются двое переведённых учеников, таинственный Кёя Онодера и читающая мысли Нана Хиираги. Но как только все начинают сливаться как товарищи по оружию, загадочные исчезновения начинают угрожать всей основе класса. [Написано MAL Rewrite]

StudioBridge

ИсточникМанга

ТемыПсихологическиеСуперсила

ДемографическиеСёнен

Мадзикои: О! Девушки-самураи

281001 6,69 20111002 Маджи де Ватаси ни Кои Шинасай!

ТВ, 2011 г. Завершен 12 эп., 23 мин

Комедия Романтика Ecchi

Самураи — очень важная часть истории Японии, и быть связанным с ними каким-либо образом — это, вероятно, одна из самых вдохновляющих вещей, на которые может надеяться юный старшеклассник. Город Каваками известен тем, что среди его жителей много предков-самураев, и в целом окружен атмосферой боевого духа, верности и преданности делу. В Maji de Watashi ni Koi Shinasai! студенты Академии Каваками ежедневно используют эти знания, готовятся ли они к экзаменам, участвуют ли в спортивных соревнованиях или стараются бережно относиться к своим традициям. Ямато Наоэ — один из таких учеников, и шесть его ближайших друзей (три мальчика и три девочки) составляют идеальную команду для дружбы, соперничества и мотивации. Однако даже у самураев есть слабости. Хотя баланс и долгая дружба их группы долгое время не нарушались, когда в группу входят две новые девушки, все становится намного интереснее. Они должны не только поддерживать то, что они считают самурайской традицией, но теперь они также должны делать это с большим количеством «отвлечений».

StudioLerche

ИсточникВизуальный роман

ТемыГаремБоевые искусстваШколаСуперсила

269615 6,39 200

Кемпфер

ТВ, 2009 г. Завершен 12 эп., 24 мин.

Действие Комедия Девушки любят Романтика Ecchi

Пробуждение, превращенное в красивую девушку, может быть предметом фантазий некоторых парней, но когда чучело тигра сообщает внезапно изнеженному Нацуру, что он теперь Кампфер, мистический боец, который должен сражаться с другими Кампферами в женском обличии. , его жизнь превращается в сущий кошмар! Если оставить в стороне очевидные «сантехнические» проблемы, оказывается, что лучший друг детства Нацуру качается в другую сторону, и ОНА влюблена в его новое женское тело. Не достаточно сложно? В школе Нацуру есть отдельные секции для мальчиков и девочек, так что теперь он и она учатся вдвоем. Ходят слухи, что он встречается с ней. И есть другие Кампферы, посещающие школу, которые хотят взять ее с собой, и он не уверен, какие из них означают «на свидании», а какие — «навсегда». О, и мы упоминали, что некоторые Кампферы используют мечи и ружья?! Гормоны, кулаки и другие части тела будут летать, поскольку смелый, новый защитник гендера должен стать соперником или умереть! (Источник: Sentai Filmworks)

StudioNomad

ИсточникЛегкий роман

ТемыMagical Sex ShiftSchoolSuper Power

268821 0 20221006 Моб Психо 100 III

ТВ, 2022Ещё не в эфире ? EPS, 0 мин

Действие комедия Сверхъестественное

Третий сезон Моб Психо 100.

StudioBones

Манга SourceWeb

ThemeSuper Power

267533 6. 33 20111005 Макен-Ки!

ТВ, 2011 Завершено 12 эп., 25 мин.

Действие Ecchi

Основанная на манге Хиромицу Такэда, эта романтическая комедия рассказывает о Такеру Охяме, типичном извращенном подростке. Его новая школа не требует вступительных экзаменов, и она стала совместным обучением! К сожалению, его мечты о счастливой школьной жизни рушатся, когда он узнает, что школа — это гораздо больше, чем кажется. Все ученики владеют особым предметом — Макеном — чтобы раскрыть свои магические способности в дуэлях! Сможет ли Такеру найти Maken, который ему подходит? Даже при попытке приспособиться к новой школе и решении всевозможных проблем с девочками? (Источник: FUNimation)

StudioAIC Spirits

ИсточникМанга

ТемыГаремБоевые искусстваШколаСуперсила

264567 5,75 20160705 Табу Тату

ТВ, 2016Готово 12 эп., 24 мин.

Действие Тайна Сверхъестественное

Сейги, ученик средней школы, обученный боевым искусствам, часто чувствует необходимость защищать более слабых людей вокруг него. Однажды он защищает бездомного от каких-то панков, а тот в ответ делает ему странную татуировку на ладони. Татуировка — секретное оружие, созданное в гонке вооружений между Америкой и Королевством Серинистан. Сейги оказывается выше головы, когда сильная девушка, используя то же секретное оружие, яростно преследует его, чтобы вернуть его. Его навыков в боевых искусствах может быть недостаточно, чтобы сохранить ему жизнь, но сможет ли он научиться вовремя активировать силу своей татуировки? (Источник: МУ)

StudioJ.C.Staff

ИсточникМанга

ТемыБоевые искусстваСуперсила

ДемографияSeinen

Black Cat

257736 7,34 20051007 Черная кошка (ТВ)

ТВ, 2005 г. Завершен 23 эп., 24 мин

Приключение Комедия Sci-Fi

Выполняя каждое задание с безжалостной точностью, Train Heartnet является печально известным убийцей, которому нет дела до человеческой жизни. Надев прозвище «Черный кот» в подземном мире, элитный убийца работает на могущественную секретную организацию, известную только как Хронос. Одной мрачной ночью пресыщенный стрелок натыкается на Саю Минацуки, загадочную охотницу за головами, и вскоре заводит с ней странную дружбу. Под влиянием позитивного взгляда Саи на жизнь Трейн начинает переосмысливать свою жизнь. Решив отказаться от своей роли Черного кота, он вместо этого выбирает добродетельный путь честного охотника за головами. Однако Хронос — и особенно Крид Дискент, собственнический подчиненный Трейна — не впечатлен внезапной переменой взглядов Трейна и клянется прибегнуть к крайним мерам, чтобы вернуть посланника неудачи. Этот убийца, ставший «бродячей кошкой», может бродить только до тех пор, пока не раздастся оглушительный звук выстрелов. [Написано MAL Rewrite]

StudioGonzo

SourceManga

ThemeSuper Power

Демографические Shounen

249390 7,50 20111007 Персона 4 Анимация

ТВ, 2011 г. Завершен 25 эп., 25 мин.

Действие Приключение Тайна Научная фантастика Сверхъестественное

Серийные убийства в последнее время преследовали Инабу, и полиция изо всех сил пытается найти какие-либо зацепки. Несмотря на это, из-за того, что его родители уезжают за границу на работу, Юу Наруками переезжает в маленький городок, чтобы жить со своим дядей в течение года. Он поступает в среднюю школу Ясогами, где знакомится и подружится с Юсуке Ханамура, Чие Сатонака и Юкико Амаги. Прогуливаясь вместе после школы, группа знакомит Юу с городской легендой, известной как «Полуночный канал» — таинственный телеканал, который появляется только в полночь в дождливые дни, когда зритель остается один. Заинтересовавшись заявлением, Юу решает настроиться той ночью, но вместо этого видит на экране следующую жертву серийных убийств. Он также оказывается вовлеченным в телевидение, которое достаточно заинтриговало его новообретенных друзей, чтобы они захотели провести расследование. В конце концов Юу попадает в мир внутри телевизора, который окутан густым туманом и кишит враждебными существами, известными как «Тени». Понимая, что этот мир каким-то образом связан с убийствами, формируется Следственная группа с целью раскрыть тайну инцидентов. [Написано MAL Rewrite]

StudioAIC ASTA

SourceGame

ThemesSchoolSuper Power

248894 7,96 201

Промаре

Фильм, 2019Завершен 1 эп, 111 мин

Действие Sci-Fi

Тридцать лет назад внезапно появилась новая раса огнедышащих мутантов, уничтожившая большую часть человечества. Эти так называемые «берниши» продолжают появляться случайным образом, оставляя за собой след смерти и разрушения. Автономная республика Промеполис — процветающая нация благодаря невероятным усилиям их лидера, Крэя Форсайта, против Бернишей. Команде пожарных, известной как Burning Rescue, поручено остановить этих ужасающих монстров, используя самые эффективные технологии, доступные благодаря их невероятному механику Люсии Фекс. Гало Тимос — энергичный молодой человек, который считает Форсайта своим героем за спасение своей жизни и является последним новобранцем спасательной команды. Террористическая группа, называющая себя Mad Burnish, сеет хаос по всей стране. После встречи с лидером Mad Burnish Лио Фотией Гало отправляется в свое судьбоносное путешествие, чтобы узнать правду об этих мутантах, что в конечном итоге заставляет его подвергнуть сомнению все, что он ранее считал правдой. [Написано MAL Rewrite]

StudioTrigger

SourceOriginal

ThemesMechaSuper Power

246047 7,74 20210716 Сонни Бой

ТВ, 2021 Завершено 12 эп. , 24 мин.

Тайна

Тридцать шесть учеников внезапно обнаруживают, что их школьное здание плывет по течению в подобном пустоте измерении. Когда в некоторых из них пробуждаются сверхъестественные силы, группу начинает разделять чувство отстраненности. Несмотря на попытки студенческого совета навести порядок, они сталкиваются со студентами, обладающими особыми способностями, которые восстают против их строгого контроля. Этот конфликт приводит их к пониманию того, что в этом мире есть свой набор правил, и следование им необходимо для выживания. После того, как один из учеников решает совершить прыжок веры, школа снова меняет измерения. В то время как они имеют дело с уникальными проблемами и обстоятельствами, которые представляет каждый мир, студенты должны разгадать таинственный феномен и найти путь домой. [Написано MAL Rewrite]

StudioMadhouse

ИсточникОригинал

ТемыIsekaiSuper Power

244968 7,93 20100127 Темнее черного: Kuro no Keiyakusha Gaiden

Специальное предложение, 2010 г. Завершено 4 эп., 24 мин.

Действие Тайна Sci-Fi

Спасаясь от последствий своего решения у Врат Ада, контрактор со сверхспособностями Хей и его компаньон Инь укрываются в тихой гостинице, приняв облик супружеской пары, чтобы не вызывать подозрений. Пытаясь оправиться от недавних событий, Хей подружился с другими гостями гостиницы. Он обнаруживает, что один из них — его коллега-подрядчик, которому поручено убить его. Их встреча в результате приводит к катастрофе как для Хэя, так и для Инь, которые вынуждены бороться за свою жизнь и бороться с эмоциональными ранами, полученными в их предыдущей совместной жизни. [Написано MAL Rewrite]

StudioBones

SourceOriginal

ThemeSuper Power

240969 7,65 20140712 К: Пропавшие без вести короли

Фильм, 2014 г. Завершен 1 эп, 73 мин.

Действие Сверхъестественное

Прошел год с момента исчезновения Широ, Серебряного Короля; Куро Ятогами и Неко усердно искали, но безрезультатно. Их расследование приводит к стычке с членами ныне расформированного Красного клана ХОМРА — Рикио Камамото и Анной Кушиной — преследуемых Зеленым кланом, которые желают использовать силы Анны в своих целях. Теперь члены Скипетра 4 призваны вместе с Куро и Неко, чтобы спасти Анну, талисман и единственную женщину-члена разрушенного Красного клана, из лап врага и, надеюсь, найти Широ, используя силы молодой девушки. В разгар кризиса группа вынуждена вступить в борьбу за власть, когда Зеленый клан угрожает захватить владения Золотого короля. Второй этап серии K Project, K: Пропавшие без вести короли, продолжает историю мальчика, оказавшегося втянутым в психическую войну между семью королями, и демонстрирует борьбу каждого персонажа после потери их соответствующих королей. [Написано MAL Rewrite]

StudioGoHands

SourceOriginal

ThemeSuper Power

My Hero Academia Season 6

239279 0 20221001 Boku no Hero Academia 6-й сезон

ТВ, 2022Ещё не в эфире ? EPS, 0 мин

Боевик

Шестой сезон Boku no Hero Academia.

StudioBones

ИсточникМанга

ТемыШколаСуперсила

ДемографияСёнен

234961 7.03 20120405 Коробка Медака

ТВ, 2012 г. Завершен 12 эп., 24 мин.

Действие Комедия Ecchi

Медака Куроками, в прямом смысле этого слова, идеальна. Красивая, умная и спортивная Медака мечтает сделать других счастливыми. Поэтому, когда она баллотируется на пост президента студенческого совета престижной академии Хаконива, вполне ожидаемо победить на выборах с 98% голосов. Самое первое, что делает неистовый новый президент, — это устанавливает «Ящик Медака», ящик для предложений, позволяющий студентам отправлять любые просьбы о помощи. Вместе с циничным Зенкичи Хитоёси, другом детства, который вынужден был помочь, Медака выполняет эти просьбы с невероятной скоростью. За каждую выполненную работу она добавляет цветы в комнату школьного совета, чтобы заполнить всю школу. Тем не менее, эти двое вскоре узнают, что помогать другим может быть намного сложнее, чем они думают, поскольку они начинают раскрывать разрушительный план, сосредоточенный на академии и даже на самой Медаке! [Написано MAL Rewrite]

StudioGainax

ИсточникМанга

ТемыБоевые искусстваШколаСуперсила

ДемографияСёнен

230704 6,89 20210401 Король шаманов (2021)

ТВ, 2021 Завершено 52 эп., 23 мин

Приключения Комедия Сверхъестественное

Шаманы — экстраординарные личности, способные общаться с призраками, духами и богами, невидимыми для обычных людей. Шаманская битва — престижный турнир, в котором шаманы со всего мира сражаются друг с другом, — проводится каждые пятьсот лет, и победитель становится коронованным королем шаманов. Этот титул позволяет нынешнему должностному лицу взывать к Великому Духу и формировать мир по своему усмотрению. Однажды вечером Манта Оямада, обычный ученик средней школы, опоздавший на урок, решает срезать путь через местное кладбище. Заметив его, одинокий мальчик, сидящий на надгробии, приглашает Манту посмотреть на звезды вместе с «ними». Понимая, что «они» относятся к мальчику и его призрачным друзьям, Манта убегает от ужаса. Позже мальчик представляется как Ю Асакура, обучающийся шаман, и демонстрирует свои силы, объединившись с призраком шестисотлетнего самурая Амидамару, чтобы спасти Манту от группы головорезов. Вы подружились с Мантой из-за его способности видеть духов, и с помощью Амидамару они намеревались достичь цели Вас — стать следующим королем-шаманом. [Написано MAL Rewrite]

StudioBridge

SourceManga

ThemeSuper Power

Демографический Shounen

Bungo Stray Dogs: Dead Apple

228989 7,92 20180303 Бродячие псы Бунгу: Мертвое яблоко

Фильм, 2018Завершен 1 эп, 90 мин

Действие Комедия Тайна Сверхъестественное

На планете происходит масштабная катастрофа. Пользователи способностей обнаруживаются после появления загадочного тумана, по всей видимости, совершившего самоубийство, поэтому Вооруженное детективное агентство намеревается расследовать эти таинственные смерти. Дело, похоже, связано с неизвестным пользователем способностей по имени «Коллекционер», человеком, который мог быть вдохновителем инцидента. Доверие и мужество подвергаются испытанию, чтобы спасти город Йокогама и пользователей способностей по всему миру от власти Коллекционера, где Вооруженное детективное агентство вступает в маловероятное партнерство с опасной портовой мафией. [Написано MAL Rewrite]

StudioBones

SourceManga

ThemeSuper Power

A Certain Magical Index III

228512 6,81 20181005 Тоару Мадзюцу но Индекс III

ТВ, 2018Готово 26 эп., 23 мин.

Действие Научная фантастика

Тома Камидзё не может передохнуть. После вторжения в Академгород, политическая напряженность продолжает расти, так как и научная, и магическая фракции сталкиваются лицом к лицу. Похоже, что Академгород намерен объявить войну Римско-католической церкви, в результате чего весь мир погрузится в глобальную войну. Вскоре Тома снова оказывается на передовой, стремясь защитить своих друзей и союзников. Toaru Majutsu no Index III служит последней частью оригинальной франшизы, поскольку Тома, Акселератор и истинный уровень 0 Шиаге Хамазура продолжают свои отдельные путешествия, ведущие к заключительному акту оригинальной серии легких новелл. [Написано MAL Rewrite]

StudioJ.C.Staff

Роман SourceLight

ThemeSuper Power

Ga-Rei-Zero

227948 7,59 20081006 Га-Рей: Ноль

ТВ, 2008 г. Завершен 12 эп., 23 мин.

Действие Сверхъестественное Suspense

В Японии существует правительственное агентство, известное как Отдел противодействия сверхъестественным бедствиям (SDCD), задачей которого является защита граждан от невидимых существ. Они могут уничтожить этих монстров быстро и без предупреждения широкой публики. Но в настоящее время они сталкиваются с другим испытанием: предательством одного из своих. После смерти ее матери несколько лет назад Кагура Цучимия была воспитана семьей Исаяма и установила тесную сестринскую связь с их дочерью Йоми. Эти двое становятся неразлучны и вместе работают на SDCD высококвалифицированными экзорцистами. Однако по мере того, как стресс и последствия их священного долга ложатся на них обоих, а в игру вступает семейная политика, Кагура и Ёми начинают медленно расходиться. Один из них усердно вживается в роль экзорциста, а другой идет по темной тропе, от которой может не быть искупления… [Написано MAL Rewrite]

StudiosAIC Spiritsпрочитано.

SourceManga

ThemeSuper Power

227629 6.08 200

11 глаз

ТВ, 2009 г. Завершен 12 эп., 25 мин.

Действие Сверхъестественное Ecchi

Когда небо становится красным, луна становится черной, а по улицам начинают бродить монстры, Сацуки Какеру не знает, что делать. Вместе со своим лучшим другом Юкой они пытаются понять, почему их отправили в этот странный мир, который кажется пустым, если не считать их самих. Однако, когда «Красная ночь» заканчивается, Какеру и Юка считают, что все это было сном, пока это не происходит снова, и они не оказываются в опасной ситуации. Они встречают еще четырех человек, оказавшихся в том же затруднительном положении: Кусакабе Мисудзу, искусную фехтовальщицу, Татибану Кукури, странную немую девушку, которая жутко похожа на покойную сестру Какеру, Хирохару Юкико, живую девушку, чья личность превращается в хладнокровного убийцу, когда она надевает очки. удалены, и Тадзима Такахиса, молодой пирокинетик. Когда шестеро из них объединяются, чтобы выжить и узнать, что представляет собой этот таинственный мир, все становится еще хуже, когда перед ними появляются шесть теней… [Написано MAL Rewrite]

StudioDoga Kobo

ИсточникВизуальный роман

ТемаSuper Power

227088 7,29 20100704 Секирей: Чистая помолвка

ТВ, 2010 г. Завершен 13 эп., 24 мин.

Действие Комедия Ecchi

Идет второй этап королевской битвы, известный как План Сэкирей. Shintou Teito был закрыт; ни Секирей, ни Асикаби не могут уйти. Минато Сахаши и его гарем Секирей теперь должны готовиться к новым битвам, поскольку в правила вносятся изменения. Однако не все группы вернутся в битву: некоторых Сэкирэй очень любят их партнеры-асикаби, которые скорее лишятся приза, чем увидят их гибель. В разгар действия кто-то из близких Минато может оказаться более вовлеченным, чем он мог себе представить, и угрозы таятся за каждым углом. Ходят даже слухи, что в бой вступили «Одиночные Числа», самый могущественный тип Секирей. В глазах «Мастера игры» Минаки Хирото все идет по плану. [Написано MAL Rewrite]

StudioSeven Arcs

ИсточникМанга

ТемыГаремСуперсила

219594 6,93 20150410 Изюминка

ТВ, 2015 Завершено 12 эп. , 23 мин

Комедия Научная фантастика Сверхъестественное Ecchi

Спасаясь от угона автобуса с помощью супергероя в маске Strange Juice, Юта Иридацу обнаруживает, что его душа отделена от тела и находится на попечении злобного кошачьего духа Чираносукэ. Как дух, Юта бродит по своей резиденции, Дому Кораи, стремясь вернуть себе тело и наблюдать за другими жителями: Мейкой Дайхатсу, гениальным изобретателем; Микатан Наругино, веселый идол; Ито Хикиотани, замкнутый NEET; и Рабура Чичибу, духовный медиум. Увидев нижнее белье Наругино, Чираносукэ показывает Юте, что он становится экспоненциально сильнее, увидев трусики. Однако, если он увидит другую пару, пока он еще является духом, его сила заставит астероид врезаться в землю, положив конец миру и убив его друзей. Punch Line следует за Ютой, который разгадывает тайны, окружающие Дом Корай, его жителей и злодейскую организацию, пытающуюся уничтожить мир. Сможет ли Юта спасти всех, или постоянная угроза трусиков приведет к их гибели? [Написано MAL Rewrite]

StudioMAPPA

SourceOriginal

ThemeSuper Power

214743 7,87 20110403 Тигр и кролик

ТВ, 2011 г. Завершен 25 эп., 24 мин.

Действие Комедия Mystery

В Stern Bild City те, у кого есть особые способности, называются «NEXT» и могут использовать свои силы во благо или во зло. Уникальная организованная группа NEXT регулярно появляется на Hero TV, где они преследуют злодеев, чтобы привлечь внимание к своим спонсорам и заработать очки Hero в надежде стать следующим «Королем героев». Котэцу Т. Кабураги, известный как «Дикий Тигр», является героем-ветераном, чья производительность в последнее время снижается, частично из-за его неспособности сотрудничать с другими героями. После разочаровывающего сезона, в котором большинство других героев намного превзошли Тигра, он оказывается в паре с совершенно новым героем, который называет себя своим настоящим именем — Барнаби Брукс-младший. Барнаби, которого его легкомысленная новая напарница прозвала «Банни», быстро дает понять, что эти двое не могут быть более разными. Хотя они смешиваются так же хорошо, как нефть и вода, Тигр и Банни должны научиться работать вместе, как ради своей карьеры, так и для того, чтобы противостоять надвигающимся угрозам внутри Stern Bild. [Написано MAL Rewrite]

StudioSunrise

SourceOriginal

ThemesAdult CastSuper Power

214568 5,37 20160416 Большой заказ (ТВ)

ТВ, 2016Готово 10 эп., 24 мин.

Действие

Десять лет назад появилась фея по имени Дейзи и спросила у мальчика Эйдзи Хошимия, какое у него единственное желание. Хотя его желание остается загадкой, последствия были катастрофическими. В событии под названием «Великое разрушение» мир начал разваливаться, когда все рухнуло и погибло бесчисленное количество людей. Теперь Эйдзи — старшеклассник, единственное, что беспокоит его больную сестру. Он не помнит, чего желал; все, что он помнит, это то, что его желание вызвало Великое Разрушение. За годы, прошедшие после этого события, тысячи других людей также получили возможность исполнить свое заветное желание. Эти люди, называемые «Орденами», считаются злыми и ненавидимы широкой публикой. Однако некоторые из этих Орденов отомстили за жизнь Эйдзи за тех, кого он убил. Сможет ли Эйдзи пережить многочисленные покушения? И самая большая загадка из всех: чего он желал и каковы были его намерения в желании того, что вызвало такое опустошение? [Написано MAL Rewrite]

Studioasread.

ИсточникМанга

ТемаСуперсила

ДемографияСёнен

214565 7.23 200 Ханаан

ТВ, 2009 г. Завершен 13 эп., 23 мин.

Действие Научная фантастика Сверхъестественное

Осава Мария — японский фотограф, в настоящее время работает в Шанхае, Китай. Вместе со своим партнером Мино она ищет потенциальные новости по всему городу. Когда на местном фестивале происходят странные события, Мария и Мино немедленно проводят расследование. Вскоре эти двое погружаются в битву между неизвестными мужчинами в масках и странной седовласой женщиной. Как раз в тот момент, когда Мария вот-вот попадет под перекрестный огонь, появляется старый друг по имени Ханаан и помогает Марии сбежать. Но вскоре развивается зловещий заговор, связанный со смертельным вирусом, и Ханаан узнает, что она должна противостоять своему прошлому, если хочет хоть какой-то шанс остановить преступника и спасти своих друзей. [Написано MAL Rewrite]

Студия П.А. Произведения

ИсточникВизуальный роман

ТемаСуперсила

ДемографияSeinen

Дети китов

210957 7.17 20171008 Кудзира но Кора ва Саджу ни Утау

ТВ, 2017Готово 12 эп., 23 мин

Драма Фантазия Тайна

В мире, покрытом бесконечным морем песка, плывет остров, известный как Грязевой кит. Внутри него находится древний город, большинство жителей которого, как говорят, «помечены» — обоюдоострая черта, которая наделяет их сверхъестественными способностями ценой безвременной смерти. Чакуро — деревенский архивариус; молодой и любопытный, он проводит время, документируя открытие вновь открытых островов. Но каждый такой же, как и все остальные — заброшенные, если не считать остатков тех, кто жил там давным-давно. Впервые за шесть месяцев на горизонте появляется еще один остров, поэтому Чакуро и его друзья присоединяются к группе разведчиков. Во время экспедиции они находят остатки архаичной цивилизации. И внутри одного из его рухнувших останков Чакуро обнаруживает девушку, которая изменит его судьбу и мир внутри Грязевого кита, каким он его знает. [Написано MAL Rewrite]

StudioJ.C.Staff

SourceManga

ThemeSuper Power

DemographicShoujo

A Certain Scientific Accelerator

209860 7. 20 201

Тоару Кагаку но Акселератор

ТВ, 2019Готово 12 эп., 23 мин

Фэнтези Сверхъестественное

Академгород находится в авангарде научно-технического прогресса, наиболее известного своими эсперами: теми, кто обладает сверхчеловеческими способностями, изменяющими правила реальности. Самыми могущественными среди них являются люди 5-го уровня, и тот, кто известен как Акселератор, безраздельно властвует, даже после того, как он был ослаблен серьезной травмой головного мозга. Рядом с ним находится молодая девушка, известная как Последний Заказ, которую, несмотря на его холодное поведение, он крепко держит и клянется защищать любой ценой. Хотя Акселератор, возможно, восстанавливается после травмы, темная сторона Академгорода никогда не отдыхает, и поэтому он невольно оказывается вовлеченным в разгар нового конфликта. Когда таинственная молодая женщина приближается к Акселератору в погоне за Последним приказом, эспер с самым высоким рангом сталкивается с ядовитой организацией, которая пустила корни в Анти-Навыке, миротворческой организации Академгорода. С опасными силами в движении, которые угрожают поставить Last Order и ее сестер в опасности, самопровозглашенный злодей готовится снова шагнуть во тьму. [Написано MAL Rewrite]

StudioJ.C.Staff

SourceManga

ThemesSchoolSuper Power

205789 7,73 20050914 Final Fantasy VII: Дети пришествия

Фильм, 2005 г. Завершен 1 эп, 101 мин

Действие Фэнтези

Два года назад мир изменился навсегда. Молодой Клауд Страйф и его группа друзей, возможно, победили Сефирота и сорвали его план по обрушению гигантского метеорита на Землю, но эта победа не обошлась без больших затрат. Густонаселенный город Мидгар был почти разорван в результате конфликта. К счастью, многие горожане смогли эвакуироваться в безопасное место, и спустя годы они создали новый дом под названием Эдж. Final Fantasy VII: Advent Children вращается вокруг Клауда и Тифы, которые пытаются начать новую жизнь для себя и окружающих в этом новом городе. Вместе они управляют курьерской службой и ухаживают за приемной дочерью своего общего друга Баррета Марлен и маленьким сиротой по имени Дензел. Дензел, Клауд и множество детей страдают от новой загадочной болезни под названием «Геостигма». Над головами городских детей нависла еще одна угроза — трое влиятельных людей по неизвестным причинам похищают зараженных детей. Клауд полон решимости спасти этих молодых не только от Геостигмы, но и от похитителей. Однако он понятия не имеет, что эти люди связаны с его старым врагом, Сефиротом, и стремление Клауда победить их снова приведет его к конфликту с демонами его прошлого. Если и есть надежда победить эти угрозы, то она заключается в узах дружбы между Клаудом и его союзниками, которые однажды спасли мир и теперь должны сделать это снова.

StudioSquare Enix

SourceGame

ThemeSuper Power

A Certain Scientific Railgun T

205289 8.19 20200110 Тоару Кагаку но Рейлган Т

ТВ, 2020Завершено 25 эп. , 24 мин.

Действие Sci-Fi

Начался фестиваль Дайхасей, и это, конечно же, означает, что средняя школа Токивадай — престижная средняя школа для девочек — тоже участвует в соревнованиях. Несмотря на участие «аса Токивадай» Микото Мисаки, другие учащиеся, которые участвуют, по-прежнему прилагают все усилия для победы, независимо от того, насколько невероятным может показаться подвиг против ее подавляющей мощи. Однако не все это развлечения и игры. Благодаря фестивалю Академгород открывается внешнему миру, и различные фракции начали продумывать способы проникновения в город. Мисака, кажется, находится на их радарах, и по мере того, как фестиваль продолжается, люди, скрывающиеся из теней, начинают появляться… Toaru Kagaku no Railgun T возвращает аса Токивадай и ее друзей, когда они все глубже погружаются в темную сторону Академгорода. В этом городе возможно все, от терактов до безжалостных подземных проектов. [Написано MAL Rewrite]

StudioJ. C.Staff

SourceManga

ThemeSuper Power

Жемчуг дракона Z: Битва богов

198896 7,39 20130330 Жемчуг дракона Z. Фильм 14: Ками Ками

Фильм, 2013 г. Завершен 1 эп, 85 мин

Действие Приключение Fantasy

После победы над великим противником Гоку Сон и его друзья живут мирной жизнью на Земле. Тем временем в космосе Берус, Бог Разрушения, пробуждается от своего долгого сна, увидев во сне сущность, известную как Супер Сайянский Бог. С помощью своего помощника Виса Берус ищет это могущественное существо, так как хочет сразиться с достойным противником. Обнаружив, что родная планета сайянов была разрушена, он выслеживает оставшихся сайянов на Земле, специально ища Гокуу. Услышав о Супер Сайянском Боге только в легендах, Гокуу и его товарищи вызывают Шен Лонга, Вечного Дракона, который, как они узнают, боится Беруса. Узнав секрет Супер Сайянского Бога, начинается напряженная битва между Гокуу и Берусом, огромная сила которой подвергает Землю ужасной опасности. [Написано MAL Rewrite]

СтудияToei Animation

ИсточникМанга

ТемыБоевые искусстваСуперсила

ДемографияСёнен

Гуррен-Лаганн Фильм: Огни в небе — это звезды

198823 8,57 200

Tengen Toppa Gurren Lagann Movie 2: Лаганн-курица

Фильм, 2009 г. Завершен 1 эп, 125 мин.

Действие Sci-Fi

Люди наслаждались своей роскошной, мирной и процветающей жизнью в течение семи лет с того дня, как всемогущий Спиральный Король был побежден — день, когда они вернули себе свою родину, Землю. Однако благо такого образа жизни оставляет их неподготовленными, когда возникает неизвестная враждебная угроза из-за постоянно растущего населения. Это бедствие — Антиспираль — грозный враг с беспримерной силой. Когда прогноз Спирального Короля, постулирующий разрушение «Спирального мира», начинает сбываться, все детали расставлены по местам, и команда Дай-Гуррен готова. Надеясь, что его покойный брат увидит лучшее будущее для человечества, Саймон вместе с Нией Теппелин и остальной командой полон решимости свергнуть могущественную Антиспираль, чтобы возродить утраченную надежду человечества. [Написано MAL Rewrite]

StudioGainax

SourceOriginal

ThemesMechaSpaceSuper Power

7,66 20081005 Иназума Одиннадцать

ТВ, 2008 г. Завершен 127 эп., 24 min

Спорт

В то время как другие школы Японии соревнуются за звание лучшей футбольной команды страны, футбольный клуб Inazuma Eleven из средней школы Раймона изо всех сил пытается подняться с грани расформирования. Внук вратаря и капитана команды Inazuma Eleven в первом поколении, Мамору Эндо, берет на себя задачу вернуть давно заброшенный клуб в форму. Для этого ему понадобится небольшая помощь и немножко удачи. Мамору Эндо находит надежду в руках Сюи Гоенджи, блестящего молодого игрока, который отказался от футбола. Мамору полон решимости во что бы то ни стало уговорить Сюю и других новобранцев присоединиться к его команде. Достаточно ли его страсти и решимости, чтобы вылечить больной клуб? Или у команды больше нет надежды?

StudioOLM

SourceGame

ТемыSuper PowerTeam Sports

Демографические Shounen

189514 7,69 20140903 Kill la Kill Specials

Специальное предложение, 2014 г. Завершено 2 эп., 18 мин.

Действие Комедия Ecchi

Мир наконец-то вернулся в Академию Хоннодзи, и теперь, когда она выполнила свою первоначальную задачу, уникальная средняя школа должна быть закрыта в течение месяца. Тем не менее, есть еще одно заключительное событие, которое должно состояться: церемония вручения дипломов. Пока каждый член студенческого совета готовится оставить свое прошлое позади, чтобы сосредоточиться на том, что они хотели бы делать в будущем, Сацуки Кирюин изо всех сил пытается найти свой собственный путь, потеряв решимость после того, как наконец одержала победу. Но незадолго до того, как она должна произнести свою речь перед студентами, церемонию прерывают таинственные существа, идентичные членам школьного совета. Когда Рюуко Матой и Элитная четверка снова готовятся к битве, они быстро обнаруживают, что тот, кто дергает за ниточки, — это старый враг, который вернулся, чтобы отомстить. [Написано MAL Rewrite]

StudioTrigger

SourceOriginal

ThemesSchoolSuper Power

My Hero Academia: World Heroes Mission

186024 7,57 20210806 Boku no Hero Academia the Movie 3: Миссия мировых героев

Кино, 2021 Завершено 1 эп, 104 мин.

Действие

В соответствии с доктринами Теории Судного Дня причуды идеологическая группа Humarise убеждена, что все люди с причудами больны и должны быть искоренены. Чтобы восстановить мир, экстремисты группы создали смертоносное устройство, известное как «Спусковая бомба», которое заставляет людей с причудами терять контроль и умирать. Их лидер, Флект Терн, избегает захвата профессиональными героями, разбросанными по всему миру. Во время учебы в стране Отеон с профессиональным героем номер один в Японии Изуку «Деку» Мидория обвиняется в преступлении, которого он не совершал. Непреднамеренно привлекая местного жителя Родди Соула, Деку вскоре оказывается в бегах с мальчиком. Теперь Роди, Деку и одноклассники Деку должны остановить заговор с триггерной бомбой, запущенный Флектом, при этом ускользая от других настойчивых членов Humarise. [Написано MAL Rewrite]

StudioBones

SourceManga

ThemeSuper Power

Демографический Shounen

Hitori no Shita — Изгой

185648 6,82 20160709 Хитори но Шита: Изгой

ТВ, 2016Готово 12 эп. , 24 мин.

Действие Сверхъестественное

Однажды, направляясь на могилу своего деда, Чжан Чулань подвергается нападению зомби на кладбище. В разгар этой ситуации его спасает загадочная девушка, которая владеет кухонными ножами, чтобы убивать врагов. Девушка говорит Чулану, который чувствует облегчение, столкнуться лицом к лицу со своими трудностями и уходит. Однако позже Чулан снова видит эту девушку в своем университете. С этого момента судьба Чжан Чуланя начинает двигаться. Один за другим будут появляться незнакомцы с особыми способностями, в битвах с участием этих способностей. Каждая серия раскрывает новую тайну.

StudioNamu Animation

SourceWeb манга

ThemeSuper Power

Моя геройская академия: обучение мертвецов

182369 7,24 20170602 Boku no Hero Academia: Тренировка мертвецов

OVA, 2017Завершено 1 эп, 25 мин.

Действие

Вернувшись со стажировки, учащиеся класса 1-А сразу же отправляются на дополнительное обучение к своему классному руководителю Сёте Айзаве. В этом упражнении к классу присоединятся четыре ученика старшей школы Академии Исаму, чтобы посоревноваться в игре на выживание. Разделившись на группы по четыре человека, ученики должны либо уничтожить друг друга, либо оставаться в тени, пока не истечет время, необходимое для победы. Тренировка также является воссоединением Цую Асуи и ее подруги из средней школы Хабуко Мангуста. Однако не все ученики Исаму дружелюбны — Кацуки Бакуго почти мгновенно затевает драку с Ромеро Фуджими. Конфликт между ними заставляет Ромеро сердито выпустить свою причуду, газ, который зомбирует любого, с кем вступает в контакт. Как оставшиеся ученики справятся с ситуацией после того, как большинство людей вокруг них превратятся в зомби? [Написано MAL Rewrite]

StudioBones

SourceManga

ThemesSchoolSuper Power

DemographicShounen

179427 7,71 20160705 D. Gray-man Hallow

ТВ, 2016Готово 13 эп., 24 мин.

Действие Приключение

Несмотря на недавнее нападение Акума, члены Черного Ордена в приподнятом настроении отправляются на новую базу. Однако сразу по прибытии Аллена Уокера внезапно вызывает Центральное агентство, и Орден насильно запечатывает его руку. Затем его приводят к неожиданной встрече со своим учителем, генералом Кроссом Марианом, который раскрывает ошеломляющие секреты, окружающие загадочного 14-го Ноя. Инцидент с вором-призраком, прибытие таинственной группы экзорцистов, смерть важного товарища и полномасштабная битва против семьи Ноя — что это значит для Аллена, Юу Канды и остальных членов Ордена? Это лишь начало серии странных, казалось бы, не связанных между собой событий, которые ведут к чему-то гораздо большему. [Написано MAL Rewrite]

StudioTMS Entertainment

ИсточникМанга

ТемыМифологияСуперсила

ДемографияСёнен

Тэнджо Тенге

178955 6,89 20040402 Тенджоу Тенге

ТВ, 2004 г. Завершен 24 эп., 23 мин.

Действие Комедия Ecchi

Для некоторых людей старшая школа представляет собой возможность начать новую жизнь. Вы можете брать новые уроки и заводить новых друзей. Однако для Соичиро Наги и Боба Макихары старшая школа означает нечто иное: шанс стать лучшим бойцом среди всех учеников! Жаль, что Академия Тодо — самое сложное место для реализации их мечты. Их новая средняя школа — не обычное учебное заведение. Вместо того, чтобы концентрироваться на классических предметах, таких как математика и естественные науки, Академия Тодо была создана с единственной целью возродить боевые искусства в Японии! В результате стремление Соитиро стать лучшим псом обрывается, когда он сталкивается с Масатакой Такаянаги и Майей Нацуме. Два старшеклассника легко останавливают буйство дуэта первокурсников в школе, но вместо того, чтобы служить сдерживающим фактором, это только разжигает их соревновательный огонь. Какие чудовищные бойцы посещают Академию Тодо? Есть ли кто-нибудь сильнее, чем Масатака и Майя? И почему младшая сестра Майи преследует Соичиро? Узнайте ответы на эти и другие вопросы в Tenjou Tenge!

StudioMadhouse

ИсточникМанга

ТемыБоевые искусстваШколаСуперсила

ДемографияСёнен

176654 7,83 20031007 Гангрейв

ТВ, 2003 г. Готово 26 эп., 25 мин.

Действие Драма Sci-Fi

Брэндон Хит и Гарри МакДауэл, два друга, настолько близкие, что их можно было бы назвать братьями, в один судьбоносный день получают резкое и жестокое напоминание о том, насколько ужасающе безжалостным может быть мир вокруг них. Вся их жизнь до этого была простой и беззаботной, состоящей в основном из местных потасовок, соблазнения женщин и совершения мелких краж, чтобы заработать на жизнь и скоротать время. Чего они не поняли, так это того, что в этом жестоком мире счастье мимолетно, а перемены неизбежны. Войдите в Millennion, крупнейший и самый печально известный мафиозный синдикат в этом районе, который принимает Брэндона и Гарри в свои ряды и запускает их в конце пищевой цепочки. У Гарри есть амбиции подняться по служебной лестнице и однажды заменить Большого Папу на посту верховного лидера Тысячелетия, в то время как Брэндон хочет только поддержать своего друга и успокоить Большого Папу, взявшего под опеку женщину, которую любит Брэндон. Основанный на видеоигре-шутере от третьего лица под тем же названием, Gungrave представляет собой эпическую историю дружбы, предательства и алчности, которая длится несколько лет и в конечном итоге возвращается к захватывающему и зловещему первому эпизоду. к захватывающему завершению истории. [Написано MAL Rewrite]

StudioMadhouse

SourceGame

ThemesAdult CastGoreOrganized CrimeSuper Power

DemographicSeinen

My Hero Academia Season 2: Hero Notebook

173688 7. 30 20170325 Boku no Hero Academia 2-й сезон: Записка героя

Специальное предложение, 2017 г. Завершено 1 эп, 23 мин.

Действие

Резюме Boku no Hero Academia, вышедшего в эфир за неделю до второго сезона.

StudioBones

SourceManga

ThemesSchoolSuper Power

DemographicShounen

170638 7.10 20100724 Черный ★ Rock Shooter (OVA)

OVA, 2010 г. Завершено 1 эп, 52 мин.

Действие Драма

В свой первый день в старшей школе Мато Курой встречает Ёми Таканаши. Хотя Йоми изначально ошеломлен прямолинейностью Мато, пара быстро становится друзьями и начинает ежедневно проводить время вместе. В знак их дружбы Мато дарит Ёми подвеску для мобильного телефона — синюю звезду, идентичную ее собственной. Однако, когда эти двое переходят на второй год обучения, их отношения начинают меняться. Перейдя в другой класс, Мато вместо этого начинает проводить больше времени с Юу Котари, девушкой, с которой она познакомилась в баскетбольной команде. На самом деле бывшие лучшие друзья расходятся настолько, что Мато нигде не может найти Ёми, как будто она исчезла совсем. В другом месте Black★Rock Shooter пытается победить Мертвого Мастера. Эти двое, хотя и противостоят друг другу, имеют связь, мало чем отличающуюся от Мато и Ёми. Когда их истории начинают пересекаться, кажется, что исчезновение Йоми может быть связано с чаром в форме синей звезды и самой легендарной стрелком. [Написано MAL Rewrite]

StudioOrdet

SourceOther

ThemesMahou ShoujoSuper Power

Charlotte: The Strong Ones

169778 7,48 20160330 Шарлотта: Цуйоймоно-тати

Специальное предложение, 2016 г. Завершено 1 эп, 24 мин.

Ясновидение Такехито Кумагами приводит его группу друзей к другому ребенку со сверхъестественными способностями: Иори Секигучи, телепату. Однако, когда они пытаются приблизиться к ней, они понимают, что ее сила делает ее почти невозможной. Будучи выбраны клубом для ведения этого дела, Нао Томори и Юу Отосака должны найти способ обойти уникальную способность ребенка, пока не стало слишком поздно. [Написано MAL Rewrite]

Студия П.А. Works

SourceOriginal

ThemesSchoolSuper Power

Dragon Ball Z Kai: The Final Chapters

169148 7,67 20140406 Жемчуг дракона Кай (2014)

ТВ, 2014 г. Завершено 61 эп., 23 мин.

Действие Приключение комедия Fantasy

Обновленная версия саги о Маджине Буу, которая больше соответствует сюжету манги.

СтудияToei Animation

ИсточникМанга

ТемыБоевые искусстваСуперсила

ДемографияСёнен

Моя геройская академия: Спасение! Спасательная подготовка

164710 7,25 20170404 Boku no Hero Academia: Сукуэ! Кюджо Кунрен!

OVA, 2017Завершено 1 эп, 25 мин.

Действие

Старшая школа UA должна восстановить доверие публики после неожиданного нападения злодея во время тренировки класса 1-A. Хотя некоторые учителя были серьезно ранены во время нападения, Изуку «Деку» Мидория и его одноклассники должны продолжать учиться и тренироваться, а также использовать свои причуды в различных условиях и обстоятельствах. Boku no Hero Academia: Сукуэ! Кюджо Кунрен! следует за классом 1-A, когда они пытаются наконец завершить свое обучение. Однако по тренировочному центру бродит фигура в маске. Вернулись ли злодеи, ответственные за предыдущий инцидент, чтобы закончить работу? Если да, то готовы ли студенты дать отпор? [Написано MAL Rewrite]

StudioBones

SourceManga

ThemesSchoolSuper Power

DemographicShounen

163326 6,55 20140712 Токио ESP

ТВ, 2014 г. Завершено 12 эп., 24 мин.

Действие Комедия Научная фантастика Сверхъестественное

Ринка Урушиба подрабатывает официанткой, чтобы помочь своему безработному отцу. По общему мнению, ее жизнь в Токио относительно нормальная, но ее чувство нормальности начинает исчезать, когда однажды она необъяснимым образом видит летающего пингвина. Преследуя его до вершины здания, она встречает новые сюрпризы, в том числе летающих золотых рыбок и еще одного человека — одноклассника по имени Кётаро Адзума, — который также может видеть эти странные вещи. После того, как Ринка теряет сознание, когда через нее проходит золотая рыбка, она просыпается эспером, способным проводить свое тело через твердую материю. Однако ее новообретенная способность — не единственная странность в ней: когда она использует свои силы, ее волосы становятся седыми. Неохотно решив использовать этот новый дар, чтобы помочь городу, она становится новым героем Токио, получившим прозвище «Белая девушка». Вместе с Кётаро, получившим способность телепортироваться, Ринка начинает исправлять ошибки в городе, сражаясь с другими эсперами, у которых гораздо менее благородные намерения. [Написано MAL Rewrite]

StudioXebec

SourceManga

ThemeSuper Power

Демографические Shounen

Re: Hamatora: Season 2

160668 7,36 20140708 Re:␣Хаматора

ТВ, 2014 г. Завершено 12 эп., 24 мин

Комедия Драма Тайна

Прошло три месяца после инцидента в Йокогаме. В Cafe Nowhere все налаживается. Мурасаки и Хадзиме объединились и снова начали расследование. После непредвиденного воссоединения Арт держит Ниццу под прицелом. Каковы его настоящие намерения? Что станет со связью между Артом и Хаматорой? (Источник: Crunchyroll)

StudioLerche

SourceOriginal

ThemeSuper Power

Dragon Ball Z: Resurrection ‘F’

160454 7.05 20150418 Жемчуг дракона Z. Фильм 15: Фуккацу но «Ф»

Фильм, 2015 г. Завершен 1 эп, 107 мин

Действие Приключение Комедия Фэнтези

На Земле снова наступил мир, но это спокойствие недолговечно. Остатки армии Фризы во главе с Сорбетом и его правой рукой Тагомой прибывают на Землю, чтобы призвать Шен Лонга с целью воскресить своего старого хозяина.

Добавить комментарий Отменить ответ

Ваш адрес email не будет опубликован. Обязательные поля помечены *

Комментарий *

Имя *

Email *

Сайт