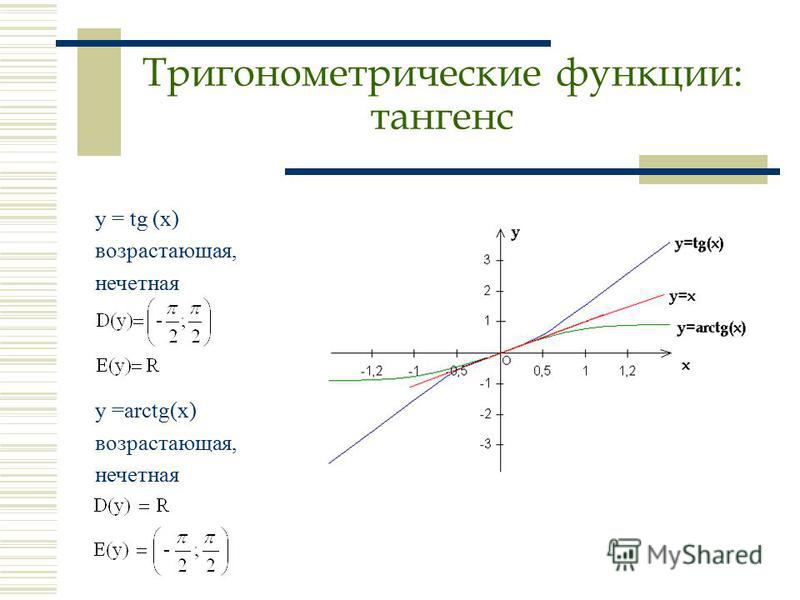
ОБРАТНЫЕ ТРИГОНОМЕТРИЧЕСКИЕ ФУНКЦИИ . Энциклопедический словарь юного математика
В ряде задач математики и ее приложений требуется по известному значению тригонометрической функции найти соответствующее значение угла, выраженное в градусной или в радианной мере. Известно, что одному и тому же значению синуса соответствует бесконечное множество углов, например, если sin α = 1/2, то угол α может быть равен и 30° и 150°, или в радианной мере π/6 и 5π/6, и любому из углов, который получается из этих прибавлением слагаемого вида 360°·k, или соответственно 2πk, где k — любое целое число. Это становится ясным и из рассмотрения графика функции y = sin x на всей числовой прямой (см. рис. 1): если на оси Oy отложить отрезок длины 1/2 и провести прямую, параллельную оси Ox, то она пересечет синусоиду в бесконечном множестве точек. Чтобы избежать возможного разнообразия ответов, вводятся обратные тригонометрические функции, иначе называемые круговыми, или аркфункциями (от латинского слова arcus — «дуга»).
Рис. 1
Основным четырем тригонометрическим функциям sin x, cos x, tg x и ctg x соответствуют четыре аркфункции arcsin x, arccos x, arctg x и arcctg x (читается: арксинус, арккосинус, арктангенс, арккотангенс). Рассмотрим функции arcsin x и arctg x, поскольку две другие выражаются через них по формулам:
arccos x = π/2 — arcsin x, arcctg x = π/2 — arctg x.
Равенство y = arcsin x по определению означает такой угол y, выраженный в радианной мере и заключенный в пределах от — π/2 до π/2, синус которого равен x, т.е. sin y = x. Функция arcsin x является функцией, обратной функции sin x, рассматриваемой на отрезке [-π/2, +π/2], где эта функция монотонно возрастает и принимает все значения от -1 до +1. Очевидно, что аргумент у функции arcsin x может принимать значения лишь из отрезка [-1,+1]. Итак, функция y = arcsin x определена на отрезке [-1,+1], является монотонно возрастающей, и ее значения заполняют отрезок [-π/2, +π/2]. График функции показан на рис. 2.
Итак, функция y = arcsin x определена на отрезке [-1,+1], является монотонно возрастающей, и ее значения заполняют отрезок [-π/2, +π/2]. График функции показан на рис. 2.
Рис. 2
При условии -1≤a≤1 все решения уравнения sin x = a представим в виде x = (-1)n arcsin a + πn, n = 0,±1,±2,…. Например, если
sin x = (√2)/2, то x = (-1)nπ/4 + πn, n = 0,±1,±2,….
Соотношение y = arctg x определено при всех значениях x и по определению означает, что угол y, выраженный в радианной мере, заключен в пределах
-π/2 < y < π/2
и тангенс этого угла равен x, т. е. tg y = x. Функция arctg x определена на всей числовой прямой, является функцией, обратной функции
-π/2 < x < π/2.
Функция y = arctg x монотонно возрастающая, ее график дан на рис. 3.
3.
Рис. 3
Все решения уравнения tg x = a могут быть записаны в виде x = arctg a + πn, n = 0,±1,±2,….
Заметим, что обратные тригонометрические функции широко используются в математическом анализе. Например, одной из первых функций, для которых было получено представление бесконечным степенным рядом, была функция arctg x. Из этого ряда Г. Лейбниц при фиксированном значении аргумента x=1 получил знаменитое представление числа π бесконечным рядом
π = 4(1 — 1/3 + 1/5 — 1/7 + …).
Обратные тригонометрические функции.
Обратные тригонометрические функции и их свойства
Содержание
- Функция y = arcsin x и ее свойства
- Функция y = arccos x и ее свойства
- Функция y = arctg x и ее свойства
- Функция y = arcctg x и ее свойства
y=x
Функция y=arcsin x и ее график
у
π / 2
y=arcsin x
y=sin x
х
-1
1
π
0
— π / 2
Функция y=arcsin x и ее свойства
- D(y) = [-

- E(y) = [- π /2 ; π /2 ] .
- arcsin (-x) = — arcsin x – функция нечетная.
- Функция возрастает на [- 1 ; 1 ] .
- Функция непрерывна.
Функция y=arcsin x
Определение
Если |а| ≤ 1 , то arcsin а – это такое число из отрезка [- π /2 ; π /2 ] , синус которого равен а .
Если |а| ≤ 1 , то
arcsin а = t
sin (arcsin a) = a
sin t = а ,
— π /2 ≤ t ≤ π /2 ;
y=x
Функция y=arccos x и ее график
у
π
y=arccos x
π /2
y= со s x
π
0
х
-1
1
Функция y=arccos x и ее свойства
- D(y) = [- 1 ; 1 ] .

- E(y) = [ 0 ; π ] .
- Функция не является ни четной, ни нечетной, arccos (-a) = π – arccos a
- Функция убывает на [- 1 ; 1 ] .
- Функция непрерывна.
Функция y=arccos x
Если |а| ≤ 1 , то arccos а – это такое число из отрезка [ 0 ; π ] , косинус которого равен а .
Если |а| ≤ 1 , то
arccos а = t
cos (arccos a) = a
cos t = а ,
0 ≤ t ≤ π ;
y=x
Функция y=arctg x и ее график
у
π / 2
y=arctg x
π /4
х
-1
1
π
0
— π /4
— π / 2
y=tg x
Функция y=arctg x и ее свойства
- D(y) = (- ; + ) .

- E(y) = (- π /2 ; π /2 ) .
- arctg (-x) = — arctg x – функция нечетная.
- Функция возрастает на (- ; + ) .
- Функция непрерывна.
Функция y=arctg x
Определение
arctg а – это такое число из интервала
( — π /2 ; π /2 ) , тангенс которого равен а .
arctg а = t
tg (arctg a) = a
tg t = а ,
— π /2 π /2 ;
y=x
Функция y=arcctg x и ее график
у
π
y= с tg x
y=arc с tg x
π / 2
— π / 2
π
х
— π
0
π / 2
Функция y=arcctg x и ее свойства
- D(y) = (- ; + ) .

- E(y) = ( 0 ; π ) .
3. Функция не является ни четной, ни нечетной, arcctg (-a) = π – arcctg a
4. Функция убывает на (- ; + ) .
5. Функция непрерывна.
Функция y=arcctgx
Определение
ar с ctg а – это такое число из интервала
( 0 ; π ) , котангенс которого равен а .
arc с tg а = t
с tg (arc с tg a) = a
с tg t = а ,
0 π ;
| 1 | Найти точное значение | грех(30) | |
| 2 | Найти точное значение | грех(45) | |
| 3 | Найти точное значение | грех(30 градусов) | |
| 4 | Найти точное значение | грех(60 градусов) | |
| 5 | Найти точное значение | ||
| 6 | Найти точное значение | угловой синус(-1) | |
| 7 | Найти точное значение | грех(пи/6) | |
| 8 | Найти точное значение | cos(pi/4) | |
| 9 | Найти точное значение | грех(45 градусов) | |
| 10 | Найти точное значение | грех(пи/3) | |
| 11 | Найти точное значение | арктан(-1) | |
| 12 | Найти точное значение | cos(45 градусов) | |
| 13 | Найти точное значение | cos(30 градусов) | |
| 14 | Найти точное значение | желтовато-коричневый(60) | |
| 15 | Найти точное значение | csc(45 градусов) | |
| 16 | Найти точное значение | загар (60 градусов) | |
| 17 | Найти точное значение | сек(30 градусов) | |
| 18 | Найти точное значение | cos(60 градусов) | |
| 19 | Найти точное значение | cos(150) | |
| 20 | Найти точное значение | грех(60) | |
| 21 | Найти точное значение | cos(pi/2) | |
| 22 | Найти точное значение | загар (45 градусов) | |
| 23 | Найти точное значение | arctan(- квадратный корень из 3) | |
| 24 | Найти точное значение | csc(60 градусов) | |
| 25 | Найти точное значение | сек(45 градусов) | |
| 26 | Найти точное значение | csc(30 градусов) | |
| 27 | Найти точное значение | грех(0) | |
| 28 | Найти точное значение | грех(120) | |
| 29 | Найти точное значение | соз(90) | |
| 30 | Преобразовать из радианов в градусы | пи/3 | |
| 31 | Найти точное значение | желтовато-коричневый(30) | |
| 32 | 92|||
| 35 | Преобразовать из радианов в градусы | пи/6 | |
| 36 | Найти точное значение | детская кроватка(30 градусов) | |
| 37 | Найти точное значение | арккос(-1) | |
| 38 | Найти точное значение | арктан(0) | |
| 39 | Найти точное значение | детская кроватка(60 градусов) | |
| 40 | Преобразование градусов в радианы | 30 | |
| 41 | Преобразовать из радианов в градусы | (2 шт. )/3 )/3 | |
| 42 | Найти точное значение | sin((5pi)/3) | |
| 43 | Найти точное значение | sin((3pi)/4) | |
| 44 | Найти точное значение | тан(пи/2) | |
| 45 | Найти точное значение | грех(300) | |
| 46 | Найти точное значение | соз(30) | |
| 47 | Найти точное значение | соз(60) | |
| 48 | Найти точное значение | соз(0) | |
| 49 | Найти точное значение | соз(135) | |
| 50 | Найти точное значение | cos((5pi)/3) | |
| 51 | Найти точное значение | cos(210) | |
| 52 | Найти точное значение | сек(60 градусов) | |
| 53 | Найти точное значение | грех(300 градусов) | |
| 54 | Преобразование градусов в радианы | 135 | |
| 55 | Преобразование градусов в радианы | 150 | |
| 56 | Преобразовать из радианов в градусы | (5 дюймов)/6 | |
| 57 | Преобразовать из радианов в градусы | (5 дюймов)/3 | |
| 58 | Преобразование градусов в радианы | 89 градусов | |
| 59 | Преобразование градусов в радианы | 60 | |
| 60 | Найти точное значение | грех(135 градусов) | |
| 61 | Найти точное значение | грех(150) | |
| 62 | Найти точное значение | грех(240 градусов) | |
| 63 | Найти точное значение | детская кроватка(45 градусов) | |
| 64 | Преобразовать из радианов в градусы | (5 дюймов)/4 | |
| 65 | Найти точное значение | грех(225) | |
| 66 | Найти точное значение | грех(240) | |
| 67 | Найти точное значение | cos(150 градусов) | |
| 68 | Найти точное значение | желтовато-коричневый(45) | |
| 69 | Оценить | грех(30 градусов) | |
| 70 | Найти точное значение | сек(0) | |
| 71 | Найти точное значение | cos((5pi)/6) | |
| 72 | Найти точное значение | КСК(30) | |
| 73 | Найти точное значение | arcsin(( квадратный корень из 2)/2) | |
| 74 | Найти точное значение | загар((5pi)/3) | |
| 75 | Найти точное значение | желтовато-коричневый(0) | |
| 76 | Оценить | грех(60 градусов) | |
| 77 | Найти точное значение | arctan(-( квадратный корень из 3)/3) | |
| 78 | Преобразовать из радианов в градусы | (3 пи)/4 | |
| 79 | Найти точное значение | sin((7pi)/4) | |
| 80 | Найти точное значение | угловой синус(-1/2) | |
| 81 | Найти точное значение | sin((4pi)/3) | |
| 82 | Найти точное значение | КСК(45) | |
| 83 | Упростить | арктан(квадратный корень из 3) | |
| 84 | Найти точное значение | грех(135) | |
| 85 | Найти точное значение | грех(105) | |
| 86 | Найти точное значение | грех(150 градусов) | |
| 87 | Найти точное значение | sin((2pi)/3) | |
| 88 | Найти точное значение | загар((2pi)/3) | |
| 89 | Преобразовать из радианов в градусы | пи/4 | |
| 90 | Найти точное значение | грех(пи/2) | |
| 91 | Найти точное значение | сек(45) | |
| 92 | Найти точное значение | cos((5pi)/4) | |
| 93 | Найти точное значение | cos((7pi)/6) | |
| 94 | Найти точное значение | угловой синус(0) | |
| 95 | Найти точное значение | грех(120 градусов) | |
| 96 | Найти точное значение | желтовато-коричневый ((7pi)/6) | |
| 97 | Найти точное значение | соз(270) | |
| 98 | Найти точное значение | sin((7pi)/6) | |
| 99 | Найти точное значение | arcsin(-( квадратный корень из 2)/2) | |
| 100 | Преобразование градусов в радианы | 88 градусов |
Обратные функции их областей и диапазонов; их графики HL Paper 1
ВопросНа следующей диаграмме показан график y = arctan( \(2x+1+\frac{\pi}{4} \)) для \(x \in \mathbb{R}\) с асимптотами at \(y=-\frac{\pi}{4}\) и \(y=\frac{3\pi}{4}\)
(a) Опишите последовательность преобразований, преобразующую граф от y = arctan x к графику y = arctan( \(2x+1+\frac{\pi}{4} \)) для \(x \in \mathbb{R}\) [3]
( б) Показать, что arctan arctan p+ arctan q= arctan \(\frac{p+q}{1-pq}\), где p , q > 0 и pq < 1 [4] 9+\)
Ответ/ОбъяснениеОтвет:
(a) Заменив $x$ в $y=\arctan x$ на $x+1$, мы получим $y=\arctan \left(x+ 1\right)$, что представляет собой перемещение на $-1$ единиц параллельно оси $x$.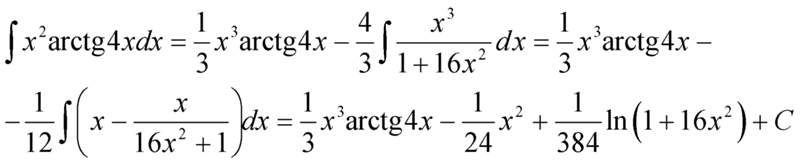
Далее, заменив $x$ в $y=\arctan \left(x+1\right)$ на $2x$, мы получим $y=\arctan \left(2x+1\right)$, т.е. участок, параллельный оси $x$, с масштабным коэффициентом $\frac{1}{2}$.
Наконец, заменив $y$ в $y=\arctan\left(2x+1\right)$ на $y-\frac{\pi}{4}$, получим $y-\frac{\pi {4}=\arctan \left(2x+1\right)$, т. е. $y=\arctan \left(2x+1\right)+\frac{\pi}{4}$, что является переводом из $\frac{\pi}{4}$ единиц, параллельных оси $y$.
(b) Взяв касательную с обеих сторон в $\arctan p+\arctan q=\arctan\left(\frac{p+q}{1-pq}\right)$, получим $\tan\left(\arctan p+\arctan q\right)=\frac{p+q}{1-pq}$
$$\begin{eqnarray}
\text{LHS} &=& \tan\left(\arctan p+\arctan q\ справа) \nonumber \\
&=& \frac{p+q}{1-pq} \nonumber \\
&=& \text{RHS}.
\end{eqnarray}$$
(c) Заметим, что $\arctan 1=\frac{\pi}{4}$. Тогда, используя (b), мы имеем
$$\begin{eqnarray}
\text{RHS} &=& \arctan \left(\frac{x}{x+1}\right)+\frac{\pi {4} \номер \\ 9+$.
Вопрос
На приведенном ниже рисунке показана граница поперечного сечения водного канала.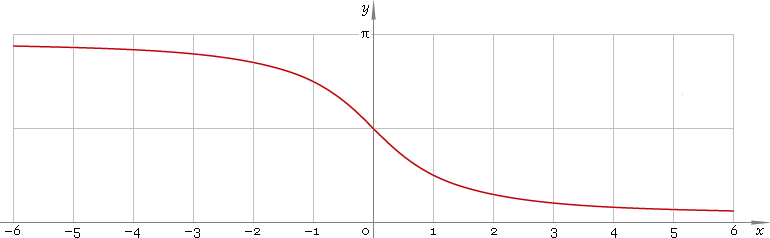
Уравнение, представляющее эту границу, имеет вид \(y = 16\sec \left( {\frac{{\pi x}}{{36}}} \right) — 32\), где x и y измеряются в см.
Верх канала находится на уровне земли и имеет ширину 24 см. Максимальная глубина канала 16 см.
Найдите ширину поверхности воды в канале, если глубина воды равна 10 см.
Дайте ответ в виде \(a\arccos b\) где \(a,{\text{ }}b \in \mathbb{R}\) .
Ответ/ПояснениеМаркировочная схема
Глубина воды 10 см соответствует \(16\сек \влево( {\frac{{\pi x}}{{36}}} \вправо) – 32 = – 6\) (A1)
Преобразование для получения уравнения вида \(\sec \left( {\frac {{\pi x}}{{36}}} \right) = k\) или эквивалентного
т. е. делает тригнометрическую функцию предметом уравнения. M1
\(\cos \left( {\frac{{\pi x}}{{36}}} \right) = \frac{8}{{13}}\) (A1 )
\(\frac{{\pi x}}{{36}} = \pm \arccos \frac{8}{{13}}\) M1
\(x = \ pm \frac{{36}}{\pi }\arccos \frac{8}{{13}}\) A1
Примечание: Не наказывать за пропуск ±.
Ширина водной поверхности \(\frac{{72}}{\pi }\arccos \frac{8}{{13}}{\text{ (см)}}\) R1 N1
Примечание: Кандидат, который начинает с 10 вместо -6, может получить две отметки M1 и отметку R1 .
[6 баллов]
Вопрос(a) Покажите, что \(\arctan \left( {\frac{1}{2}} \right) + \arctan \left( {\frac{1}{3}} \right) = \ гидроразрыва {\ пи} {4} \) .
(b) Отсюда или иначе найдите значение \(\arctan (2) + \arctan (3)\) .
Ответ/ПояснениеМаркировочная схема
(a) МЕТОД 1
пусть \(x = \arctan \frac{1}{2} \Rightarrow \tan x = \frac{1}{2}\) и \(y = \ arctan \ frac {1} {3} \ Rightarrow \ tan y = \ frac {1} {3} \)
\(\ tan (x + y) = \ frac {{\ tan x + \tan y}}{{1 – \tan x\tan y}} = \frac{{\frac{1}{2} + \frac{1}{3}}}{{1 – \frac{1 {2} \times \frac{1}{3}}} = 1\) M1
Итак, \(x + y = \arctan 1 = \frac{\pi} {4}\) A1AG
МЕТОД 2 {\text,
для {}}y > 0\) , \(\arctan x + \arctan y = \arctan\left( {\frac{{x + y}}{{1 — xy}}} \right)\) если \( xy < 1\) M1поэтому, \(\ arctan \ frac {1} {2} + \ arctan \ frac {1} {3} = \ arctan \ left ( {\ frac {{\ frac {1}{2} + \frac{1}{3}}}{{1 – \frac{1}{2} \times \frac{1}{3}}}} \right) = \frac{\ пи {4}\) A1AG
МЕТОД 3
соответствующий эскиз
Правильная аргументация, ведущая к \ (\ frac {\ pi} {4} \) R1AG
(b) Метод 1
\ (2) (2) (2) (2) (2) (2) (2) (2) (2) (2) (2) (2) (2) (2) (2) (2) (2) (2) (2) (2) (2) (2) (2) (2) (2) (2) (2) (2) (2) (2) (2) (2) (2). ) = \ frac {\ pi {2} — \ arctan \ left ( {\ frac {1} {2}} \ right) + \ frac {\ pi {2} — \ arctan \ left ( {\ frac { 1}{3}} \справа)\) (M1)
) = \ frac {\ pi {2} — \ arctan \ left ( {\ frac {1} {2}} \ right) + \ frac {\ pi {2} — \ arctan \ left ( {\ frac { 1}{3}} \справа)\) (M1)
\( = \pi – \left( {\arctan \left({\frac{1}{2}} \right) + \arctan \left({\frac{1}{3}} \right )} \right)\) (A1)
Примечание: Может подразумеваться только один из двух предыдущих знаков.
\( = \pi – \frac{\pi }{4} = \frac{{3\pi }}{4}\) A1 N1
901 МЕТОД 2 902 пусть \(x = \arctan 2 \Rightarrow \tan x = 2\) и \(y = \arctan 3 \Rightarrow \tan y = 3\) \(\tan (x + y) = \frac{{\tan x + \tan y}}{{1 — \tan x\tan y}} = \frac{{2 + 3}}{{1 – 2 \times 3}} = – 1\) (M1) как \(\frac{\pi }{4} < x < \frac{\pi }{2}\,\,\ ,\,\,\left( {{\text{accept}}0 и \(\frac{\pi}{4} < y < \ frac {\ pi} {2} \, \, \, \, \, \ left ( {{\ text {accept}} 0 < y < \ frac {\ pi} {2}} \ right) \ ) \(\ frac{\pi }{2} < x + y < \pi \,\,\,\,\,{\text{(принять}}0 < x + y <\pi )\) (R1) Примечание: Может подразумеваться только один из двух предыдущих знаков. Итак, \(x + y = \frac{{3\pi}}{4}\) A1 N1 {}} y > 0 \) , \(\ arctan x + \ arctan y = \ arctan \ left ( {\ frac {{x + y}} {{1 — xy}}} \ right) + \ pi {\ text{ if }}xy > 1\) (M1) поэтому \(\ arctan 2 + \ arctan 3 = \ arctan \left( {\ frac {{2 + 3}} {{1 — 2 \times 3}}} \right) + \pi \) (A1) Примечание: Может подразумеваться только один из двух предыдущих знаков. \( = \frac{{3\pi }}{4}\) A1 N1 METHOD 4 an appropriate sketch M1 e.g. правильные рассуждения, ведущие к \(\frac{{3\pi }}{4}\) R1A1 [5 баллов] 92}x\) \(r = \frac{{2\sin x\cos x}}{{\sin x}} = 2\cos x\) A1 Примечание: Принять \(\frac{{\sin 2x}}{{\sin x}}\). [1 балл] (b) ЛИБО \(\left| r \right| < 1 \Стрелка вправо \left| {2\cos x} \right| < 90\) 4 M1 

ИЛИ
\( – 1 < r < 1 \Стрелка вправо – 1 < 2\cos x < 1\) M1
ЗАТЕМ
\(0 < \cos x < \frac{1}{2}{\text{ for }} – \frac{\pi }{2} < x < \frac {\pi} {2}\)
\( — \ frac{\pi }{2} < x < - \ frac{\pi }{3}{\text{или }}\frac{\pi }{ 3} < x < \frac{\pi} {2}\) A1A1
[3 балла]
(c) \({S_\infty} = \frac {{\sin x}}{{1 – 2\cos x}}\) M1
\({S_\infty} = \frac{{\sin\left({\arccos\left( {\frac{1 }{4}} \right)} \right)}}{{1 – 2\cos \left( {\arccos \left({\frac{1}{4}} \right)} \right)}}\ )
\( = \frac{{\frac{{\frac{{\sqrt {15}}}{4}}}{{\frac{1}{2}}}\) A1A1
Примечание: Награда A1 за правильный числитель и A1 за правильный знаменатель.
\ (= \ frac {{\ sqrt {15}}} {2} \) AG
[3 Marks]
110907 [3 Marks] 11111109924 4. 111111111109907 ВопросРассмотрим следующие функции:
\(h(x) = \arctan (x),{\text{}}x \in\mathbb{R}\)
\(g(x) = \frac{1}{x}\) , \(x\in \mathbb{R}\), \({\text{}}x \ne 0\)
Нарисуйте график \(y = h(x)\).[2]
а.
Найдите выражение для составной функции \(h \circ g(x)\) и укажите ее область определения.[2]
б.
Учитывая, что \(f(x) = h(x) + h \circ g(x)\),
(i) найти \(f'(x)\) в упрощенной форме;
(ii) покажите, что \(f(x) = \frac{\pi }{2}\) для \(x > 0\).[7]
г.
Найджел утверждает, что \(f\) — нечетная функция, а Том утверждает, что \(f\) — четная функция.
(i) Укажите, кто прав, и обоснуйте свой ответ.
(ii) Следовательно, найдите значение \(f(x)\) для \(x < 0\). [3]
[3]
д.
Answer/ExplanationMarkscheme
A1A1
Note: A1 for correct shape, A1 for asymptotic behaviour at \(y = \pm \frac{\pi {2}\). 92}}} \)
\ (= 0 \) A1
(II) Метод 1
F — это констант R1. )
\(f(1) = \frac{\pi }{4} + \frac{\pi }{4}\) M1A1
\( = \frac{\pi }{2} \) AG
МЕТОД 2
из диаграммы
\(\theta = \arctan \frac{1}{x}\) A1
\(\alpha = \arctan x\) A1
\(\theta + \alpha = \frac{\pi }{2}\) R1
следовательно \(f(x) = \frac{\pi }{2}\) AG
МЕТОД 3
\(\tan \left( {f(x)} \right) = \ tan \left( {\arctan (x) + \arctan \left({\frac{1}{x}} \right)} \right)\) M1
\( = \ frac{{x + \frac{1}{x}}}{{1 – x\left( {\frac{1}{x}} \right)}}\) A1
знаменатель = 0, поэтому \(f(x) = \frac{\pi} {2}{\text{ (для }}x > 0)\) R1
[7 баллов]
в.
(i) Найджел прав. A1
МЕТОД 1
\(\arctan (x)\) нечетная функция и \(\frac{1}{x}\) нечетная функция
композиция двух нечетных функций — нечетная функция, а сумма двух нечетных функций — нечетная функция R1
МЕТОД 2
\(f( – x) = \arctan ( – x) + \arctan \left( { – \frac{1}{x}} \right) = – \ arctan (x) – \ arctan \left( {\frac {1}{x}} \right) = – f(x)\)
, поэтому f является нечетной функцией. R1
(ii) \(f(x) = – \frac{\pi }{2}\) A1
[3 marks]
d.
Вопрос 92}=\sqrt{2} \Стрелка вправо … \Стрелка вправо x=\frac{\sqrt{2}}{4}\) Вопрос (a) Запишите область определения и область значений функции f(x) = arctan x.
(b) Применяя тангенс, найдите значения
\(A=arctan\frac{1}{3}+arctan\frac{1}{2},\) \(B=arctan 2 + arctan 3\)
\(C=arctan\frac{1}{3}-arctan2\) \(D=arctan\frac{2}{3}+arctan\frac{3}{2}\)
Ans
(a) x∈R, \(-\frac{\pi}{2}
\(tan C=-1\Rightarrow C=-\frac{\pi}{4}\), (C является -тивным) tan D не определено \(\Rightarrow D=\frac{\pi }{2}\)Вопросы 23–25: без GDC.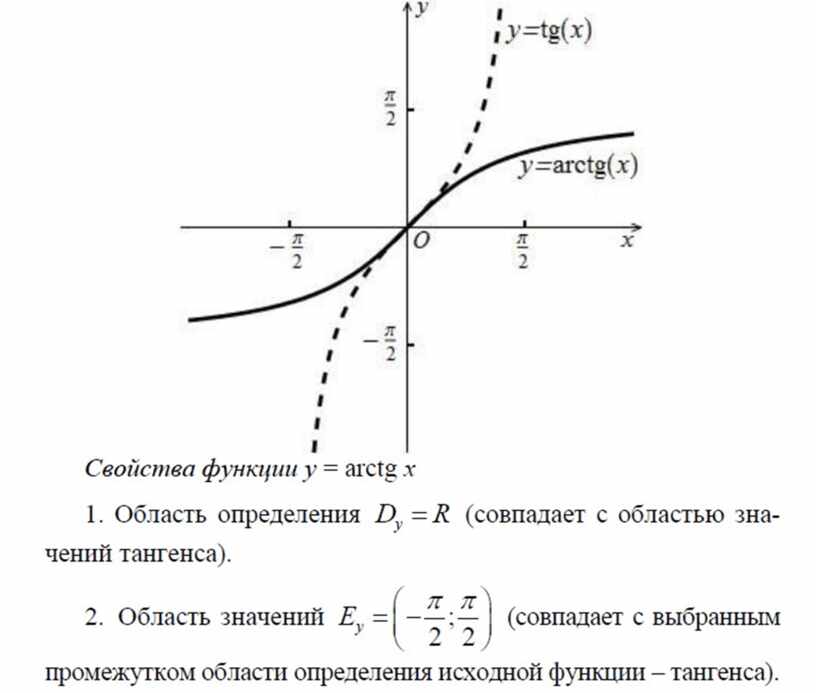
Решите 2 sin x = tan x, где \(-\frac{\pi}{2} Ответ Телевизионный экран ВС высотой один метр встроен в стену. Нижняя часть телевизионного экрана в точке B находится на один метр выше уровня глаз наблюдателя. Углы места (АОС, АОВ) от глаза наблюдателя в точке О до верхней и нижней части телевизионного экрана равны α и β радианам соответственно. Расстояние по горизонтали от глаза наблюдателя до стены с экраном телевизора равно х метров. Угол зрения наблюдателя (BOC) равен радиусу θ, как показано ниже. 92+b}\), где a,b∈R Ответ
\(2sinx =tanx\)
\(\Rightarrow 2sinx cosx-sinx =0\) 9{-1}{4}\)
(c) Найдите максимальное значение угла θ и значение x, при котором этот максимум достигается.
(d) Найдите, где должен стоять наблюдатель, чтобы угол обзора был равен 15 o .
Попытка выразить α и β через арктангенс
α = арктан\(\frac{2}{x}\) и \(β=arctan\frac{1}{x }\)
\(θ=arctan\frac{2}{x}-arctan\frac{1}{x}\)
(b) Использование tan θ =\(\frac{tanα-tanβ}{1+tanαtanβ }\), чтобы получить tanθ через x.

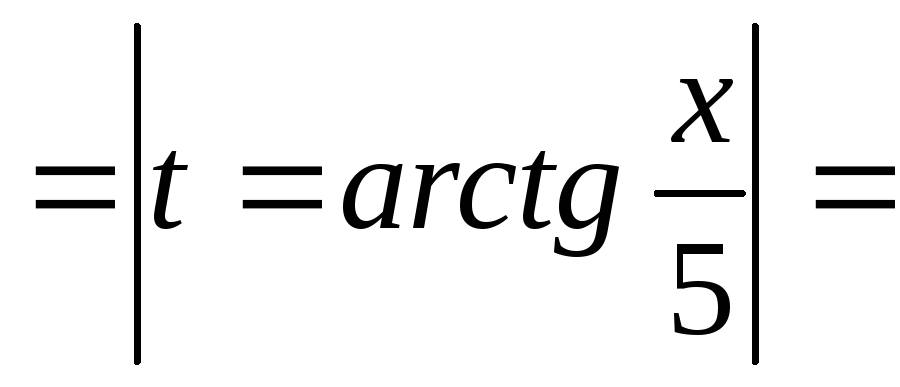
-and-arctan(x).gif)