Построить таблицу истинности логической функции: Онлайн-калькулятор по информатике

4. Логические выражения и таблицы истинности

13

4.1.Логические выражения

Каждое составное высказывание можно выразить в виде формулы (логического выражения), в которую входят логические переменные, обозначающие высказывания, и знаки логических операций, обозначающие логические функции.

Для записи составного высказывания в виде логического выражения на формальном языке (языке алгебры логики) в составном высказывании нужно выделить простые высказывания и логические связи между ними.

Запишем в форме логического выражения составное высказывание

«(2·2=5 или 2·2=4) и (2·2≠5 или 2·2≠4)».

Проанализируем составное высказывание. Оно содержит два простых высказывания:

А = «2•2=5»—ложно (0), В = «2•2=4»—истинно (1).

Тогда составное высказывание можно записать в следующей форме: «(А или В) и (Ā или В)».

Теперь необходимо записать высказывание в форме логического выражения с учётом последовательности выполнения логических операций. При выполнении логических операций определён следующий порядок их выполнения:

инверсия, конъюнкция, дизъюнкция.

Для изменения указанного порядка могут использоваться скобки:

F = (A v В) & (Ā v В).

Истинность или ложность составных высказываний можно определять чисто формально, руководствуясь законами алгебры высказываний, не обращаясь к смысловому содержанию высказываний.

Подставим в логическое выражение значения логических переменных и, используя таблицы истинности базовых логических операций, получим значение логической функции:

F = (A v В) & (Ā v В) = (0 v 1) & (1 v 0) = 1 & 1 = 1.

14

4.2.Таблицы истинности

Таблицы, в которых логические операции отражают результаты вычислений сложных высказываний при различных значениях исходных простых высказываний, называются таблицами истинности.

Простые высказывания обозначаются переменными (например, A и B).

При построении таблиц истинности целесообразно руководствоваться определённой последовательностью действий:

1) необходимо определить количество строк в таблице истинности.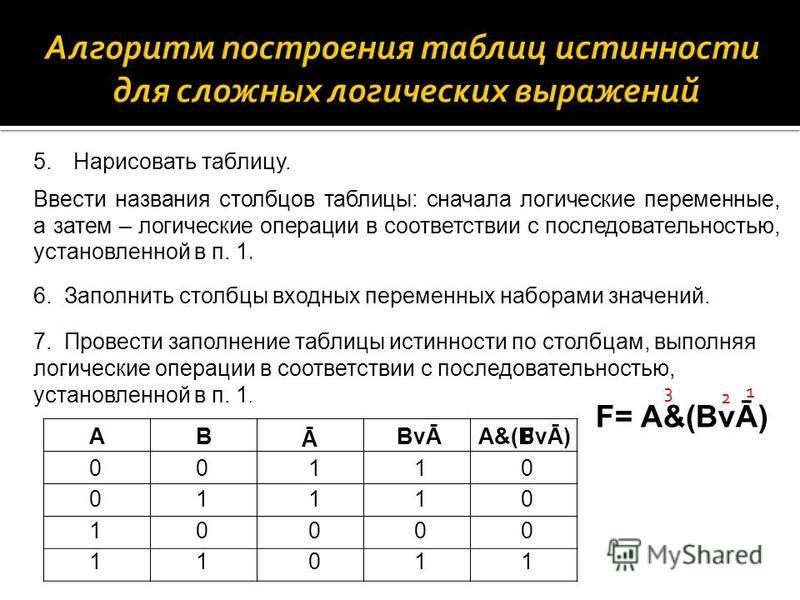 Оно равно количеству возможных комбинаций значений логических переменных, входящих в логическое выражение. Если количество логических переменных равно п, то:

количество строк = 2n.

В нашем случае логическая функция имеет 2 переменные и, следовательно, количество строк в таблице истинности должно быть равно 4;

2)необходимо определить количество столбцов в таблице истинности, которое равно количеству логических переменных плюс количество логических операций.

В нашем случае количество переменных равно двум: А и В, а количество логических операций — пяти (таблица 8), то есть количество столбцов таблицы истинности равно семи;

3)необходимо построить таблицу истинности с указанным количеством строк и столбцов, обозначить столбцы и внести в таблицу возможные наборы значений исходных логических переменных;

4)необходимо заполнить таблицу истинности по столбцам, выполняя базовые логические операции в необходимой последовательности и в соответствии с их таблицами истинности.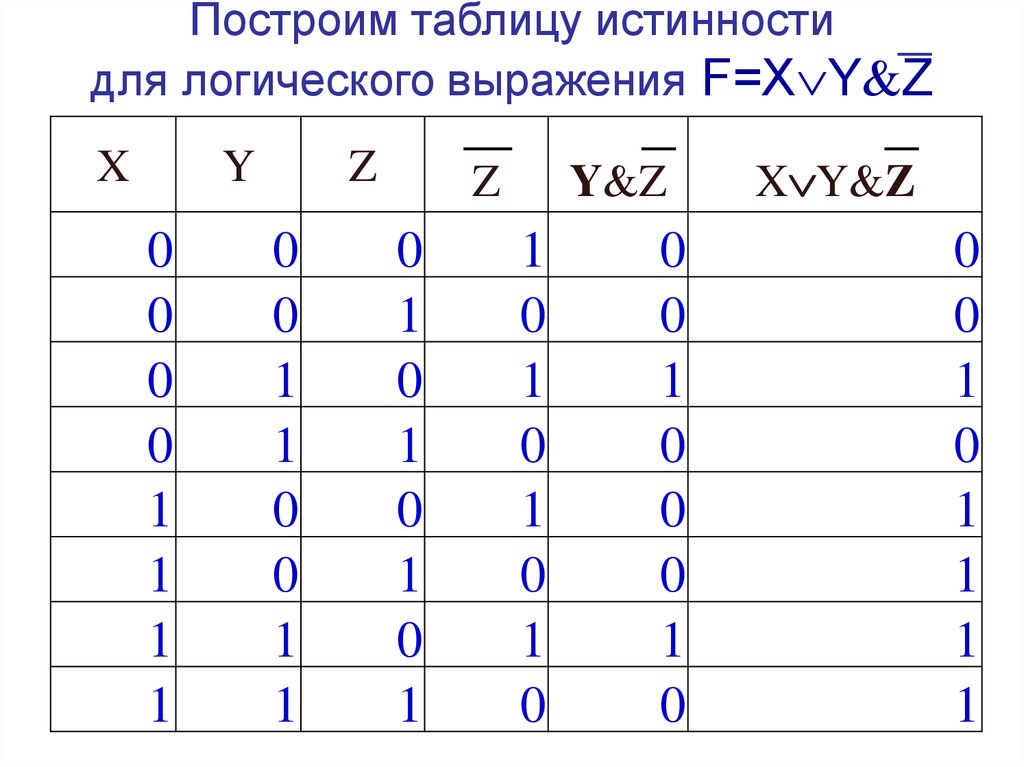

Теперь мы можем определить значение логической функции для любого набора значений логических переменных.

15

Таблица 8 – Таблица истинности логической функции

4.3.Равносильные логические выражения

Логические выражения, у которых последние столбцы таблиц истинности сов-

падают, называются равносильными. Для обозначения равносильных логических выражений используется знак «=».

Докажем, что логические выражения равносильны. Построим сначала таблицу истинности логического выражения (табли-

ца 9).

Таблица 9 – Таблица истинности логического выражения

А	В
0	0	1	1	1
0	1	1	0	0
1	0	0	1	0
1	1	0	0	0

Теперь построим таблицу истинности логического выражения (таблица 10).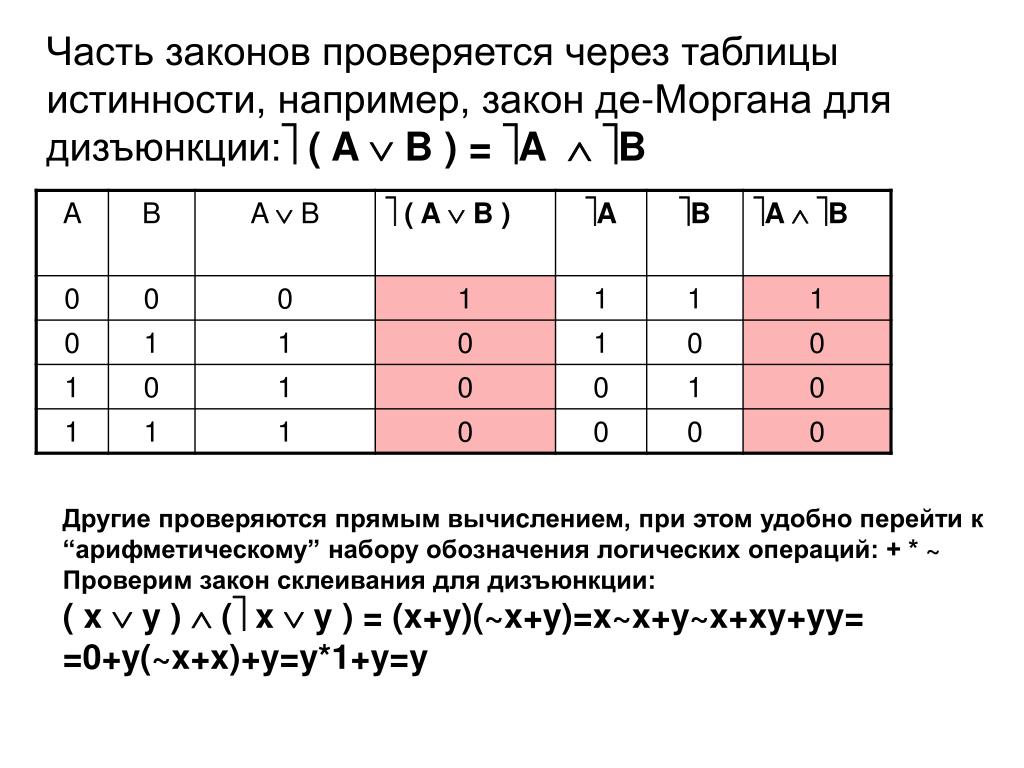

Таблица 10 – Таблица истинности логического выражения

А	В	А v В
0	0	0	1
0	1	1	0
1	0	1	0
1	1	1	0

Значения в последних столбцах таблиц истинности совпадают, следовательно, логические выражения равносильны:

=.

16

5. Построение таблиц истинности для сложных выражений

Согласно определению, таблица истинности логической формулы выражает соответствие между всевозможными наборами значений переменных и значениями формулы.

Для формулы, которая содержит две переменные, таких наборов значений

переменных всего четыре:
(0, 0),	(0, 1),	(1, 0),	(1, 1).

Если формула содержит три переменные, то возможных наборов значений

переменных восемь:
(0, 0, 0),	(0, 0, 1),	(0, 1, 0),	(0, 1, 1),	(1, 0, 0),	(1, 0, 1),	(1, 1, 0),	(1, 1, 1).

Количество наборов для формулы с четырьмя переменными равно шестнадцати и т.д.

Удобной формой записи при нахождении значений формулы является таблица, содержащая кроме значений переменных и значений формулы также и значения промежуточных формул.

Пример 1 1. Составим таблицу истинности для формулы, которая содержит две пере-

менные X и Y. В первых двух столбцах таблицы запишем четыре возможных пары значений этих переменных, в последующих столбцах — значения промежуточных формул и в последнем столбце — значение формулы. В результате получим таблицу 11:

Таблица 11 – Таблица истинности для формулы с переменными Х и У

Пример 2

Cоставить таблицу истинности сложного логического выражения: D = неA & (B+C).

А, В, С – три простых высказывания, поэтому:

количество строк = 23 +2 = 10 (n=3, т.к. на входе три элемента А, В, С) количество столбцов (таблица 12):

1)А,

2)В,

Урок по теме: Логические выражения и таблицы истинности | План-конспект урока по информатике и икт (9 класс) по теме:

Урок по информатике: Логические выражения и таблицы истинности

Цели: построение таблиц истинности логических выражений.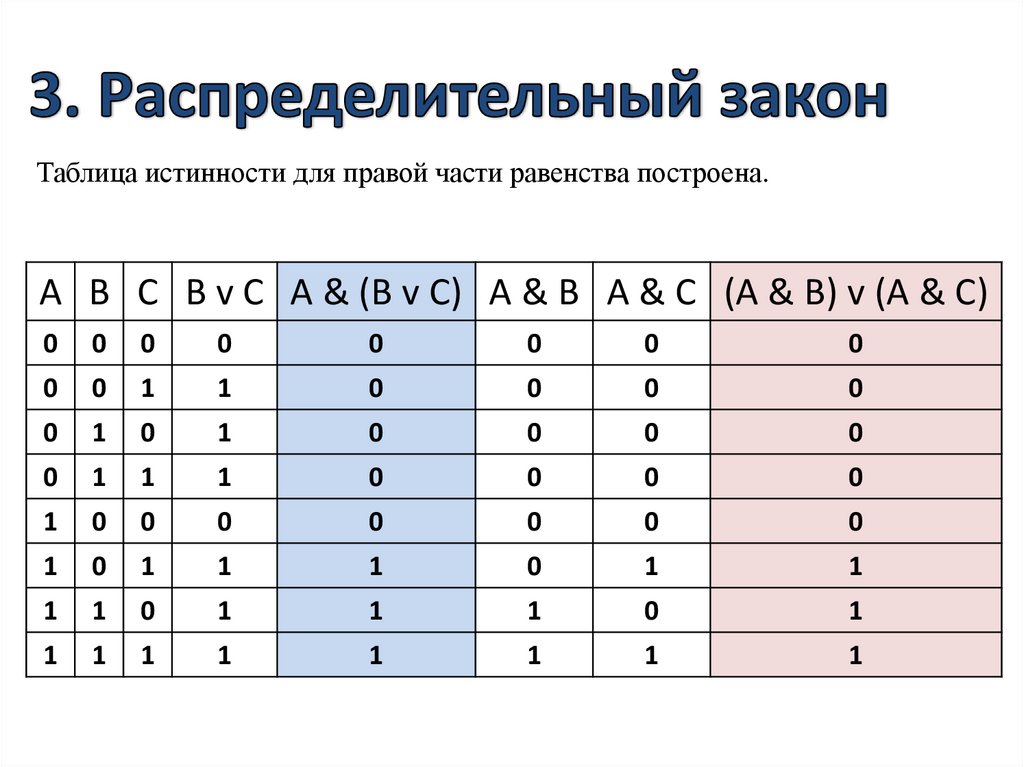

Задачи:

1. Научить составлять логические выражения из высказываний;
2. Ввести понятие “таблица истинности логического выражения”;
3. Изучить последовательность действий построения таблиц истинности;
4. Научить находить значение логических выражений посредством построения таблиц истинности;
5. Ввести понятие равносильности логических выражений;
6. Научить доказывать равносильность логических выражений, используя таблицы истинности;
7. Закрепить навыки нахождения значений логических выражений посредством построения таблиц истинности.

Ожидаемые результаты обучения:

Учащиеся должны знать:

• таблицы истинности логических операций;

• этапы составления таблиц истинности логических выражений;
• понятие равносильные логические выражения.

Учащиеся должны уметь:

• строить  и заполнять таблицу истинности логического выражения;
• находить значение логических выражений посредством построения таблиц истинности;
• доказывать равносильность логических выражений, используя таблицы истинности.

Ход урока

I. Оргмомент.

Здравствуйте, ребята. Мы продолжаем изучать основы логики и тема нашего сегодняшнего урока «Составление логических выражений. Таблицы истинности». Изучив данную тему, вы научитесь, как из высказываний составляются логические формы, и определять их истинность посредством составления таблиц истинности.

II. Проверка домашнего задания.

III. Изложение нового материала.

1. Построение таблиц истинности.

Мы уже несколько уроков используем понятие “таблица истинности”, определим же его.

Опр.1 Таблица истинности — это таблица, устанавливающая соответствие между возможными наборами значений логических переменных и значениями функций.

При построении таблиц истинности есть определенная последовательность действий:

1. Необходимо определить количество строк в таблице истинности: количество строк равно 2n, где n — количество логических переменных.
2. Необходимо определить количество столбцов в таблице истинности, которое равно количеству логических переменных плюс количество логических операций.
3. Необходимо построить таблицу истинности с указанным количеством строк и столбцов, ввести названия столбцов таблицы в соответствии с последовательностью выполнения логических операций с учетом скобок и приоритетов;
4. Заполнить столбцы входных переменных наборами значений;
5. Провести заполнение таблицы истинности по столбцам, выполняя логические операции в соответствии с установленной последовательностью.

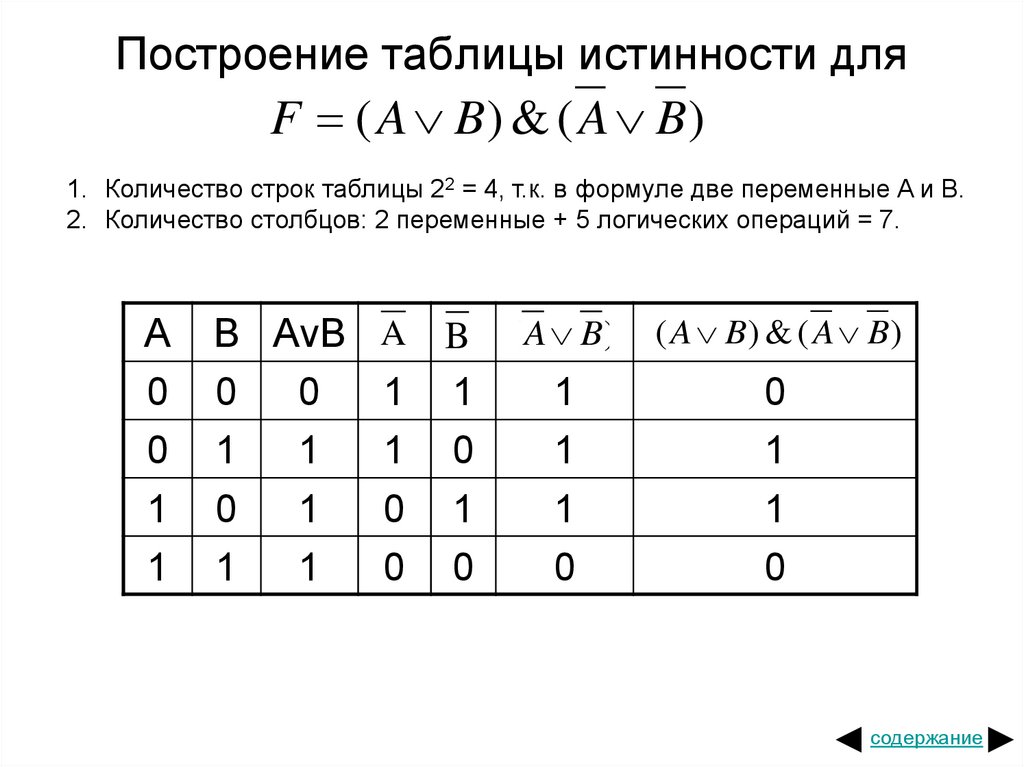
Пример. Построить таблицу истинности для составного высказывания:

1). Определим количество строк в таблице. Для этого: считаем количество переменных, в нашем случае логическая функция содержит 2 переменные: А и В.

Количество строк в таблице истинности должно быть равно 22=4.

2). Определяем количество столбцов. Это количество логических переменных плюс количество логических операций.

 В нашем случае количество переменных равно двум, а количество логических операции — пяти, то есть количество столбцов таблицы истинности равно семи.

3). Строим таблицу с указанным количеством строк и столбцов, обозначаем столбцы и вносим в таблицу возможные наборы значений исходных логических переменных и заполняем таблицу истинности по столбцам.

Можно сначала выполнить логическое отрицание или найти значение сначала в первой скобке, затем инверсию и значение во второй скобке, затем значение между этими скобками.

A	B
0	0	0	1	1	1	0
0	1	1	1	0	1	1
1	0	1	0	1	1	1
1	1	1	0	0	0	0

Теперь мы можем определить значение логической функции для любого набора значений логических переменных.

2. Равносильные логические выражения.

Логические выражения, у которых последние столбцы таблиц истинности совпадают, называются равносильными. Для обозначения равносильных логических выражений используется знак “ = “.

Пример. Докажем, что логические выражения  и  равносильны.

Построим сначала таблицу истинности логического выражения:

1). Определим количество строк в таблице. Для этого: считаем количество переменных, в нашем случае логическая функция содержит 2 переменные: А и В.

Количество строк в таблице истинности должно быть равно 22=4.

2). Определяем количество столбцов. Это количество логических переменных плюс количество логических операций.

В нашем случае количество переменных равно двум, а количество логических операции — трем, то есть количество столбцов таблицы истинности равно пяти.

3). Строим таблицу с указанным количеством строк и столбцов, обозначаем столбцы и вносим в таблицу возможные наборы значений исходных логических переменных и заполняем таблицу истинности по столбцам.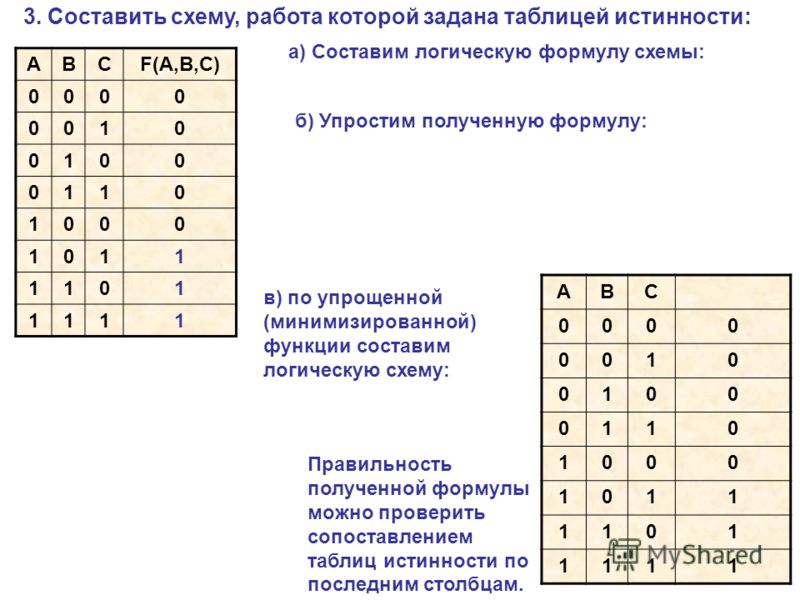

Сначала необходимо выполнить логическое отрицание А, а затем логическое отрицание В. Последним действием выполним логическое сложение.

A	B
0	0	1	1	1
0	1	1	0	0
1	0	0	1	0
1	1	0	0	0

Теперь построим таблицу истинности логического выражения:

1). Определим количество строк в таблице. Для этого: считаем количество переменных, в нашем случае логическая функция содержит 2 переменные: А и В.

Количество строк в таблице истинности должно быть равно 22=4.

2). Определяем количество столбцов. В нашем случае количество переменных равно двум, а количество логических операции — двум, то есть количество столбцов таблицы истинности равно четырем.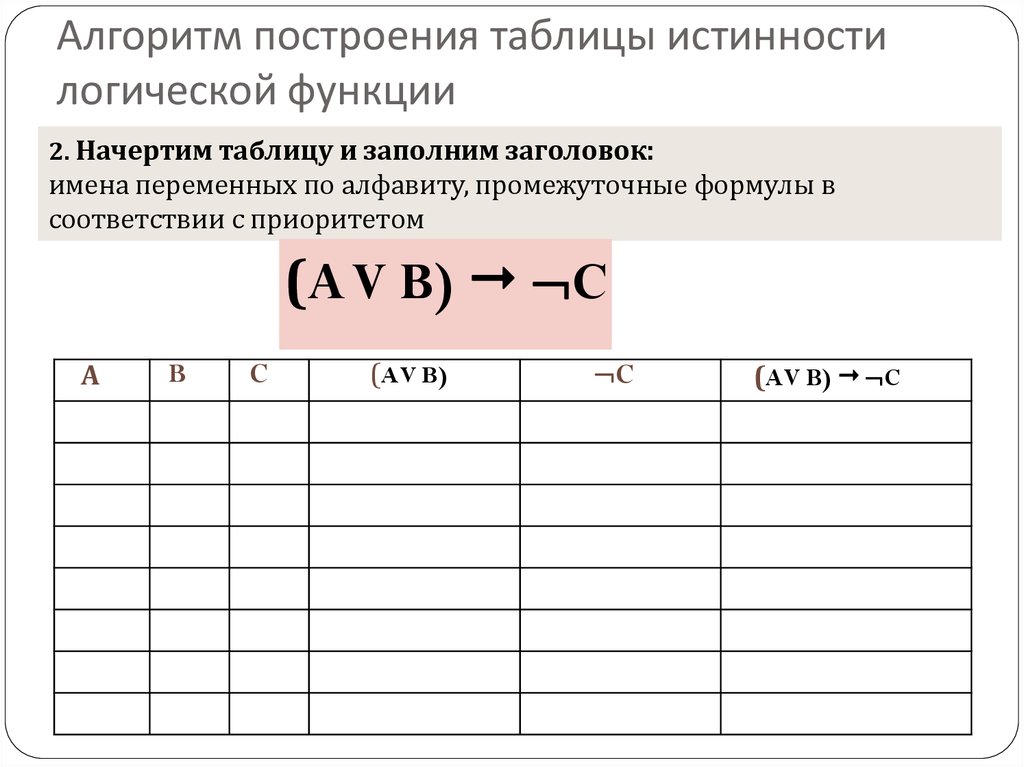

3). Строим таблицу с указанным количеством строк и столбцов, обозначаем столбцы и вносим в таблицу возможные наборы значений исходных логических переменных и заполняем таблицу истинности по столбцам.

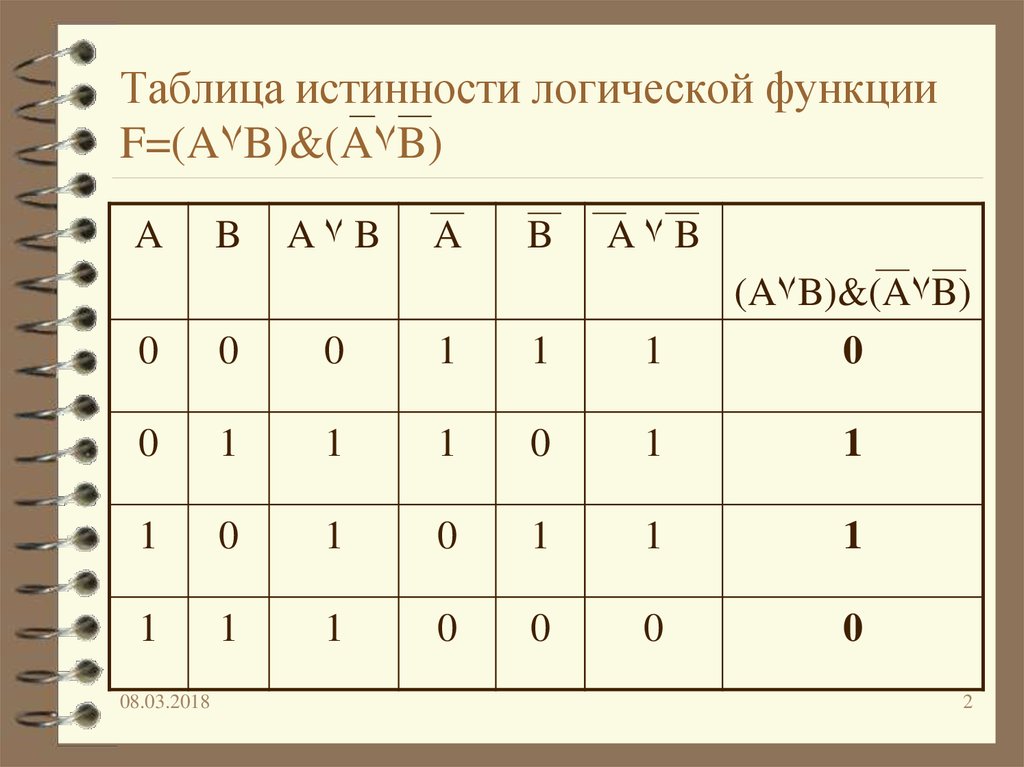
Сначала необходимо выполнить действие в скобках, а затем логическое отрицание.

A	B
0	0	0	1
0	1	1	0
1	0	1	0
1	1	1	0

Построили таблицы. Теперь давайте, сравним значения в последних столбцах таблиц истинности, т.к. именно последние столбцы являются результирующими:

=

IV. Закрепление изученного материала.

1. Построить таблицу истинности для формулы: .

1).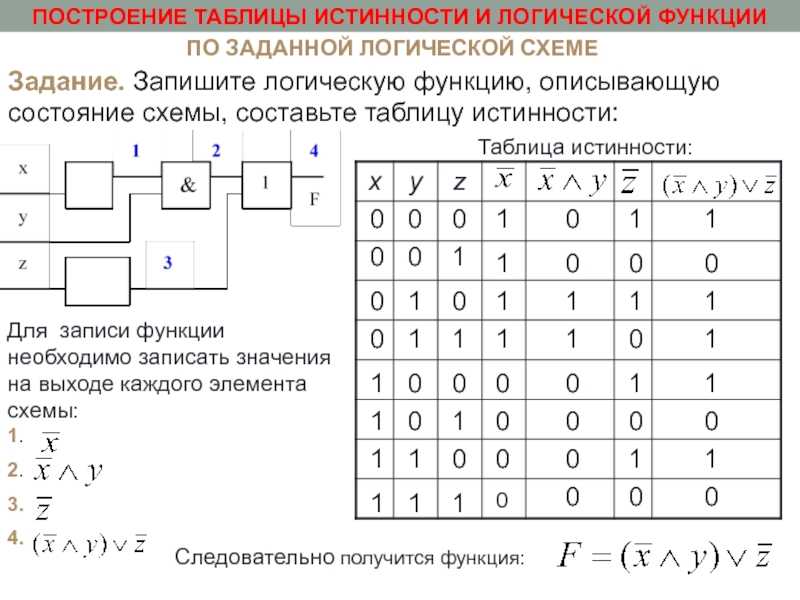 Определим количество строк в таблице. Для этого: считаем количество переменных, в нашем случае логическая функция содержит 3переменные: А, В и С.

Количество строк в таблице истинности должно быть равно 23=8.

2). Определяем количество столбцов. В нашем случае количество переменных равно трем, а количество логических операции — пяти, то есть количество столбцов таблицы истинности равно восьми.

3). Строим таблицу с указанным количеством строк и столбцов, обозначаем столбцы и вносим в таблицу возможные наборы значений исходных логических переменных и заполняем таблицу истинности по столбцам.

Последовательность операций: инверсия, операции в скобках, операция за скобкой.

A	B	C
0	0	0	1	1	1	1	1
0	0	1	1	0	1	0	0
0	1	0	0	1	1	1	1
1	0	0	1	1	1	1	1
0	1	1	0	0	1	0	0
1	1	0	0	1	1	1	1
1	0	1	1	0	1	0	1
1	1	1	0	0	1	0	1

2. Докажите с помощью таблиц истинности равносильность следующих логических выражений:  и .

Построим сначала таблицу истинности логического выражения: .

1). Определим количество строк в таблице: 22=4.

2). Определяем количество столбцов: 2+1=3.

3). Строим таблицу с указанным количеством строк и столбцов.

A	B
0	0	1
0	1	1
1	0	0
1	1	1

Построим таблицу истинности логического выражения: .

1). Определим количество строк в таблице: 22=4.

2). Определяем количество столбцов: 2+2=4.

3). Строим таблицу с указанным количеством строк и столбцов.

A	B
0	0	1	1
0	1	0	0
1	0	1	1
1	1	0	1

Вывод: данные логические выражения не равносильны.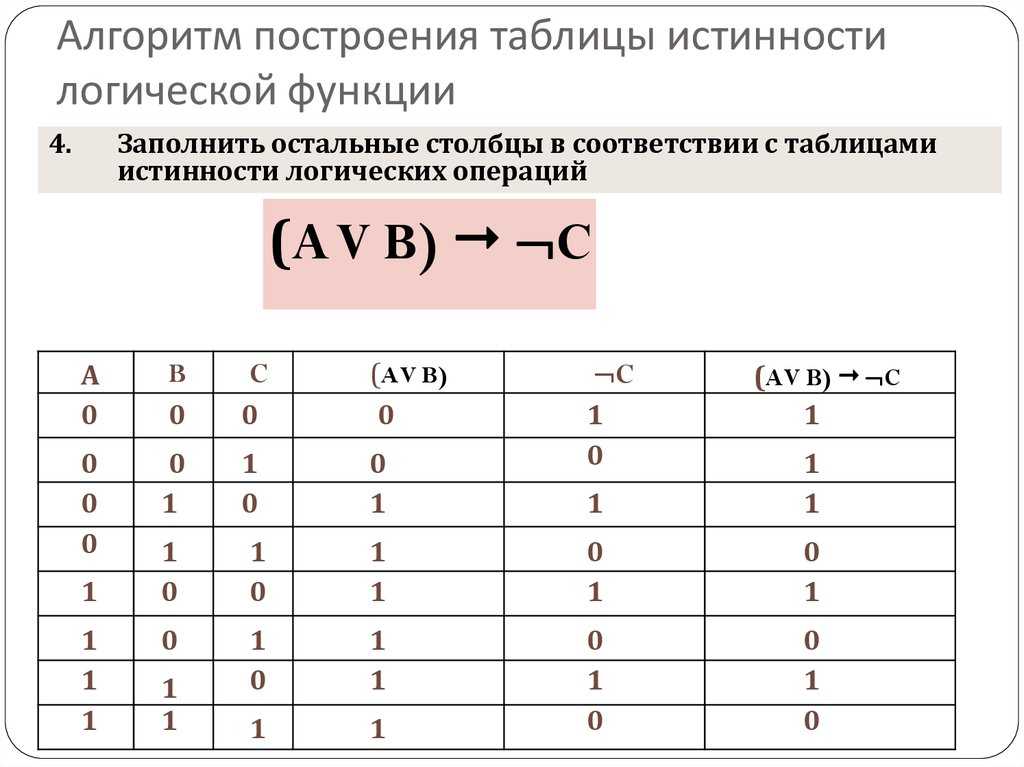

V. Итог урока.

Обобщить пройденный материал, оценить работу активных учеников.

VI. Домашнее задание.

1. Доказать, используя таблицы истинности, что логические выражения  и  равносильны.

Построить таблицу истинности для формулы:

Примечания к таблице истинности и логическим утверждениям

Таблица истинности логической функции содержит списки всех возможных значений, которые функция может получить для данного входа. Таблица истинности состоит из множества строк и столбцов, причем верхняя строка указывает логические переменные и их комбинации, а нижняя строка показывает конечную функцию с возрастающей сложностью. Таблица истинности логической системы представляет выходные данные системы для данного входа в виде строк и столбцов. Чтобы назвать столбцы таблицы истинности, используются входы и выходы со строками, представляющими все потенциальные входы и выходы схемы.

Что такое логические операторы?

Логическое утверждение — это утверждение, которое возвращает либо истину, либо ложь, т. е. 0 или 1. Если оно возвращает истину, оно позволяет нам получить известный набор фактов или получить из них новый факт. Пример: Диагонали прямоугольника имеют одинаковую длину.

Здесь он вернет либо истину, либо ложь в зависимости от оператора. Это декларативный тип оператора, который возвращает true или false.

Некоторые примеры логических утверждений:

Примеры предложений, которые являются (или содержат) истинными утверждениями:

• «Том Круз — мужчина».
• «У треугольника три стороны».
• «Милан — столица Италии».

Примеры ложных предложений:

• «Все кулеры сделаны из чистого золота».
• «Два плюс два равно девять».

Примеры предложений, которые не являются (или не составляют) утверждениями: Эмоции, чувства, вопросы и т. д. не могут быть включены в логические утверждения.

• «Кто ты?»
• «Беги!»
• «Королева Англии мудра».
• «Пегас существует».

Операции в логической функции:

В логической функции есть три основные операции НЕ, ИЛИ и И: 

• НЕ: Это также называется инверсией или отрицанием. Обозначается -. Это означает прямо противоположное или отрицательное значение.
• ИЛИ: Это также называется дизъюнкцией или сложением. Обозначается +. Это похоже на простое добавление значений. Функция возвращает истину, если хотя бы одно из ее значений истинно.
•  И: Это также называется соединением или умножением. Он обозначается *. Это похоже на износ умножения для функции, возвращающей истину, оба значения должны быть истинными.

Таблицы истинности для унарных операторов:

Унарные логические операторы содержат только один логический оператор. Это может быть либо Логическая Истина, либо Логическая Ложь.

Таблица истинности для логической истины: для каждого логического входа возвращается истинное значение.

Вход	Output
T	T
F	T

Truth Table for Logical false: For each logical input, it returns a false Значение

Вход	Выход
T	F
F 9003
9192 F
1912 F 9003
91111003
191219 9003
	. 0074	F

Таблица истинности для комплимента: возвращает значение, прямо противоположное логическому входу.

Input	Output(~)
T	F
F	T

Truth Tables for Binary Операторы:  

В двоичных операциях есть два логических входа. Над этими операторами выполняются операции И, ИЛИ и НЕ.

Таблица истинности для операции ИЛИ: Возвращает истину, если любой из входных данных верен, и ложь, если оба входа ложны.

A	B	A OR B
T	T	T
T	F	Т
Ф	T	T
F	F	F

Tall Table For For For For For Empormance: It True On True On True Tons Thes This This This This This This This This This This This This This False Thes This False Tons On True Tons Thes Thes Thes This.

A	B	A AND B
T	T	T
T	F	F
F	T	F
F	F	F

Правила назначения:

Значения функций могут быть 0 или 1. Где логический 0 означает ложь, а логическая 1 означает истину. Таким образом, применяются следующие правила:

Если A = 0, то -A = 1

Если A = 1, то -A = 0

A+B = 0, если A = 0 и B = 0

A+B = 1, за исключением случаев, когда A = 0 и B = 0

A*B = 1 если A = 1 и B = 1

A*B = 0, за исключением случаев, когда A = 1 и B = 1

Как оценить значения логической функции:

Пример: показать процесс оценки значений логическая функция -(A+B) * -(A*B).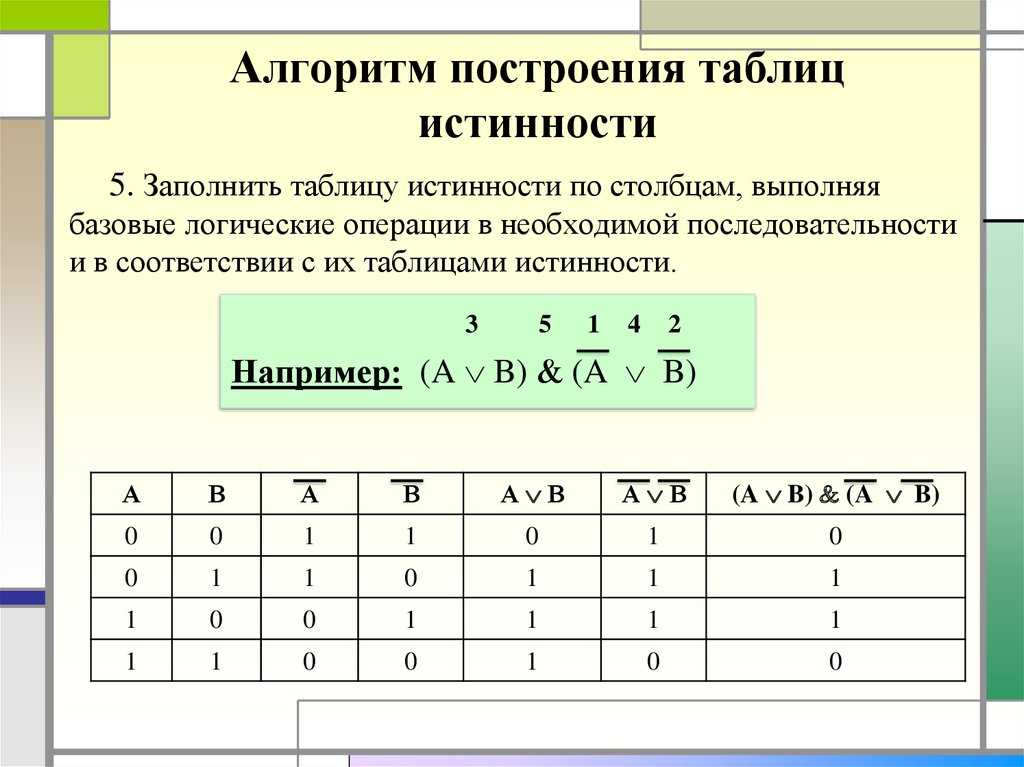

Определяется путем разбиения на более мелкие составные функции и вычисления их значений для достижения последнего шага. Это последовательный процесс. Необходимо выполнить следующие шаги:-

1.  Две логические переменные, A и B, перечислены вверху первых двух столбцов. Все возможные комбинации значений для A и B перечислены в этих столбцах путем подсчета двоичными числами: 00, 01, 10, 11.
2. В третьем столбце значение (A+B) вычисляется с помощью операции ИЛИ. .
3. В четвертом столбце минус (дополнение) третьего столбца берется, чтобы найти значения, связанные с функцией -(A+B)
4. В пятом столбце мы вычисляем значения (A*B) с помощью AND операция.
5. Мы находим отрицательное значение (A*B), чтобы вычислить значение -(A*B)
6. В седьмом столбце мы находим И значений в четвертом столбце и шестом столбце, чтобы получить значение -(A+B )*-(A*B)

Таким же образом мы вычисляем таблицу истинности и значения для всех функций. Ниже приведена таблица выражения для -(A+B) * -(A*B).

А	В	(А+В)	-(А+В)	(A*B)	-(A*B)	-(A+B) * -(A*B)
0	0	0	1	0	1	1
0	1	1	0	0	1	0
1	0	1	0	0	1	0
1	1	1	0	1	0	0

Крайний правый (седьмой) столбец содержит последнюю функцию, которая должна быть оценена.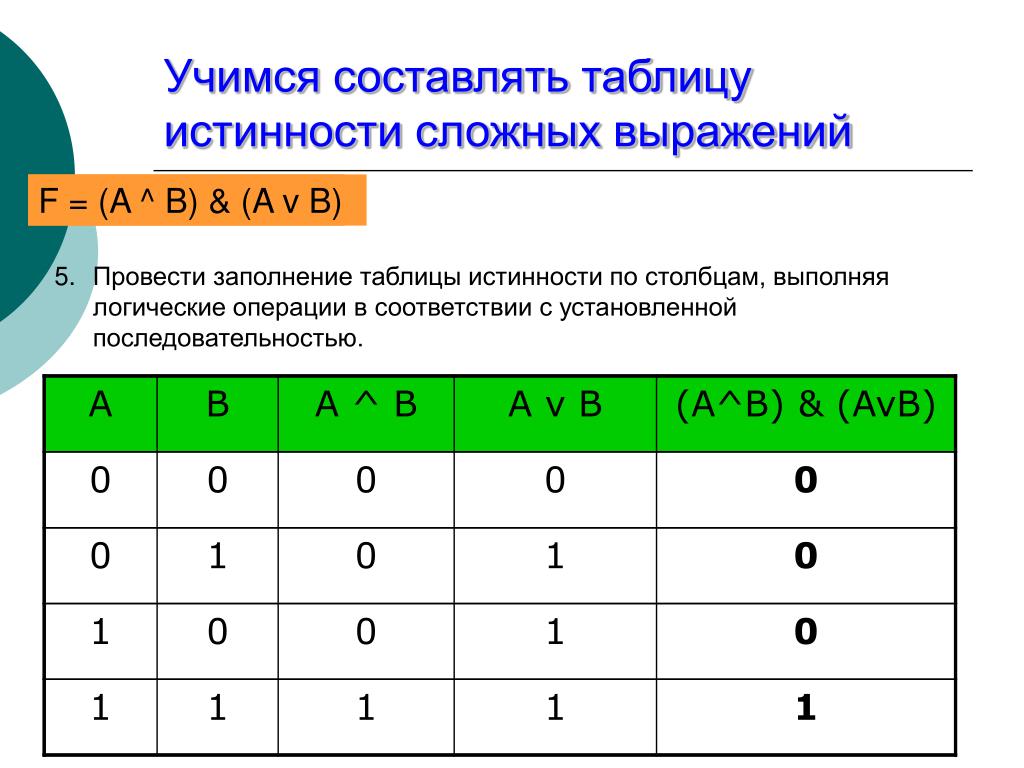 Другие значения в других столбцах (3-й-6-й) определяются путем определения сложения и умножения, а затем отрицания значений.

Применение таблиц истинности и логических утверждений:

Для все более сложных логических функций компьютеры используются для построения таблиц истинности. Некоторые функции имеют большое количество входных переменных и состоят из нескольких составляющих функций; может получиться таблица с сотнями строк и столбцов.

Мы можем использовать таблицы истинности, чтобы определить, правильна ли структура логического аргумента. Они широко используются в логике запросов к базе данных, а также в их оптимизации. Кроме того, для приложений, связанных с общей логикой, таких как экспертные системы. Любой анализ, вероятно, должен реализовать их в той или иной форме. Кроме того, они используются в структурах базовых решений (IF, Case/Switch, IIF и т. д.). Вы можете построить любое количество логических слоев, и было бы полезно их использовать. Они там на фоне системы.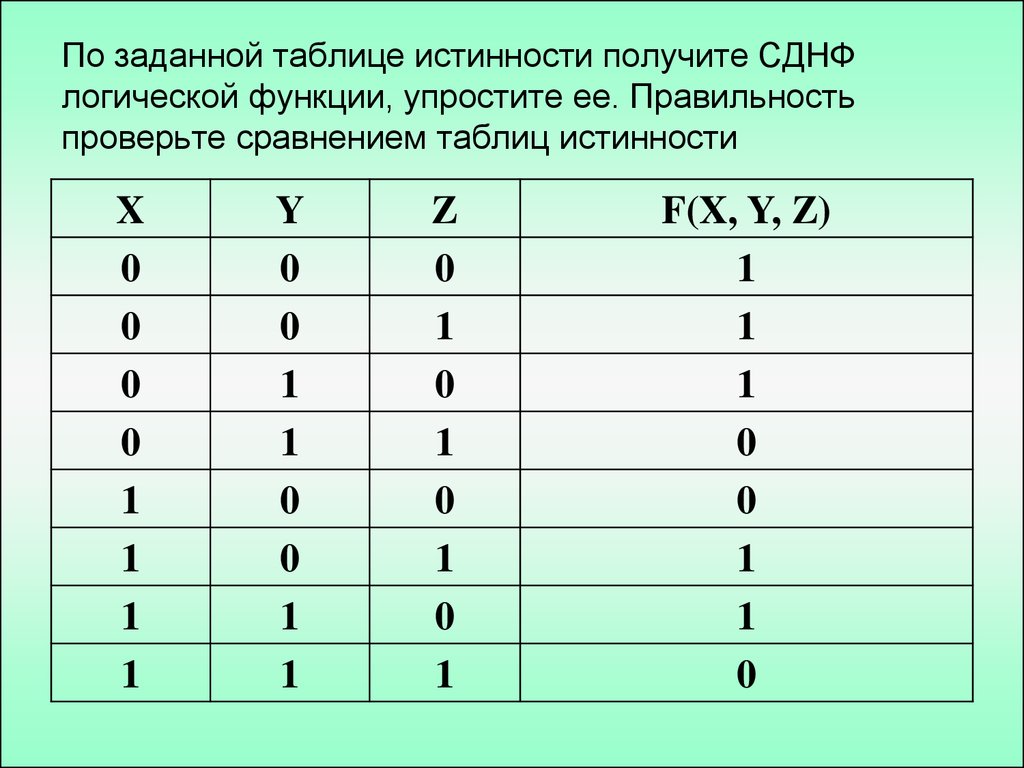

Использование булевых теорем является альтернативой таблице истинности. Этот процесс используется для определения простейшей схемы, которая будет выполнять необходимую логическую функцию. Это уменьшает количество операций, необходимых для выполнения данной задачи, и, следовательно, повышает эффективность системы.

Создание таблиц истинности — обучающиеся машины

Короткий на сегодня: в этом посте мы узнаем, как легко создавать таблицы истинности с помощью R, и внесем наш код в растущий репозиторий

Код Розетты . Я надеюсь, что вы узнаете несколько трюков по пути, так что читайте дальше!

Мы рассмотрели фрагменты кода, которые я добавлял в Rosetta Code в этом блоге ранее (см. Категорию: Rosetta Code). На этот раз мы хотим решить следующую задачу:

Таблица истинности
Таблица истинности представляет собой отображение входных и выходных данных булевой функции, организованной в виде таблицы, где каждая строка содержит одну комбинацию входных значений и соответствующее значение функции.

Задача

1. Введите логическую функцию от пользователя в виде строки, затем вычислите и распечатайте форматированную таблицу истинности для данной функции.
   (Можно предположить, что ввод пользователя правильный).
2. Распечатать и показать вывод для логических функций с двумя и тремя входными переменными, но ни одна программа не должна ограничиваться таким количеством переменных в функции.
3. Разрешены выражения как с обратной шлифовкой, так и с инфиксной нотацией.

Ядром таблицы истинности является перестановка всех утверждений TRUE и FALSE для всех переменных (= букв), которые мы извлекаем из булевой функции x . К счастью, несколько сообщений назад мы создали такую ​​функцию перестановки (см. Изучение R: перестановки и комбинации с базой R), так что мы можем адаптировать ее соответствующим образом: expand.grid(rep(list(c(FALSE, TRUE)), длина(вары))) .