Y cos 2: Mathway | Популярные задачи

2

Mathway | Популярные задачи

1	Найти точное значение	sin(30)
2	Найти точное значение	sin(45)
3	Найти точное значение	sin(30 град. )
4	Найти точное значение	sin(60 град. )
5	Найти точное значение	tan(30 град. )
6	Найти точное значение	arcsin(-1)
7	Найти точное значение	sin(pi/6)
8	Найти точное значение	cos(pi/4)
9	Найти точное значение	sin(45 град. )
10	Найти точное значение	sin(pi/3)
11	Найти точное значение	arctan(-1)
12	Найти точное значение	cos(45 град. )
13	Найти точное значение	cos(30 град. )
14	Найти точное значение	tan(60)
15	Найти точное значение	csc(45 град. )
16	Найти точное значение	tan(60 град. )
17	Найти точное значение	sec(30 град. )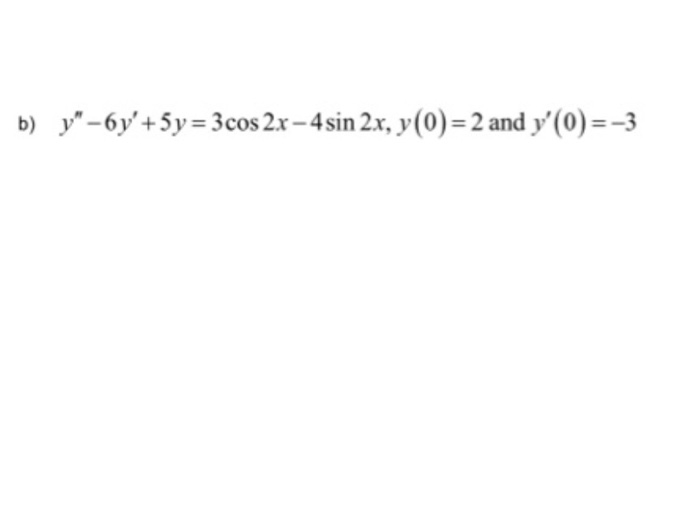
18	Найти точное значение	cos(60 град. )
19	Найти точное значение	cos(150)
20	Найти точное значение	sin(60)
21	Найти точное значение	cos(pi/2)
22	Найти точное значение	tan(45 град. )
23	Найти точное значение	arctan(- квадратный корень из 3)
24	Найти точное значение	csc(60 град. )
25	Найти точное значение	sec(45 град. )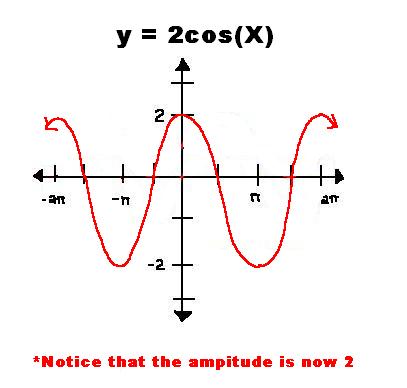
26	Найти точное значение	csc(30 град. )
27	Найти точное значение	sin(0)
28	Найти точное значение	sin(120)
29	Найти точное значение	cos(90)
30	Преобразовать из радианов в градусы	pi/3
31	Найти точное значение	tan(30)
32	Преобразовать из градусов в радианы	45
33	Найти точное значение	cos(45)
34	Упростить	sin(theta)^2+cos(theta)^2
35	Преобразовать из радианов в градусы	pi/6
36	Найти точное значение	cot(30 град. )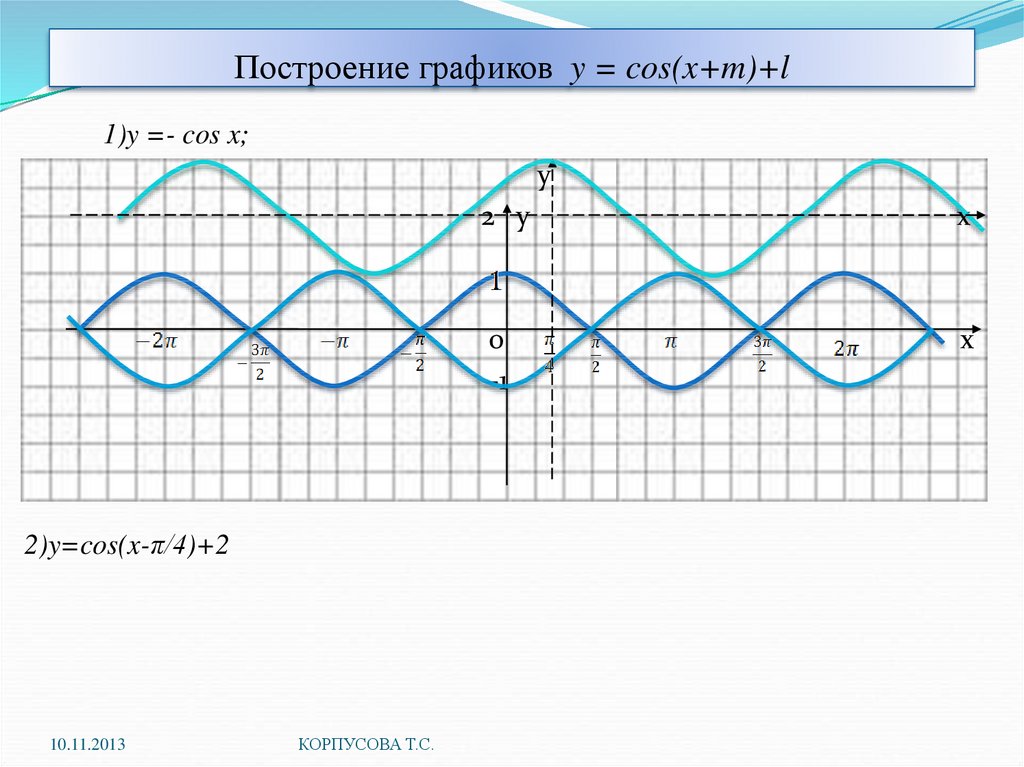
37	Найти точное значение	arccos(-1)
38	Найти точное значение	arctan(0)
39	Найти точное значение	cot(60 град. )
40	Преобразовать из градусов в радианы	30
41	Преобразовать из радианов в градусы	(2pi)/3
42	Найти точное значение	sin((5pi)/3)
43	Найти точное значение	sin((3pi)/4)
44	Найти точное значение	tan(pi/2)
45	Найти точное значение	sin(300)
46	Найти точное значение	cos(30)
47	Найти точное значение	cos(60)
48	Найти точное значение	cos(0)
49	Найти точное значение	cos(135)
50	Найти точное значение	cos((5pi)/3)
51	Найти точное значение	cos(210)
52	Найти точное значение	sec(60 град. )
53	Найти точное значение	sin(300 град. )
54	Преобразовать из градусов в радианы	135
55	Преобразовать из градусов в радианы	150
56	Преобразовать из радианов в градусы	(5pi)/6
57	Преобразовать из радианов в градусы	(5pi)/3
58	Преобразовать из градусов в радианы	89 град.
59	Преобразовать из градусов в радианы	60
60	Найти точное значение	sin(135 град. )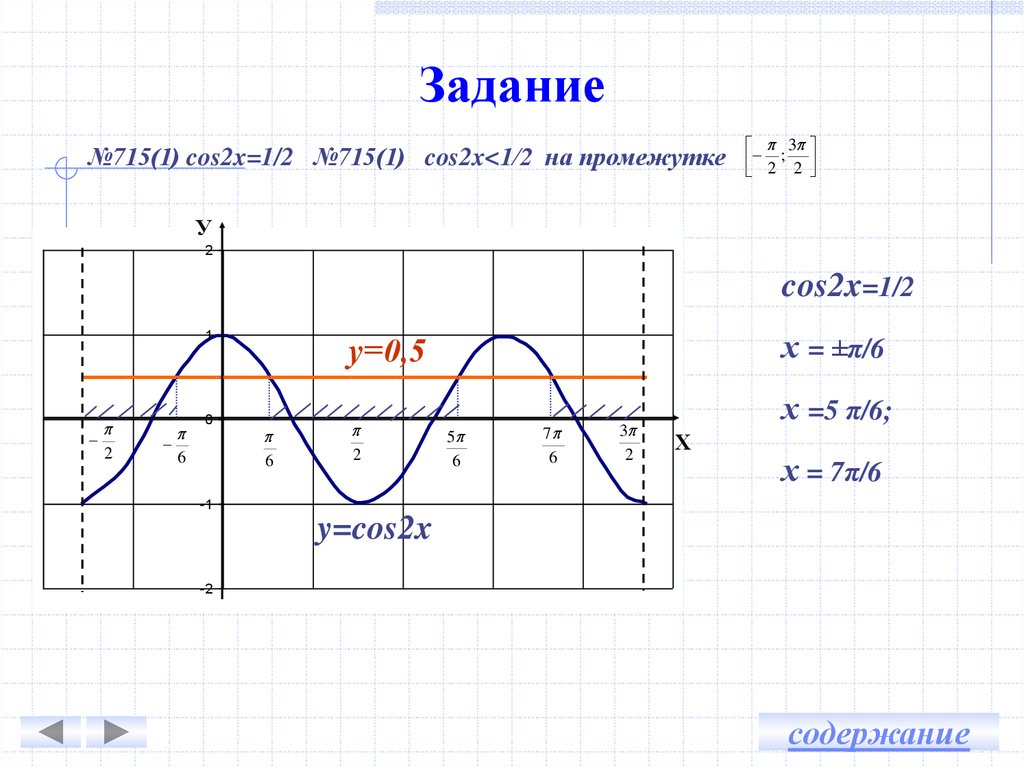
61	Найти точное значение	sin(150)
62	Найти точное значение	sin(240 град. )
63	Найти точное значение	cot(45 град. )
64	Преобразовать из радианов в градусы	(5pi)/4
65	Найти точное значение	sin(225)
66	Найти точное значение	sin(240)
67	Найти точное значение	cos(150 град. )
68	Найти точное значение	tan(45)
69	Вычислить	sin(30 град. )
70	Найти точное значение	sec(0)
71	Найти точное значение	cos((5pi)/6)
72	Найти точное значение	csc(30)
73	Найти точное значение	arcsin(( квадратный корень из 2)/2)
74	Найти точное значение	tan((5pi)/3)
75	Найти точное значение	tan(0)
76	Вычислить	sin(60 град. )
77	Найти точное значение	arctan(-( квадратный корень из 3)/3)
78	Преобразовать из радианов в градусы	(3pi)/4
79	Найти точное значение	sin((7pi)/4)
80	Найти точное значение	arcsin(-1/2)
81	Найти точное значение	sin((4pi)/3)
82	Найти точное значение	csc(45)
83	Упростить	arctan( квадратный корень из 3)
84	Найти точное значение	sin(135)
85	Найти точное значение	sin(105)
86	Найти точное значение	sin(150 град. )
87	Найти точное значение	sin((2pi)/3)
88	Найти точное значение	tan((2pi)/3)
89	Преобразовать из радианов в градусы	pi/4
90	Найти точное значение	sin(pi/2)
91	Найти точное значение	sec(45)
92	Найти точное значение	cos((5pi)/4)
93	Найти точное значение	cos((7pi)/6)
94	Найти точное значение	arcsin(0)
95	Найти точное значение	sin(120 град. )
96	Найти точное значение	tan((7pi)/6)
97	Найти точное значение	cos(270)
98	Найти точное значение	sin((7pi)/6)
99	Найти точное значение	arcsin(-( квадратный корень из 2)/2)
100	Преобразовать из градусов в радианы	88 град.

3-8 9 Оценить квадратный корень из 12 10 Оценить квадратный корень из 20 11 Оценить квадратный корень из 50 94 18 Оценить квадратный корень из 45 19 Оценить квадратный корень из 32 20 Оценить квадратный корень из 18 92

Если x sin θ — y cos θ = √(x2 + y2) и cos2 θ/a2 + sin2 θ/b2 = 1/(x2 + y2), то докажите, что y2/a2 + x2/b2 = 1

Тригонометрические тождества — это уравнения, которые верны для любого значения переменной в области и относятся к различным тригонометрическим функциям. Это качества, которые существуют для всех значений переменных в уравнении. Синус, косинус, тангенс, косеканс, секанс и котангенс — тригонометрические отношения, используемые в этих тождествах. Стороны прямоугольного треугольника, такие как смежная сторона, противоположная сторона и сторона гипотенузы, используются для определения всех этих тригонометрических отношений. Эти тригонометрические тождества действительны только в прямоугольном треугольнике.

Синус-косинусное тождество

В тригонометрии синус-косинусное тождество является пифагорейским тригонометрическим тождеством, поскольку оно основано на теореме Пифагора. В нем говорится, что сумма квадратов синуса и косинуса для любого угла θ равна единице.

SIN ² θ + COS ² θ = 1

ДЕРИВАНИЯ

.

Применение теоремы Pythagoras на этот треугольник, мы получаем

AC ² = AB ² + BC ²

, разделяя обе стороны на AC ² , мы получаем

9

6, мы получим

8,

7

6. = AB ² /AC ² + BC ² /AC ²

(AB/AC) ² + (BC/AC) ^{90 7 9090 (1 6} = 1 знаем) , для угла θ,

sin θ = Перпендикуляр/Гипотенуза

sin θ = AB/AC ⇢  (2)

Кроме того,

cos θ = основание/гипотенуза

cos θ = BC/AC⇢ (3)

Используя (2) и (3) в (1),

sin ^{2 cos 2 θ = 1}

Это доказывает идентичность отношений синуса и косинуса.

. x

² + y ² ), то докажите, что y ² /a ² + x ² /b ² = 1.

Solution:

x sin θ – y cos θ = √(x ² + y ² )

Squaring both sides we get,

=> x ² sin ² θ + y ² cos ² θ – 2xy sin θ cos θ = x ² + y ²

=> x ² sin ² θ + y ² cos ² θ – 2xy sin θ cos θ – x ² – y ² = 0

=> x ² (sin ² θ – 1) + y ² (cos ² θ -9) – 2xy sin θ = 90 0 0 = 9 0 0 0 > – x ² cos ² θ – y ² sin ² θ – 2xy sin θ cos θ = 0

=> x ² cos ² θ + y ² sin ² θ + 2xy sin θ cos θ = 0

=> (x cos θ + y sin θ) ² = 0

=> x cos θ = -y sin θ

=> x/sin θ = -y/cos θ

=> x ² /sin ² θ = y ² /cos ² θ

=> tan ² θ = x ² /y ²

=> sin ² θ = x ² /(x ² + y ² ) and cos ² θ = y ² /(x ² + y ² )

Подставьте вышеуказанные значения в уравнение cos ² θ/a ² + sin ² θ/b ² = 1/(х ² + у ² ).

=> (у ² /(х ² + у ² ))/а ² + (х ² /(х ² + у ^{18)) 2 0} + у ^{8 2} = 1/(x ² + y ² )

=> y ² /a ² + x ² /b ² = 1

Similar problems

Problem 1 : Если x = a cos θ − b sin θ и y = a sin θ + b cos θ, то докажите, что x ² + у ² = а ² + б ² .

Решение:

x = a cos θ − b sin θ и y = a sin θ + b cos θ

θ − b sin θ) ² + (a sin θ + b cos θ) ²

= a ² cos ² θ + b ² sin 9 ² sin θs ^{2 + a 2 sin 2 θ + b 2 cos 2 θ + 2ab sin θ cos θ}

= A ² (COS ² θ + SIN ² θ) + B ² (COS ² θ + SIN ² (COS ² θ + SIN ² (COS ² θ + SIN ² (COS ² θ + SIN ² (COS ² θ + ² (COS ² θ + ² (COS ² . ² + b ²  

= RHS

Отсюда доказано.

Задача 2. Если x = a sin θ + b cos θ и y = a cos θ − b sin θ, докажите, что x ² + y ² = a ² + b ² .

Решение:

x = a sin θ + b cos θ и y = a cos θ – b sin θ.

Здесь LHS = x ² + y ²

= (a sin θ + b cos θ) ² + (a cos θ – b sin θ) ^{2 a 09067}

SIN ² θ + B ² COS ² θ + 2AB SIN θ COS θ + A ² COS ² θ + B ² SIN ² θ + B ² SIN ² θ + B ² SIN ² θ + B ² SIN ² θ θ θ 2 . a ² (sin ² θ + cos ² θ) + b ² (cos ² θ + sin ² θ)

= a ² + b ²

= RHS

Отсюда доказано.

Задача 3. Если x/a cos θ + y/b sin θ = 1 и x/a sin θ – y/b cos θ = 1, докажите, что x ² /a ² + y ² /B ² = 2.

Решение:

x /a cos θ + y /b sin θ = 1

квалификации с обеих сторон, мы получаем

x

1111111111111111906 гг. 2 cos ² θ + y ² /b ² sin ² θ + 2 (x/a) (y/b) cos θ sin θ = 1 ⇢ (1)

Также дано ,

x/a sin θ – y/b cos θ = 1

Возводя обе стороны в квадрат, получаем

x ² /a ² sin ² θ 9 0 9 9 ^{2 cos 2 θ – 2 (x/a) (y/b) cos θ sin θ = 1 ⇢ (2)}

Сложение (1) и (2),

x ² /a ² cos ² θ + у ² /b ² sin ² θ + 2 (x/a) (y/b) cos θ sin θ + x ² /a ² sin ² / 1 9901 + y 29091 b ² cos ² θ – 2 (x/a) (y/b) cos θ sin θ = 1 + 1

x ² /a ² (cos ² 09 θ θ) + y ² /b ² (sin ² θ + cos ² θ) = 2

x ² /a ² + y ² /b ² = 2

Значит доказано.

Задача 4. Если x/a sin θ + y/b cos θ = 1 и x/a cos θ – y/b sin θ = 1, докажите, что x ² /a ² + y ² /b ² = 2.

Решение:

x /a sin θ + y /b cos θ = 1

квадрат с обеих сторон, мы получаем

x

2

117 2

17 2

17 2

906. 2 sin ² θ + y ² /b ² cos ² θ + 2 (x/a) (y/b) sin θ cos θ = 1 ⇢ (1)

Кроме того,

x/a cos θ – y/b sin θ = 1

Возводя обе стороны в квадрат, получаем

x ² /a ² cos ^{2 917 9090 + 2} sin ² θ – 2 (x/a) (y/b) cos θ sin θ = 1 ⇢ (2)

Сложение (1) и (2) дает

x ² /a ² sin2 θ + y ² /b ² cos ² θ + 2 (x/a) (y/b) cos θ sin θ + x ² /a ^{2 8} cos θ + у ² /b ² sin ² θ – 2 (x/a) (y/b) cos θ sin θ = 1 + 1

x ² /a ² (sin 2 + cos ² θ) + y ² /b ² (cos ² θ + sin ² θ) = 2

x ² /a ² + y ² /b ² = 2

Отсюда доказано.

Задача 5. Если x = a cos ² θ sin θ и y = a sin ² θ cos θ, то докажите, что (x ² + у ² ) ³ /(х ² у ² ) = а ² .

Solution:

x = a cos ² θ sin θ and y = a sin ² θ cos θ

Here, LHS = (x ² + y ² ) ³ /(x ² y ² )

= (A ² COS ⁴ SIN ² θ + A ² SIN ⁴ θ + A ² SIN ⁴ θ + A ² 4 θ + ² 4 θ + ² 4 θ + ² 4 θ + ² 4 θ + ² 4 .18 /[(a ² cos ⁴ θ sin ² θ) (a ² sin ⁴ θ cos ² θ)]

= (a ² cos ² θ sin ² θ (sin ² θ + cos ² θ)) ³ /(a ⁴ cos ⁶ θ sin ⁶ θ)

= (a ² cos ² θ sin ² θ) ³ /(a ⁴ cos ⁶ θ sin ⁶ θ)

= (a ⁶ cos ⁶ θ sin ⁶ θ)/(a ⁴ cos ⁶ θ sin ⁶ θ)

= a7 2 .

No related posts.