интервал сходимости ряда
Вы искали интервал сходимости ряда? На нашем сайте вы можете получить ответ на любой математический вопрос здесь. Подробное решение с описанием и пояснениями поможет вам разобраться даже с самой сложной задачей и интервал сходимости степенного ряда, не исключение. Мы поможем вам подготовиться к домашним работам, контрольным, олимпиадам, а так же к поступлению в вуз. И какой бы пример, какой бы запрос по математике вы не ввели — у нас уже есть решение. Например, «интервал сходимости ряда».
Применение различных математических задач, калькуляторов, уравнений и функций широко распространено в нашей
жизни. Они используются во многих расчетах, строительстве сооружений и даже спорте. Математику человек
использовал еще в древности и с тех пор их применение только возрастает. Однако сейчас наука не стоит на
месте и мы можем наслаждаться плодами ее деятельности, такими, например, как онлайн-калькулятор, который
может решить задачи, такие, как интервал сходимости ряда,интервал сходимости степенного ряда,как найти область сходимости ряда,как найти область сходимости степенного ряда,найти интервал и радиус сходимости степенного ряда онлайн,найти интервал сходимости ряда,найти интервал сходимости степенного ряда,найти интервал сходимости степенного ряда онлайн с подробным решением,найти область сходимости,найти область сходимости ряда,найти область сходимости ряда онлайн,найти область сходимости степенного ряда,найти область сходимости степенного ряда онлайн,найти область сходимости степенного ряда онлайн калькулятор с решением,найти область сходимости степенного ряда онлайн с решением,найти область сходимости степенного ряда онлайн с решением калькулятор,найти радиус и интервал сходимости степенного ряда онлайн,найти радиус сходимости и интервал сходимости степенного ряда,найти радиус сходимости степенного ряда,найти радиус сходимости степенного ряда онлайн,область сходимости найти,область сходимости онлайн,область сходимости ряда,область сходимости ряда как найти,область сходимости ряда онлайн,область сходимости ряда онлайн калькулятор,область сходимости степенного ряда,область сходимости степенного ряда онлайн,область сходимости степенного ряда онлайн калькулятор,онлайн калькулятор область сходимости степенного ряда,радиус сходимости ряда,радиус сходимости ряда онлайн,радиус сходимости степенного ряда,радиус сходимости степенного ряда онлайн,радиус сходимости степенного ряда онлайн калькулятор,степенные ряды примеры решения,сходимость степенного ряда,сходимость степенного ряда онлайн.
Решить задачу интервал сходимости ряда вы можете на нашем сайте https://pocketteacher.ru. Бесплатный онлайн решатель позволит решить онлайн задачу любой сложности за считанные секунды. Все, что вам необходимо сделать — это просто ввести свои данные в решателе. Так же вы можете посмотреть видео инструкцию и узнать, как правильно ввести вашу задачу на нашем сайте. А если у вас остались вопросы, то вы можете задать их в чате снизу слева на странице калькулятора.
Область сходимости степенного ряда. Примеры решения задач
Образовательные онлайн сервисы: теория и практика
- Главная
- Примеры
- Математический анализ
- Векторная алгебра и аналитическая геометрия
- Линейная алгебра
- Теория вероятностей и математическая статистика
- Математическое программирование
Методы оптимизации - Математика в экономике
Экономическая статистика
- Видео-уроки
- Математический анализ
- Векторная алгебра и Аналитическая геометрия
- Линейная алгебра
- Теория вероятностей и математическая статистика
- Математическое программирование.
Методы оптимизации
- Готовые работы
- Математический анализ
- Векторная алгебра и аналитическая геометрия
- Линейная алгебра
- Теория вероятностей и математическая статистика
- Математическое программирование
Методы оптимизации - Математика в экономике
Экономическая статистика - Другое
- Контакты
Методы оптимизации
Полезные материалы:
- Учебники
- Справочники
- Помощь в решении
- Онлайн занятия в Zoom
Область сходимости степенного ряда
Задача Найти область сходимости степенного ряда
Заданный ряд является степенным рядом.
Согласно признаку Даламбера, для абсолютной сходимости ряда достаточно, чтобы .
Для решаемой задачи , .
Так как , то ряд будет абсолютно сходиться при значениях , удовлетворяющих неравенству .
Решением этого неравенства является интервал , следовательно, при исследуемый степенной ряд будет абсолютно сходиться.
Исследуем поведение ряда на концах интервала, то есть при и .
При получаем числовой ряд . Это знакочередующийся ряд, удовлетворяющий условиям теоремы Лейбница: , . Поэтому ряд сходится, и граница интервала принадлежит области сходимости. В область абсолютной сходимости ряда эта граница не входит, так как ряд расходится.
Итак, областью сходимости степенного ряда является полуинтервал
, а областью абсолютной сходимости степенного ряда является интервал
.
Задать вопрос
Заказать помощь
Отзывы
+7-911-7987704
vk.
com/id286009794
Написать в Whatsapp
Написать в Viber
@matem96
Skype: matem96.ru
н???Теперь, когда у нас есть представление в виде степенного ряда для данной функции, мы можем найти радиус сходимости, используя критерий соотношения.
Так как тест отношений говорит нам, что ряд сходится, если ???L<1??? когда
???L=\lim_{n\to\infty}\left|\frac{a_{n+1}}{a_n}\right|???
нам просто нужно найти ???a_n??? и ???a_{n+1}???, а затем подставьте их в уравнение для ???L???. Используя степенной ряд, который мы сгенерировали для нашей функции, мы скажем, что
9{1}2xn}{n+1}\право|??????L=\lim_{n\to\infty}\left|\frac{-2xn}{n+1}\right|???
Скобки абсолютного значения отменяют ???-1???, поэтому мы получаем
???L=\lim_{n\to\infty}\left|\frac{2xn}{n+1}\ верно |???
Ограничение касается только ???n???, а не ???x???, поэтому мы можем вытянуть ???2x??? вне предела, пока мы держим его в барах абсолютного значения.
???L=\влево|2x\вправо|\lim_{n\to\infty}\влево|\frac{n}{n+1}\вправо|???
???L=\left|2x\right|\lim_{n\to\infty}\left|\frac{n}{n+1}\left(\frac{\frac{1}{n} }{\frac{1}{n}}\right)\right|???
???L=\left|2x\right|\lim_{n\to\infty}\left|\frac{\frac{n}{n}}{\frac{n}{n}+\frac {1}{n}}\право|???
???L=\left|2x\right|\lim_{n\to\infty}\left|\frac{1}{1+\frac{1}{n}}\right|???
???L=\left|2x\right|\left|\frac{1}{1+\frac{1}{\infty}}\right|???
???L=\влево|2x\вправо|\влево|\frac{1}{1+0}\вправо|???
???L=\влево|2x\вправо|\влево|1\вправо|???
???L=\влево|2x\вправо|???
Так как из теста отношения мы знаем, что ряд будет сходиться, когда ???L<1???, положим
???\влево|2x\вправо|<1???
???\влево|х\вправо|<\frac12???
Имея неравенство вида ???\left|x-a\right| ???R=\frac12??? Чтобы найти интервал сходимости ряда Маклорена, мы удалим бары абсолютного значения из радиуса сходимости.
???\влево|х\вправо|<\frac12???
???-\frac12 Но прежде чем мы сможем назвать это интервалом сходимости, мы должны проверить, сходится ли ряд в одной или обеих конечных точках, ???x=-1/2??? и ???х=1/2???. Для этого мы подключим каждую конечную точку к исходной серии. 9{2n+1}\frac{1}{n}??? Это чередующийся ряд, где ???a_n=\frac{1}{n}??? , что означает, что мы можем использовать тест переменного ряда, чтобы сказать, сходится он или нет. Помните, тест переменного ряда говорит нам, что ряд сходится, если ???\lim_{n\to\infty}a_n=0???. ???\lim_{n\to\infty}a_n??? ???\lim_{n\to\infty}\frac1n??? ???\frac{1}{\infty}??? ???0??? Поскольку предел равен ???0???, ряд сходится по критерию чередующихся рядов, что означает, что ряд Маклорена сходится в левой конечной точке интервала, ???x=-1/2???. 9{n+1}\frac{1}{n}??? Это чередующийся ряд, где ???a_n=\frac{1}{n}??? Это тот же самый ряд, который мы использовали для нахождения сходимости левой конечной точки интервала, и мы уже знаем, что он сходится с помощью проверки переменного ряда. Поскольку ряд сходится на обоих концах интервала, интервал сходимости ряда Маклорена ???f(x)=\ln(1+2x)??? ???-\frac12\le{x}\le\frac12???
Следовательно, мы можем сказать, что ряд также сходится на правом конце интервала, ???x=1/2???. Получить доступ к полному курсу Исчисление 2
Калькулятор интервала сходимости — значение, использование, серия
В современном мире мы не можем представить и дня без вычислений. От ведения счетов до космических полетов — все требует расчетов. Но по мере развития науки экспоненциально растет и потребность в новых и продвинутых калькуляторах. В этой статье мы узнаем все о калькуляторе интервала сходимости и о том, как его рассчитать.
Содержание
Что такое калькулятор интервала сходимости Первое, что должно прийти вам на ум, это точно интервал сходимости? Интервал сходимости ряда представляет собой набор значений, при которых ряд сходится. Более того, интервал связан с данным степенным рядом таким образом, что ряд расходится для всех значений значений вне интервала и сходится для всех значений внутри него.
Интервал сходимости можно представить как интервал, в котором конкретный ряд показывает абсолютную сходимость для степенного ряда. Он выражается в интервальной нотации. Например, предположим, что имеется ряд, показывающий сходимость между 2 (включительно) и 8 (исключительно). В результате мы можем записать это как (2, 8) или как 2 меньше, чем x, и x меньше, чем 8.
Другими словами, степенной ряд показывает бесконечный ряд формы:
∑n=0∞cn(x–a)n
Где cn представляет собой коэффициент, зависящий от n. Кроме того, ряд работает как функция x, где члены изменяются в зависимости от n-го члена ряда.
Кроме того, степенной ряд может добавлять бесконечное количество последовательных членов. Сумма членов может быть как бесконечной, так и конечной.
Читайте также: Дивергентная и конвергентная эволюция: определения
Ряд сходится, если сумма членов является конечным числом.
Ряд расходящийся, если сумма членов бесконечна. Находя интервал сходимости, мы находим диапазон значений x в |x – a| меньше R, так что ряд сходится.
Излишне говорить, что компьютеры имеют преимущество перед людьми в определенных типах вычислений, но сталкиваются с трудностями при выполнении сложных вычислений. Таким образом, мы можем успешно запрограммировать неспособный иначе компьютер косвенно находить решения с помощью степенных рядов, если мы научимся находить интервал сходимости.
Чтобы вычислить ex с большим показателем степени, компьютеру калькулятора приходится снова и снова умножать большие, беспорядочные числа на большие, беспорядочные числа. Компьютеры обычно хранят числа с плавающей запятой и создают ошибки округления. В результате этот процесс может значительное время и даже после этого давать вам неточный ответ..
К счастью, степенной ряд f(x) = xn⁄n! представляет выражение ex, когда оно применяется ко многим терминам.
Мы находим, что это ∞ меньше, чем x меньше, чем ∞ , когда мы проверяем интервал сходимости для степенного ряда. Проще говоря, это означает, что степенной ряд будет сходиться везде и может использоваться для примера со всеми возможными входными значениями x. Если мы сможем запрограммировать эту процедуру на компьютер, мы сможем заставить ее точно находить значение ex при любом значении x. Это всего лишь один небольшой пример того, как использование интервала сходимости может повлиять на нашу технологию.
Когда мы пытаемся найти сходимость степенного ряда, мы получаем несколько вариантов теста на выбор. Они бывают двух типов: очень распространенный тест отношения и тест корня.
В тесте отношения мы используем отношение степенного ряда и модифицированную (n + 1) версию самого себя для решения x. Нам нужно убедиться, что он соответствует критериям сходимости. Формула для теста отношения:
Сходимость, когда L меньше 1,
L=limn→∞|an+1an|
Где «an» представляет собой степенной ряд, а «an + 1» представляет степенной ряд, в котором все члены n заменены на n + 1.
Первый этап проверки соотношения заключается в сопоставлении исходной и модифицированной версий степенного ряда. на соответствующие места в формуле. Затем обратите внимание на предел, когда n стремится к бесконечности. Подставив бесконечность вместо n, выражение может показаться неразрешимым. Затем мы начинаем вырезать члены, которые незначительны по сравнению с бесконечностью, и исключаем из выражения фактические члены бесконечности.
После упрощения результирующего выражения и правильной оценки предела нужно составить выражение так, чтобы L было меньше 1. В результате теперь мы получим неравенство, напоминающее вид 1⁄c×|x – a | что меньше 1. При этом константа c в данном уравнении может быть не дробной или дробной.
Как вычислить степенной ряд интервала сходимости Теперь вам нужно найти правую и левую конечные точки, чтобы убедиться, что они удовлетворяют окончательному неравенству. Это интервал границ сходимости. Мы должны знать, является ли каждая граница включающей или исключающей.
Для этого мы проверяем сходимость/расхождение рядов в этих точках.
Значение левой конечной точки подставлено в x = a1 вместо x в исходном ряду степеней. Затем мы берем предел, когда n приближается к бесконечности. Если результат не равен нулю или не определен, ряд в этой точке расходится. Дивергенция показывает исключительную конечную точку, а конвергенция показывает включающую конечную точку. Мы повторяем процесс для правого конца x = a2, чтобы завершить интервал сходимости. Вот как вы используете степенной ряд в интервале калькулятора сходимости.
Как найти интервал сходимости калькуляторЭтот калькулятор интервала сходимости написан в основном на JavaScript (JS). Поскольку подпрограмма вычислений — это JS, веб-сайт работает в режиме реального времени. Это дает нам мгновенные решения наших математических задач.
Процедура вычислений также использует систему компьютерной алгебры (CAS) на основе JS. Он выполняет различные символьные операции на протяжении всей подпрограммы, такие как полиномиальное деление и оценка предела.
Подпрограмма использует тест отношения, заполняя формулу с заданным степенным рядом.
Интервал калькулятора сходимости с шагамиПроцедура использования калькулятора сходимости следующая:
Шаг 1: Введите функцию и диапазон в заданном пространстве
Шаг 2: Теперь нажмите кнопку «Вычислить», чтобы получить результат
И Шаг 3: Наконец, точка сходимости для данного ряда будет отображаться в новом окне
Часто задаваемые вопросы по калькулятору интервала сходимостиЧто такое интервал сходимости?
Интервал сходимости степенного ряда можно представить как интервал входных значений, для которых ряд сходится.
Как найти интервал сходимости?
Чтобы полностью найти интервал сходимости, мы должны определить, будет ли сходиться степенной ряд для (x=a−R x = a − R) или (x=a+R x = a + R) . Если степенной ряд сходится для одного или обоих этих значений, мы включим это в значения сходимости.
Как найти интервал и радиус сходимости?
Радиус схождения равен половине длины интервала схождения. Если обозначить радиус сходимости как R, то интервал сходимости будет включать открытый интервал: (a − R, a + R). Вам нужно использовать тест отношения, чтобы найти радиус сходимости, R.
1. Каков радиус сходимости калькулятора ряда Тейлора?
Существуют определенные шаги для использования радиуса сходимости:
Шаг 1: Введите функцию и диапазон в данное поле ввода.
Шаг 2: Теперь нажмите кнопку «Рассчитать», чтобы получить результат.
И Шаг 3: Наконец, вы увидите точку схождения для данного ряда, отображаемую в новом окне.
4. Как найти интервал?
Интервалы возрастания или убывания функции соответствуют интервалам, на которых ее производная является отрицательной или положительной. Таким образом, чтобы найти интервалы, в которых функция увеличивается или уменьшается, нам нужно взять производную и проанализировать ее, чтобы определить, будет ли она положительной или отрицательной.
Если степенной ряд сходится только для x = a, то в этом случае радиус сходимости равен R = 0. С другой стороны, если степенной ряд сходится для всех значений x, то радиус сходимости равно R = ∞
6. Как найти интервал степенного ряда?
Интервал сходимости степенного ряда представляет собой набор всех значений x, для которых степенной ряд показывает сходимость. Теперь, чтобы найти интервал сходимости ∞∑n=0xnn. =|х|⋅1=|х| менее 1,
Это будет стремиться к -1 меньше, чем x меньше 1, что означает, что степенной ряд сходится по крайней мере на (−1,1)
7. Как найти интервал сходимости ряда Маклорена?
Чтобы найти интервал сходимости ряда Маклорена, нужно из радиуса сходимости вычесть абсолютную величину.
8. Каков радиус сходимости ряда?
Радиус сходимости степенного ряда представляет собой радиус наибольшего круга в центре ряда, в котором ряд сходится, на языке математики.
9. Что такое интервальный калькулятор?
Калькулятор музыкальных интервалов поможет вам определить интервал между двумя нотами. Чтобы найти интервал между двумя нотами, выберите один из звуков в девяти октавах и найдите простое и составное название для любого расстояния, превышающего октаву.
10. Какой интервал в математическом примере?
Интервал представляет числа, лежащие между двумя заданными числами.
11. К какому значению сходится степенной ряд?Поскольку члены степенного ряда включают переменную x, ряд может сходиться для определенных значений x. Не только это, но оно также может расходиться для других значений x. Для степенного ряда с центром в точке x=a значение ряда в точке x=a определяется как c0. Следовательно, степенной ряд всегда сходится в своем центре.
12. Что происходит, когда радиус сходимости равен 0?
Радиус сходимости представляет собой расстояние между центром интервала сходимости степенного ряда и его конечными точками.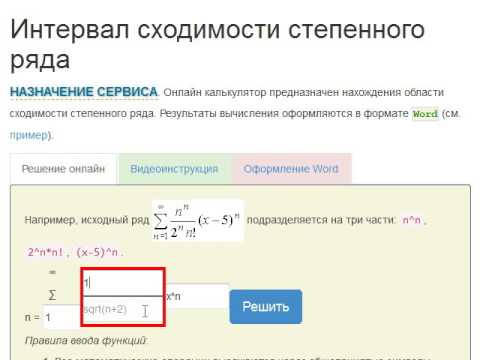
Если ряд сходится только в одной точке, радиус сходимости равен 0. Если ряд сходится в нескольких точках, радиус сходимости равен ∞.
Для любого ненулевого значения x предел бесконечен, если L=∞. Следовательно, ряд сходится только тогда, когда x стремится к 0. Значение 1/L представляет собой радиус сходимости ряда, а интервал, на котором ряд сходится, является интервалом сходимости.
14. Может ли интервал сходимости быть равен 0?
Да, радиус сходимости может быть равен 0. Несмотря на все это, он в конечном итоге сойдется в точке x=0, но больше нигде.
15. Какой интервал между C и E?
В минорном интервале на один полутон меньше, чем в мажорном. Например: поскольку от C до E — большая терция (4 полутона), C до Eb — малая терция (3 полутона). Например: поскольку от C до E — большая терция (4 полутона), C до Eb — минорная терция (3 полутона).
16.
