Тригонометрические тождества примеры решения: Примеры на доказательство тригонометрических тождеств

Основные тригонометрические тождества. Решение задач

Похожие презентации:

Элементы комбинаторики ( 9-11 классы)

Применение производной в науке и в жизни

Проект по математике «Математика вокруг нас. Узоры и орнаменты на посуде»

Знакомство детей с математическими знаками и монетами

Тренажёр по математике «Собираем урожай». Счет в пределах 10

Методы обработки экспериментальных данных

Лекция 6. Корреляционный и регрессионный анализ

Решение задач обязательной части ОГЭ по геометрии

Дифференциальные уравнения

Подготовка к ЕГЭ по математике. Базовый уровень Сложные задачи

Пускай кому- то мил английский,
Кому – то химия важна,
Без математики же всем нам
Но ни туда и ни сюда
Нам уравнения, как поэмы
А синусы поддерживают дух
Нам косинусы, будто песни,
А формулы тригонометрии
Ласкают слух!
Тема урока:
“ Основные тригонометрические
тождества. Решение задач”.
Цель урока:

Знать:
Уметь:
ЗНАЮ!
УМЕЮ!
РЕШУ!
Что называется единичной
окружностью?
у
R
α
х
Какие направления поворота
единичного радиуса известны?
у
R
α
х
В каких единицах измеряется
угол поворота единичного
у
радиуса?
R
α
х
Что такое угол в один радиан?
Сколько приблизительно градусов
содержит угол в 1 радиан ? у
R
α
х
Сформулируйте правила перевода
из градусной меры угла в
радианную меру и наоборот.
Сформулируйте правила перевода
из градусной меры угла в
радианную меру и наоборот.
0
30
π
2
450
π
2π
Какие тригонометрические
функции вы знаете?
Какие тригонометрические
функции вы знаете?
От чего зависит значение
тригонометрических функций?
Углом какой четверти является угол α , если:
α =15°
α =190°
α =100°
Углом какой четверти является угол α , если:
α =-20°
α =-110°
α =289°
Работа в группах
Правила работы в группе:
1. Группа совместно обсуждает и решает, выдвигает
идеи или опровергает их.
2.Каждый член группы должен работать в полную
меру своих сил.
3.Во время работы с уважением относитесь
к товарищам: принимая или отвергая идею, делайте
это вежливо. Помните, что каждый имеет право
на ошибку.
4.Помните, что успех группы зависит от того,
насколько каждый проявит свои достоинства.
Работа в группах
Таблица значений тригонометрической функции
0°
30°
45°
60°
90°
sin
0
1
cos
1
0
tg
ctg
0
1
—
—
1
0
1
2
A
cos sin
2
2
2
B
3
sin 2 1
C
4
1 cos 2
D
5
1 tg
E
6
7
cos
2
1
ctg
Установить
соответствие между
левой и правой
частью тождества.
sin2α
H
ctg через tg
8
1 ñtg 2
9
ctg
10
tg
через
через
K
L 1-sin2α
sin
и
cos
sin и cos
M
1
N -cos2α
Критерии оценивания:
10 заданий – оценка «5».
8-9 заданий – оценка «4».
5-7 заданий – оценка «3».
1-4 заданий – оценка «2».
1
cos 2 sin 2
M
1
2
L
1-sin2α
3
sin 2 1
N
4
1 cos 2
-cos2α
E
sin2α
5
1 tg 2
B
6
1
ctg
C
2
7
8
cos
ctg через tg
A
1 ñtg 2
9
ctg
10
tg
через
через
K
cos
H
sin и cos
D
sin
Установить
соответствие между
левой и правой
частью тождества.
и
Критерии оценивания:
10 заданий – оценка «5».
8-9 заданий – оценка «4».
5-7 заданий – оценка «3».
1-4 заданий – оценка «2».
Основное тригонометрическое тождество
2
2
cos sin 1
«тригонометрическая единица»
Основное тригонометрическое тождество
2
2
cos sin 1
«тригонометрическая единица»
Косинус квадрат
Очень рад.
К нему едет брат
Синус квадрат!
Когда они встретятся
Окружность удивиться:
Выйдет целая семья,
То есть единица!
Получите имя математика, в книге которого
впервые встречается термин –
1. 3 sin2 α+ 3 cos2 α
2. (1 – cos α)(1 + cos α) при α =90°
«тригонометрия».
3. 1- sin2 400
4. 2-2cos(-600)
5.
tgα∙ctgα
6. (ctg2α+ 1)(1 – sin2α)
7. tgα∙ctgα -1
8. cos2 α+ ctg2α+ sin2α
и
с
1
1
П
2
и
3
т
т
П
к
у
cos2 40°
3
ctg2α
0
4
и
5
с
6
к
7
у
8
с
Питискус
Аль-Батуни
Аль-Хорезми
Бхаскара
Насиреддин
Туси
Леонард Эйлер
По заданному значению
тригонометрической функции
найдите значение другой функции
Четверть
Дано:
Найти:
I
sinα=0,6
II
cosα=
sinα
III
tgα=
ctgα
tgα
IV
cosα=
Решение:
По заданному значению
тригонометрической функции
найдите значение другой функции
Четверть
I
Дано:
sinα=0,6
Найти:
Решение:
По заданному значению
тригонометрической функции
найдите значение другой функции
Четверть
II
Дано:
Найти:
cosα=
sinα
Решение:
=
=
По заданному значению
тригонометрической функции
найдите значение другой функции
Четверть
III
Дано:
tgα=
Найти:
ctgα
Решение:
ctgα =
=
=
По заданному значению
тригонометрической функции
найдите значение другой функции
Четверть
Дано:
Найти:
tgα
IV
cosα =
Решение:
tgα=
=
=
=
=
=
Применение тригонометрии в жизни человека.

32. Домашнее задание

•Сообщение:
«Тригонометрия в
жизни человека»
•№304 с.111
y=sinx
y=sinx
Спасибо за урок!
Определите знак выражения
1 sin 240°
—
8
cos 290°
2 tg 98°
—
9
tg(-120°)
3 sin 70°
+
10 sin
4 ctg 200°
+
—
11 cos
—
12 cos
13 sin
+
+
+
14 tg
—
5 cos 113°
6 sin ( — 140° )
7 cos (-300° )
+
+
+

English     Русский Правила

Тригонометрические тождества

МЕТОДИЧЕСКИЕ РЕКОМЕНДАЦИИ К ИЗУЧЕНИЮ ТЕМЫ ТОЖДЕСТВА(§ 26. Тригонометрические тождества)

Вопрос о существовании такого математического объекта, как тригонометрическое тождество уже затрагивался. Однако не достаточно внимания уделялось четкому определению понятия тождества, применительно к тригонометрии, а так же не приобретен необходимый навык доказательства тригонометрических тождеств. Учащиеся могут привести примеры тригонометрических тождеств (основное тригонометрическое), сформулировать определение тождества: равенство, верное при допустимых значениях входящих в него букв называетсятождеством. Тут требуется обратить особое внимание учащихся на то, что буквы могут принимать допустимые значения. Это наиболее актуально для функций тангенс и котангенс. Ограничения, о которых идет речь получаются из определения тангенса и котангенса.

(например, для тангенса , так как на нуль делить нельзя. С решением данного тригонометрического неравенства учащиеся справятся, используя единичную окружность)

Мы уже отмечали, что при рассмотрении данного параграфа необходимо формировать навык доказательства тригонометрических тождеств. Совместно с учащимися, еще раз, выделим способы доказательства тождеств. Причем в дальнейшем, при проведении доказательства, следует указывать каким способом оно проведено.

Можно выделить формулы, используемые при доказательстве тождеств: ;;;;;;;, а так же достаточное владение такой моделью как единичная окружность, в частности умения связанные с решением простейших тригонометрических уравнений и неравенств.

Описанную работу можно провести на разных этапах урока:

Перед непосредственным доказательством тождеств, как планирование результата и способа деятельности.

После того как доказано некоторое количество тождеств, то есть учащиеся имеют опыт доказательства и могут выделить теоретический базас.

Необходимо так же выделить типы решаемых задач, задач связанных с понятием тождества. Подход к этой работе может быть аналогичным описанному ранее: либо до непосредственного проведения некоторого количества доказательств, либо после накопления соответствующего опыта.

ТИПЫ ЗАДАЧ:

Доказать тождество

Упростить выражение

Найти значение выражения

Решить уравнение

ТИП ЗАДАЧИ	Соответствующий № учебника (автор Ш.А.Алимова)
1. Доказать тождество	465, 468, 470
2. Упростить выражение	466, 467, 469
3. Найти значение выражения	467, 471, 472, 473
4. Решить уравнение	474

ПРИМЕРЫ РЕШЕНИЯ ЗАДАЧ:

Тип 1. (№470(5))

Доказать тождество

Доказательство:

, что и требовалось доказать.

Способ доказательства: сведение левой части тождества к правой.

Базис: основное тригонометрическое тождество.

Тип 2. (№469(1))

Упростить выражение:

Решение:

Ответ: 0.

Базис:

Тип 3. (№472)

Найти значение выражения , если

Решение:

Выражение значение, которого требуется найти, можно преобразовать, используя формулу сокращенного умножения – разность кубов:

Первый множитель в полученном произведении равен 0,2. Таким образом, нам требуется найти значение выражения: .

Итак,

.

Ответ: .

Базис: знание ФСУ; специальный прием выражения произведения через разность или сумму, основанный на ФСУ; основное тригонометрическое тождество.

Заметим, что знание одних лишь тригонометрических формул не ведет к успеху при решении задач, требуется, кроме того, знать и уметь применять к новым математическим объектам приемы и методы которые были известны ранее.

Тип 4. (№474(1))

Решить уравнение:

Решение:

Упростим выражение, стоящее в левой части

Учтем, что — это ордината точки числовой окружности. Значит, нам нужно найти на числовой окружности точки с ординатой и записать, каким числам они соответствуют.

Прямая пересекает единичную окружность в точках М и К. Точка М получается поворотом точки на угол , а значит и на любой из следующих угловсоответствует числу. Точка К – на угол , а значит, и на углы .Таким образом, получили две серии корней: и .

Ответ: ; .

Базис: основное тригонометрическое тождество; владение моделью – единичная окружность; умение решать простейшие тригонометрические уравнения, используя единичную окружность.

Адрес публикации: https://www.prodlenka.org/metodicheskie-razrabotki/233965-trigonometricheskie-tozhdestva

Проблемы по тригонометрическим идентичностям с решениями

Проблема 1:

Докажите:

(1 — COS ² θ) CSC ² θ = 1

Решение:

Пусть a = (1 — cos ^2. θ) CSC ² θ и B = 1.

A = (1 — COS ² θ) CSC ² θ

Потому что SIN ² θ+COS ² θ, мы

sin ² θ = 1 — cos ² θ

Тогда

A = SIN ² θ ⋅ CSC ² θ

A = SIN ² θ ⋅ (1/SIN ² θ)

A = SIN ² θ ² θ

a = 1

a = b (доказано)

Задача 2:

Доказать:

с θ √ (1 — sin ² θ) = 1

Решение:

Пусть a = sec θ √ ( 1 — sin ² θ)  и B  =  1.

A  =  sec θ √(1 — sin ² θ)

Потому что sin ² θ+cos ² θ = 1, мы имеем

COS ² θ = 1 — SIN ² θ

Затем,

A = Sec θ √cos ² θ

A = Sec θ √cos ² θ

A = sec θ ⋅ cos θ

a = sec θ ⋅ (1 /с θ)

a = sec θ /sec θ

a = 1

a = b (доказано)

Проблема 3:

Достаток:

tan θ sin θ + cos θ  =  sec θ

Решение:

Пусть A  = tan θ sin θ + cos θ  и B =  sec θ.

A = tan θ sin θ + cos θ

A  = (sin θ/cos θ) ⋅ sin θ + cos θ

A  =  (sin ² θ/cos 0 θ) + 9 0 cos sin ² θ / cos θ) + (cos ² θ / cosθ)

a = (sin ² θ + cos ² θ) / cos θ

a = 1 / cos θ

A =  sec θ

A  =  B  (Proved)

Задача 4 :

Докажите :

(1 — cos θ)(1 + cos θ)(1 + cot ² θ) : 0 90 90 0 0

Пусть A = (1 — cos θ)(1 + cos θ)(1 + cot ² θ)  =  1 и B  = 1.

A  =  (1 — cos θ)(1 + cos θ)( 1 + COT ² θ)

A = (1 — COS ² θ) (1 + COT ² θ)

Потому что SIN ² θ + COS ² θ = 1, мы имеем

SIN ² θ = 1 -COS ² θ

THEN,

A = SIN ² θ ⋅ (1 + COT ² θ)

A = SIN ² θ + SIN θ)

A = SIN ² θ + SIN )0008 2 θ ⋅ Cot ² θ

a = sin ² θ+sin ² θ ⋅ (cos ² θ/sin ² θ)

a = sin ² θ+cos cos cos cos cos ² θ

A = 1

A = B (доказано)

Задача 5:

Доказать:

Cot θ + tan θ = sec θ CSC θ

Решение:

. θ + tan θ и B = sec θ csc θ.

A  = cot θ + tan θ

A  =  (cos θ/sin θ) + (sin θ/cos θ)

a = (cos ² θ/sin θ cos θ) + (sin ² θ/sin θ cos θ)

a = (cos ² θ + sin ² θ)/sin θ cos θ

A  = 1 / sin θ cos θ

A  =  (1/cos θ) ⋅ (1/sin θ)

A  =  sec θ csc θ

A  =  sec θ csc θ

0 2

A  = Доказана Задача :

Докажите :

cos θ/(1 — tan θ) + sin θ/(1 — cot θ)  =  sin θ + cos θ

Решение :

Пусть A =  cos θ/(1 — tan θ) + sin θ/(1 — кроватка θ) и

B  =  sin θ + cos θ

A  =  cos θ/{1 — (sin θ/cos θ)} + sin θ/{1 — (cos θ/sin θ)}

A  =  cos ² θ/(cos θ — sin θ) + sin ² θ/(sin θ — cos θ) 

A  =  cos ² θ/(cos θ — sin θ) — sin ² θ/(cos θ — sin θ)

A  =  (cos ² θ — sin ² θ) / (cos θ — sin θ) 

A  =  [(cos θ + sin θ)(cos θ — sin θ))] / (cos θ — sin θ)

A  =  (cos θ + sin θ)

A  =  B  (доказано)

Задача 7:

Докажите:

TAN ⁴ θ+ TAN ² θ = SEC ⁴ θ- SEC ² θ

Решение:

Пусть A = TAN ⁴ θ+ TAN TAN TAN TAN. ² θ и B = сек ⁴ θ + сек ² θ.

A = TAN ⁴ θ+ TAN ² θ

A = TAN ² θ (TAN ² θ+ 1)

Мы знаем, что,

TAN ² θ = SEC ^{2 2} θ — 1

TAN ² θ + 1 = SEC ² θ

Тогда,

A = (SEC ² θ- 1) (SEC ² θ)

A = Sec ⁴ θ- Sec)

A = Sec ⁴ θ- Sec) ² θ

a = b (доказано)

Задача 8:

Доказать:

√ {(Sec θ — 1)/(Sec θ + 1)} = cosec θ — cot θ

Решение :

Пусть A  =  √{(sec θ – 1)/(sec θ + 1)} и B  =  cosec θ — cot θ.

A = √{(сек θ – 1)/(сек θ + 1)}

A  =  √[{(сек θ – 1) (сек θ – 1)}/{(сек θ + 1) (сек θ – 1)}]

A  =  √{(сек θ – 1) ² / (сек ² θ — 1)}

A  =  √{(сек θ — 1) ²  / tan ² θ}

A 09 0 = 1 (сек θ) 9 0 – 3 θ

A  =  (sec θ/tan θ) – (1/tan θ)

A  =  {(1/cos θ)/(sin θ/cos θ)} — cot θ

A  =  {(1/cos θ ) ⋅ (cos θ/sin θ)} — кроватка θ

A  =  (1/sin θ) — кроватка θ

A  = cosec θ — кроватка θ

A = B (доказано)

Задача 9 : 

Докажите :

(1 — sin A)/(1 + sin A)  =  (sec A — tan A) ²

Решение 4:

2 A = (1 – sin A)/(1 + sin A) и B = (sec A – tan A)

² .

A  =  (1 — sin A) / (1 + sin A)

A  =   (1 — sin A) ²  / (1 — sin A) (1 + sin A)

A  =  (1 — sin A) ²  / (1 — sin ² A) 

A  =  (1 — sin A) ² / (cos ² A)

A  =  (1 — sin A) ²  / (cos A) ²

A  =  {(1 } sin 0 cos A) /0 0

A  =  {(1/cos A) — (sin A/cos A)} ²

A  =  (sec A – tan A) ²

A 02 900 (03) Задача 10:

Докажите:

(tan θ + sec θ — 1)/(tan θ — sec θ + 1) = (1 + sin θ)/cos θ

Решение:

Пусть A = (tan θ + сек θ — 1)/(tan θ — сек θ + 1) и 

B  =  (1 + sin θ)/cos θ.

A  = (tan θ + sec θ — 1)/(tan θ — sec θ + 1)

A  =  [(tan θ + sec θ) — (sec ² θ — tan ² θ)] /(tan θ — sec θ + 1)

A  =  {(tan θ + sec θ) (1 — sec θ + tan θ)}/(tan θ — sec θ + 1) 

A  =  {(tan θ + sec θ) (tan θ — sec θ + 1)}/(tan θ — sec θ + 1)

 A  =  tan θ + sec θ

A  =  (sin θ/cos θ) + (1/cos θ)

A = (sin θ + 1)/cos θ

A  = (1 + sin θ)/cos θ

A  = B   (Proved)

Пожалуйста, отправьте ваш отзыв по адресу v4formath@gmail. com

Мы всегда ценим ваши отзывы.

©Все права защищены. onlinemath5all.com

Тригонометрические тождества — SAT II Math I

Все ресурсы SAT II Math I

6 диагностических тестов 113 практических тестов Вопрос дня Карточки Learn by Concept

← Предыдущая 1 2 Следующая →

SAT II Математика I Помощь » Тригонометрия » Тригонометрические тождества

Упростите выражение.

Возможные ответы:

Правильный ответ:

Объяснение:

Найдите общий знаменатель

Умножьте числители и оставьте множители

Сложите числители

4

02

Комбинировать, как Условия

Числоватор по факту

Уменьшить

Взаимная идентичность

Сообщайте о ошибке

, если и, оценить.

Возможные ответы:

Правильный ответ:

 

Объяснение:

Здесь проще всего использовать идентификацию:

 

Подставляя данные значения, мы получаем:

Сообщить об ошибке

Что из следующего является упрощенной версией ?

Возможные ответы:

Правильный ответ:

Объяснение:

Чтобы решить эту задачу, нам нужно переписать ее в терминах  и .

Переписывая котангенс получаем следующее.

Переписывая секанс, получаем следующее.

Таким образом, мы можем подставить эти тождества в исходную задачу и упростить ее.

Отчет о ошибке

Использование тригонометрических идентификаторов.

Неверно

Правильный ответ:

Верно

Объяснение:

Мы можем работать с любой частью уравнения по своему усмотрению. Мы работаем с правой частью уравнения, поскольку здесь очевиден двойной угол. Мы можем факторизовать числитель, чтобы получить следующее:

Далее мы записываем формулу уменьшения степени для синуса, чтобы мы могли извлечь необходимые компоненты следующим образом:

Формулу уменьшения степени необходимо инвертировать, что дает:

Теперь мы можем распределить и уменьшить:

4

Наконец, вспоминая основное тождество для котангенса:

Это доказывает эквивалентность.

Сообщить об ошибке

Используйте формулы уменьшения степени для тригонометрических функций, чтобы сократить и упростить следующее уравнение:

Возможные ответы:

Правильный ответ:

Объяснение:

Формулы уменьшения степени для синуса и косинуса отличаются только операцией в числителе. Применяя здесь формулы уменьшения степени, мы получаем:

Умножая биномы в числителе и умножая знаменатели:

Сокращая числитель:

Мы снова используем формулу уменьшения степени для косинуса следующим образом:

Объединение числителя путем определения общего знаменателя:

Теперь просто уменьшив двойную фракцию:

Отчет о ошибке

Использование тригонометрических идентичностей, определить, является ли следующее. Ответы:

Неточно

Верно

Допустимо только в диапазоне: 

Действительно только в диапазоне: 

Ложь

Правильный ответ:

Неверно

Объяснение:

В этом случае мы решили работать с той стороной, которая кажется более простой, левой стороной. Начнем с использования формул уменьшения степени:

Далее выполняем умножение на числитель:

Следующим шагом является удаление двойного угла, так как в предполагаемом решении нет двойного угла:

Наконец, мы умножаем биномы в числителе в левой части, чтобы определить, выполняется ли эквивалентность:

Мы видим, что эквивалентность не выполняется.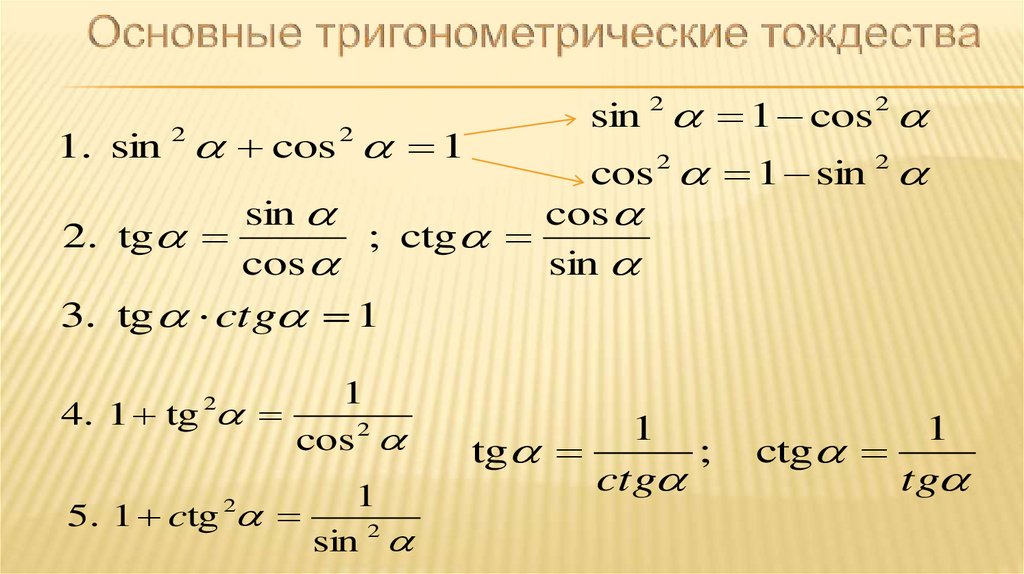

Сообщить об ошибке

Упростите выражение:

Возможные ответы:

Правильный ответ:

Объяснение:

Первым шагом в решении этого уравнения является распределение:

 

На этом этапе упростите, используя известные тождества Пифагора. Левая величина упрощает такую:

и правильное количество упрощает такое:

Таким образом, мы получаем:

,

, что согласно нашему пифагорейскому тождеству эквивалентно .

Таким образом,

Отчет о ошибке

Упрощайте, используя идентификаторы:

Возможные ответы:

Правильный ответ:

23 Пояснение:

Сначала разложим обратные тождества в дробную форму:

Инвертируем нижнюю дробь и распределяем в верхнюю, отслеживая отрицательное значение:

Используя тождество Пифагора, наше уравнение принимает следующий вид:

Сообщить об ошибке

Определите значение:  

Возможные ответы:

Правильный ответ:

Объяснение:

Чтобы решить , сначала определите все узнаваемые личности.

Для этого сценария можно использовать следующие идентификаторы:

Первым идентификатором также можно манипулировать.

Замените правильными идентификаторами и упростите.

 

 

Сообщить об ошибке

Что из следующего эквивалентно:  ?

 

Возможные ответы:

Правильный ответ:

Объяснение:

Мы можем умножить основание на сопряженное и получить:

Затем мы можем использовать тождество Пифагора для косинусов и синусов:

Наконец, мы можем разделить дроби и преобразовать их в тригонометрическое тождество:

В качестве альтернативы вы можете взять этот и другие варианты ответа и действовать в обратном порядке, переведя все тригонометрические отношения в синусы и косинусы, используя тождества.