Геометрическая прогрессия убывающая: Геометрическая прогрессия — урок. Алгебра, 9 класс.

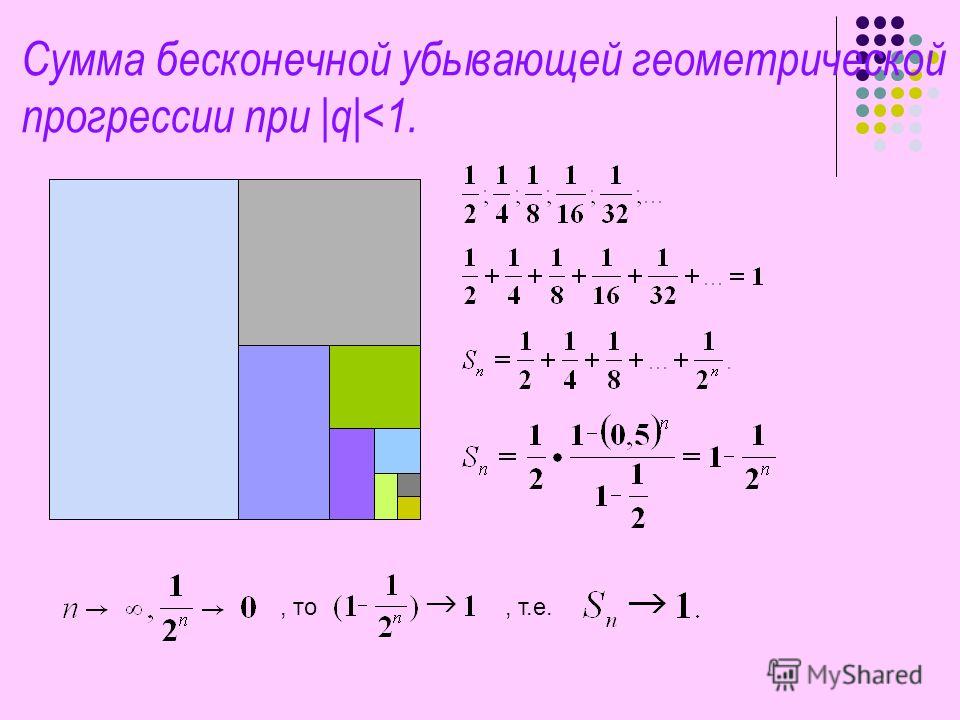
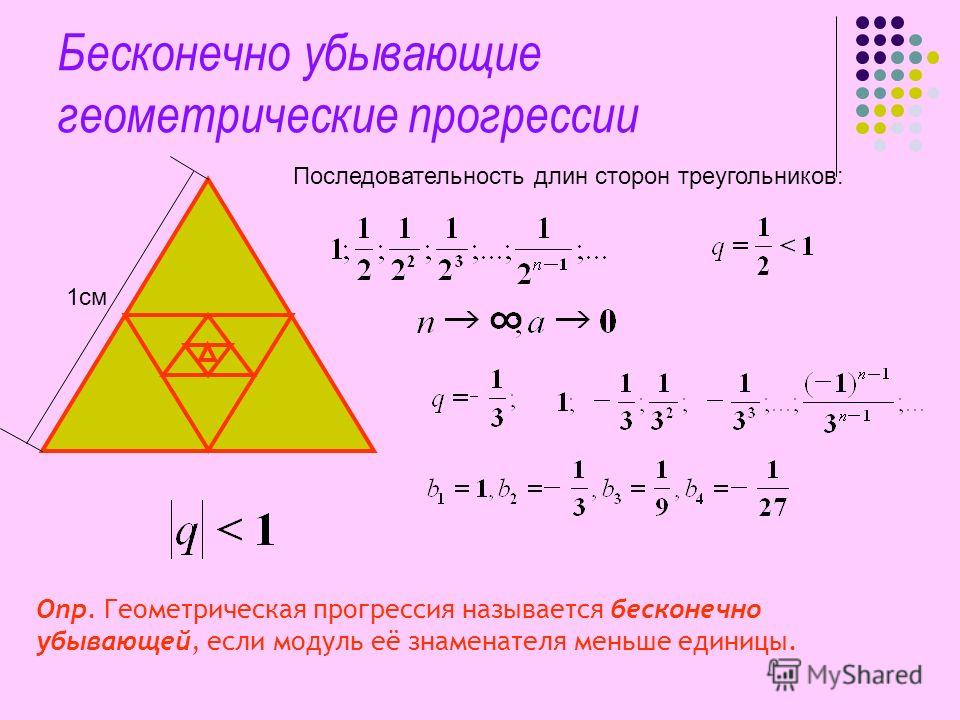
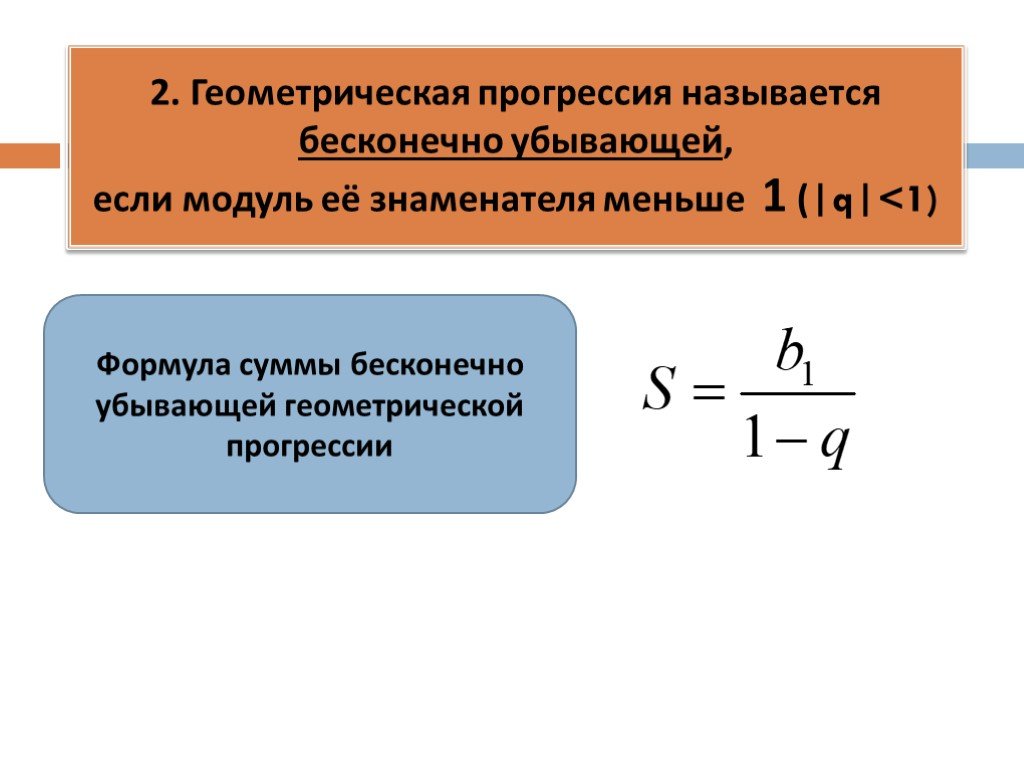
Бесконечная убывающая геометрическая прогрессия и ее формулы

ОПРЕДЕЛЕНИЕ

Численная последовательность \(\ B=\left\{b_{1}, b_{2}, \dots, b_{n}, \dots\right\} \) , каждый член которой равен предыдущей, умноженной на постоянное число \(\ q \) для этой последовательности, называется геометрической прогрессией. Число q называется знаменателем прогрессии.

Если знаменатель \(\ |q|Количество бесконечно уменьшающейся геометрической прогрессии

Сумма бесконечно убывающей прогрессии — это число, к которому сумма первых n членов убывающей прогрессии приближается без ограничений, поскольку число n стремится к бесконечности. Сумма бесконечно уменьшающейся геометрической прогрессии рассчитывается по формуле:

\(\ S_{n}=\frac{b_{1}}{1-q} \)

Примеры решения проблем

ПРИМЕР 1

Задача

Чтобы найти сумму бесконечной геометрической прогрессии \(\ 1, \frac{1}{3}, \frac{1}{9}, \dots \)

Решение.

Эта последовательность чисел будет бесконечно уменьшающейся прогрессией, поскольку

\(\ q=\frac{b_{2}}{b_{1}}=\frac{1}{3}Сумма этой бесконечно уменьшающейся геометрической прогрессии рассчитывается по формуле:

\(\ S_{n}=\frac{b_{1}}{1-q}=\frac{1}{1-\frac{1}{3}}=\frac{3}{2} \)

Ответ

\(\ S_{n}=\frac{3}{2} \)

ПРИМЕР 2

Задача

Представить число \(\ 0 \) в виде обычной фракции, \(\ (6) \)

Решение.

Написание числа как \(\ 0,(6) \) означает периодическую долю \(\ 0.6666 \dots \), которая может быть представлена в виде следующей суммы:

\(\ 0,(6)=0,6+0,06+0,006+\dots \)

Эта сумма представляет собой сумму бесконечной геометрической прогрессии с первым членом \(\ b_{1}=0,6 \) и знаменателем \(\ \mathrm{q}=\mathrm{O}_{.1} \). Найдите эту сумму по формуле

\(\ S_{n}=\frac{b_{1}}{1-q}=\frac{0,6}{1-0,1}=\frac{0,6}{0,9}=\frac{6}{9}=\frac{2}{3} \)

Поэтому \(\ 0,(6)=\frac{2}{3} \)

Ответ

\(\ 0,(6)=\frac{2}{3} \)

Физика

166

Реклама и PR

31

Педагогика

80

Психология

72

Социология

7

Астрономия

9

Биология

30

Культурология

86

Экология

8

Право и юриспруденция

36

Политология

13

Экономика

49

Финансы

9

История

16

Философия

8

Информатика

20

Право

35

Информационные технологии

6

Экономическая теория

7

Менеджент

719

Математика

338

Химия

20

Микро- и макроэкономика

1

Медицина

5

Государственное и муниципальное управление

2

География

542

Информационная безопасность

2

Аудит

11

Безопасность жизнедеятельности

3

Архитектура и строительство

1

Банковское дело

1

Рынок ценных бумаг

6

Менеджмент организации

2

Маркетинг

238

Кредит

3

Инвестиции

2

Журналистика

1

Конфликтология

15

Этика

9

Формулы дифференцирования Формула n-го члена геометрической прогрессии Формула n-го члена арифметической прогрессии Формула знаменателя геометрической прогрессии Формула разности арифметической прогрессии

Узнать цену работы

Узнай цену

своей работы

Имя

Выбрать тип работыЧасть дипломаДипломнаяКурсоваяКонтрольнаяРешение задачРефератНаучно — исследовательскаяОтчет по практикеОтветы на билетыТест/экзамен onlineМонографияЭссеДокладКомпьютерный набор текстаКомпьютерный чертежРецензияПереводРепетиторБизнес-планКонспектыПроверка качестваЭкзамен на сайтеАспирантский рефератМагистерскаяНаучная статьяНаучный трудТехническая редакция текстаЧертеж от рукиДиаграммы, таблицыПрезентация к защитеТезисный планРечь к дипломуДоработка заказа клиентаОтзыв на дипломПубликация в ВАКПубликация в ScopusДиплом MBAПовышение оригинальностиКопирайтингДругое

Принимаю  Политику  конфиденциальности

Подпишись на рассылку, чтобы не пропустить информацию об акциях

111.

Геометрическая прогрессия

Геометрическая прогрессия – это числовая последовательность, первый член которой отличен от нуля, а каждый член, начиная со второго, равен предыдущему, умноженному на одно и то же отличное от нуля число , где – знаменатель прогрессии: ().

Общий вид геометрической прогрессии:

:: ; ; ; …; ; …

Геометрическая прогрессия является возрастающей при и убывающей при .

Например, :: 2; 6; 18; 54; …; – возрастающая прогрессия; :: 250; 50; 10; …; – убывающая прогрессия.

Если заданы первый член и знаменатель , то -й член геометрической прогрессии определяют по формуле

:

.

Сумму первых членов Геометрической прогрессии находят по формуле: .

Свойства геометрической прогрессии.

1. Квадрат каждого среднего члена прогрессии равен произведению равноотстоящих от него членов:

; ().

2. В конечной геометрической прогрессии произведения двух членов, равноотстоящих от ее концов, равны между собой и равны произведению крайних членов:

:: ; ; ; . ..; ; ; …; ; ;

.

Пример 7. Найдите первый и последний члены геометрической прогрессии, которая состоит из четырех членов, если и .

Решение. Подставим исходные данные в формулу:

.

Найдем по формуле и получим: .

Ответ. и .

Пример 8. В геометрической прогрессии (): . Найдите сумму восьми первых членов прогрессии .

Решение. ; ; , тогда запишем исходную систему так: .

Разделим почленно второе уравнение на первое. Получим:

.

Найдем из первого уравнения системы: .

По формуле для суммы найдем: .

Ответ. .

Пример 9. Шесть чисел составляют геометрическую прогрессию. Сумма первых трех чисел равна 168, а сумма последних трех чисел равна 21. Найдите эти числа.

Решение. Из условия задачи составим систему уравнений:

Найдем , для этого разделим первое уравнение на второе: .

Найдем из первого уравнения: .

Ответ. 96; 48; 24; 12; 6; 3.

Пример 10. Найдите сумму , .

Решение. По условию задания можно сделать вывод о том, что: – это геометрическая прогрессия. Найдем первый член прогрессии, знаменатель и общее количество ее членов: ; ; . Тогда .

Ответ. .

Бесконечно убывающая геометрическая прогрессия

– это такая бесконечная геометрическая прогрессия (), у которой знаменатель .

Сумму бесконечно убывающей геометрической прогрессии находят по формуле:

.

Пример 11. Запишите периодическую дробь 0,4545…=0,(45) как обыкновенную.

Решение. Запишем периодическую дробь в виде бесконечной суммы обыкновенных дробей: .

Слагаемые представляют собой бесконечно убывающую геометрическую прогрессию со знаменателем и первым членом , а полученная сумма – это сумма этой прогрессии.

Используя формулу суммы бесконечно убывающей геометрической прогрессии, получим: .

Ответ. .

Пример 12. Найдите бесконечно убывающую геометрическую прогрессию, если , а сумма .

Решение. Используя формулу суммы бесконечно убывающей геометрической прогрессии найдем:

.

Ответ. :: ; ; ; …

Пример 13. Найдите бесконечно убывающую геометрическую прогрессию, если ее сумма равна , а сумма ее первых четырех членов равна .

Решение. Из условия задачи запишем систему:

.

Подставим правую часть первого уравнения во второе уравнение:

И .

Тогда найдем два значения :

1) ; 2) .

Ответ. 1) :: ; ; ; ; …; 2) :: ; ; ; ; … .

Пример 14. Сумма бесконечно убывающей геометрической прогрессии , а сумма квадратов всех ее членов . Найти четвертый член прогрессии.

Решение. Найдем знаменатель прогрессии, которая состоит из квадратов членов: ; ; ; …; ; … : .

Тогда составим систему уравнений: .

Возведем первое уравнение в квадрат: .

Разделим второе уравнение системы на первое:

Тогда ; .

Ответ. .

< Предыдущая		Следующая >

Объяснение урока: Геометрические последовательности | Nagwa

В этом объяснителе мы научимся вычислять обыкновенное отношение, найдем следующее члены в геометрической последовательности и проверьте, увеличивается или уменьшается последовательность.

Последовательность {𝑎,𝑎,𝑎,…} — это пронумерованный набор чисел (или другие объекты), которые обычно следуют шаблону. Отдельные элементы в последовательность, 𝑎 для 𝑛∈ℕ, называются термами и помечаются индекс 𝑛, который сообщает вам позицию данного термина в последовательности.

Существует множество реальных применений геометрических последовательностей в науке. бизнес, личные финансы и здоровье. Например, физики используют геометрические последовательности для расчета количества радиоактивного материала, оставшегося после любого заданного количество периодов полураспада вещества.

В течение каждого периода полураспада вещество распадается на 50%.

Прежде чем мы начнем с математического описания геометрической прогрессии, полезно рассмотреть несколько простых примеров, которые помогут нам визуализировать то, что структура геометрической последовательности выглядит как в реальном мире. Один из самые известные примеры геометрической последовательности относятся к изобретению шахмат. Согласно легенде, великий визирь Сисса Бен Дахир изобрел игру в шахматы. и подарил индийскому королю Шаиму шахматную доску. В благодарность за подарок, великому визирю предлагалась любая награда, какую он просил, лишь бы она звучало разумно для короля. Великий визирь сделал, казалось бы, скромное запрос с рисом на шахматной доске. Он попросил, чтобы одно зерно риса поставить на первую клетку две на вторую, четыре на четвертую и т.д., удваивая количество рисовых зерен каждый раз от предыдущего квадрата до конец шахматной доски (на которой 64 поля).

Король, впечатленный скромной просьбой, обязал и приказал, чтобы рис был привезли в мешках. Первые несколько квадратов вроде бы все шло хорошо, но к 21-му квадрату их было более миллион (1‎ ‎048‎ ‎576) зерен риса; сумка была опустошена, и другая должна была быть принесенный, который тотчас же опустел на проходящей площади. К 41-му квадрату их было более триллион (1‎ ‎099‎ ‎511‎ ‎627‎ ‎776) зерен риса и как эта прогрессия продолжался, удваивая каждый раз, в финале было больше рисовых зёрен квадратов, чем существует во всем мире, даже не считая всех рисовые зерна на всех предыдущих квадратах. Просто зерна на последнем квадрате превысит мировое производство риса более чем 1 000 лет. Количество рисовых зерен на каждой клетке шахматной доски составляет геометрическая последовательность, описываемая {1,2,4,8,16,32,64,128,256,512,…}, где каждый последующий член последовательности в два раза больше предыдущего; Это называется возрастающей геометрической прогрессией.

Мы также можем эквивалентно изобразить это как

Теперь предположим, что мы хотим исследовать поведение прыгающего теннисного мяча. Если сначала бросаем мяч с высоты 10 м и измерьте его положение над время мы можем заметить, что шар теряет свою первоначальную высоту после каждого подпрыгивать.

Мяч теряет 20% своей энергии каждый раз, когда отскакивает, и кинетическая энергия пропорциональна высоте, с которой он упал. Это значит, что мяч теряет 20% своей высоты после каждого отскока; в других слов, каждая высота составляет 80% от предыдущей. Это позволяет нам предсказать высоту мяча после каждого отскока. После первого отскока, высота мяча будет 80% 10 м: 0,8×10=8,мм

А после второго рикошета будет 80% 8 м: 0,8×8=6,4 мм

Если мы продолжим эту процедуру, высота мяча после каждого отскока сформирует последовательность: {10,8,6,4,5,12,4,096,…}, или эквивалентно изображенному как

Это известно как убывающая геометрическая последовательность, где каждый член является убывающим и определяется предыдущим путем умножения его на определенное число; в данном случае число равно 0,8.

Теперь давайте определим, что такое геометрическая последовательность математически.

Определение: геометрическая последовательность

Геометрическая последовательность, также известная как геометрическая прогрессия, представляет собой последовательность ненулевые числа {𝑎,𝑎,𝑎,𝑎,…}, имеющие ненулевое постоянное знаменательное отношение 𝑟≠1 между любыми двумя последовательными членами: 𝑟=𝑎𝑎𝑛=1,2,3,….для

Геометрическую последовательность в общем случае можно также изобразить как

Для рисовых зерен на каждой клетке шахматной доски отношение между любыми двумя последовательных терминов 𝑟=2, это число, на которое мы умножаем каждый член в последовательности, чтобы получить следующий член в последовательности.

Стоит отметить, что геометрические последовательности не всегда увеличиваются в цене; они также может уменьшаться, как с высотой теннисного мяча, или чередоваться в знак. Другой пример убывающей геометрической последовательности: {48,24,12,6,3,32,…}, и пример чередующейся последовательности {3,−6,12,−24,48,−96,192,…}.

Убывающая последовательность имеет общее отношение 𝑟=12 и чередующаяся последовательность имеет общее отношение 𝑟=−2. В общем, обычное соотношение 𝑟 управляет тем, как ведут себя члены геометрической последовательности, хотя нам может понадобиться учитывать знак начального значения, 𝑎, узнать, увеличивается оно или уменьшается.

• Если |𝑟|>1 (эквивалентно 𝑟>1 или 𝑟−1), величина членов геометрической последовательности, |𝑎|, увеличится до бесконечности; это известно как расходящаяся последовательность.
  • Если 𝑎>0 и 𝑟>1, условия в геометрическая последовательность будет возрастать и расходиться до бесконечности. Например, с 𝑎=1 и 𝑟=2 геометрическая последовательность будет: {1,2,4,8,16,32,…}.
  • Если 𝑎0 и 𝑟>1, условия в геометрическая последовательность будет уменьшаться и расходиться к отрицательной бесконечности. Например, при 𝑎=−1 и 𝑟=2, геометрический последовательность будет: {−1,−2,−4,−8,−16,−32,…}.
  • Если 𝑟−1 для любого начального значения 𝑎, члены геометрической последовательности будут чередоваться по знаку, но их величина будет возрастать и расходиться до бесконечности. Например, с 𝑎=1 и 𝑟=−2 геометрическая последовательность будет: {1,−2,4,−8,16,−32,…}, или с 𝑎=−1 и 𝑟=−2 геометрический последовательность будет: {−1,2,−4,8,−16,32,…}.
• Если |𝑟|1 (эквивалентно −1𝑟1), величина слагаемых в геометрии последовательность, |𝑎|, будет приближаться к нуль; это известно как сходящаяся последовательность.
  • Если 𝑎>0 и 0𝑟1, члены геометрической последовательности будут уменьшаться и стремиться к нулю. Например, с 𝑎=1 и 𝑟=12, геометрическая последовательность будет такой: 1,12,14,18,116,132,….
  • Если 𝑎0 и 0𝑟1, члены геометрической последовательности будут возрастать и стремиться к нулю. Например, при 𝑎=−1 и 𝑟=12, геометрическая последовательность будет: −1,−12,−14,−18,−116,−132,….
  • Если −1𝑟0 для любого начального значения 𝑎 члены геометрической последовательности будут чередоваться по знаку, но их величина будет уменьшаться и стремиться к нулю. Например, с 𝑎=1 и 𝑟=−12, геометрическое последовательность будет: 1,−12,14,−18,116,−132,…, или с 𝑎=−1 и 𝑟=−12, геометрическая последовательность будет: −1,12,−14,18,−116,132,….

Чтобы вычислить знаменатель данной геометрической последовательности, мы можем разделить любой термин из последовательности на член, который непосредственно предшествует ему. Для например, мы могли бы разделить третий член на второй член или второй член по первому члену последовательности; в любом случае должно давать одно и то же число для геометрическая последовательность.

В первом примере мы определим обыкновенное отношение для данного геометрического последовательность, описывающая количество бактерий в лабораторном эксперименте.

Пример 1. Нахождение общего отношения геометрической последовательности

В таблице показано количество бактерий в лабораторном эксперименте для четырех дней подряд. Количество бактерий можно описать геометрическим последовательность. Найдите знаменатель этой последовательности.

День	1-й	2-й	3-й	4-й
Количество бактерий	2 643	2‎ ‎572	10‎ ‎288	41‎ ‎152

Ответ

описание количества бактерий в лабораторном эксперименте.

Напомним, что последовательность является геометрической, если между любыми два срока подряд. Как нам говорят, что мы смотрим на геометрическое последовательность, нам не нужно проверять, что отношение согласовано между каждые два срока подряд. Вместо этого мы можем выбрать любые два последовательных условия. Общее отношение можно найти из 2-го и 1-го членов как 𝑟=𝑎𝑎=2572643=4.

Мы могли бы также найти это из отношения 3-го и 2-го слагаемых или 4-й и 3-й члены дают тот же результат. Отметим также, что поскольку 𝑎>0 и 𝑟>1, геометрическое последовательность возрастающая и расходящаяся.

Таким образом, знаменатель геометрической прогрессии равен 4.

В последнем примере мы определяем знаменатель отношения из 2-го и 1-го членов, но мы могли бы также использовать 3-й и 2-й или 4-й и 3-й члены, чтобы получить тот же результат: 𝑟=𝑎𝑎=102882572=4, или 𝑟=𝑎𝑎=4115210288=4.

Нас также могут попросить найти последовательные члены геометрической прогрессии. Этот включает в себя сначала нахождение обыкновенного отношения, а затем его использование для вычисления дополнительные условия путем умножения предыдущих условий на 𝑟.

Теперь давайте рассмотрим пример, в котором мы находим следующий член данного убывающая геометрическая последовательность.

Пример 2. Нахождение следующего члена заданной геометрической последовательности

Поиск следующего члена геометрической последовательности −5,−54,−516,−564,….

Ответ

В этом примере мы хотим определить следующий член данного геометрического последовательность.

Напомним, что последовательность является геометрической, если между любыми два срока подряд. Первым шагом является установление общего отношения 𝑟 геометрической прогрессии, которую мы можем найти из отношение любых двух последовательных членов. Мы можем использовать соотношение 2-го и 1-го члены в последовательности, чтобы получить 𝑟=𝑎𝑎=−5=14.

Заметим, что, поскольку 𝑎0 и 0𝑟1, геометрическая прогрессия возрастает и стремится к нулю.

Наконец, мы можем определить следующий член последовательности, 𝑎, умножив предыдущее слагаемое на 𝑟 чтобы получить 𝑎=𝑟𝑎=14×−564=−5256. 

В последнем примере мы видели, что можем определить следующий член заданного последовательность, сначала найдя знаменатель и умножив на него последний член. Если мы повторим эту процедуру, мы сможем перечислить столько членов в последовательности как требуется.

В следующем примере мы определим следующие четыре члена данного возрастающего геометрическая последовательность.

Пример 3. Поиск пропущенных членов заданной геометрической последовательности

Найдите следующие четыре члена в геометрической последовательности 1165 155 355,….

Ответ

В этом примере мы хотим определить следующие четыре члена в данном геометрическая последовательность.

Напомним, что последовательность является геометрической, если между любыми два срока подряд. Первым шагом является установление общего отношения 𝑟 геометрической прогрессии, которую мы можем найти из отношение любых двух последовательных членов. Мы можем использовать соотношение 2-го и 1-го члены в последовательности, чтобы получить 𝑟=𝑎𝑎==3.

Заметим, что поскольку 𝑎>0 и 𝑟>1, геометрическая прогрессия возрастает и расходящийся. Следующие четыре члена, 𝑎,𝑎,𝑎,𝑎, можно найти повторно умножив предыдущие члены на это обыкновенное соотношение: 𝑎=𝑟𝑎=3×355=955,𝑎=𝑟𝑎=3×955=2755,𝑎=𝑟𝑎=3×2755=8155,𝑎=𝑟𝑎=3×8155=24355. Таким образом, следующие четыре члена геометрической последовательности равны 955 2755 8155 24355.

Как видно из определения и предыдущих примеров, рекурсивная формула для геометрической прогрессии можно записать как 𝑎=𝑟𝑎.

В некоторых случаях нам может быть задана геометрическая последовательность как отношение в такой форме, которое мы можем использовать для определения обыкновенного отношения.

В следующем примере мы определим знаменатель данного геометрического последовательность, заданная в терминах рекурсивной формулы.

Пример 4. Нахождение общего отношения геометрической последовательности по ее общему виду Член

Найдите знаменатель геометрической прогрессии, удовлетворяющий соотношению 𝑎=98𝑎, где 𝑛≥1.

Ответ

В этом примере мы хотим определить знаменатель геометрического последовательность, определяемая конкретным рекурсивным отношением.

Напомним, что последовательность является геометрической, если существует знаменатель 𝑟, между любыми двумя последовательными терминами: 𝑟=𝑎𝑎.

Мы также можем преобразовать эту рекурсивную формулу для геометрической прогрессии в виде 𝑎=𝑟𝑎.

Заметим, что это отличается от формы, данной в вопросе, где отношение умножается на 𝑎. Теперь, если мы перепишем заданное соотношение в таком виде, мы получаем 𝑎=89𝑎.

Таким образом, обыкновенное отношение равно 𝑟=89.

Заметим, что начиная с 0𝑟1 этот геометрический последовательность сходится к нулю; увеличивается или уменьшается зависит на начальном значении 𝑎.

Если нам также дано начальное значение, 𝑎, с рекурсивной формулы, мы можем перечислить первые несколько членов в последовательность; это то же самое, что и в предыдущих примерах, где мы умножаем обыкновенное отношение с термином в последовательности, чтобы получить следующий термин.

Теперь давайте рассмотрим пример, где нам нужно найти первые пять членов заданной геометрической последовательности и начального значения.

Пример 5. Нахождение членов последовательности по ее общему члену и значению Первый член

Найдите первые пять членов последовательности 𝑎, учитывая 𝑎=14𝑎, 𝑛≥1, и 𝑎=−27.

Ответ

В этом примере мы хотим найти члены геометрической последовательности из заданное отношение и первый член.

Заметим, что, поскольку 𝑎0 и 0𝑟1 из заданной рекурсивной формулы как 𝑟=14, геометрическая последовательность возрастает и сходящиеся к нулю.

Начнем с нахождения второго члена, подставив 𝑛=1 в соотношение: 𝑎=14𝑎=14×−27=−274.

Затем мы повторяем эту процедуру, чтобы найти три других члена с 𝑛=2,3,4: 𝑎=14𝑎=14×−274=−2716,𝑎=14𝑎=14×−2716=−2764,𝑎=14𝑎=14×−2764=−27256.

Таким образом, первые пять членов последовательности −27,−274,−2716,−2764,−27256.

Также можно делать вещи, противоположные предыдущему примеру. То есть, предположив, что у нас есть несколько первых членов последовательности, мы можем найти ее обыкновенное отношение и первый член. В самом деле, если мы обозначим первый термин как 𝑎=𝑎 для простоты, общая форма геометрического последовательность

Второй член геометрической прогрессии вычисляется путем умножения первого члена, 𝑎, на 𝑟, чтобы получить 𝑎𝑟, тогда третий член равен второму члену, умноженному на 𝑟, дать 𝑎𝑟 и так далее.

Другими словами, каждое слагаемое умножается на одно и то же число 𝑟, чтобы получить следующее срок. В следующем примере мы увидим применение этой идеи.

Пример 6. Определение первого члена и знаменателя сходящейся геометрической фигуры Последовательность

Геометрическая последовательность представляет собой список термов, который можно записать в виде 𝑎,𝑎𝑟,𝑎𝑟,𝑎𝑟,…, где 𝑎 — первый член, а 𝑟 — обыкновенное отношение (число, на которое умножается одно слагаемое, чтобы получить следующее слагаемое в последовательность, 𝑟≠1).

Определите 𝑎 и 𝑟 в следующей последовательности: 250,50,10,2,….

Ответ

В этом примере мы хотим определить первый член, 𝑎, и обыкновенное отношение 𝑟 данной геометрической прогрессии.

Первый член по проверке равен 𝑎=250. Второй срок, из заданной формы 𝑎𝑟=50. Подставляя значение 𝑎 во второе выражение и решение для 𝑟 дает нам общее отношение, которое мы также можем определить из любых двух последовательных терминов: 𝑟=50𝑎=50250=15.

Заметим, что, поскольку 𝑎>0 и 0𝑟1, геометрическая последовательность убывает и сходящиеся к нулю.

Итак, имеем 𝑎=250, 𝑟=15.

Очень похоже на то, как мы можем использовать свойства геометрической последовательности для определения отношения или конкретных условий, мы можем проверить, является ли последовательность геометрическим или нет, проверив свойства, которыми он обладает. В следующем примере мы увидим применение этого.

Пример 7. Идентификация геометрических последовательностей

Что из перечисленного не является геометрической прогрессией?

1. 𝑤7𝑥,−16,7𝑥36𝑤,−49𝑥216𝑤,…
2. (11,−44,176,−704,…)
3. 𝑏,𝑏,𝑏,𝑏,…loglogloglog
4. 119,−157,1171,−1513,…

Ответ

правильно следует определению геометрической прогрессии.

Напомним, что геометрическая последовательность определяется как имеющая общий отношение, 𝑟, между последовательными терминами.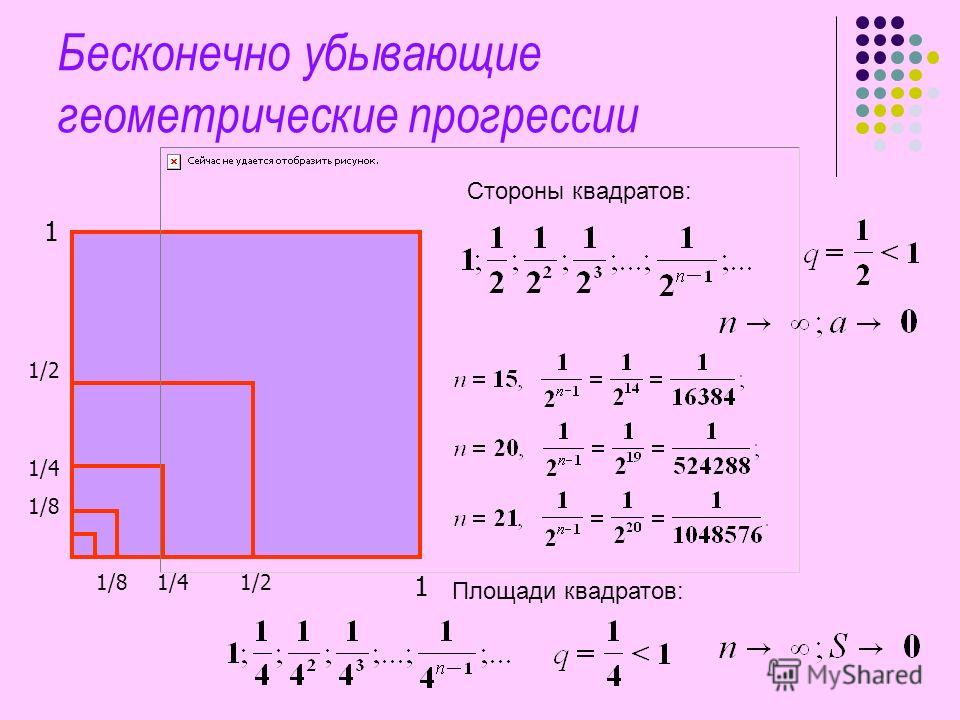 То есть, 𝑟=𝑎𝑎.

Поначалу может показаться сложной попытка определить, какие последовательности (некоторые из которых кажутся довольно сложными) подчиняются этому принципу. Однако, существует простая процедура, которой мы можем следовать в каждом случае, чтобы проверить последовательности; а именно, мы можем разделить второе слагаемое на первое член, чтобы получить соотношение, а затем мы можем умножить второй член на это отношение, чтобы увидеть, получим ли мы третий член или нет. Если мы его получим, тогда отношение является обыкновенным отношением, а последовательность является геометрической.

Итак, применим эту процедуру. Для варианта A 𝑎 равно 𝑤7𝑥 и 𝑎 −16, поэтому отношение равно 𝑟=𝑎𝑎=−16÷𝑤7𝑥=−16×7𝑥𝑤=−7𝑥6𝑤.

Далее умножаем второе слагаемое на это соотношение: 𝑟𝑎=−7𝑥6𝑤×−16=7𝑥36𝑤.

Поскольку 𝑎 действительно равно 7𝑥36𝑤, это подтверждает, что соотношение соответствует между первыми тремя терминами. Кроме того, мы можем проверить 𝑎 и убедиться, что оно равно к 𝑟𝑎. Таким образом, вариант А представляет собой геометрическую прогрессию.

Для варианта B соотношение между 𝑎 и 𝑎 равно 𝑟=𝑎𝑎=−4411=−4.

Затем умножаем 𝑎 на отношение, чтобы получить 𝑟𝑎=−4×−44=176, что 𝑎. Кроме того, 𝑎=𝑟𝑎 (т. е. −704=−4×176), что показывает, что вариант B также геометрический.

Для варианта C соотношение между первыми двумя членами равно 𝑟=𝑏𝑏=2𝑏𝑏=2,логлоглоглог где мы использовали свойство loglog𝑥=𝑦𝑥 для упростить выражение. Однако, если мы умножим 𝑎 на 𝑟 получаем 𝑟𝑎=2𝑏=𝑏.loglog

Это не равно 𝑎; скорее, это на самом деле 𝑎. Таким образом, последовательность не может быть геометрической, так как соотношение между членами не является постоянным.

Для полноты картины рассмотрим вариант D. Мы можем рассчитать соотношение между первыми двумя членами 𝑟=-157÷119=-157×191=-1957=-13.

Вычисляя это отношение, умноженное на 𝑎, получаем 𝑟𝑎=−13×−157=1171.

Это равно 𝑎. Мы также можем убедиться, что 𝑎=𝑟𝑎. Таким образом, эта последовательность является геометрической.

В заключение, вариант C является единственной негеометрической последовательностью.

Мы также можем определить значения неизвестных параметров, появляющихся в членов геометрической прогрессии, используя свойства геометрических последовательностей, в частности, обыкновенное отношение является постоянным для любых двух последовательные термины.

Теперь давайте рассмотрим пример, в котором нам даны три термина в геометрическая последовательность, заданная через неизвестный параметр, которую мы определить из свойств геометрических последовательностей.

Пример 8. Использование свойств геометрических последовательностей для поиска неизвестного члена

Найдите значение 𝑚 по заданной геометрической последовательности −4,𝑚,2𝑚+3,….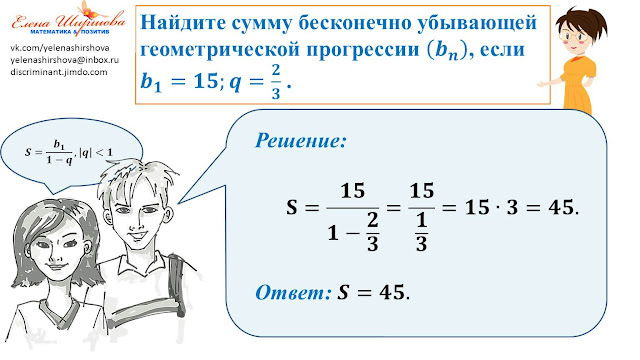

Ответ

В этом примере мы будем использовать свойства геометрической последовательности в чтобы определить неизвестный параметр 𝑚, фигурирующий в условия последовательности.

Напомним, что последовательность является геометрической, если между любыми два срока подряд. Как нам говорят, у нас есть геометрическая последовательность, мы знаем что отношение между любыми двумя последовательными терминами является постоянным числом 𝑟. Из 2-го и 1-го слагаемых имеем 𝑟=𝑎𝑎=𝑚−4, а из 3-го и 2-го слагаемых имеем 𝑟=𝑎𝑎=2𝑚+3𝑚.

Эти отношения будут одинаковыми для геометрической последовательности, и мы получим Квадратное уравнение −𝑚4=2𝑚+3𝑚−𝑚=4(2𝑚+3)𝑚+8𝑚+12=0(𝑚+6)(𝑚+2)=0,

Таким образом, решение 𝑚=−6 или 𝑚 =-2. Мы обратите внимание, что эти решения приводят к различным типам геометрических последовательности. Для 𝑚 = −6 обычное отношение равно 𝑟=−6−4=32, и, поскольку 𝑎0 и 𝑟>1, мы имеют убывающую и расходящуюся геометрическую прогрессию. Для 𝑚=−2, обыкновенное отношение равно 𝑟=−2−4=12, и, поскольку 𝑎0 и 0𝑟1, это возрастающая и сходящаяся геометрическая прогрессия.

В предыдущем примере мы видели, что неизвестный параметр появился в члены геометрической прогрессии имеют два решения, каждое из которых имеет разный тип геометрической последовательности, возрастающей или убывающей.

В последнем примере мы определим значение двух неизвестных параметров появляется в двух из четырех членов данной геометрической последовательности, используя ее характеристики.

Пример 9. Использование свойств геометрических последовательностей для нахождения значений неизвестных Условия

Найдите 𝑥 и 𝑦 по геометрическому последовательность (1,4𝑥,4𝑦,64,…).

Ответ

В этом примере мы будем использовать свойства геометрической последовательности в для определения неизвестных параметров 𝑥 и 𝑦 появляется в условиях последовательности.

Напомним, что последовательность является геометрической, если между любыми два срока подряд. Как нам говорят, у нас есть геометрическая последовательность, мы знаем что отношение между любыми двумя последовательными терминами является постоянным числом 𝑟. Из 4-го и 3-го слагаемых имеем 𝑟=𝑎𝑎=644𝑦=16𝑦, а из 3-го и 2-го слагаемых имеем 𝑟=𝑎𝑎=4𝑦4𝑥=𝑦𝑥, а из 2-го и 1-го слагаемых имеем 𝑟=𝑎𝑎=4𝑥1=4𝑥.

Эти отношения будут одинаковыми для геометрической последовательности, и мы получим квадратные уравнения 4𝑥=16𝑦,4𝑥=𝑦𝑥,16𝑦=𝑦𝑥.

После перестановки эти уравнения становятся 𝑥𝑦=4,𝑦=4𝑥,𝑦=16𝑥.

Подстановка второго уравнения в третье дает квадратное уравнение уравнение (4𝑥)=16𝑥𝑥−𝑥=0𝑥(𝑥−1)=0.

Таким образом, мы имеем 𝑥=0 и 𝑥=1, но мы можем игнорировать первое решение, так как оно не удовлетворяет первому уравнению 𝑥𝑦=4. Используя первое уравнение, значение 𝑦 можно найти как 𝑦=4.

Следовательно, значения 𝑥 и 𝑦, которые появляются в геометрической последовательности 𝑥=1, 𝑦=4.

Заметим, что для этого решения обыкновенное отношение равно 𝑟=4. А поскольку 𝑎>0 и 𝑟>1, имеем возрастающую и расходящуюся геометрическую прогрессию.

Давайте закончим резюмированием ключевых моментов, которые мы узнали в этом объяснитель.

Ключевые моменты

• Геометрическая последовательность — это последовательность ненулевых чисел, определяемая постоянное ненулевое знаменатель отношения 𝑟≠1 между любыми двумя последовательные члены в последовательности 𝑟=𝑎𝑎. Данная геометрическая последовательность может быть определена в терминах набора чисел {𝑎,𝑎,𝑎,…}, рекурсивная формула или явная формула.
• Обычно обыкновенное отношение 𝑟 определяет, как члены ведет себя геометрическая последовательность, хотя нам, возможно, придется принять во внимание подпишите начальное значение, 𝑎, чтобы узнать, увеличивается или уменьшается.
  • Если |𝑟|>1 (эквивалентно 𝑟>1 или 𝑟−1), величина слагаемых в геометрической последовательность, |𝑎|, увеличится до бесконечность; это известно как расходящаяся последовательность.
    • Если 𝑎>0 и 𝑟>1, члены геометрической последовательности будут возрастать и расходиться к бесконечность.
    • Если 𝑎0 и 𝑟>1, члены геометрической последовательности будут уменьшаться и расходиться к отрицательная бесконечность.
    • Если 𝑟−1 для любого начального значения 𝑎, члены геометрической последовательности будут чередоваться по знаку, но их величина будет возрастать и расходиться до бесконечности.
  • Если |𝑟|1 (эквивалентно −1𝑟1), величина слагаемых в последовательность геометрии, |𝑎|, получит ближе к нулю; это известно как сходящаяся последовательность.
    • Если 𝑎>0 и 0𝑟1, члены геометрической прогрессии будут уменьшаться и стремиться к нулю.
    • Если 𝑎0 и 0𝑟1, члены геометрической последовательности будут возрастать и стремиться к нулю.
    • Если −1𝑟0 для любого начального значения 𝑎 члены геометрической последовательности будут чередоваться по знаку, но их величина будет уменьшаться и стремиться к нулю.
• Рекурсивное отношение, следующее из определения общего соотношение вместе с заданным начальным значением 𝑎 позволяет нам перечислить члены в геометрической последовательности: 𝑎=𝑟𝑎. Это означает, что каждый член геометрической последовательности находится путем умножения предыдущего члена по обыкновенному соотношению.
• Если обозначить начальное значение как 𝑎=𝑎 для простоты, общее форма геометрической прогрессии {𝑎,𝑎𝑟,𝑎𝑟𝑎𝑟,…}. 
• Используя свойства геометрических последовательностей, мы также можем определить значения неизвестных параметров, входящих в некоторые члены данного геометрического последовательность.

Определение геометрического в алгебре.

(прилагательное)

увеличение или уменьшение в геометрической прогрессии, т.е. умножение на константу.

• Геометрические последовательности

  • Геометрическая прогрессия , также известная как геометрическая последовательность , представляет собой последовательность чисел, в которой каждый член после первого находится путем умножения предыдущего на фиксированное ненулевое число, называемое знаменателем $r$.
  • Например, последовательность $2, 6, 18, 54, \cdots$ представляет собой геометрическую прогрессию со знаменателем $3$.
  • Точно так же $10,5,2.5,1.25,\cdots$ является геометрическим 9Последовательность 0351 со знаменателем $\frac{1}{2}$.
  • Например: $1,-3,9,-27,81,-243, \cdots$ — это геометрическая последовательность со знаменателем $-3$.
  • Поведение геометрической последовательности зависит от значения обыкновенного отношения.

• Бесконечный геометрический ряд

  • Геометрические ряды — один из простейших примеров бесконечных рядов с конечными суммами.
  • Геометрический ряд — это бесконечный ряд, члены которого находятся в геометрическая прогрессия, или последовательные члены которой имеют общее отношение.
  • Если члены геометрического ряда стремятся к нулю, сумма его членов будет конечной.
  • Говорят, что геометрический ряд с конечной суммой сходится.
  • Найдите сумму бесконечного геометрического ряда $64+ 32 + 16 + 8 + \cdots$

• Применение геометрического ряда

  • Формула суммы геометрический ряд можно использовать для преобразования десятичной дроби в дробную:
  • В случае снежинки Коха ее площадь может быть описана геометрическим рядом .
  • За исключением начальной 1, этот ряд представляет собой геометрических с постоянным отношением $r = \frac{4}{9}$.
  • Первый член геометрического ряда равен $a = 3 \frac{1}{9} = \frac{1}{3}$, поэтому сумма равна
  • Применение геометрических последовательностей и рядов к различным физическим и математическим темам

• Суммирование первых n членов геометрической последовательности

  • Используя обыкновенное отношение и первый член геометрической последовательности , мы можем просуммировать ее члены.
  • Члены геометрического ряда образуют геометрическую прогрессию , что означает, что отношение последовательных членов в ряду постоянно.
  • Ниже приведены несколько геометрических серий с различными общими коэффициентами.
  • Для $r\neq 1$ сумма первых $n$ членов геометрического ряда равна:
  • Вычислить сумму первых $n$ членов в геометрической последовательности

• Суммы и ряды

  • Если сложить все члены геометрической последовательности (в которой каждая запись представляет собой предыдущую запись, умноженную на константу), вы получите геометрическую последовательность .
  • Типичный пример тренда, следующего за геометрический ряд — это количество людей, зараженных вирусом, так как каждый человек передает его еще нескольким.
  • Еще раз сделайте паузу, чтобы убедиться, что это будет работать на всех геометрических серии , но только на геометрических сериях .
  • Наконец — еще раз — мы можем применить этот трюк к общему геометрическому ряду , чтобы найти формулу.
  • Таким образом, общее число инфицированных соответствует геометрическому ряду .

• Рекурсивные определения

  • Геометрическая последовательность следует формуле $a_n=r\cdot a_{n-1}.$ Это еще один пример рекурсивной формулы.
  • Прикладной пример геометрической последовательности включает распространение вируса гриппа.
  • Предположим, что каждый зараженный человек заразит еще двоих, так что члены следуют геометрической последовательности .
  • Используя это уравнение, рекурсивное уравнение для этого геометрического последовательность: $a_n=2 \cdot a_{n-1}.$
  • Каждый человек заражает еще двух человек вирусом гриппа, что делает число недавно инфицированных людей n-м членом в геометрической последовательности .

• Комплексные числа в полярных координатах

  • Это приводит к способу визуализации умножения и деления комплексных чисел геометрически .
  • Иногда полезно думать о комплексных числах в другом геометрическом способ.
  • Прежняя геометрическая идея, в которой число $z=a+bi$ сопоставляется с точкой $(a,b)$ в обычной системе координат $xy$, называется прямоугольными координатами.
  • Такой способ мышления об умножении и делении комплексных чисел дает геометрический способ мышления об этих операциях.

• Комплексные конъюгаты

  • Два комплексно-сопряженных друг друга умножаются, чтобы получить действительное число с 92.

    No related posts.