Y cosx sinx график: Mathway | Популярные задачи

alexxlab / / Разное

Mathway | Популярные задачи

1Найти точное значениеsin(30)
2Найти точное значениеsin(45)
3Найти точное значениеsin(30 град. )
4Найти точное значениеsin(60 град. )
5Найти точное значениеtan(30 град. )
6Найти точное значениеarcsin(-1)
7Найти точное значениеsin(pi/6)
8
Найти точное значение		cos(pi/4)
9Найти точное значениеsin(45 град. )
10Найти точное значениеsin(pi/3)
11Найти точное значениеarctan(-1)
12Найти точное значениеcos(45 град. )
13Найти точное значениеcos(30 град. )
14Найти точное значениеtan(60)
15
Найти точное значение		csc(45 град. )
16Найти точное значениеtan(60 град. )
17Найти точное значениеsec(30 град. )
18Найти точное значениеcos(60 град. )
19Найти точное значениеcos(150)
20Найти точное значениеsin(60)
21Найти точное значениеcos(pi/2)
22Найти точное значениеtan(45 град. )
23Найти точное значениеarctan(- квадратный корень из 3)
24Найти точное значениеcsc(60 град. )
25Найти точное значениеsec(45 град. )
26Найти точное значениеcsc(30 град. )
27Найти точное значение
sin(0)
28Найти точное значениеsin(120)
29Найти точное значениеcos(90)
30Преобразовать из радианов в градусыpi/3
31Найти точное значениеtan(30)
32Преобразовать из градусов в радианы45
33Найти точное значениеcos(45)
34Упроститьsin(theta)^2+cos(theta)^2
35Преобразовать из радианов в градусыpi/6
36Найти точное значениеcot(30 град. )
37Найти точное значениеarccos(-1)
38Найти точное значениеarctan(0)
39Найти точное значениеcot(60 град. )
40Преобразовать из градусов в радианы30
41Преобразовать из радианов в градусы(2pi)/3
42Найти точное значениеsin((5pi)/3)
43Найти точное значениеsin((3pi)/4)
44Найти точное значениеtan(pi/2)
45Найти точное значениеsin(300)
46Найти точное значениеcos(30)
47Найти точное значениеcos(60)
48Найти точное значениеcos(0)
49Найти точное значениеcos(135)
50Найти точное значениеcos((5pi)/3)
51Найти точное значениеcos(210)
52Найти точное значениеsec(60 град. )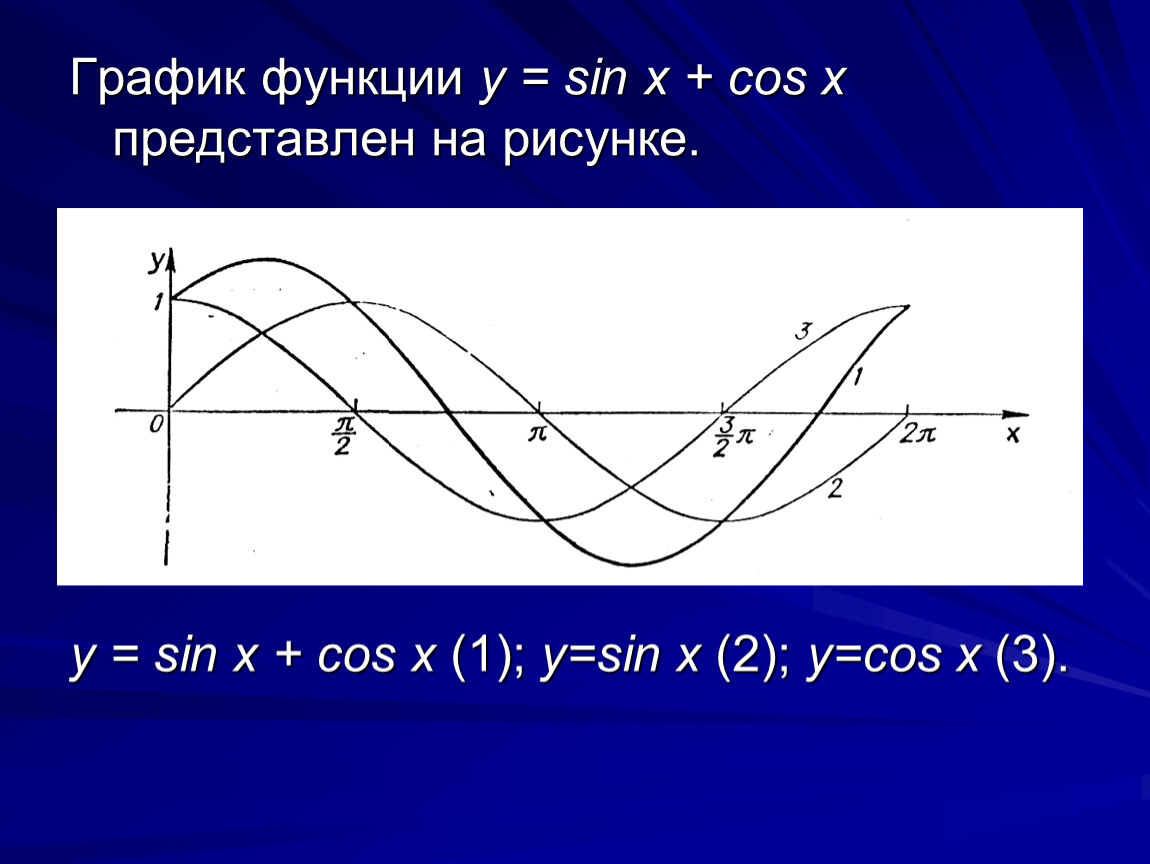
53Найти точное значениеsin(300 град. )
54Преобразовать из градусов в радианы135
55Преобразовать из градусов в радианы150
56Преобразовать из радианов в градусы(5pi)/6
57Преобразовать из радианов в градусы(5pi)/3
58Преобразовать из градусов в радианы89 град.
59Преобразовать из градусов в радианы60
60Найти точное значениеsin(135 град. )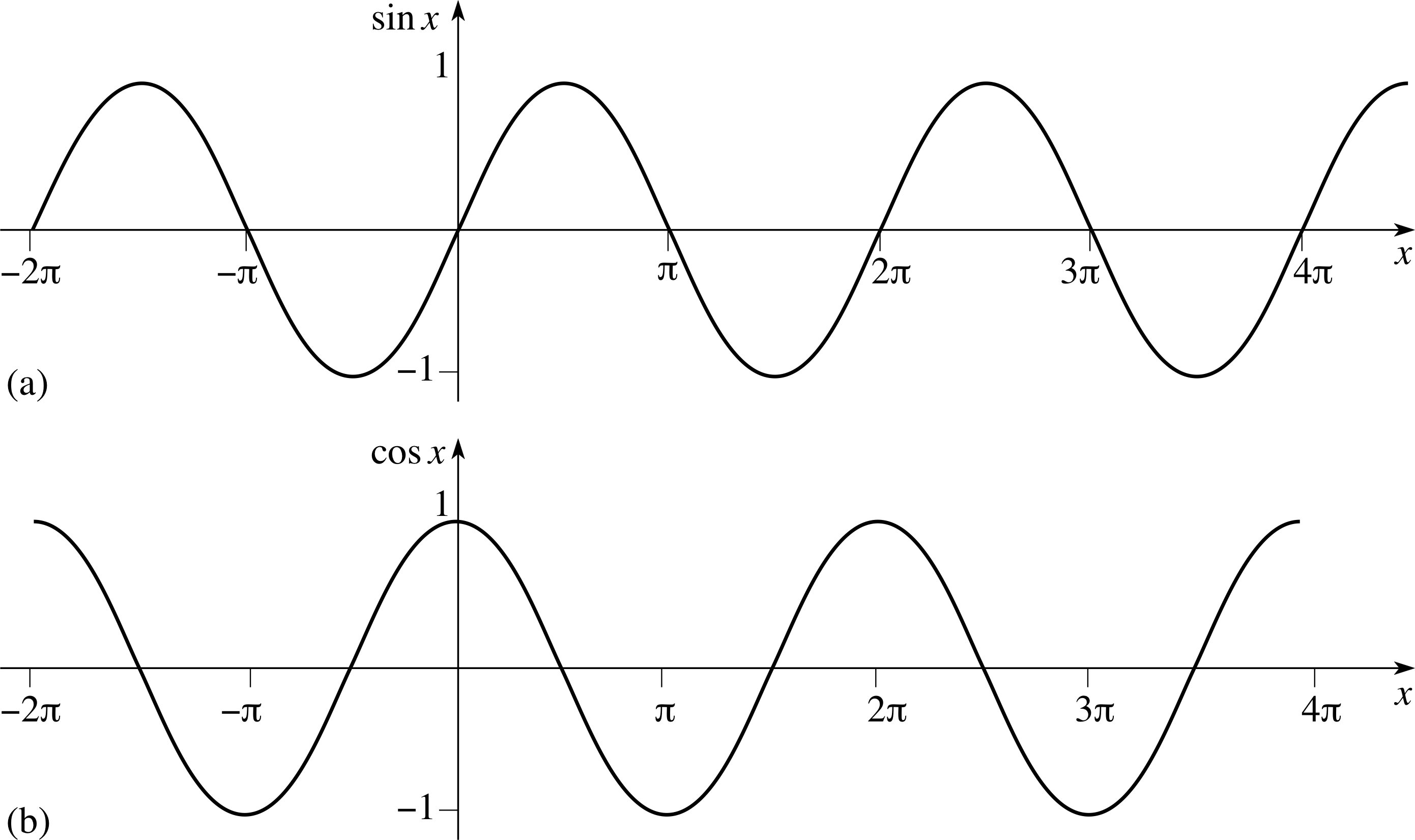
61Найти точное значениеsin(150)
62Найти точное значениеsin(240 град. )
63Найти точное значениеcot(45 град. )
64Преобразовать из радианов в градусы(5pi)/4
65Найти точное значениеsin(225)
66Найти точное значениеsin(240)
67Найти точное значениеcos(150 град. )
68Найти точное значениеtan(45)
69Вычислитьsin(30 град. )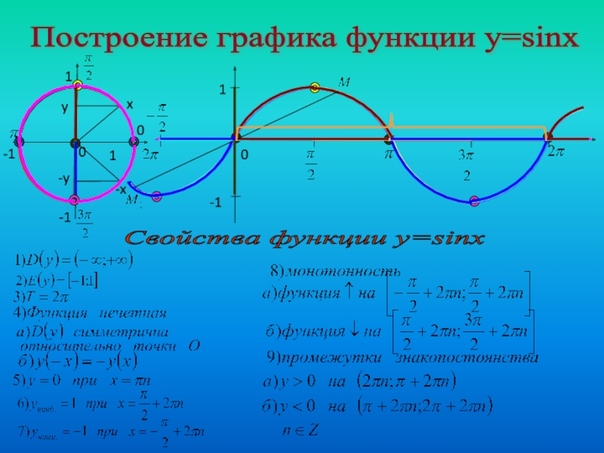
70Найти точное значениеsec(0)
71Найти точное значениеcos((5pi)/6)
72Найти точное значениеcsc(30)
73Найти точное значениеarcsin(( квадратный корень из 2)/2)
74Найти точное значениеtan((5pi)/3)
75Найти точное значениеtan(0)
76Вычислитьsin(60 град. )
77Найти точное значениеarctan(-( квадратный корень из 3)/3)
78Преобразовать из радианов в градусы(3pi)/4
79Найти точное значениеsin((7pi)/4)
80Найти точное значениеarcsin(-1/2)
81Найти точное значениеsin((4pi)/3)
82Найти точное значениеcsc(45)
83Упроститьarctan( квадратный корень из 3)
84Найти точное значениеsin(135)
85Найти точное значениеsin(105)
86Найти точное значениеsin(150 град. )
87
Найти точное значение		sin((2pi)/3)
88Найти точное значениеtan((2pi)/3)
89Преобразовать из радианов в градусыpi/4
90Найти точное значениеsin(pi/2)
91Найти точное значениеsec(45)
92Найти точное значениеcos((5pi)/4)
93Найти точное значениеcos((7pi)/6)
94Найти точное значениеarcsin(0)
95Найти точное значениеsin(120 град. )
96Найти точное значениеtan((7pi)/6)
97Найти точное значениеcos(270)
98Найти точное значениеsin((7pi)/6)
99Найти точное значениеarcsin(-( квадратный корень из 2)/2)
100Преобразовать из градусов в радианы 88 град.

ФУНКЦИИ y=sinx, y=cosx их свойства и графики


Для начала предлагаю вам посмотреть видео урок


А теперь ещё раз пробежимся по свойствам функцийy=sinx и 
y=cosx


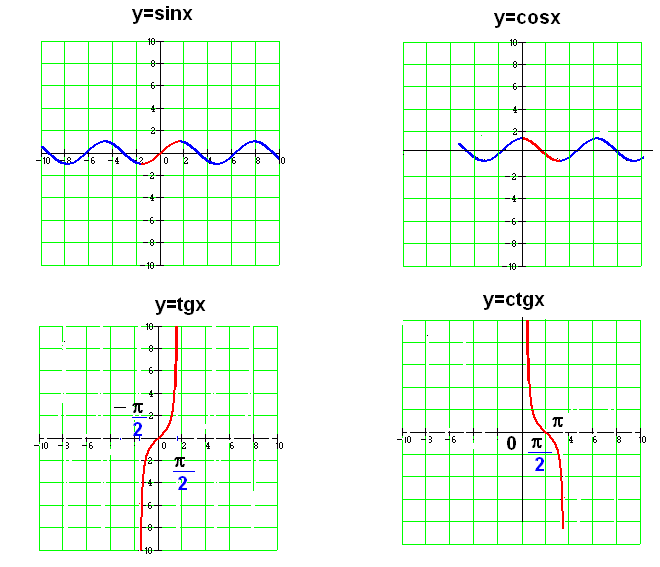
Функция y=cosx

Функция y=cosx определена на всей числовой прямой и множеством её значений является отрезок [−1;1]

Следовательно, график этой функции расположен в полосе между прямыми y=−1 и y=1

Так как функция y=cosx периодическая с периодом 2π, то достаточно построить её график на каком-нибудь промежутке длиной 2π, например на отрезке −π≤x≤π, тогда на промежутках, получаемых сдвигами выбранного отрезка на 2πn,n∈Z, график будет таким же.

Функция y=cosx является чётной. Поэтому её график симметричен относительно оси Oy.

Для построения графика на отрезке −π≤x≤π достаточно построить его для 0≤x≤π, а затем симметрично отразить его относительно оси Oy.

Найдём несколько точек, принадлежащих графику на этом отрезке 0≤x≤π cos0=1;cosπ6=3√2;cosπ4=2√2;cosπ3=12;cosπ2=0;cosπ=−1 

Итак, график функции y=cosx построен на всей числовой прямой.

Свойства функции y=cosx

1. Область определения — множество R всех действительных чисел

2. Множество значений — отрезок [−1;1]

3. Функция y=cosx периодическая с периодом 2π 

4. Функция y=cosx — чётная

5. Функция y=cosx принимает:

— значение, равное 0, при x=π2+πn,n∈Z; 

— наибольшее значение, равное 1, при x=2πn,n∈Z 

— наименьшее значение, равное −1, при  x=π+2πn,n∈Z  

— положительные значения на интервале (−π2;π2) и на интервалах, получаемых сдвигами этого интервала на 2πn,n∈Z

— отрицательные значения на интервале (π2;3π2) и на интервалах, получаемых сдвигами этого интервала на 2πn,n∈Z

6. Функция y=cosx

— возрастает на отрезке [π;2π] и на отрезках, получаемых сдвигами этого отрезка на 2πn,n∈Z

— убывает на отрезке [0;π] и на отрезках, получаемых сдвигами этого отрезка на 2πn,n∈Z


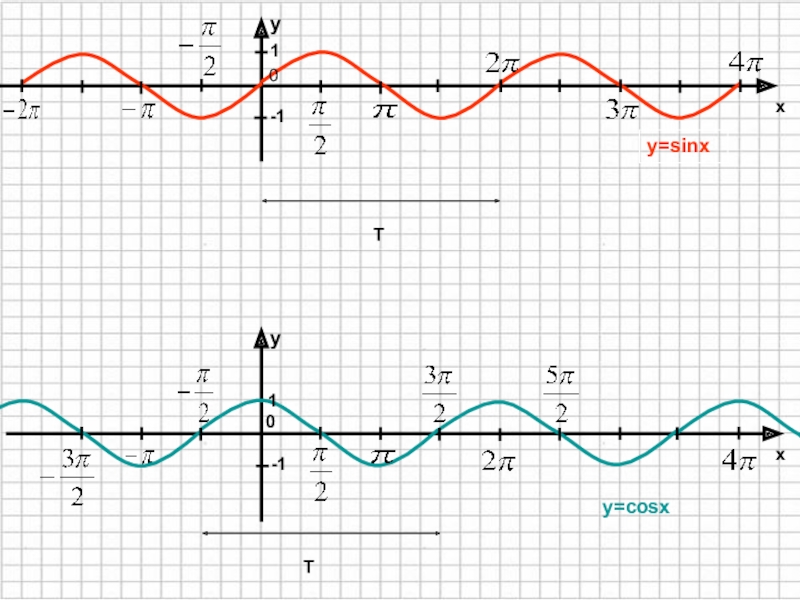
Функция y=sinx

y=sinx Функция 

y=sinx определена на всей числовой прямой, является нечётной и периодической с периодом 

2π.  

График этой функции можно построить таким же способом, как и график функции y=cosx, начиная с построения, например,  на отрезке [0;π]. 

Однако проще применить формулу sinx=cos(x−π2), которая показывает, что график функции y=sinx можно получить сдвигом графика функции  y=cosx вдоль оси абсцисс вправо на π2 

Свойства функции y=sinx

1. Область определения — множество R всех действительных чисел.


2. Множество значений — отрезок [−1;1]


3. Функция y=sinx периодическая с периодом T=2π 


4. Функция y=sinx- нечётная.


5. Функция y=sinx принимает:
— значение, равное 0, при  x=πn,n∈Z
— наибольшее значение, равное 1, при x=π2+2πn,n∈Z
— наименьшее значение, равное −1, при x=−π2+2πn,n∈Z
— положительные значения на интервале (0;π) и на интервалах, получаемых сдвигами этого интервала на 2πn,n∈Z

— отрицательные значения на интервале (π;2π) и на интервалах, получаемых сдвигами этого интервала на 2πn,n∈Z

6. Функция y=sinx

— возрастает на отрезке

 [−π2;π2] и на отрезках, получаемых сдвигами этого отрезка на 2πn,n∈Z
— убывает на отрезке

 [π2;3π2] и на отрезках, получаемых сдвигами этого отрезка на 2πn,n∈Z

И вновь хочу предложить вам игру, но в этот раз усложним её. 

Вам необходимо из всех предложенных свойств функций  выбрать только те, которые

соответствуют только синусу и косинусу произвольного угла

Готовы? ВПЕРЁД!!!

Мэтуэй | Популярные задачи

92
1 Найти точное значение грех(30)
2 Найти точное значение грех(45)
3 Найти точное значение грех(30 градусов)
4 Найти точное значение грех(60 градусов)
5 Найти точное значение загар (30 градусов)
6 Найти точное значение угловой синус(-1)
7 Найти точное значение грех(пи/6)
8 Найти точное значение cos(pi/4)
9 Найти точное значение грех(45 градусов)
10 Найти точное значение грех(пи/3)
11 Найти точное значение арктан(-1)
12 Найти точное значение cos(45 градусов)
13 Найти точное значение cos(30 градусов)
14 Найти точное значение желтовато-коричневый(60)
15 Найти точное значение csc(45 градусов)
16 Найти точное значение загар (60 градусов)
17 Найти точное значение сек(30 градусов)
18 Найти точное значение cos(60 градусов)
19 Найти точное значение cos(150)
20 Найти точное значение грех(60)
21 Найти точное значение cos(pi/2)
22 Найти точное значение загар (45 градусов)
23 Найти точное значение arctan(- квадратный корень из 3)
24 Найти точное значение csc(60 градусов)
25 Найти точное значение сек(45 градусов)
26 Найти точное значение csc(30 градусов)
27 Найти точное значение грех(0)
28 Найти точное значение грех(120)
29 Найти точное значение соз(90)
30 Преобразовать из радианов в градусы пи/3
31 Найти точное значение желтовато-коричневый(30)
32
35 Преобразовать из радианов в градусы пи/6
36 Найти точное значение детская кроватка(30 градусов)
37 Найти точное значение арккос(-1)
38 Найти точное значение арктан(0)
39 Найти точное значение детская кроватка(60 градусов)
40 Преобразование градусов в радианы 30
41 Преобразовать из радианов в градусы (2 шт. )/3
42 Найти точное значение sin((5pi)/3)
43 Найти точное значение sin((3pi)/4)
44 Найти точное значение тан(пи/2)
45 Найти точное значение грех(300)
46 Найти точное значение соз(30)
47 Найти точное значение соз(60)
48 Найти точное значение соз(0)
49 Найти точное значение соз(135)
50 Найти точное значение cos((5pi)/3)
51 Найти точное значение cos(210)
52 Найти точное значение сек(60 градусов)
53 Найти точное значение грех(300 градусов)
54 Преобразование градусов в радианы 135
55 Преобразование градусов в радианы 150
56 Преобразовать из радианов в градусы (5pi)/6
57 Преобразовать из радианов в градусы (5 дюймов)/3
58 Преобразование градусов в радианы 89 градусов
59 Преобразование градусов в радианы 60
60 Найти точное значение грех(135 градусов)
61 Найти точное значение грех(150)
62 Найти точное значение грех(240 градусов)
63 Найти точное значение детская кроватка(45 градусов)
64 Преобразовать из радианов в градусы (5 дюймов)/4
65 Найти точное значение грех(225)
66 Найти точное значение грех(240)
67 Найти точное значение cos(150 градусов)
68 Найти точное значение желтовато-коричневый(45)
69 Оценить грех(30 градусов)
70 Найти точное значение сек(0)
71 Найти точное значение cos((5pi)/6)
72 Найти точное значение КСК(30)
73 Найти точное значение arcsin(( квадратный корень из 2)/2)
74 Найти точное значение загар((5pi)/3)
75 Найти точное значение желтовато-коричневый(0)
76 Оценить грех(60 градусов)
77 Найти точное значение arctan(-( квадратный корень из 3)/3)
78 Преобразовать из радианов в градусы (3 пи)/4 
79 Найти точное значение sin((7pi)/4)
80 Найти точное значение угловой синус(-1/2)
81 Найти точное значение sin((4pi)/3)
82 Найти точное значение КСК(45)
83 Упростить арктан(квадратный корень из 3)
84 Найти точное значение грех(135)
85 Найти точное значение грех(105)
86 Найти точное значение грех(150 градусов)
87 Найти точное значение sin((2pi)/3)
88 Найти точное значение загар((2pi)/3)
89 Преобразовать из радианов в градусы пи/4
90 Найти точное значение грех(пи/2)
91 Найти точное значение сек(45)
92 Найти точное значение cos((5pi)/4)
93 Найти точное значение cos((7pi)/6)
94 Найти точное значение угловой синус(0)
95 Найти точное значение грех(120 градусов)
96 Найти точное значение желтовато-коричневый ((7pi)/6)
97 Найти точное значение соз(270)
98 Найти точное значение sin((7pi)/6)
99 Найти точное значение arcsin(-( квадратный корень из 2)/2)
100 Преобразование градусов в радианы 88 градусов

тригонометрия — график $\sin(x) + \sin(y)= \cos(x) + \cos(y)$

спросил

Изменено 2 года, 10 месяцев назад

Просмотрено 513 раз

$\begingroup$

Я играл с неявными графиками вида $f(x,y) = g(x,y)$ и заметил, что если построить на плоскости следующее уравнение: $\sin(x) + \ sin(y)= \cos(x) + \cos(y)$ получаем следующий график:

Мой вопрос: почему эта тригонометрическая функция дает нам эти квадраты, охватывающие всю плоскость?

  • тригонометрия
  • графические функции
  • неявные функции
$\endgroup$

1

$\begingroup$

Использование формул простафаэреза

$$2\sin\dfrac{x+y}2\cos\dfrac{x-y}2=\cos\dfrac{x+y}2\cos\dfrac{x-y}2$$

Если $\cos\dfrac{x-y}2=0\имплицитно\dfrac{x-y}2=(2n+1)\dfrac\pi2, x-y=(2n+1)\pi$

иначе $\sin\ dfrac {x + y} 2 = \ cos \ dfrac {x + y} 2 \ iff \ tan \ dfrac {x + y} 2 = 1 \ подразумевает \ dfrac {x + y} 2 = m \ pi + \ dfrac \ pi4 \iff x+y=\dfrac{(4m+1)\pi}2$

Итак, мы получаем непрерывные перпендикулярные и равноудаленные прямые линии.

В первом случае расстояние между двумя последовательными прямыми равно $$\dfrac{2(m+1)+1-(2m+1)}{\sqrt2}\cdot\pi$$

, а во втором , $$\dfrac{2\pi}{\sqrt2}$$

Итак, мы получаем бесконечное количество квадратов с каждой стороной $=\sqrt2\pi$

$\endgroup$

$\begingroup$

$$\sin(x)+\sin(y)=\cos(x)+\cos(y)\iff$$

$$\sin(x)-\cos(x)=\cos( y)-\sin(y)\iff$$

$$\sqrt{2}\sin(x-\frac{\pi}{4})=\sqrt{2}\sin(\frac{\pi {4}-y)\iff$$

$$x=-y+\frac{\pi}{2}+2k\pi$$ или $$x=y+\pi+2k\pi$$ таким образом, есть два вида линий: возрастающие линии с уравнением $$y=x+(2k+1)\pi$$ и убывающие $$y=-x+(\frac 12+2k)\pi$$

где $ k\in \Bbb Z.$

$\endgroup$

$\begingroup$

\begin{выравнивание*} \sin(x)-\cos(x)&=\cos(y)-\sin(y)\стрелка вправо \sin\left(x-\frac{\pi}4\right)=\sin\left(\ frac{\pi}4-y\right)\\ &\Стрелка вправо x-\frac{\pi}4=2n\pi+\left(\frac{\pi}4-y\right)\\ &=x+y=2n\pi+\frac{\pi}2 \конец{выравнивание*} Повторить для $x-\frac{\pi}4=n\pi-\left(\frac{\pi}4-y\right)$

Семейство прямых 🙂

$\endgroup$

$\begingroup$

$$\sin(x)-\cos(x)=\cos(y)-\sin(y)$$ $$(\sin(x)-\cos(x))/\sqrt 2=(\cos(y)-\sin(y))/\sqrt 2$$

$$ \sin(x-\pi /4) = \sin (\pi/4-y) $$

Поясним для двух главных функций обратных синусов

$$x- \pi/4= \pi/4-y \rightarrow x+y = \ пи/2$$ $$x- \pi/4= \pi-[\pi/4-y] \rightarrow y=x-\pi$$

На графике вокруг начала координат вы видите две прямые линии.

No related posts.

Добавить комментарий

Ваш адрес email не будет опубликован. Обязательные поля помечены *