Формулы по геометрии 8 класс: Формулы по геометрии

Определения, теоремы и формулы геометрия 8 класс

Определения

Многоугольник-геометрическая фигура, составленная из отрезков так, что смежные отрезки не лежат на одной прямой, а несмежные-не имеют общих точек.

Выпуклый многоугольник, если он лежит по одну сторону от каждой прямой, проходящей через  две его соседние вершины.

Параллелограмм-четырехугольник, у которого противоположные стороны попарно параллельны.

Трапеция-четырёхугольник, у которого две стороны параллельны, а две другие-не параллельны.

Основания трапеции-её параллельные стороны, две другие не параллельные-боковые стороны трапеции.

Равнобедренна трапеция, если её боковые стороны равны.

Прямоугольная трапеция, если один из её углов прямой.

Прямоугольник-параллелограмм, у которого все углы прямые.

Ромб-параллелограмм, у которого все стороны равны.

Квадрат-прямоугольник, у которого все стороны равны.

Точки А и А₁симметричны относительно прямой, если эта прямая проходит через середину отрезка АА₁ и перпендикулярна к нему.

Фигура симметрична относительно прямой, если для каждой точки фигуры симметричная ей точка относительно данной прямой также принадлежит этой фигуре(это осевая симметрия).

Ось симметрии-данная прямая, относительно которой происходит симметрия.

Точки А и А₁симметричны относительно точки О, если О середина отрезка АА₁.

Фигура симметрична относительно точки, если для каждой точки фигуры симметричная ей точка относительно точки О также принадлежит этой фигуре(это центральная симметрия).

Отношение отрезков АВ и СD-отношение их длин, т.е. .

Отрезки АВ и СD пропорциональны отрезкам А₁В₁ и С₁D₁, если .

Стороны треугольника

АВ и А₁В₁, ВС и В₁С₁, СА и С₁А₁сходственны, если .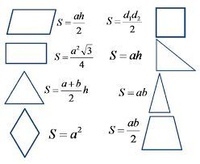

Два треугольника подобны, если их углы соответственно равны и стороны одного треугольника пропорциональны сходственным сторонам другого

, 

где k- коэффициент подобия.

Средняя линия треугольника-отрезок, соединяющий середины двух сторон треугольника.

Синус острого угла прямоугольного треугольника- отношение противолежащего катета к гипотенузе.

Косинус острого угла прямоугольного треугольника- отношение прилежащего катета к гипотенузе.

Тангенс острого угла прямоугольного треугольника – отношение противолежащего катета к прилежащему.

Тангенс острого угла прямоугольного треугольника – отношение синуса к косинусу этого угла.

Касательная к окружности-прямая, имеющая с окружностью только одну общую точку-точку касания прямой и окружности.

Полуокружность-дуга, если отрезок, соединяющий её концы, является диаметром окружности.

Центральный угол-угол с вершиной в центре окружности.

Серединный перпендикуляр к отрезку-прямая, проходящая через середину отрезка и перпендикулярная к нему.

Окружность, вписанная в многоугольник, если все стороны многоугольника касаются окружности. А многоугольник, описанный  около этой окружности.

Окружность, описанная около многоугольника, если все вершины многоугольника лежат на окружности. А многоугольник, вписанный в окружность.

Вектор(направленный отрезок)-отрезок, для которого указано, какой его конец является началом, а какой-концом.

Нулевой вектор

, если начало совпадает с его концом.

Длина или модуль вектора — длина отрезка АВ.

Векторы коллинеарные , если они лежат либо на одной прямой, либо на параллельных прямых. Нулевой вектор коллинеарен любому вектору.

Векторы сонаправленные , если они направлены в одну сторону.

Векторы противоположно направленные , если они направлены в разные стороны.

Векторы равны, если они сонаправлены и их длины равны.

Сумма двух векторов  (правило треугольника)-вектор с началом в начале первого вектора и концом в конце второго вектора.

Сумма n— векторов (правило многоугольника), если А₁,А₂,…,А_n-произвольные точки плоскости, то , где n_количество векторов.

Разность двух векторов  и — вектор , равный сумме векторов  и .

Произведение вектора  на число k-вектор , длина которого , причем и при  и при .

Средняя линия трапеции-отрезок, соединяющий середины её боковых сторон или середины её оснований (вторая средняя линия трапеции).

Правила и теоремы

5.1. Сумма углов выпуклого n-угольника равна , где n-количество сторон многоугольника.

5.2. Сумма углов выпуклого четырехугольника равна 360⁰.

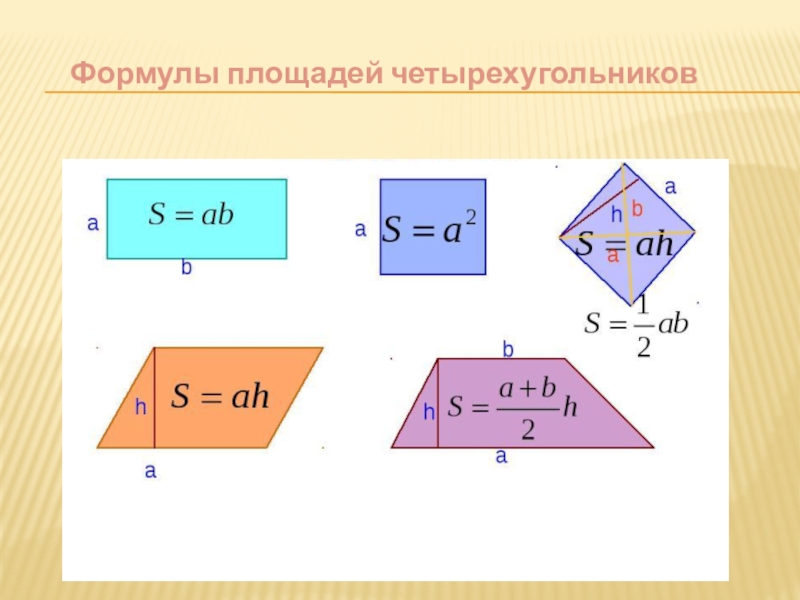
5.3. Свойства параллелограмма:

1⁰. В параллелограмме противоположные стороны равны и противоположные углы равны.

2⁰. Диагонали параллелограмма точкой пересечения делятся пополам.

5.4. Признаки параллелограмма:

1⁰. Если в четырехугольнике две стороны равны и параллельны, то этот четырёхугольник параллелограмм.

2⁰. Если в четырехугольнике противоположные стороны попарно равны, то этот четырёхугольник параллелограмм.

3⁰. Если в четырехугольнике диагонали пересекаются и точкой пересечения делятся пополам, то этот четырёхугольник параллелограмм.

5.5. Теорема Фалеса. Если на одной из двух прямых отложить последовательно несколько равных отрезков и через их концы провести параллельные прямые, пересекающие вторую прямую, то они отсекут на второй прямой равные между собой отрезки.

5.6. Свойство прямоугольника:

1⁰. Диагонали прямоугольника равны.

5.7. Признак  прямоугольника:

1⁰. Если в параллелограмме диагонали равны, значит этот параллелограмм-прямоугольник.

5.8. Свойство ромба:

1⁰. Диагонали ромба взаимно перпендикулярны и делят его углы пополам.

5.9. Свойства квадрата:

1⁰. Все углы квадрата прямые.

2⁰. Диагонали квадрата равны, взаимно перпендикулярны, точкой пересечения делятся пополам и делят углы квадрата пополам.

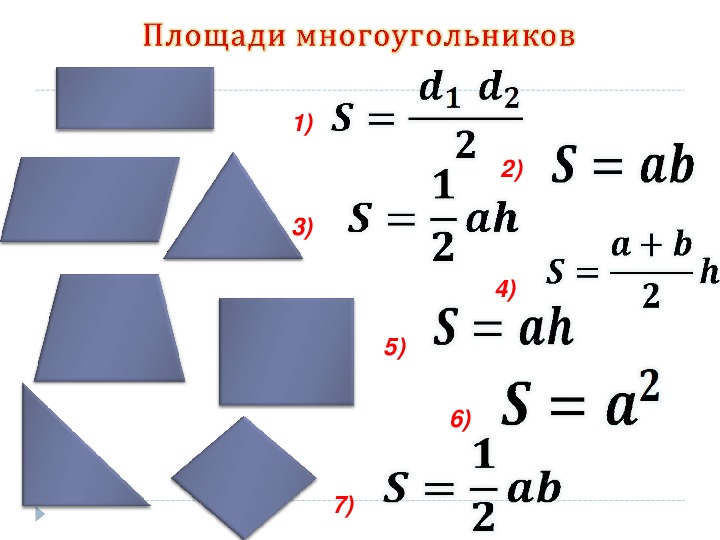
6.1. Свойства суммы многоугольников:

1⁰. Равные многоугольники имеют равные площади.

2⁰. Если многоугольник составлен из нескольких многоугольников, то его площадь равна сумме площадей этих многоугольников.

3⁰. Площадь квадрата равна квадрату его стороны.

6.2. Теорема (о площади прямоугольника). Площадь прямоугольника равна произведению его смежных сторон.

6.3. Теорема (о площади параллелограмма). Площадь параллелограмма равна произведению его основания на высоту.

6.4. Теорема (о площади треугольника).

Площадь треугольника равна половине произведения его основания на высоту.

Следствия из теоремы:

1.     Площадь прямоугольного треугольника равна половине произведения его катетов.

2.     Если высоты двух треугольников равны, то их площади относятся как основания.

6.5. Теорема (о площади двух треугольников). Если угол одного треугольника равен углу другого треугольника, то площади этих треугольников относятся как произведения сторон, заключающих равные углы.

6.6. Теорема (о площади трапеции). Площадь трапеции равна произведению полу суммы её оснований на высоту.

6.7. Теорема Пифагора. В прямоугольном треугольнике квадрат гипотенузы равен сумме квадратов катетов.

6.8.

Обратная теорема Пифагора. Если квадрат одной стороны треугольника равен сумме квадратов двух других сторон, то треугольник прямоугольный.

6.9. Свойства биссектрис параллелограмма:

1⁰. Биссектриса угла параллелограмма отсекает от него равнобедренный треугольник.

2⁰. Биссектрисы смежных углов параллелограмма пересекаются под прямым углом.

3⁰. Биссектрисы противоположных углов, равны и параллельны.

6.10. Свойства биссектрис трапеции:

1⁰. Биссектриса отсекается от основания (или его продолжения на прямой за пределами самой фигуры) отрезок такой же длины, что и боковая сторона. .

2⁰. Биссектрисы углов при боковой стороне трапеции пересекаются под прямым углом.

3⁰. Точка пересечения биссектрис трапеции, прилежащих к боковой стороне, лежит на средней линии трапеции.

4⁰. Точка пересечения биссектрис тупых углов при основании трапеции принадлежит другому основанию.

6.11. Свойство второй средней линии  трапеции: Пусть средняя КN-вторая средняя линия трапеции с основаниями ВС и АD, проходящая через точку пересечения диагоналей трапеции М. Тогда .

7.1. Теорема (об отношение площадей подобных треугольников).Отношение площадей двух подобных треугольников равно квадрату коэффициента подобия.

7.2. Биссектриса треугольника делит противоположную сторону на отрезки, пропорциональные прилежащим сторонам треугольника.

7.3. Признаки подобия треугольников:

Теорема 1. Если два угла одного треугольника соответственно равны двум углам другого, то эти треугольники подобны.

Теорема 2. Если две стороны одного треугольника пропорциональны двум сторонам другого треугольника и углы, заключенные между этими сторонами, равны, то эти треугольники подобны.

Теорема 3. Если три стороны одного треугольника пропорциональны трём сторонам другого, то эти треугольники подобны.

7.4. Теорема (о средней линии треугольника). Средняя линия треугольника параллельна одной из его сторон и равна половине этой стороны.

7. 5. Свойство медианы треугольника:

1⁰. Медианы треугольника пересекаются в одной точке, которая делит каждую медиану в отношение 2:1, считая от вершины.

7.6. Высота прямоугольного треугольника, проведенная из вершины прямого угла, делит треугольник на два подобных прямоугольных треугольника, каждый из которых подобен данному треугольнику.

7.7. Если острый угол одного прямоугольного треугольника равен острому углу другого прямоугольного треугольника, то синусы, косинусы и тангенсы этих углов равны.

8.1. Если расстояние от центра окружности до прямой меньше радиуса окружности (d<r), то прямая и окружность имеют две общие точки.

8.2. Если расстояние от центра окружности до прямой равно радиусу окружности (d=r), то прямая и окружность имеют только одну общую точку.

8.3. Если расстояние от центра окружности до прямой больше радиуса окружности (d>r), то прямая и окружность не имеют общих точек.

8.4. Теорема (о касательной и радиусе). Касательная к окружности перпендикулярна к радиусу, проведенному в точку касания.

8.5. Отрезки касательных к окружности, проведенные из одной точки. Равны и составляют равные углы с прямой, проходящей через эту точку и центр окружности.

8.6. Теорема (признак касательной). Если прямая проходит через конец радиуса, лежащий на окружности, и перпендикулярна к этому радиусу, то она является касательной.

8.7. Теорема (о касательной и секущей). Если из точки М, лежащей вне окружности, проведены касательная МС и секущая МВ, то квадрат длины касательной равен произведению секущей на ее внешнюю часть

, где А и В-точки пересечения с окружностью секущей соответственно, считая от М.

8.8. Если дуга АВ окружности с центром О меньше полуокружности или является полуокружностью, то её градусная мера считается равной градусной мере центрального угла АОВ. Если же дуга АВ больше полуокружности, то её градусная мера считается равной .

8.9. Сумма градусных мер двух дуг окружности с общими концами равна 360⁰.

8.10. Теорема (о вписанном угле). Вписанный угол измеряется половиной дуги, на которую он опирается.

Следствия из теоремы:

1.     Вписанные углы, опирающиеся на одну и ту же дугу, равны.

2.     Вписанный угол, опирающийся на полуокружность, -прямой.

8.11. Теорема (о произведении отрезков пересекающихся хорд). Если две хорды окружности пересекаются, то произведение отрезков одной хорды равно произведению отрезков другой хорды.

8.12. Четыре замечательные точки треугольника: точка пересечения медиан, точка пересечения биссектрис, точка пересечения серединных перпендикуляров к сторонам и точка пересечения высот (или их продолжения).

Теорема (о биссектрисе угла). Каждая точка биссектрисы неразвернутого угла равноудалена от его сторон. Обратно: каждая точка, лежащая внутри угла и равноудаленная от сторон угла, лежит на его биссектрисе.

Следствие из теоремы: Биссектрисы треугольника пересекаются в одной точке.

Теорема (о серединном перпендикуляре к отрезку). Каждая точка серединного перпендикуляра  к отрезку равноудалена от концов этого отрезка. Обратно: каждая точка, равноудаленная от концов отрезка, лежит на серединном перпендикуляре к нему.

Следствие из теоремы: Серединные перпендикуляры к сторонам треугольника пересекаются в одной точке.

Теорема (о пересечении высот треугольника). Высоты треугольника (или их продолжения) пересекаются в одной точке.

8.13. Теорема (об окружности, вписанной в треугольник). В любой треугольник можно вписать только одну окружность.

8.14. В любом описанном четырехугольнике суммы противоположных сторон равны.

8.15. Теорема (об окружности, описанной около треугольника). Около любого треугольника можно описать только одну окружность.

8.16. В любом вписанном четырехугольнике сумма противоположных углов равна 180⁰.

8.17. Если сумма противоположных углов четырёхугольника равна 180⁰, то около него можно описать окружность.

8.18. Свойства равностороннего треугольника:

1⁰. Высота, медиана и биссектриса, проведённые к каждой из сторон равностороннего треугольника, совпадают.

2⁰. Точка пересечения высот, биссектрис и медиан называется центром правильного треугольника и является центром вписанной и описанной окружностей (то есть в равностороннем треугольнике центры вписанной и описанной окружностей совпадают).

3⁰. Расстояние от точки пересечения высот, биссектрис и медиан до любой вершины    треугольника равно радиусу описанной окружности.

4⁰. Все высоты равностороннего треугольника равны.

9.1. От любой точки можно отложить только один вектор, равный данному.

9.2. Теорема (правило параллелограмма). Для любых векторов и справедливы равенства:

1.  (переместительный закон)

2.  (сочетательный закон).

9.3. Теорема (о разности векторов). Для любых векторов  и справедливо равенство .

9.4. Произведение любого вектора на 0-это нулевой вектор.

9.5. Векторы  и коллинеарны при любых  и .

9.6. Свойства произведения вектора на число:

1⁰.  (сочетательный закон)

2⁰.  (первый распределительный закон)

3⁰.  (второй распределительный закон)

9.7. Теорема (о средней линии трапеции). Средняя линия трапеции параллельна основаниям и равна их полу сумме.

9.8. Сумма противолежащих углов трапеции равна 180⁰.

Формулы

Основное тригонометрическое тождество

Таблица углов

Радиан.	0
	0				1			0		-1	0
	1				0			-1		0	1
	0		1		—		-1	0		—	0
градусы	00	300	450	600	900	1200	1350	1800	2400	2700	3600

*знать таблицу наизусть для 8 класса (зелёный), для 9 класса (зелёный и жёлтый).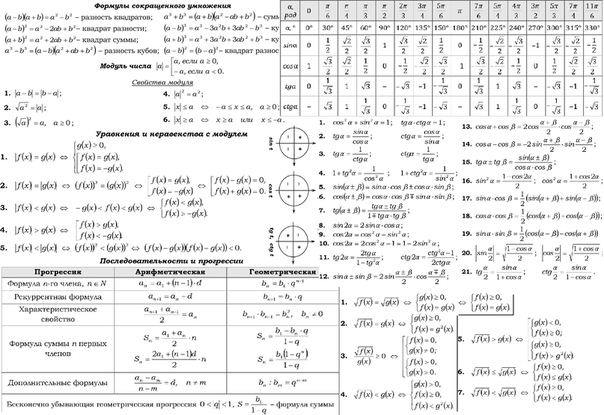

все классы, все формулы, все темы

Дорогие школьники, студенты! На сайте вы найдете темы по математике за 5-11 класс и лекции по высшей математике. Мы не только изучаем теоретический материал, но и решаем задачи — подробно их разбираем. Уделяем внимание и разбору интересных задач ЕГЭ по математике. У нас вы найдете все формулы по математике за 5-11 класс, научитесь рассуждать и решать уравнения, неравенства, системы уравнений и неравенств, анализировать функции, брать производные и интегралы. Особое внимание мы уделили важному разделу математики — «Геометрии». Решение пространственных задач, рассуждения, схемы и многое другое ждет вас в этом разделе.
Тригонометрия — еще один важный раздел в математике, он связывает воедино и геометрию и алгебру, помогает осмыслить пространство. Подробно разобраны в этом разделе тригонометрические уравнения и неравенства. Приведены все необходимые формулы.

7 класс. Алгебра.

Решить неравенство t^2≤5t

06. 7k.26 января 2023

Больше или меньше? А если «меньше или равно»? Как решить неравенство? В этом уроке мы решим неравенство

5 класс. Математика.

Таблица умножения на 3

13.7k.23 января 2023

Сколько будет трижды три? Девять. А откуда мы это знаем? Из таблицы умножения на 3. О ней и пойдет речь

6 класс. Математика.

Решите примеры: 8 5/6+4 3/8 и 8 5/6-4 3/8

12.7k.18 января 2023

Два примера на проверку умений складывать и вычитать смешанные числа, то есть такие числа, которые содержат

5 класс. Математика.

Выполните действия: а) 3 2 /3+2 /3 б) 4 1/6 — 1 1/ 5 в) 12×5/18 г) 6: 1 1/5

01.2k.17 января 2023

Решать примеры с дробями можно легко и просто, если знать всего несколько правил — определение общего

5 класс. Математика.

Таблица умножения на 3

13.7k.

Сколько будет трижды три? Девять. А откуда мы это знаем?

5 класс. Математика.

Выполните действия: а) 3 2 /3+2 /3 б) 4 1/6 — 1 1/ 5 в) 12×5/18 г) 6: 1 1/5

01.2k.

Решать примеры с дробями можно легко и просто, если

5 класс. Математика.

Сколько всего двузначных чисел

12.5k.

Как записать, что у Маши двадцать пять карандашей

5 класс. Математика.

Сколько трёхзначных чисел

13.7k.

Подсчитаем сколько всего трехзначных чисел.

5 класс. Математика.

Таблица умножения на 2

3858

Как умножать на два? Что это вообще означает?

5 класс. Математика.

5 5 5 5 5 расставить знаки и скобки чтобы получилось 6, 7, 8, 9, 10

1937

Логическая задача. Даны числа 5 5 5 5 5, расставить

6 класс. 2

01k.

Вычислите. 1) 2) 3) 4) Вычисление: 1) В первом примере

7 класс. Алгебра.

Абсолютная погрешность

1607

Не всегда получается точно измерить длину отрезка или

7 класс. Алгебра.

Формулы сокращенного умножения

01.4k.

Чтобы быстро умножить одно число на другое, придумали

7 класс. Алгебра.

Разность квадратов

12.7k.

Как быстро умножать алгебраические выражения?

7 класс. Алгебра.

Линейная функция y=kx+b и ее график

02.9k.

Если функция задана формулой , где и  — некоторые числа

8 класс. Алгебра.

Дискриминант — определение, свойства, геометрический смысл

87k.

Важная характеристика квадратных уравнений — их дискриминант.

8 класс. Алгебра.

Теорема Виета

23. 2

11.9k.2 декабря 2022

Правильное решение получить иногда совсем не просто, хотя под корнем кажется все прекрасно извлекается, но.

9 класс. Алгебра.

9.3.3. Определение арифметической прогрессии. Примеры

02.3k.22 декабря 2013

Числовую последовательность, каждый член которой, начиная со второго, равен предыдущему, сложенному с

9 класс. Алгебра.

9.3.1. Числовая последовательность

022.3k.6 декабря 2013

Функция an=f (n) натурального аргумента n (n=1; 2; 3; 4;…) называется числовой последовательностью. Числа a1;

9 класс. Алгебра.

9.3.2. Арифметическая прогрессия. Теория

06.8k.25 сентября 2012

Числовую последовательность, каждый член которой, начиная со второго, равен предыдущему, сложенному с

10 класс. Алгебра.

Формулы приведения

116.9k.

Формулы приведения относятся к тригонометрической функции

10 класс. Алгебра.

10.3.0. Вычисление производных

015.1k.

На этом занятии мы будем учиться применять формулы

10 класс. Алгебра.

10.2.6. Решение тригонометрических неравенств. Часть 6

03.1k.

На предыдущих занятиях мы решали тригонометрические

11 класс. Алгебра.

Показательные уравнения и методы решения показательных уравнений

56.3k.

В 10-11 классе в курсе алгебры изучаются показательные

11 класс. Алгебра.

Площадь криволинейной трапеции, ограниченной линиями

02.8k.

Как найти площадь криволинейной трапеции ограниченной прямыми?

11 класс. Алгебра.

11.1.9.2. Площадь криволинейной трапеции, прилегающей к оси Оу

03k.

Если криволинейная трапеция прилегает к оси Оу (рис.

11 класс. Алгебра.

11.1.9.2. Площадь криволинейной трапеции. Примеры

042.5k.

Площадь криволинейной трапеции, ограниченной сверху

Геометрия

Площадь трапеции

44k.

Формулы для вычисления площади всех видов трапеции

Геометрия

Площадь прямоугольника

214.9k.

Площадь прямоугольника очень часто требуется найти

Геометрия

Как рассчитать площадь круга — все формулы

117k.

Площадь круга часто требуется рассчитать в различных

5 класс. Тесты.

Тренажер таблицы умножения на 2 по возрастанию

0431

Порядок умножения на 2, в котором мы все начинаем учить

5 класс. Тесты.

Тренажер таблицы умножения на 2 (в разброс)

1298

Потренируйтесь в знании таблицы умножения на 2 на нашем

5 класс.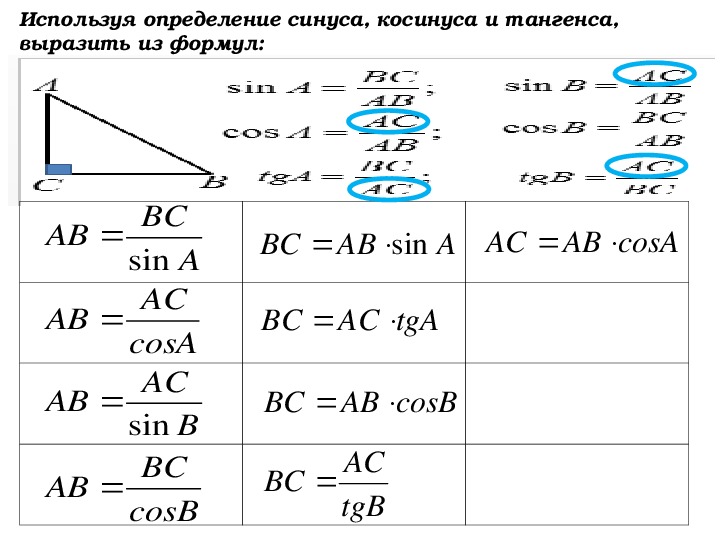 Тесты.

Тренажер таблицы умножения на 2 с окошками для введения ответа

0330

Это интерактивный онлайн тренажер таблицы умножения на 2.

6 класс. Тесты.

Тест 6.9.2.1. Линейная функция и ее график

02.3k.

Математика. 6 класс.              Тест 9.

Геометрические формулы для 8 класса

• Формула

В математике область, изучающая формы, размеры, свойства пространства и взаимное расположение фигур, называется геометрией. В то время люди использовали геометрические формулы для вычисления длины, площади и объема. Расширенная геометрия делится на две категории или группы, т. е. планиметрию и объемную геометрию. Различные формы, такие как треугольник, круг, квадрат, прямоугольник и т. д., являются частью планиметрии. С другой стороны, расчеты периметра, площади, длины и объема различных геометрических фигур и форм относятся к объемной геометрии. Что касается студентов, изучающих геометрию, так это геометрическая формула. Геометрия — это вещь, которую мы используем каждый день в жизни, поэтому ее формулы составляют ее основу, и их очень важно знать.

Список геометрических формул для 8-го класса

Чтобы легко решать геометрические задачи, нам нужно знать формулы, поэтому вот они, формулы важных геометрических фигур приведены ниже.

Квадрат 

                                  [Изображение будет загружено в ближайшее время]

Периметр квадрата: 4 x сторона 010

Прямоугольник 

                                          [Изображение будет загружено в ближайшее время]

Периметр прямоугольника: 2 x (длина + ширина) квадратная единица   

Площадь прямоугольника: длина x ширина 

Круг 

                                     [Изображение будет загружено в ближайшее время]

Диаметр круга: 2 × r

Окружность круга: 2 × π × r 

Площадь круга: π × r2

Треугольник

                                      [Изображение будет скоро загружено]

Мы можем найти площадь и периметр треугольника, используя формула:

Периметр треугольника: сторона a + сторона b + сторона c 

Площадь треугольника: ½ основания треугольника x высота треугольника.

Куб

                             [Изображение будет загружено в ближайшее время]

Общая площадь поверхности куба: 6a2 в квадратной единице

Объем куба: a3 кубической единицы  900 10

Прямоугольник

Периметр куба: 4 x (длина + ширина + высота)

Общая площадь прямоугольного параллелепипеда: 2 x [(длина x ширина) + (ширина x высота) + (длина x высота)]

Объем прямоугольного параллелепипеда: длина x ширина x высота

Прямая призма

Общая площадь поверхности прямоугольной призмы: периметр основания x высота + 2 x площадь основания

Объем прямой призмы : площадь основания x высота   

Правый круглый цилиндр

                                       [Изображение будет загружено в ближайшее время]

Общая площадь правого кругового цилиндра: 2 π r (h + r) квадратных единиц

Объем правого Круглый цилиндр: πr2h

Правая пирамида

                                        [Изображение будет загружено в ближайшее время]

Общая площадь поверхности пирамиды: площадь основания + ½ (количество сторон основания x наклон высота x длина основания)  

Объем пирамиды: ⅓ x площадь основания x высота

Прямой круглый конус

                                                   [Изображение будет загружено в ближайшее время]

м) р

Объем прямого кругового конуса: 1/3 πr2h

Сфера

                                    [Изображение будет загружено в ближайшее время]

Диаметр сферы: 2 r

Площадь поверхности сферы: 4 πr2

Объем сферы: (4 ⁄ 3) πr3

Решенные примеры

Пример 1) Если стороны многоугольника равны 5 см, 4 см и 2 см, найдите периметр.

Решение 1) a = 5 см, b = 4 см и c = 2 см 

Периметр = a + b + c 

                 = 5 + 4 + 2 

                                   = 11 см 

Пример 2) Какой будет длина окружности если его радиус равен 7 см?

Решение 2) Используя формулу 2πr

Подставив ее 2 x (22/7) x 7

22 x 7

154 см2

Дата последнего обновления: 02 мая 2023

•

Всего просмотров: 293.1k

•

Просмотров сегодня: 2.58k

Недавно обновленные страницы

Диагональ квадратной формулы — значение, вывод и примеры решения

Формула дисперсионного анализа — определение, полная форма, статистика и примеры

Формула среднего значения — методы отклонения, примеры решения и часто задаваемые вопросы

Формула процентного дохода — APY, атомная экономика и решение Пример

Формула ряда – определение, примеры решений и часто задаваемые вопросы

Формула площади поверхности квадратной пирамиды – определение и вопросы

Диагональ формулы квадрата – значение, вывод и примеры решения

Формула дисперсионного анализа — определение, полная форма, статистика и примеры

Формула среднего — методы отклонения, примеры решений и часто задаваемые вопросы

Формула процентного выхода — APY, атомная экономика и пример решения

Формула ряда — определение, примеры решения и часто задаваемые вопросы

Формула площади поверхности квадратной пирамиды – определение и вопросы

Актуальные темы

Формулы геометрии – все формулы геометрии

Формулы геометрии используются для нахождения размеров, периметра, площади, площади поверхности, объема и т.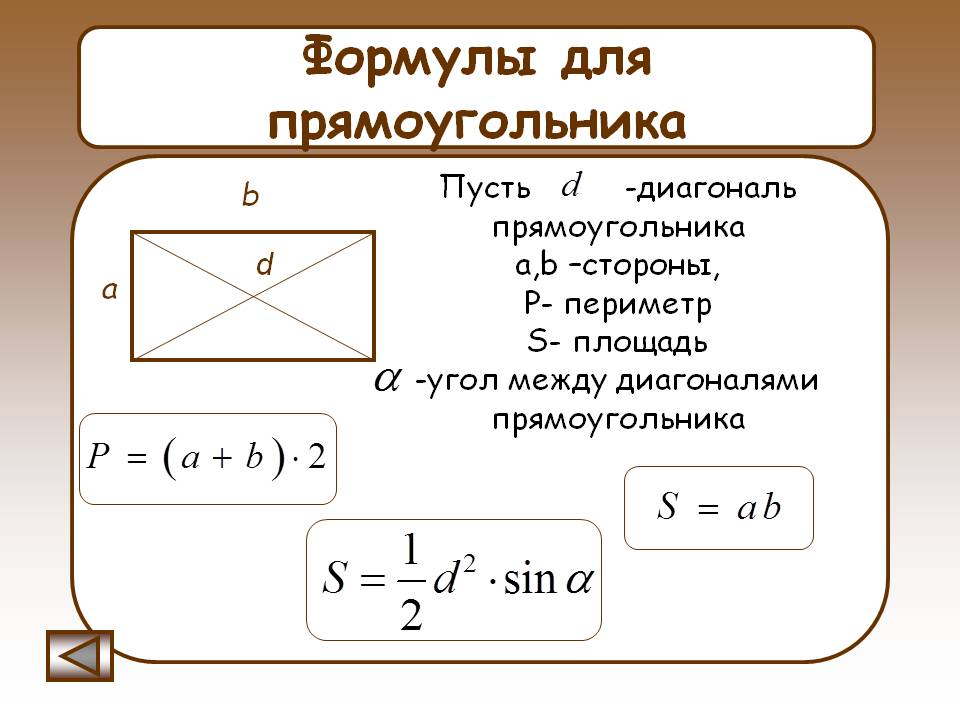 д. геометрических фигур. Геометрия — это часть математики, которая имеет дело с отношениями точек, линий, углов, поверхностей, измерением тел и свойствами. Существует два типа геометрии: 2D или плоскостная геометрия и 3D или объемная геометрия.

2D-фигуры — это плоские фигуры, которые имеют только два измерения: длину и ширину, такие как квадраты, круги, треугольники и т. д. 3D-объекты — это твердые объекты, которые имеют три измерения, длину, ширину и высоту или глубину, как в кубе, параллелепипеде, сфере, цилиндре, конусе. Давайте учиться все геометрические формулы вместе с несколькими решенными примерами в следующих разделах.

Что такое геометрические формулы?

Формулы, используемые для нахождения размеров, периметра, площади, площади поверхности, объема и т. д. двумерных и трехмерных геометрических фигур, известны как формулы геометрии. 2D-формы состоят из плоских фигур, таких как квадраты, круги, треугольники и т. д., а куб, прямоугольный параллелепипед, сфера, цилиндр, конус и т.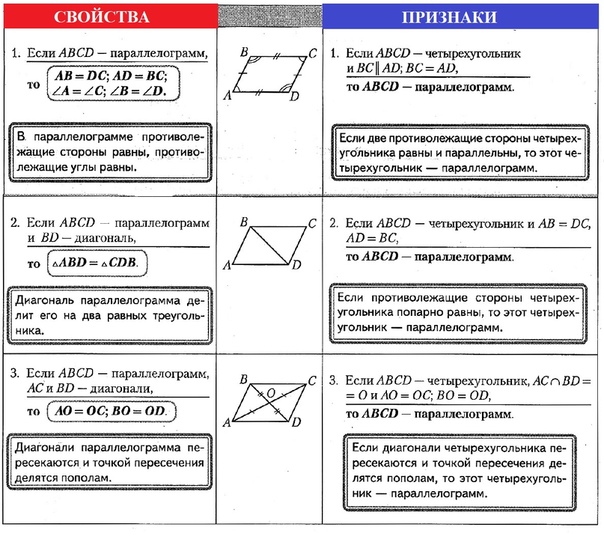 д. являются некоторыми примерами трехмерных форм. Основные формулы геометрии даны следующим образом:

Формулы базовой геометрии

Давайте посмотрим список всех формул базовой геометрии здесь.

Формулы 2D-геометрии

Вот список различных формул 2D-геометрии в соответствии с геометрической формой. Он также включает несколько формул, в которых используется математическая константа π(pi).

• Периметр квадрата = 4 (сторона)
• Периметр прямоугольника = 2 (длина + ширина)
• Площадь квадрата = сторона ²
• Площадь прямоугольника = длина × ширина
• Площадь треугольника = ½ × основание × высота
• Площадь трапеции = ½ × (основание ₁ + основание ₂ ) × высота
• Площадь круга = A = π×r ²
• Длина окружности = 2πr

Формулы трехмерной геометрии

Ниже приведены основные формулы трехмерной геометрии. Следует отметить, что в следующих формулах использовалась математическая константа π(pi)

• Площадь криволинейной поверхности цилиндра = 2πrh
• Общая площадь поверхности цилиндра = 2πr(r + h)
• Объем цилиндра = V = πr ² ч
• Площадь криволинейной поверхности конуса = πrl
• Общая площадь поверхности конуса = πr(r+l) = πr[r+√(h ² +r ² )]
• Объем конуса = V = ⅓×πr ² ч
• Площадь поверхности сферы = S = 4πr ²
• Объем сферы = V = 4/3×πr ³

где

• r = радиус;
• ч = высота. и,
• l = Наклонная высота

В таблице формул представлены формулы 2D-геометрии и формулы 3D-геометрии.

ФОРМЫ	ФОРМУЛЫ
1. Прямоугольный треугольник	Теорема Пифагора: основание 2 + высота 2 = гипотенуза 2 Площадь = ½ × основание × высота Периметр = основание + высота + гипотенуза
2. Треугольник	Периметр, P = a + b + c Где a, b и c — стороны треугольника. Площадь, A = ½ основания × высота
3. Прямоугольник	Периметр = 2(д + ш) Площадь = lw Диагональ, d = √(l 2 + w 2 ) Где, l = длина прямоугольника w = ширина прямоугольника
4.Параллелограмм	Периметр, P = 2(a + b) Где а и b стороны параллелограмма Площадь параллелограмма, A = основание × высота Высота, h = площадь/основание Основание, b = площадь/высота
5. Трапеция	Площадь, A = ½(a + b)h Где, а и b — параллельные стороны h = расстояние между двумя параллельными сторонами
6. Круг	Окружность = 2πr Площадь = πr 2 Диаметр = 2r Где, r = радиус окружности
7. Квадрат	Периметр, P = 4a Площадь, А = а 2 Диагональ, d = a√2 Сторона, а = √A Где, а = сторона квадрата
8. Дуга	Длина дуги, L = rθ Здесь θ — центральный угол в радианах, r = радиус
9. Куб	Площадь, А = 6а 2 Объем, В = а 3 Край, a = объем ⅓ Пространственная диагональ = a√3 Где, а = сторона куба
10. Прямоугольный	Площадь поверхности, A = 2 (lb + bh + hl) Объем, В = фунты-час Пространственная диагональ, d = √( l 2 + b 2 +h 2 ) Где, l= длина b= ширина h= высота
11. Цилиндр	Общая площадь поверхности, A = 2πrh + 2πr 2 Площадь изогнутой поверхности, A c = 2πrh Объем, В = πr 2 ч Базовая зона, A b = πr 2 Радиус, r = √(В/πh) Где, r= радиус цилиндра h= высота цилиндра
12. Конус	Общая площадь поверхности, A = πr(r+l) = πr[r+√(h 2 +r 2 )] Площадь изогнутой поверхности, A c = πrl Объем, V = ⅓πr 2 ч Наклонная высота, l = √(h 2 +r 2 ) Базовая зона, А б = πr 2 Где, r= радиус конуса h= высота конуса l = наклонная высота
13. Сфера	Площадь поверхности, A = 4πr 2 Объем, В = ⁴⁄₃πr 3 Диаметр = 2r Где, r= радиус сферы

Cuemath — одна из ведущих мировых обучающих платформ по математике, которая предлагает онлайн-уроки по математике в прямом эфире один на один для классов K-12. Наша миссия — изменить то, как дети изучают математику, чтобы помочь им преуспеть в школе и на конкурсных экзаменах. Наши опытные преподаватели проводят 2 или более живых занятий в неделю в темпе, соответствующем потребностям ребенка в обучении.

Отличное обучение в старшей школе с помощью простых сигналов

Увлекаясь зубрежкой, вы, скорее всего, забудете понятия. С Cuemath вы будете учиться визуально и будете удивлены результатами.

Запишитесь на бесплатный пробный урок

Давайте посмотрим на решенные примеры, чтобы понять основные формулы геометрии.

Примеры решения с использованием формул геометрии

Пример 1: Вычислите длину окружности, площадь и окружность с помощью формул геометрии, если радиус окружности равен 21 единице.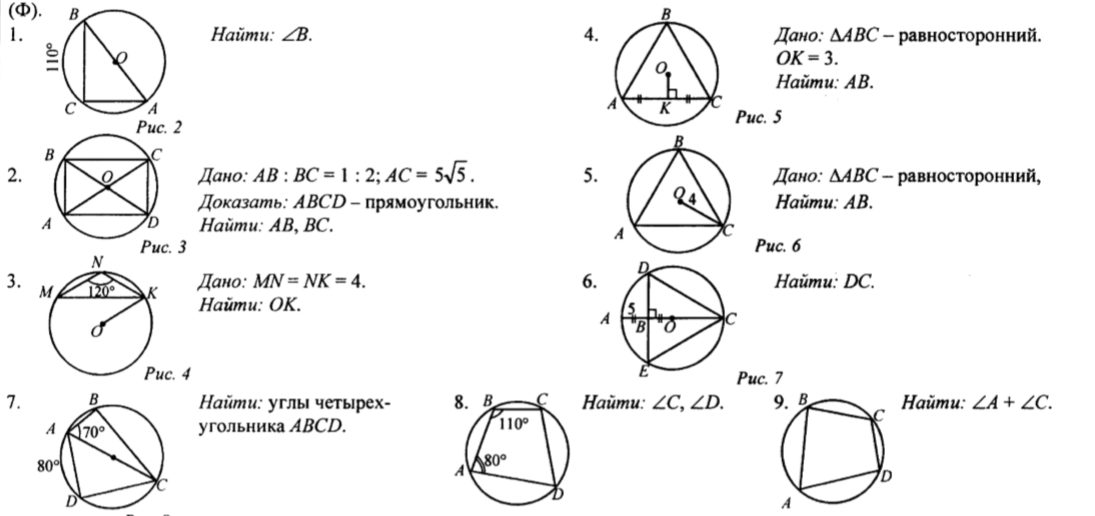

Решение:

Чтобы найти площадь и длину окружности.

Дано: Радиус круга = 21 единица

Используя формулы геометрии для круга,

Площадь круга = π × r ²

= 3,142857 × 21 ² 900 10

= 1385,44

Теперь длина окружности окружности,

Используя формулы геометрии для окружности,

Длина окружности = 2πr

= 2(3,142857)(21)

= 131,95

Ответ: Площадь круга равна 1385,44 квадратных единиц, а длина окружности 131,95 единиц.

Пример 2: Какова площадь прямоугольного парка, длина и ширина которого равны 90 м и 60 м соответственно?

Решение:
Чтобы найти площадь прямоугольного парка:

Дано: Длина парка = 90 м

Ширина парка = 60 м
Используя формулы геометрии для прямоугольника,

Площадь прямоугольника = (Длина × Ширина)

= (90 × 60) м ²

= 5400 м ²

Ответ: Площадь прямоугольного парка равна 5400 м ² .

Пример 3: Используя формулы геометрии куба, вычислите площадь поверхности и объем куба, ребро которого равно 6 единицам.

Решение:
Найти: площадь поверхности и объем куба, длина ребра которого равна 6 единицам

Используя формулы геометрии куба,
Площадь поверхности куба = A = 6a ²
А = 6 (6) ²
А = 6 × 36 = 216 шт. ²
Объем куба, V = a ³
V = (6) ³
V = 216 единиц ³

Ответ: площадь поверхности куба 216 единиц ² . Объем куба 216 единиц ³

Часто задаваемые вопросы по формулам геометрии

Что такое формулы геометрии кубоида?

Формулы геометрии прямоугольного параллелепипеда перечислены ниже:

• Площадь поверхности прямоугольного параллелепипеда, A = 2 (lb + bh + hl)
• Объем прямоугольного параллелепипеда, V = lbh
• Пространственная диагональ прямоугольного параллелепипеда, d = √(l ² + b ² +h ² )

Где,

• l= длина
• b= ширина
• h= высота

Какие формулы геометрии прямоугольника?

Геометрические формулы прямоугольника перечислены ниже:

• Периметр прямоугольника = 2(l + w)
• Площадь прямоугольника = lw
• Диагональ прямоугольника, d = √(l ² + w ² )

Где,

• l = длина прямоугольника
• w = ширина прямоугольника

Какие формулы геометрии конуса?

Формулы геометрии конуса приведены ниже:

• Общая площадь поверхности конуса, A = πr(r+l) = πr[r+√(h ² +r ² )]
• Площадь криволинейной поверхности конуса, A _c = πrl
• Объем конуса, V = ⅓πr ² ч
• Наклонная высота конуса, l = √(h ² +r ² )
• Базовая зона, A _b = πr ²

Где,

• r= радиус конуса
• h= высота конуса
• l = наклонная высота

Какие формулы геометрии окружности?

Геометрические формулы окружности приведены ниже:

• Окружность = 2πr
• Площадь = πr ²
• Диаметр = 2r

Где r = радиус окружности

Какие геометрические формулы сферы?

Две важные геометрические формулы сферы — площадь и объем сферы.