Таблица квадратов натуральных чисел.
Таблица квадратов натуральных чисел.Таблица квадратов натуральных чисел от 1 до 100. Квадрат числа определение: квадратом числа называется результат умножения числа на точно такое число. Говорят, что для того, чтобы возвести число в квадрат, нужно это число умножить само на себя. За математическую точность приведенных определений я ответственности не несу, написал, как понимаю. Для бюрократов от математики советую воспользоваться учебником и выучить определение оттуда. Таблица квадратов натуральных чисел представляет собой натуральные числа от 1 до 100 в степени 2. Все результаты возведения натуральных чисел в квадрат или в степень 2 сведены в таблицу, эту таблицу квадратов натуральных чисел любой желающий может скачать бесплатно.
В таблице квадратов натуральных чисел числа представлены по десяткам, как в таблице умножения. В первом квадратике вы найдете квадраты однозначных чисел до 10 включительно.
Степень 2 для любого числа показывает, что это число умножается само на себя. Любое отрицательное число в степени 2 дает положительный результат потому, что минус на минус при умножении дает плюс. Поэтому приведенная выше таблица является также таблицей квадратов целых чисел. Если вам нужно найти результат возведения отрицательного числа в степень 2, то смело отбрасывайте знак минус перед числом и результат ищите по таблице — он всегда будет положительным. Формулы возведения положительного и отрицательного числа в квадрат или в степень 2 будут выглядеть так:
a² = a · a
(-a)² = (-a) · (-a) = a · a
Рассмотрим несколько примеров. Начинается таблица с единицы. 1 в квадрате или единица во второй степени равняется единице. Минус единица -1 в квадрате так же равняется единице.
1² = 1 · 1 = 1
(-1)² = (-1) · (-1) = 1
2 в квадрате или 2 в степени 2 будет равно четырем.
Если двойка отрицательная возводится во 2 степень, -2 в квадрате, это тоже равно четыре. Дважды два равно четыре — эта классика детской математики показывает результат возведения числа 2 в квадрат.
2² = 2 · 2 = 4
(-2)² = (-2) · (-2) = 4
Квадрат числа три или 3 в степени 2 равняется девяти. Трижды три равно девять. Минус три в квадрате равно девять. Не забываем, что минус умножить на минус дает плюс.
3² = 3 · 3 = 9
(-3)² = (-3) · (-3) = 9
Квадрат числа четыре или 4 в степени 2 равняется шестнадцати. Четырежды четыре равно шестнадцать. Минус четыре во второй степени тоже дает шестнадцать.
4² = 4 · 4 = 16
(-4)² = (-4) · (-4) = 16
Квадрат числа пять или 5 в степени 2 равняется двадцати пяти. Пять у пять — двадцать пять. Минус пять в степени два дает опять двадцать пять.
5² = 5 · 5 = 25
(-5)² = (-5) · (-5) = 25
27 ноября 2010 года — 22 сентября 2019 года.
© 2006 — 2021 Николай Хижняк. Все права защищены.
Возведение многочленов в квадрат | Математика
Рассмотрим теперь возведение в квадрат двучлена и, применяясь к арифметической точке зрения, будем говорить о квадрате суммы, т. е. (a + b)² и о квадрате разности двух чисел, т. е. (a – b)².
Так как (a + b)² = (a + b) ∙ (a + b),
то найдем: (a + b) ∙ (a + b) = a² + ab + ab + b² = a² + 2ab + b², т. е.
(a + b)² = a² + 2ab + b²
Этот результат полезно запомнить и в виде вышеописанного равенства и словами: квадрат суммы двух чисел равен квадрату первого числа плюс произведение двойки на первое число и на второе число, плюс квадрат второго числа.
Зная этот результат, мы можем сразу написать, напр.:
(x + y)² = x² + 2xy + y²
(3ab + 1)² = 9a² b² + 6ab + 1
(xn + 4x)² = x2n + 8xn+1 + 16x2
Разберем второй из этих примеров.
Нам требуется возвести в квадрат сумму двух чисел: первое число есть 3ab, второе 1. Должно получиться: 1) квадрат первого числа, т. е. (3ab)², что равно 9a²b²; 2) произведение двойки на первое число и на второе, т. е. 2 ∙ 3ab ∙ 1 = 6ab; 3) квадрат 2-го числа, т. е. 1² = 1 – все эти три члена должно сложить между собою.
Совершенно также получим формулу для возведения в квадрат разности двух чисел, т. е. для (a – b)²:
(a – b)² = (a – b) (a – b) = a² – ab – ab + b² = a² – 2ab + b².
Итак,
(a – b)² = a² – 2ab + b²,
т. е. квадрат разности двух чисел равен квадрату первого числа, минус произведение двойки на первое число и на второе, плюс квадрат второго числа.
Зная этот результат, мы можем сразу выполнять возведение в квадрат двучленов, представляющих с точки зрения арифметики разность двух чисел.
Напр.:
(m – n)² = m² – 2mn + n²
(5ab3 – 3a2b)2 = 25a2b6 – 30a3b4 + 9a4b2
(an-1 – a)2 = a2n-2 – 2an + a2 и т.
п.
Поясним 2-ой пример. Здесь мы имеем в скобках разность двух чисел: первое число 5ab3 и второе число 3a2b. В результате должно получиться: 1) квадрат первого числа, т. е. (5ab 3)2 = 25a2b6, 2) произведение двойки на 1-ое и на 2-ое число, т. е. 2 ∙ 5ab3 ∙ 3a2b = 30a3b4 и 3) квадрат второго числа, т. е. (3a2b)2 = 9a4b2; первый и третий члены надо взять с плюсом, а 2-ой с минусом, получим 25a2b6 – 30a3b4 + 9a4b2. В пояснение 4-го примера заметим лишь, что 1) (an-1)2 = a2n-2 … надо показателя степени умножить на 2 и 2) произведение двойки на 1-ое число и на 2-ое = 2 ∙ an-1 ∙ a = 2an.
Если встать на точку зрения алгебры, то оба равенства: 1) (a + b)² = a² + 2ab + b² и 2) (a – b)² = a² – 2ab + b² выражают одно и тоже, а именно: квадрат двучлена равен квадрату первого члена, плюс произведение числа (+2) на первый член и на второй, плюс квадрат второго члена.
1) (a + b)² = (+a)² + (+2) ∙ (+a) (+b) + (+b)²
2) (a – b)² = (+a)² + (+2) ∙ (+a) (–b) + (–b)²
В некоторых случаях так именно и удобно толковать полученные равенства:
(–4a – 3b)² = (–4a)² + (+2) (–4a) (–3b) + (–3b)²
Здесь возводится в квадрат двучлен, первый член которого = –4a и второй = –3b. Далее мы получим (–4a)² = 16a², (+2) (–4a) (–3b) = +24ab, (–3b)² = 9b² и окончательно:
(–4a – 3b)² = 6a² + 24ab + 9b²
Возможно было бы также получить и запомнить формулу для возведения в квадрат трехчлена, четырехчлена и вообще любого многочлена. Однако, мы этого делать не будем, ибо применять эти формулы приходится редко, а если понадобится какой-либо многочлен (кроме двучлена) возвести в квадрат, то станем сводить дело к умножению. Например:
31. Применим полученные 3 равенства, а именно:
(a + b) (a – b) = a² – b²
(a + b)² = a² + 2ab + b²
(a – b)² = a² – 2ab + b²
к арифметике.
Пусть надо 41 ∙ 39. Тогда мы можем это представить в виде (40 + 1) (40 – 1) и свести дело к первому равенству – получим 40² – 1 или 1600 – 1 = 1599. Благодаря этому, легко выполнять в уме умножения вроде 21 ∙ 19; 22 ∙ 18; 31 ∙ 29; 32 ∙ 28; 71 ∙ 69 и т. д.
Пусть надо 41 ∙ 41; это все равно, что 41² или (40 + 1)² = 1600 + 80 + 1 = 1681. Также 35 ∙ 35 = 35² = (30 + 5)² = 900 + 300 + 25 = 1225. Если надо 37 ∙ 37, то это равно (40 – 3)² = 1600 – 240 + 9 = 1369. Подобные умножения (или возведение в квадрат двузначных чисел) легко выполнять, при некотором навыке, в уме.
2 = 3 2 Квадрат – это двумерная фигура, две стороны которой имеют одинаковую длину. Площадь квадрата определяется произведением двух его измерений. Например, если длина ребра квадрата равна «a» сантиметров, площадь квадрата определяется произведением «a × a», которое равно a 
Значит, его площадь:
a 2 = a × a × a = a 2 = 4 × 4 × 4 = 64 единицы или кубические сантиметры (64 см 2 ) (если мы выберем в качестве единицы измерения площади квадратные сантиметры).
Полный квадрат — это число, которое можно представить как произведение двух равных целых чисел.
Полный квадрат, также называемый квадратным числом, — это число, записанное по формуле S n = n 2 , где n — целое число.
Изображение предоставлено: mathsisfun.com
Обратите внимание:
- 0 в квадрате равно 0 (просто сделайте n = 0 в формуле S n = n 2 )
- 1 в квадрате равно 1 (просто сделайте n = 1)
- Отрицательный 0 в квадрате равен 0 (просто сделайте n = 0)
- Отрицательное значение 1 в квадрате равно 1 (просто сделайте n = 1)
Числовые в квадрате или Таблица идеальных квадратов от 0 до 100
2| Таблица чисел в квадрате от 0 до 50 2 |
|---|
| 0 или -0 в квадрате равно 0 |
| 1 или -1 в квадрате равно 1 |
| 2 или -2 в квадрате равно 8 |
| 3 или -3 в квадрате равно 27 |
| 4 или -4 в квадрате равно 64 | 5 или -5 в квадрате равно 125 |
| 6 или -6 в квадрате равно 216 |
| 7 или -7 в квадрате равно 343 |
| 8 или -8 в квадрате равно 512 |
| 9 или -9 в квадрате равно 729 |
| 10 или -10 в квадрате равно 1000 |
| 11 или -11 в квадрате равно 1331 |
| 12 или -12 в квадрате равно 1728 |
| 13 или -13 в квадрате равно 2197 |
| 15 или -15 в квадрате равно 3375 |
| 16 или -16 в квадрате равно 4096 |
| 17 или -17 в квадрате равно 4913 |
| 18 или -18 в квадрате равно 5832 |
| 19 или -19 в квадрате равно 6859 |
| 20 или -20 в квадрате равно 8000 |
| 21 или -21 в квадрате равно 9261 |
| 22 или -22 в квадрате равно 10648 |
| 23 или -23 в квадрате равно 12167 |
| 24 или -24 квадрат равен 13824 |
| 25 или -25 квадрат равен 15625 |
| 26 или -26 квадрат равен 17576 |
| 27 или -2 7 в квадрате равно 19683 |
| 28 или -28 в квадрате равно 21952 |
| 29 или -29 в квадрате равно 24389 |
| 30 или -30 в квадрате равно 27000 |
| 31 или -31 в квадрате равно 2 9791 |
| 32 или -32 в квадрате равно 32768 |
| 33 или -33 в квадрате равно 35937 |
| 34 или -34 в квадрате равно 39304 |
| 35 или -35 в квадрате равно 42875 |
| 3 6 или -36 в квадрате равно 46656 |
| 37 или -37 в квадрате равно 50653 |
| 38 или -38 в квадрате равно 54872 |
| 39 или -39 в квадрате равно 59319 |
| 40 или -40 в квадрате равно 64000 |
| 41 или -41 в квадрате равно 68921 |
| 42 или -42 в квадрате равно 74088 |
| 43 или -43 в квадрате равно 79507 |
| 44 или -44 в квадрате равно 85184 |
| 45 или -45 в квадрате равно 91125 |
| 46 или -46 в квадрате равно 97336 |
| 47 или -47 в квадрате равно 103823 |
| 48 или -48 в квадрате равно 110592 |
| 49 или -49 в квадрате равно 117649 |
| 50 или -50 в квадрате равно 125000 |
| Таблица чисел в квадрате 51 2 до 100 2 |
|---|
| 51 или -51 в квадрате равно 132651 |
| 52 или -52 в квадрате равно 140608 |
| 53 или -53 в квадрате равно 148877 |
| 54 или -54 в квадрате равно 157464 |
| 55 или -55 в квадрате равно 166375 |
| 56 или -56 в квадрате равно 175 616 |
| 57 или -57 в квадрате равно 185193 |
| 58 или -58 в квадрате равно 195112 |
| 59 или -59 в квадрате равно 205379 |
| 60 или -60 в квадрате равно 216000 |
| 61 или -61 в квадрате равно 226981 |
| 62 или -62 в квадрате равно 238328 |
| 63 или -63 в квадрате равно 250047 |
| 64 или -64 в квадрате равно 262144 |
| 65 или -65 в квадрате равно 274 625 |
| 66 или -66 в квадрате равно 287496 |
| 67 или -67 в квадрате равно 300763 |
| 68 или -68 в квадрате равно 314432 |
| 69 или -69 в квадрате равно 328509 |
| 70 или -70 в квадрате равно 343000 |
| 71 или -71 в квадрате равно 357911 |
| 72 или -72 в квадрате равно 373248 |
| 73 или -73 в квадрате равно 389017 |
| 74 или -74 в квадрате равно 405224 |
| 75 или -75 в квадрате равно 421875 |
| 76 или -76 в квадрате равно 438976 |
| 77 или -77 в квадрате равно 456533 |
| 78 или -78 в квадрате равно 474552 |
| 80 или -80 в квадрате равно 512000 |
| 81 или -81 в квадрате равно 531441 |
| 82 или -82 в квадрате равно 551368 |
| 83 или -83 в квадрате равно 571 787 |
| 84 или -84 в квадрате равно 592704 |
| 85 или -85 в квадрате равно 614125 |
| 86 или -86 в квадрате равно 636056 |
| 87 или -87 в квадрате равно 658503 |
| 88 или -88 в квадрате равно 681472 |
| 89 или -89квадрат равен 704969 |
| 90 или -90 квадрат равен 729000 |
| 91 или -91 квадрат равен 753571 |
| 92 или -92 в квадрате равно 778688 |
| 93 или -93 в квадрате равно 804357 |
| 94 или -94 в квадрате равно 830584 |
| 95 или -95 в квадрате равно 857375 |
| 96 или -96 в квадрате равно 884736 | 97 или -97 в квадрате равно 912673 |
| 98 или -98 в квадрате равно 941192 |
| 99 или -99 в квадрате равно 970299 |
| 100 или -100 в квадрате равно 1000000 |
| 101 или -101 в квадрате равно 1030301 |
Образец Squared или Perfect Squares
- 96 в квадрате
- -10 в квадрате
- -66 в квадрате
- 33 в квадрате
- 43 в квадрате
- -69 в квадрате
Узнайте, что означает слово «квадрат» в математике и как его использовать
Термин «возведение в квадрат» часто используется в математике для обозначения конкретной операции, которая умножает число само на себя.
Что именно означает квадрат в математике?
Квадрат — это математический термин, обозначающий число 2, умноженное само на себя. Другими словами, это означает «два, возведенные в степень двойки».
Если вам нужна помощь в понимании математики в квадрате, лучше всего нанять квалифицированного репетитора по математике. Репетитор по математике может помочь вам понять, что означает квадрат и как использовать его в различных уравнениях, например, в алгебре, геометрии и исчислении.
А пока мы попытаемся раскрыть для вас понятие квадрата.
Что такое символ квадратного корня и что он означает в математике?
Символ квадратного корня — неотъемлемая часть математики, указывающая на отношение количества к числу «2». извлекает один множитель числа, значение которого было возведено в квадрат в уравнении.0003
В математических уравнениях числа вокруг этого символа обычно представляют любые значения, от простых чисел до более сложных формул, таких как тригонометрические функции и многочлены.
Поместив такую мощную математическую операцию в один символ, мы создали важный инструмент для упрощения вычислений и придания смысла уравнениям, которые в противном случае было бы трудно понять.
Например, когда x = 3, тогда x2 = 9. Другими словами, умножение значения 3 само на себя дает нам результат 9. Избавившись от необходимости выполнять несколько вычислений, мы можем легко вычислить результаты без необходимости записывать и вычислять каждый шаг.
Этот символ очень силен, потому что может обозначать несколько вещей одновременно. Процесс возведения числа в квадрат может быть представлен уравнением, например, x2 = x • x, но гораздо проще распознать и использовать единственный символ для «возведения в квадрат».
Возможность таким образом представлять сложные вычисления делает квадратный символ одним из самых важных символов в математике. Он используется для всего, от простых математических задач до сложных алгебраических уравнений. Кроме того, его можно использовать для вычисления площади фигур и других геометрических объектов путем умножения длины одной стороны на саму себя.
Как найти квадратный корень числа
Найти квадратный корень числа довольно просто. Чтобы найти квадратный корень, нужно взять исходное число и разделить его само на себя.
Например, если бы вас попросили найти квадратный корень из 9, вы бы разделили 9 на 9. Вы бы решили это как:
= 9/9
= 1
Квадратный корень из 9 равен 1
Если число, из которого вас просят найти квадратный корень, не является точным квадратом, то это будет десятичное число. Примером этого может быть нахождение квадратного корня из 10. Ответ равен 3,1622776601, что округляется до 3,162.
Итак, если вас просят найти квадратный корень из числа, лучший способ сделать это — разделить исходное число само на себя. Если число, из которого вы пытаетесь найти квадратный корень, не является точным квадратом, вы получите десятичный ответ.
В этом случае вы можете округлить свой ответ до определенной степени точности, в зависимости от того, для чего он вам нужен.
Как можно использовать символ квадратного корня для упрощения уравнений?
Символ квадратного корня является важной частью алгебры и может значительно упростить понимание уравнений. Находя квадратный корень из числа, вы, по сути, делите одно число на два.
При работе с уравнениями, которые имеют более одной переменной, легко получить быстрые ответы или приблизительные оценки, используя символ квадратного корня и простое деление.
Важно помнить, что при поиске только положительных значений следует избегать как положительных, так и отрицательных значений (вместо того, чтобы просто взять половину уравнения).
Более того, если вы ищете неупрощенный корень, воспользуйтесь эмпирическим правилом, согласно которому любой полный квадрат, умноженный сам на себя, будет равен начальному числу, деленному на другие члены уравнения. 92 и 3, которые при умножении дают 12.
В результате корень равен 12, разделенному на остальные члены уравнения, что равно 1/2 (1 — 11).
Использование этого процесса упрощения сэкономит много времени и энергии при решении сложных уравнений!
Каковы реальные применения символа квадратного корня в математике?
Символ квадратного корня обычно ассоциируется с математикой, но он имеет множество применений в реальной жизни, например:
- В финансовых расчетах для определения совокупных годовых темпов роста и оценок волатильности
- В строительстве помогает рассчитать площади полов и крыш
- В инженерии инженеры используют его для решения классических задач устойчивости, таких как жесткость пружины и прочность балки
- Сельское хозяйство также использует этот символ для анализа почвы и оценки продуктивности растений.
- Авиация использует символ квадратного корня для расчета коэффициентов подъемной силы для самолетов.
Как видно из этих примеров, знание того, как использовать символ квадратного корня вне урока математики, может быть очень полезным во многих областях.
Почему символ квадратного корня так важен в математических уравнениях?
Символ квадратного корня является важной частью математических уравнений по ряду причин. Это означает, что данное число должно быть возведено в степень половины. Это важно для решения многих уравнений, когда переменные имеют степень больше единицы.
Символ квадратного корня можно также использовать в других типах уравнений, например, с корнями и радикалами. Это позволяет математикам определять точные значения более сложных переменных.
Кроме того, этот символ может помочь вам увидеть основные закономерности в некоторых наборах задач и показать, как различные переменные связаны друг с другом.
Извлекая, например, квадратный корень из переменной, математики могут выяснить, является ли это полным квадратом, а затем использовать эту информацию для решения более сложных уравнений.
Наконец, использование символа квадратного корня может облегчить математикам поиск решений, обладающих простыми свойствами, например состоящих только из положительных или действительных чисел.
Это полезно для определения вершины параболы или других графических решений.
Математики во многих областях, таких как физика, инженерия и экономика, используют способность быстро находить решения с определенными свойствами как очень полезный навык.
Понимая силу символа квадратного корня, практикующие специалисты могут более эффективно решать сложные уравнения и сложные задачи. Таким образом, сила символа квадратного корня является не только бесценным инструментом для математиков, но и ценным активом для многих профессий.
Как запомнить определение квадрата при решении математических задач?
Запоминание определения квадрата может быть трудным, но есть несколько простых приемов, которые помогут вам запомнить.
Хороший способ начать — разобрать определение: «возвести в квадрат» означает умножить число само на себя. Если вы думаете об этом таким образом, это может быть легче понять.
Кроме того, это может помочь визуализировать концепцию с помощью диаграмм или рисунков.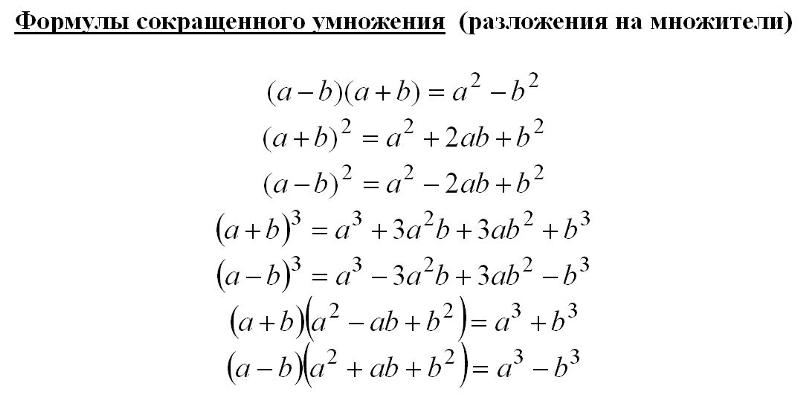
Например, рисование квадрата, каждая сторона которого имеет длину в одну единицу, показывает, что когда вы возводите в квадрат число в одну единицу длины, площадь равна четырем единицам. 92 может помочь вам вспомнить, что это означает возведение числа в квадрат.
Наконец, практика делает совершенным. Решая уравнения с числами в квадрате, вы привыкнете к этой идее и сможете легко запомнить ее в будущем.
Независимо от того, какой метод вы выберете, изучение квадратов чисел поможет вам улучшить математические способности и упростить решение уравнений. С небольшой практикой и пониманием любой может освоить эту концепцию.
Получите квалифицированную помощь квалифицированного репетитора по математике
Символ квадратного корня является очень важной частью математики и одним из наиболее часто используемых символов в уравнениях.
Часто используется для упрощения сложных уравнений и поиска реальных приложений для математических задач.
Если вам трудно понять символ квадратного корня или научиться эффективно его использовать, подумайте о том, чтобы нанять для вашего ребенка репетитора по математике.