17 распространенных типов графиков функций и их формул • BUOM
25 ноября 2021 г.
Графики берут числовые данные и переводят их в целостное визуальное отображение. Статистические графики используют собранные данные и отображают эти данные в таких формах, как гистограммы или гистограммы, в то время как функциональные графики отображают данные, сгенерированные конкретными математическими функциями, и отображают их с помощью линий, соединяющих точки данных. Те, кто работает в областях, основанных на математике и физике, часто используют эти графики, поэтому, если вы интересуетесь этими областями, их полезно знать. В этой статье мы рассмотрим 17 различных графиков функций и их формулы.
Графики полиномиальных функций
Полиномиальные функции выражают данные вертикальной оси y по отношению к горизонтальной оси x. Это означает, что y является функцией x, также показанной как f(x). Полиномиальные функции имеют несколько членов и включают коэффициенты, показатели степени и целые числа, которые влияют на форму графика. Они часто обозначаются в формулах такими буквами, как a, b, c, e и m. Вот список из шести различных полиномиальных функций и их графики:
Они часто обозначаются в формулах такими буквами, как a, b, c, e и m. Вот список из шести различных полиномиальных функций и их графики:
1. Константа
В постоянной функции y=a. Это означает, что график представляет собой прямую линию, которая проходит параллельно оси x и пересекает ось y под номером a. Таким образом, если y=6, то график будет пересекать ось y на 6 единиц выше оси x.
2. Линейный
Линейные графики — один из самых узнаваемых типов графиков полиномиальных функций. Также называемые линейными графиками, функция y=mx+b, где m — коэффициент или множитель x, а b — точка, в которой линия пересекает ось y. Если m — положительное число, линия идет от нижнего левого края к верхнему правому краю графика, а если m отрицательное, линия идет от верхнего левого края к нижнему правому краю. Коэффициент m также определяет угол наклона линии. Если b положительное, линия пересекает ось y выше оси x, а если b отрицательное, линия пересекает ось ниже x.
3.
 Квадратичный
КвадратичныйКвадратичные функции имеют формулу y=ax2+bx+c. Показатель первого члена, 2 в ax**2, является степенью функции. Графики полиномиальных функций выражают кривые при использовании показателей степени, а график образует на один виток меньше числа степени. Квадратичные функции образуют U-образный график, называемый параболой. Коэффициенты при каждом члене определяют, в каком направлении раскрывается парабола, а целое число c определяет графики, расположенные на оси Y.
4. Кубический
Кубические функции имеют формулу y=ax3+x2+cx+d. Эта формула создает график с двумя поворотами, причем два конца графика идут в противоположных направлениях. Коэффициент каждого члена определяет угол наклона и направление каждой секции графика.
5. Квартик
Формула функции четвертой степени: y=ax4+bx3+cx2+dx+e. Граф четвертой степени имеет три поворота, и, подобно параболе, образованной квадратичной формулой, оба конца графа обращены в одном направлении. Каждый коэффициент влияет на разные участки графика.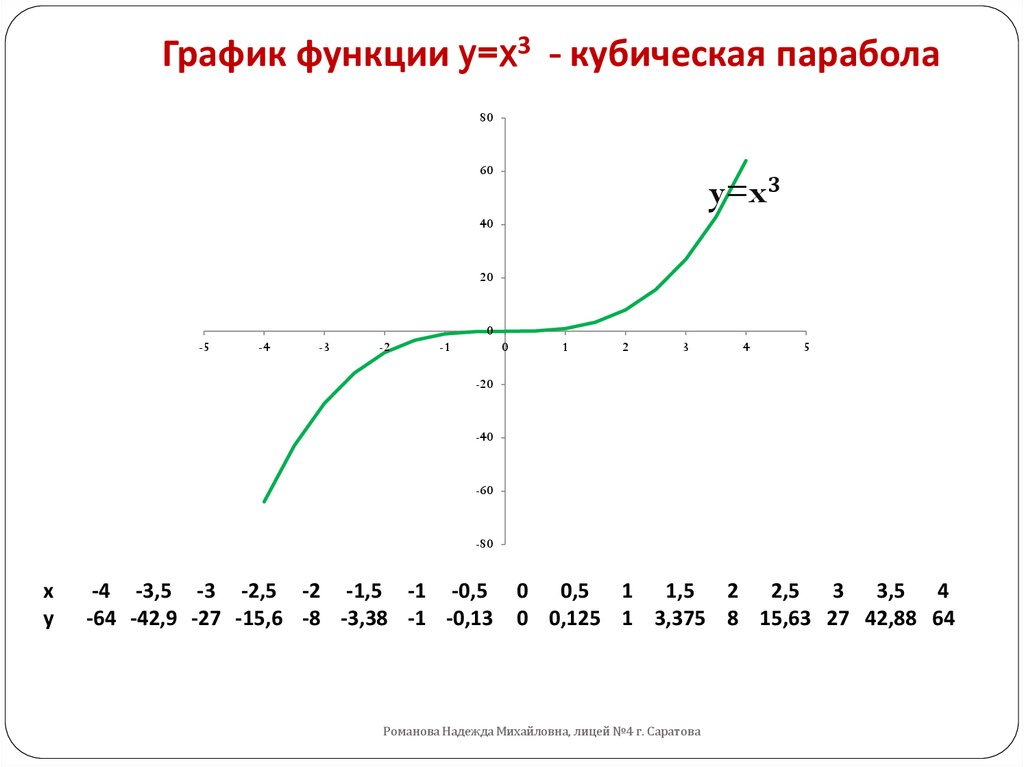
6. Квинтик
Формула функции пятой степени начинается с члена ax**5 и следует той же схеме убывания показателей степени. Граф пятой степени имеет четыре поворота, причем два конца графа обращены в противоположные стороны. Как и в случае графов кубической и четвертой степени, график формируется в соответствии с каждым коэффициентом формулы.
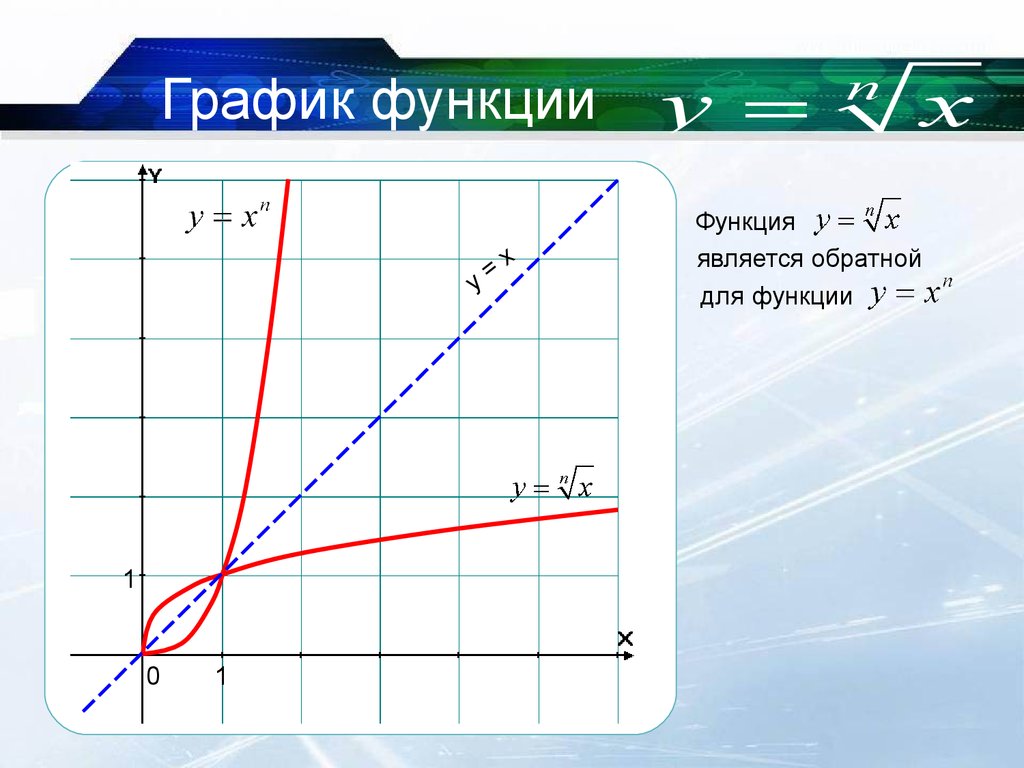
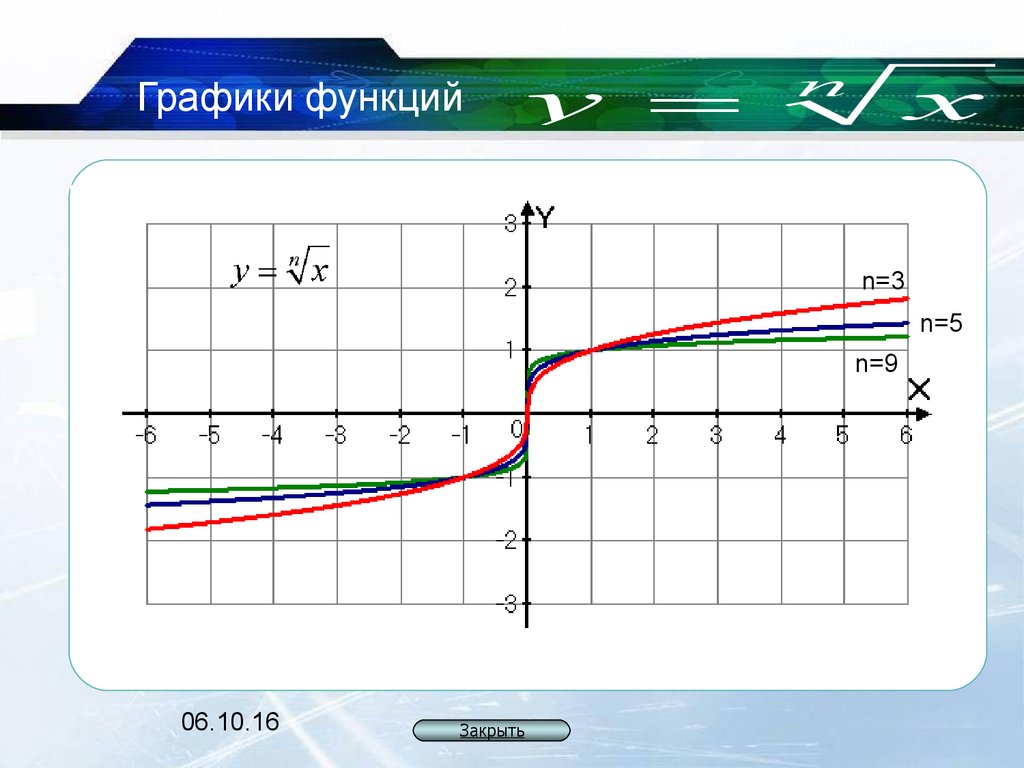
Графики функции мощности
Степенные функции — это одночленные формулы, в которых для определения формы графика используются показатели степени. Вот пять различных графиков функции мощности:
1. Квадрат
Формула квадратичной функции: y=ax**2. Как и квадратичная формула, график представляет собой параболу. Разница между графиком квадратичной функции и графиком квадратичной функции заключается в том, что квадратичный график может двигаться вдоль любой из осей в зависимости от других членов формулы, а квадратная функция привязывается к пересечению осей. Если а является положительным числом, график открывается вверх, а если а является отрицательным, график открывается вниз.
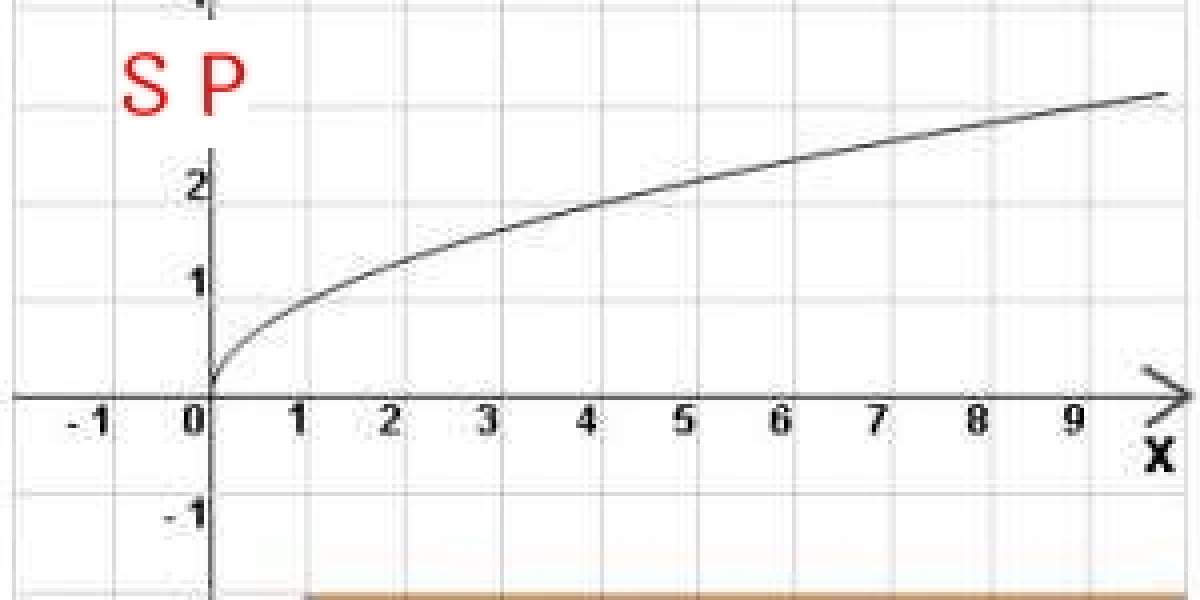
2. Квадратный корень
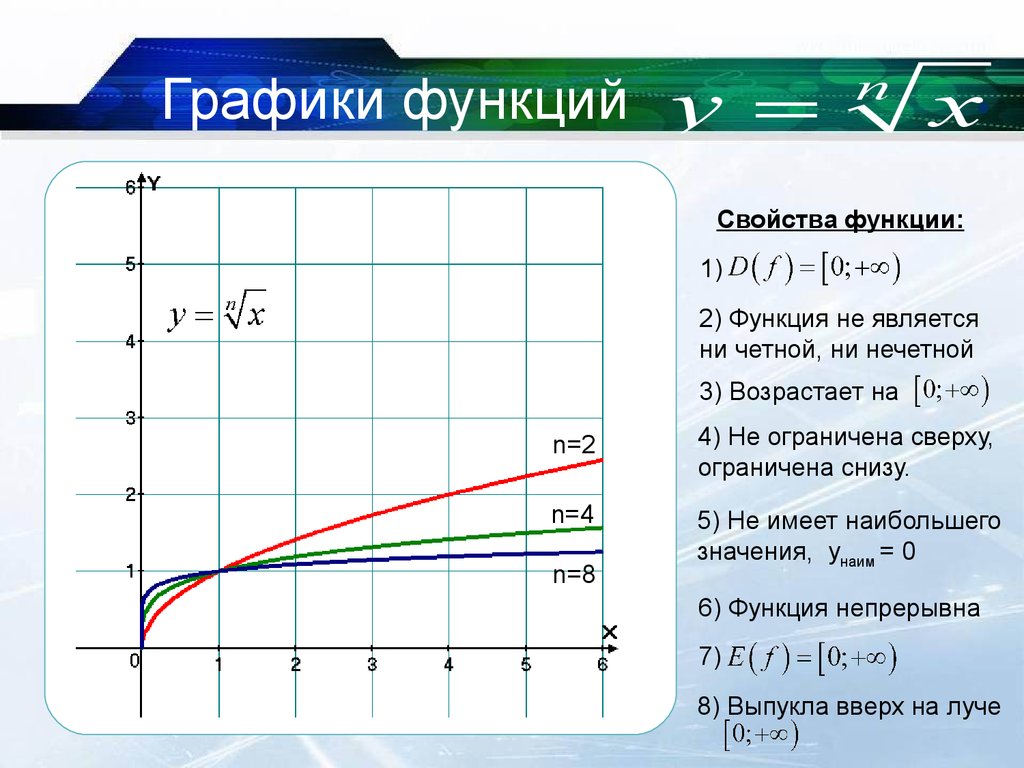
Функция квадратного корня обратна функции квадрата. Функция квадратного корня y=a√x. Этот график выглядит как половина параболы и обращен к оси x. Если коэффициент a является положительным числом, график начинается с пересечения осей и изгибается над осью x. Если a отрицательно, график изгибается под осью x.
3. Куб
Функция куба имеет формулу y=ax**3. График функции куба имеет два оборота, как и его полиномиальный аналог. Каждый конец графика продолжается в другом направлении, и они следуют по оси Y. Если a положительно, график начинается в левом нижнем углу и проходит через центр осей вверх вправо. Если a отрицательно, график перемещается из верхнего левого угла в нижний правый.
4. Кубический корень
Кубический корень — это обратная функция куба. Формула y=a3√x. Этот график имеет ту же форму, что и график функции куба, но он вращается так, что каждый его конец перемещается вдоль оси X. Коэффициент a оказывает такое же влияние на эту функцию, как и на функцию куба, когда он положительный или отрицательный.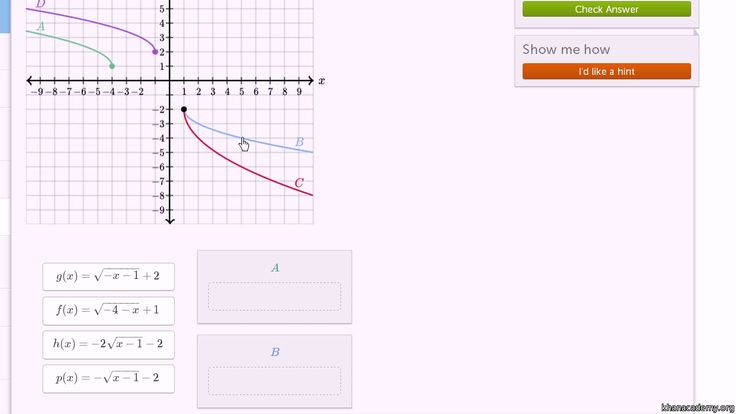
5. Взаимный
Обратная функция относится к термину, используемому для перевернутых дробей. Эта формула у=а/х. Этот график состоит из двух отдельных частей, которые приближаются к обеим осям, но не касаются их, так как x ≠ 0. Две половины этого графика зеркально отражают друг друга из диагонально противоположных четвертей графика. Каждая половина имеет одну кривую, которая находится рядом с пересечением осей, а концы линии проходят рядом с осью X и осью Y. При положительном а половинки располагаются в верхней правой и нижней левой четвертях, а при отрицательном а эти кривые получаются в верхней левой и нижней правой четвертях.
Тригонометрический
Тригонометрические функции, или круговые функции, описывают отношения между окружностями и прямоугольными треугольниками внутри них. Тригонометрические функции имеют соответствующие обратные и обратные функции. На этих графиках используются единицы измерения пи (π) вместо целых чисел по оси X. Три тригонометрические функции:
1.
 Синус
СинусФормула функции синуса: y=sin(ax). Синусоидальный график представляет собой ровный и повторяющийся волновой узор, который пересекает пересечение двух осей и перемещается выше и ниже оси x, пересекая ось с интервалом π. Коэффициент а влияет на ширину волны, когда она пересекает ось x. У синуса есть три связанные функции: обратная, обратная и обратная обратная. Обратная величина, косеканс, равна y=cosec(x). Инверсия синуса — это арксинус, y=arcsin(x) или y=sin-1(x). Обратная обратная величина — арккосеканс, y=arccosec(x)=cos-1(x).
2. Косинус
Формула функции косинуса: y=cos(ax). Как и синус, график косинуса также представляет собой четную и повторяющуюся волну. График косинуса пересекает ось x с интервалом в половину π и пересекает ось y на одну единицу выше оси x. Ширина волны изменяется в зависимости от a. Обратная величина косинуса — это секанс, обратная — арккосинус, а обратная — арк-секанс. Эти формулы: y=sec(x), y=arccos(x)=cos-1(x) и y=arcsec(x)=sec-1(x).
3. Тангенс
Тангенс — последняя из круговых функций. Формула функции тангенса: y=tan(ax). В отличие от синуса и косинуса, график тангенса не является волновым рисунком. Касательные графики имеют повторяющиеся формы, похожие на функцию куба. График пересекает пересечение осей, а один конец движется вверх, приближаясь к вертикальной линии, называемой асимптотой. Другой конец движется вниз к аналогичной асимптоте. Этот образец повторяется, с асимптотами, расположенными вдоль оси x в половине π, трех половинах π и далее. Коэффициент а влияет на ширину касательного графика.
Соответствующие формулы тангенса: обратный котангенс, y=cot(x), арктангенс арктангенса, y=arctan(x)=tan-1(x), и арктангенс обратного арккотангенса, y=arccot(x)=cot- 1(х).
Связанный: 20 лучших вакансий для математических специальностей
Абсолютная величина
Функция абсолютного значения, также называемая функцией модуля, имеет вид y=|x|. На этом графике есть две линии, которые встречаются под прямым углом на пересечении осей и продолжаются по диагонали вверх в обоих направлениях. Поскольку абсолютное значение числа всегда положительно, этот график перемещается вверх только по левой и правой сторонам графика.
Поскольку абсолютное значение числа всегда положительно, этот график перемещается вверх только по левой и правой сторонам графика.
экспоненциальный
Основная экспоненциальная функция y=a**x. Этот график имеет несколько параметров, которые им управляют. Во-первых, a≠0, и график имеет горизонтальную асимптоту вдоль оси x. Если a=1, график представляет собой горизонтальную линию, проходящую через ось Y в точке 1.
Если 0, график представляет собой кривую, которая пересекает ось y в точке 1 и движется вверх по левой стороне графика к оси x по правой стороне графика. Если a>1, график по-прежнему представляет собой кривую с горизонтальной асимптотой на оси x и пересекает ось y в точке 1, но движется к оси x с левой стороны и движется вверх с правой стороны.
Логарифмический
Логарифмическая функция обратна экспоненциальной функции, и эта формула имеет вид y=loga(x). Как и экспоненциальная функция, логарифмический график имеет несколько определяющих параметров.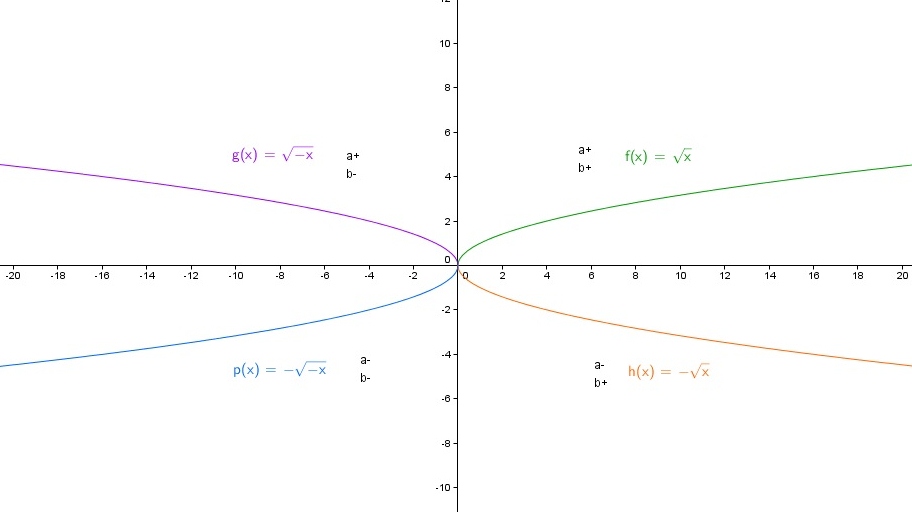 Этот график имеет вертикальную асимптоту вдоль оси y, и есть три условия для a. Когда a=1, график не определен или не отображается. Если 0, график представляет собой кривую, которая пересекает ось x в точке 1 и продолжается вверх к оси y и вниз через нижнюю правую четверть. Когда a>1, график представляет собой кривую, которая пересекает ось x в точке 1 и движется вниз к оси y и вверх через верхнюю правую четверть.
Этот график имеет вертикальную асимптоту вдоль оси y, и есть три условия для a. Когда a=1, график не определен или не отображается. Если 0, график представляет собой кривую, которая пересекает ось x в точке 1 и продолжается вверх к оси y и вниз через нижнюю правую четверть. Когда a>1, график представляет собой кривую, которая пересекает ось x в точке 1 и движется вниз к оси y и вверх через верхнюю правую четверть.
Технологическая карта урока Функция y=√x, ее свойства и график. | План-конспект урока по алгебре (8 класс) на тему:
Технологическая карта урока
Ф. И. О. учителя Тойлонова Надежда Владимировна
Класс 8 Дата 12. 11. 2014 г.
Предмет математика (алгебра)
№ урока по расписанию 2 по программе 48
Тема урока: Функция , ее свойства и график.
Тип урока: изучение нового материала
Цель урока: формирование прочных умений и навыков вычислять квадратный корень из чисел неотрицательного числа; знакомство с графиком функции , с правилом построения графика данной функции и её свойствами.
Задачи урока:
Образовательные: повторить и закрепить умения и навыки вычислять квадратный корень из неотрицательного числа, познакомить с функцией , ее графиком и свойствами; ввести понятие выпуклости и области значения;
Развивающие: развивать вычислительные навыки учащихся, умения работать с материалом, логическое мышление и память;
Воспитательные: воспитывать самостоятельность, аккуратность при построении графиков функций; воспитывать математическую грамотность умение говорить и писать на математическом языке; воспитывать чувство взаимоуважения в детском коллективе.
Оборудование: доска, карточки с вариантами для выполнения самостоятельной работы, наглядность для устной работы, учебник и задачник.
Этапы | Время | Цель этапа | Содержание | Методы обучен. | ФОУД | Деятельность учителя | Деятельность учащихся |
Орг. | 2 | Эмоциональная подготовка к уроку | Через персонажей мультфильма Смешарики эмоционально подготовить учащихся к успешному уроку. | Игровой | И | Дает учащимся персонажи мультика Смешарики | Выбирают персонажи для того, чтобы помочь учащимся. |
Обучающая самост. раб | 7 | Проверить вычислительные навыки учащихся | Самостоятельная работа на 7 минут обучающего характера по вариантам (приложение1) Во время данной самостоятельной работы, учитель отвечает на все вопросы, возникающие по ходу решения. Ответы проверяются на уроке, в журнал оценки выставляются выборочно. | Практический | П | Дает диффиринцированную работу в карточках по вариантам | Учащиеся в парах выполняют работу в крточках |
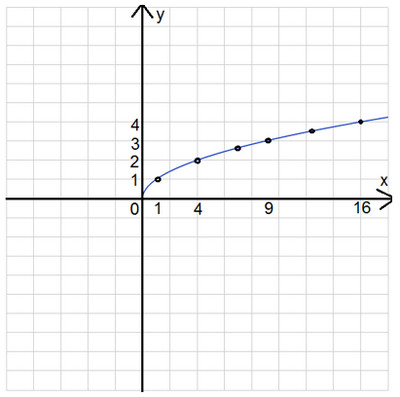
Изучение нового материала | 15 | Знакомство с графиком функции , ее свойствами | Учитель на доске показывает построение графика функции . Вместе с учащимися записывает свойства данной функции: 1. Область определения [0, +∞). 2. y = 0 при x = 0, y >0 при x > 0. 3. Функция является непрерывной на луче [0, +∞). 4. Функция ограничена снизу, но не ограничена сверху. 5. ymin=0 при x=0; ymaxне сущ. 6. Данная функция возрастает на интервале [0, +∞). Далее учитель объясняет понятие выпуклости, области значений. К свойствам функции добавляется еще два: 7. 8. Область значений данной функции: луч [0, +). | Нагляд-ные, частично-поисковые. | Г | Учитель на доске показывает построение графика функции . Вместе с учащимися записывает свойства данной функции. Дает понятие выпуклости функции и затем добавляет еще 2 свойства для изучаемой функции. | Строят график функции , рассматривают его свойства. Знакомятся с понятием выпуклости графика функции, далее вводят еще свойства функции. |
материала | 18 | Закрепление изученного материала, через практическую работу. | 1. Рассмотреть задания из задачника №13.2, №13.3 (г), №13.7 (г), №13.9 (а,г), №13.16. 2. Устно выполнить задания на сравнение иррациональных выражений: (приложение 2) | Практический, работа с материалом | П И | Дает задания на самостоятельную работу по задачнику. Рассматриваются задания для устного сравнения иррациональ | Выполняют упражнения из учебника, работают активно и выполняют задания на сравнение иррациональных |
Закрепление изученного | Для обучающихся с высоким уровнем подготовки объяснить правило сравнения выражений, содержащих знак корня; разобрать примеры на сравнение: а)2и ; б) и в) и ; г) и д) и ; е) и | ных чисел | чисел | ||||
Итоги урока | 3 | Рефлексия | Поговорить с персонажами мультика Смешарики, научились ли они строить график квадратичной функции, и читать ее, достигнуты ли цели урока. | Игровой | И | Учитель спрашивает у персонажей мультика, что им понравилось на уроке, получили ли они чего-то нового. | Отвечают на вопросы учителя как персонажи мультика Смашарики. |
Домашнее задание: прочитать материал параграфа 13, выучить свойства функции . Выполнить решение примеров (б, в) из заданий № 13.9; 13.18. | — | И | Дает домашнее задание | Записывают задание на дом и выставляют оценки. |
Приложение 1.
Вариант 1
1. Вычислите:
а) б)
2. Подберите два последовательных целых числа между которыми заключено число:
а)
3. используя определение квадратного корня, решите уравнение:
а)
Вариант 2
1. Вычислите:
Вычислите:
а) б)
2. Подберите два последовательных целых числа между которыми заключено число:
а)
3. используя определение квадратного корня, решите уравнение:
а)
Приложение 2.
2
График квадратного корня, кубического корня и кусочных функций
Все ресурсы по алгебре II
10 диагностических тестов 630 практических тестов Вопрос дня Карточки Learn by Concept
← Предыдущая 1 2 Следующая →
Алгебра II Помощь » Математические отношения и основные графики » Радикалы » Решение и графическое изображение радикалов » График квадратного корня, кубического корня и кусочных функций
Укажите домен функции:
Возможные ответы:
Правильный ответ:
Объяснение:
Поскольку выражение под корнем не может быть отрицательным,
.
Найдите x:
Это домен или возможные значения
Сообщить об ошибке
Какой из следующих вариантов правильно описывает область определения графика функции?
Возможные ответы:
Все действительные числа
Правильный ответ:
5
55
5
Объяснение: Поскольку член внутри радикала в числителе должен быть больше или равен нулю, в нашей области есть ограничение; чтобы описать это ограничение, мы решаем неравенство для :
Добавьте к обеим частям, и в результате неравенство:
или
Далее рассмотрим знаменатель, квадратичный; мы знаем, что не можем делить на ноль, поэтому мы должны найти значения x, при которых знаменатель равен нулю, и исключить их из нашей области значений:
наше выражение оставляет нас с:
Следовательно, есть 3 ограничения на домен функции:
Сообщить об ошибке
Что из следующего является графиком ?
Возможные ответы:
Правильный ответ:
Объяснение:
График такой:
Этот график сдвинут на 2 единицы влево и на 4 единицы вниз от графика , который выглядит так: квадратный корень, скажите нам, что нам нужно сдвинуть график вниз на четыре единицы. Если вы возьмете то, что находится под квадратным корнем, установите его равным 0, а затем решите, вы получите x = -2, что вы можете интерпретировать как сдвиг влево на две единицы.
Если вы возьмете то, что находится под квадратным корнем, установите его равным 0, а затем решите, вы получите x = -2, что вы можете интерпретировать как сдвиг влево на две единицы.
Каждый из приведенных ниже графиков, которые неверны, либо неправильно сдвигает график вправо (а не влево), вверх (вместо вниз) или и вправо, и вверх.
Сообщить об ошибке
Является ли следующий график функцией?
Возможные ответы:
Правильный ответ:
Нет
Объяснение:
Приведенный выше график не является функцией. Чтобы быть функцией, график должен пройти тест вертикальной линии. Если вы посмотрите на x=2, вы увидите, что x=2 является значением как на зеленом, так и на фиолетовом графиках. Следовательно, он не проходит тест вертикальной линии и не является функцией.
Сообщить об ошибке
Является ли следующий график функцией?
Возможные ответы:
Правильный ответ:
Да
Объяснение:
Этот график является функцией.
Мы называем этот тип функции кусочной (или ступенчатой) функцией. Этот тип функции определяется определенным образом для определенных значений x, а затем по-разному для других значений x. Тем не менее, он все еще проходит тест на вертикальную линию, так что это функция! Сообщить об ошибке
Каковы область определения и диапазон этой кусочной функции?
Возможные ответы:
Домен:
Диапазон:
Домен:
. домен и диапазон.
Правильный ответ:
Домен:
Диапазон:
Объяснение:
Во-первых, это функция, так как она проходит тест вертикальной линии.
Чтобы найти домен, начните с крайней левой части графика, начиная с красной части. Вы можете следовать по нему непрерывно, пока не дойдете до точки (-5,-5). В этот момент он прыгает вверх к зеленому графику.
В то время как значения y скачут, в значениях x нет разрыва. Вы можете проследить слева направо по зеленому графику, пока не дойдете до x=2. Затем график переходит к фиолетовым значениям. Еще раз, нет разрыва в значениях x. Фиолетовый график непрерывен и продолжается до положительной бесконечности. Следовательно, областью определения этого графа являются все действительные числа или . Теперь давайте снова начнем с нижней части графика (выделено красным), на этот раз глядя на значения y. Мы начинаем с отрицательной бесконечности и можем непрерывно отслеживать, пока не доберемся до точки (-5,-5). Существует разрыв между значениями y красного и зеленого графиков. Мы используем символ («объединение») для соединения несвязных частей графа. Зеленый график начинается с -1,71, а значения y продолжают расти, пока не достигают 1,256. Опять же, в диапазоне есть разрыв, поэтому мы снова используем символ объединения. Значения y возвращаются в точку (2,4) и продолжают расти до бесконечности.
Следовательно, диапазон этой функции . Сообщить об ошибке
Что из следующего является графиком ?
Возможные ответы:
Правильный ответ:
Объяснение:
График это
Имейте в виду, что вы не можете положить отрицательное число под квадратным корнем и получить ответ в виде действительного числа. Если бы мы попытались подставить -2 вместо x, это было бы неопределенно. Вот почему на графике показаны только положительные значения x.
Другие графики, изображенные ниже, , и . Сообщить об ошибке
Что из следующего является графиком ?
Возможные ответы:
Правильный ответ:
Объяснение:
График это
.
Другие показанные графики относятся к , и .
Сообщить об ошибке
Что из следующего является графиком ?
Возможные ответы:
Правильный ответ:
Объяснение:
График – это
. Другие изображенные графики , , и .
Сообщить об ошибке
Укажите точку пересечения по осям X, Y, домен и диапазон функции , как показано на рисунке ниже.
Возможные ответы:
x-intercept: нет
y-intercept: нет
Домен:
Диапазон:
X-Intercept: None
Y-Intercept: None
Домен:
Диапазон:
X-Intercept: x = 0
Y-Intercept: Y = 0
Домен:
:
4 Пересечение по оси x: x=0
Пересечение по оси y: y=0
Домен:
Диапазон:
Правильный ответ:
Пересечение по оси x: x=0
Пересечение по оси y: 0y=090
Домен:
Диапазон:
Объяснение:
Этот график пересекает ось x только один раз и ось y только один раз, и они совпадают в точке (0,0). Следовательно, точка пересечения x находится в точке x=0, а точка пересечения y находится в точке y=0. График будет продолжаться бесконечно вправо. Однако самая левая точка — это (0,0). Точно так же график будет бесконечно высоко, но его самая нижняя точка также будет (0,0). Следовательно, его домен и его диапазон также .
Следовательно, точка пересечения x находится в точке x=0, а точка пересечения y находится в точке y=0. График будет продолжаться бесконечно вправо. Однако самая левая точка — это (0,0). Точно так же график будет бесконечно высоко, но его самая нижняя точка также будет (0,0). Следовательно, его домен и его диапазон также .
Сообщить об ошибке
← Предыдущая 1 2 Следующая →
Уведомление об авторских правах
Все ресурсы по алгебре II
10 диагностических тестов
630 практических тестов
Вопрос дня
Карточки
Learn by Concept
графическое представление функции cube_root(x)
Программное обеспечение для построения графиков онлайн , также известное как графопостроитель ,
представляет собой онлайн-построитель кривых , который позволяет отображать функции в режиме онлайн.
Просто введите выражение в соответствии с x функции, которую нужно построить, используя обычные математические операторы.
9Плоттер 0017 кривой особенно подходит для функционального исследования ,
позволяет получить графическое представление функции из уравнения кривой,
его можно использовать для определения вариации, минимума, максимума функции. Онлайн-плоттер также может рисовать параметрические кривые.
и рисовать полярные кривые, а для функций достаточно ввести выражение для представления по параметру t.
9Для мощности
/ Для отдела Это программное обеспечение для построения кривых позволяет использовать следующие обычных математических функций :
- абс (абсолютное значение),
график абсолютного значения
- арккос (арккосинус),
арккосинус участка
- арксинус (арксинус),
арксинус графика
- арктангенс (арктангенс),
арктангенс графика
- ch (гиперболический косинус),
построить гиперболический косинус
- cos (косинус),
график косинус
- косек (косеканс),
косеканс участка
- котан (котангенс),
котангенс участка
- coth (гиперболический котангенс),
построить гиперболический котангенс
- эксп (экспоненциальная),
экспоненциальный график
- ln (напировский логарифм),
построить напьеровский логарифм
- log (логарифм),
логарифм графика
- cube_root (кубический корень),
построить кубический корень
- сек (секанс),
секущая участка
- ш (гиперболический синус),
построить гиперболический синус
- sin (синус),
график синуса
- sqrt (квадратный корень),
участок квадратный корень
- тангенс (тангенс),
участок касательной
- th (гиперболический тангенс),
построить гиперболический тангенс
- абс.
 (абсолютное значение),
график абсолютного значения
(абсолютное значение),
график абсолютного значения - арккос (арккосинус),
арккосинус участка
- арксинус (арксинус),
арксинус графика
- арктангенс (арктангенс),
арктангенс графика
- ch (гиперболический косинус),
построить гиперболический косинус
- cos (косинус),
график косинус
- косек (косеканс),
косеканс участка
- котанг (котангенс),
котангенс участка
- coth (гиперболический котангенс),
построить гиперболический котангенс
- cube_root (кубический корень),
построить кубический корень
- эксп (экспоненциальная),
экспоненциальный график
- ln (напировский логарифм),
построить напьеровский логарифм
логарифм- (логарифм),
логарифм графика
- сек (секанс),
секущая участка
- ш (гиперболический синус),
построить гиперболический синус
- sin (синус),
график синуса
- sqrt (квадратный корень),
участок квадратный корень
- тангенс (тангенс),
участок касательной
- th (гиперболический тангенс),
построить гиперболический тангенс
- Графические функции онлайн
Этот онлайн-плоттер позволяет вам рисовать несколько кривых одновременно ,
просто введите выражение функции, которую нужно построить, и нажмите «Добавить», графическое представление функции появляется мгновенно, можно повторить операцию для построения других кривых онлайн .
Переменная, которая будет использоваться для представления функций, — «x».
Координаты точек на кривой можно получить с помощью курсора.
Для этого нажмите на кривую, чтобы появился этот курсор, а затем перетащите вдоль кривой, чтобы увидеть ее координаты.
Кривые можно удалить из плоттера:
- Чтобы удалить кривую, выберите кривую, затем нажмите кнопку удаления в меню.
- Чтобы удалить все кривые с графика, нажмите кнопку удалить все в меню.
Можно изменить кривую, представленную на графике, выбрав ее, отредактировав ее выражение и затем щелкнув
на кнопку редактирования.
онлайн-плоттер имеет несколько опций, позволяющих настроить график.
Чтобы получить доступ к этим параметрам, нажмите кнопку параметров. Затем можно определить границы графов,
чтобы подтвердить эти изменения, необходимо снова нажать кнопку параметров.
- Проведение касательной функции к точке
Онлайн-плоттер позволяет провести тангенс функции в точке сделать это,
вы просто рисуете нужную функцию, затем, как только функция нарисована, нажмите на меню,
параметры, а затем кнопку касательной, которая появляется на экране, после чего будет нарисована касательная,
можно изменить точку касательной, что приводит к перерисовке касательной.
Калькулятор позволяет определить
уравнение касательной очень просто,
с уравнением кривой.
- График производной функции
Онлайн-плоттер позволяет вам построить производную функции для этого,
вы просто рисуете нужную функцию, затем после того, как функция нарисована,
нажмите на меню, на параметры, затем на появившуюся производную кнопку,
затем строится производная функции.
9Построитель кривых 0017 также можно использовать для вычисления производной функции и
к участок он для этой цели,
вам нужно нарисовать нужную функцию, затем, как только функция будет нарисована, выберите ее, щелкнув по ней,
на кривой появится красный курсор. Затем нажмите на меню, на параметры, затем на производную кнопку «выражение», которая появляется на экране,
затем строится и вычисляется производная функции. («Выражение» представляет собой выражение, которое необходимо получить и нанести на график).
Построить параметрическую кривую онлайн Плоттер позволяет рисовать параметрическую кривую , для этого
вам просто нужно ввести абсциссу, ординату как функцию от t,
затем нажмите кнопку «Построить параметрическую кривую»,
кривая автоматически отображается с двумя курсорами для отображения нужных точек.
Построить полярную кривую онлайн Построитель кривых можно использовать для построения полярной кривой .
Для этого просто введите выражение полярной кривой в зависимости от t,
затем нажмите кнопку «Построить полярную кривую», кривая автоматически отобразится с двумя курсорами для отображения нужных точек.
Переместите курсор на кривую Есть возможность двигаться по кривым и получать координаты точки, на которой находится курсор,
Для этого необходимо ввести курсор и перемещать его по графику, координаты X и Y отображаются под графиком.
Доступные графические опции Можно изменить область графика, для этого необходимо зайти в меню, затем нажать на опции,
Затем можно изменить пределы графического дисплея.
Графический калькулятор предлагает возможность масштабировать и перемещать область графика. Сделать это,
используйте область в правом нижнем углу графиков.
Сделать это,
используйте область в правом нижнем углу графиков.
- Кнопка + позволяет увеличить масштаб кривых,
- — позволяет уменьшить масштаб кривых,
- Стрелки используются для перемещения кривых,
Экспорт кривых Можно экспортировать построенные кривые с помощью графического калькулятора , экспорт осуществляется как
изображение в формате PNG. Для этого вам нужно зайти в меню графика, затем в подменю экспорта графиков.
Затем калькулятор отображает построенные кривые в виде изображения, просто щелкните правой кнопкой мыши, чтобы экспортировать изображение,
также возможно скопировать изображение.
Чтобы вернуться к обычному отображению калькулятора, используйте кнопку Выход из режима изображения.
Поскольку член внутри радикала в числителе должен быть больше или равен нулю, в нашей области есть ограничение; чтобы описать это ограничение, мы решаем неравенство для :
Добавьте к обеим частям, и в результате неравенство:
или
Далее рассмотрим знаменатель, квадратичный; мы знаем, что не можем делить на ноль, поэтому мы должны найти значения x, при которых знаменатель равен нулю, и исключить их из нашей области значений:
наше выражение оставляет нас с:
Следовательно, есть 3 ограничения на домен функции:
Сообщить об ошибке
Что из следующего является графиком ?
Возможные ответы:
Правильный ответ:
Объяснение:
График такой:
Этот график сдвинут на 2 единицы влево и на 4 единицы вниз от графика , который выглядит так: квадратный корень, скажите нам, что нам нужно сдвинуть график вниз на четыре единицы.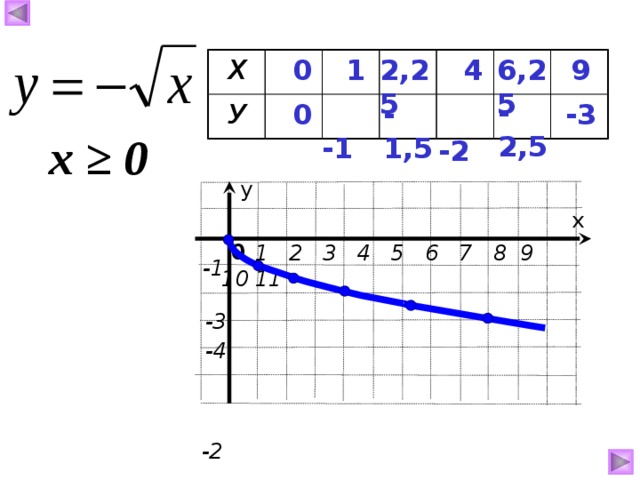 Если вы возьмете то, что находится под квадратным корнем, установите его равным 0, а затем решите, вы получите x = -2, что вы можете интерпретировать как сдвиг влево на две единицы.
Если вы возьмете то, что находится под квадратным корнем, установите его равным 0, а затем решите, вы получите x = -2, что вы можете интерпретировать как сдвиг влево на две единицы.
Каждый из приведенных ниже графиков, которые неверны, либо неправильно сдвигает график вправо (а не влево), вверх (вместо вниз) или и вправо, и вверх.
Сообщить об ошибке
Является ли следующий график функцией?
Возможные ответы:
Правильный ответ:
Нет
Объяснение:
Приведенный выше график не является функцией. Чтобы быть функцией, график должен пройти тест вертикальной линии. Если вы посмотрите на x=2, вы увидите, что x=2 является значением как на зеленом, так и на фиолетовом графиках. Следовательно, он не проходит тест вертикальной линии и не является функцией.
Сообщить об ошибке
Является ли следующий график функцией?
Возможные ответы:
Правильный ответ:
Да
Объяснение:
Этот график является функцией.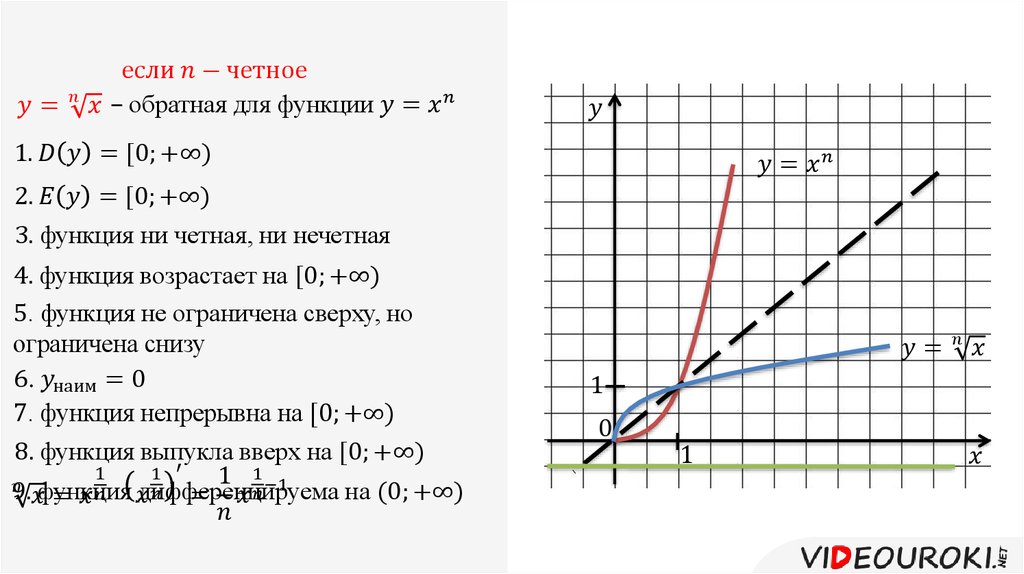
Сообщить об ошибке
Каковы область определения и диапазон этой кусочной функции?
Возможные ответы:
Домен:
Диапазон:
Домен:
. домен и диапазон.
Правильный ответ:
Домен:
Диапазон:
Объяснение:
Во-первых, это функция, так как она проходит тест вертикальной линии.
Чтобы найти домен, начните с крайней левой части графика, начиная с красной части. Вы можете следовать по нему непрерывно, пока не дойдете до точки (-5,-5). В этот момент он прыгает вверх к зеленому графику.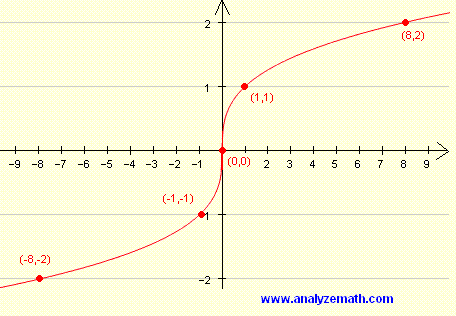
Теперь давайте снова начнем с нижней части графика (выделено красным), на этот раз глядя на значения y. Мы начинаем с отрицательной бесконечности и можем непрерывно отслеживать, пока не доберемся до точки (-5,-5). Существует разрыв между значениями y красного и зеленого графиков. Мы используем символ («объединение») для соединения несвязных частей графа. Зеленый график начинается с -1,71, а значения y продолжают расти, пока не достигают 1,256. Опять же, в диапазоне есть разрыв, поэтому мы снова используем символ объединения. Значения y возвращаются в точку (2,4) и продолжают расти до бесконечности.
Сообщить об ошибке
Что из следующего является графиком ?
Возможные ответы:
Правильный ответ:
Объяснение:
График это
Имейте в виду, что вы не можете положить отрицательное число под квадратным корнем и получить ответ в виде действительного числа. Если бы мы попытались подставить -2 вместо x, это было бы неопределенно. Вот почему на графике показаны только положительные значения x.
Сообщить об ошибке
Что из следующего является графиком ?
Возможные ответы:
Правильный ответ:
Объяснение:
График это
.
Другие показанные графики относятся к , и .
Сообщить об ошибке
Что из следующего является графиком ?
Возможные ответы:
Правильный ответ:
Объяснение:
График – это
. Другие изображенные графики , , и .
Сообщить об ошибке
Укажите точку пересечения по осям X, Y, домен и диапазон функции , как показано на рисунке ниже.
Возможные ответы:
x-intercept: нет
y-intercept: нет
Домен:
Диапазон:
X-Intercept: None
Y-Intercept: None
Домен:
Диапазон:
X-Intercept: x = 0
Y-Intercept: Y = 0
Домен:
:
4 Пересечение по оси x: x=0
Пересечение по оси y: y=0
Домен:
Диапазон:
Правильный ответ:
Пересечение по оси x: x=0
Пересечение по оси y: 0y=090
Домен:
Диапазон:
Объяснение:
Этот график пересекает ось x только один раз и ось y только один раз, и они совпадают в точке (0,0). Следовательно, точка пересечения x находится в точке x=0, а точка пересечения y находится в точке y=0. График будет продолжаться бесконечно вправо. Однако самая левая точка — это (0,0). Точно так же график будет бесконечно высоко, но его самая нижняя точка также будет (0,0). Следовательно, его домен и его диапазон также .
Следовательно, точка пересечения x находится в точке x=0, а точка пересечения y находится в точке y=0. График будет продолжаться бесконечно вправо. Однако самая левая точка — это (0,0). Точно так же график будет бесконечно высоко, но его самая нижняя точка также будет (0,0). Следовательно, его домен и его диапазон также .
Сообщить об ошибке
← Предыдущая 1 2 Следующая →
Уведомление об авторских правах
Все ресурсы по алгебре II
10 диагностических тестов 630 практических тестов Вопрос дня Карточки Learn by Concept
графическое представление функции cube_root(x)
Программное обеспечение для построения графиков онлайн , также известное как графопостроитель ,
представляет собой онлайн-построитель кривых , который позволяет отображать функции в режиме онлайн.
Просто введите выражение в соответствии с x функции, которую нужно построить, используя обычные математические операторы.
Онлайн-плоттер также может рисовать параметрические кривые. и рисовать полярные кривые, а для функций достаточно ввести выражение для представления по параметру t. 9Для мощности
Это программное обеспечение для построения кривых позволяет использовать следующие обычных математических функций :
- абс (абсолютное значение), график абсолютного значения
- арккос (арккосинус), арккосинус участка
- арксинус (арксинус), арксинус графика
- арктангенс (арктангенс), арктангенс графика
- ch (гиперболический косинус), построить гиперболический косинус
- cos (косинус), график косинус
- косек (косеканс), косеканс участка
- котан (котангенс), котангенс участка
- coth (гиперболический котангенс), построить гиперболический котангенс
- эксп (экспоненциальная), экспоненциальный график
- ln (напировский логарифм), построить напьеровский логарифм
- log (логарифм), логарифм графика
- cube_root (кубический корень), построить кубический корень
- сек (секанс), секущая участка
- ш (гиперболический синус), построить гиперболический синус
- sin (синус), график синуса
- sqrt (квадратный корень), участок квадратный корень
- тангенс (тангенс), участок касательной
- th (гиперболический тангенс), построить гиперболический тангенс
- абс.
 (абсолютное значение),
график абсолютного значения
(абсолютное значение),
график абсолютного значения - арккос (арккосинус), арккосинус участка
- арксинус (арксинус), арксинус графика
- арктангенс (арктангенс), арктангенс графика
- ch (гиперболический косинус), построить гиперболический косинус
- cos (косинус), график косинус
- косек (косеканс), косеканс участка
- котанг (котангенс), котангенс участка
- coth (гиперболический котангенс), построить гиперболический котангенс
- cube_root (кубический корень), построить кубический корень
- эксп (экспоненциальная), экспоненциальный график
- ln (напировский логарифм), построить напьеровский логарифм логарифм
- (логарифм), логарифм графика
- сек (секанс), секущая участка
- ш (гиперболический синус), построить гиперболический синус
- sin (синус), график синуса
- sqrt (квадратный корень), участок квадратный корень
- тангенс (тангенс), участок касательной
- th (гиперболический тангенс), построить гиперболический тангенс
- Графические функции онлайн
Этот онлайн-плоттер позволяет вам рисовать несколько кривых одновременно ,
просто введите выражение функции, которую нужно построить, и нажмите «Добавить», графическое представление функции появляется мгновенно, можно повторить операцию для построения других кривых онлайн .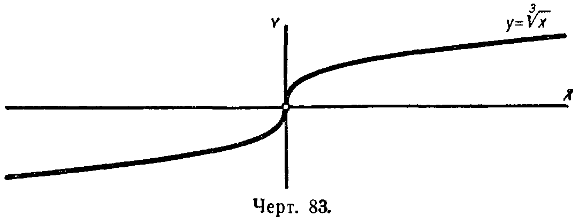
Переменная, которая будет использоваться для представления функций, — «x».
Координаты точек на кривой можно получить с помощью курсора. Для этого нажмите на кривую, чтобы появился этот курсор, а затем перетащите вдоль кривой, чтобы увидеть ее координаты.
Кривые можно удалить из плоттера:
- Чтобы удалить кривую, выберите кривую, затем нажмите кнопку удаления в меню.
- Чтобы удалить все кривые с графика, нажмите кнопку удалить все в меню.
Можно изменить кривую, представленную на графике, выбрав ее, отредактировав ее выражение и затем щелкнув на кнопку редактирования.
онлайн-плоттер имеет несколько опций, позволяющих настроить график.
Чтобы получить доступ к этим параметрам, нажмите кнопку параметров. Затем можно определить границы графов,
чтобы подтвердить эти изменения, необходимо снова нажать кнопку параметров.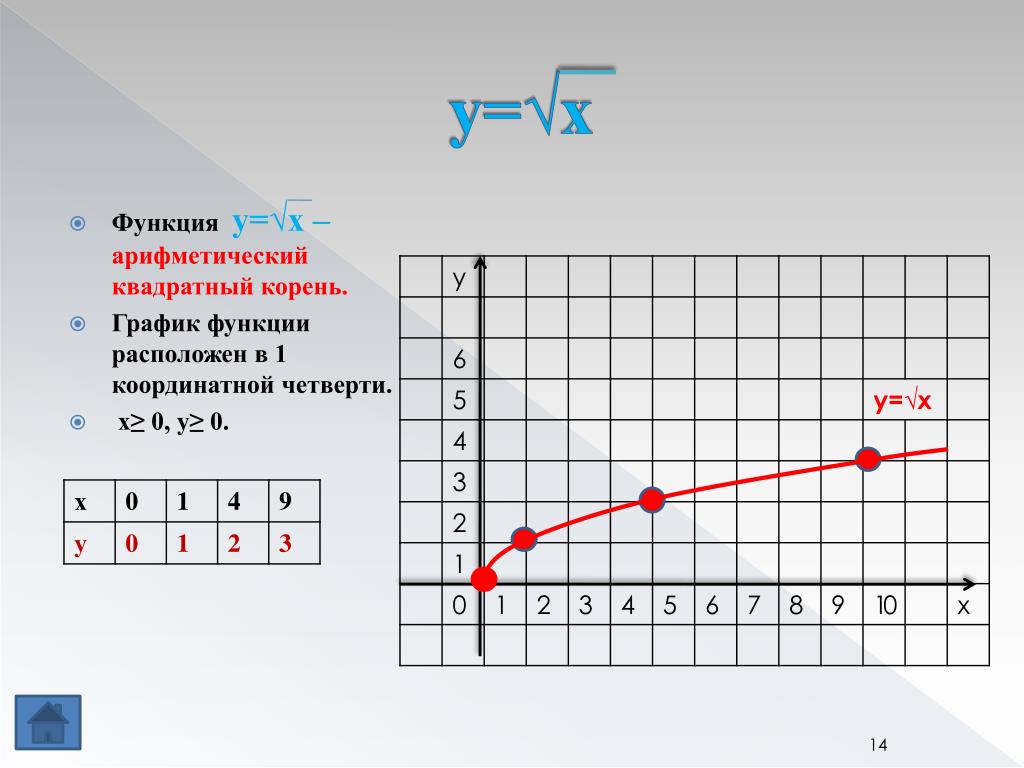
- Проведение касательной функции к точке
- График производной функции
Онлайн-плоттер позволяет провести тангенс функции в точке сделать это, вы просто рисуете нужную функцию, затем, как только функция нарисована, нажмите на меню, параметры, а затем кнопку касательной, которая появляется на экране, после чего будет нарисована касательная, можно изменить точку касательной, что приводит к перерисовке касательной. Калькулятор позволяет определить уравнение касательной очень просто, с уравнением кривой.
Онлайн-плоттер позволяет вам построить производную функции для этого,
вы просто рисуете нужную функцию, затем после того, как функция нарисована,
нажмите на меню, на параметры, затем на появившуюся производную кнопку,
затем строится производная функции.
9Построитель кривых 0017 также можно использовать для вычисления производной функции и к участок он для этой цели, вам нужно нарисовать нужную функцию, затем, как только функция будет нарисована, выберите ее, щелкнув по ней, на кривой появится красный курсор. Затем нажмите на меню, на параметры, затем на производную кнопку «выражение», которая появляется на экране, затем строится и вычисляется производная функции. («Выражение» представляет собой выражение, которое необходимо получить и нанести на график).
Плоттер позволяет рисовать параметрическую кривую , для этого
вам просто нужно ввести абсциссу, ординату как функцию от t,
затем нажмите кнопку «Построить параметрическую кривую»,
кривая автоматически отображается с двумя курсорами для отображения нужных точек.
Построитель кривых можно использовать для построения полярной кривой . Для этого просто введите выражение полярной кривой в зависимости от t, затем нажмите кнопку «Построить полярную кривую», кривая автоматически отобразится с двумя курсорами для отображения нужных точек.
Есть возможность двигаться по кривым и получать координаты точки, на которой находится курсор, Для этого необходимо ввести курсор и перемещать его по графику, координаты X и Y отображаются под графиком.
Можно изменить область графика, для этого необходимо зайти в меню, затем нажать на опции, Затем можно изменить пределы графического дисплея.
Графический калькулятор предлагает возможность масштабировать и перемещать область графика. Сделать это,
используйте область в правом нижнем углу графиков.
Сделать это,
используйте область в правом нижнем углу графиков.
- Кнопка + позволяет увеличить масштаб кривых,
- — позволяет уменьшить масштаб кривых,
- Стрелки используются для перемещения кривых,
Можно экспортировать построенные кривые с помощью графического калькулятора , экспорт осуществляется как
изображение в формате PNG. Для этого вам нужно зайти в меню графика, затем в подменю экспорта графиков.
Затем калькулятор отображает построенные кривые в виде изображения, просто щелкните правой кнопкой мыши, чтобы экспортировать изображение,
также возможно скопировать изображение.
Чтобы вернуться к обычному отображению калькулятора, используйте кнопку Выход из режима изображения.

 мо-нт
мо-нт
 Данная функция выпукла вверх.
Данная функция выпукла вверх.
 (абсолютное значение),
график абсолютного значения
(абсолютное значение),
график абсолютного значения