Электронный справочник по математике для школьников тригонометрия тригонометрические функции кратных углов вывод с помощью комплексных чисел
| Справочник по математике | Тригонометрия |
Рассмотрим комплексное число
| z = cos α + i sin α , | (1) |
модуль которого равен 1, а аргумент равен α (см. раздел «Комплексные числа» нашего справочника). Если комплексное число (1) возвести в квадрат, то, с одной стороны,
| z 2 = cos 2α + i sin 2α , | (2) |
а, с другой стороны,
| z 2 = (cos α + i sin α) 2 = = cos 2α + + 2i cos α sin α – – sin 2α , | (3) |
откуда, приравнивая вещественные и мнимые части комплексных чисел (2) и (3), мы получаем тригонометрические формулы «Косинус двойного угла» и «Синус двойного угла»:
cos 2α = cos 2α – sin 2α ,
sin 2α = 2cos α sin α .
Если же комплексное число (1) возвести в куб, то, с одной стороны,
| z 3 = cos 3α + i sin 3α , | (4) |
а, с другой стороны,
| z 3 = (cos α + i sin α) 3 = = cos 3α + + 3cos 2α (i sin α) + + 3cos α (i sin α)2 + + (i sin α)3 = = cos 3 α – 3cos α sin2α + + 3i cos2α sin α – – i sin3α = = cos 3 α – 3cos αsin2α + + i (3cos2α sin α – sin3α). | (5) |
Следовательно,
z 3 = cos 3 α – 3cos α sin2 α +
+ i (3cos 2α sin α – sin3α) ,
откуда, приравнивая вещественные и мнимые части комплексных чисел (4) и (5), мы получаем соотношения
cos 3α =
= cos3α – 3cos α sin2 α =
= cos3α –
– 3cos α (1 – cos2α) =
= 4cos3α – 3cos α ,
sin 3α =
= 3cos2α sin α – sin3α =
= 3(1 – sin2α) sin α –
– sin3α =
= 3sin α – 4sin3α .
Таким образом,
cos 3α = 4cos3α – 3cos α ,
sin 3α = 3sin α – 4sin3α ,
и вывод тригонометрических формул «Косинус тройного угла» и «Синус тройного угла» завершен.
Совершенно аналогично можно вывести формулы для cos nα и sin nα, где n – произвольное натуральное число.
Формулы кратных углов
Тригонометрические функции являются неотъемлемой частью школьного курса математики, в частности — алгебры. Кто-то про все эти «косинусы», «синусы», «тангенсы» и «котангенсы» забывает, получив аттестат, а кто-то сталкивается с ними все свою последующую жизнь. Однако суть остается одна – тригонометрия является одним из самых важных разделов алгебры, который, ко всему прочему, затрагивает и геометрию.
Однако знать все тригонометрические функции недостаточно, нужно иметь их преобразовывать. Разумеется, функции преобразовываются в процессе решения той или иной задачи и способов их преобразования множество, ничуть не меньше, чем у простых чисел (если не сказать, что больше).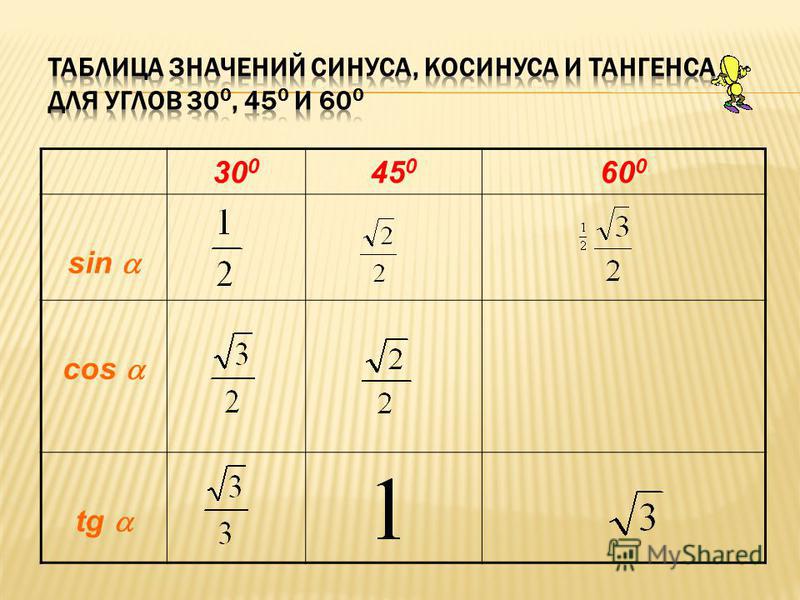
Интересно знать, что формулу cos3a, математик Франсуа Виет использовал при решении кубических уравнений. Он же и нашел выражения для sin na и cos na, которые позже получили более простым путем из всем известной формулы Муавра.
Если же в формулах двойного аргумента произвести замену a на a/2, то данные тригонометрические формулы превращаются в формулы половинных углов.
| sin2α = 2sinαcosα | |||||||||||
| |||||||||||
| |||||||||||
| |||||||||||
| |||||||||||
| |||||||||||
| |||||||||||
| |||||||||||
| |||||||||||
| |||||||||||
| |||||||||||
| |||||||||||
| |||||||||||
| |||||||||||
Что такое формулы множественных углов? Примеры
Множественные углы обычно встречаются в тригонометрических функциях.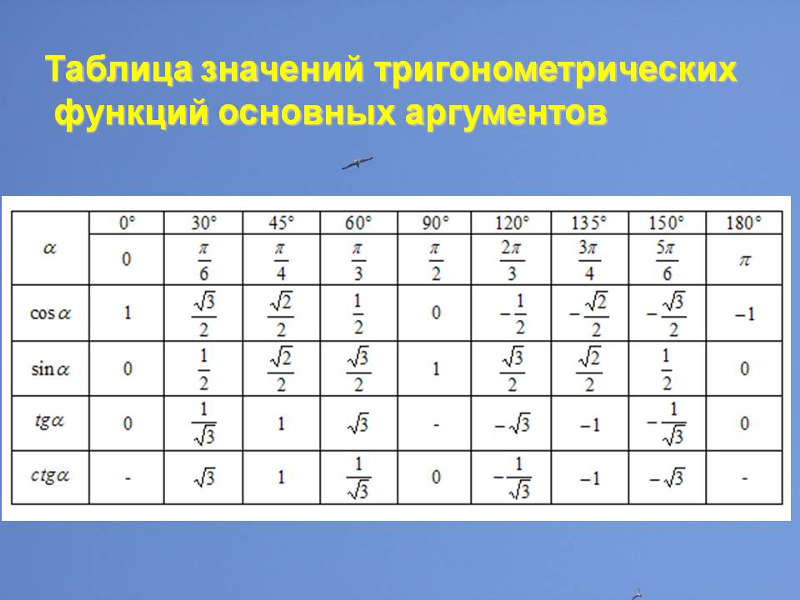 Значения нескольких углов невозможно найти напрямую, но их значения можно рассчитать, выразив каждую тригонометрическую функцию в ее расширенной форме. Тригонометрическая функция нескольких углов также известна как формула нескольких углов. Формула двойного и тройного углов используется в формулах кратных углов. Синус, тангенс и косинус являются общими функциями, которые используются в формуле множественного угла. Давайте узнаем больше о формулах множественных углов в следующих разделах. 9{n-k}\theta \;cos\left [\frac{1}{2}\left(n-k\right)\pi\right]\)
Значения нескольких углов невозможно найти напрямую, но их значения можно рассчитать, выразив каждую тригонометрическую функцию в ее расширенной форме. Тригонометрическая функция нескольких углов также известна как формула нескольких углов. Формула двойного и тройного углов используется в формулах кратных углов. Синус, тангенс и косинус являются общими функциями, которые используются в формуле множественного угла. Давайте узнаем больше о формулах множественных углов в следующих разделах. 9{n-k}\theta \;cos\left [\frac{1}{2}\left(n-k\right)\pi\right]\)
, где n = 1,2,3
Общая формула имеет вид :
cos2θ = cos 2 θ — sin 2 θ
cos3θ = 4cos 3 θ — 3cosθ
Формула 3: Тангационные формулы
\ (tan \; n \ theta = \ frac { sin\;n\theta}{cos\;n\theta}\)
Где n = 1,2,3….
Давайте посмотрим, как использовать формулы кратных углов в следующих решенных примерах. раздел. 9{3}\, \тета – 3 cos\, \тета}=загар\;3\тета\). {2}\,x}\)
{2}\,x}\)
\(=\frac{sin\,x(1+2cos\,x)}{cos\,x(2\,cos\,x+1)}\)
RHS = tanx
Ответ: Отсюда доказано \(\frac{sin\,x+sin\,2x}{1+cos\,x+cos\,2x}=tan\,x\).
Тригонометрические функции суммы и разности двух углов
Тригонометрия — раздел математики, изучающий углы, длины и высоты треугольников и их соотношения. Это сыграло важную роль для вычисления сложных функций или больших расстояний, которые невозможно было вычислить без тригонометрии. При решении задач по тригонометрии мы сталкивались со многими ситуациями, когда приходится вычислять тригонометрические решения для суммы углов или разности углов. Например.
Здесь
Это касательное тригонометрическое отношение с углом, противоположным BC.
tan(θ+Φ) =
Если θ = 30° и Φ = 45°. Мы знаем тригонометрические углы 45° и 30°, но не знаем тригонометрический угол (45° + 30° = 75°). Таким образом, чтобы упростить эти типы проблем. Мы изучим тригонометрические формулы или тождества суммы и разности двух углов, что облегчит задачу.
Прежде чем двигаться дальше, сначала мы увидим знаки тригонометрических функций в четырех квадрантах. Эти знаки играют важную роль в тригонометрии.
Тригонометрические тождестваТеперь найдем тригонометрические тождества. Поскольку мы знаем, что
sin(-x) = – sin x
cos(-x) = cos x
Потому что только cos и sec положительны в четвертом квадранте. Итак, теперь мы докажем некоторые результаты относительно суммы и разности углов:
Рассмотрим единичный круг (с радиусом равным 1) с центром в начале координат. Пусть x будет ∠DOA, а y будет ∠AOB. Тогда (x + y) — это ∠DOB. Также пусть (– y) будет ∠DOC.
Следовательно, координаты A, B, C и D равны
A = (cos x, sin x)
B = [cos (x + y), sin (x + y)]
C = [ cos (– y), sin (– y)]
D = (1, 0).
AS, ϪaOB = Ϫcod
Добавление, с обеих сторон ntboc, мы получаем
↑AOB + ↑BOC = ↑COD + ↑BOC
↑AOC = ↑BOD
в △ AOC и △ BOD
OA = OB (радиус окружности)
∠AOC = ∠BOD (доказано ранее)
OC = OD (радиус окружности)
△ AOC ≅ △ БПК согласно SAS.
Используя формулу расстояния, для
AC 2 = [cos x – cos (– y)] 2 + [sin x – sin(–y] 2
AC 2 2 = 2 (cos x cos y – sin x sin y) …………….(i)
И, теперь
Аналогично, используя формулу расстояния, получаем
BD 2 = [1 – cos (x + у)] 2 + [0 – sin (x + y)] 2
BD 2 = 2 – 2 cos (x + y) …………….(ii)
As, △ AOC ≅ △ БПК
AC = BD, поэтому AC 2 = BD 2
Из уравнения (i) и уравнения (ii) получаем
2 – 2 (cos x cos y – sin x sin y) = 2 – 2 cos (x + y)
Итак,
cos (x + y) = cos x cos y – sin x sin y
Возьмем y = -y, получим
cos (x + (-y)) = cos x cos (-y) – sin x sin (-y)
cos (x – y) = cos x cos y + sin x sin y
Сейчас , взяв
потому что (-(x + y)) = cos ((-x) – y) (cos (-θ) = sin θ)
sin (x – y) = sin x cos y – cos x sin y
возьмем y = -y, получим
sin (x – (-y)) = sin x cos (-y) – cos x sin (-y)
sin (x + y) = sin x cos y + cos x sin y
Полученные формулы для тригонометрических отношений составных углов следующие:
sin (A + B) = sin A cos B + cos A sin B ……………….
.(1)
sin (A – B) = sin A cos B – cos A sin B ………………..(2)
cos (A + B) = cos A cos B – sin A sin B .. ………………(3)
cos (A – B) = cos A cos B + sin A sin B ………………..(4)
Используя эти формулы, мы можем получить важную и наиболее часто используемую форму:
(1) Возьмем A =
В уравнении (1) и (3) мы получим
sin (+B) = cos B
cos (+B) = – sin A
(2 ) Возьмем, A = π
В уравнениях (1), (2), (3) и (4) мы получаем
sin (π + B) = – sin B
sin (π – B) = sin B
cos ( π ± B) = – cos B
(3) Возьмем A = 2π
В уравнении (2) и (4) получаем
sin (2π – B) = – sin B
cos (2π – B) = cos B
Аналогично для cot A, tan A, sec A и cosec A
(4)
Здесь A, B и (A + B) не являются нечетное число, кратное π/2, поэтому cosA, cosB и cos(A + B) отличны от нуля
tan(A + B) = sin(A + B)/cos(A + B)
Из уравнения (1) и (3) мы получаем
tan(A + B) = sin A cos B + cos A sin B/cos A cos B – sin A sin B
Теперь разделим числитель и знаменатель на cos A cos B, получим
tan(A + B) =
(5)
3
4
Поскольку мы знаем, что
Итак, полагая B = -B, мы получаем
(6)
Здесь A, B и (A + B) не кратны π, поэтому sinA, sinB и sin(A + B) отличны от нуля
cot(A + B) = cos(A + B)/sin(A + B)
Из уравнения (1) и (3) мы получаем
cot(A + B) = cos A cos B – sin A sin B/sin A cos B + cos A sin B
Теперь разделим числитель и знаменатель на sin A sin B, получим
cot(A + B) =
(7)
Поскольку мы знаем, что
Итак, поставив B = -B, мы получим
Здесь мы установим два набора формул преобразования: формулы факторизации и дефакторизации.
Формулы дефакторизации
В тригонометрии дефакторизация означает преобразование произведения в сумму или разность. Формулы дефакторизации:
(1) 2 sin A cos B = sin (A + B) + sin (A – B)
Доказательство:
Поскольку мы знаем, что
sin (A + B) = sin A cos B + cos A sin B …………………………(1)
sin (A – B) = sin A cos B – cos A sin B ……………………… …(2)
Складывая уравнение (1) и (2), мы получаем
2 sin A cos B = sin (A + B) + sin (A – B)
(2) 2 cos A sin B = sin (A + B) – sin (A – B)
Доказательство:
Поскольку мы знаем, что
sin (A + B) = sin A cos B + cos A sin B …………………………(1)
sin (A – B) = sin A cos B – cos A sin B ………………………(2)
Вычитая уравнение (2) из (1), получаем
2 cos A sin B = sin (A + B) – sin (A – B)
(3) 2 cos A cos B = cos (A + B) + cos (A – B)
Доказательство:
Поскольку мы знаем, что
cos (A + B) = cos A cos B – sin A sin B ……………………………(1) B) = cos A cos B + sin A sin B ………………………(2)
Складывая уравнения (1) и (2), мы получаем
2 cos A cos B = cos (A + B) + cos (A – B)
(4) 2 sin A sin B = cos (A – B) – cos (A + B)
Доказательство:
cos (A + B) = cos A cos B – sin A sin B ………………………(1)
cos (A – B) = cos A cos B + sin A sin B ………………………(2)
Вычитая уравнение (3) из (4), мы получаем
2 sin A sin B = cos (A – B) – cos (A + B)
Пример 1. Преобразуйте каждое из следующих произведений в сумму или разность.
Преобразуйте каждое из следующих произведений в сумму или разность.
(i) 2 SIN 40 ° COS 30 °
(II) 2 SIN 75 ° SIN 15 °
(III) COS 75 ° COS 15 °
Раствор:
4444444449 :444444444449:
44444444449(и) Дано: A = 40° и B = 30°
Теперь подставим все эти значения в формулу
2 sin A cos B = sin (A + B) + sin (A – B)
Получим
2 sin 40° cos 30° = sin (40 + 30) + sin (40 – 30)
= sin (70°) + sin (10°)
(ii) Дано: A = 75° и B = 15°
Теперь подставим все эти значения в формулу
2 sin A sin B = cos (A – B) – cos (A + B)
Получим
2 sin 75° sin 15° = cos (75-15) – cos (75+15)
= cos (60°) – cos (90°)
(iii) Дано: A = 75° и B = 15°
Теперь подставьте все эти значения в формулу
2 cos A cos B = cos (A + B) + cos (A – B)
Получаем
cos 75° cos 15° = 1/2(cos (75+15) + cos (75-15))
= 1/ 2 (cos (90°) + cos (60°))
Пример 2.
Найдите
Решение:
Используя формулу
+ 2 cos A cos B = cos (A cos B) + cos (А – В)
=
=
=
Следовательно,
= 0
Факторизация. Формулы
Формулы факторизации:
(1) sin (C) + sin (D) = 2 sin cos
Доказательство:
B) + sin (A – B) ………………………(1)
Итак, теперь мы берем
A + B = C и A – B = D
Тогда A = и B =
Теперь поместите все эти значения в уравнение (1), мы получим
2 sin () cos () = sin (C ) + sin (D)
Или
sin (C) + sin (D) = 2 sin () cos ()
(2) sin (C) – sin (D) = 2 cos sin
Доказательство:
Имеем
2 cos A sin B = sin (A + B) – sin (A – B) ………………………(1)
Итак, теперь, мы берем
A + B = C и A – B = D
Тогда A = и B =
Теперь поместите все эти значения в уравнение (1), мы получим
2 cos () sin () = sin (C) – sin (D)
Или
sin ( C) – sin (D) = 2 cos () sin ()
(3) cos (C) + cos (D) = 2 cos cos
Доказательство:
902 cos A cos B = cos (A + B) + cos (A – B) …………………………(1)
Итак, теперь мы берем
A + B = C и A – B = D
Тогда A = и B =
Теперь поместите все эти значения в уравнение (1), мы получим
2 cos () cos () = cos (C) + cos (D)
Или
cos (C) + cos (D) = 2 cos () cos ()
(4) cos (C) – cos (D) = 2 sin sin
Доказательство:
A – B) – cos (A + B) …………………………(1)
Итак, теперь мы берем
A + B = C и A – B = D
Тогда, А = и В =
Теперь поместите все эти значения в уравнение (1), мы получим
2 sin () sin () = cos (C) – cos (D)
Или
cos (C) – cos (D) = 2 sin () sin ()
Объясните 1. Выразите каждое из следующих чисел в виде произведения
Выразите каждое из следующих чисел в виде произведения
(i) sin 40° + sin 20°
(ii) sin 60° – sin 20°
(iii) cos 40° + cos 80°
Решение:
(i) Дано: C = 40° и D = 20°
Теперь подставим все эти значения в формулу
sin (C) + sin (D) = 2 sin cos
Получим
sin 40° + sin 20° = 2 sin cos
= 2 sin cos
= 2 sin 30° cos 10°
(ii) Дано: C = 60° и D = 20° 2 cos sin
Получаем
sin 60° – sin 20° = 2 cos sin
= 2 cos sin
= 2 cos 40° sin 20°
(iii) Дано: C = 80°, D = 40° cos 40° + cos 80° = 2 cos cos
= 2 cos cos
= 2 cos 60° cos 20°
Пример 2. Докажите, что: 1 + cos 2x + cos 4x + cos 6x = 4 x cos 2x cos 3x
Решение:
Возьмем LHS
1 + cos 2x + cos 4x + cos 6x
Здесь, cos 0x = 1
Итак,
(cos 0x + cos 2x) + (cos 4x + cos 6x)
Используя формулу
cos (C) + cos (D) = 2 cos cos
Получаем(2 cos cos) + (2 cos cos)
(2 cos x cos x) + (2 cos 5x cos x)
Взяв 2 cos x общие, имеем
2 cos x (cos x + cos 5x)
Снова используя формулу
cos (C) + cos (D) = 2 cos cos
Получаем
2 cos x (2 cos cos)
2 cos x (2 cos 3x cos 2x)
4 cos x cos 2x cos 3x
LHS = RHS
Отсюда доказано угла в прямоугольном треугольнике определяют отношение между углом и длиной его сторон.
sin 2x или cos 2x и т. д. также являются одной из таких тригонометрических формул, также известных как формула двойного угла, поскольку в ней есть двойной угол.
(1) sin 2A = 2 sin A cos A
Доказательство:
Поскольку мы знаем, что
sin (A + B) = sin A cos B + cos A sin B ………………..(1)
Теперь примем B = A , в уравнении (1) мы получаем
sin (A + A) = sin A cos A + cos A sin A
sin 2A = 2 sin A cos A
(2) cos 2A = cos 2 (1) )
Теперь принимая B = A, в уравнении (1) мы получаем
cos (A + A) = cos A cos A + sin A sin A
cos 2A = cos 2 A – sin 2 A
(3) COS 2A = 2COS 2 A — 1
Доказательство:
Как мы знаем,
COS 2A = COS 2 A — SIN 2 A… ………..(1)
Мы также знаем, что
sin 2 A + cos 2 A = 1
Итак, sin 2 A = 1 – cos 2 A
Теперь подставим значение sin 2 A в уравнение (1), получим
cos 2A = cos 2 A – (1 – cos9 2 2 0 A)
COS 2A = COS 2 A — 1 + COS 2 A
COS 2A = 2COS 2 A — 1
(4) COS 2A = 1 — 2SIN 2 A
Доказательство:
Поскольку мы знаем, что
cos 2A = 2cos 2 A – 1 ……………….
.(1)
Мы также знаем, что
SIN 2 A + COS 2 A = 1
SO, COS 2 A = 1 — SIN 2 A
Сейчас положите значение SIN 2 A в уравнении (1) мы получаем
cos 2A = 2(1 – sin 2 A) – 1
cos 2A = 2 – 2sin 2 A) – 1
cos 2A = 1 – 2sin 2 A
(5) cos 2A =
Доказательство:
Как мы знаем,
cos 2A = cos 2 A – sin 2 A
Итак, делим теперь на sin 2 A + cos 2 A = 1, получаем
0A 9 деление 0Acos Числователь и знаменатель от COS 2 A, мы получаем
COS 2A =
COS 2A =
(6) SIN 2A =
Доказательство:
Как мы знаем,
SIN (
Как мы знаем,
SIN (
AS WELL, что 9003
SIN (
.
A + B) = sin A cos B + cos A sin B ………………..(1)
Теперь принимая B = A, в уравнении (1) мы получаем
sin (A + A) = sin A cos A + cos A sin A
sin 2A = 2 sin A cos A
Поскольку мы также знаем, что sin 2 A + cos 2 A = 1
Итак, делим теперь на sin 2 A + cos 2 A = 1, получаем
sin 2A = числитель
,и знаменатель на cos 2 А, получаем
sin 2A =
(7) tan 2A =
Доказательство:
Поскольку мы знаем, что
………………..(1)
Теперь, взяв B = A, в уравнении (1) мы получим
tan(A + A) =
TAN 2A =
Пример: докажите, что
(I) = TAN θ
(II) = COT θ
(III) COS 4X 4X = 4X = 4X = 4X = 4X = 4X = 4X = 4X = 4X = 4X = 4X = 4X = 4X = 4X = 4X = 4X = 4X = 8 θ
(III).
2 x cos 2 x
Решение:
(i) sin 2θ = 2 sin θ cos θ ………..(из тождества 1)
и, 1 + cos 2θ = 2cos 2 θ ……… .. (из идентичности 3)
=
= tan θ
Отсюда доказано
(ii) sin 2θ = 2 sin θ cos θ ………..(из тождества 1)
и, 1 – cos 2θ = 2sin 2 θ ………..(из тождества 4)
=
= ctg θ
2 Отсюда Доказано
(iii) cos 4x = cos 2(2x)
= 1 – 2sin 2 (2x) (используя 16)
= 1 – 2(sin(2x)) 2
= 1 – 2(2 sin x cos x) 2 (с использованием тождества 1)
= 1 – 2(4 sin 2 x cos 2 x) = 1
cos 8 sin 2 x cos 2 x
Отсюда доказано
Тригонометрические отношения кратных углов (3A) через угол A
Тригонометрические отношения угла в прямоугольном треугольнике определяют отношение между углом и длина его сторон.
sin 3x или cos 3x и т. д. также являются одной из таких тригонометрических формул, также известных как формула тройного угла, поскольку в ней есть тройной угол.
(1) SIN 3A = 3SIN A — 4 SIN 3 A
Доказательство:
Let’s Take LHS
SIN 3A = SIN (2A + A)
Используя личность
SIN (2A + A)
. A + B) = sin A cos B + cos A sin B
Получаем
sin 3A = sin 2A cos A + cos 2A sin A
= 2sin A cos A cos A + (1 – 2 sin 2 A)sin A
= 2sin A(1 – sin 2 A) + sin A – 2 sin 3 A
= 2SIN A — 2SIN 3 A + SIN A — 2 SIN 3 A
SIN 3A = 3SIN A — 4 SIN 3 A
(2) COS 3A = 4 COS . 3 A – 3cos A
Доказательство:
Возьмем LHS
sin 3A = sin(2A + A)
Используя тождество
A cos B – A cos B – A cos Acos (
) cos sin B
Получаем
cos 3A = cos 2A cos A – sin 2A sin A
= (2cos
2 A – 1)cos A – 2sin A cos A sin A = (2cos 2 A – 1)cos A – 2cos A(1 – cos 2 A)
= 2cos 3 A – COS A — 2COS A + 2COS 3 A)
COS 3A = 4 COS 3 A — 3COS A
(3) TAN 3A =
Доказательство:
tan 3A = tan(2A + A)
Используя идентификатор
Получаем
tan 3A =
=
=
=
Пример 1.


 .(1)
.(1) 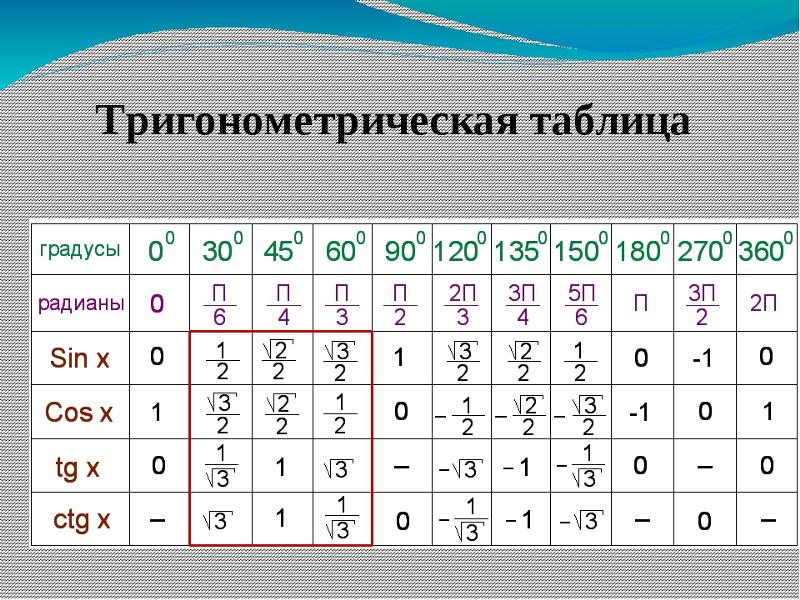 Найдите
Найдите  sin 2x или cos 2x и т. д. также являются одной из таких тригонометрических формул, также известных как формула двойного угла, поскольку в ней есть двойной угол.
sin 2x или cos 2x и т. д. также являются одной из таких тригонометрических формул, также известных как формула двойного угла, поскольку в ней есть двойной угол.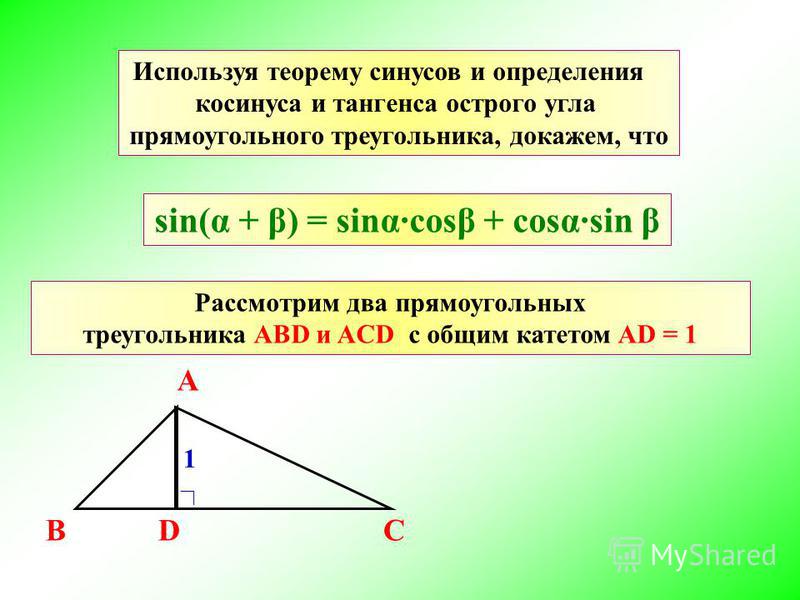 .(1)
.(1) A + B) = sin A cos B + cos A sin B ………………..(1)
A + B) = sin A cos B + cos A sin B ………………..(1) 2 x cos 2 x
2 x cos 2 x  sin 3x или cos 3x и т. д. также являются одной из таких тригонометрических формул, также известных как формула тройного угла, поскольку в ней есть тройной угол.
sin 3x или cos 3x и т. д. также являются одной из таких тригонометрических формул, также известных как формула тройного угла, поскольку в ней есть тройной угол.