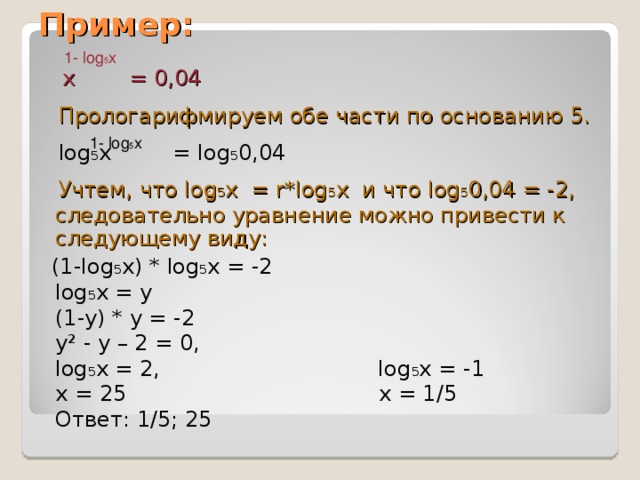
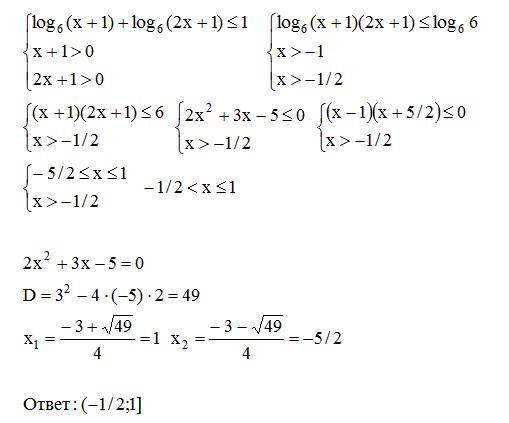Презентация на тему: «Y=log 2x-1 (x 2
1 y=log 2x-1 (x 2 — 2x-7) L o g l o g 2 2 x x x = c o s 3 0 x Логарифмические уравнения и неравенства. Методы решения
2 Exit Логарифмы в истории Логарифмы в истории Логарифмы в истории Логарифмы в истории Логарифм Логарифм Логарифм Логарифмическая функция f(x)=log a x Логарифмическая функция f(x)=log a x Логарифмическая функция f(x)=log a x Логарифмическая функция f(x)=log a x Логарифмические уравнения Логарифмические уравнения Логарифмические уравнения Логарифмические уравнения Логарифмические неравенства Логарифмические неравенства Логарифмические неравенства Логарифмические неравенства
3
Открытие логарифмов — еще одна историческая цепочка знаний, которая связана не только с математикой, но и, казалось бы, совсем не имеющей к ней отношение музыкой.
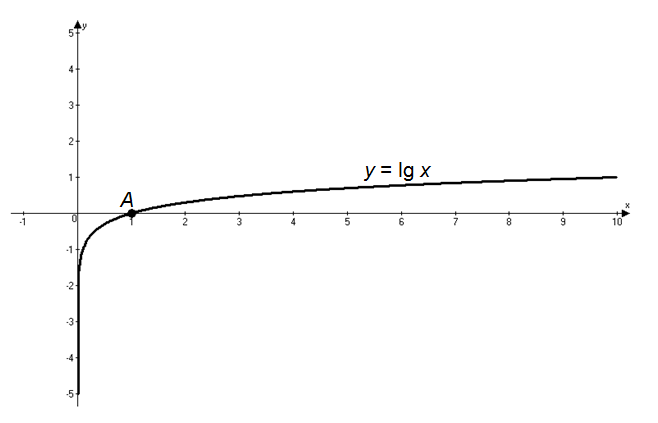
4
Идея логарифма возникла также в Древней Греции. Так, в сочинении «Псамлигт» Архимеда ( гг. до н.э.) мы читаем: «Если будет дан ряд чисел в непрерывной пропорции начиная от 1 и если два его члена перемножить, то произведение будет членом того же ряда, настолько удаленным от большего множителя, насколько меньший удален от единицы, и одним членом меньше против того, насколько удалены оба множителя вместе». Здесь под «непрерывной пропорцией» Архимед разумеет геометрическую прогрессию, которую мы записали бы так: 1, а, а 2.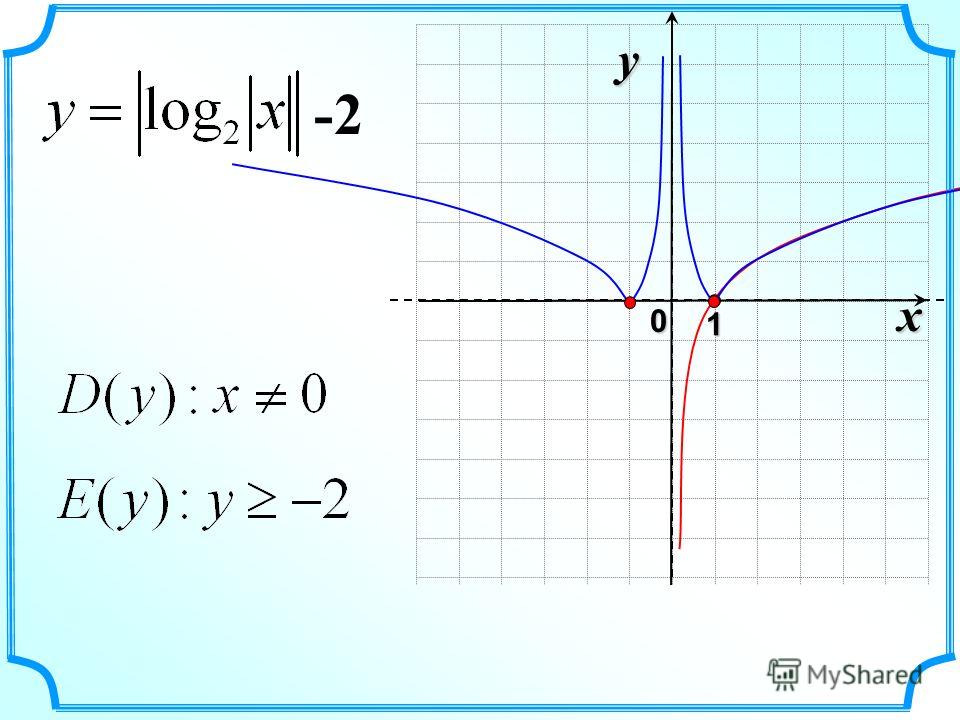
5 Что такое логарифм? log a b=c log a b=c a c =b Основное логарифмическое тождество
6
Основные свойства логарифмов 1) Логарифм произведения положительных сомножителей равен сумме логарифмов этих сомножителей: log a N 1 ·N 2 = log a N 1 + log a N 2 (a > 0, a 1, N1 > 0, N2 > 0).
7
3) Логарифм степени положительного числа равен произведению показателя степени на логарифм этого числа: log a N k = k log a N (a > 0, a 1, N > 0).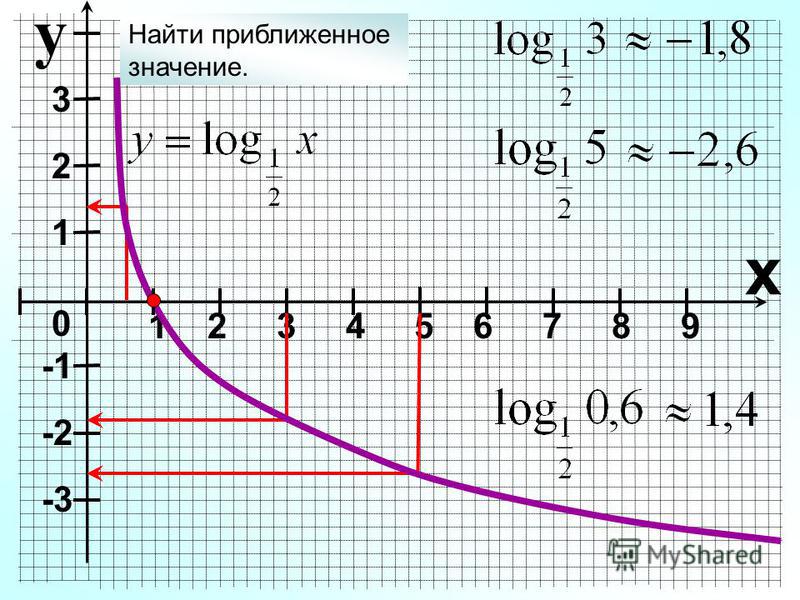
Замечание. Если k — четное число (k = 2s), то log a N 2s = 2s log a |N| (a > 0, a 1, N 0). 4) Формула перехода к другому основанию: (a > 0, a 1, c > 0, c 1, b > 0), в частности, если b = c, получим (a > 0, a 1, b > 0, b 1).
9 x y a y=log a x y=a x y=x
10
1.
Область определения логарифмической функции есть множество положительных чисел. 2.Область значений логарифмической функции — множество действительных чисел. 3.При a > 1 логарифмическая функция строго возрастает (0 log a x 1 log a x 1 >log a x 2 ). 4.log a 1 = 0 и log a a = 1 (a > 0, a 1). 5.Если a > 1, то логарифмическая функция отрицательна при x Î (0;1) и положительна при x Î (1;+ ), а если 0 1, то логарифмическая функция выпукла вверх, а если a Î (0;1) — выпукла вниз.
11 x y y=log a x 1 1 a y x 1 a a>1 0
12
2) log a f(x) = log a g(x) Уравнение, содержащее неизвестное под знаком логарифма или (и) в его основании, называется логарифмическим уравнением.
13 4) log h(x) f(x) = log h(x) g(x) f(x) > 0, h(x) 1, h(x) > 0, f(x) = g(x), g(x) > 0. h(x) 1, h(x) > 0, f(x) = g(x), Потеря решений при неравносильных переходах log a f(x) = log a g(x) f(x) = g(x)
14 Методы решения логарифмических уравнений Использование определения логарифма Использование определения логарифма log a b = c b = a c Пример log 2 (5 + 3log 2 (x — 3)) = 3 log 2 (5 + 3log 2 (x — 3)) = 3 Решение Решение 5+3log 2 (x-3)=2 3 log 2 (x — 3) = 1 x=5
15
Методы решения логарифмических уравнений Использование свойств логарифма Использование свойств логарифма log a b = c b = a c Пример log 3 x + log 3 (x + 3) = log 3 (x + 24), log 3 x + log 3 (x + 3) = log 3 (x + 24), Решение Решение О.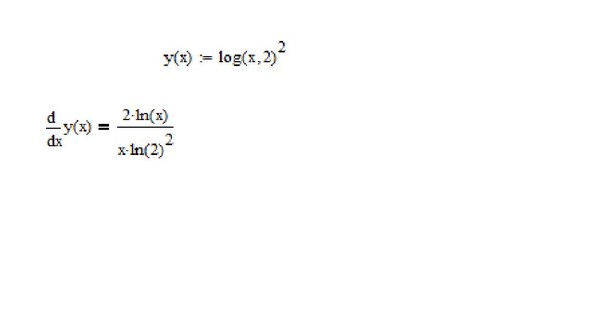
Д.З.: x>0, x(x+3)=x+24 x 2 + 2x — 24 = 0 x={-6;4} x(x+3)=x+24 x 2 + 2x — 24 = 0 x={-6;4} x>0 x>0 x=4 x=4
16 Методы решения логарифмических уравнений Метод подстановки Метод подстановки f(log a x)=0 t=log a x f(t)=0 f(t)=0Пример lg 2 x — 3lgx + 2 = 0 lg 2 x — 3lgx + 2 = 0Решение lg x = t lgx=1 t 2 -3t+2=0 lgx=2 x={10;100}
17 Пример 5 lg x = 25 5 lgx = 50 — x lg5 5 lgx = lgx 5 lg x = 25 x=100 x=100
18
Методы решения логарифмических уравнений Уравнения, содержащие выражения вида Уравнения, содержащие выражения видаПример Решение Решение log 2 (x+2)=t, t 2 -t-2=0.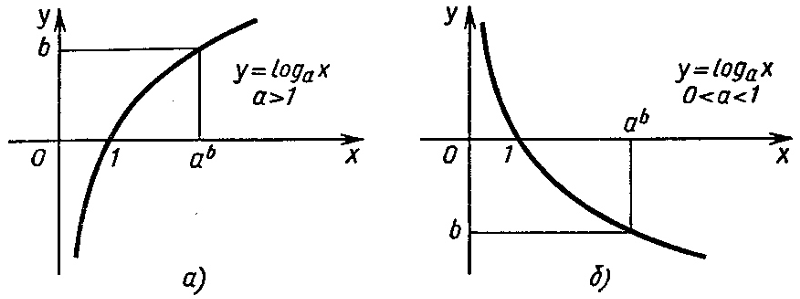
19 Методы решения логарифмических уравнений Метод оценки левой и правой частей Метод оценки левой и правой частейПример log 2 (2x – x ) = x 2 – 2x + 5. log 2 (2x – x ) = x 2 – 2x + 5. Решение Решение 1) 2x – x = – (x 2 – 2x – 15) = –((x 2 – 2x + 1) –1 –15)= = (16 – (x – 1) 2 ) 16 log 2 (2x – x ) 4. 2) x 2 – 2x + 5 = (x 2 – 2x + 1) – = (x – 1) ; log 2 (2x – x )=4, x 2 – 2x + 5 =4. x=1
20
Методы решения логарифмических уравнений Использование монотонности функций.
Подбор корней. Использование монотонности функций. Подбор корней.Пример log 2 (2x – x ) = x 2 – 2x + 5. log 2 (2x – x ) = x 2 – 2x + 5. Решение2x–x 2 +15=t, t>0 Решение2x–x 2 +15=t, t>0 x 2 –2x+5=20–t log 2 t=20-t y=log 2 t – возрастающая, y=20–t – убывающая. Геометрическая интерпретация дает понять, что исходное уравнение имеет единственный корень, который нетрудно найти подбором, t=16. Решив уравнение 2x–x 2 +15=16, находим, что x=1
21
1) log a f(x) > log a g(x) Неравенство, содержащее неизвестное под знаком логарифма или (и) в его основании, называется логарифмическим уравнением.
Логарифмические неравенства f(x)>g(x)>0, a>
22 3) log h(x) f(x)>log h(x) g(x) (h(x)-1)(f(x)-g(x))>0, h(x)>0, f(x)>0, g(x)>0. 4) f(log a x)>0 t=log a x, f(t)>0.
23
Методы решения логарифмических неравенств с переменным основанием Быстрое избавление от логарифмов Пример log 2x (x 2 -5x+6)0.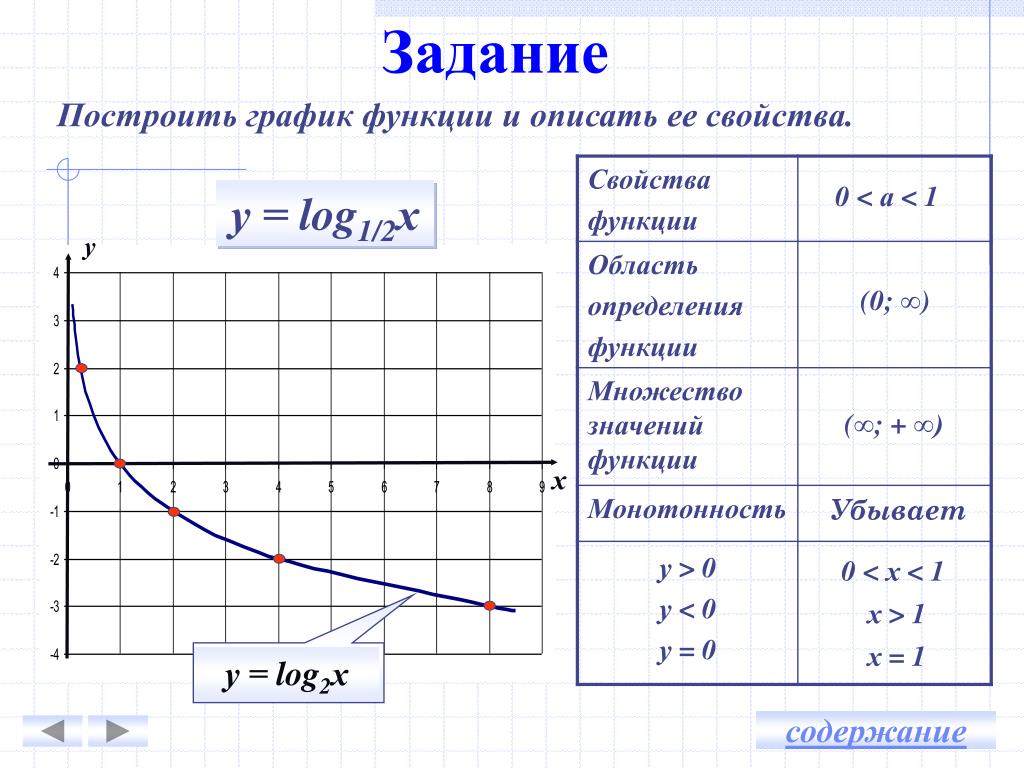
24 Правило знаков Очевидно, что lg x, как и log a x по любому основанию a > 1, имеет тот же знак, что и число x – 1. В более общем случае от логарифма по произвольному основанию a можно перейти к основанию 10: Таким образом, знак величины log a x совпадает со знаком числа (x – 1)/(a – 1) или (x – 1)(a – 1). 1
25
Пример log 2x (x-4) log x-1 (6-x)0, x>0, x1/2, x>1,x-11.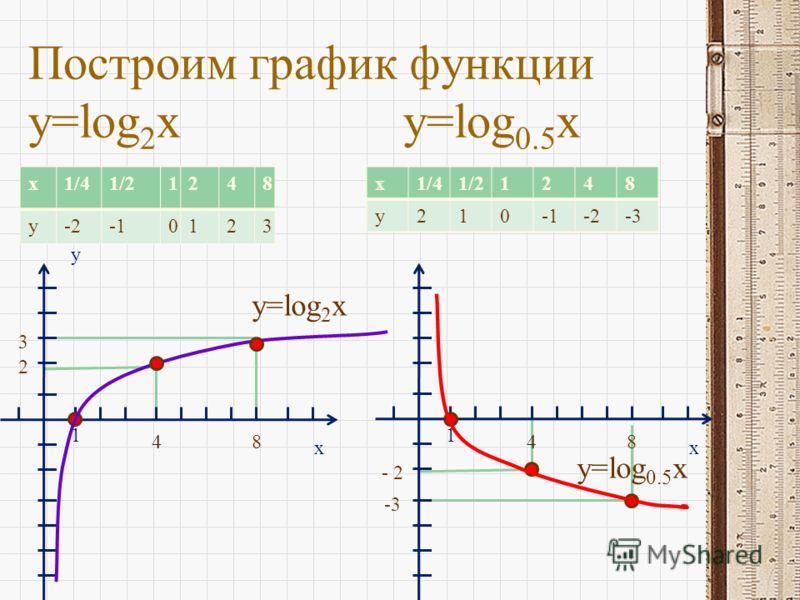
x (4;5) (5;6)
26
Тесты Логарифмические уравнения 11 класс с ответами
Тесты по алгебре 11 класс. Тема: «Логарифмические уравнения»
Правильный вариант ответа отмечен знаком +
1. Как выглядит простейшее логарифмическое уравнение?
a. logax = b +
b. logaa = 1 —
c. 3log = b —
d. logbx = a —
2. log31/9 = …
a.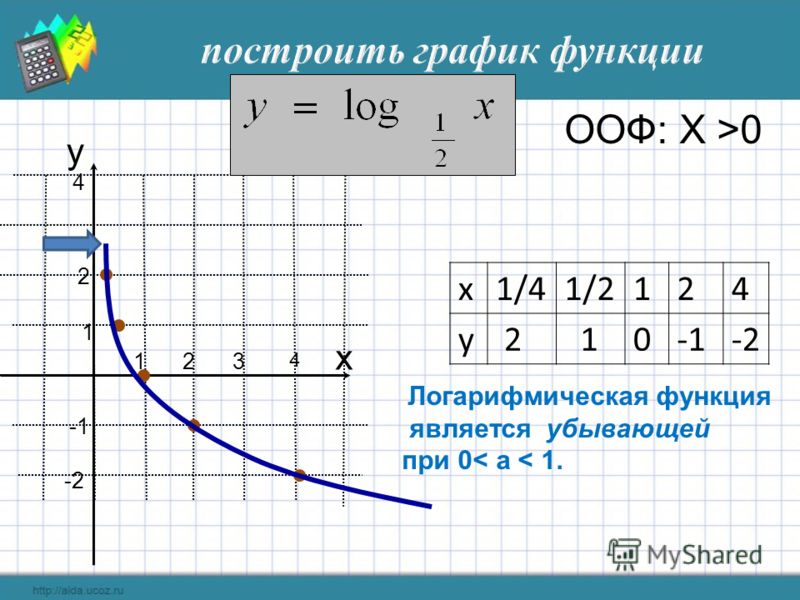
27 —
b. 2 —
c. 12 —
d. -2 +
3. Чему равен x в уравнении log4x = 3?
a. 12 —
b. 64 +
c. 7 —
d. 81 —
4. Что такое логарифмическое уравнение?
a. это уравнение, в котором неизвестные переменные находятся вне логарифмов —
b. это уравнение, в котором отсутствуют неизвестные переменные —
c. это уравнение, в котором неизвестные переменные находятся внутри логарифмов +
d. это уравнение, в котором неизвестные переменные представлены в виде логарифмов —
5. Из-за какого значения уравнение 1 + 2x = log2(3x + 1) нельзя назвать логарифмическим?
a. 1 —
b. 2x +
c. 3x + 1 —
d. log2 —
6. log3x = … при x = ⅓
a. -1 +
b. 3 —
c. 1 —
d. 1/9 —
7. Действие, которое является обратным логарифмированию по некоторому основанию, — это …
a.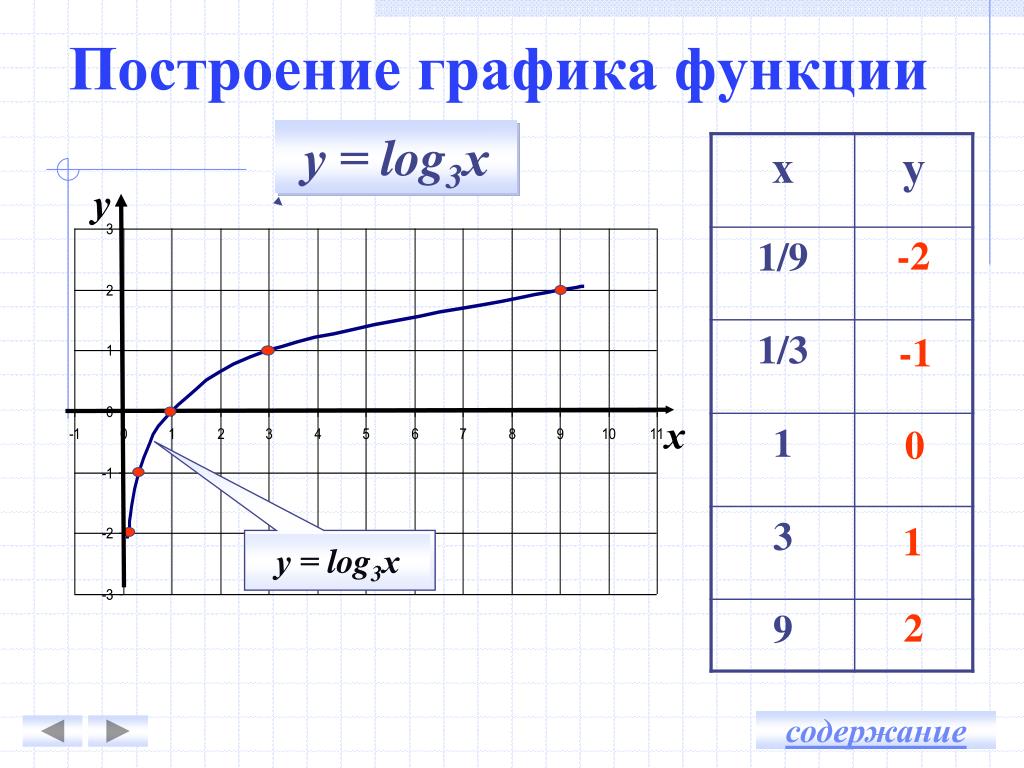
аддитивность —
b. потенцирование +
c. инвариант —
d. тривиальность —
8. Чему равна область определения функции y=logax при a > 0, a≠1?
a. x > 0 +
b. x < 0 —
c. x = 0 —
d. x ⩽ 0 —
9. Какой математик является одним из изобретателей логарифмов?
a. Исаак Ньютон —
b. Джон Непер +
c. Андрей Колмогоров —
d. Леонтий Магницкий —
тест 10. График какого логарифма изображен на картинке?
a. натурального —
b. десятичного +
c. двоичного —
d. логарифма числа b по основанию a —
11. Между какими числами установлено равенство в уравнении logab=c?
a. a и b —
b. a и c —
c. a, b и c +
d. b и c —
12. Чему равен x в уравнении log2x = 3?
a. 9 —
b. 6 —
c. 5 —
d. 8 +
13. Как расшифровывается Одз логарифма?
a.
область допустимых значений логарифма +
b. общее действительное значение логарифма —
c. однозначность логарифма —
d. одинарное значение логарифма —
14. log2 x2 + х = log2(х + 9) при x = …
a. 6 —
b. 3 +
c. 10 —
d. 4 —
15. Логарифмическое неравенство – это неравенство вида logab(x) > logac(x),где а … 0, a ≠ 1
a. < —
b. = —
c. ≫ —
d. > +
16. Область значений логарифмической функции y = logax равна …
a. (-1; +♾) —
b. (-♾; +♾) +
c. (-♾; 1) —
d. -1; 0) —
17. Чему равен логарифм произведения положительных сомножителей?
a. сумме логарифмов этих сомножителей +
b. разности логарифмов этих сомножителей —
c. частному логарифмов этих сомножителей —
d. произведению логарифмов этих сомножителей —
18. Как будет выглядеть уравнение log3(2х-5) = log3х после применения потенцирования?
a.
log2x — 1 = 2 —
b. log3(2х-1) = 2 +
c. log2(2х-1) = 2 —
d. log3(2х-1) = 2 —
19. Какого метода решения логарифмических уравнений не бывает?
a. применения основного логарифмического тождества —
b. метода введения новой переменной —
c. метода логарифмирования —
d. метода превращения логарифмов в десятичные дроби +
тест-20. В каких случаях можно убрать логарифмы из уравнения?
a. если в левой и правой частях уравнения одинаковые основания +
b. если в левой и правой частях уравнения разные степени —
c. если в левой и правой частях уравнения имеются одинаковые степени —
d. если в левой и правой частях уравнения разные основания —
21. Чему равен x в уравнении ?
a. 4 —
b. 3 +
c. 2 —
d. 7 —
22. Кем была изобретена логарифмическая линейка?
a. Эдмундом Гантером +
b.
Вильгельмом Лейбницем —
c. Бернардом Риманом —
d. Пифагором —
23. log5(x — 4) = 2 при x = …
a. 29 +
b. 16 —
c. 11 —
d. 7 —
24. Какое общее основание имеет уравнение log816 + log84 = 2?
a. 8 —
b. log4 —
c. log —
d. log8 +
25. log…125 = 3
a. 5 +
b. 8 —
c. 2 —
d. 9 —
26. Как будет выглядеть уравнение log24x — 2log4x — 3 = 0 после введения новой переменной m?
a. m4 — 5 = 0 —
b. 2m + 3 = 0 —
c. m2 — 2m — 3 = 0 +
d. 4m2 — 2m = 3 —
27. Какой метод решения применим к уравнению log3x = 2?
a. метод по определению логарифма +
b. метод подстановки —
c. метод потенцирования —
d. метод логарифмирования —
28. Из какой страны математик Джон Непер, автор работы «Описание удивительной таблицы логарифмов»?
a.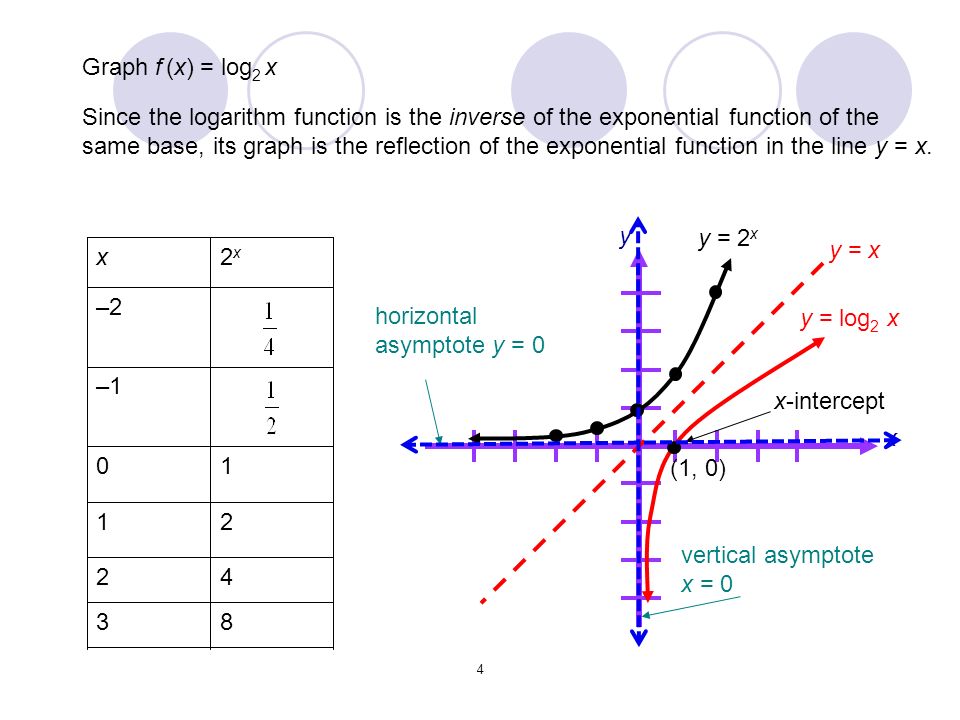
Бельгия —
b. Шотландия +
c. Япония —
d. Англия —
29. Чему равен x в уравнении log5x = 0?
a. 1 +
b. 0 —
c. 2 —
d. -1 —
тест_30. Какое из уравнений не решается методом логарифмирования?
a. 2xlog2 x = 32 —
b. log2((2 + log3(3 + x)) = 0 +
c.loglog2 x = 32 —
d. xlg x= 10 —
3-8Выполнение логарифмических вычислений в программировании на R — функции log(), log10(), log1p() и log2()
Улучшить статью
Сохранить статью
- Последнее обновление:
05 июня 2020 г.
функция log() на языке R возвращает натуральный логарифм (логарифм по основанию e) аргумента, переданного в параметре.
Синтаксис: log(x)
Параметр:
x: Заданное значение.Возвраты: Возвращает натуральный логарифм указанного значения, бесконечность для 0 и NaN для отрицательного значения.
Example 1:
| |
903)
9099)6))
[1] 0
[1] 3.
401197
[1] -Инф
[1] NaN
Предупреждение:
В журнале (-44): произведено NaN
log(x, base = y)
log(x, base=y) — это встроенная функция в R, которая используется для вычисления логарифма указанного значения по основанию y, бесконечности для 0 и NaN для отрицательного значения.
Синтаксис: log(x, основание = y)
Параметры:
x и основание y.Возвраты: Возвращает логарифм указанного значения по основанию y, бесконечность для 0 и NaN для отрицательного значения.
Example 2:
| |
Output:
[1] 1 [1] 4 [1] -Инф [1] NaN Предупреждение: В печати (журнал (-44, база = 4)) : произведено NaN
Функция log10()
log10() — это встроенная функция в R, которая используется для вычисления логарифма указанного значения по основанию 10, бесконечности для 0 и NaN для отрицательного значения.
Синтаксис: log10(x)
Параметры:
x: Заданные значения.Возвраты: Возвращает логарифм указанного значения по основанию 10, бесконечность для 0 и NaN для отрицательного значения.
Example 2:
| |
Output:
[1] 0 [1] 1 [1] -Инф [1] NaN Предупреждение: В печати (log10 (-44)) : произведено NaN
log1p()
log1p() — это встроенная функция в R, которая используется для вычисления точного натурального логарифма 1+x, где x — указанное значение, и возвращает бесконечность для 0 и NaN для отрицательного значения.
.
Синтаксис: log1p(x)
Параметры:
x: Заданные значения.Возвраты: Возвращает точный натуральный логарифм 1+x, где x — заданное значение, и возвращает бесконечность для 0 и NaN для отрицательного значения.
Example:
| |
