Y log2x: Решить y=log2x | Microsoft Math Solver

y = log2*(|x|)

Графики функций, Построение графиков Работа проверена: sargy Время решения: 6 мин Сложность: 3.7

Дано

$$f{left (x right )} = log{left (2 right )} left|{x}right|$$

График функции

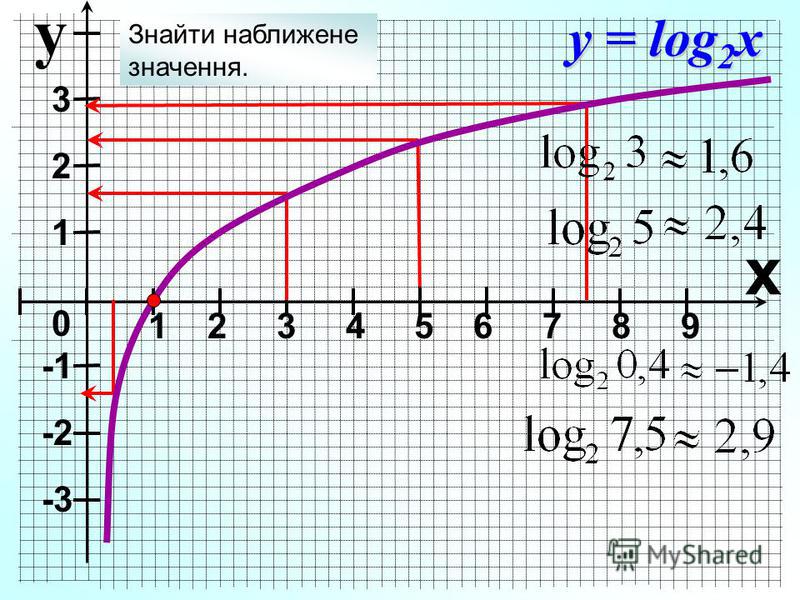
Точки пересечения с осью координат X

График функции пересекает ось X при f = 0
значит надо решить уравнение:
$$log{left (2 right )} left|{x}right| = 0$$
Решаем это уравнение
Точки пересечения с осью X:

Аналитическое решение
$$x_{1} = 0$$
Численное решение
$$x_{1} = 0$$

Точки пересечения с осью координат Y

График пересекает ось Y, когда x равняется 0:
подставляем x = 0 в log(2)*|x|.
$$log{left (2 right )} left|{0}right|$$
Результат:
$$f{left (0 right )} = 0$$

Точка:

(0, 0)

Экстремумы функции

Для того, чтобы найти экстремумы, нужно решить уравнение
$$frac{d}{d x} f{left (x right )} = 0$$
(производная равна нулю),
и корни этого уравнения будут экстремумами данной функции:
$$frac{d}{d x} f{left (x right )} = $$
Решаем это уравнение
Корни этого ур-ния
$$x_{1} = 0$$
Зн. экстремумы в точках:

(0, 0)

Интервалы возрастания и убывания функции:
Найдём интервалы, где функция возрастает и убывает, а также минимумы и максимумы функции, для этого смотрим как ведёт себя функция в экстремумах при малейшем отклонении от экстремума:
Минимумы функции в точках:
$$x_{1} = 0$$
Максимумов у функции нет
Убывает на промежутках

[0, oo)

Возрастает на промежутках

(-oo, 0]

Горизонтальные асимптоты

Горизонтальные асимптоты найдём с помощью пределов данной функции при x->+oo и x->-oo
$$lim_{x to -infty}left(log{left (2 right )} left|{x}right|right) = infty$$
Возьмём предел
значит,
горизонтальной асимптоты справа не существует

Наклонные асимптоты

Наклонную асимптоту можно найти, подсчитав предел функции log(2)*|x|, делённой на x при x->+oo и x ->-oo
$$lim_{x to -infty}left(frac{left|{x}right|}{x} log{left (2 right )}right) = – log{left (2 right )}$$
Возьмём предел
значит,
уравнение наклонной асимптоты справа:
$$y = x log{left (2 right )}$$

Чётность и нечётность функции

Проверим функци чётна или нечётна с помощью соотношений f = f(-x) и f = -f(-x).
Итак, проверяем:
$$log{left (2 right )} left|{x}right| = log{left (2 right )} left|{x}right|$$
– Да
$$log{left (2 right )} left|{x}right| = – log{left (2 right )} left|{x}right|$$

– Нет
значит, функция
является
чётной

   

3-8 9 Оценить квадратный корень из 12 10 Оценить квадратный корень из 20 11 Оценить квадратный корень из 50 94 18 Оценить квадратный корень из 45 19 Оценить квадратный корень из 32 20 Оценить квадратный корень из 18 92

Логарифмические функции и их графики

4.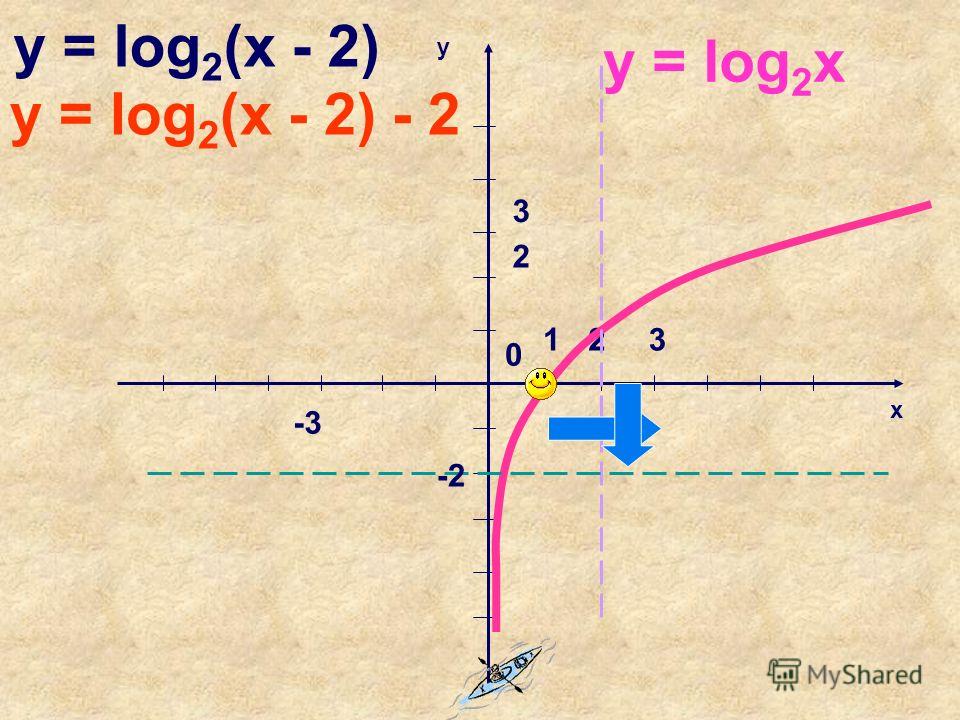 2 — Логарифмические функции и их графики

Обратная экспоненциальная функция

В разделе об экспоненциальных функциях мы заявили, что экспоненциальные функции были взаимно однозначными. Один к одному функции обладали тем особым свойством, что они имеют обратные это тоже функции. И, как многие из вас говорили в классе, и я так рад, что вы помните, функции один-к-одному могут применяться к обеим частям уравнения. Они также проходят тест горизонтальной линии.

Этот раздел посвящен обратной экспоненциальной функция. Обратной экспоненциальной функцией является логарифмическая функция. Помните, что инверсия функция получается путем переключения координат x и y. Это отражает график относительно прямой y=x. Как видно из графика справа, логарифмическая кривая является отражением экспоненциальной кривой.

В таблице ниже показано, как значения x и y точек на экспоненциальной кривую можно переключать, чтобы найти координаты точек на логарифмической изгиб.

Точка на экспоненциальной кривой	Соответствующая точка на логарифмической кривой
(-3, 1/8)	(1/8, -3)
(-2, 1/4)	(1/4, -2)
(-1, 1/2)	(1/2, -1)
(0, 1)	(1, 0)
(1, 2)	(2, 1)
(2, 4)	(4, 2)
(3, 8)	(8, 3)

Сравнение экспоненциальной и логарифмической функций

Давайте посмотрим на некоторые свойства из двух функций.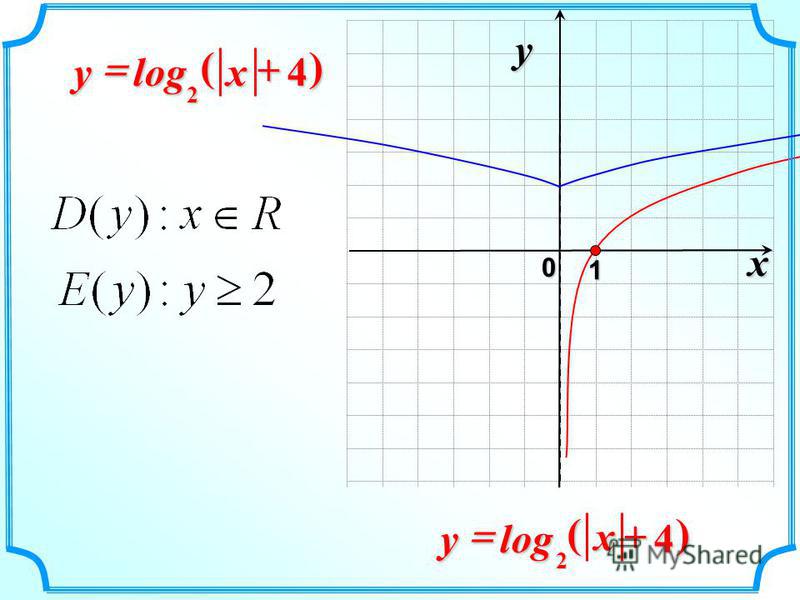

Стандартная форма логарифмической функции: y = log _a x

Обратите внимание, если «а» в приведенном выше выражении не является нижним индексом (ниже, чем «лог»), тогда вам нужно обновить свой веб-браузер.

	Экспоненциальный	Логарифмический
Функция	у=а х , а>0, а≠1	у=log а х, а>0, а≠1
Домен	все реалы	х > 0
Диапазон	г > 0	все реалы
перехват	г = 1	х = 1
увеличение	при > 1	при > 1
по убыванию	, когда 0 < а < 1	, когда 0 < а < 1
асимптота	ось x (y=0)	ось Y (x=0)
непрерывный	да	да
гладкая	да	да

Рабочее определение логарифма

В экспоненциальной функции x был показателем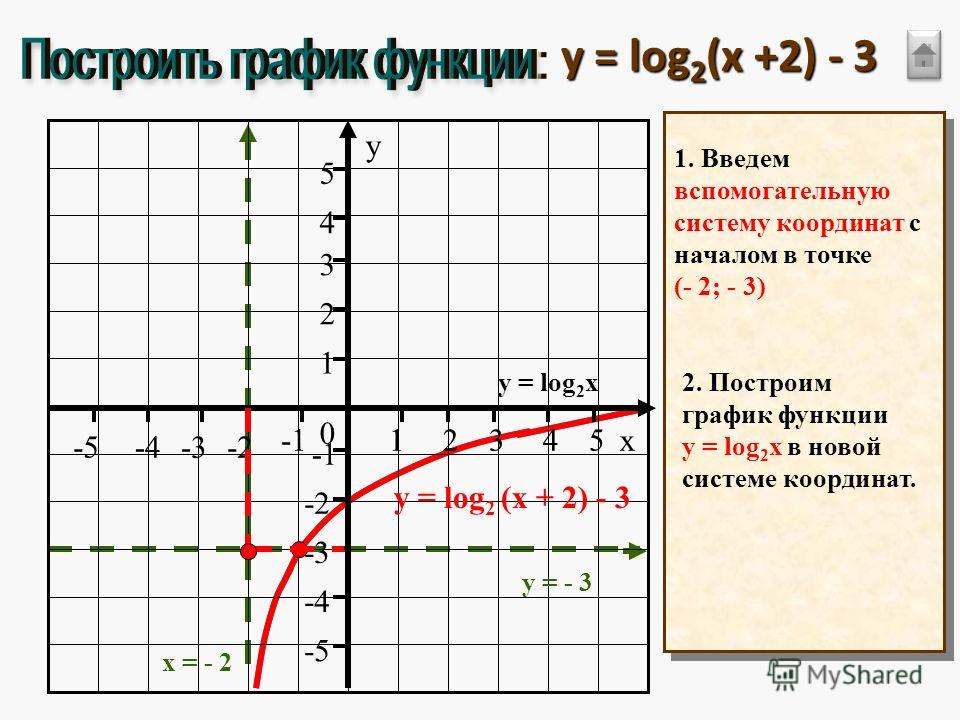 степени. Цель обратной функции чтобы сообщить вам, какое значение x было использовано, когда вы уже знаете значение y. Итак, целью логарифм, чтобы сказать вам показатель степени.

Таким образом, наше простое определение логарифма состоит в том, что он является показателем степени.

Другой способ взглянуть на выражение «log _a x» — это «в какую степень (показатель степени) нужно возвести а получить х?»

Эквивалентные формы

Логарифмическая форма уравнения y=log

a x эквивалентна экспоненциальной форме x=a ^y .

Чтобы переписать одну форму в другую, оставьте основу прежней и поменяйте местами две другие стороны ценности.

Свойства логарифмов

журнал _a 1 = 0, потому что a ⁰ = 1

Независимо от базы, если она разрешена, логарифм 1 всегда равен 0. Это потому что логарифмические кривые всегда проходят через (1,0)

log _a a = 1, потому что a ¹ = a

Любое значение, возведенное в первую степень, такое же значение.

журнал _а а ^х = х

Основание логарифма x и a в степени x являются обратными функциями. Всякий раз, когда инверсия функции применяются друг к другу, они инвертируются, и у вас остается в аргумент, в данном случае x.

log _a x = log _a y означает, что x = y

Если два бревна с одинаковым основанием равны, то аргументы должны быть равны.

log _a x = log _b x означает, что a = b

Если два логарифма с одним и тем же аргументом равны, то основания должны быть равны.

Обычные бревна и бревна

На вашем калькуляторе есть две кнопки логарифмирования. Один помечен как «журнал» и другой отмечен «лн». Ни в одном из них не записана база. База может быть определена, однако, взглянув на обратную функцию, которая написана над ключом и доступ по 2 ^и ключ.

Десятичный логарифм (основание 10)

Когда вы видите написанное «журнал» без основания, примите, что основание равно 10.
То есть: log x = log ₁₀ x.

Некоторые приложения, использующие десятичные логарифмы, относятся к pH (для измерения кислотности), децибелам. (сила звука), шкала Рихтера (землетрясения).

Интересное (возможно) примечание о рН. «Глава 50: Канализация» деревни Кодекса Форсайта требует запрещает сброс отходов с рН менее 5,5 или выше 10,5 (раздел 50.07).

Обычные журналы служат и другой цели. Каждое увеличение десятичного логарифма на 1 является результатом 10-кратного аргумента. То есть землетрясение силой 6,3 имеет 10 раз превышает величину землетрясение силой 5,3 балла. Уровень децибел громкой рок-музыки или бензопилы (115 децибел = 11,5 бел) в 10 раз громче, чем куры внутри здания (105 децибел = 10,5 бел)

Натуральные логарифмы (основание e)

Помните тот номер e , который у нас был из предыдущего раздела? Знаешь, тот, который был примерно 2,718281828 (но не повторяется и не заканчивается). Это основа естественного логарифм.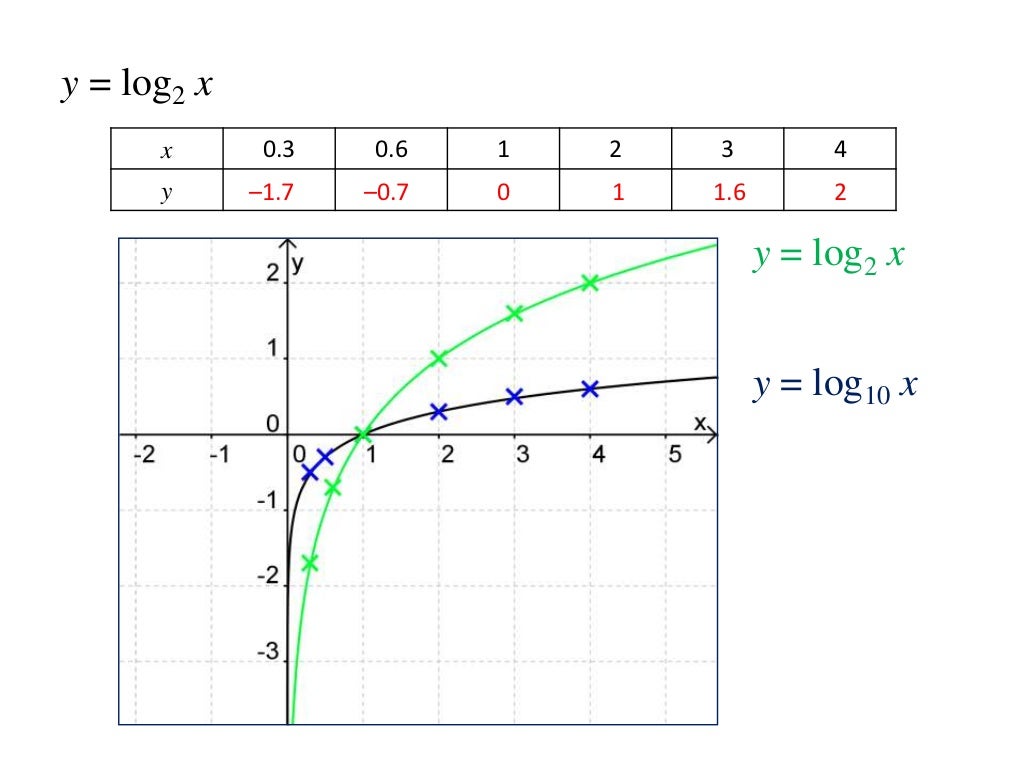

Когда вы видите написанное «ln», основание равно e .
То есть: ln x = log _e x

Модели экспоненциального роста и затухания — одно из приложений, использующих натуральные логарифмы. Этот включает непрерывное накопление, радиоактивный распад (период полураспада), рост населения. Обычно приложения, в которых постоянно происходит процесс. Теперь эти приложения были первыми упоминается в экспоненциальном разделе, но вы сможете решить для других переменных участие (после раздела 4) с использованием логарифмов.

В высшей математике натуральный логарифм является предпочтительным логарифмом. Есть несколько особые свойства функции натурального логарифма и ее обратной функции, которые делают жизнь намного интереснее. проще в расчетах.

Поскольку «ln x» и « e ^x » являются обратными функциями друг друга, всегда, когда «ln» и «e» появляются правильно рядом друг с другом, между которыми абсолютно ничего нет (то есть, когда они составлены друг с другом), затем они инвертируются, и у вас остается Аргумент.