Определение log. Для решения неравенств полезно знать
Начнем со свойства логарифма единицы . Его формулировка такова: логарифм единицы равен нулю, то есть, log a 1=0 для любого a>0 , a≠1 . Доказательство не вызывает сложностей: так как a 0 =1 для любого a , удовлетворяющего указанным выше условиям a>0 и a≠1 , то доказываемое равенство log a 1=0 сразу следует из определения логарифма.
Приведем примеры применения рассмотренного свойства: log 3 1=0 , lg1=0 и .
Переходим к следующему свойству: логарифм числа, равного основанию, равен единице , то есть, log a a=1 при a>0 , a≠1 . Действительно, так как a 1 =a для любого a , то по определению логарифма log a a=1 .
Примерами использования этого свойства логарифмов являются равенства log 5 5=1 , log 5,6 5,6 и lne=1 .
К примеру, log 2 2 7 =7 , lg10 -4 =-4 и .
Логарифм произведения двух положительных чисел x и y равен произведению логарифмов этих чисел: log a (x·y)=log a x+log a y
 Докажем свойство логарифма произведения. В силу свойств степени a log a x+log a y =a log a x ·a log a y
, а так как по основному логарифмическому тождеству a log a x =x
и a log a y =y
, то a log a x ·a log a y =x·y
. Таким образом, a log a x+log a y =x·y
, откуда по определению логарифма вытекает доказываемое равенство.
Докажем свойство логарифма произведения. В силу свойств степени a log a x+log a y =a log a x ·a log a y
, а так как по основному логарифмическому тождеству a log a x =x
и a log a y =y
, то a log a x ·a log a y =x·y
. Таким образом, a log a x+log a y =x·y
, откуда по определению логарифма вытекает доказываемое равенство.Покажем примеры использования свойства логарифма произведения: log 5 (2·3)=log 5 2+log 5 3 и .
Свойство логарифма произведения можно обобщить на произведение конечного числа n положительных чисел x 1 , x 2 , …, x n как log a (x 1 ·x 2 ·…·x n)= log a x 1 +log a x 2 +…+log a x n . Данное равенство без проблем доказывается .
Например, натуральных логарифм произведения можно заменить суммой трех натуральных логарифмов чисел 4 , e , и .
Логарифм частного двух положительных чисел x
и y
равен разности логарифмов этих чисел. Свойству логарифма частного соответствует формула вида , где a>0
, a≠1
, x
и y
– некоторые положительные числа.
Приведем пример использования этого свойства логарифма: .
Переходим к свойству логарифма степени . Логарифм степени равен произведению показателя степени на логарифм модуля основания этой степени. Запишем это свойство логарифма степени в виде формулы: log a b p =p·log a |b| , где a>0 , a≠1 , b и p такие числа, что степень b p имеет смысл и b p >0 .
Сначала докажем это свойство для положительных b . Основное логарифмическое тождество позволяет нам представить число b как a log a b , тогда b p =(a log a b) p , а полученное выражение в силу свойство степени равно a p·log a b . Так мы приходим к равенству b p =a p·log a b , из которого по определению логарифма заключаем, что log a b p =p·log a b .
Осталось доказать это свойство для отрицательных b
. Здесь замечаем, что выражение log a b p
при отрицательных b
имеет смысл лишь при четных показателях степени p
(так как значение степени b p
должно быть больше нуля, в противном случае логарифм не будет иметь смысла), а в этом случае b p =|b| p
. Тогда b p =|b| p =(a log a |b|) p =a p·log a |b|
, откуда log a b p =p·log a |b|
.
Тогда b p =|b| p =(a log a |b|) p =a p·log a |b|
, откуда log a b p =p·log a |b|
.
Например, и ln(-3) 4 =4·ln|-3|=4·ln3 .
Из предыдущего свойства вытекает свойство логарифма из корня : логарифм корня n -ой степени равен произведению дроби 1/n на логарифм подкоренного выражения, то есть, , где a>0 , a≠1 , n – натуральное число, большее единицы, b>0 .
Доказательство базируется на равенстве (смотрите ), которое справедливо для любых положительных b , и свойстве логарифма степени: .
Вот пример использования этого свойства: .
Теперь докажем формулу перехода к новому основанию логарифма вида . Для этого достаточно доказать справедливость равенства log c b=log a b·log c a
. Основное логарифмическое тождество позволяет нам число b
представить как a log a b
, тогда log c b=log c a log a b
. Осталось воспользоваться свойством логарифма степени: log c a log a b =log a b·log c a
. Так доказано равенство log c b=log a b·log c a
, а значит, доказана и формула перехода к новому основанию логарифма .
Покажем пару примеров применения этого свойства логарифмов: и .
Формула перехода к новому основанию позволяет переходить к работе с логарифмами, имеющими «удобное» основание. Например, с ее помощью можно перейти к натуральным или десятичным логарифмам, чтобы можно было вычислить значение логарифма по таблице логарифмов . Формула перехода к новому основанию логарифма также позволяет в некоторых случаях находить значение данного логарифма, когда известны значения некоторых логарифмов с другими основаниями.
Часто используется частный случай формулы перехода к новому основанию логарифма при c=b вида . Отсюда видно, что log a b и log b a – . К примеру, .
Также часто используется формула , которая удобна при нахождении значений логарифмов. Для подтверждения своих слов покажем, как с ее помощью вычисляется значение логарифма вида . Имеем . Для доказательства формулы достаточно воспользоваться формулой перехода к новому основанию логарифма a : .
Осталось доказать свойства сравнения логарифмов.
Докажем, что для любых положительных чисел b 1 и b 2 , b 1 log a b 2 , а при a>1 – неравенство log a b 1
Наконец, осталось доказать последнее из перечисленных свойств логарифмов. Ограничимся доказательством его первой части, то есть, докажем, что если a 1 >1 , a 2 >1 и a 1 1 справедливо log a 1 b>log a 2 b . Остальные утверждения этого свойства логарифмов доказываются по аналогичному принципу.
Воспользуемся методом от противного. Предположим, что при a 1 >1 , a 2 >1 и a 1 1 справедливо log a 1 b≤log a 2 b . По свойствам логарифмов эти неравенства можно переписать как и соответственно, а из них следует, что log b a 1 ≤log b a 2 и log b a 1 ≥log b a 2 соответственно. Тогда по свойствам степеней с одинаковыми основаниями должны выполняться равенства b log b a 1 ≥b log b a 2 и b log b a 1 ≥b log b a 2 , то есть, a 1 ≥a 2 . Так мы пришли к противоречию условию a 1
Список литературы.
- Колмогоров А.
 Н., Абрамов А.М., Дудницын Ю.П. и др. Алгебра и начала анализа: Учебник для 10 — 11 классов общеобразовательных учреждений.
Н., Абрамов А.М., Дудницын Ю.П. и др. Алгебра и начала анализа: Учебник для 10 — 11 классов общеобразовательных учреждений. - Гусев В.А., Мордкович А.Г. Математика (пособие для поступающих в техникумы).
Логарифмом числа N по основаниюа называется показатель степених , в которую нужно возвестиа , чтобы получить числоN
При условии, что
,
,
Из определения логарифма
следует, что
,
т.е.
— это равенство является основным
логарифмическим тождеством.
Логарифмы по основанию 10
называются десятичными логарифмами.
Вместо
пишут
.
Логарифмы по основанию e называются натуральными и обозначаются
.
Основные свойства логарифмов.
Логарифм единицы при любом основании равен нулю
Логарифм произведения равен сумме логарифмов сомножителей.
3) Логарифм частного равен разности логарифмов
Множитель
называется модулем перехода от логарифмов
при основанииa к логарифмам при основании b .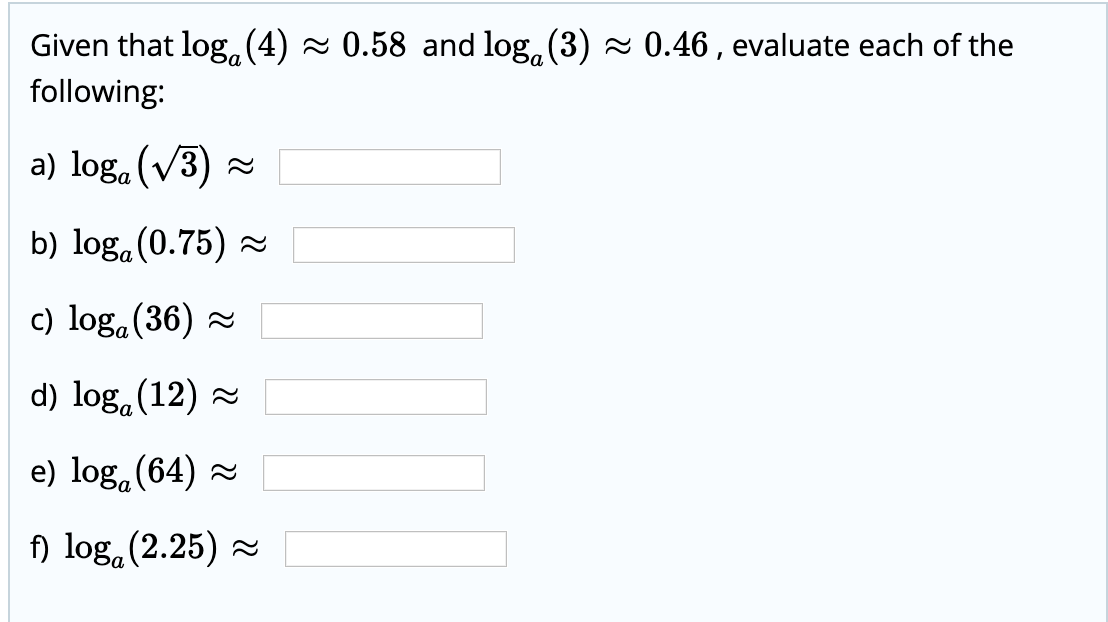
С помощью свойств 2-5 часто удается свести логарифм сложного выражения к результату простых арифметических действий над логарифмами.
Например,
Такие преобразования логарифма называются логарифмированием. Преобразования обратные логарифмированию называются потенцированием.
Глава 2. Элементы высшей математики.
1. Пределы
Пределом функции
является конечное число А, если при
стремлении xx 0 для каждого наперед заданного
,
найдется такое число
,
что как только
,
то
.
Функция, имеющая предел, отличается от
него на бесконечно малую величину:
,
где- б.м.в., т.е.
.
Пример. Рассмотрим функцию
.
При стремлении
,
функцияy стремится к нулю:
1.1. Основные теоремы о пределах.
Предел постоянной величины равен этой постоянной величине
.
Предел
суммы (разности) конечного числа функций
равен сумме (разности) пределов этих
функций.
Предел произведения конечного числа функций равен произведению пределов этих функций.
Предел частного двух функций равен частному пределов этих функций, если предел знаменателя не равен нулю.
Замечательные пределы
,
,
где
1.2. Примеры вычисления пределов
Однако, не все пределы вычисляются так просто. Чаще вычисление предела сводится к раскрытию неопределенности типа: или .
.
2. Производная функции
Пусть мы имеем функцию
,
непрерывную на отрезке
.
Аргумент
получил некоторое приращение
.
Тогда и функция получит приращение
.
Значению аргумента соответствует значение функции
.
Значению аргумента
Следовательно, .
Найдем предел этого отношения при
.
Если этот предел существует, то он
называется производной данной функции.
Определение 3Производной данной функции
по
аргументу
называется предел отношения приращения
функции к приращению аргумента, когда
приращение аргумента произвольным
образом стремится к нулю.
Производная функции
может быть обозначена следующим образом:
; ; ; .
Определение 4Операция нахождения производной от функции называетсядифференцированием.
2.1. Механический смысл производной.
Рассмотрим прямолинейное движение некоторого твердого тела или материальной точки.
Пусть в некоторый момент времени
движущаяся
точка
находилась на расстоянии
от начального положения
.
Через некоторый
промежуток времени
она переместилась на расстояние
. Найдем предел этого отношения, учитывая что
.
Следовательно, определение мгновенной скорости движения материальной точки сводится к нахождению производной от пути по времени.
2.2. Геометрическое значение производной
Пусть у нас
есть графически заданная некоторая
функция
.
Рис. 1. Геометрический смысл производной
Если
,
то точка
,
будет перемещаться по кривой, приближаясь
к точке
.
Следовательно
,
т.е. значение производной при данном
значении аргумента
численно равняется тангенсу угла
образованного касательной в данной
точке с положительным направлением оси
.
2.3. Таблица основных формул дифференцирования.
Степенная функция
Показательная функция
Логарифмическая функция
Тригонометрическая функция
Обратная тригонометрическая функция
2.4. Правила дифференцирования.
Производная от
Производная суммы (разности) функций
Производная произведения двух функций
Производная частного двух функций
2.5. Производная от сложной функции.
Пусть дана функция
такая, что ее можно представить в виде
и
,
где переменнаяявляется промежуточным аргументом,
тогда
Производная сложной функции равна
произведению производной данной функции
по промежуточному аргументу на производную
промежуточного аргумента по x.
Пример1.
Пример2.
3. Дифференциал функции.
Пусть есть
,
дифференцируемая на некотором отрезке
и пустьу этой функции есть производная
,
тогда можно записать
(1),
где — бесконечно малая величина,
так как при
Умножая все члены равенства (1) на
имеем:
Где
—
б.м.в. высшего порядка.
Величина
называется дифференциалом функции
и обозначается
.
3.1. Геометрическое значение дифференциала.
Пусть дана функция
.
Рис.2. Геометрический смысл дифференциала.
.
Очевидно, что дифференциал функции
равен приращению ординаты касательной
в данной точке.
3.2. Производные и дифференциалы различных порядков.
Если есть
,
тогда
называется первой производной.
Производная от первой производной
называется производной второго порядка
и записывается
.
Производной n-го порядка
от функции
называется производная (n-1)-го
порядка и записывается:
.
Дифференциал от дифференциала функции называется вторым дифференциалом или дифференциалом второго порядка.
.
.
3.3 Решение биологических задач с применением дифференцирования.
Задача1.
Исследования показали, что рост колонии
микроорганизмов подчиняется закону
,
гдеN – численность микроорганизмов (в тыс.),t –время (дни).
б) Будет ли в этот период численность колонии увеличиваться или уменьшаться?
Ответ. Численность колонии будет увеличиваться.
Задача 2. Вода в озере периодически тестируется для контроля содержания болезнетворных бактерий. Черезt дней после тестирования концентрация бактерий определяется соотношением
.
Когда в озере наступит минимальная концентрация бактерий и можно будет в нем купаться?
РешениеФункция достигает max или min, когда ее производная равна нулю.
,
Определим max или min будет через 6 дней.
Для этого возьмем вторую производную.
Ответ: Через 6 дней будет минимальная концентрация бактерий.
Соблюдение Вашей конфиденциальности важно для нас. По этой причине, мы разработали Политику Конфиденциальности, которая описывает, как мы используем и храним Вашу информацию. Пожалуйста, ознакомьтесь с нашими правилами соблюдения конфиденциальности и сообщите нам, если у вас возникнут какие-либо вопросы.
Сбор и использование персональной информации
Под персональной информацией понимаются данные, которые могут быть использованы для идентификации определенного лица либо связи с ним.
От вас может быть запрошено предоставление вашей персональной информации в любой момент, когда вы связываетесь с нами.
Ниже приведены некоторые примеры типов персональной информации, которую мы можем собирать, и как мы можем использовать такую информацию.
Какую персональную информацию мы собираем:
- Когда вы оставляете заявку на сайте, мы можем собирать различную информацию, включая ваши имя, номер телефона, адрес электронной почты и т.
 д.
д.
Как мы используем вашу персональную информацию:
- Собираемая нами персональная информация позволяет нам связываться с вами и сообщать об уникальных предложениях, акциях и других мероприятиях и ближайших событиях.
- Время от времени, мы можем использовать вашу персональную информацию для отправки важных уведомлений и сообщений.
- Мы также можем использовать персональную информацию для внутренних целей, таких как проведения аудита, анализа данных и различных исследований в целях улучшения услуг предоставляемых нами и предоставления Вам рекомендаций относительно наших услуг.
- Если вы принимаете участие в розыгрыше призов, конкурсе или сходном стимулирующем мероприятии, мы можем использовать предоставляемую вами информацию для управления такими программами.
Раскрытие информации третьим лицам
Мы не раскрываем полученную от Вас информацию третьим лицам.
Исключения:
- В случае если необходимо — в соответствии с законом, судебным порядком, в судебном разбирательстве, и/или на основании публичных запросов или запросов от государственных органов на территории РФ — раскрыть вашу персональную информацию.
 Мы также можем раскрывать информацию о вас если мы определим, что такое раскрытие необходимо или уместно в целях безопасности, поддержания правопорядка, или иных общественно важных случаях.
Мы также можем раскрывать информацию о вас если мы определим, что такое раскрытие необходимо или уместно в целях безопасности, поддержания правопорядка, или иных общественно важных случаях. - В случае реорганизации, слияния или продажи мы можем передать собираемую нами персональную информацию соответствующему третьему лицу – правопреемнику.
Защита персональной информации
Мы предпринимаем меры предосторожности — включая административные, технические и физические — для защиты вашей персональной информации от утраты, кражи, и недобросовестного использования, а также от несанкционированного доступа, раскрытия, изменения и уничтожения.
Соблюдение вашей конфиденциальности на уровне компании
Для того чтобы убедиться, что ваша персональная информация находится в безопасности, мы доводим нормы соблюдения конфиденциальности и безопасности до наших сотрудников, и строго следим за исполнением мер соблюдения конфиденциальности.
Сегодня мы поговорим о формулах логарифмов и дадим показательные примеры решения .
Сами по себе подразумевают шаблоны решения согласно основным свойствам логарифмов. Прежде применять формулы логарифмов для решения напомним для вас, сначала все свойства:
Теперь на основе этих формул(свойств), покажем примеры решения логарифмов .
Примеры решения логарифмов на основании формул.
Логарифм положительного числа b по основанию a (обозначается log a b) — это показатель степени, в которую надо возвести a, чтобы получить b, при этом b > 0, a > 0, а 1.
Согласно определения log a b = x, что равносильно a x = b, поэтому log a a x = x.
Логарифмы , примеры:
log 2 8 = 3, т.к. 2 3 = 8
log 7 49 = 2, т.к. 7 2 = 49
log 5 1/5 = -1, т.к. 5 -1 = 1/5
Десятичный логарифм — это обычный логарифм, в основании которого находится 10. Обозначается как lg.
log 10 100 = 2, т.к. 10 2 = 100
Натуральный логарифм — также обычный логарифм логарифм, но уже с основанием е (е = 2,71828. .. — иррациональное число). Обозначается как ln.
.. — иррациональное число). Обозначается как ln.
Формулы или свойства логарифмов желательно запомнить, потому что они понадобятся нам в дальнейшем при решении логарифмов, логарифмических уравнений и неравенств. Давайте еще раз отработаем каждую формулу на примерах.
- Основное логарифмическое тождество
a log a b = b8 2log 8 3 = (8 2log 8 3) 2 = 3 2 = 9
- Логарифм произведения равен сумме логарифмов
log a (bc) = log a b + log a clog 3 8,1 + log 3 10 = log 3 (8,1*10) = log 3 81 = 4
- Логарифм частного равен разности логарифмов
log a (b/c) = log a b — log a c9 log 5 50 /9 log 5 2 = 9 log 5 50- log 5 2 = 9 log 5 25 = 9 2 = 81
- Свойства степени логарифмируемого числа и основания логарифма
Показатель степени логарифмируемого числа log a b m = mlog a b
Показатель степени основания логарифма log a n b =1/n*log a b
log a n b m = m/n*log a b,
если m = n, получим log a n b n = log a b
log 4 9 = log 2 2 3 2 = log 2 3
- Переход к новому основанию
log a b = log c b/log c a,если c = b, получим log b b = 1
тогда log a b = 1/log b a
log 0,8 3*log 3 1,25 = log 0,8 3*log 0,8 1,25/log 0,8 3 = log 0,8 1,25 = log 4/5 5/4 = -1
Как видите, формулы логарифмов не так сложны как кажутся. Теперь рассмотрев примеры решения логарифмов мы можем переходить к логарифмическим уравнениям. Примеры решения логарифмических уравнений мы более подробно рассмотрим в статье: » «. Не пропустите!
Теперь рассмотрев примеры решения логарифмов мы можем переходить к логарифмическим уравнениям. Примеры решения логарифмических уравнений мы более подробно рассмотрим в статье: » «. Не пропустите!
Если у вас остались вопросы по решению, пишите их в комментариях к статье.
Заметка: решили получить образование другого класса обучение за рубежом как вариант развития событий.
Итак, перед нами степени двойки. Если взять число из нижней строчки, то можно легко найти степень, в которую придется возвести двойку, чтобы получилось это число. Например, чтобы получить 16, надо два возвести в четвертую степень. А чтобы получить 64, надо два возвести в шестую степень. Это видно из таблицы.
А теперь — собственно, определение логарифма:
Логарифм по основанию a от аргумента x — это степень, в которую надо возвести число a , чтобы получить число x .
Обозначение: log a
x
= b
, где a
— основание, x
— аргумент, b
— собственно, чему равен логарифм.
Например, 2 3 = 8 ⇒ log 2 8 = 3 (логарифм по основанию 2 от числа 8 равен трем, поскольку 2 3 = 8). С тем же успехом log 2 64 = 6 , поскольку 2 6 = 64 .
Операцию нахождения логарифма числа по заданному основанию называют логарифмированием. Итак, дополним нашу таблицу новой строкой:
| 2 1 | 2 2 | 2 3 | 2 4 | 2 5 | 2 6 |
| 2 | 4 | 8 | 16 | 32 | 64 |
| log 2 2 = 1 | log 2 4 = 2 | log 2 8 = 3 | log 2 16 = 4 | log 2 32 = 5 | log 2 64 = 6 |
К сожалению, далеко не все логарифмы считаются так легко. Например, попробуйте найти log 2 5 . Числа 5 нет в таблице, но логика подсказывает, что логарифм будет лежать где-то на отрезке . Потому что 2 2
Такие числа называются иррациональными: цифры после запятой можно писать до бесконечности, и они никогда не повторяются. Если логарифм получается иррациональным, его лучше так и оставить: log 2 5 , log 3 8 , log 5 100 .
Важно понимать, что логарифм — это выражение с двумя переменными (основание и аргумент). Многие на первых порах путают, где находится основание, а где — аргумент. Чтобы избежать досадных недоразумений, просто взгляните на картинку:
Перед нами — не что иное как определение логарифма. Вспомните: логарифм — это степень , в которую надо возвести основание, чтобы получить аргумент. Именно основание возводится в степень — на картинке оно выделено красным. Получается, что основание всегда находится внизу! Это замечательное правило я рассказываю своим ученикам на первом же занятии — и никакой путаницы не возникает.
С определением разобрались — осталось научиться считать логарифмы, т.е. избавляться от знака «log». Для начала отметим, что из определения следует два важных факта:
- Аргумент и основание всегда должны быть больше нуля. Это следует из определения степени рациональным показателем, к которому сводится определение логарифма.
- Основание должно быть отличным от единицы, поскольку единица в любой степени все равно остается единицей.
 Из-за этого вопрос «в какую степень надо возвести единицу, чтобы получить двойку» лишен смысла. Нет такой степени!
Из-за этого вопрос «в какую степень надо возвести единицу, чтобы получить двойку» лишен смысла. Нет такой степени!
Такие ограничения называются областью допустимых значений (ОДЗ). Получается, что ОДЗ логарифма выглядит так: log a x = b ⇒ x > 0 , a > 0 , a ≠ 1 .
Заметьте, что никаких ограничений на число b (значение логарифма) не накладывается. Например, логарифм вполне может быть отрицательным: log 2 0,5 = −1 , т.к. 0,5 = 2 −1 .
Впрочем, сейчас мы рассматриваем лишь числовые выражения, где знать ОДЗ логарифма не требуется. Все ограничения уже учтены составителями задач. Но когда пойдут логарифмические уравнения и неравенства, требования ОДЗ станут обязательными. Ведь в основании и аргументе могут стоять весьма неслабые конструкции, которые совсем необязательно соответствуют приведенным выше ограничениям.
Теперь рассмотрим общую схему вычисления логарифмов. Она состоит из трех шагов:
- Представить основание a
и аргумент x
в виде степени с минимально возможным основанием, большим единицы.
 Попутно лучше избавиться от десятичных дробей;
Попутно лучше избавиться от десятичных дробей; - Решить относительно переменной b уравнение: x = a b ;
- Полученное число b будет ответом.
Вот и все! Если логарифм окажется иррациональным, это будет видно уже на первом шаге. Требование, чтобы основание было больше единицы, весьма актуально: это снижает вероятность ошибки и значительно упрощает выкладки. Аналогично с десятичными дробями: если сразу перевести их в обычные, ошибок будет в разы меньше.
Посмотрим, как работает эта схема на конкретных примерах:
Задача. Вычислите логарифм: log 5 25
- Представим основание и аргумент как степень пятерки: 5 = 5 1 ; 25 = 5 2 ;
- Получили ответ: 2.
Составим и решим уравнение:
log 5 25 = b
⇒ (5 1) b
= 5 2 ⇒ 5 b
= 5 2 ⇒ b
= 2 ;
Задача. Вычислите логарифм:
Задача. Вычислите логарифм: log 4 64
- Представим основание и аргумент как степень двойки: 4 = 2 2 ; 64 = 2 6 ;
- Составим и решим уравнение:
log 4 64 = b ⇒ (2 2) b = 2 6 ⇒ 2 2b = 2 6 ⇒ 2b = 6 ⇒ b = 3 ; - Получили ответ: 3.

Задача. Вычислите логарифм: log 16 1
- Представим основание и аргумент как степень двойки: 16 = 2 4 ; 1 = 2 0 ;
- Составим и решим уравнение:
log 16 1 = b ⇒ (2 4) b = 2 0 ⇒ 2 4b = 2 0 ⇒ 4b = 0 ⇒ b = 0 ; - Получили ответ: 0.
Задача. Вычислите логарифм: log 7 14
- Представим основание и аргумент как степень семерки: 7 = 7 1 ; 14 в виде степени семерки не представляется, поскольку 7 1
- Из предыдущего пункта следует, что логарифм не считается;
- Ответ — без изменений: log 7 14.
Небольшое замечание к последнему примеру. Как убедиться, что число не является точной степенью другого числа? Очень просто — достаточно разложить его на простые множители. Если в разложении есть хотя бы два различных множителя, число не является точной степенью.
Задача. Выясните, являются ли точными степенями числа: 8; 48; 81; 35; 14 .
8 = 2 · 2 · 2 = 2 3 — точная степень, т. к. множитель всего один;
к. множитель всего один;
48 = 6 · 8 = 3 · 2 · 2 · 2 · 2 = 3 · 2 4 — не является точной степенью, поскольку есть два множителя: 3 и 2;
81 = 9 · 9 = 3 · 3 · 3 · 3 = 3 4 — точная степень;
35 = 7 · 5 — снова не является точной степенью;
14 = 7 · 2 — опять не точная степень;
Заметим также, что сами простые числа всегда являются точными степенями самих себя.
Десятичный логарифм
Некоторые логарифмы встречаются настолько часто, что имеют специальное название и обозначение.
Десятичный логарифм от аргумента x — это логарифм по основанию 10, т.е. степень, в которую надо возвести число 10, чтобы получить число x . Обозначение: lg x .
Например, lg 10 = 1; lg 100 = 2; lg 1000 = 3 — и т.д.
Отныне, когда в учебнике встречается фраза типа «Найдите lg 0,01», знайте: это не опечатка. Это десятичный логарифм. Впрочем, если вам непривычно такое обозначение, его всегда можно переписать:
lg x
= log 10 x
Все, что верно для обычных логарифмов, верно и для десятичных.
Натуральный логарифм
Существует еще один логарифм, который имеет собственное обозначение. В некотором смысле, он даже более важен, чем десятичный. Речь идет о натуральном логарифме.
Натуральный логарифм от аргумента x — это логарифм по основанию e , т.е. степень, в которую надо возвести число e , чтобы получить число x . Обозначение: ln x .
Многие спросят: что еще за число e
? Это иррациональное число, его точное значение найти и записать невозможно. Приведу лишь первые его цифры:
e
= 2,718281828459…
Не будем углубляться, что это за число и зачем нужно. Просто помните, что e
— основание натурального логарифма:
ln x
= log e
x
Таким образом, ln e = 1 ; ln e 2 = 2 ; ln e 16 = 16 — и т.д. С другой стороны, ln 2 — иррациональное число. Вообще, натуральный логарифм любого рационального числа иррационален. Кроме, разумеется, единицы: ln 1 = 0.
Для натуральных логарифмов справедливы все правила, которые верны для обычных логарифмов.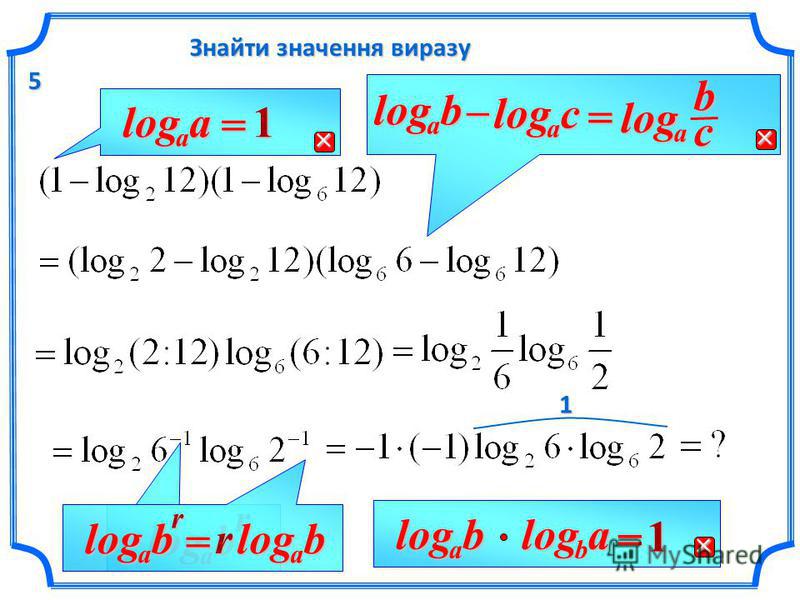
Стоматология Ас-Дент
Добро пожаловать!
Стоматология для нас — не просто профессия, это наше семейное дело. Уже три поколения нашей семьи занимаются стоматологией. За эти годы мы накопили огромный опыт и базу знаний, выработали свои методы и подходы. Но у нас есть не только богатое прошлое: мы смотрим в будущее!
Кроме опыта и традиций наша клиника может предложить Вам новейшие технологии и достижения науки. Наши доктора постоянно совершенствуются. Мы посещаем международные конгрессы и семинары по всему миру, где у нас есть возможность повысить свою квалификацию, перенять опыт иностранных коллег и поделиться своим. Сотрудники нашей клиники являются членами различных российских и международных стоматологических групп и обществ, что позволяет нам никогда не стоять на месте и развиваться.
Наши услуги
Полный спектр услуг стоматологической клиники
Терапия
- Композиты в стоматологии
- Лечение альвеолита зуба
- Лечение зуба — пломбирование каналов
- Эндодонтия зубов
- Коффердам в стоматологии
- Лечение кист зубов
- Лечение кариеса
Хирургия
- Имплантация зубов
- Синус-лифтинг
- Регенерация костной ткани
- Удаление без боли
Отропедия
- Реставрация зубов
- Безметалловые коронки
- Микропротезирование зубов
- Протезирование зубов
- Виниры
Гигиена
- Профессиональная чистка
- Профессиональная гигиена полости рта и зубов
- Отбеливание зубов
Ортодонтия
- Установка брекетов
- Методы лечения в ортодонтии
- Консультация ортодонта
- Ортодонтичческая коррекция
- Исправление прикуса
Наш подход к работе
Проведем комплексную проверку (CHECKUP)
Предлагаем программу ежегодного профилактического осмотра и профессиональной гигиены полости рта (CHECKUP).
1
Комплексный осмотр и консультация
панорамный снимок зубов, осмотр полости рта специалистами (хирургом, терапевтом и ортопедом при необходимости) для выявления возможных проблем, консультация по лечению и составление плана и сметы лечения (при необходимости)
2
Профессиональная гигиена полости рта
Удаление зубных отложений Air-Flow, профессиональная гигиена полости рта и десен на ультразвуковом аппарате Vector или Perioscan, шлифовка и полировка зубов специальными пастами Реминерализация эмали зубов
3
Встретимся через 12 месяцев!
Мы напомним Вам заранее о следующем рекомендуемом посещении стоматологии и согласуем удобное для Вас время.
Врачи клиники
Команда профессионалов
Калинин Андрей Юрьевич
ортопед, стоматолог
Генеральный Директор
Стаж работы с 1991 года
Калинина Татьяна Викторовна
стоматолог, терапевт, хирург
Стаж работы с 1994 года
Нусуев Юрий Ильич
имплантолог, ортопед, терапевт, хирург
Стаж работы с 2012 года.
Калинина Анна Игоревна
Подробнее
Почему нас выбирают
Нас рекомендуют семьями и поколениями
Любим свое дело
Наш семейный центр основан потомственными дантистами, горячо любящими профессию.
Заботимся о вас
Считаем, что в нашей профессии трудно работать без улыбки. Все клиенты чувствуют нашу заботу и внимание.
Высокое качество
Гарантируем каждому пациенту высокий уровень сервиса, индивидуальный подход и комфортные условия лечения.
Запишитесь на бесплатную консультацию
Записаться
Полезная информация
Новости и публикации
Обновление сайта Ас-Дент
29 июля 2020
Уважаемые клиенты, друзья и партнеры! Рады сообщить вам об обновлении официального сайта стоматологической клиники Ас-Дент на Удальцова, 50.
Подробнее
Работа в условиях вируса covid-19
26 мая 2020
В условиях периода распространения корона вируса covid-19 мы считаем важным довести до вас важную информацию.
Подробнее
Подробнее
Запись на прием
Каково значение log(ab2) — log(ac) + log(abc4) — 3log(bc)?
- 2,6 тыс. просмотров
Ответ: Д. 1…
Каково значение log(ab 2 ) – log(ac) + log(abc 4 ) – 3log(bc)?
A. 2
B. 0
C. -2
D. 1
Ответ: D. 1… log(ab 2 log(ab 2 ) 4 – 3log(bc)
= log ab 2 – logac + log abc 4 – log b 3 c 3
= log a (ab 2 /ac) x (abc 4 /b 3 c 3 90 32 = журнал а а = 1
Связанные теги
- вопросы и ответы на интервью adani enterpris,
- вопросы и ответы на интервью adani green energy ltd,
- вопросы и ответы на интервью adani ports ltd,
- вопросы и ответы на интервью adani total gas ltd,
- Adani Transmission Ltd интервью вопросы и ответы,
- ambuja цементы интервью вопросы и ответы,
- вопросы логарифма amcat,
- вопросы интервью и ответы в больнице Аполлона,
- aurobindo pharm вопросы и ответы интервью,
- avenue supermarts ltd вопросы интервью и ответы,
- ось банк ответы,
- вопросы и ответы на собеседовании bajaj auto,
- вопросы и ответы на интервью bajaj Finance,
- вопросы и ответы на интервью bajaj finserv ltd,
- Balkrishna Industries вопросы и ответы на интервью,
- Bandhan Bank вопросы и ответы на интервью,
- Berger Paints вопросы и ответы на интервью,
- Bharat Petroleum Corporation Ltd вопросы и ответы на интервью,
- Biocon вопросы и ответы на интервью,
- britannia Industries ltd вопросы и ответы на собеседовании,
- cadila вопросы и ответы на собеседование о здоровье,
- Coal India Ltd интервью вопросы и ответы,
- Cognizant Interview Questions,
- Colgate вопросы и ответы для интервью,
- Dabur India ltd вопросы и ответы для интервью,
- divis labs вопросы и ответы для интервью,
- dlf вопросы и ответы для интервью,
- Dr.
 2 / аб) ?,
2 / аб) ?, - gail (India) Ltd вопросы и ответы на собеседовании,
- iron pharma ltd вопросы и ответы на собеседование,
- godrej Consumer Products Ltd вопросы и ответы на интервью,
- godrej properties вопросы и ответы на интервью,
- grasim Industries ltd вопросы и ответы на собеседование ответы,
- gujarat gas ltd вопросы и ответы на интервью,
- havells India ltd вопросы и ответы на интервью,
- hdfc life Insurance Company Ltd интервью вопросы и ответы,
- вопросы и ответы на интервью с hero motocorp,
- вопросы и ответы на интервью с Hindustan Industries Ltd,
- вопросы и ответы на интервью с Hindustan Unilever Ltd,
- вопросы и ответы на интервью с Hindustan Zinc Ltd,
- как считать логарифмы, 9000 3 как найти значение журнала 16,
- как решать логарифмы,
- ICICI Ломбардные вопросы и ответы на интервью,
- icici вопросы и ответы на интервью по пруденциальному страхованию жизни, 90,3010 = 2,
- , если a 2 и b 1, то каково значение log a b )( a 2 b 2,
- , если log 2 0,3010 значение log 80,
- , если log2 0,3010 найти количество цифр in 4 29,
- Indian Oil Corporation Ltd вопросы и ответы на интервью,
- indus towers ltd вопросы и ответы на интервью,
- indusind bank вопросы и ответы,
- вопросы и ответы на интервью Interglobe Aviation вопросы и ответы,
- вопросы на интервью jsw steel и ответы,
- jubilant foodworks ltd вопросы и ответы на собеседовании,
- kotak mahindra bank вопросы и ответы на собеседование,
- L&T Infotech вопросы и ответы на собеседование,
- larsen & toubro Ltd вопросы и ответы на собеседование,
- законы логарифмов, log
5
5
5
- равно
- log ab log bc log ca,
- log xy = 100 и log x2 = 10,
- log(a2/bc) + log(b2/ca(c2/ab) is,
- log10 ( 10) + log10 (100) + log10 (1000) + log10 (10000) + log10 (100000) равно ?,
- логарифм,
- основы логарифмирования,
- формула логарифма,
- правила логарифмирования,
- рабочий лист логарифма,
- логарифмическое дифференцирование,
- логарифм примеры математических уравнений,
- логарифмические функции,
- вопросы и ответы на интервью с Люпеном,
- вопросы и ответы на интервью M&M,
- вопросы и ответы на интервью marico,
- вопросы и ответы на интервью maruti suzuki,
- вопросы и ответы на интервью Motherson Sumi Systems,
- вопросы и ответы на интервью muthoot Finance hdfc amc,
- вопросы и ответы на интервью Nestle,
- вопросы и ответы на интервью nmdc ltd,
- вопросы и ответы на интервью ntpc ltd,
- вопросы и ответы на интервью Oil and Natural Gas Corporation (ONGC) и ответы,
- вопросы и ответы на собеседование с pi Industries Ltd,
- вопросы и ответы на интервью с Pidilite Industries,
- электросетевая корпорация Индии, вопросы и ответы на интервью,
- свойства логарифмов,
- ril частично оплачиваемые вопросы и ответы на собеседование,
- вопросы о размещении Sapient Nitro,
- вопросы и ответы на интервью с картой sbi,
- вопросы и ответы на собеседование на sbi life insura,
- вопросы на интервью shree цементы и ООО ответы,
- Siemens вопросы и ответы на интервью,
- srf ограниченные вопросы и ответы на интервью,
- государственный банк Индии (SBI) интервью вопросы и ответы,
- Steel Authority of India Ltd (SAIL) вопросы и ответы на собеседовании,
- вопросы и ответы на интервью Sun Pharma,
- вопросы и ответы на интервью Tata Consumer Products Ltd,
- вопросы и ответы на интервью Tata Motors,
- вопросы на интервью Tata Steel и ответы,
- значение log 4 log 5 log 2 равно,
- значение log 9/8 – log 27/32 + log3/4 равно ?,
- значение log2 (1/64) равно? ,
- затем найти значение log0,125 (125) ?,
- тогда значение y равно,
- вопросы и ответы на собеседование в компанию titan,
- вопросы и ответы на интервью с торрент-фармацевтикой,
- вопросы и ответы на интервью на ультратех цемент,
- вопросы и ответы на интервью в United Phosphorus Ltd (UPL),
- вопросы и ответы на интервью с United Spirits,
- вопросы и ответы на интервью с vedanta ltd,
- вопросы на интервью с Zoho Corporation,
- вопросы и ответы на интервью с zomato
Значение log(b)a.
 log(c)b.log(a)c равно
log(c)b.log(a)c равно- Курс
- NCERT
- Класс 12
- Класс 11
- Класс 10
- Класс 50 90
- Класс 9 09003 5
- Класс 7
- Класс 6
- IIT JEE
- NCERT
- Экзамен
- JEE MAINS
- XBOARD ADVANCED 9 0005 0005
- XII СОСТАВ
- NEET
- Предыдущий год (по годам)
- Физика Предыдущий год
- Химия Предыдущий год
- Биология Предыдущий год
- Нет Все образцы работ
- Образцы работ Биология
- Образцы работ Физика
- Образцы работ Химия
60 0
900 0006
- Загрузить PDF-файлы
- Класс 12
- Класс 11
- Класс 10
- Класс 9
- Класс 8
- Класс 7
- Класс 6
- Экзаменационный уголок0005
- Онлайн-класс
- Викторина
- Задать вопрос в WhatsApp
- Поиск Doubtnut Словарь
5
9006 900 05
- Toppers Talk
- Блог
- О нас
- Карьера
- Скачать
- Получить приложение
Вопрос
Обновлено: 21.
15 видео 07.2021 ) (Вопросы с несколькими вариантами ответов)
07.2021 ) (Вопросы с несколькими вариантами ответов)РЕКЛАМА
लिखित उत्तर
B
logabc
Ответ
Abina Padka 8
ads ке
Khareedo DN Pro и дехо сари видео бина киси объявление ки rukaavat ке!
संबंधित वीडियो
Значение log(log_(b)a.log_(c)b*log_(d)c.log_(a)d) равно
18900 9000
008
Если х, г, г находятся в Г.П. над топором=by=cz , затем (лог)ба=(лог)ас б. (лог)cb=(лог)ac в. (лог) ba = (лог) cb д. ни один из этих
31380
02:17
10 Найдите значение logba.logcb.logac.
33744
00:43
Если a,b,c — различные положительные действительные числа, каждое из которых отлично от единицы, такое, что (log_(a)a.log_(c)a-log_(a)a)+(log_( a)b*log_(c)b-log b_(b))+(log_(a)c.log_(a)c-log_(c)c)=0, затем докажите, что abc=1
1
0
04 :48
Если a,b,c — различные вещественные числа, отличные от 1, такие, что
(logba. logca-logaa)+(logab.logcb.logcb-logbb)+(logac.logbc-logcC)=0, тогда abc равно
logca-logaa)+(logab.logcb.logcb-logbb)+(logac.logbc-logcC)=0, тогда abc равно39181286
03:02
Если в прямоугольном треугольнике a и b — длины сторон, c — длина гипотенузы, а c−b≠1,c+b≠1, то покажите, что
logc +ba+logc-ba=2logc+ba.logc-ba.39181294
02:55
Учитывая a2+b2=c2. Докажите, что
logb+ca+logc-ba=2logc+ba.logc-ba,∀a>0,a≠1
c−b>0,c+b>0
c−b≠1,c+b≠ 1.114771031
05:36
logba.logab=………….
161130935
00:53
Докажите, что :
(vii) log√ab.log√bc.log√ca=8.213713466
02:14
logba.logcb.logac का मान है
643168199
02:27 Дано
01:23 с2. Докажите, что
logb+ca+logc-ba=2logc+ba.logc-ba,∀a>0,a≠1
c−b>0,c+b>0
c−b≠1,c+b≠ 1.644007284
05:11
Если a, b, c — различные положительные числа, каждое из которых отлично от 1, такое, что
(logba.logca-logaa)+(logab.logcb-logbb)
+(logac.
- Загрузить PDF-файлы

 Н., Абрамов А.М., Дудницын Ю.П. и др. Алгебра и начала анализа: Учебник для 10 — 11 классов общеобразовательных учреждений.
Н., Абрамов А.М., Дудницын Ю.П. и др. Алгебра и начала анализа: Учебник для 10 — 11 классов общеобразовательных учреждений.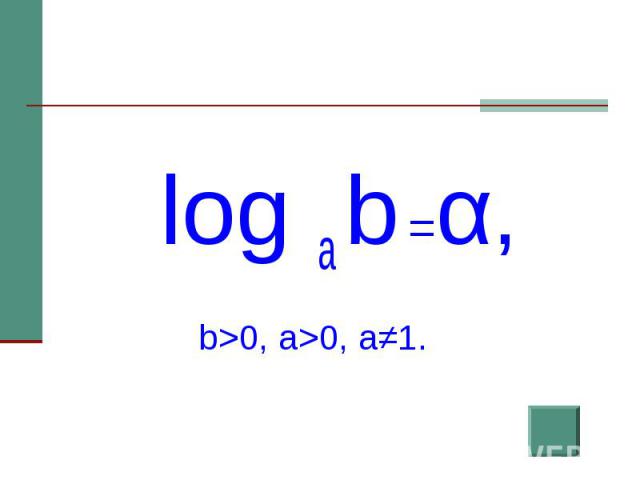 д.
д. Мы также можем раскрывать информацию о вас если мы определим, что такое раскрытие необходимо или уместно в целях безопасности, поддержания правопорядка, или иных общественно важных случаях.
Мы также можем раскрывать информацию о вас если мы определим, что такое раскрытие необходимо или уместно в целях безопасности, поддержания правопорядка, или иных общественно важных случаях. Из-за этого вопрос «в какую степень надо возвести единицу, чтобы получить двойку» лишен смысла. Нет такой степени!
Из-за этого вопрос «в какую степень надо возвести единицу, чтобы получить двойку» лишен смысла. Нет такой степени! Попутно лучше избавиться от десятичных дробей;
Попутно лучше избавиться от десятичных дробей;
 2 / аб) ?,
2 / аб) ?, 07.2021 ) (Вопросы с несколькими вариантами ответов)
07.2021 ) (Вопросы с несколькими вариантами ответов) logca-logaa)+(logab.logcb.logcb-logbb)+(logac.logbc-logcC)=0, тогда abc равно
logca-logaa)+(logab.logcb.logcb-logbb)+(logac.logbc-logcC)=0, тогда abc равно