Найти производную y=sin(lnx) — Школьные Знания.com
поможить з ось цим дуже срочно
Приведи подобные слагаемые: -3х + 6х 100 БАЛЛОВ Приведи подобные слагаемые: 3х + 7у — х — 10у = Решите уравнение: 6,3у — у = — 10,6 Приведи подобные с … лагаемые:: — 4,8а + 5,4а = Приведи подобные слагаемые: -8,5у + 8,5у Приведи подобные слагаемые: — х + 6,7х Приведи подобные слагаемые: 9х — х = Приведи подобные слагаемые:: — 4,8а — 5,4а =
Турист прошел за 3 дня 48 км.За первый день он прошел 25% всего пути,что составляет 80% расстояния,пройденного за второй день.Сколько км он прошел за … третий день?
Методы решения уравнений 1.Наиболее важные выводы (5-10) 2. 3-5 примеров с решениями 3.Комментарии, оценка приобретения темы
В треугольниках АВС и А1В1С1 равны углы при вершинах А и А1, а также С и С1. Даны стороны: АВ = 20 см, АС = 24 см и А1В1 = 15 см. Найди остальные стор
… оны треугольников, если известно, что сторона ВС на 4 см длинее стороны В1С1.
Помогите срочно решить задание Три сотрудника могут составить один и тот же документ. Вероятность представить готовый документ без ошибок для них соот … ветственно равны p1,p2,p3 . Составить закон распределения случайной величины X – числа готовых документов без ошибок, найти её математическое ожидание, дисперсию и среднее квадратическое отклонение. p1-0.4, p2-0.9, p3-0.5,
Помогите решить! (Даю 20 балов) Перевод: 1) Найти: а) область определения функции; b) исследовать на четность (нечетность) функции; 2) вычислить гран … ицы; 3)продифференцировать функцию; 4)найти значение производной функции в точке; 5)найти производную функции, заданной параметрически.
|х-1|=2 Как это решить помогите пожалуйста, срочно
| 1 | Trovare la Derivata — d/dx | натуральный логарифм x | |
| 2 | Вычислим интеграл | интеграл натурального логарифма x по x | |
| 3 | Trovare la Derivata — d/dx | e^x | |
| 4 | Вычислим интеграл | интеграл e^(2x) относительно x | |
| 5 | Trovare la Derivata — d/dx | 1/x | |
| 6 | Trovare la Derivata — d/dx | x^2 | |
| 7 | Trovare la Derivata — d/dx | 1/(x^2) | |
| 8 | Trovare la Derivata — d/dx | sin(x)^2 | |
| 9 | Trovare la Derivata — d/dx | sec(x) | |
| 10 | Вычислим интеграл | интеграл e^x относительно x | |
| 11 | Вычислим интеграл | интеграл x^2 относительно x | |
| 12 | Вычислим интеграл | интеграл квадратного корня x по x | |
| 13 | Trovare la Derivata — d/dx | cos(x)^2 | |
| 14 | Вычислим интеграл | интеграл 1/x относительно x | |
| 15 | Вычислим интеграл | интеграл sin(x)^2 относительно x | |
| 16 | Trovare la Derivata — d/dx | x^3 | |
| 17 | Trovare la Derivata — d/dx | sec(x)^2 | |
| 18 | Вычислим интеграл | интеграл cos(x)^2 относительно x | |
| 19 | Вычислим интеграл | интеграл sec(x)^2 относительно x | |
| 20 | Trovare la Derivata — d/dx | e^(x^2) | |
| 21 | Вычислим интеграл | интеграл в пределах от 0 до 1 кубического корня 1+7x по x | |
| 22 | Trovare la Derivata — d/dx | sin(2x) | |
| 23 | Trovare la Derivata — d/dx | tan(x)^2 | |
| 24 | Вычислим интеграл | интеграл 1/(x^2) относительно x | |
| 25 | Trovare la Derivata — d/dx | 2^x | |
| 26 | График | натуральный логарифм a | |
| 27 | Trovare la Derivata — d/dx | cos(2x) | |
| 28 | Trovare la Derivata — d/dx | xe^x | |
| 29 | Вычислим интеграл | интеграл 2x относительно x | |
| 30 | Trovare la Derivata — d/dx | ( натуральный логарифм x)^2 | |
| 31 | Trovare la Derivata — d/dx | натуральный логарифм (x)^2 | |
| 32 | Trovare la Derivata — d/dx | 3x^2 | |
| 33 | Вычислим интеграл | интеграл xe^(2x) относительно x | |
| 34 | Trovare la Derivata — d/dx | 2e^x | |
| 35 | Trovare la Derivata — d/dx | натуральный логарифм 2x | |
| 36 | Trovare la Derivata — d/dx | -sin(x) | |
| 37 | Trovare la Derivata — d/dx | 4x^2-x+5 | |
| 38 | Trovare la Derivata — d/dx | y=16 корень четвертой степени 4x^4+4 | |
| 39 | Trovare la Derivata — d/dx | 2x^2 | |
| 40 | Вычислим интеграл | интеграл e^(3x) относительно x | |
| 41 | Вычислим интеграл | интеграл cos(2x) относительно x | |
| 42 | Trovare la Derivata — d/dx | 1/( квадратный корень x) | |
| 43 | Вычислим интеграл | интеграл e^(x^2) относительно x | |
| 44 | Вычислить | e^infinity | |
| 45 | Trovare la Derivata — d/dx | x/2 | |
| 46 | Trovare la Derivata — d/dx | -cos(x) | |
| 47 | Trovare la Derivata — d/dx | sin(3x) | |
| 48 | Trovare la Derivata — d/dx | 1/(x^3) | |
| 49 | Вычислим интеграл | интеграл tan(x)^2 относительно x | |
| 50 | Вычислим интеграл | интеграл 1 относительно x | |
| 51 | Trovare la Derivata — d/dx | x^x | |
| 52 | Trovare la Derivata — d/dx | x натуральный логарифм x | |
| 53 | Trovare la Derivata — d/dx | x^4 | |
| 54 | Оценить предел | предел (3x-5)/(x-3), если x стремится к 3 | |
| 55 | Вычислим интеграл | интеграл от x^2 натуральный логарифм x по x | |
| 56 | Trovare la Derivata — d/dx | f(x) = square root of x | |
| 57 | Trovare la Derivata — d/dx | x^2sin(x) | |
| 58 | Вычислим интеграл | интеграл sin(2x) относительно x | |
| 59 | Trovare la Derivata — d/dx | 3e^x | |
| 60 | Вычислим интеграл | интеграл xe^x относительно x | |
| 61 | Trovare la Derivata — d/dx | y=x^2 | |
| 62 | Trovare la Derivata — d/dx | квадратный корень x^2+1 | |
| 63 | Trovare la Derivata — d/dx | sin(x^2) | |
| 64 | Вычислим интеграл | интеграл e^(-2x) относительно x | |
| 65 | Вычислим интеграл | интеграл натурального логарифма квадратного корня x по x | |
| 66 | Trovare la Derivata — d/dx | e^2 | |
| 67 | Trovare la Derivata — d/dx | x^2+1 | |
| 68 | Вычислим интеграл | интеграл sin(x) относительно x | |
| 69 | Trovare la Derivata — d/dx | arcsin(x) | |
| 70 | Оценить предел | предел (sin(x))/x, если x стремится к 0 | |
| 71 | Вычислим интеграл | интеграл e^(-x) относительно x | |
| 72 | Trovare la Derivata — d/dx | x^5 | |
| 73 | Trovare la Derivata — d/dx | 2/x | |
| 74 | Trovare la Derivata — d/dx | натуральный логарифм 3x | |
| 75 | Trovare la Derivata — d/dx | x^(1/2) | |
| 76 | Trovare la Derivata — d/d@VAR | f(x) = square root of x | |
| 77 | Trovare la Derivata — d/dx | cos(x^2) | |
| 78 | Trovare la Derivata — d/dx | 1/(x^5) | |
| 79 | Trovare la Derivata — d/dx | кубический корень x^2 | |
| 80 | Вычислим интеграл | интеграл cos(x) относительно x | |
| 81 | Вычислим интеграл | интеграл e^(-x^2) относительно x | |
| 82 | Trovare la Derivata — d/d@VAR | f(x)=x^3 | |
| 83 | Вычислим интеграл | интеграл 4x^2+7 от 0 до 10 относительно x | |
| 84 | Вычислим интеграл | интеграл от ( натуральный логарифм x)^2 по x | |
| 85 | Trovare la Derivata — d/dx | логарифм x | |
| 86 | Trovare la Derivata — d/dx | arctan(x) | |
| 87 | Trovare la Derivata — d/dx | натуральный логарифм 5x | |
| 88 | Trovare la Derivata — d/dx | 5e^x | |
| 89 | Trovare la Derivata — d/dx | cos(3x) | |
| 90 | Вычислим интеграл | интеграл x^3 относительно x | |
| 91 | Вычислим интеграл | интеграл x^2e^x относительно x | |
| 92 | Trovare la Derivata — d/dx | 16 корень четвертой степени 4x^4+4 | |
| 93 | Trovare la Derivata — d/dx | x/(e^x) | |
| 94 | Оценить предел | предел arctan(e^x), если x стремится к 3 | |
| 95 | Вычислим интеграл | интеграл (e^x-e^(-x))/(e^x+e^(-x)) относительно x | |
| 96 | Trovare la Derivata — d/dx | 3^x | |
| 97 | Вычислим интеграл | интеграл xe^(x^2) относительно x | |
| 98 | Trovare la Derivata — d/dx | 2sin(x) | |
| 99 | Вычислить | sec(0)^2 | |
| 100 | Trovare la Derivata — d/dx | натуральный логарифм x^2 |
Дифференциальные уравнения.
 Пошаговый калькулятор
Пошаговый калькуляторПорядок производной указывается штрихами —y»’ или числом после одного штриха —y’5
Ввод распознает различные синонимы функций, как asin, arsin, arcsin
Знак умножения и скобки раставляются дополнительно — запись2sinx сходна2*sin(x)
Список математических функций и констант:
•d(x) — дифференциал
•ln(x) — натуральный логарифм
•sin(x) — синус
•cos(x) — косинус
•tg(x) — тангенс
•ctg(x) — котангенс
•arcsin(x) — арксинус
•arccos(x) — арккосинус
•arctg(x) — арктангенс
•arcctg(x) — арккотангенс
•sh(x) — гиперболический синус
•ch(x) — гиперболический косинус
•th(x) — гиперболический тангенс
•cth(x) — гиперболический котангенс
•sch(x) — гиперболический секанс
•csch(x) — гиперболический косеканс
•arsh(x) — обратный гиперболический синус
•arch(x) — обратный гиперболический косинус
•arth(x) — обратный гиперболический тангенс
•arcth(x) — обратный гиперболический котангенс
•sec(x) — секанс
•cosec(x) — косеканс
•arcsec(x) — арксеканс
•arccsc(x) — арккосеканс
•arsch(x) — обратный гиперболический секанс
•arcsch(x) — обратный гиперболический косеканс
•abs(x) — модуль
•sqrt(x) — корень
•exp(x) — экспонента в степени x
•pow(a,b) — \(a^b\)
•sqrt7(x) — \(\sqrt[7]{x}\)
•sqrt(n,x) — \(\sqrt[n]{x}\)
•log3(x) — \(\log_3\left(x\right)\)
•log(a,x) — \(\log_a\left(x\right)\)
•pi — \(\pi\)
alpha — \(\alpha\)
beta — \(\beta\)
•sigma — \(\sigma\)
gamma — \(\gamma\)
nu — \(\nu\)
•mu — \(\mu\)
phi — \(\phi\)
psi — \(\psi\)
•tau — \(\tau\)
eta — \(\eta\)
rho — \(\rho\)
•a123 — \(a_{123}\)
x_n — \(x_{n}\)
mu11 — \(\mu_{11}\)
| 1 | Найдите производную — d / dx | натуральное журнал x | |
| 2 | Оцените интеграл | интеграл натурального логарифма x относительно x | |
| 3 | Найдите производную — d / dx | е ^ х | |
| 4 | Оцените интеграл | интеграл от e ^ (2x) относительно x | |
| 5 | Найдите производную — d / dx | 1 / х | |
| 6 | Найдите производную — d / dx | х ^ 2 | |
| 7 | Найдите производную — d / dx | 1 / (х ^ 2) | |
| 8 | Найдите производную — d / dx | грех (х) ^ 2 | |
| 9 | Найдите производную — d / dx | сек (x) | |
| 10 | Оцените интеграл | интеграл e ^ x относительно x | |
| 11 | Оцените интеграл | интеграл x ^ 2 относительно x | |
| 12 | Оцените интеграл | интеграл квадратного корня x относительно x | |
| 13 | Найдите производную — d / dx | соз (х) ^ 2 | |
| 14 | Оцените интеграл | интеграл от 1 / x по отношению к x | |
| 15 | Оцените интеграл | интеграл sin (x) ^ 2 относительно x | |
| 16 | Найдите производную — d / dx | х ^ 3 | |
| 17 | Найдите производную — d / dx | сек (x) ^ 2 | |
| 18 | Оцените интеграл | интеграл cos (x) ^ 2 относительно x | |
| 19 | Оцените интеграл | интеграл от sec (x) ^ 2 относительно x | |
| 20 | Найдите производную — d / dx | е ^ (х ^ 2) | |
| 21 | Оцените интеграл | интеграл от 0 до 1 кубического корня из 1 + 7x относительно x | |
| 22 | Найдите производную — d / dx | грех (2x) | |
| 23 | Найдите производную — d / dx | загар (x) ^ 2 | |
| 24 | Оцените интеграл | интеграл 1 / (x ^ 2) относительно x | |
| 25 | Найдите производную — d / dx | 2 ^ х | |
| 26 | График | натуральное бревно из | |
| 27 | Найдите производную — d / dx | cos (2x) | |
| 28 | Найдите производную — d / dx | хе ^ х | |
| 29 | Оцените интеграл | интеграл от 2x относительно x | |
| 30 | Найдите производную — d / dx | (натуральный логарифм x) ^ 2 | |
| 31 | Найдите производную — d / dx | натуральный логарифм (x) ^ 2 | |
| 32 | Найдите производную — d / dx | 3x ^ 2 | |
| 33 | Оцените интеграл | интеграл xe ^ (2x) относительно x | |
| 34 | Найдите производную — d / dx | 2e ^ x | |
| 35 | Найдите производную — d / dx | натуральное бревно 2x | |
| 36 | Найдите производную — d / dx | -sin (х) | |
| 37 | Найдите производную — d / dx | 4x ^ 2-x + 5 | |
| 38 | Найдите производную — d / dx | y = 16 корень четвертой степени из 4x ^ 4 + 4 | |
| 39 | Найдите производную — d / dx | 2x ^ 2 | |
| 40 | Оцените интеграл | интеграл e ^ (3x) относительно x | |
| 41 | Оцените интеграл | интеграл от cos (2x) относительно x | |
| 42 | Найдите производную — d / dx | 1 / (квадратный корень из x) | |
| 43 | Оцените интеграл | интеграл e ^ (x ^ 2) относительно x | |
| 44 | Оценить | e ^ бесконечность | |
| 45 | Найдите производную — d / dx | х / 2 | |
| 46 | Найдите производную — d / dx | -cos (x) | |
| 47 | Найдите производную — d / dx | грех (3x) | |
| 48 | Найдите производную — d / dx | 1 / (х ^ 3) | |
| 49 | Оцените интеграл | интеграл tan (x) ^ 2 относительно x | |
| 50 | Оцените интеграл | интеграл 1 по x | |
| 51 | Найдите производную — d / dx | х ^ х | |
| 52 | Найдите производную — d / dx | x натуральное бревно x | |
| 53 | Найдите производную — d / dx | х ^ 4 | |
| 54 | Оценить предел | предел, когда x приближается к 3 из (3x-5) / (x-3) | |
| 55 | Оцените интеграл | интеграл x ^ 2 натуральный логарифм x относительно x | |
| 56 | Найдите производную — d / dx | f (x) = квадратный корень из x | |
| 57 | Найдите производную — d / dx | х ^ 2sin (х) | |
| 58 | Оцените интеграл | интеграл sin (2x) относительно x | |
| 59 | Найдите производную — d / dx | 3e ^ x | |
| 60 | Оцените интеграл | интеграл xe ^ x относительно x | |
| 61 | Найдите производную — d / dx | у = х ^ 2 | |
| 62 | Найдите производную — d / dx | квадратный корень из x ^ 2 + 1 | |
| 63 | Найдите производную — d / dx | грех (x ^ 2) | |
| 64 | Оцените интеграл | интеграл от e ^ (- 2x) относительно x | |
| 65 | Оцените интеграл | интеграл натурального логарифма квадратного корня x относительно x | |
| 66 | Найдите производную — d / dx | е ^ 2 | |
| 67 | Найдите производную — d / dx | х ^ 2 + 1 | |
| 68 | Оцените интеграл | интеграл sin (x) относительно x | |
| 69 | Найдите производную — d / dx | арксин (х) | |
| 70 | Оценить предел | предел, когда x приближается к 0 of (sin (x)) / x | |
| 71 | Оцените интеграл | интеграл e ^ (- x) относительно x | |
| 72 | Найдите производную — d / dx | х ^ 5 | |
| 73 | Найдите производную — d / dx | 2 / х | |
| 74 | Найдите производную — d / dx | натуральное бревно из 3х | |
| 75 | Найдите производную — d / dx | х ^ (1/2) | |
| 76 | Найдите производную — d / d @ VAR | f (x) = квадратный корень из x | |
| 77 | Найдите производную — d / dx | соз (х ^ 2) | |
| 78 | Найдите производную — d / dx | 1 / (х ^ 5) | |
| 79 | Найдите производную — d / dx | кубический корень из x ^ 2 | |
| 80 | Оцените интеграл | интеграл cos (x) относительно x | |
| 81 | Оцените интеграл | интеграл e ^ (- x ^ 2) относительно x | |
| 82 | Найдите производную — d / d @ VAR | е (х) = х ^ 3 | |
| 83 | Оцените интеграл | интеграл от 0 до 10 из 4x ^ 2 + 7 по x | |
| 84 | Оцените интеграл | интеграл (натуральный логарифм x) ^ 2 относительно x | |
| 85 | Найдите производную — d / dx | журнал x | |
| 86 | Найдите производную — d / dx | арктан (x) | |
| 87 | Найдите производную — d / dx | натуральное бревно 5x | |
| 88 | Найдите производную — d / dx | 5e ^ x | |
| 89 | Найдите производную — d / dx | cos (3x) | |
| 90 | Оцените интеграл | интеграл x ^ 3 относительно x | |
| 91 | Оцените интеграл | интеграл x ^ 2e ^ x относительно x | |
| 92 | Найдите производную — d / dx | 16 корень четвертой степени из 4x ^ 4 + 4 | |
| 93 | Найдите производную — d / dx | х / (е ^ х) | |
| 94 | Оценить предел | предел, когда x приближается к 3 от arctan (e ^ x) | |
| 95 | Оцените интеграл | интеграл от (e ^ x-e ^ (- x)) / (e ^ x + e ^ (- x)) относительно x | |
| 96 | Найдите производную — d / dx | 3 ^ х | |
| 97 | Оцените интеграл | интеграл xe ^ (x ^ 2) относительно x | |
| 98 | Найдите производную — d / dx | 2sin (х) | |
| 99 | Оценить | сек (0) ^ 2 | |
| 100 | Найдите производную — d / dx | натуральный логарифм x ^ 2 |
Правило цепочки — стр.
 2}}}}.\ prime}}
2}}}}.\ prime}} = {\ frac {{\ cancel {2} \ cos 2x}} {{\ cancel {2} \ sqrt {\ sin 2x + 1}}}}
= {\ frac {{\ cos 2x) }} {{\ sqrt {\ sin 2x + 1}}}.}
\]
Производная этой функции не определена в точках, где знаменатель равен нулю, то есть когда
\ [
{\ sin 2x + 1 = 0, \; \;} \ Rightarrow
{\ sin 2x = — 1, \; \;} \ Rightarrow
{2x = \ frac {{3 \ pi}} { 2} + 2 \ pi n, \; \;} \ Rightarrow
{x = \ frac {{3 \ pi}} {4} + \ pi n, \; n \ in \ mathbb {Z}.}
\ ]
Пример 27.4}}} \; \; \ left ({x \ ne 1} \ right).}
\]
Домен, диапазон и состав функций
Домен, диапазон и состав функцийОбласть, диапазон и состав функций
Студентам было предложено дать решение второй задачи для
третий семинар. Центральным аспектом этой проблемы было рассмотрение
сложной формулы, определяющей функцию. Формула была
состав из 4 (а может и 5, в зависимости от того, как вы «читаете»)
функции.Каждая деталь была «легкой» или (по крайней мере, я надеялся) хорошо
известен. Это были:
Это были:
ln arctan в кубе (формула: x 3 ) квадратный корень (ing) (формула:
sqrt (x) или x & frac12 ) минус 1 (формула: x – 1)
Судя по решениям, которые я прочитал, это было очень сложно проблема. Я не предполагал, что решение будет таким недоступным и сложно писать. Может быть, здесь я могу показать более простые примеры состав, и вы можете увидеть, в чем заключаются трудности.Мастерская проблема была довольно сложной.
Итак, давайте посмотрим на область, диапазон и графики двух функций: I надеюсь, что то, что следует здесь, вам знакомо. После этого мы увидим некоторые примеры композиций и обсудить, что происходит с доменами, диапазоны и графики.
| синус График периодический и повторяется каждые 2Π. я думаю, эта функция должна быть вам знакома. | ||
| Домен Все реальные номера: R , также записывается как (–∞, + ∞). 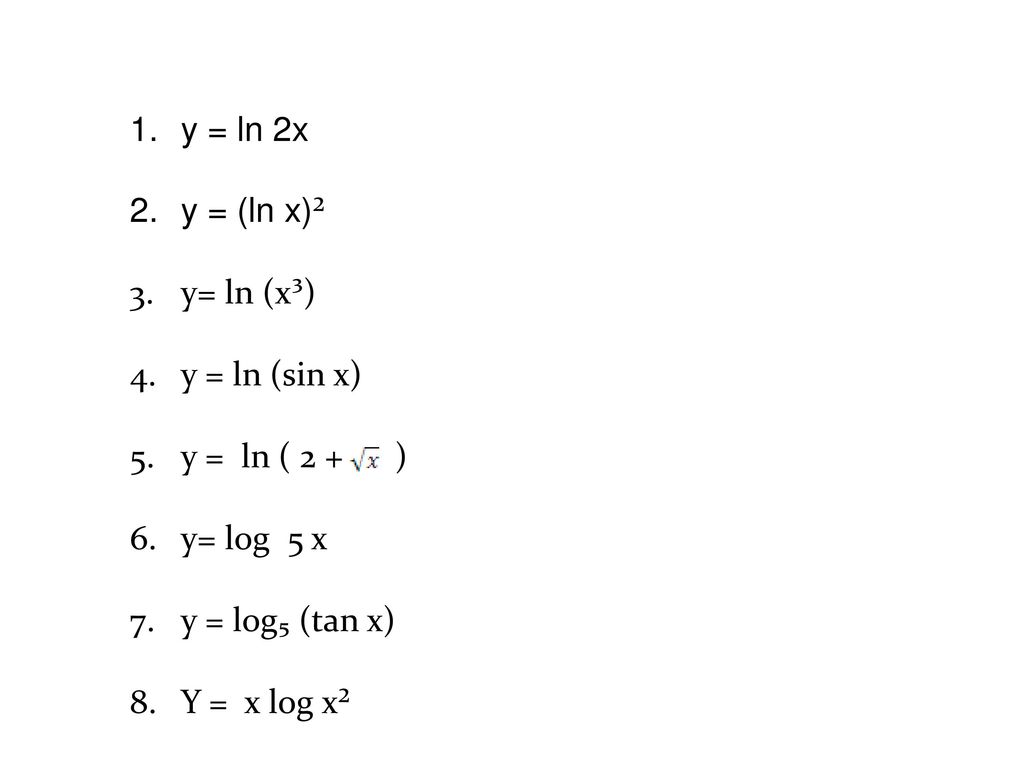 Мы можем введите любое действительное число. Мы можем введите любое действительное число. | Диапазон Выход из функционального блока «синус» (извините, правда думайте так!) ограничено числами от –1 до 1, включая обе конечные точки. Так что это [–1,1]. | График Или достаточно в этом разобраться, надеюсь! |
| ln Слева от оси Y нет ничего, а то, что справа, на самом деле довольно «простое» — оно просто идет вверх, начиная с От –∞ до + ∞.Надеюсь, это тоже знакомо. | ||
| Домен Мы можем ввести только положительные числа. Таким образом, домен равен (0, + ∞). | Диапазон Выход для ln равен неограниченный: возможно любое действительное число. Так что диапазон R или (–∞, + ∞). | График Или достаточно в этом разобраться, надеюсь! |
Теперь попробуем поработать с этими функциями.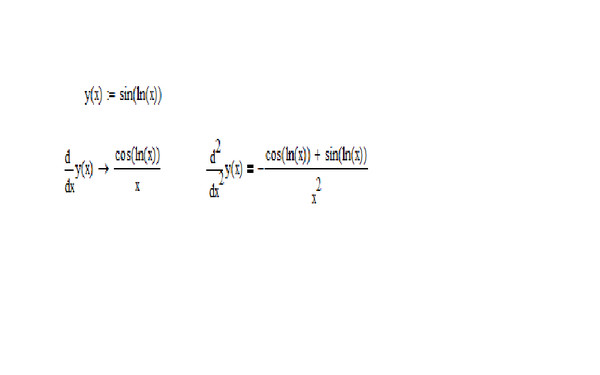 Я посмотрю на некоторые
композиции.
Я посмотрю на некоторые
композиции.
sin (ln (x))
Ну, логический «поток» выглядит примерно так:
x → ln (x) → sin (ln (x). Первая стрелка накладывает ограничение на
домен. Лучше не кормить ничем ≤0. Вторая стрелка
«возьмет» что угодно, потому что область синуса — это все R . Следовательно, область этой композиции
(0, ∞). А как насчет диапазона? Поскольку на выходе ln все R , совокупность входов, которые «скармливаются» синусу, реальна
числа. И мы знаем, что набор результатов для этого
набор входных данных равен [–1,1].Так что я уверен, что вывод
sin (ln (x)), диапазон равен [–1,1].
Справа есть изображение графика y = sin (ln (x)), но предупреждение: этот график на самом деле намного сложнее
и страннее, чем то, что показано на этой картинке. График показан в
довольно обычное окно, с координатами x от 0 до 5 и y от
–1 к 1. Большая часть информации скрыта. Поскольку x приближается к 0
(в наших обозначениях x → 0 — ), ln (x) убывает и
уменьшается и уменьшается, и дается все больше и больше отрицательных чисел
как входы в синус.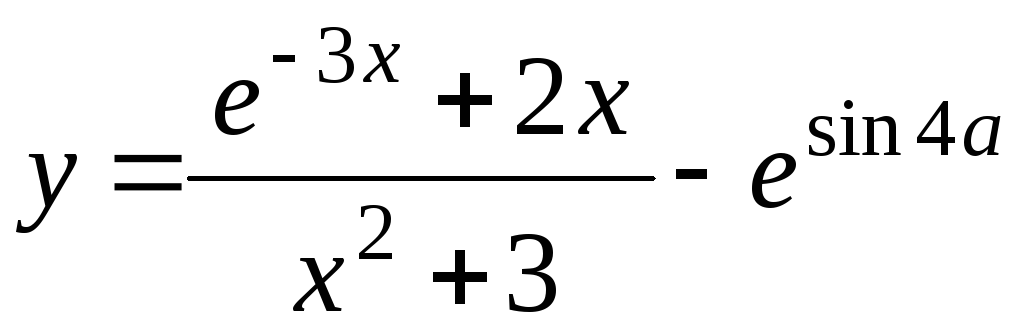 Но затем синус колеблется. Получаем все выходы
соответствующие входам синуса (-∞, 0). Есть более точные
изображения ниже, которые также более запутаны.
Но затем синус колеблется. Получаем все выходы
соответствующие входам синуса (-∞, 0). Есть более точные
изображения ниже, которые также более запутаны.
| Это менее обычное окно, в нем что происходит для x в интервале [≈0, .5]. | В этом окне x находится в [≈0, .05]. Есть еще шевеление и вниз в качестве входных сигналов для синусоидального марша, кратного 2Π. На самом деле существует бесконечно много колебаний вверх и вниз до непосредственно справа от 0.Это все колебания синуса в (–∞, 0) как бы переупаковывается все быстрее и быстрее при x → 0 + . Я считаю, что «колебание» более достойно, чем «покачивание» но они означают то же самое. | Ну вот и другая сторона, и сильно измененный горизонтальный масштаб. (присмотритесь, пожалуйста). ln (x) возрастает при x → ∞, и на самом деле все положительные действительные числа в конечном итоге становятся выходными.  Ну это значит
что существует также бесконечно много колебаний , когда x становится
большие, но волны прибывают все медленнее и медленнее.Итак, вершины
неровности становятся все дальше и дальше друг от друга. Так что это тоже сбивает с толку
картина. Эти колебания представляют собой все колебания синуса в
(0, ∞) вроде переупакованы с другими часами, становятся медленнее
и медленнее. Ну это значит
что существует также бесконечно много колебаний , когда x становится
большие, но волны прибывают все медленнее и медленнее.Итак, вершины
неровности становятся все дальше и дальше друг от друга. Так что это тоже сбивает с толку
картина. Эти колебания представляют собой все колебания синуса в
(0, ∞) вроде переупакованы с другими часами, становятся медленнее
и медленнее. |
лин (sin (x))
Попробуем это так: x → sin (x) → ln (sin (x)). Конечно есть
нет ограничений на входов на синус, но есть сильный
ограничение на входы в ln: они должны быть положительными. Итак, каждый интервал
где значения синуса (то, что я называл , выводит )
не положительны, должны быть выброшены, чтобы эта композиция была
определенный.Посмотрим: в [0,2Π] синус положителен ровно в (0,)
(обратите внимание, что конечных точек там нет!), так что домен
ln (sin (x)) включает интервал (0, Π).
Вещи повторяются для каждого
кратно 2Π, поскольку синус периодичен с периодом 2Π и
поэтому область определения ln (sin (x) включает (2Π, 3Π) и
(4Π, 5Π) и (6Π, 7Π) и т.
Но что может быть интереснее, так это ассортимент. В значения синуса на (0, Π) — это просто числа от 0 до 1. Быть точнее, эти числа представляют собой интервал (0,1]. Когда (0,1] скармливается в ln, ну, мы получаем только , поскольку выводит значений, которые соответствуют этим входам. Я знаю, что ln (1) равно 0. И я знаю что ln имеет все отрицательные числа как выходы для чисел от 0 до 1. Таким образом, выходы для этой композиции равны (–∞, 0]. состав ln (sin (x)) НЕ имеет тот же диапазон, что и просто ln.Его диапазон составляет всего (–∞, 0], что значительно меньший набор чисел.
Что вы должны извлечь из этого, пожалуйста?
Состав очень странный . Состав функций может сделать
как домен , так и диапазон функций меняется странно
способами.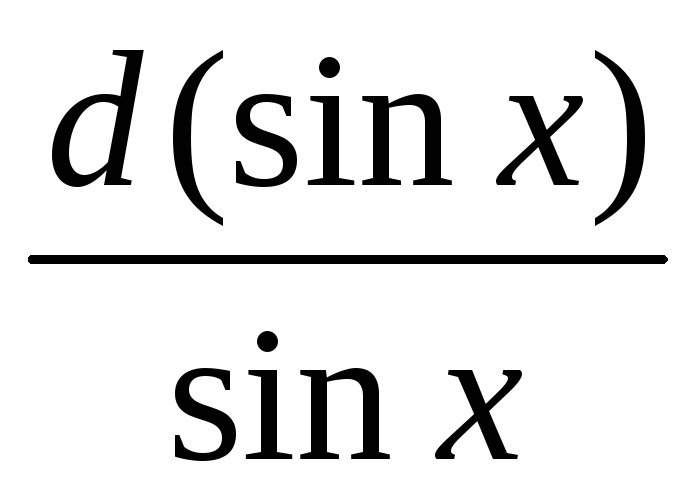 Ниже приводится краткое изложение того, что мы видели.
Ниже приводится краткое изложение того, что мы видели.
| Функция | Домен | Диапазон |
|---|---|---|
| sin (x) | (- & infin, ∞) | [–1,1] |
| ln (x) | (0, ∞) | (- & infin, ∞) |
| sin (ln (x)) | (0, ∞) | [–1,1] |
| ln (sin (x)) | ( 0, Π) и все интервалы, полученные «перемещением» этого интервала на целые кратные (положительное или отрицательное) из 2Π | (–∞, 0] |
Дополнительные комментарии
Учащиеся сделали интересные и полезные комментарии в классе и после
класс об этом обсуждении.Эти комментарии были оценены.
Например, г-жа О’Салливан заметила
что ее изображение (на графическом калькуляторе) y = ln (sin (x))
выглядело не так аккуратно и красиво, как на картинке выше.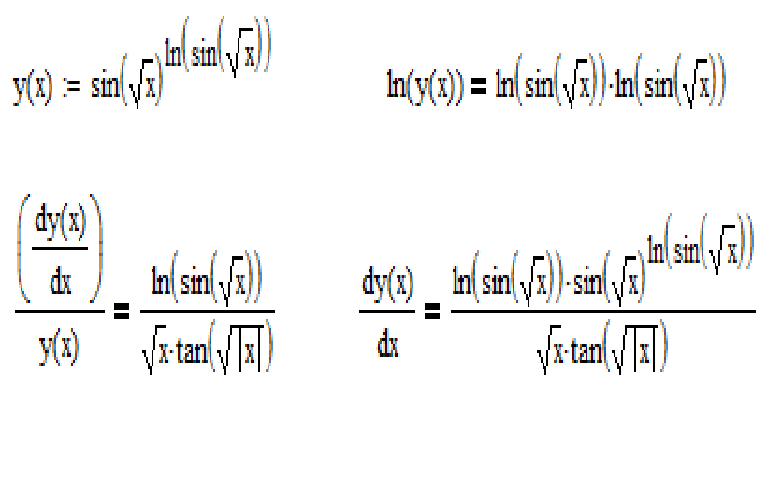 Этот
потому что (по сути) то, что делает калькулятор для отображения графика,
оценить функцию на 87 равных по горизонтали значениях в
ширину окна по горизонтали, а затем включить или подсветить, как
ну как можно пиксели, расположение на экране калькулятора,
соответствующие этим значениям.Если расстояние между образцами не совпадает
хорошо с кратными, которые важны для функции,
тогда изображение не будет хорошо выглядеть или не будет соответствовать фактическому
график функции. Справа — график, полученный путем выборки 87.
значения. Вы можете видеть, что части кривой не выглядят
одно и тоже. На моем графике выше было , а не , моя первая попытка создать
изображение для этих заметок. Мне действительно нужно около полдюжины
пытается. Картинка, которую я использовал, имела частоту дискретизации около 350 точек, и я
очень тщательно подбирали окно, чтобы картинка выглядела так надо ! Технологии очень мощные, но компьютеры обычно делают
именно то, что им велят делать.Иногда нужна осторожность!
Этот
потому что (по сути) то, что делает калькулятор для отображения графика,
оценить функцию на 87 равных по горизонтали значениях в
ширину окна по горизонтали, а затем включить или подсветить, как
ну как можно пиксели, расположение на экране калькулятора,
соответствующие этим значениям.Если расстояние между образцами не совпадает
хорошо с кратными, которые важны для функции,
тогда изображение не будет хорошо выглядеть или не будет соответствовать фактическому
график функции. Справа — график, полученный путем выборки 87.
значения. Вы можете видеть, что части кривой не выглядят
одно и тоже. На моем графике выше было , а не , моя первая попытка создать
изображение для этих заметок. Мне действительно нужно около полдюжины
пытается. Картинка, которую я использовал, имела частоту дискретизации около 350 точек, и я
очень тщательно подбирали окно, чтобы картинка выглядела так надо ! Технологии очень мощные, но компьютеры обычно делают
именно то, что им велят делать.Иногда нужна осторожность!
Другой студент (имя которого я, к сожалению, не знаю) обсуждал
Проблема с семинаром у меня после нашего анализа функций здесь. В
Задача мастерской запрашивает домен и диапазон (arctan (ln (sqrt (x) -1))) 3 . Он сказал, что возможно
он мог только «беспокоиться» об арктане и кубе. Мой комментарий был таким
запись, в которой объясняется решение проблемы, потребует
рассмотреть все «кусочки» композиции, и что
объяснение должно быть довольно осторожным.В двух более простых
композиции, обсуждаемые здесь, я попытался объяснить, как соображения
домен и диапазон потребовали, чтобы мы рассмотрели обе задействованные функции и то, как
эти функции взаимодействовали друг с другом. Это взаимодействие обеспечивает
большинство раздражающих особенностей (извините, «интересные аспекты» могут быть
более дипломатичная фраза) примера. Итак, для задачи мастерской,
некоторое обсуждение взаимодействия каждой части композиции
нужно.
В
Задача мастерской запрашивает домен и диапазон (arctan (ln (sqrt (x) -1))) 3 . Он сказал, что возможно
он мог только «беспокоиться» об арктане и кубе. Мой комментарий был таким
запись, в которой объясняется решение проблемы, потребует
рассмотреть все «кусочки» композиции, и что
объяснение должно быть довольно осторожным.В двух более простых
композиции, обсуждаемые здесь, я попытался объяснить, как соображения
домен и диапазон потребовали, чтобы мы рассмотрели обе задействованные функции и то, как
эти функции взаимодействовали друг с другом. Это взаимодействие обеспечивает
большинство раздражающих особенностей (извините, «интересные аспекты» могут быть
более дипломатичная фраза) примера. Итак, для задачи мастерской,
некоторое обсуждение взаимодействия каждой части композиции
нужно.
Поддерживается greenfie @ math.rutgers.edu, последнее изменение — 02.10.2009.
5. Производная логарифмической функции
М. Борн
Сначала давайте посмотрим на график функции журнала с основанием e , то есть:
f ( x ) = log e ( x ) (обычно пишется «ln x »).
Касательная x = 2 включена на график.
Наклон тангенса угла y = ln x при x = 2 равен 1/2.(Мы можем наблюдать это на графике, посмотрев на отношение подъема / хода).
Если y = ln x ,
| x | 1 | 2 | 3 | 4 | 5 |
|---|---|---|---|---|---|
| наклон графика | `1` | `1/2` | `1/3` | `1/4` | `1/5` |
| `1 / x` | `1` | `1/2` | `1/3` | `1/4` | `1/5` |
Мы видим, что наклон графика для каждого значения x равен «1 / x».Это работает для любого положительного значения x (конечно, у нас не может быть логарифма отрицательного числа).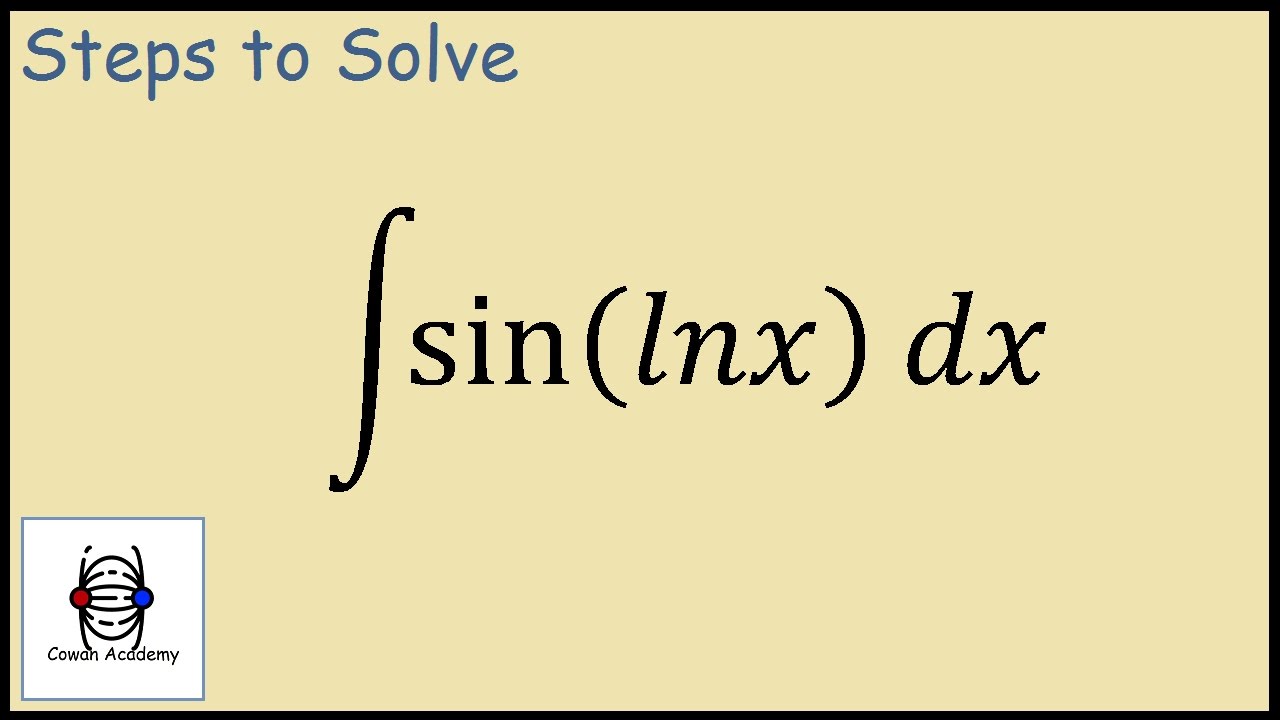
Если бы мы сделали еще много примеров, мы могли бы сделать вывод, что производная функции логарифма y = ln x равна
`dy / dx = 1 / x`
Примечание 1: На самом деле, этот результат исходит из первых принципов.
Примечание 2: Мы используем логарифмы с основанием e . Если вам нужно напоминание о функциях журнала, ознакомьтесь с базой журнала и ранее.
Производная логарифма
y = ln xПроизводная логарифмической функции y = ln x определяется по формуле:
`d / (dx) (ln \ x) = 1 / x`
Вы также увидите, что это написано несколькими другими способами. Следующие эквиваленты:
`d / (dx) log_ex = 1 / x`
Если y = ln x , то `(dy) / (dx) = 1 / x`
Теперь мы покажем, откуда взялась формула для производной от log_e x, используя первые принципы. {1 «/» t} `приближается к значению` e ~~ 2.71828`.)
{1 «/» t} `приближается к значению` e ~~ 2.71828`.)
Я напишу `log (x)` для обозначения `log_e (x) = ln (x)`, чтобы облегчить чтение.
У нас есть `f (x) = log (x)`, поэтому производная будет равна:
`(df) / (dx) = lim_ {h-> 0} (log (x + h) -log (x)) / h`
Теперь верхняя часть нашей фракции —
`log (x + h) -log (x)` `= log ((x + h) / x)` `= log (1 + h / x)`.
Чтобы упростить алгебру, мы теперь подставляем `t = h / x`, и это дает нам` h = xt`.{1 «/» t}) `
`= 1 / x log (e)`
`= 1 / x`
Подсказка
Для некоторых задач мы можем использовать законы логарифмирования, чтобы упростить логарифмическое выражение перед его дифференцированием.
Пример 1
Найдите производную от
y = ln 2 x
Ответ
Мы используем логарифмический закон:
журнал ab = журнал a + журнал b
Мы можем написать наш вопрос как:
y = ln 2 x = ln 2 + ln x
Теперь производная константы равна 0, поэтому
`d / (dx) ln \ 2 = 0`
Итак, у нас осталось (из нашей формулы выше)
`d / (dx) (ln \ x) = 1 / x`
Окончательный ответ:
`(dy) / (dx) = 1 / x`
Из следующего графика видно, что наклон y = ln 2 x (кривая зеленого цвета, касательная пурпурного) совпадает с наклоном y = ln x (кривая серого цвета, касательная пунктирно серым) в точке x = 2.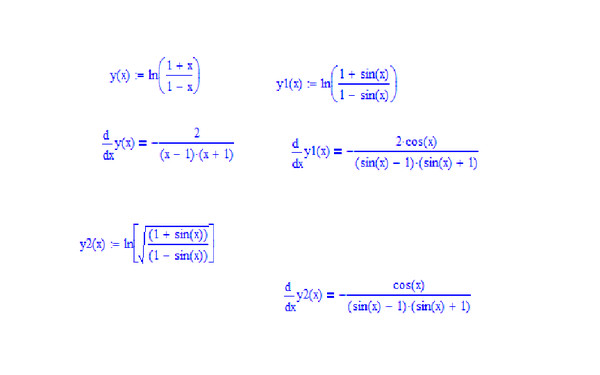
Пример 2
Найдите производную от
y = ln x 2
Ответ
Мы используем логарифмический закон:
журнал a n = n журнал a
Итак, мы можем написать вопрос как
y = ln x 2 = 2 ln x
Производная будет просто в 2 раза больше производной ln x .2) «на самом деле имеет 2« руки », одно на отрицательной стороне, а другое на положительной. На приведенном выше графике для простоты показано только положительное плечо.
Производная от
y = ln u (где u — функция от x )К сожалению, мы можем использовать только законы логарифма, чтобы помочь нам в ограниченном количестве типов вопросов логарифмической дифференциации.
Чаще всего нам нужно найти производную логарифма некоторой функции x . Например, нам может потребоваться найти производную от y = 2 ln (3 x 2 — 1).
Например, нам может потребоваться найти производную от y = 2 ln (3 x 2 — 1).
Для решения таких задач нам понадобится следующая формула.
Если
y = ln u
и u — некоторая функция от x , тогда:
`(dy) / (dx) = (u ‘) / u`
, где u ‘ — производная от u
Другой способ записать это —
`(dy) / (dx) = 1 / u (du) / (dx)`
Вы также можете увидеть следующую форму.Это означает то же самое.
Если
y = ln f ( x ),
, тогда производная y дается по формуле:
`(dy) / (dx) = (f ‘(x)) / (f (x)`
Пример 3
Найти производную из
y = 2 ln (3 x 2 — 1).
2 + 1)`
Дифференцирование логарифмических функций с основанием, отличным от
eЕсли
u = f ( x ) является функцией x ,
и
y = log b u — логарифм с основанием b ,
, то мы можем получить производную функции логарифма с основанием b , используя:
`(dy) / (dx) = (log_be) (u ‘) / u`
где
u является производным от u
log b e — постоянная величина.См. Изменение базового правила, чтобы узнать, как вычислить такие константы на вашем калькуляторе.)
Примечание 1: Эта формула основана на первых принципах.
Примечание 2: Если мы выберем e в качестве основы, то производная от ln u , где u является функцией x , просто даст нам нашу формулу выше:
`(dy) / (dx) = (u ‘) / u`
[Напомним, что журнал e e = 1.
]
[См. Главу, посвященную экспоненциальным и логарифмическим функциям, основание и , если вам нужно освежить все это.]
Пример 6
Найти производную из y = журнал 2 6 x .
Ответ
Начнем с использования следующего правила журнала, чтобы упростить наш вопрос:
журнал ab = журнал a + журнал b
Мы можем написать наш вопрос как:
y = журнал 2 6 x = журнал 2 6 + журнал 2 x
Первый член, log 2 6, является константой, поэтому его производная равна 0.
Производная второго члена выглядит следующим образом по нашей формуле:
`(dy) / (dx) = (log_2e) (1 / x) = (log_2e) / x`
Член сверху, log 2 e , является константой.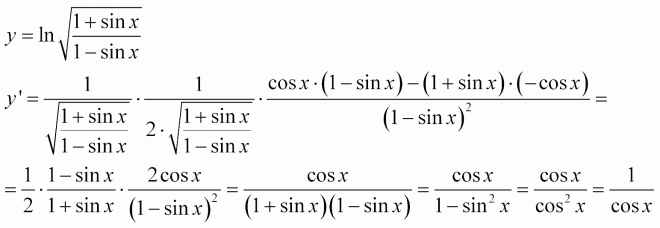 3-x`
3-x`
`x ≠ ± sqrt (0.5) `,
`x ≠ 0`
ПРИМЕЧАНИЕ: Мы должны быть осторожны с областью этого решения, так как это верно только для определенных значений из x .
График y = ln (2 x 3 — x ) 2 (который имеет степень 2 ) определен для всех x , кроме
`± sqrt (0,5), 0`
Его график выглядит следующим образом:
График y = 2 ln (2 x 3 — x ), однако (он имеет 2 x спереди) определен только для более ограниченного домен (поскольку у нас не может быть логарифма отрицательного номер.)
Таким образом, мы можем иметь только x в диапазоне `-sqrt 0,5 sqrt0.5.`
Итак, когда мы находим дифференцирование логарифма с помощью
ярлык, указанный выше, мы должны быть осторожны, чтобы домен
указаны функция и область определения производной. 2`
2`
3.x (x \ cot \ x + ln (sin x)) `
График функции в упражнении 5 довольно интересен:
График y = (sin x ) x .
Найдите область определения функции ydfracxsqrtsin ln xcos class 12 maths CBSE
Подсказка: Область вещественной функции — это набор вещественных значений x, для которых определена функция y.Предположим, что данная функция является функцией с действительным знаком (от действительного набора до действительного набора чисел). Затем проанализируйте заданную функцию и выясните, для какого значения x, y является действительным числом. Используемая формула:
$ \ cos x \ sin y- \ sin x \ cos y = \ sin \ left (xy \ right) $
Полное пошаговое решение:
Давайте сначала поймем, что такое область функции. Область определения функции с действительным знаком — это набор действительных значений x, для которых определена функция y. Здесь функция задается равной
Здесь функция задается равной
$ y = \ dfrac {x} {\ sqrt {\ sin (\ ln x) — \ cos (\ ln x)}} $
. Теперь мы должны найти эти реальные значения x, для которого существует значение y. Мы видим, что числитель функции — x, который всегда действительный. Однако знаменатель содержит квадратный корень. Число под квадратным корнем всегда должно быть положительным действительным числом. В противном случае результатом будет мнимое число, которое не является реальным. Это означает, что для действительного значения y $ \ sin (\ ln x) — \ cos (\ ln x)> 0 $.
Теперь умножьте и разделите полученное выше неравенство на $ \ sqrt {2} $, как показано ниже.
$ \ sqrt {2} \ left (\ dfrac {1} {\ sqrt {2}} \ sin (\ ln x) — \ dfrac {1} {\ sqrt {2}} \ cos (\ ln x) \ right)> 0 $
Мы знаем, что $ \ dfrac {1} {\ sqrt {2}} = \ cos \ left (\ dfrac {\ pi} {4} \ right) = \ sin \ left (\ dfrac {\ pi} {4} \ right) $.
Тогда мы можем записать неравенство как
$ \ sqrt {2} \ left (\ cos \ dfrac {\ pi} {4} \ sin (\ ln x) — \ sin \ dfrac {\ pi} {4} \ cos (\ ln x) \ right)> 0 $
Считаем, что $ \ sqrt {2} $> 0
Тогда
$ \ Rightarrow \ cos \ dfrac {\ pi} {4} \ sin (\ ln x ) — \ sin \ dfrac {\ pi} {4} \ cos (\ ln x)> 0 $
Теперь мы можем написать, что $ \ cos \ dfrac {\ pi} {4} \ sin (\ ln x) — \ sin \ dfrac {\ pi} {4} \ cos (\ ln x) = \ sin \ left (\ ln x- \ dfrac {\ pi} {4} \ right) $.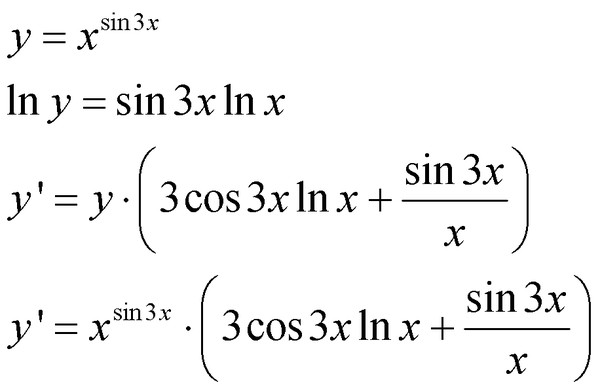 {\ dfrac {(4n + 1) \ pi} {4}}}
{\ dfrac {(4n + 1) \ pi} {4}}}
Примечание: Некоторые студенты могут утверждать, что число под квадратным корнем может быть нулем, поскольку квадратный корень из нуля равен нулю, и это действительное число. . Однако обратите внимание, что квадратный корень находится в знаменателе, и для существования действительного значения y знаменатель не может быть равен нулю.
Домашнее задание по исчислению и дифференциальным уравнениям
Домашнее задание по исчислению и дифференциальным уравнениямМатематика 69.105, Раздел D, Зима, 1998.
Неделя 1: Раздел 15.1 # 1-10 (нечетный)
Раздел 15.2 №1, 3, 5, 7, 9
Раздел 15.2 № 15, 17, 19, 25
Неделя 2:
Раздел 15.2 # 25
Раздел 12.3 № 3 — 16 (нечетный)
Раздел 12.3 № 17 — 33 (нечетный)
Неделя 3:
Раздел 15.3 №1–13 (нечетный)
Раздел 15.3 № 15-16
Раздел 15.3 № 23, 25, 27
Неделя 4:
Раздел 15. 4 # 5-19 (нечетный)
4 # 5-19 (нечетный)
Раздел 15.5 №1-17 (нечетный)
Раздел 15.5 # 21, 23
Раздел 15.5 # 29, 31, 33
Неделя 5:
Раздел 15.6 # 1 — 10 (нечетный)
Посмотрите дополнительные примеры здесь .. («Примеры с использованием изменения параметров»).
Неделя 6:
Домашнее задание по уравнениям Коши-Эйлера
1. Найдите общее решение уравнения
x 2 y «- 3xy ‘+ 4y = x + x 2 ln (x)Ответ : y = c 1 x 2 + c 2 x 2 ln (x) + x + x 2 ln 3 (x) / 6.
2. Найдите общее решение уравнения x 2 y «- 2xy ‘+ 2y = ln 2 (x) — ln (x 2 )Ответ : y = c 1 x + c 2 x 2 + (1/4) + {ln (x) + ln 2 (x)} / 2.
3. Найдите общее решение уравнения x 2 y «- xy ‘+ 4y = cos (ln (x)) + x sin (ln (x))Ответ : y = c 1 x cos (sqrt (3) ln (x)) + c 2 x sin (sqrt (3) ln (x)) + {x sin (ln (x))} / 2 + {3 cos (ln (x)) — 2 sin (ln (x))} / 13
Домашнее задание по уравнению Клеро
1.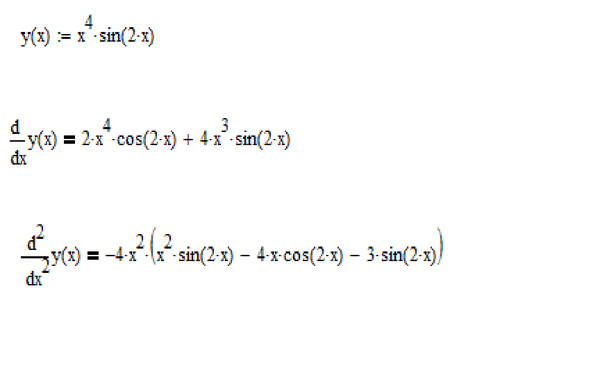 Найти общее решение уравнения
Найти общее решение уравнения
Ответ: … y = y (x) = Cx + 3 C 3
2. Решите дифференциальное уравнение
x e y ‘(x) + x 2 y’ (x) = x y (x) Ответ: … y = y (x) = Cx + e CДомашнее задание по элементарным системам уравнений
1. Найдите общее решение системы уравнений 2 на 2
x ‘+ 2x + y’ + y = t5x + y ‘+ 3y = t 2 ……… Обратите внимание на опечатку!
Ответ: … y = y (t) = c 1 cos (t) + c 2 sin (t) + 2 t 2 — 3t — 4
x = x (t) = { c 1 -3 c 2 } sin (t) / 5 — {3 c 1 + c 2 } cos (t) / 5 — t 2 + t + 3.
Седьмая неделя была Неделей чтения ……………..
Неделя 8: Последовательности и серии
Раздел 10.1 № 1-39 (нечетный)
Раздел 10.2 № 1-31 (нечетный)
Раздел 10. 3 # 1-21 (нечетные)
3 # 1-21 (нечетные)
Неделя 9:
Последовательности и серии
Раздел 10.3 # 25, 27
Остатки …
Неделя 10:
Последовательности и серии
Раздел 10.4 # 1-31 (нечетный)
Раздел 10.5 # 1-19, 25, 27, 29 (нечетный)
Раздел 10.6 # 1-31 (нечетный)
НОВОЕ: Раздел 10.7 # 1-19 (нечетный)
Неделя 11:
Последовательности и серии
НОВОЕ: Раздел 10.8 # 3-19 (нечетный)
Раздел 10.10 # 1, 3, 7, 9, 11 (нечетные)
Раздел 10.10 # 17-25 (нечетные)
Раздел 10.10 # 27, 29
Последовательности и серии
Раздел 10.11 № 1-9, (нечетный)
Раздел 15.8 № 1-11, (нечетный)
Найти уравнение касательной в данной точке неявное дифференцирование
Используйте неявное дифференцирование, чтобы найти уравнение касательной к кривой в данной точке. Используйте неявное дифференцирование, чтобы найти уравнение касательной к кривой в данной точке .2 = 1` представляет собой пару параллельных прямых. dy = 3x 2. dx. Градиент касательной, когда x = 2, равен 3 × 2 2 = 12. Следовательно, из раздела координатной геометрии уравнение касательной имеет следующий вид: y — 8 = 12 (x — 2), поскольку градиент касательной равен 12, и мы знаем что он проходит через (2, 8), поэтому y = 12x — 16. Найдите все точки на графике уравнения x 2 + y 2 = 4, где касательные параллельны прямой x + y = 2 Решение примера 3 : Перепишите данную линию x + y = 2 в форму пересечения наклона: y = -x + 2 и определите наклон как m = -1.3 = -149 а. найти dy / dx b. написать уравнение касательной к кривой в точке (4, -1) c. Существует такой номер k, что точка (4.2, k) находится на. исчисление. Используйте неявное дифференцирование, чтобы найти уравнение касательной к кривой в данной точке. x2 … Мы сделали много примеров, в которых мы просто использовали неявные производные, но мы не вычисляли фактический наклон касательной в данной точке.
Используйте неявное дифференцирование, чтобы найти уравнение касательной к кривой в данной точке .2 = 1` представляет собой пару параллельных прямых. dy = 3x 2. dx. Градиент касательной, когда x = 2, равен 3 × 2 2 = 12. Следовательно, из раздела координатной геометрии уравнение касательной имеет следующий вид: y — 8 = 12 (x — 2), поскольку градиент касательной равен 12, и мы знаем что он проходит через (2, 8), поэтому y = 12x — 16. Найдите все точки на графике уравнения x 2 + y 2 = 4, где касательные параллельны прямой x + y = 2 Решение примера 3 : Перепишите данную линию x + y = 2 в форму пересечения наклона: y = -x + 2 и определите наклон как m = -1.3 = -149 а. найти dy / dx b. написать уравнение касательной к кривой в точке (4, -1) c. Существует такой номер k, что точка (4.2, k) находится на. исчисление. Используйте неявное дифференцирование, чтобы найти уравнение касательной к кривой в данной точке. x2 … Мы сделали много примеров, в которых мы просто использовали неявные производные, но мы не вычисляли фактический наклон касательной в данной точке. И это то, что я хочу сделать в этом видео. Итак, я хочу выяснить, что наклон в точке x равен 1.Итак, когда x равно 1. Решение. Мы неявно дифференцируем обе части уравнения по x (мы рассматриваем левую часть как составную функцию и используем цепное правило): d dx (x2 + 2xy + 2y2) = d dx (1), ⇒ 2x + 2 ( y + xy ′) + 4yy ′ = 0, ⇒ x + y + xy ′ + 2yy ′ = 0. Когда y = 1, исходное уравнение принимает вид. Учебные видеоуроки по математике онлайн и на компакт-диске. вопрос Используйте неявное дифференцирование, чтобы найти уравнение касательной к кривой в данной точке P. cos (xy) + y = x 4, P (1, 0) и.2 = 1` представляет собой пару параллельных прямых. Неявное дифференцирование / найти уравнение касательной с помощью производной Hot Network Вопросы Что Базз сделал с Кевином в сцене Рождественского конкурса? Используйте неявное дифференцирование, чтобы найти уравнение касательной к кривой в данной точке. 30. x 2/3 + y 2/3 = 4, (- 3 3, 1) (астроид) Используйте неявное дифференцирование, чтобы найти уравнение касательной к кривой в данной точке.
И это то, что я хочу сделать в этом видео. Итак, я хочу выяснить, что наклон в точке x равен 1.Итак, когда x равно 1. Решение. Мы неявно дифференцируем обе части уравнения по x (мы рассматриваем левую часть как составную функцию и используем цепное правило): d dx (x2 + 2xy + 2y2) = d dx (1), ⇒ 2x + 2 ( y + xy ′) + 4yy ′ = 0, ⇒ x + y + xy ′ + 2yy ′ = 0. Когда y = 1, исходное уравнение принимает вид. Учебные видеоуроки по математике онлайн и на компакт-диске. вопрос Используйте неявное дифференцирование, чтобы найти уравнение касательной к кривой в данной точке P. cos (xy) + y = x 4, P (1, 0) и.2 = 1` представляет собой пару параллельных прямых. Неявное дифференцирование / найти уравнение касательной с помощью производной Hot Network Вопросы Что Базз сделал с Кевином в сцене Рождественского конкурса? Используйте неявное дифференцирование, чтобы найти уравнение касательной к кривой в данной точке. 30. x 2/3 + y 2/3 = 4, (- 3 3, 1) (астроид) Используйте неявное дифференцирование, чтобы найти уравнение касательной к кривой в данной точке. y \ sin 2x = x \ cos 2y, (\ pi / 2, \ pi / 4) 🎉 Объявлен номер выигрышного билета «Study-to-Win»! 25–30 Используйте неявное дифференцирование, чтобы найти уравнение для (а) Найти.у. неявным дифференцированием. касательная к кривой в данной точке. (b) Решите … Неявная функция — это функция, заданная F: f (x, y, z) = k, где k — постоянная. В отличие от двух других примеров, касательную плоскость к неявно определенной функции найти гораздо сложнее. Как и в случае с графиками и параметрическими графиками, мы должны использовать другое устройство в качестве инструмента для поиска плоскости. Это устройство известно как градиент. Используйте неявное дифференцирование, чтобы найти уравнение касательной к кривой в данной точке.30. x 2/3 + y 2/3 = 4, (- 3 3, 1) (астроид)
y \ sin 2x = x \ cos 2y, (\ pi / 2, \ pi / 4) 🎉 Объявлен номер выигрышного билета «Study-to-Win»! 25–30 Используйте неявное дифференцирование, чтобы найти уравнение для (а) Найти.у. неявным дифференцированием. касательная к кривой в данной точке. (b) Решите … Неявная функция — это функция, заданная F: f (x, y, z) = k, где k — постоянная. В отличие от двух других примеров, касательную плоскость к неявно определенной функции найти гораздо сложнее. Как и в случае с графиками и параметрическими графиками, мы должны использовать другое устройство в качестве инструмента для поиска плоскости. Это устройство известно как градиент. Используйте неявное дифференцирование, чтобы найти уравнение касательной к кривой в данной точке.30. x 2/3 + y 2/3 = 4, (- 3 3, 1) (астроид)
8 февраля 2018 г. · Найдите \ (y ‘\), решив уравнение для y и производя прямое дифференцирование. Найдите \ (y ‘\) неявным дифференцированием. Убедитесь, что производные в (a) и (b) совпадают.
10 Для x2 + y2 = 13 найдите наклон касательной в точке (−2,3). 11 Для x2 + xy − y2 = 1 найдите уравнения касательных в точке, где x = 2. 12 Для xsin2y = ycos2x найдите уравнения касательной и нормали к графику в точке π 4, π 2 ⎛ ⎝⎜ ⎞ ⎠⎟.2 = 3. При заданном …
11 Для x2 + xy − y2 = 1 найдите уравнения касательных в точке, где x = 2. 12 Для xsin2y = ycos2x найдите уравнения касательной и нормали к графику в точке π 4, π 2 ⎛ ⎝⎜ ⎞ ⎠⎟.2 = 3. При заданном …
Используя неявное дифференцирование, мы можем найти уравнение касательной к графику кривой. В следующих упражнениях используйте неявное дифференцирование, чтобы найти [latex] \ frac {dy} {dx} [/ latex]. 1.
Неявная функция — это функция, заданная F: f (x, y, z) = k, где k — постоянная. В отличие от двух других примеров, касательную плоскость к неявно определенной функции найти гораздо сложнее. Как и в случае с графиками и параметрическими графиками, мы должны использовать другое устройство в качестве инструмента для поиска плоскости.2 …
Решение для Найдите уравнение касательной прямой к xy + 4y = 2 в точке (2, -1) Подсказка: используйте неявное% 3D дифференцирование.
Мы можем найти уравнение касательной, применив форму точки наклона уравнения прямой. Наклон можно получить путем дифференцирования. Координаты точки уже приведены в …
Координаты точки уже приведены в …
Использование неявного дифференцирования для нахождения уравнения касательной линии лишь немного отличается от нахождения уравнения касательной прямой с использованием регулярного дифференцирования.Помните, что мы выполняем следующие шаги, чтобы найти уравнение касательной с помощью нормального дифференцирования: Возьмите производную заданной функции.
Узнайте, как использовать неявное дифференцирование для вычисления уравнения касательной к кривой в определенной точке. Используйте неявное дифференцирование, чтобы найти …
Калькулятор неявного дифференцирования найдет первую и вторую производные неявной функции, обрабатывая либо y как функцию от x, либо x как функцию от y, с указанными шагами….
Итак, наклон касательной равен 1/2. Используйте форму Point-Slope уравнения прямой: yy 1 = m (xx 1) y — π / 4 = 1/2 (x — π / 2) y = 1 / 2x — π / 4 + π / 4 Итак, y = 1/2 x — уравнение касательной в точке (π / 2, π / 4)
Учебная помощь по математике видеоуроки онлайн и на компакт-диске.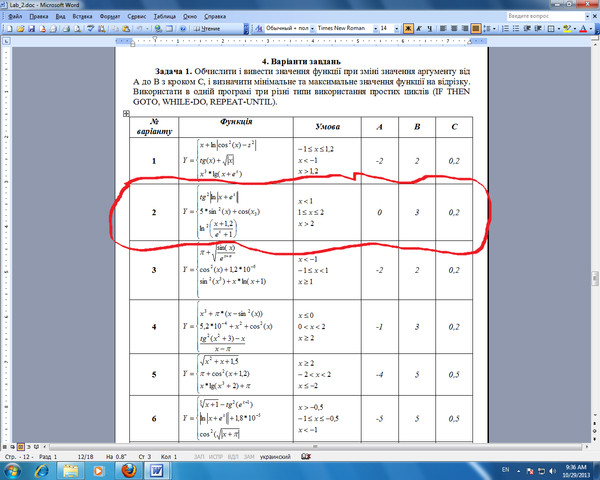 2 + 1}, \: \ left (0, \: 1 \ right) $.касательная к y = √x2 + 1, (0, 1) калькулятор касательных линий. en.
2 + 1}, \: \ left (0, \: 1 \ right) $.касательная к y = √x2 + 1, (0, 1) калькулятор касательных линий. en.
Помните, что значение производной в данной точке равно наклону касательной в этой точке. Помните также, что неявное дифференцирование означает, что вы берете производную всего этого, помните, что y является функцией x, поэтому вы должны использовать правило цепочки всякий раз, когда вы дифференцируете y.
y ‘= -x-1/3 / y-1/3. Теперь используйте свою точку, чтобы найти m: m = y ‘(- 3sqrt (3), 1) = — (- 3sqrt (3) -1/3) / 1-1 / 3.m = sqrt (3) Уравнение касательной: y — y1 = m (x — x1) y — 1 = sqrt (3) * (x + 3sqrt (3)) y — 1 = sqrt (3) x + 9. y = sqrt (3) x + 10.
Производная функции интерпретируется как наклон касательной к кривой функции в определенной заданной точке. В этом разделе мы исследуем значение производной функции, а также узнаем, как найти форму точки наклона уравнения касательной, а также нормальных линий к кривой в нескольких заданных точках.2 .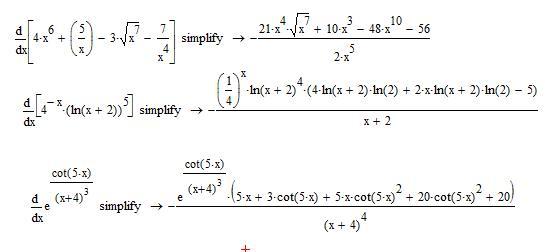

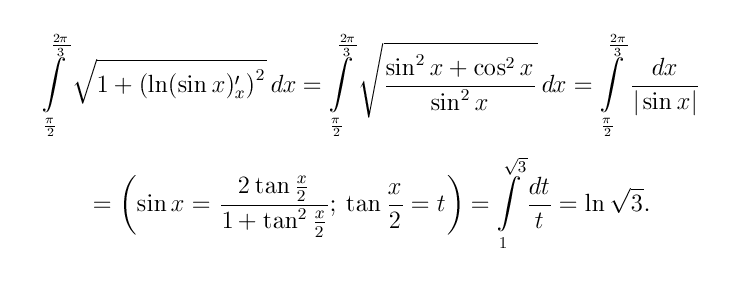
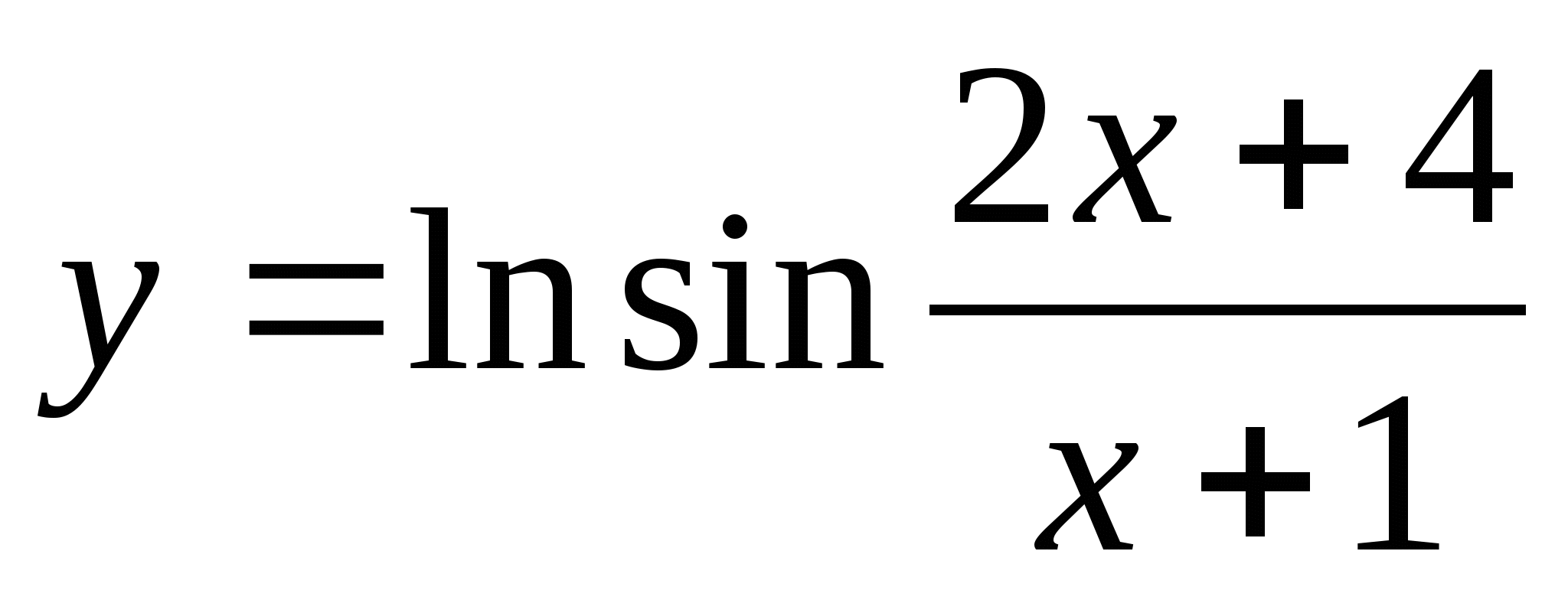 2 + 1)`
2 + 1)`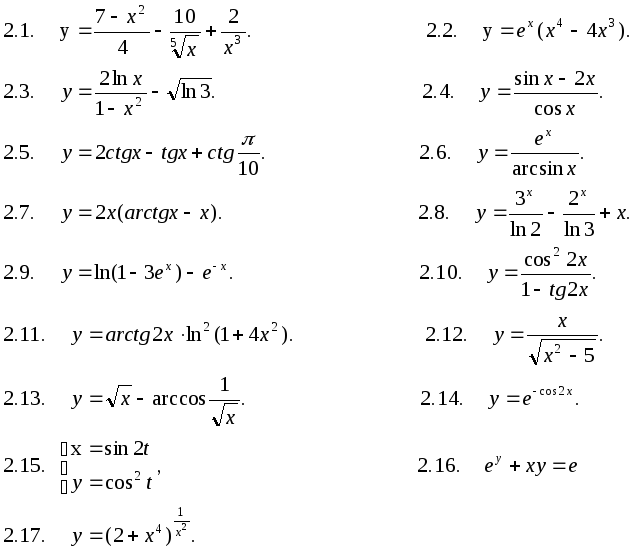 ]
]