Исследование функции с помощью производной онлайн · Как пользоваться Контрольная Работа РУ
Вы можете выполнить исследование функции с помощью производной. Для этого воспользуйтесь онлайн калькулятором с подробным решением, как исследовать функцию.
Для это введите свою функцию в калькулятор:

Где при исследовании функции пригодится помощь производной?
Здесь перечислим, где используется производная, чтобы исследовать функцию:
- Чтобы найти точки экстремумов: найти наименьшее или наибольшее значение функции, а также промежутки возрастания и убывания функции
- Также чтобы найти точки перегибов функции — интервалы выпуклости и вогнутости (здесь используется производная второго порядка).
Рассмотрим пример
Найдём с помощью производной экстремумы и точки перегибов для функции (x^2 — 1)/(x^2 + 1):
Получим результат:
Для того, чтобы найти экстремумы, нужно решить уравнение
(производная равна нулю),
и корни этого уравнения будут экстремумами данной функции:
Первая производная
/ 2 \
2*x 2*x*\x - 1/
------ - ------------ = 0
2 2
x + 1 / 2 \
\x + 1/ Решаем это уравнение
Корни этого ур-ния
Зн. экстремумы в точках:
Интервалы возрастания и убывания функции:
Найдём интервалы, где функция возрастает и убывает, а также минимумы и максимумы функции, для этого смотрим как ведёт себя функция в экстремумах при малейшем отклонении от экстремума:
Минимумы функции в точках:
Максимумов у функции нет
Убывает на промежутках
Возрастает на промежутках
Найдем точки перегибов, для этого надо решить уравнение
(вторая производная равняется нулю),
корни полученного уравнения будут точками перегибов для указанного графика функции:
Вторая производная
/ 2 2 2 / 2\\
| -1 + x 4*x 4*x *\-1 + x /|
2*|1 - ------- - ------ + --------------|
| 2 2 2 |
| 1 + x 1 + x / 2\ |
\ \1 + x / /
----------------------------------------- = 0
2
1 + x Решаем это уравнение
Корни этого ур-ния
Интервалы выпуклости и вогнутости:
Найдём интервалы, где функция выпуклая или вогнутая, для этого посмотрим, как ведет себя функция в точках перегибов:
Вогнутая на промежутках
Выпуклая на промежутках
(-oo, -sqrt(3)/3] U [sqrt(3)/3, oo)
| 1 | Trovare la Derivata — d/dx | квадратный корень x | |
| 2 | Trovare la Derivata — d/dx | натуральный логарифм x | |
| 3 | Вычислим интеграл | интеграл натурального логарифма x по x | |
| 4 | Trovare la Derivata — d/dx | e^x | |
| 5 | Вычислим интеграл | интеграл e^(2x) относительно x | |
| 6 | Trovare la Derivata — d/dx | 1/x | |
| 7 | Trovare la Derivata — d/dx | x^2 | |
| 8 | Вычислим интеграл | интеграл e^(-x) относительно x | |
| 9 | Trovare la Derivata — d/dx | 1/(x^2) | |
| 10 | Trovare la Derivata — d/dx | sin(x)^2 | |
| 11 | Trovare la Derivata — d/dx | sec(x) | |
| 12 | Вычислим интеграл | интеграл e^x относительно x | |
| 13 | Вычислим интеграл | интеграл x^2 относительно x | |
| 14 | Вычислим интеграл | интеграл квадратного корня x по x | |
| 15 | Вычислить | натуральный логарифм 1 | |
| 16 | Вычислить | e^0 | |
| 17 | Вычислить | sin(0) | |
| 18 | Trovare la Derivata — d/dx | cos(x)^2 | |
| 19 | Вычислим интеграл | интеграл 1/x относительно x | |
| 20 | Вычислить | cos(0) | |
| 21 | Вычислим интеграл | интеграл sin(x)^2 относительно x | |
| 22 | Trovare la Derivata — d/dx | x^3 | |
| 23 | Trovare la Derivata — d/dx | sec(x)^2 | |
| 24 | Trovare la Derivata — d/dx | 1/(x^2) | |
| 25 | Вычислим интеграл | интеграл arcsin(x) относительно x | |
| 26 | Вычислим интеграл | интеграл cos(x)^2 относительно x | |
| 27 | Вычислим интеграл | интеграл sec(x)^2 относительно x | |
| 28 | Trovare la Derivata — d/dx | e^(x^2) | |
| 29 | Вычислим интеграл | интеграл в пределах от 0 до 1 кубического корня 1+7x по x | |
| 30 | Trovare la Derivata — d/dx | sin(2x) | |
| 31 | Вычислим интеграл | интеграл натурального логарифма x по x | |
| 32 | Trovare la Derivata — d/dx | tan(x)^2 | |
| 33 | Вычислим интеграл | интеграл e^(2x) относительно x | |
| 34 | Вычислим интеграл | интеграл 1/(x^2) относительно x | |
| 35 | Trovare la Derivata — d/dx | 2^x | |
| 36 | График | натуральный логарифм a | |
| 37 | Вычислить | e^1 | |
| 38 | Вычислим интеграл | интеграл 1/(x^2) относительно x | |
| 39 | Вычислить | натуральный логарифм 0 | |
| 40 | Trovare la Derivata — d/dx | cos(2x) | |
| 41 | Trovare la Derivata — d/dx | xe^x | |
| 42 | Вычислим интеграл | интеграл 1/x относительно x | |
| 43 | Вычислим интеграл | интеграл 2x относительно x | |
| 44 | Trovare la Derivata — d/dx | ( натуральный логарифм x)^2 | |
| 45 | Trovare la Derivata — d/dx | натуральный логарифм (x)^2 | |
| 46 | Trovare la Derivata — d/dx | 3x^2 | |
| 47 | Вычислить | натуральный логарифм 2 | |
| 48 | Вычислим интеграл | интеграл xe^(2x) относительно x | |
| 49 | Trovare la Derivata — d/dx | 2e^x | |
| 50 | Trovare la Derivata — d/dx | натуральный логарифм 2x | |
| 51 | Trovare la Derivata — d/dx | -sin(x) | |
| 52 | Вычислить | tan(0) | |
| 53 | Trovare la Derivata — d/dx | 4x^2-x+5 | |
| 54 | Trovare la Derivata — d/dx | y=16 корень четвертой степени 4x^4+4 | |
| 55 | Trovare la Derivata — d/dx | 2x^2 | |
| 56 | Вычислим интеграл | интеграл e^(3x) относительно x | |
| 57 | Вычислим интеграл | интеграл cos(2x) относительно x | |
| 58 | Вычислим интеграл | интеграл cos(x)^2 относительно x | |
| 59 | Trovare la Derivata — d/dx | 1/( квадратный корень x) | |
| 60 | Вычислим интеграл | интеграл e^(x^2) относительно x | |
| 61 | Вычислить | sec(0) | |
| 62 | Вычислить | e^infinity | |
| 63 | Вычислить | 2^4 | |
| 64 | Trovare la Derivata — d/dx | x/2 | |
| 65 | Вычислить | 4^3 | |
| 66 | Trovare la Derivata — d/dx | -cos(x) | |
| 67 | Trovare la Derivata — d/dx | sin(3x) | |
| 68 | Вычислить | натуральный логарифм 1/e | |
| 69 | Вычислим интеграл | интеграл x^2 относительно x | |
| 70 | Упростить | 1/( кубический корень от x^4) | |
| 71 | Trovare la Derivata — d/dx | 1/(x^3) | |
| 72 | Вычислим интеграл | интеграл e^x относительно x | |
| 73 | Вычислим интеграл | интеграл tan(x)^2 относительно x | |
| 74 | Вычислим интеграл | интеграл 1 относительно x | |
| 75 | Trovare la Derivata — d/dx | x^x | |
| 76 | Trovare la Derivata — d/dx | x натуральный логарифм x | |
| 77 | Вычислим интеграл | интеграл sin(x)^2 относительно x | |
| 78 | Trovare la Derivata — d/dx | x^4 | |
| 79 | Оценить предел | предел (3x-5)/(x-3), если x стремится к 3 | |
| 80 | Вычислим интеграл | интеграл от x^2 натуральный логарифм x по x | |
| 81 | Trovare la Derivata — d/dx | f(x) = square root of x | |
| 82 | Trovare la Derivata — d/dx | x^2sin(x) | |
| 83 | Вычислим интеграл | интеграл sin(2x) относительно x | |
| 84 | Trovare la Derivata — d/dx | 3e^x | |
| 85 | Вычислим интеграл | интеграл xe^x относительно x | |
| 86 | Trovare la Derivata — d/dx | y=x^2 | |
| 87 | Trovare la Derivata — d/dx | квадратный корень x^2+1 | |
| 88 | Trovare la Derivata — d/dx | sin(x^2) | |
| 89 | Вычислим интеграл | интеграл e^(-2x) относительно x | |
| 90 | Вычислим интеграл | интеграл натурального логарифма квадратного корня x по x | |
| 91 | Вычислить | 2^5 | |
| 92 | Trovare la Derivata — d/dx | e^2 | |
| 93 | Trovare la Derivata — d/dx | x^2+1 | |
| 94 | Вычислим интеграл | интеграл sin(x) относительно x | |
| 95 | Вычислить | 2^3 | |
| 96 | Trovare la Derivata — d/dx | arcsin(x) | |
| 97 | Оценить предел | предел (sin(x))/x, если x стремится к 0 | |
| 98 | Вычислить | e^2 | |
| 99 | Вычислим интеграл | интеграл e^(-x) относительно x | |
| 100 | Вычислим интеграл | интеграл 1/x относительно x |
| Основные функции
модуль x: abs(x)
| 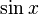 : sin[x] или Sin[x] : sin[x] или Sin[x]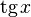 : tan[x] или Tan[x] : tan[x] или Tan[x]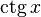 : cot[x] или Cot[x] : cot[x] или Cot[x] : sec[x] или Sec[x] : sec[x] или Sec[x]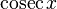 : csc[x] или Csc[x] : csc[x] или Csc[x]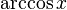 : ArcCos[x] : ArcCos[x]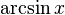 : ArcSin[x] : ArcSin[x]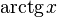 : ArcTan[x] : ArcTan[x]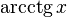 : ArcCot[x] : ArcCot[x]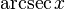 : ArcSec[x] : ArcSec[x]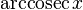 : ArcCsc[x] : ArcCsc[x]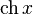 : cosh[x] или Cosh[x] : cosh[x] или Cosh[x] | 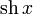 : sinh[x] или Sinh[x] : sinh[x] или Sinh[x]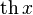 : tanh[x] или Tanh[x] : tanh[x] или Tanh[x]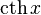 : coth[x] или Coth[x] : coth[x] или Coth[x]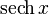 : sech[x] или Sech[x] : sech[x] или Sech[x]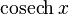 : csch[x] или Csch[е] : csch[x] или Csch[е]  : ArcSinh[x] : ArcSinh[x] : ArcTanh[x] : ArcTanh[x] : ArcCoth[x] : ArcCoth[x]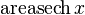 : ArcSech[x] : ArcSech[x]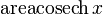 : ArcCsch[x] : ArcCsch[x] |
| 1 | Trovare la Derivata — d/dx | квадратный корень x | |
| 2 | Trovare la Derivata — d/dx | натуральный логарифм x | |
| 3 | Вычислим интеграл | интеграл натурального логарифма x по x | |
| 4 | Trovare la Derivata — d/dx | e^x | |
| 5 | Вычислим интеграл | интеграл e^(2x) относительно x | |
| 6 | Trovare la Derivata — d/dx | 1/x | |
| 7 | Trovare la Derivata — d/dx | x^2 | |
| 8 | Вычислим интеграл | интеграл e^(-x) относительно x | |
| 9 | Trovare la Derivata — d/dx | 1/(x^2) | |
| 10 | Trovare la Derivata — d/dx | sin(x)^2 | |
| 11 | Trovare la Derivata — d/dx | sec(x) | |
| 12 | Вычислим интеграл | интеграл e^x относительно x | |
| 13 | Вычислим интеграл | интеграл x^2 относительно x | |
| 14 | Вычислим интеграл | интеграл квадратного корня x по x | |
| 15 | Вычислить | натуральный логарифм 1 | |
| 16 | Вычислить | e^0 | |
| 17 | Вычислить | sin(0) | |
| 18 | Trovare la Derivata — d/dx | cos(x)^2 | |
| 19 | Вычислим интеграл | интеграл 1/x относительно x | |
| 20 | Вычислить | cos(0) | |
| 21 | Вычислим интеграл | интеграл sin(x)^2 относительно x | |
| 22 | Trovare la Derivata — d/dx | x^3 | |
| 23 | Trovare la Derivata — d/dx | sec(x)^2 | |
| 24 | Trovare la Derivata — d/dx | 1/(x^2) | |
| 25 | Вычислим интеграл | интеграл arcsin(x) относительно x | |
| 26 | Вычислим интеграл | интеграл cos(x)^2 относительно x | |
| 27 | Вычислим интеграл | интеграл sec(x)^2 относительно x | |
| 28 | Trovare la Derivata — d/dx | e^(x^2) | |
| 29 | Вычислим интеграл | интеграл в пределах от 0 до 1 кубического корня 1+7x по x | |
| 30 | Trovare la Derivata — d/dx | sin(2x) | |
| 31 | Вычислим интеграл | интеграл натурального логарифма x по x | |
| 32 | Trovare la Derivata — d/dx | tan(x)^2 | |
| 33 | Вычислим интеграл | интеграл e^(2x) относительно x | |
| 34 | Вычислим интеграл | интеграл 1/(x^2) относительно x | |
| 35 | Trovare la Derivata — d/dx | 2^x | |
| 36 | График | натуральный логарифм a | |
| 37 | Вычислить | e^1 | |
| 38 | Вычислим интеграл | интеграл 1/(x^2) относительно x | |
| 39 | Вычислить | натуральный логарифм 0 | |
| 40 | Trovare la Derivata — d/dx | cos(2x) | |
| 41 | Trovare la Derivata — d/dx | xe^x | |
| 42 | Вычислим интеграл | интеграл 1/x относительно x | |
| 43 | Вычислим интеграл | интеграл 2x относительно x | |
| 44 | Trovare la Derivata — d/dx | ( натуральный логарифм x)^2 | |
| 45 | Trovare la Derivata — d/dx | натуральный логарифм (x)^2 | |
| 46 | Trovare la Derivata — d/dx | 3x^2 | |
| 47 | Вычислить | натуральный логарифм 2 | |
| 48 | Вычислим интеграл | интеграл xe^(2x) относительно x | |
| 49 | Trovare la Derivata — d/dx | 2e^x | |
| 50 | Trovare la Derivata — d/dx | натуральный логарифм 2x | |
| 51 | Trovare la Derivata — d/dx | -sin(x) | |
| 52 | Вычислить | tan(0) | |
| 53 | Trovare la Derivata — d/dx | 4x^2-x+5 | |
| 54 | Trovare la Derivata — d/dx | y=16 корень четвертой степени 4x^4+4 | |
| 55 | Trovare la Derivata — d/dx | 2x^2 | |
| 56 | Вычислим интеграл | интеграл e^(3x) относительно x | |
| 57 | Вычислим интеграл | интеграл cos(2x) относительно x | |
| 58 | Вычислим интеграл | интеграл cos(x)^2 относительно x | |
| 59 | Trovare la Derivata — d/dx | 1/( квадратный корень x) | |
| 60 | Вычислим интеграл | интеграл e^(x^2) относительно x | |
| 61 | Вычислить | sec(0) | |
| 62 | Вычислить | e^infinity | |
| 63 | Вычислить | 2^4 | |
| 64 | Trovare la Derivata — d/dx | x/2 | |
| 65 | Вычислить | 4^3 | |
| 66 | Trovare la Derivata — d/dx | -cos(x) | |
| 67 | Trovare la Derivata — d/dx | sin(3x) | |
| 68 | Вычислить | натуральный логарифм 1/e | |
| 69 | Вычислим интеграл | интеграл x^2 относительно x | |
| 70 | Упростить | 1/( кубический корень от x^4) | |
| 71 | Trovare la Derivata — d/dx | 1/(x^3) | |
| 72 | Вычислим интеграл | интеграл e^x относительно x | |
| 73 | Вычислим интеграл | интеграл tan(x)^2 относительно x | |
| 74 | Вычислим интеграл | интеграл 1 относительно x | |
| 75 | Trovare la Derivata — d/dx | x^x | |
| 76 | Trovare la Derivata — d/dx | x натуральный логарифм x | |
| 77 | Вычислим интеграл | интеграл sin(x)^2 относительно x | |
| 78 | Trovare la Derivata — d/dx | x^4 | |
| 79 | Оценить предел | предел (3x-5)/(x-3), если x стремится к 3 | |
| 80 | Вычислим интеграл | интеграл от x^2 натуральный логарифм x по x | |
| 81 | Trovare la Derivata — d/dx | f(x) = square root of x | |
| 82 | Trovare la Derivata — d/dx | x^2sin(x) | |
| 83 | Вычислим интеграл | интеграл sin(2x) относительно x | |
| 84 | Trovare la Derivata — d/dx | 3e^x | |
| 85 | Вычислим интеграл | интеграл xe^x относительно x | |
| 86 | Trovare la Derivata — d/dx | y=x^2 | |
| 87 | Trovare la Derivata — d/dx | квадратный корень x^2+1 | |
| 88 | Trovare la Derivata — d/dx | sin(x^2) | |
| 89 | Вычислим интеграл | интеграл e^(-2x) относительно x | |
| 90 | Вычислим интеграл | интеграл натурального логарифма квадратного корня x по x | |
| 91 | Вычислить | 2^5 | |
| 92 | Trovare la Derivata — d/dx | e^2 | |
| 93 | Trovare la Derivata — d/dx | x^2+1 | |
| 94 | Вычислим интеграл | интеграл sin(x) относительно x | |
| 95 | Вычислить | 2^3 | |
| 96 | Trovare la Derivata — d/dx | arcsin(x) | |
| 97 | Оценить предел | предел (sin(x))/x, если x стремится к 0 | |
| 98 | Вычислить | e^2 | |
| 99 | Вычислим интеграл | интеграл e^(-x) относительно x | |
| 100 | Вычислим интеграл | интеграл 1/x относительно x |
| Основные функции
модуль x: abs(x)
| 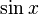 : sin[x] или Sin[x] : sin[x] или Sin[x]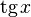 : tan[x] или Tan[x] : tan[x] или Tan[x]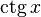 : cot[x] или Cot[x] : cot[x] или Cot[x] : sec[x] или Sec[x] : sec[x] или Sec[x]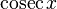 : csc[x] или Csc[x] : csc[x] или Csc[x]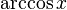 : ArcCos[x] : ArcCos[x]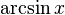 : ArcSin[x] : ArcSin[x]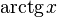 : ArcTan[x] : ArcTan[x]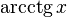 : ArcCot[x] : ArcCot[x]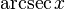 : ArcSec[x] : ArcSec[x]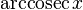 : ArcCsc[x] : ArcCsc[x]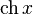 : cosh[x] или Cosh[x] : cosh[x] или Cosh[x] | 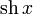 : sinh[x] или Sinh[x] : sinh[x] или Sinh[x]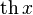 : tanh[x] или Tanh[x] : tanh[x] или Tanh[x]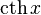 : coth[x] или Coth[x] : coth[x] или Coth[x]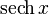 : sech[x] или Sech[x] : sech[x] или Sech[x]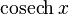 : csch[x] или Csch[е] : csch[x] или Csch[е]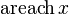 : ArcCosh[x] : ArcCosh[x]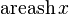 : ArcSinh[x] : ArcSinh[x]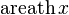 : ArcTanh[x] : ArcTanh[x]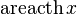 : ArcCoth[x] : ArcCoth[x]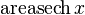 : ArcSech[x] : ArcSech[x]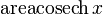 : ArcCsch[x] : ArcCsch[x] |
исследование на монотонность функции онлайн
Вы искали исследование на монотонность функции онлайн? На нашем сайте вы можете получить ответ на любой математический вопрос здесь. Подробное решение с описанием и пояснениями поможет вам разобраться даже с самой сложной задачей и исследовать на монотонность и экстремумы функцию онлайн, не исключение. Мы поможем вам подготовиться к домашним работам, контрольным, олимпиадам, а так же к поступлению в вуз. И какой бы пример, какой бы запрос по математике вы не ввели — у нас уже есть решение. Например, «исследование на монотонность функции онлайн».

Применение различных математических задач, калькуляторов, уравнений и функций широко распространено в нашей жизни. Они используются во многих расчетах, строительстве сооружений и даже спорте. Математику человек использовал еще в древности и с тех пор их применение только возрастает. Однако сейчас наука не стоит на месте и мы можем наслаждаться плодами ее деятельности, такими, например, как онлайн-калькулятор, который может решить задачи, такие, как исследование на монотонность функции онлайн,исследовать на монотонность и экстремумы функцию онлайн,исследуйте функцию на монотонность и экстремумы калькулятор,монотонность функции онлайн,монотонность функции онлайн калькулятор,найдите промежутки возрастания и убывания функции онлайн,найти интервалы монотонности и экстремумы функции онлайн калькулятор,найти монотонность функции онлайн,найти промежутки возрастания и убывания функции онлайн калькулятор,онлайн калькулятор на непрерывность функции онлайн,промежутки знакопостоянства онлайн,экстремумы и интервалы монотонности функции онлайн. На этой странице вы найдёте калькулятор, который поможет решить любой вопрос, в том числе и исследование на монотонность функции онлайн. Просто введите задачу в окошко и нажмите «решить» здесь (например, исследуйте функцию на монотонность и экстремумы калькулятор).
Где можно решить любую задачу по математике, а так же исследование на монотонность функции онлайн Онлайн?
Решить задачу исследование на монотонность функции онлайн вы можете на нашем сайте https://pocketteacher.ru. Бесплатный онлайн решатель позволит решить онлайн задачу любой сложности за считанные секунды. Все, что вам необходимо сделать — это просто ввести свои данные в решателе. Так же вы можете посмотреть видео инструкцию и узнать, как правильно ввести вашу задачу на нашем сайте. А если у вас остались вопросы, то вы можете задать их в чате снизу слева на странице калькулятора.
| Основные функции
модуль x: abs(x)
| 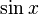 : sin[x] или Sin[x] : sin[x] или Sin[x]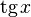 : tan[x] или Tan[x] : tan[x] или Tan[x]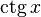 : cot[x] или Cot[x] : cot[x] или Cot[x] : sec[x] или Sec[x] : sec[x] или Sec[x]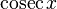 : csc[x] или Csc[x] : csc[x] или Csc[x]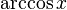 : ArcCos[x] : ArcCos[x]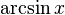 : ArcSin[x] : ArcSin[x]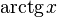 : ArcTan[x] : ArcTan[x]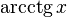 : ArcCot[x] : ArcCot[x]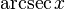 : ArcSec[x] : ArcSec[x]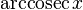 : ArcCsc[x] : ArcCsc[x]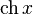 : cosh[x] или Cosh[x] : cosh[x] или Cosh[x] | 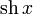 : sinh[x] или Sinh[x] : sinh[x] или Sinh[x]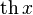 : tanh[x] или Tanh[x] : tanh[x] или Tanh[x]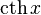 : coth[x] или Coth[x] : coth[x] или Coth[x]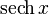 : sech[x] или Sech[x] : sech[x] или Sech[x]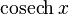 : csch[x] или Csch[е] : csch[x] или Csch[е] : ArcCosh[x] : ArcCosh[x] : ArcSinh[x] : ArcSinh[x] : ArcTanh[x] : ArcTanh[x] : ArcCoth[x] : ArcCoth[x]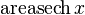 : ArcSech[x] : ArcSech[x]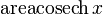 : ArcCsch[x] : ArcCsch[x] |
Функции увеличения и уменьшения
Увеличение функций
Функция «увеличивается», когда значение y увеличивается, когда значение x увеличивается, например:
Легко видеть, что y = f (x) имеет тенденцию повышаться на вверх на по мере того, как идет вдоль .
Квартира?
А что насчет того плоского бита в начале? Это нормально?
- Да, это нормально, когда мы говорим, что функция Увеличение
- Но это не в порядке , если мы скажем, что функция строго возрастает (плоскостность не допускается)
Использование алгебры
Что делать, если мы не можем построить график, чтобы увидеть, увеличивается ли он? В этом случае нам понадобится определение с использованием алгебры.
Для функции y = f (x) :
| , когда x 1 | Увеличение | |
| , если x 1 | Строгое увеличение |
Это должно быть верно для любых x 1 , x 2 , а не только некоторых хороших, которые мы могли бы выбрать.
Пример:
| Это также возрастающая функция , хотя скорость увеличения уменьшается |
на интервал
Обычно нас интересует только некоторый интервал , например, этот:
Эта функция — , увеличивающая для показанного интервала
(в другом месте она может увеличиваться или уменьшаться)
Убывающие функции
Значение y уменьшается по мере увеличения значения x :
Для функции y = f (x) :
| , если x 1 | Уменьшение | |
| , если x 1 | Строго убавления |
Обратите внимание, что f (x 1 ) теперь больше (или равно) f (x 2 ).
Пример
Давайте попробуем найти, где функция увеличивается или уменьшается.
Пример: f (x) = x 3 −4x, для x в интервале [−1,2]
Построим его, включая интервал [−1,2]:
Начиная с −1 (начало интервала [−1,2] ):
- при x = −1 функция убывает,
- продолжает уменьшаться до около 1.2
- затем увеличивается оттуда, после x = 2
Без точного анализа мы не можем точно определить, где кривая переходит от убывания к возрастанию, поэтому давайте просто скажем:
В интервале [−1,2] :
- кривая убывает в интервале [-1, приблизительно 1,2]
- кривая увеличивается в интервале [приблизительно 1,2, 2]
Постоянные функции
Постоянная функция — это горизонтальная линия:
Строки
На самом деле линии либо увеличиваются, либо уменьшаются, либо постоянны.
Уравнение прямой:
y = mx + b
Наклон m говорит нам, увеличивается ли функция, убывает или остается постоянной:
| м <0 | уменьшение | |
| м = 0 | постоянная | |
| м> 0 | увеличение |
Индивидуальные встречи
Строго возрастающие (и строго убывающие) функции имеют специальное свойство, называемое «инъективным» или «один к одному», что просто означает, что мы никогда не получим одно и то же значение «y» дважды.
Общие функции
«Инъективный» (индивидуально)
Почему это полезно? Поскольку инъективные функции могут быть обратными !
Мы можем перейти от значения «y» назад к , значение «x» (чего мы не можем сделать, когда существует более одного возможного значения «x»).
Прочтите Injective, Surjective и Bijective, чтобы узнать больше.
.интервалов увеличения и уменьшения
Интервалы увеличения и уменьшения
Процедура определения того, где функция увеличивается или уменьшается:
- Сначала нам нужно найти первую производную
- Затем установить f ‘(x) = 0
- Поместить решения в числовую строку
- Разделить интервалы
- выбрать случайное значение из интервала и проверить их в первой производной
- Если мы получим положительное число для выбранных значений, мы можем сказать, что функция увеличивается в этом конкретном интервале
- Если мы получим отрицательное число для выбранных значений , мы можем сказать, что функция убывает в этом конкретном интервале.
Пример 1:
Найдите интервалы, в которых f (x) = 2x³ + x² — 20 x увеличивается или уменьшается
Решение:
f (x) = 2x³ + x² — 20 x
f ‘(x) = 2 (3x²) + 2 x — 20
f’ (x) = 6x² + 2 x — 20
÷ на 2 ⇒ 3x² + x — 10
f ‘(x) = 0
3x² + x — 10 = 0
(3x — 5) (x + 2) = 0
(3x — 5) = 0 (x + 2) = 0
3 x = 5 x = — 2
x = 5/3
Мы можем разделить это на три интервала (-∞, -2) (-2,5 / 3) (5/3, ∞).Теперь давайте посмотрим, в какие интервалы данная функция увеличивается или уменьшается.
| Интервал | (3x-5) | (x + 2) | f ‘(x) | Интервалы увеличения / уменьшения |
|---|---|---|---|---|
| -∞ | – | – | + | увеличивается на (-∞, -2] |
| -2 | + | – | – | убывающая на [-2,5 / 3] |
| 5/3 | + | + | + | увеличивается на [5/3, -∞) |
Значение увеличивается на (-∞, -2] ∪ [5/3, -∞) и уменьшается на [-2,5 / 3]
Пример 2:
Найдите интервалы, в которых f (x) = x³ — 3 x + 1 увеличивается или уменьшается
Решение:
f (x) = x³ — 3 x + 1
f ‘(x) = (3x²) — 3 (1)
f’ (x) = 3x² — 3
÷ на 3 ⇒ x² — 1
f ‘(x) = 0
x² — 1 = 0
(x + 1) (x — 1) = 0
(x + 1) = 0 (x — 1) = 0
x = -1 x = 1
Мы можем разделить это на три интервала (-∞, -1) (-1,1) (1, ∞).Теперь давайте посмотрим, в какие интервалы данная функция увеличивается или уменьшается.
| Интервал | (x + 1) | (х-1) | f ‘(x) | Интервалы увеличения / уменьшения |
|---|---|---|---|---|
| -∞ | – | – | + | увеличивается на (-∞, -1] |
| -1 | + | – | – | в убывании на [-1,1] |
| 1 | + | + | + | увеличивается на [1, ∞) |
Значение увеличивается на (-∞, -1] ∪ [1, ∞) и уменьшается на [-1,1]
Пример 3:
Найдите интервалы, в которых f (x) = x — 2 sin x увеличивается или уменьшается
Решение:
f (x) = x — 2 sin x
f ‘( x) = 1-2 cos x
f ‘(x) = 0
1-2 cos x = 0
-2 cos x = -1
cos x = 1/2
x = cos ⁻ ¹ (1/2)
x = Π / 3,5Π / 3
x = Π / 3 x = 5Π / 3
интервалов увеличения и уменьшения интервалов увеличения и уменьшения
Мы можем разделить это на три интервала (0, Π / 3) (Π / 3,5Π / 3) (5Π / 3,2Π).Теперь давайте посмотрим, в какие интервалы данная функция увеличивается или уменьшается.
| Интервал | 1-2 cos x | f ‘(x) | Интервалы увеличения / уменьшения |
|---|---|---|---|
| 0 | – | – | Уменьшение на (0, Π / 3] |
| Π / 3 | + | + | Увеличение на [Π / 3,5, Π / 3] |
| 5Π / 3 | – | – | Уменьшение на [5Π / 3,2Π) |
Значение увеличивается на [Π / 3,5, Π / 3] и уменьшается на (0, Π / 3]
∪ [5Π / 3,2Π).
Это примеры в теме увеличения и уменьшения интервалов. Практикуя подобные задачи, вы сможете ясно понять эту тему.
Связанные темы
Цитата по математике
«Математика, без этого мы можем ничего не делать в нашей жизни. Все вокруг нас — математика.
Математика — это не только решение задач и поиск решений, и он также делает многое в нашей повседневной жизни.Они есть:
Удаляет грусть и добавляет счастья в Наша жизнь.
Он разделяет печаль и умножает прощение и любовь.
Некоторые люди не могут принять, что предмет «Математика» легко понять. Это потому; они не могут понять как жизнь сложна. Задачи по предмету Математика легче решать чем решать проблемы в нашей реальной жизни. Когда мы люди умеем решать все проблемы в сложной жизни, почему мы не можем решить простую математику проблемы?
Многие думают, что математика всегда сложно, и он существует, чтобы делать вещи от простого к сложному.Но реальное существование предмета математики состоит в том, чтобы сделать вещи от сложных до просто.»
увеличение и уменьшение интервалов до монотонной функции .Функции увеличения / уменьшения
Функции увеличения / уменьшения
Производная функции может использоваться для определения того, увеличивается или уменьшается функция на любых интервалах в ее области определения. Если f ′ (x) > 0 в каждой точке интервала I, то говорят, что функция возрастает на I. f ′ (x) <0 в каждой точке интервала I, тогда функция Говорят, что на меньше .Поскольку производная равна нулю или не существует только в критических точках функции, она должна быть положительной или отрицательной во всех других точках, где существует функция.При определении интервалов, в которых функция увеличивается или уменьшается, вы сначала находите значения области, где будут встречаться все критические точки; затем проверьте все интервалы в области определения функции слева и справа от этих значений, чтобы определить, является ли производная положительной или отрицательной. Если f ‘(x) > 0, то f увеличивается на интервале, а если f’ (x) <0, то f убывает на интервале.Эта и другая информация может использоваться, чтобы показать достаточно точный набросок графика функции.
Пример 1: Для f (x) = x 4 — 8 x 2 определяют все интервалы, в которых f увеличивается или уменьшается.
Область f (x) — все действительные числа, и ее критические точки находятся при x = −2, 0 и 2. Тестирование всех интервалов слева и справа от этих значений для f ′ (x ) = 4 x 3 — 16 x , вы обнаружите, что

, следовательно, f увеличивается на (−2,0) и (2, + ∞) и убывает на (−∞, −2) и (0,2).
Пример 2: Для f (x) = sin x + cos x на [0,2π], определите все интервалы, где f увеличивается или уменьшается.
Область f (x) ограничена закрытым интервалом [0,2π], а ее критические точки находятся на π / 4 и 5π / 4. Проверяя все интервалы слева и справа от этих значений для f ′ (x) = cos x — sin x , вы обнаружите, что

, следовательно, f увеличивается на [0, π / 4] (5π / 4, 2π) и уменьшается на (π / 4, 5π / 4).
.Калькулятор процентного увеличения
Использование калькулятора
Калькулятор процентного увеличения находит увеличение от одного значения к другому в процентах.
Введите начальное и конечное значения, чтобы найти увеличение в процентах.
Как рассчитать увеличение в процентах
- Вычесть конечное значение минус начальное значение
- Разделите эту сумму на абсолютное значение начального значения
- Умножьте на 100, чтобы получить процентное увеличение
- Если процент отрицательный, это означает, что произошло уменьшение, а не увеличение.
Формула процентного увеличения
Вы можете использовать формулу процентного увеличения для расчета любого процентного увеличения:
\ (\ text {Увеличение в процентах} = \\ \ dfrac {\ text {Окончательное значение} — \ text {Начальное значение}} {\ left | \ text {Начальное значение} \ right |} \ times 100 \)
Пример проблемы: увеличение в процентах
В прошлом году ваши любимые джинсы стоили 36 долларов за пару.В этом году они стоят 45 долларов за пару. Каков процент повышения цен на эти джинсы с прошлого года по сравнению с этим годом?
Увеличение в процентах = [(Конечное значение — Начальное значение) / | Начальное значение | ] × 100
45 — 36 = 9
9/36 = 0,25
0,25 × 100 = 25%
Итак, цена на ваши любимые джинсы выросла на 25% по сравнению с прошлым годом.
Связанные калькуляторы
Используйте Калькулятор процентного уменьшения, чтобы найти процентное уменьшение от одного значения к другому.
Используйте Калькулятор процентной разницы, когда вы сравниваете два значения и хотите найти процентную разницу между ними.
Калькулятор процентного изменения находит изменение между двумя числами в процентах. Это похоже на поиск увеличения или уменьшения в процентах, но это изменение не помечается как увеличение или уменьшение.
.
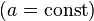
 : x^a
: x^a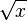 : Sqrt[x]
: Sqrt[x]![\sqrt[n]{x}](/800/600/https/upload.wikimedia.org/math/5/e/4/5e4352778f3b156f05ef056f9793ec36.png) : x^(1/n)
: x^(1/n)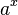 : a^x
: a^x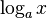 : Log[a, x]
: Log[a, x]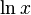 : Log[x]
: Log[x]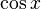 : cos[x] или Cos[x]
: cos[x] или Cos[x]