Лекция 10
Лекция 10.Теория комплексных чисел.
Комплексные числа были введены в связи со следующей задачей. Известно, что действительных чисел недостаточно для того, чтобы решить любое квадратное уравнение. Простейшее из квадратных уравнений, не имеющих корней среди действительных чисел, есть уравнение .
Возникла задача: расширить систему действительных чисел до такой системы чисел, в которой указанное уравнение имеет решение.
Покажем, что среди комплексных чисел есть число, квадрат которого равен -1. Это будет, например, число (0,1). Действительно, (0,1)(0,1)=(-1,0)= -1.
Комплексное число (0,1) называется мнимой единицейи обозначаетсяj(илиi). Итак,j=(0,1) – мнимая единица.
Комплексное число z=(x,y) имеет три формы записи.
Алгебраическая форма комплексного числа
.
— алгебраическая форма комплексного числа.
Координатную плоскость хОу, точки которой отождествлены с комплексными числами, будем называть комплексной плоскостью. Ох – вещественная ось, служит для изображения действительной части комплексных чисел. Оу – мнимая ось, служит для изображения мнимой части числа.
Комплексно-сопряженные числа
Комплексные числа 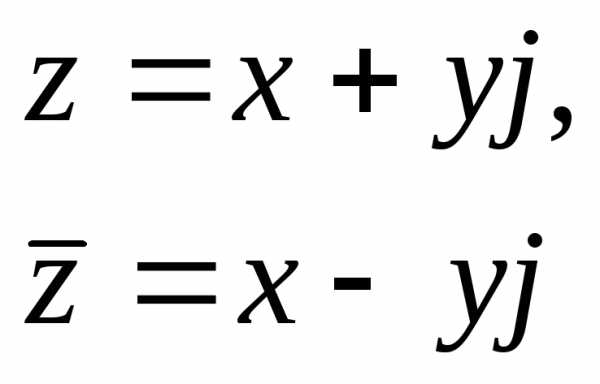 называются комплексно сопря-женными.
называются комплексно сопря-женными.
Геометрическая интерпретация: комплексно-сопряженные числа и отождествляются с точками (х,у) и (х,-у), симметричными относительно оси Ох.
Свойствакомплексно-сопряженных чисел:
1..
2..
3..
4.. (Проверить!)
Операции над комплексными числами в алгебраической форме.
1. .
При сложении (вычитании) комплексных чисел складывают (вычитаются) их вещественные и мнимые части соответственно.
2. Учитывая, что 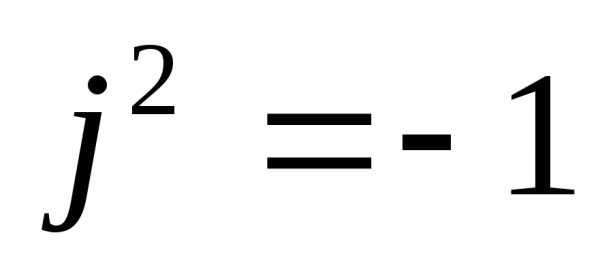 :
:
Итак, комплексные числа умножаются по правилу умножения многочленов, т.е. почленно.
3. 
Итак, при делении  на
на числитель и знаменатель умножают на
число
числитель и знаменатель умножают на
число .
.
Тригонометрическая форма комплексного числа
, где-модуль
 —аргументчислаz,
т.е. любое решение системы уравнений
—аргументчислаz,
т.е. любое решение системы уравнений 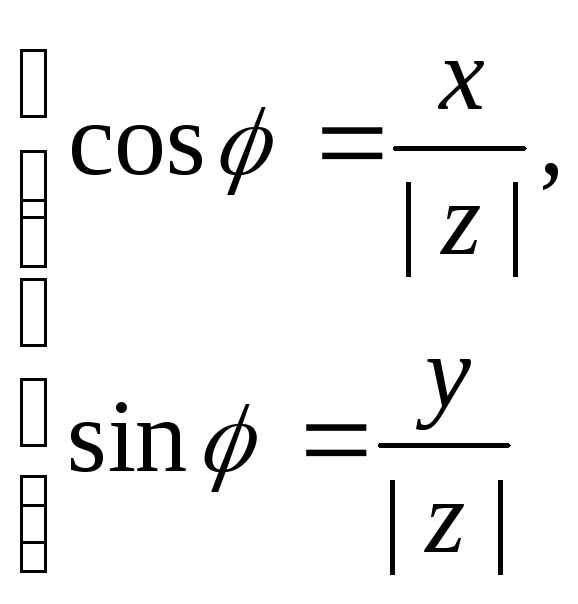
и обозначается символом .Модулькомплексного числа есть число неотрицательное и определяется однозначно.
Аргумент комплексного числа  ,
определяемый только врадианах,
имеет бесконечное множество своих
значений.
,
определяемый только врадианах,
имеет бесконечное множество своих
значений.
Они отличаются друг от друга на числа,
кратные  ,
и только одно значение (обозначим его
,
и только одно значение (обозначим его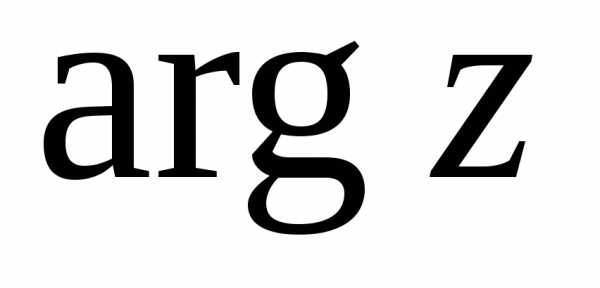 )
удовлетворяет условию:.
Его будем называтьглавным значением аргумента числаz.
Множество всех значений аргументаzможно записать так:.
)
удовлетворяет условию:.
Его будем называтьглавным значением аргумента числаz.
Множество всех значений аргументаzможно записать так:.
Если 
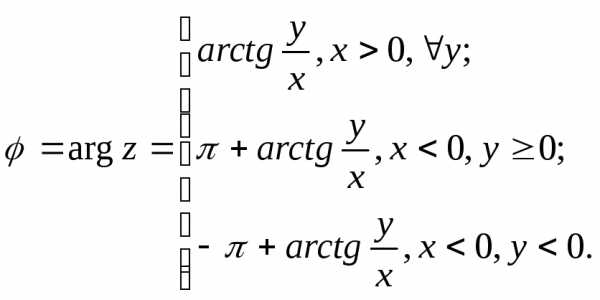 (рис. 31)
(рис. 31)
Геометрическая интерпретация модуля и аргумента числаz
Если число
изображается точкой М(х,у) на координатной
плоскости Оху (рис. 28), то |z|
— длина радиус-вектора точки М, а
точки М, а — угол между осью Ох и этим радиус-вектором.
— угол между осью Ох и этим радиус-вектором.
Пример.Представить числоz= -1+jв тригонометрической форме.
.
Ответ: .
Пример.Представить число –jв тригонометрической форме.
.
Ответ: .
Операции над комплексными числами в тригонометрической форме
Итак, при умножении комплексных чисел их модули перемножаются, т.е. , а аргументы складываются, т.е..
Делениекомплексных чисел.
При делении комплексных чисел  на
на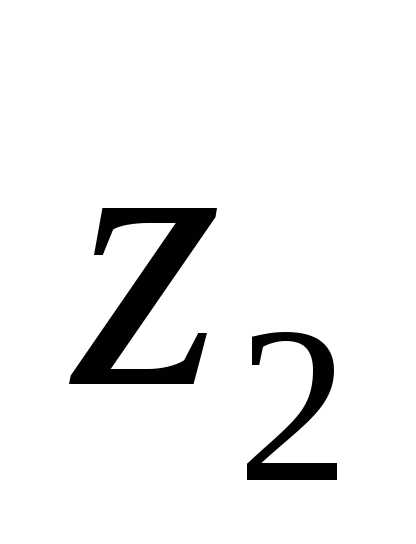 (
(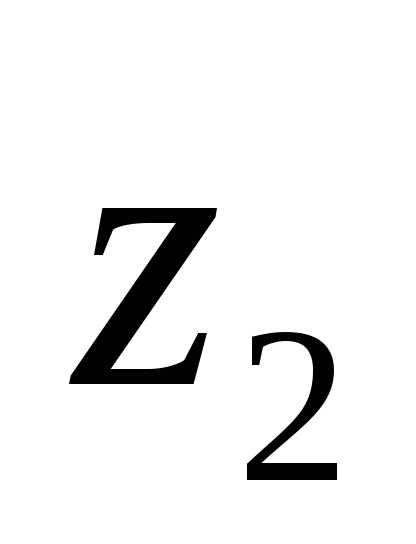 0)
модули их делятся, т.е.
0)
модули их делятся, т.е.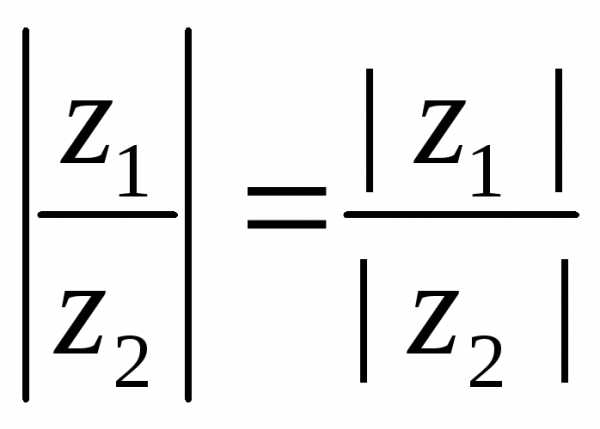 ,
а аргументы вычитаются, т.е..
(Проверить!).
,
а аргументы вычитаются, т.е..
(Проверить!).
3. Возведение комплексного числа в целую положительную степень
 -n-я степень числаz.
-n-я степень числаz.
Если , то.
При  равенство примет вид:.
равенство примет вид:.
Эта формула носит название формулы Муавра.
4. Извлечение корня
Число wназывается корнем
степени 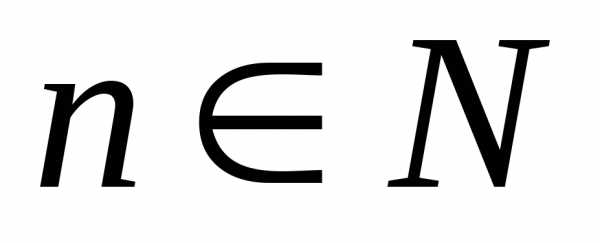 из числаz, если
из числаz, если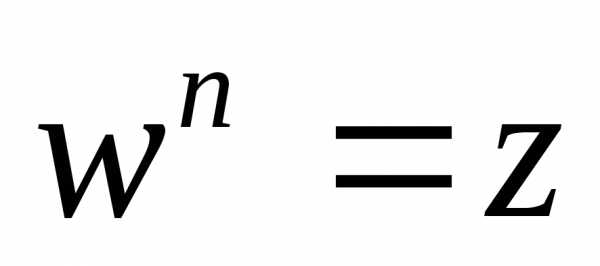 .
Используется обозначение
.
Используется обозначение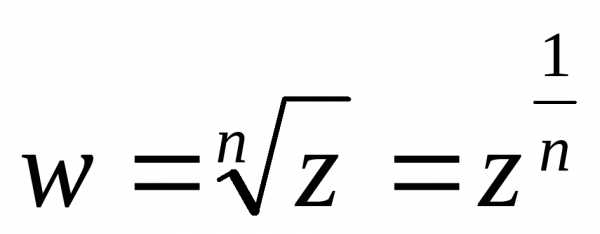 .
.
Если положить
,
гдеи,
то равенство примет вид:.
примет вид:.
Зная, что модули равных чисел равны
между собой, а аргументы отличаются
друг от друга на число, кратное 2,
имеем два равенства: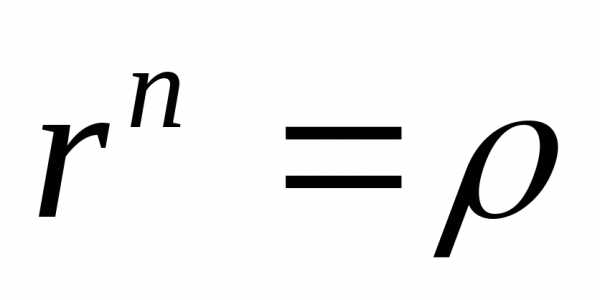 и(корень
арифметический),
и(корень
арифметический),
.
Итак, .
Формула определяет бесконечное множество значений корня n-ой степени изz. И толькоnиз них различные.
Полагаяk=0,1,2,…,n-1, получаемnразличных значений корня.
Геометрическая интерпретация 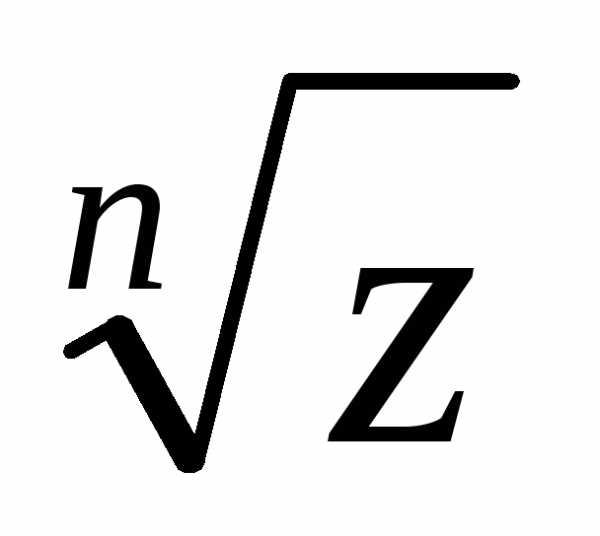
— различные значения корня — вершины правильногоn-угольника,
вписанного в окружность с центром в
начале координат и радиусом
— вершины правильногоn-угольника,
вписанного в окружность с центром в
начале координат и радиусом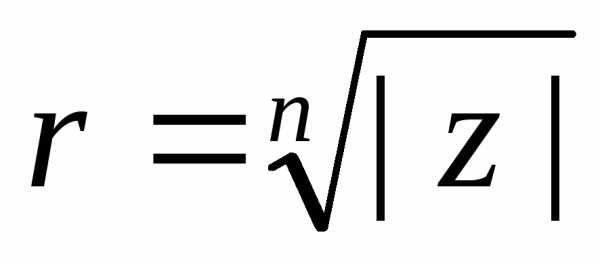 .
.
Пример

Показательная форма комплексного числа
Действие возведения числа е (неперово
число) в комплексную степень z=x+yjопределяется равенством (10.1).
(10.1).
Это определение может показаться
искусственным. Заметим в его оправдание,
что при у=0, т.е. 
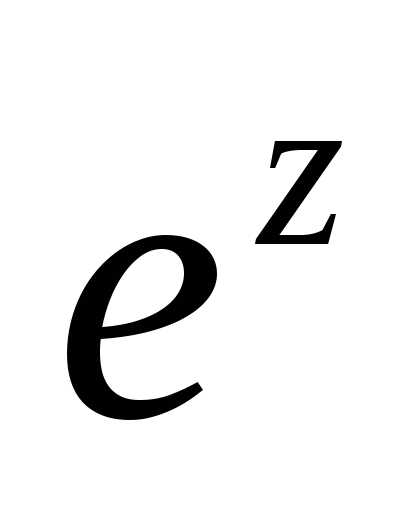 сводится к обычной степени
сводится к обычной степени ,
а также комплексная степень числа е
сохраняетсвойствавещественных
степеней:
,
а также комплексная степень числа е
сохраняетсвойствавещественных
степеней:1.;
2.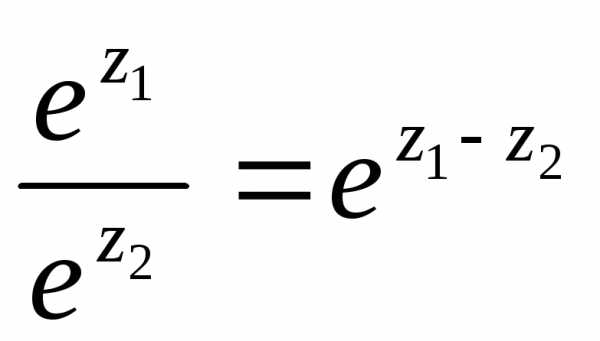 .
(Проверить!)
.
(Проверить!)
Комплексная степень 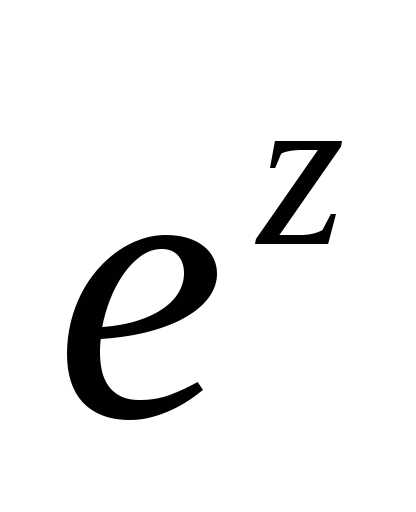 обладает также и новыми свойствами,
отсутствующими у действительных
степеней.
обладает также и новыми свойствами,
отсутствующими у действительных
степеней.
Например, свойство периодичности.
Докажем, что
.
Действительно, .
Отсюда следует периодичность комплексной
степени  ;
;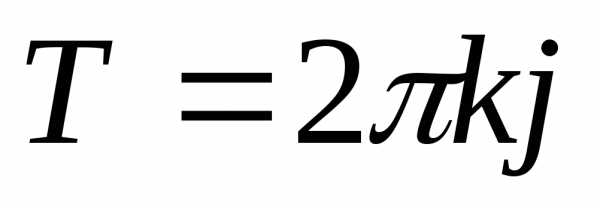 — ее периоды,
— ее периоды,
Полагая в формуле (10.1) х=0, 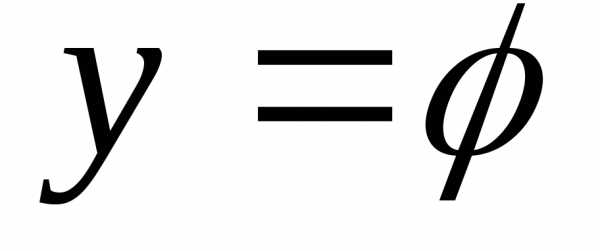 ,
получим.
,
получим.
Это равенство носит название формулы Эйлера (Эйлер – немецкий математик, академик Российской Академии наук).
Пользуясь формулой Эйлера, можно
представить комплексное число zв виде.
Итак, — показательная форма комплексного
числа.
— показательная форма комплексного
числа.
Пример
studfiles.net
Комплексные числа – теория и общие формулы.
⇐ ПредыдущаяСтр 3 из 4Следующая ⇒
Прежде всего, отметим, что энтузиасты-поклонники примитива вытеснили из школьной математической программы многие основополагающие понятия и разделы Математики. Одним из пострадавших разделов является Теория многочленов.
Сколько труда и изобретательности проявила человеческая мысль, доказав справедливость утверждения – Основная теорема алгебры комплексных чисел: всякий многочлен, степень которого не меньше единицы, имеет хотя бы один корень, в общем случае комплексный! Эту Теорему считают одним из крупнейших достижений математики: трудно назвать область науки, которая не использовала бы утверждение этой теоремы.
Из Основной теоремы получили Следствие: всякий многочлен — степени с любыми комплексными коэффициентами может быть представлен в виде произведения линейных множителей: = .
Из выражения легко следует: числа , в общем случае комплексные, есть корни многочлена (по определению). Возникает вопрос – что это за числа, которые обеспечивают существование корней для любого многочлена – степени? Что такое комплексные числа?..
☺☺
Пример 2–01: Пусть имеем многочлен: = . В соответствии с разложением этот многочлен должен иметь 2 корня. А школьная программа в части алгебры многочленов утверждает, что этот многочлен корней (действительных) не имеет!.. Как это понимать доверчивому юному математику?
Решение:
1). Попробуем руководствоваться определением корня, и станем формально выполнять привычные действия: .
2). Пусть . Проверим, является ли корнем заданного многочлена = . Запишем: . Это значит, что есть корень многочлена . Легко заметить, что и является корнем многочлена .
Замечание: По определению корнем многочлена называют любое число, которое, будучи подставлено в выражение многочлена, обращает его в тождество!
3). В нашем случае мы получили нечто: и , у которого свойство быть корнем имеется, но в привычном понимании это нечто не есть число! Для выхода из возникшего затруднения было предложено назвать корень – число = единица мнимая и обозначить: . В таком случае имеем: =
Ответ: разложение: = .
Пример 2–02: Задан многочлен: = . Учитывая результат предыдущего примера, найти его корни.
Решение:
1). Воспользуемся общей формулой = для нахождения корней многочлена: . В нашем случае: = = .
2). Пусть = и = . Так как названо числом, то и тоже числа. Действительно, выражения и есть числа, так как произведение чисел 3 и есть число. Значит и , – тоже числа, только необычные!..
Ответ: корни: = и = .
☻
В соответствии с исторической традицией число будем называть комплексное числов алгебраической форме, где называют действительной частью, а число – мнимой частью, причём и – произвольные действительные числа. Если =0, то множество действительных чисел можем рассматривать как подмножество множества комплексных чисел .
Назвав выражение числом, необходимо определить для этих чисел операции: сложения и умножения, причём так, чтобы для чисел выполнялись все, установленные для действительных чисел свойства. Пусть имеем и – два комплексных числа. Определим операции:
Сумма: . Разность – обратная операция.
Произведение: . Учитывая , можем записать: . В частном случае, когда число , имеем умножение комплексного числа на число вещественное: .
Деление: .
Замечание: Деление, как и разность, можно было определить как обратную операцию умножения, но в данном случае иллюстрация вычисления деления числа на число выразительно иллюстрирует сохранение всех свойств действительных чисел, в том числе – недопустимость деления на ноль!
Нетрудно заметить, что операции суммы комплексных чисел и произведения комплексного числа на произвольное вещественное число аналогичны линейным операциям с двумерными векторами. В таком случае логично воспользоваться представлением комплексного числа как вектора на плоскости прямоугольных координат : = .
Используя векторную модель комплексного числа, определим его модуль: = и координаты: и , где — угол, который вектор образует с осью . Это значит, произвольное комплексное число может быть представлено в виде: = — комплексное числов тригонометрической форме.
Если воспользоваться тождеством Эйлера: = , можем получить запись комплексного числа как: = . Более того, учитывая периодичность тригонометрических функций, в общем случае можем записать: = , .
Используя формулу , нетрудно записать выражения для операций произведения и деления комплексных чисел = и = , а также возведения комплексного числа = в степень (целую или дробную):
= , = .
= , = , .
Замечание: Формулы называют формулами Муавра. Заметим, что при извлечении корня — ой степени из любого комплексного числа получают различных комплексных чисел, которые располагаются на окружности радиуса с центром в точке и делят эту окружность на равных частей.
•• ☻☻ ••
Пример 1–421: Вычислить произведение комплексных чисел: . Результат записать в алгебраической форме.
Решение:
1). Раскрыв скобки и выполняя тождественные преобразования, запишем: = = .
2). Запись: = — алгебраическая форма комплексного числа.
Ответ: = .
Пример 2–423: Вычислить комплексное число: = . Результат записать в алгебраической форме. (1)
Решение:
1). Применим формулу для разности кубов двух чисел. Выполнив тождественные преобразования, запишем: = = .
2). Запись: = — алгебраическая форма комплексного числа.
Ответ: = .
Пример 3–425: Вычислить комплексное число: = . Результат записать в алгебраической форме.
Решение:
1). Применим формулу деления двух комплексных чисел в алгебраической форме. Выполнив тождественные преобразования, запишем: = = .
2). Запись: = — алгебраическая форма комплексного числа.
Ответ: = .
Пример 4–427: Вычислить комплексное число: = . Результат записать в алгебраической форме.
Решение:
1). Применим формулу деления двух комплексных чисел в алгебраической форме. Выполнив тождественные преобразования, запишем: = .
2). Тогда, воспользовавшись тем, что , запишем: = — алгебраическая форма комплексного числа.
Ответ: = .
Пример 5–429: Вычислить комплексное число: = . Результат записать в алгебраической форме.
Решение:
1). Воспользуемся таблицей степеней числа , именно: , , , . Тогда можем записать: и .
2). Тогда = . Вычислим сначала дробь = , затем запишем: = .
3). Запись: = — алгебраическая форма комплексного числа.
Ответ: = .
Пример 6–435: Представить комплексное число: = в тригонометрической форме и изобразить на комплексной плоскости .
Решение:
1). Воспользуемся общей записью: = . В нашем случае: = — тригонометрическая форма комплексного числа.
2). Изобразим заданное число на плоскости : его можно изобразить как по записи в алгебраической форме, так и воспользовавшись тригонометрической формой.
Ответ: = , см. рисунок.
Пример 7–437: Представить комплексное число: = в тригонометрической форме и изобразить на комплексной плоскости .
Решение:
1). Воспользуемся общей записью: = . В нашем случае: = — тригонометрическая форма комплексного числа.
2). Изобразим заданное число на плоскости : его можно изобразить как по записи в алгебраической форме, так и воспользовавшись тригонометрической формой.
Ответ: = , см. рисунок.
Пример 8–448(а): Вычислить: и , если , .
Решение:
1). В соответствии с определением сопряжённого числа запишем: и .
2). Тогда = = и = = , после чего: = .
Ответ: = , = .
Пример 9–487: Вычислить: = , используя формулу Муавра.
Решение:
1). Запишем: и .
2). Тогда (формула Муавра): = = = . Аналогично вычислим = = .
3). Вычислим: = = .
Ответ: = .
Пример 10–497: Вычислить все значения корня: .
Решение:
1). Запишем: . Тогда = .
2). Для всех указанных значений запишем соответствующие комплексные числа:
=0 → = = ,
=1 → = = ,
=2 → = = ,
=3 → = = ,
Ответ: , , , ; также см. рисунок.
Пример 11–499: Вычислить все значения корня: .
Решение:
1). Запишем: = = . Тогда = .
2). Для всех указанных значений запишем соответствующие комплексные числа:
=0 → = = ,
=1 → = = ,
Ответ: , ; также см. рисунок.
•• ☻☻ ••
Вопросы для самопроверки:
1. Что такое комплексное число?
2. Каковы основные операции с комплексными числами, их свойства?
3. Что такое тригонометрическая форма записи комплексного числа?
4. Формула Муавра, как её получили?
5. Сколько значений имеет корень – ой степени их числа 1?
Задачи для самоподготовки:
Пример C2–1: Вычислить комплексное число: . Результат записать в алгебраической форме.
Пример C2–2: Вычислить комплексное число: . Результат записать в алгебраической форме.
Пример C2–3: Вычислить комплексное число: = . Результат записать в алгебраической форме.
Пример C2–4: Вычислить комплексное число: = . Результат записать в алгебраической форме.
Пример C2–5: Представить комплексное число: = в тригонометрической форме и изобразить на комплексной плоскости .
Пример C2–6: Представить комплексное число: = в тригонометрической форме и изобразить на комплексной плоскости .
Пример C2–7: Вычислить: и , если , .
Пример C2–8: Вычислить: , используя формулу Муавра.
Пример C2–9: Вычислить все значения корня: .
Пример C2–10: Вычислить все значения корня: .
Пример C2–11: Вычислить все значения корня: .
•• ☻☻ ••
Рекомендуемые страницы:
lektsia.com
4. Теория функций комплексного переменного. Операционное исчисление
4.1. Комплексные числа
Комплексным
числом  называется арифметическое выражение
вида
называется арифметическое выражение
вида
, | (4.1) |
где 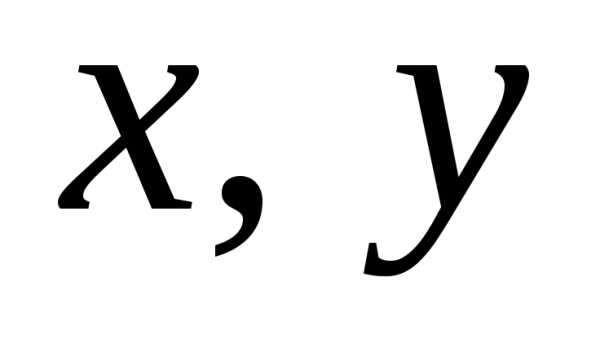 — действительные числа, а
— действительные числа, а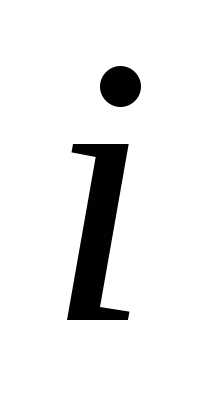 — специальный символ, который называетсямнимой
единицей.
Для мнимой единицы по определению
считается, что
— специальный символ, который называетсямнимой
единицей.
Для мнимой единицы по определению
считается, что 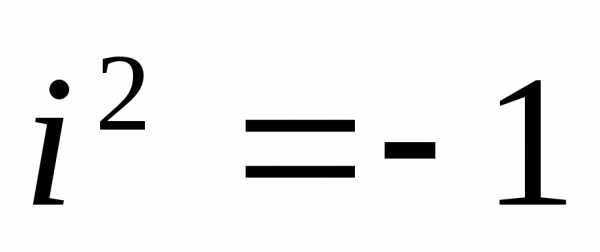 .
.
(4.1)
– алгебраическая
форма комплексного числа, причем
называетсядействительной
частью комплексного числа, а 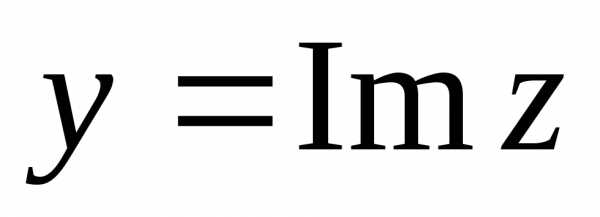 —мнимой
частью.
—мнимой
частью.
Число называетсякомплексно сопряженным к числу .
Пусть даны два комплексных числа ,.
1. Суммой 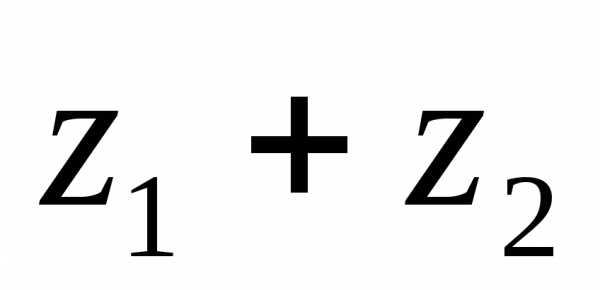 комплексных чисел
комплексных чисел и
и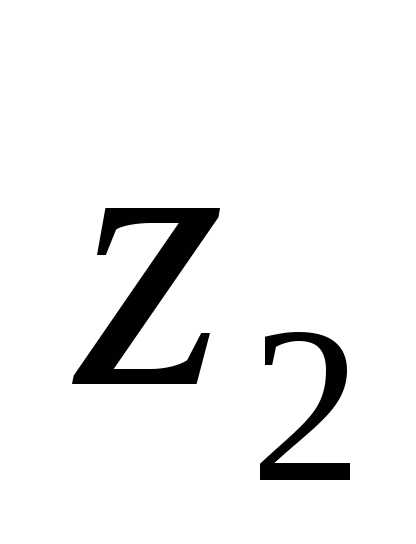 называется комплексное число
называется комплексное число
.
2. Разностью 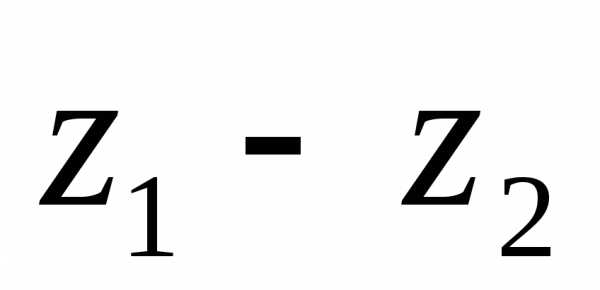 комплексных чисел
комплексных чисел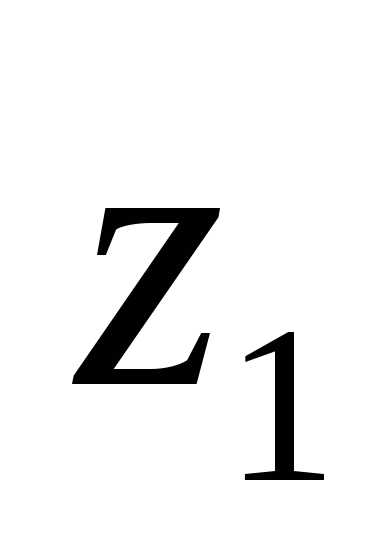 и
и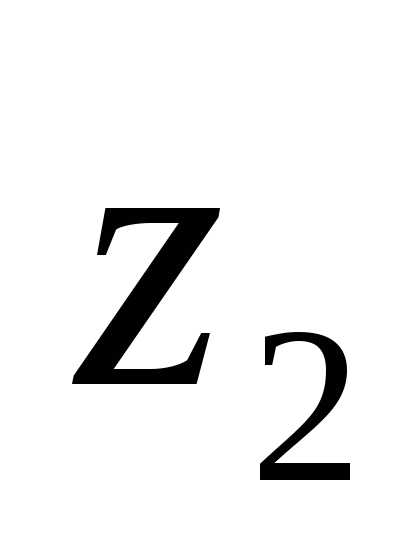 называется комплексное число
называется комплексное число
.
3. Произведением 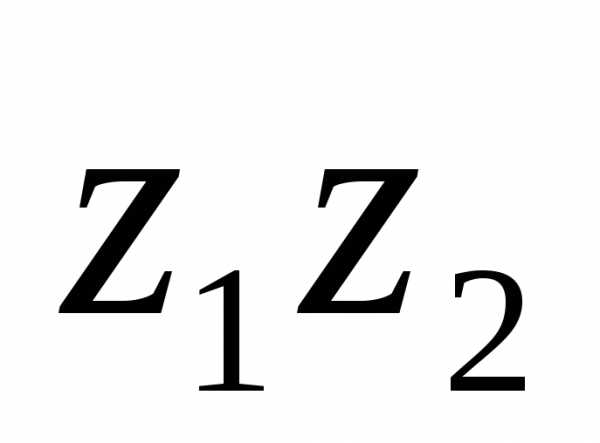 комплексных чисел
комплексных чисел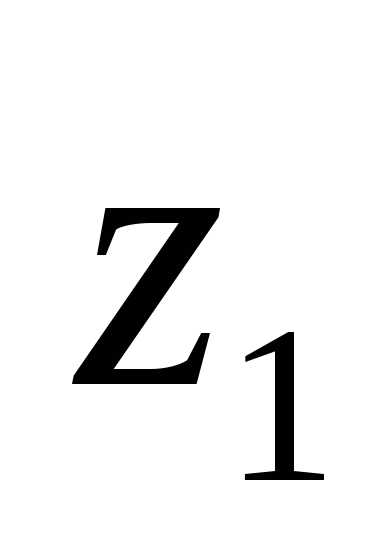 и
и называется комплексное число
называется комплексное число
.
4. Частным 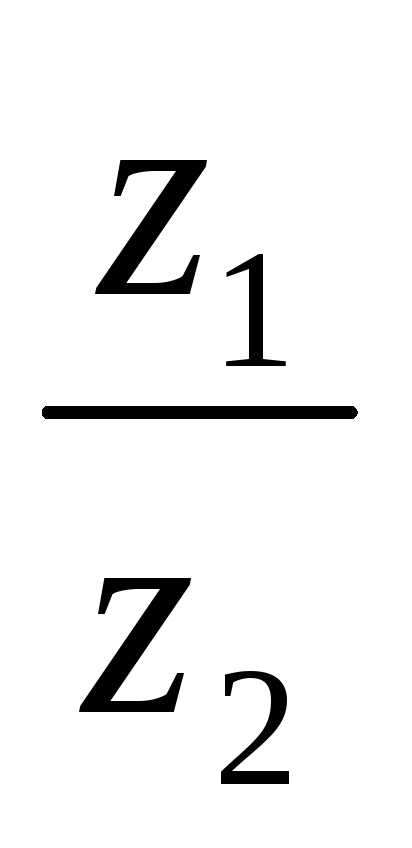 от деления комплексного числа
от деления комплексного числа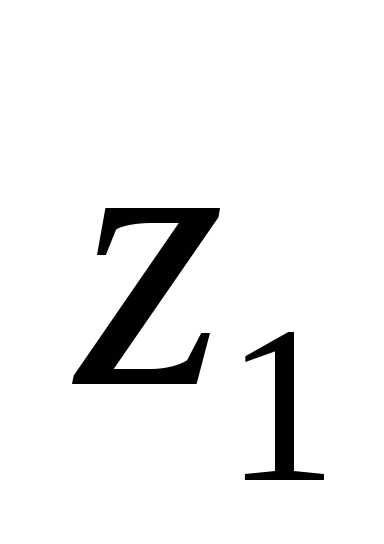 на комплексное число
на комплексное число называется комплексное число
называется комплексное число
.
Замечание 4.1. То есть операции над комплексными числами вводятся по обычным правилам арифметических операций над буквенными выражениями в алгебре.
Пример 4.1. Даны комплексные числа . Найти
.
Решение. 1) .
2) .
3)
.
4) Домножая числитель и знаменатель на комплексно сопряженное знаменателю число, получаем
.
Тригонометрическая форма комплексного числа:
,
где
— модуль комплексного числа,- аргумент комплексного числа. Угол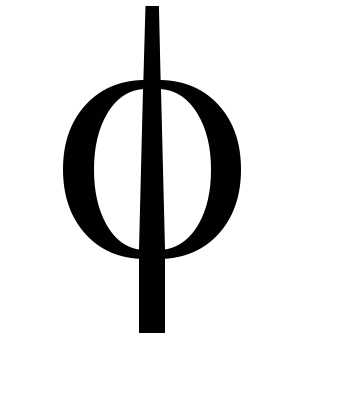 определен неоднозначно, с точностью до
слагаемого
определен неоднозначно, с точностью до
слагаемого :
:
, 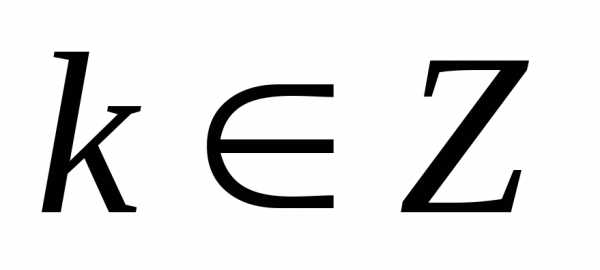 .
.
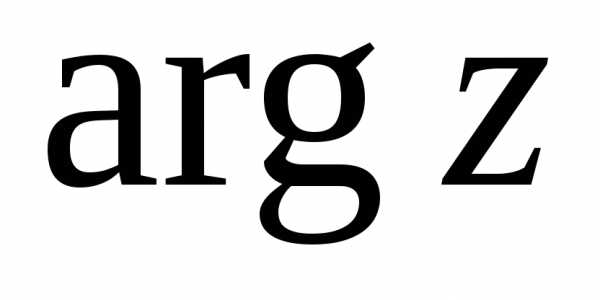 —
главное значение аргумента, определяемое
условием
—
главное значение аргумента, определяемое
условием
, (или ).
Показательная форма комплексного числа:
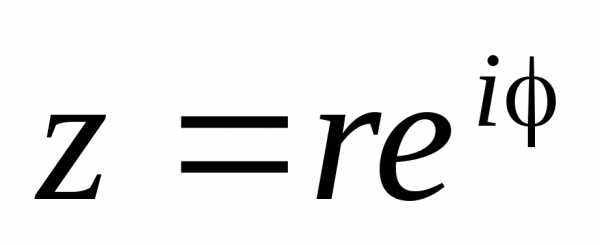 .
.
Корень  й
степени числа
й
степени числа имеет
имеет  различных значений, которые находятся
по формуле
различных значений, которые находятся
по формуле
, | (4.2) |
где .
Точки,
соответствующие значениям 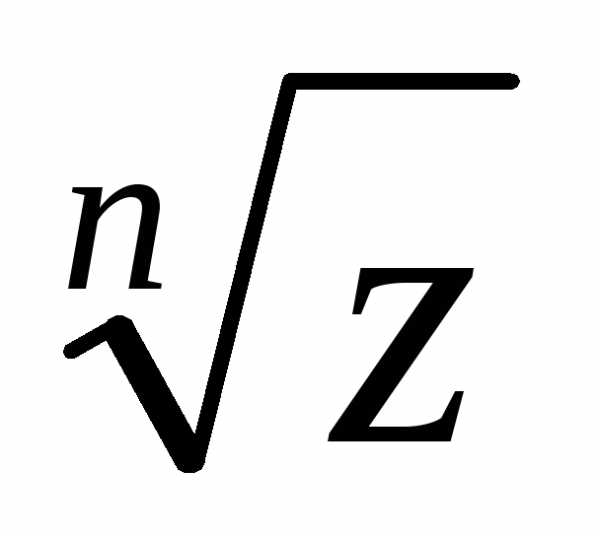 ,
являются вершинами правильного
,
являются вершинами правильного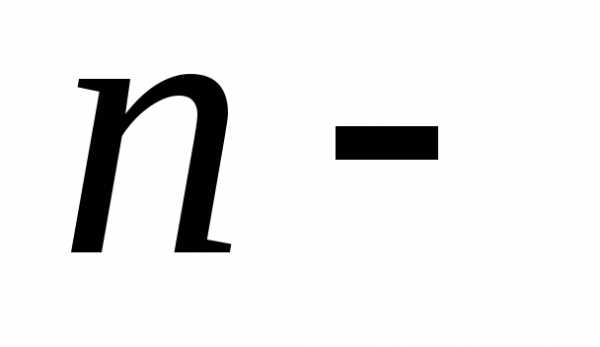 угольника,
вписанного в окружность радиуса
угольника,
вписанного в окружность радиуса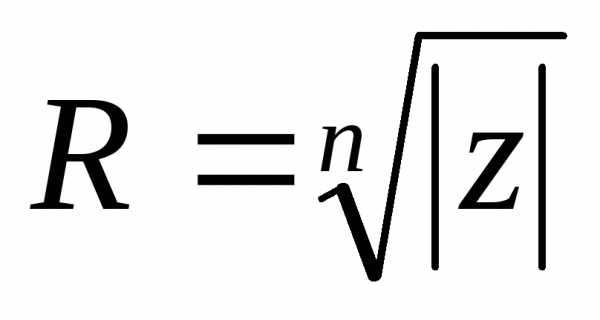 с центром в начале координат.
с центром в начале координат.
Пример
4.2. Найти
все значения корня 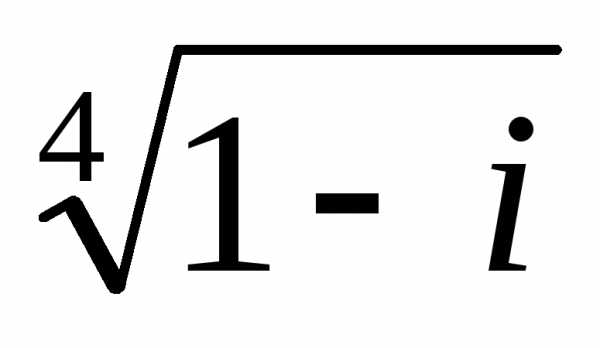 .
.
Решение. Представим
комплексное число 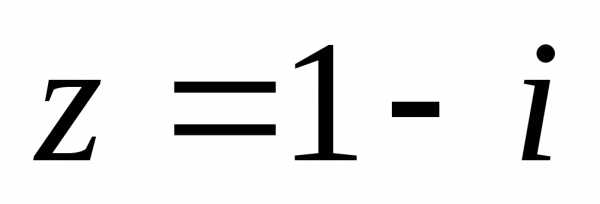 в тригонометрической форме:
в тригонометрической форме:
,
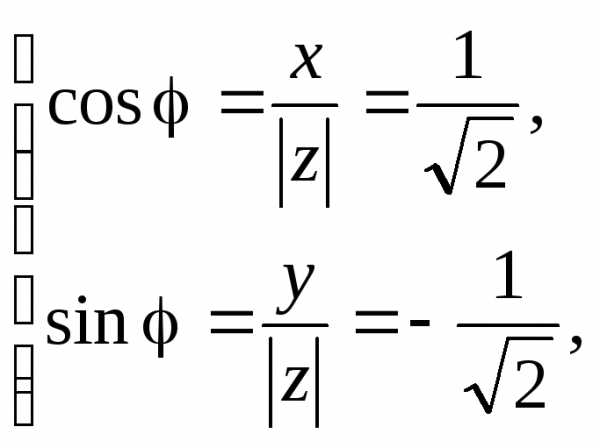 ,
откуда
,
откуда 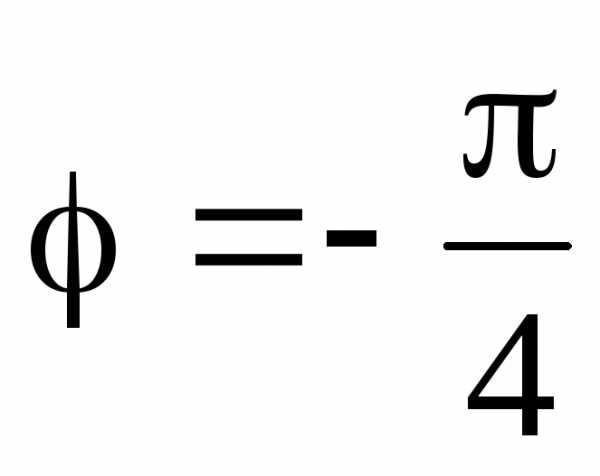 .
.
Тогда
.
Следовательно, по формуле (4.2)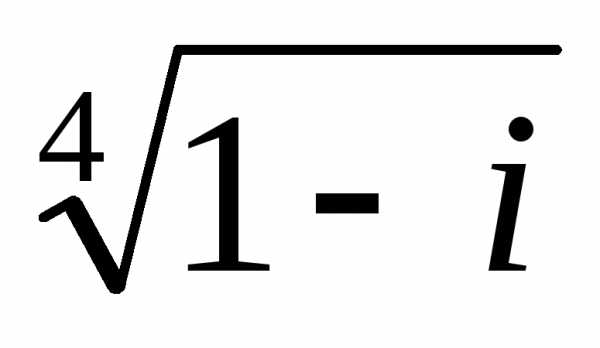 имеет четыре значения:
имеет четыре значения:
, .
Полагая , находим
, ,
, .
Здесь мы преобразовывали значения аргумента к его главному значению.
Множества на комплексной плоскости
Комплексное
число
изображается на плоскости точкой
точкой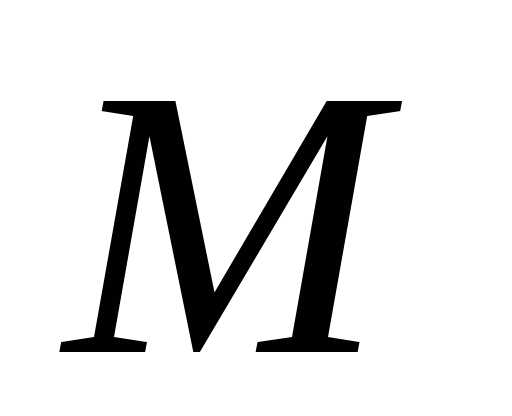 с координатами
с координатами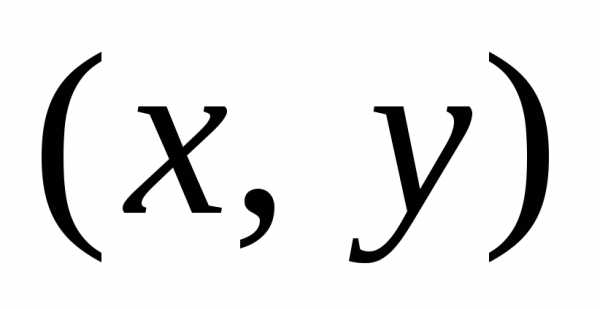 .
Модуль
.
Модуль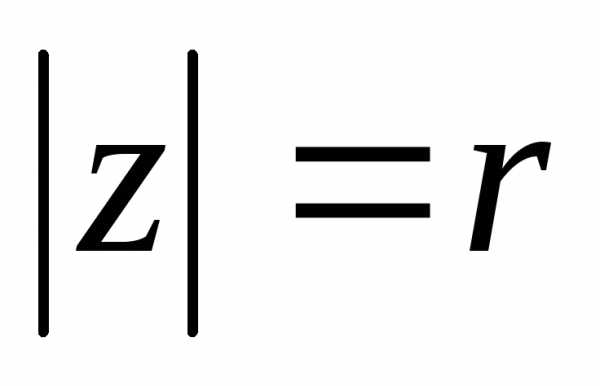 и аргументсоответствуют полярным координатам
точки
и аргументсоответствуют полярным координатам
точки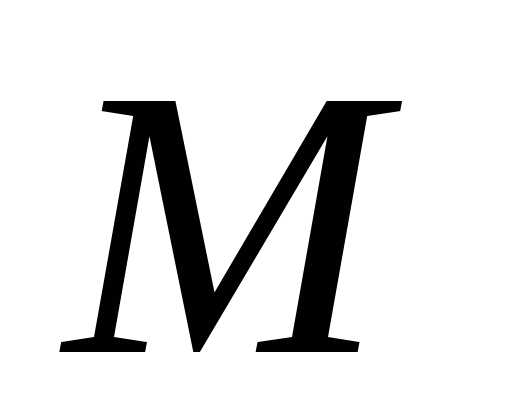 .
.
Полезно
помнить, что неравенство 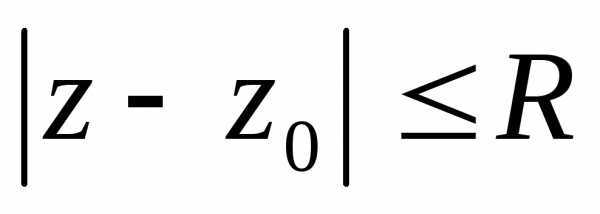 задает круг с центром в точке
задает круг с центром в точке радиуса
радиуса .
Неравенствозадает полуплоскость, расположенную
правее прямой
.
Неравенствозадает полуплоскость, расположенную
правее прямой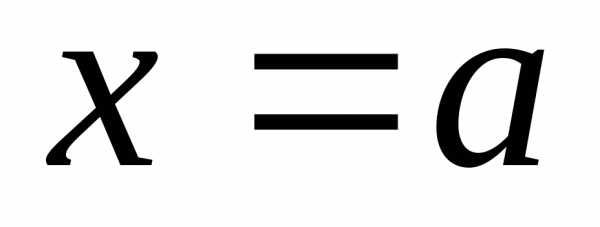 ,
а неравенство- полуплоскость, расположенную выше
прямой
,
а неравенство- полуплоскость, расположенную выше
прямой .
Кроме того, система неравенствзадает угол между лучами
.
Кроме того, система неравенствзадает угол между лучами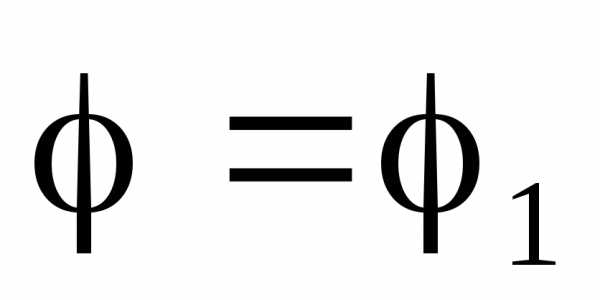 и
и ,
выходящими из начала координат.
,
выходящими из начала координат.
Пример
4.3. Нарисовать
область, заданную неравенствами: 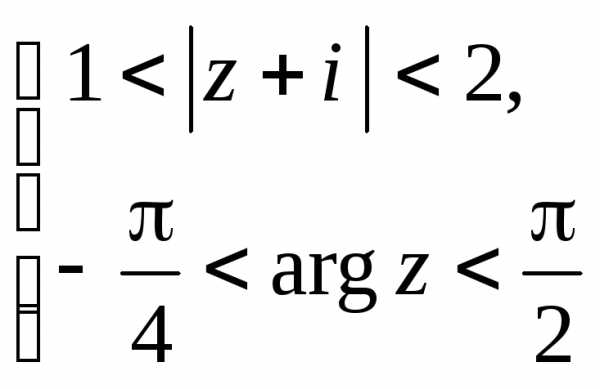 .
.
Решение. Первому
неравенству соответствует кольцо с
центром в точке  и двумя радиусами 1 и 2, окружности в
область не входят (рис. 4.1).
и двумя радиусами 1 и 2, окружности в
область не входят (рис. 4.1).
Второму
неравенству соответствует угол между
лучами 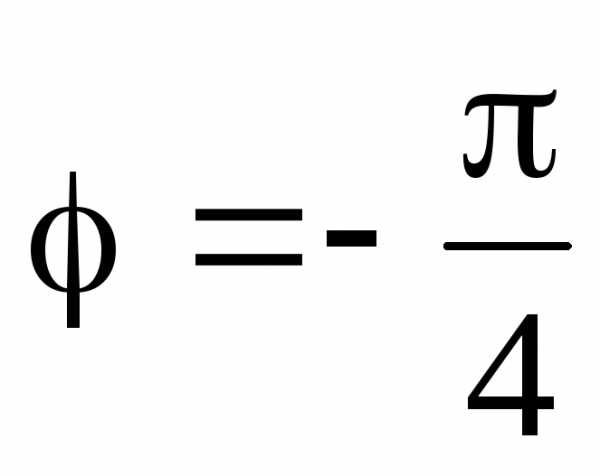 (биссектриса 4 координатного угла) и
(биссектриса 4 координатного угла) и (положительное направление оси
(положительное направление оси ).
Сами лучи в область не входят (рис. 4.2).
).
Сами лучи в область не входят (рис. 4.2).
Искомая область является пересечением двух полученных областей (рис. 4.3)
рис. 4.1 | рис. 4.2 | рис. 4.3 |
4.2. Функции комплексного переменного
Пусть
однозначная функция  определена и непрерывна в области
определена и непрерывна в области ,
а
,
а — кусочно-гладкая замкнутая или незамкнутая
ориентированная кривая, лежащая в
— кусочно-гладкая замкнутая или незамкнутая
ориентированная кривая, лежащая в .
Пусть, как обычно,,,
где,- действительные функции переменных
.
Пусть, как обычно,,,
где,- действительные функции переменных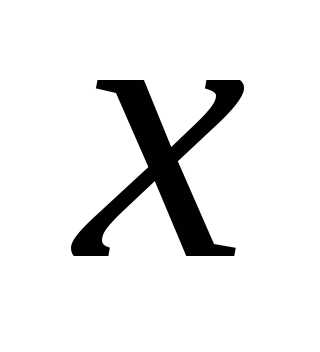 и
и .
.
Вычисление
интеграла от функции 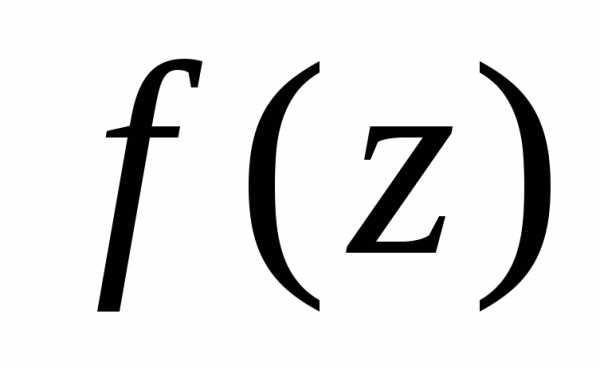 комплексного переменного
комплексного переменного сводится к вычислению обычных криволинейных
интегралов, а именно
сводится к вычислению обычных криволинейных
интегралов, а именно
. | (4.3) |
Если
функция  аналитична в односвязной области
аналитична в односвязной области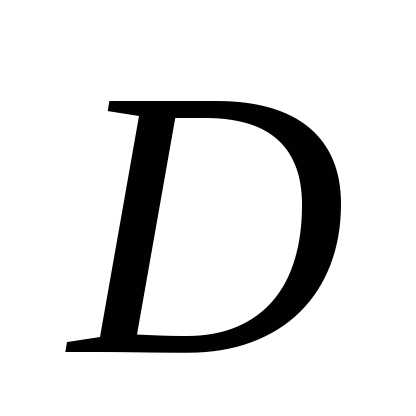 ,
содержащей точки
,
содержащей точки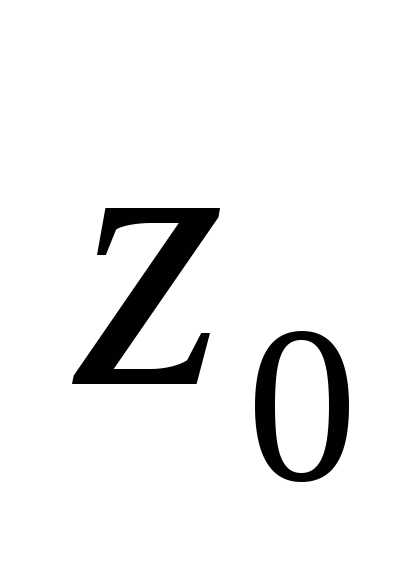 и
и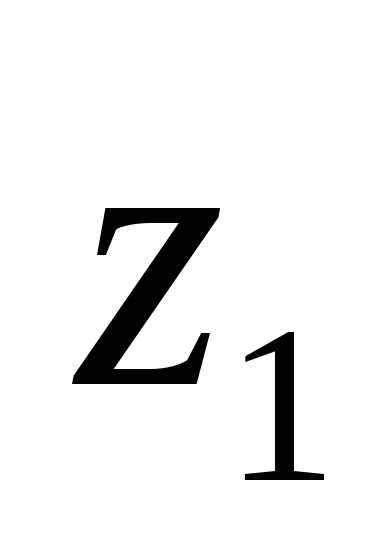 ,
то имеет место формула Ньютона-Лейбница:
,
то имеет место формула Ньютона-Лейбница:
, | (4.4) |
где 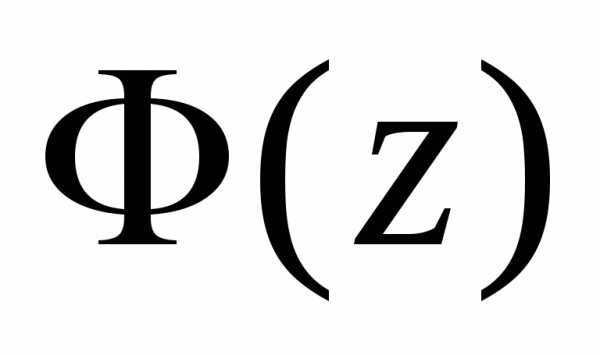 — какая-либо первообразная для функции
— какая-либо первообразная для функции ,
то естьв области
,
то естьв области .
.
В интегралах от функций комплексного переменного можно производить замену переменной, и интегрирование по частям аналогично тому, как это делается при вычислении интегралов от функций действительного переменного.
Заметим
также, что если путь интегрирования
является частью прямой, выходящей из
точки 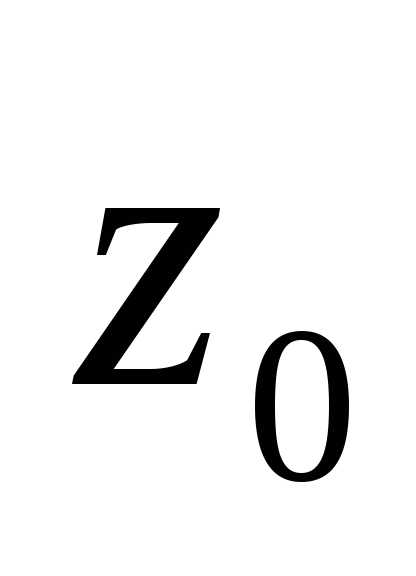 ,
или частью окружности с центром в точке
,
или частью окружности с центром в точке ,
то полезно делать замену переменной
вида.
В первом случае,
а
,
то полезно делать замену переменной
вида.
В первом случае,
а — действительная переменная интегрирования;
во втором случае,
а
— действительная переменная интегрирования;
во втором случае,
а — действительная переменная интегрирования.
— действительная переменная интегрирования.
Пример
4.4. Вычислить 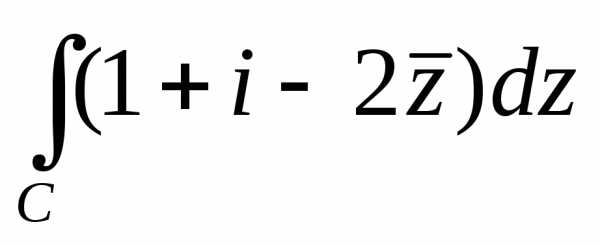 по параболе
по параболе от точки
от точки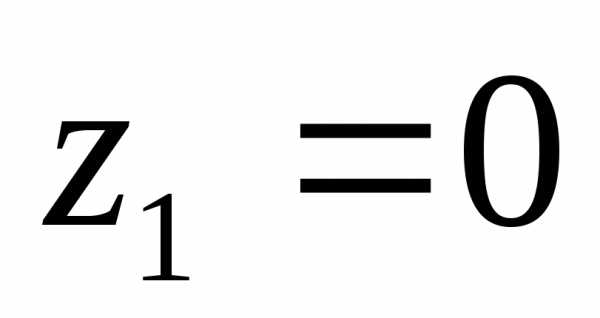 до точки
до точки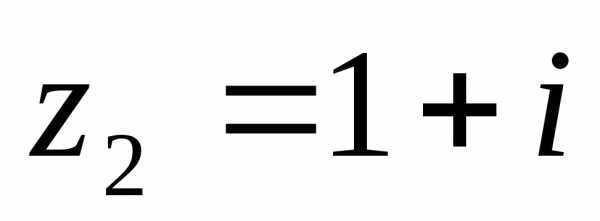 (рис 4.4).
(рис 4.4).
.
Пример
4.5. Вычислить
интеграл 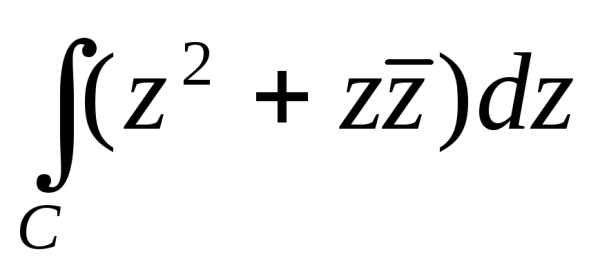 ,
где
,
где — дуга окружности
— дуга окружности ,(рис. 4.5) .
,(рис. 4.5) .
Функция 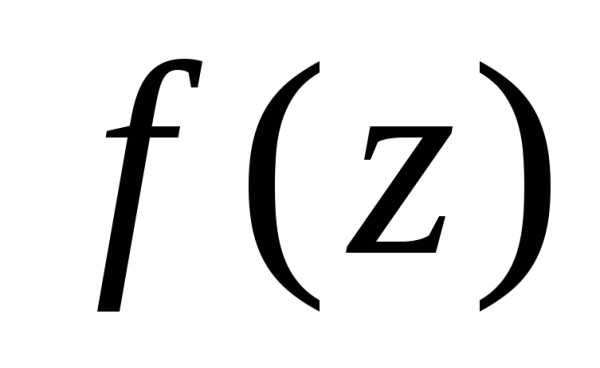 ,
однозначная и аналитическая в кольце,
разлагается в этом кольце вряд
Лорана
,
однозначная и аналитическая в кольце,
разлагается в этом кольце вряд
Лорана
. | (4.5) |
В
формуле (4.5) ряд
называетсяглавной
частью ряда Лорана, а ряд 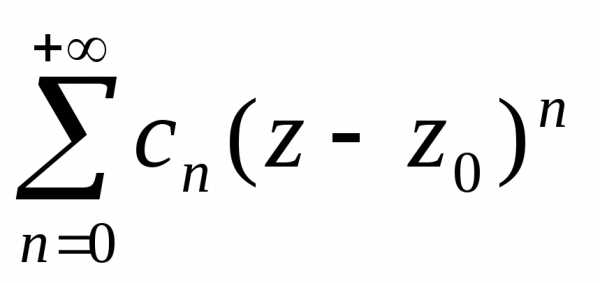 называетсяправильной
частью ряда Лорана.
называетсяправильной
частью ряда Лорана.
Определение
4.1. Точка  называетсяизолированной
особой точкой функции
называетсяизолированной
особой точкой функции  ,
если существует окрестность этой точки,
в которой функция
,
если существует окрестность этой точки,
в которой функция аналитична всюду, кроме самой точки
аналитична всюду, кроме самой точки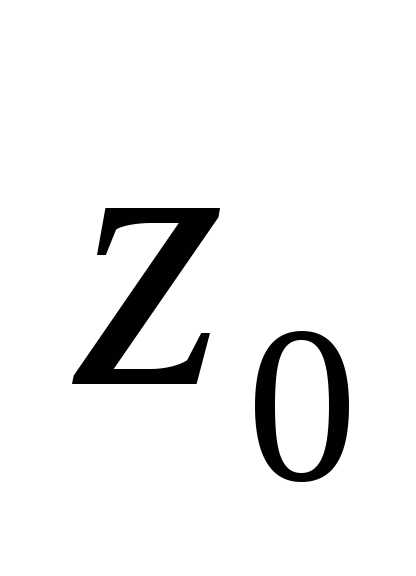 .
.
Функцию 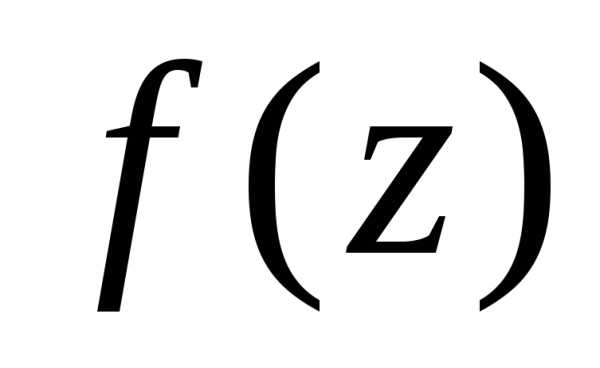 в окрестности точки
в окрестности точки  можно разложить в ряд Лорана. При этом
возможны три различных случая, когда
ряд Лорана:
можно разложить в ряд Лорана. При этом
возможны три различных случая, когда
ряд Лорана:
1) не содержит членов с отрицательными
степенями разности 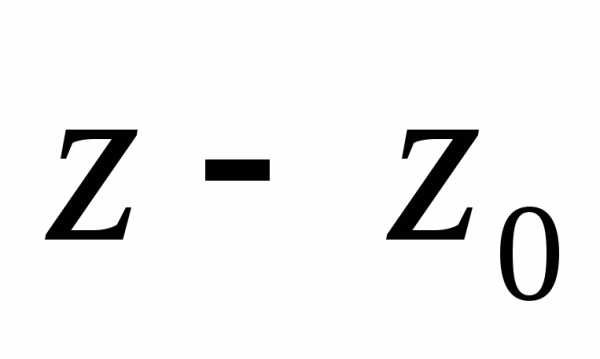 ,
то есть
,
то есть
(ряд
Лорана не содержит главной части). В
этом случае  называется устранимой
особой точкой функции
называется устранимой
особой точкой функции 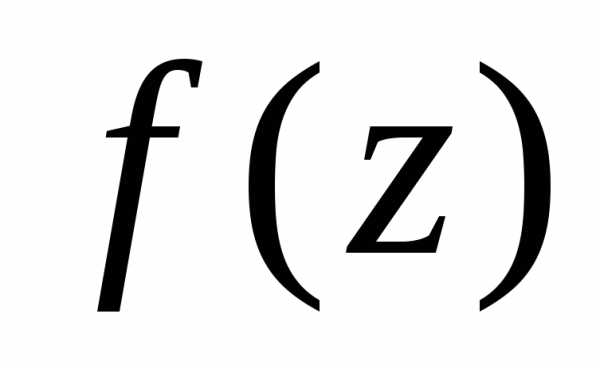 ;
;
2) содержит конечное число членов с
отрицательными степенями разности 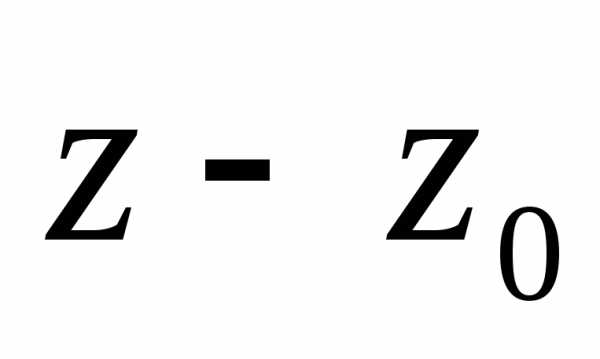 ,
то есть
,
то есть
,
причем 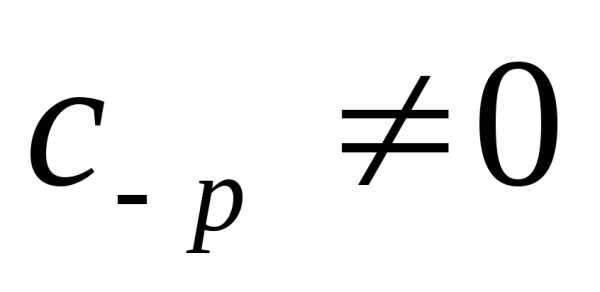 .
В этом случае точка
.
В этом случае точка 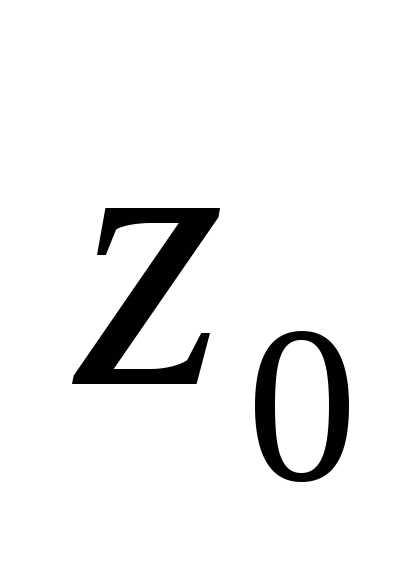 называется полюсом
порядка
называется полюсом
порядка 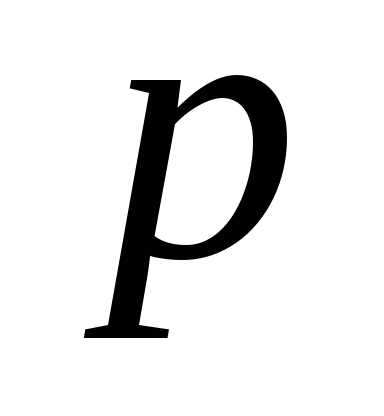 функции
функции 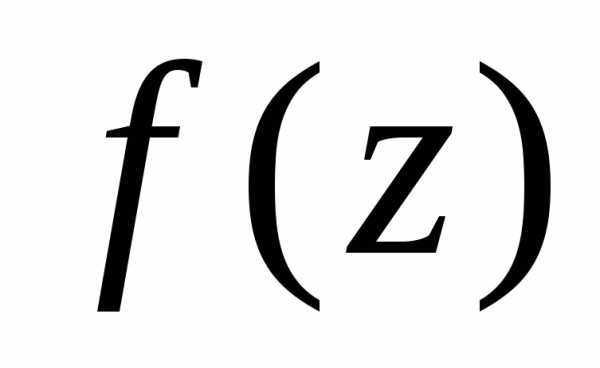 ;
;
3) содержит бесконечное число членов с отрицательными степенями:
.
В
этом случае точка 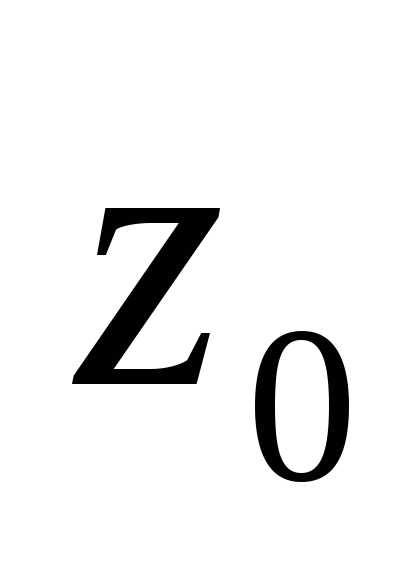 называется существенно
особой точкой функции
называется существенно
особой точкой функции 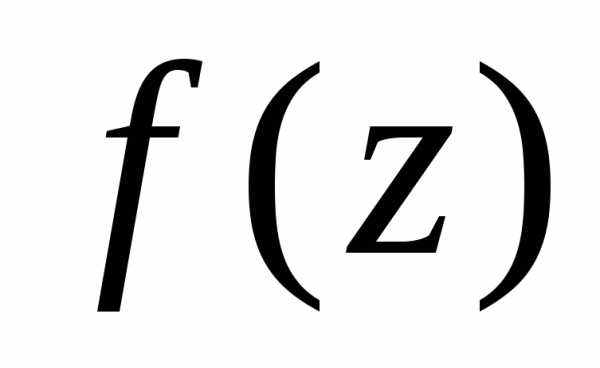 .
.
При определении характера изолированной особой точки не обязательно искать разложение в ряд Лорана. Можно использовать различные свойства изолированных особых точек.
1) 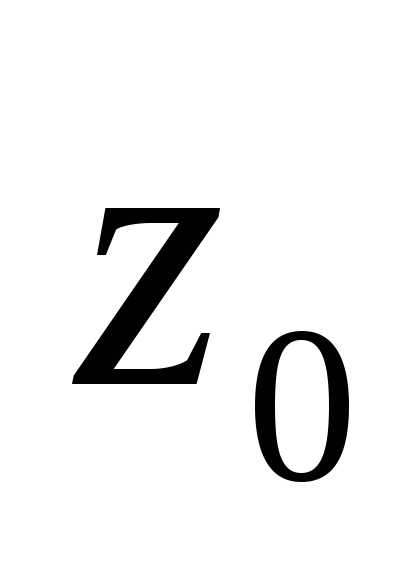 является устранимой особой точкой
функции
является устранимой особой точкой
функции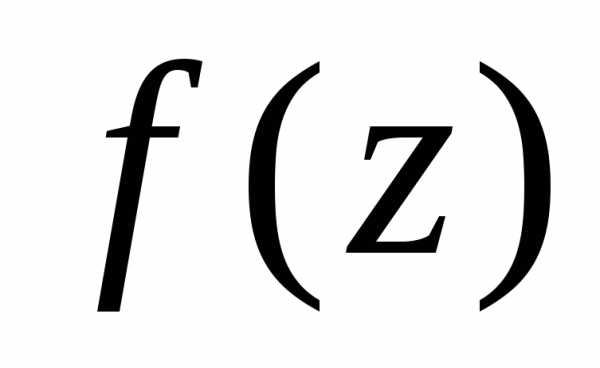 ,
если существует конечный предел функции
,
если существует конечный предел функции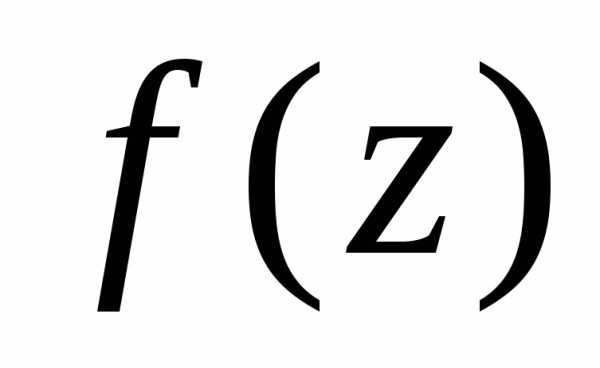 в точке
в точке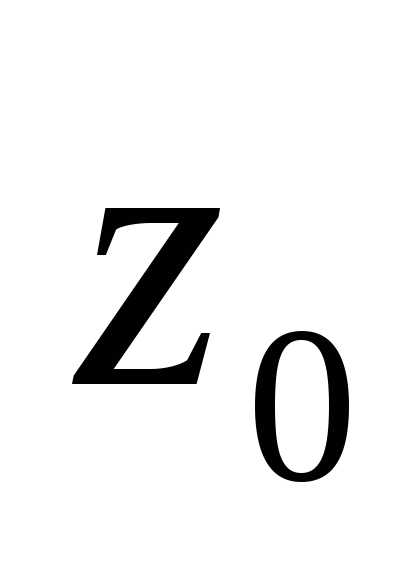 :
:
.
2) 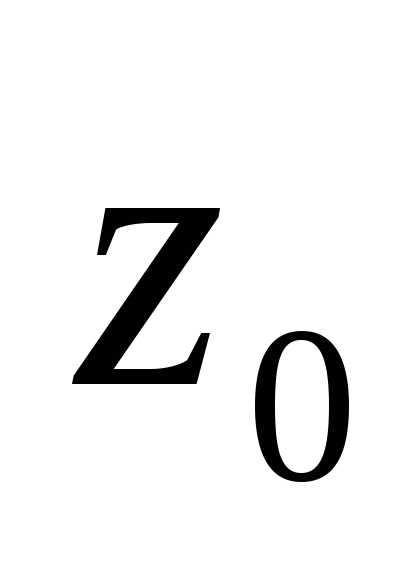 является полюсом функции
является полюсом функции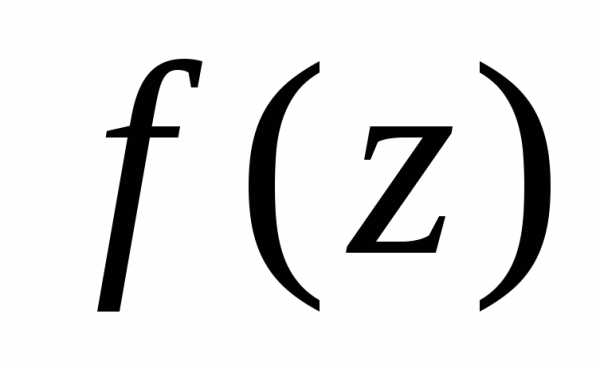 ,
если
,
если
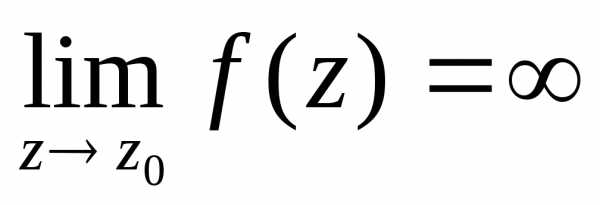 .
.
3) 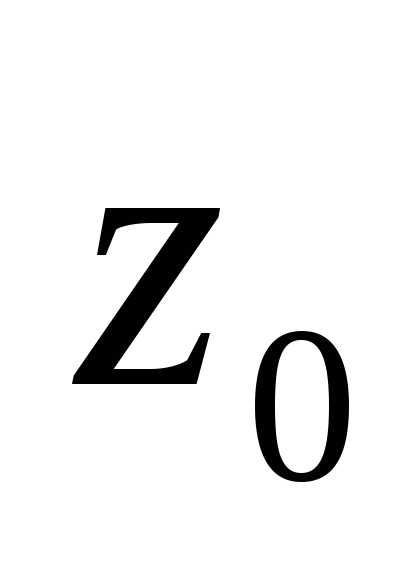 является существенно особой точкой
функции
является существенно особой точкой
функции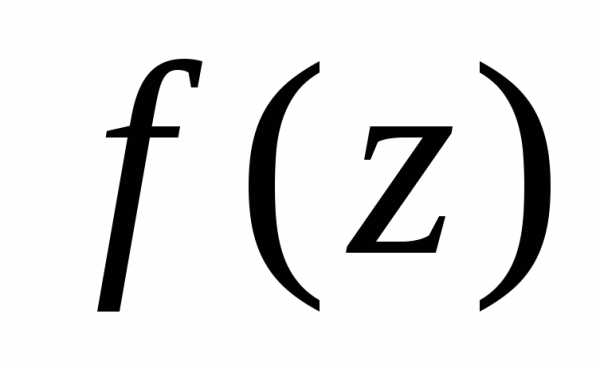 ,
если при
,
если при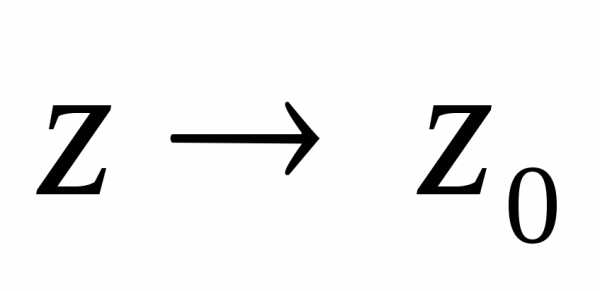 функция не имеет предела, ни конечного,
ни бесконечного.
функция не имеет предела, ни конечного,
ни бесконечного.
Определение
4.2. Точка 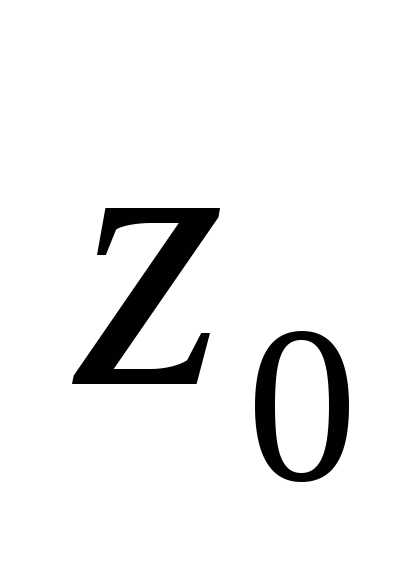 называетсянулем
называетсянулем  го
порядка(или
кратности
го
порядка(или
кратности 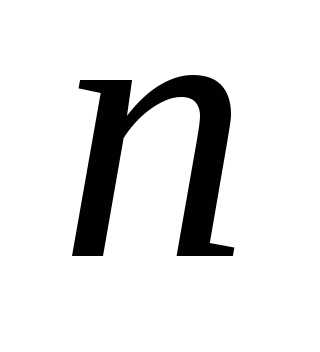 ) функции
) функции  ,
если выполняются условия:
,
если выполняются условия:
 …, .
…, .
Замечание
4.2. Точка 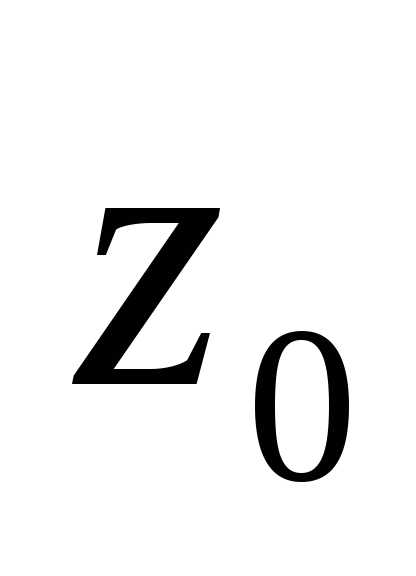 тогда и только тогда является нулем
тогда и только тогда является нулем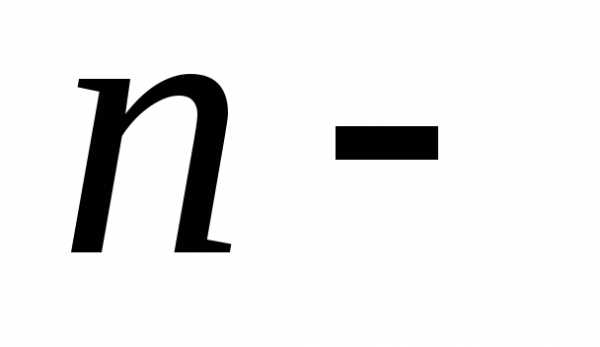 го
порядка функции
го
порядка функции  ,
когда в некоторой окрестности этой
точки имеет место равенство
,
когда в некоторой окрестности этой
точки имеет место равенство
,
где
функция 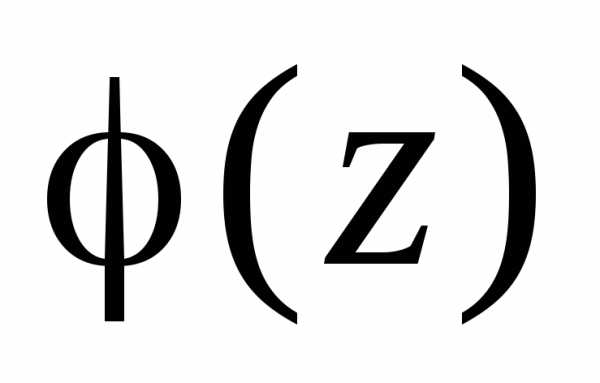 аналитична в точке
аналитична в точке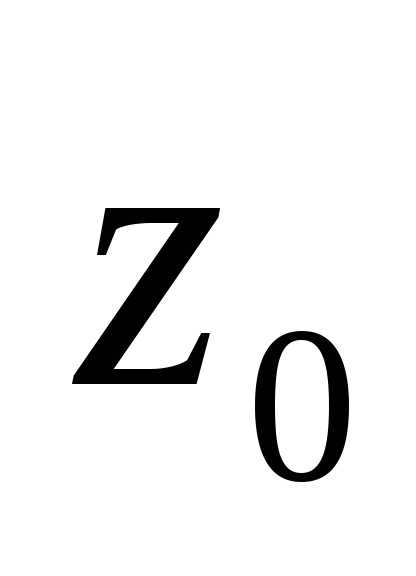 и
и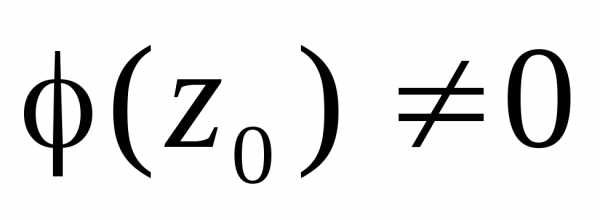
4)
точка 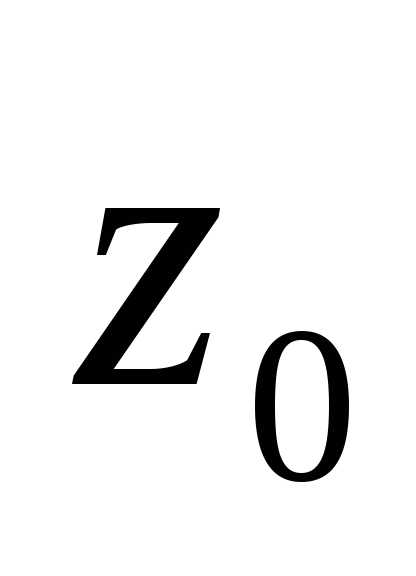 является полюсом порядка
является полюсом порядка  (
(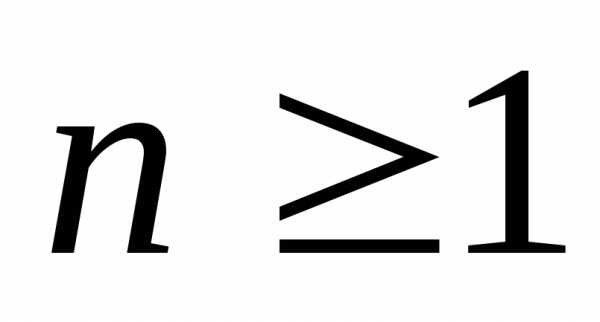 )
функции
)
функции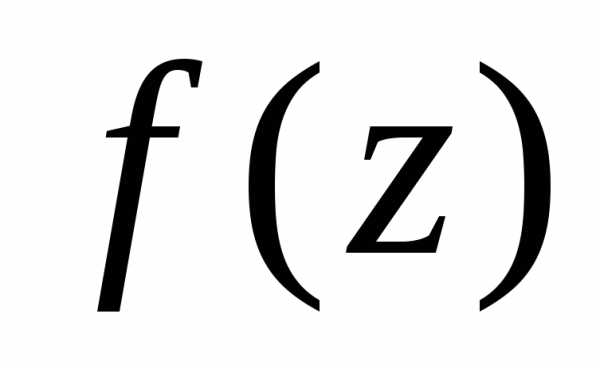 ,
если эта точка является нулем порядка
,
если эта точка является нулем порядка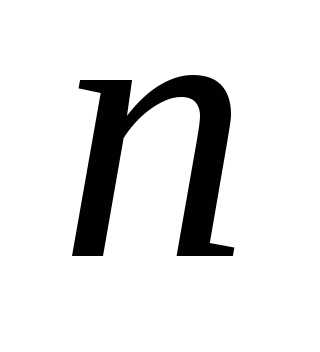 для функции
для функции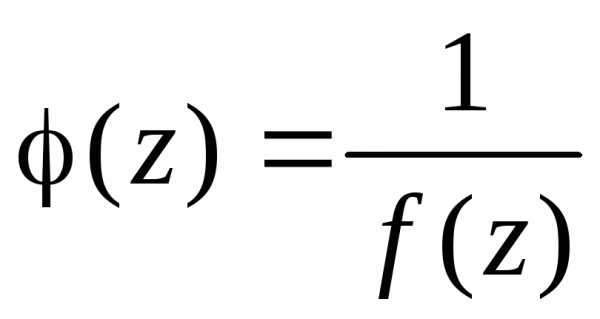 .
.
5)
пусть 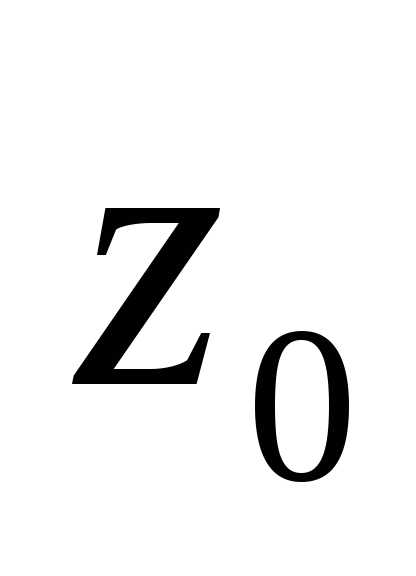 —изолированная
особая точка функции
—изолированная
особая точка функции  ,
где- функции аналитические в точке
,
где- функции аналитические в точке  .
И пусть точка
.
И пусть точка 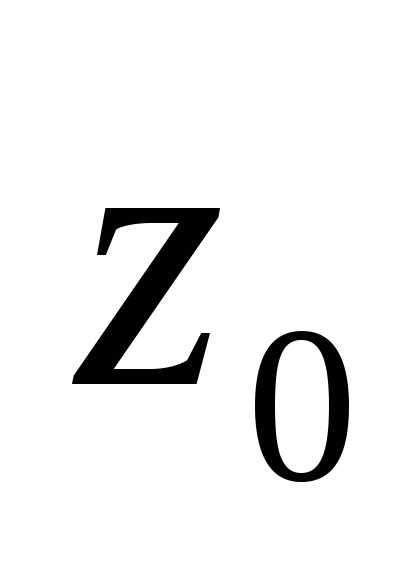 является нулем порядка
является нулем порядка 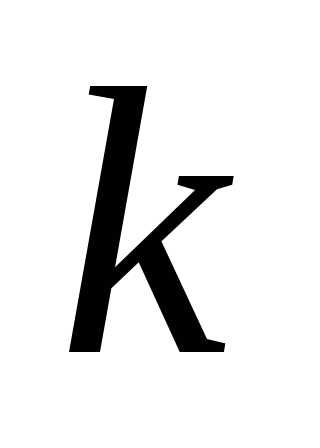 функции
функции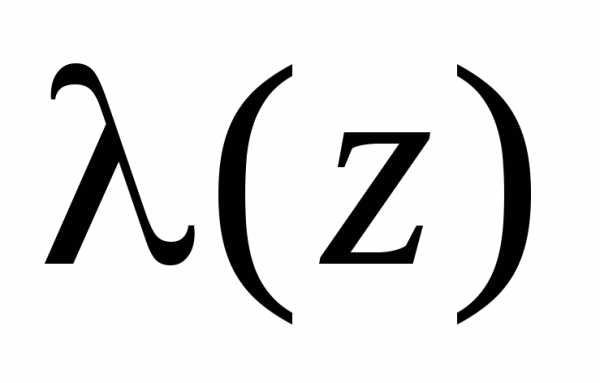 и нулем порядка
и нулем порядка функции
функции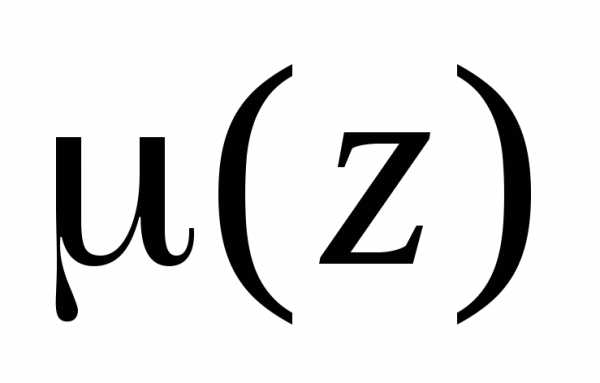 .
.
При 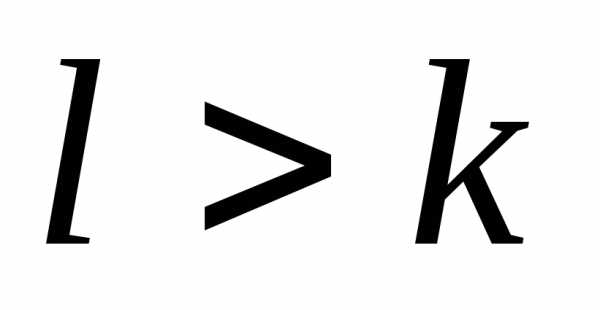 точка
точка 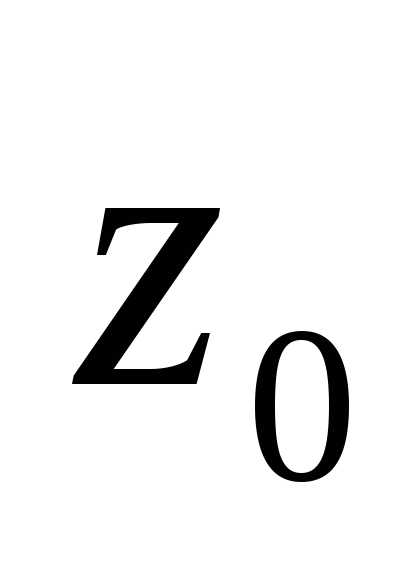 является полюсом порядка
функции
является полюсом порядка
функции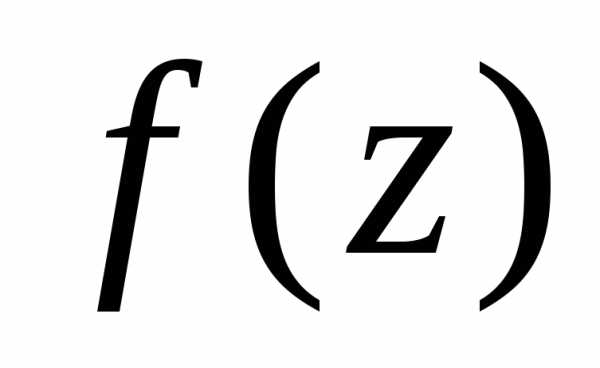 .
.
При 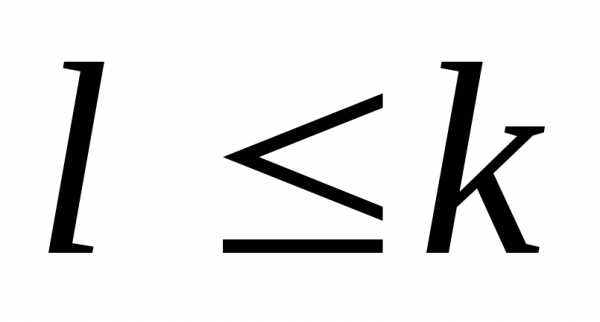 точка
точка 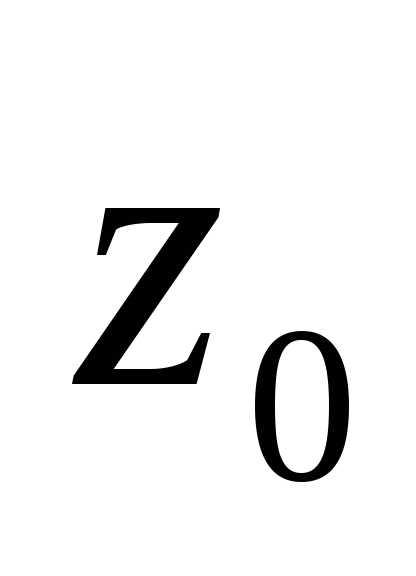 является устранимой особой точкой
функции
является устранимой особой точкой
функции 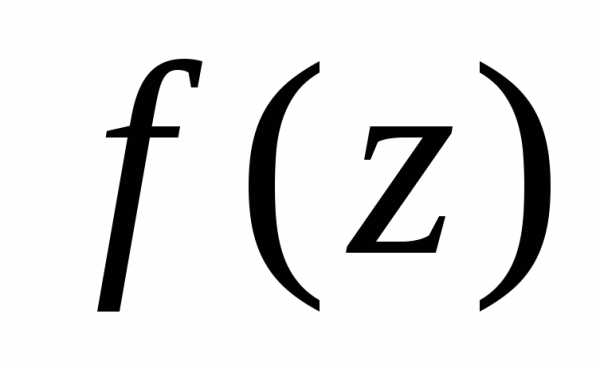 .
.
Пример
4.6. Найти
изолированные точки и определить их
тип для функции 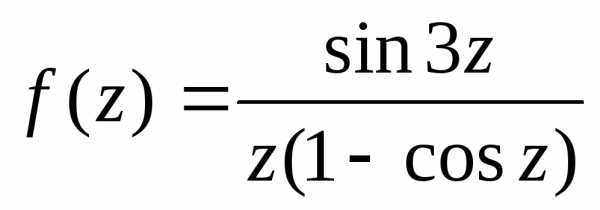 .
.
Решение. Функции
и- аналитические во всей комплексной
плоскости. Значит, особыми точками
функции являются нули знаменателя, то есть
точки, где
являются нули знаменателя, то есть
точки, где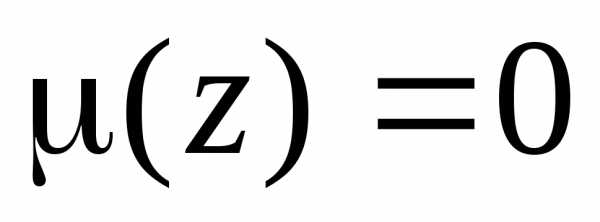 .
Таких точек бесконечно много. Во-первых,
это точка
.
Таких точек бесконечно много. Во-первых,
это точка ,
а также точки, удовлетворяющие уравнению.
Отсюдаи.
,
а также точки, удовлетворяющие уравнению.
Отсюдаи.
Рассмотрим
точку 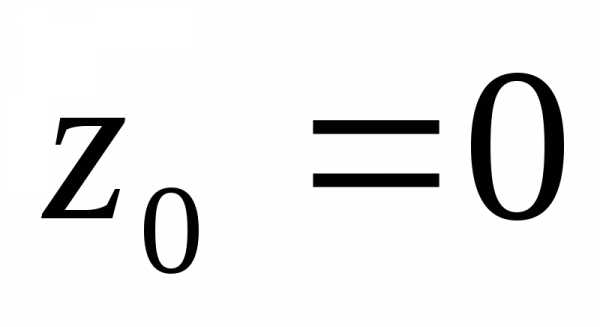 .
В этой точке получим:
.
В этой точке получим:
, 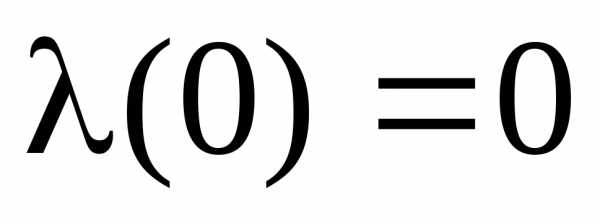 ,
,
, .
Порядок
нуля равен  .
.
, 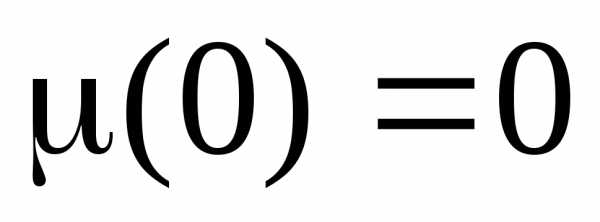 ,
,
, 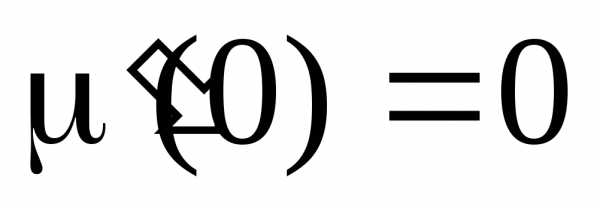 ,
,
, ,
, .
Порядок
нуля знаменателя равен 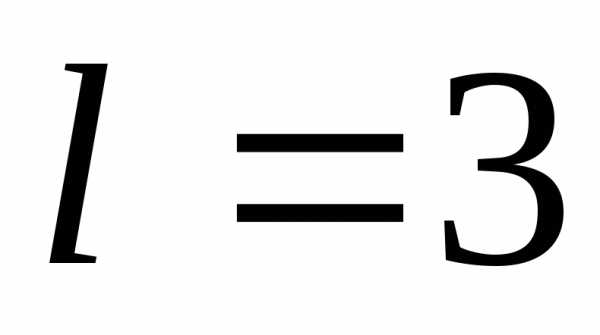 .
.
Значит,
точка 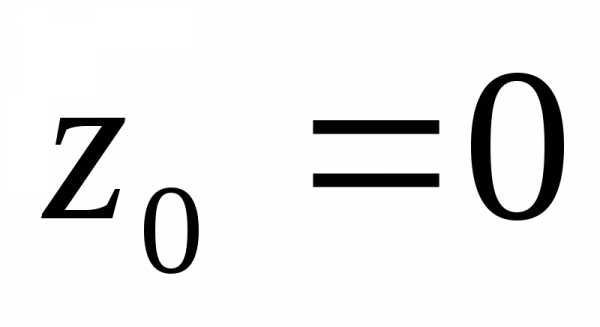 является полюсом второго порядка ().
является полюсом второго порядка ().
. Тогда
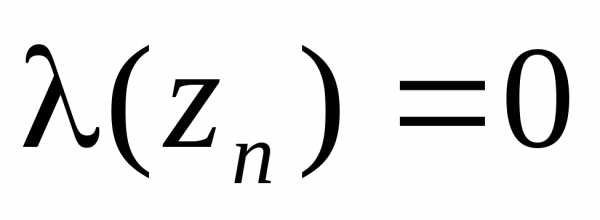 ,
.
,
.
Порядок
нуля числителя равен 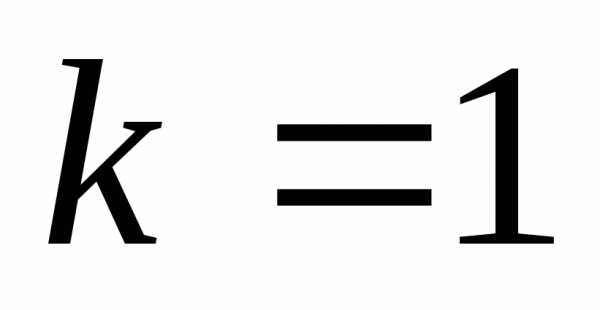 .
.
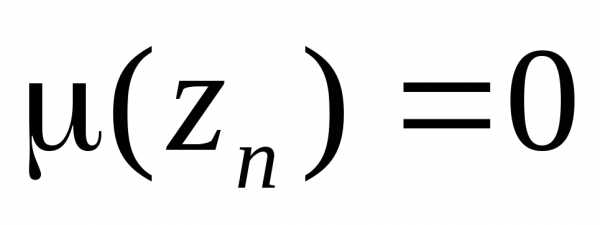 ,
, 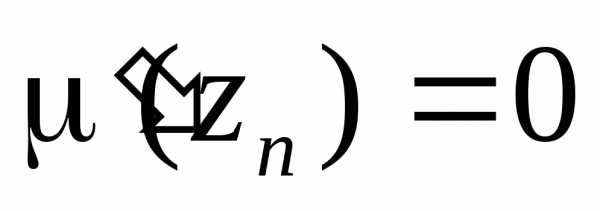 ,.
,.
Порядок
нуля знаменателя равен 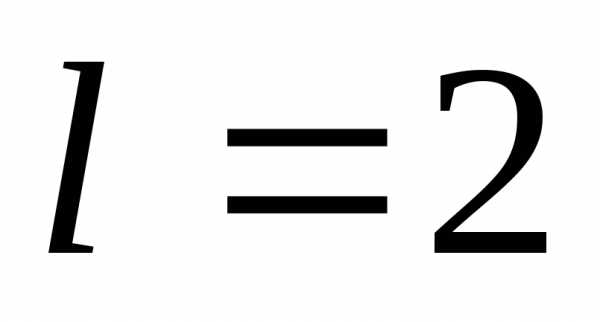 .
Следовательно, точки
.
Следовательно, точки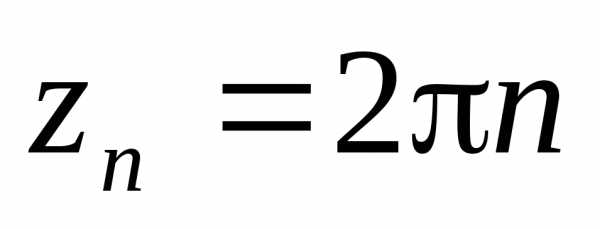 при
при являются полюсами первого порядка
(простыми
полюсами).
являются полюсами первого порядка
(простыми
полюсами).
Теорема
4.1. (Теорема
Коши о вычетах). Если
функция 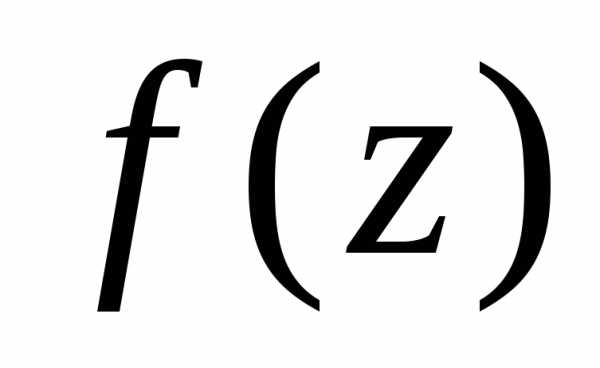 является аналитической на границе
является аналитической на границе области
области и всюду внутри области, за исключением
конечного числа особых точек,
то
и всюду внутри области, за исключением
конечного числа особых точек,
то
.
При
вычислении интегралов стоит аккуратно
найти все особые точки функции 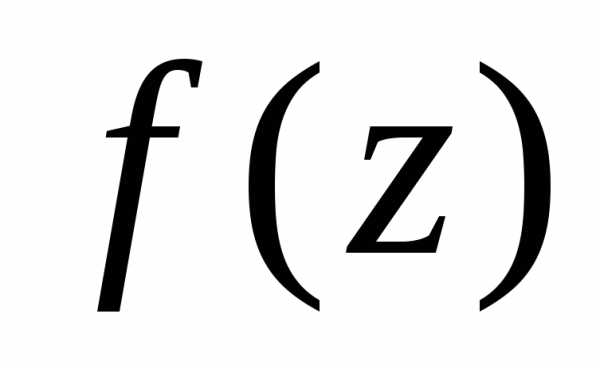 ,
затем нарисовать контур и особые точки,
и после этого выбрать только те точки,
которые попали внутрь контура
интегрирования. Сделать правильный
выбор без рисунка часто бывает
затруднительно.
,
затем нарисовать контур и особые точки,
и после этого выбрать только те точки,
которые попали внутрь контура
интегрирования. Сделать правильный
выбор без рисунка часто бывает
затруднительно.
Способ
вычисления вычета 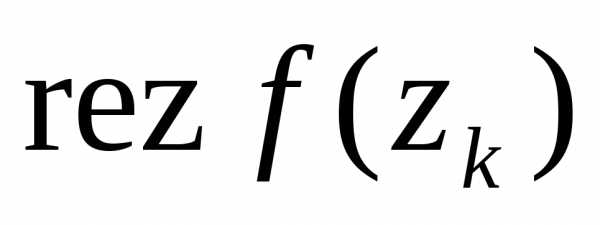 зависит от типа особой точки. Поэтому,
прежде чем вычислять вычет, нужно
определить тип особой точки.
зависит от типа особой точки. Поэтому,
прежде чем вычислять вычет, нужно
определить тип особой точки.
1)
вычет функции в точке 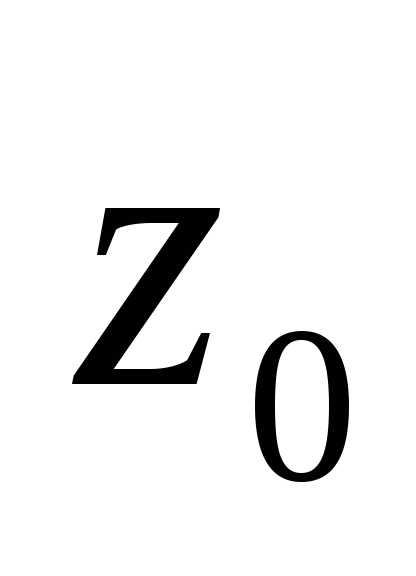 равен коэффициенту при минус первой
степени в лорановском разложении
равен коэффициенту при минус первой
степени в лорановском разложении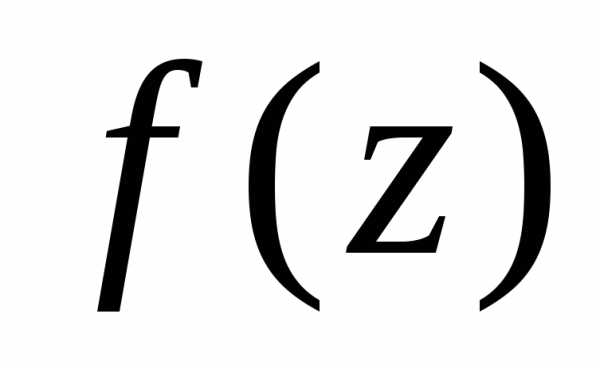 в окрестности точки
в окрестности точки :
:
.
Это утверждение справедливо для всех типов изолированных точек, и поэтому в данном случае определять тип особой точки не обязательно.
2) вычет в устранимой особой точке равен нулю.
3)
если 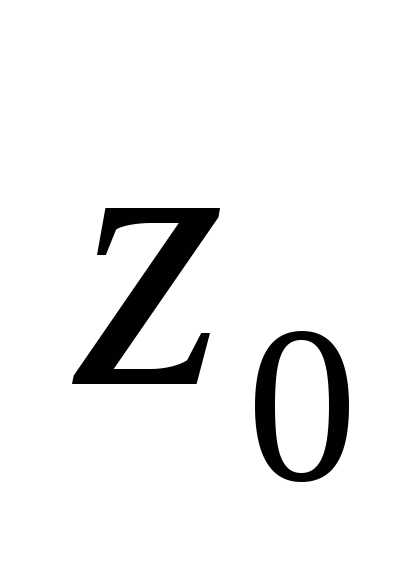 — простой полюс (полюс первого порядка),
а функцию
— простой полюс (полюс первого порядка),
а функцию можно
представить в виде
можно
представить в виде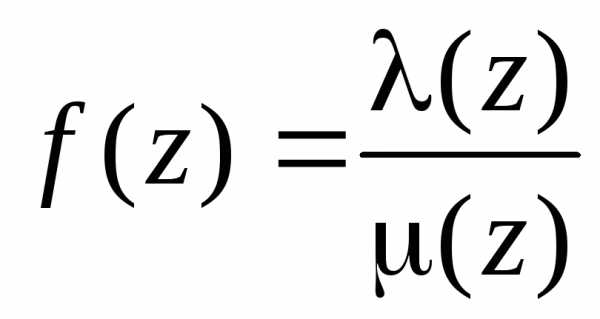 ,
где
,
где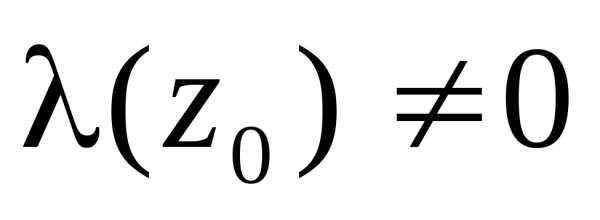 ,
, (заметим, что в этом случае
(заметим, что в этом случае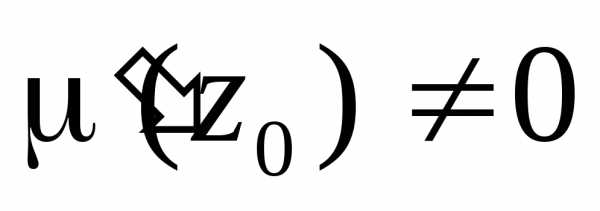 ),
тогда вычет в точке
),
тогда вычет в точке равен
равен
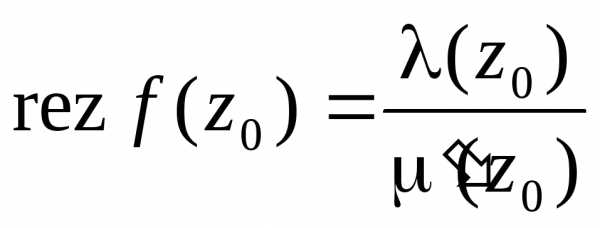 .
.
В
частности, если 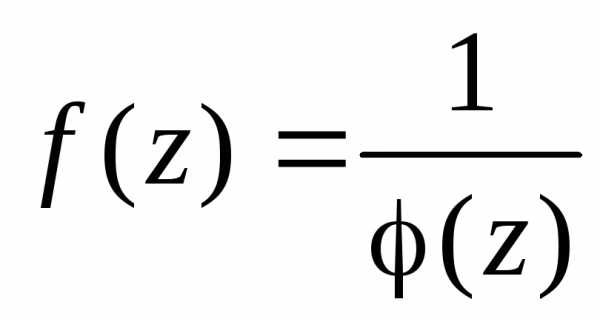 ,
то
,
то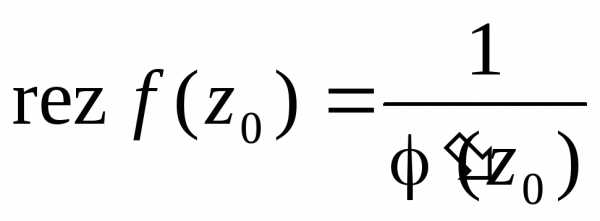 .
.
4)
если 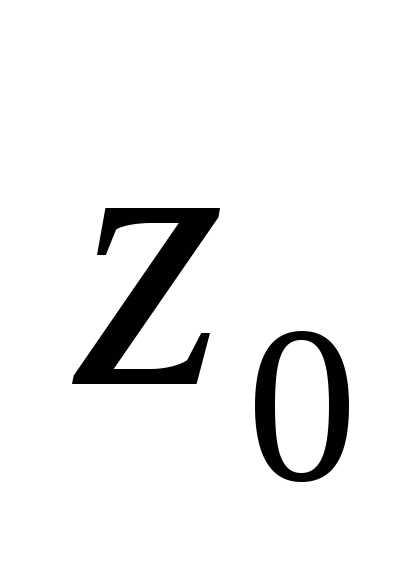 — простой полюс, то
— простой полюс, то
. | (4.6) |
5)
если 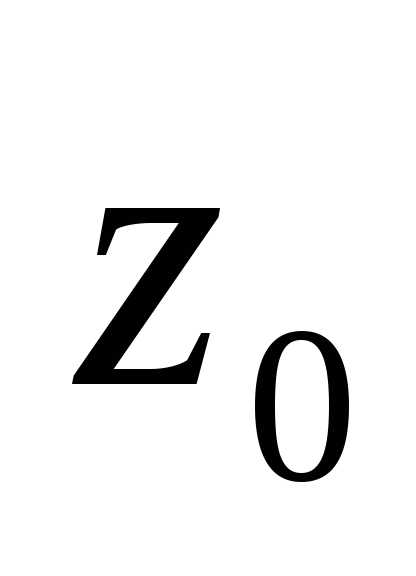 — полюс
— полюс го
порядка функции
го
порядка функции ,
то
,
то
. | (4.7) |
Пример 4.7. Вычислить интеграл .
Тогда по формуле (4.7) находим вычет в этой точке:
.
В силу теоремы 4.1 находим
.
studfiles.net
Комплексные числа
Напомним необходимые сведения о комплексных числах.
Комплексное число — это выражение вида a + bi, где a, b — действительные числа, а i — так называемая мнимая единица, символ, квадрат которого равен –1, то есть i2 = –1. Число a называется действительной частью, а число b — мнимой частью комплексного числа z = a + bi. Если b = 0, то вместо a + 0i пишут просто a. Видно, что действительные числа — это частный случай комплексных чисел.
Арифметические действия над комплексными числами те же, что и над действительными: их можно складывать, вычитать, умножать и делить друг на друга. Сложение и вычитание происходят по правилу (a + bi) ± (c + di) = (a ± c) + (b ± d)i, а умножение — по правилу (a + bi) · (c + di) = (ac – bd) + (ad + bc)i (здесь как раз используется, что i2 = –1). Число = a – bi называется комплексно-сопряженным к z = a + bi. Равенство z · = a2 + b2 позволяет понять, как делить одно комплексное число на другое (ненулевое) комплексное число:
.(Например, .)
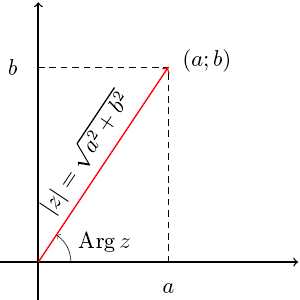
У комплексных чисел есть удобное и наглядное геометрическое представление: число z = a + bi можно изображать вектором с координатами (a; b) на декартовой плоскости (или, что почти то же самое, точкой — концом вектора с этими координатами). При этом сумма двух комплексных чисел изображается как сумма соответствующих векторов (которую можно найти по правилу параллелограмма). По теореме Пифагора длина вектора с координатами (a; b) равна . Эта величина называется модулем комплексного числа z = a + bi и обозначается |z|. Угол, который этот вектор образует с положительным направлением оси абсцисс (отсчитанный против часовой стрелки), называется аргументом комплексного числа z и обозначается Arg z. Аргумент определен не однозначно, а лишь с точностью до прибавления величины, кратной 2π радиан (или 360°, если считать в градусах) — ведь ясно, что поворот на такой угол вокруг начала координат не изменит вектор. Но если вектор длины r образует угол φ с положительным направлением оси абсцисс, то его координаты равны (r · cos φ; r · sin φ). Отсюда получается тригонометрическая форма записи комплексного числа: z = |z| · (cos(Arg z) + i sin(Arg z)). Часто бывает удобно записывать комплексные числа именно в такой форме, потому что это сильно упрощает выкладки. Умножение комплексных чисел в тригонометрической форме выглядит очень просто: z1 · z2 = |z1| · |z2| · (cos(Arg z1 + Arg z2) + i sin(Arg z1 + Arg z2)) (при умножении двух комплексных чисел их модули перемножаются, а аргументы складываются). Отсюда следуют формулы Муавра: zn = |z|n · (cos(n · (Arg z)) + i sin(n · (Arg z))). С помощью этих формул легко научиться извлекать корни любой степени из комплексных чисел. Корень n-й степени из числа z — это такое комплексное число w, что wn = z. Видно, что , а , где k может принимать любое значение из множества {0, 1, …, n – 1}. Это означает, что всегда есть ровно n корней n-й степени из комплексного числа (на плоскости они располагаются в вершинах правильного n-угольника).
Далее: Фрактальные размерности
elementy.ru
Комплексные числа — Циклопедия
Комплексные числа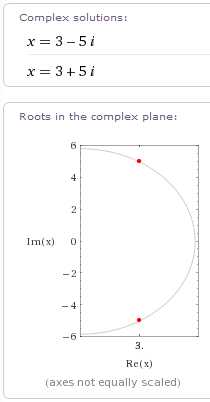 Комплексная плоскость (в программе Wolfram Mathematica)
Комплексная плоскость (в программе Wolfram Mathematica)Комплексные числа (complexus — «соплетённый», составной, сложный) — математическая концепция чисел-сумм вещественного и чисто мнимого числа — вещественного множителя абстрактной квази-величины мнимая единица i, которая инверсивно определяется через утверждение, что её квадрат равен минус единице.
Более формально: комплексное число — это число, которое записывается в алгебраической форме в виде [math]a + b \cdot i[/math], где a и b — любые вещественные чи́сла, и считается, что для числа́ [math]i[/math] выполняется тождество [math]i^2=-1[/math].
Множество комплексных чисел в традиционной нотации обозначается зна́ком [math]\mathbb C[/math].
Комплексные числа появились в XVI веке, когда математики попытались решить квадратные уравнения с отрицательными дискриминантами (такие уравнения не имеют вещественных корней). Оказалось, что квадратный корень из отрицательного числа приходится извлекать при решении кубического уравнения по формуле, хотя все корни исходного кубического уравнения могут быть вещественными. Тогда же появилось описание действий над комплексными числами в их современном понимании (эти действия было необходимо проводить с комплексными числами для корректного решения кубического уравнения по формуле).
Значимый вклад в теорию комплексных чисел внес великий математик Леонард Эйлер (XVIII век), разработавший привычные алгебраическую, тригонометрическую и показательную записи комплексного числа. В XIX веке появилось отображение комплексных чисел на координатной плоскости, методы комплексного анализа.
Основная теорема алгебры утверждает, что всякий многочлен n-й степени с комплексными коэффициентами может быть разложен на n линейных сомножителей, и, таким образом, у всякого полиномиального уравнения n-й степени есть n корней в поле комплексных чисел с учетом их кратностей (до появления комплексных чисел у полиномиального уравнения могло не быть корней вовсе).
В алгебраической форме комплексное число записывается как [math]a + b \cdot i[/math], где под [math]i[/math] понимается [math]\sqrt{-1}[/math], то есть выполняется тождество [math]i^2=-1[/math]. Мнимая часть появляется при извлечении квадратного корня из отрицательного вещественного числа: [math]\sqrt{-16} = \sqrt{-1 \cdot 16} = \sqrt{16} \cdot i = ±4 \cdot i[/math].
Над комплексными числами можно проводить операции сложения (вычитания), умножения (по правилам перемножения многочленов), деления.
Формула деления комплексных чисел:
- [math]\frac{a + bi}{c + di} = \frac{(a + bi)(c — di)}{(c + di)(c — di)} = \frac{ac + bd}{c^2 + d^2} + \frac{bc — ad}{c^2 + d^2}i[/math],
то есть для каждого ненулевого комплексного число можно найти обратное к нему по умножению.
Поэтому они образуют поле, которое расширяет поле вещественных чисел: [math]\mathbb{R} \subset \mathbb{C}[/math]. Вещественные числа в этой модели — комплексные, коэффициент при мнимой части которых равен 0.
Пара сопряженных комплексных чисел является решением квадратного уравнения при [math]D \lt 0[/math]. Например, в уравнении [math]x² + 6x + 34 = 0[/math] имеем [math]D = −100[/math]; в таком случае [math]\sqrt{D} = ±10i[/math], где [math]i = \sqrt{-1}[/math]. Решения уравнения, соответственно [math]-3 ± 5i[/math].
Сумма и произведение сопряженных комплексных чисел представляют собой вещественные числа.
Комплексные числа изучаются в специальном разделе математического анализа — комплексном анализе, в алгебре они доставляют пример алгебраически замкнутого поля, имеют значительное применение в физике.
[править] Геометрическая интерпретация
Комплексное число z = a + bi может быть изображено точкой (a; b) на комплексной плоскости, на которой по оси x располагаются вещественные числа, по оси y — чисто мнимые.
Тригонометрическая форма отражает вектор, отложенный от начала координат до этой точки.
Тригонометрическая форма комплексного числа: [math]z = \left | z \right | \cdot (\cos \varphi + i \sin \varphi)[/math], где |z| («модуль z») — расстояние на комплексной плоскости от начала координат до точки, обозначающей число z, а «аргумент» [math]\varphi[/math] = [math]\operatorname{arctg}\ \frac{b}{a}[/math] (если [math]a \gt 0[/math]), [math]\pi + \operatorname{arctg}\ \frac{b}{a}[/math] (если [math]a \lt 0 \wedge b \gt 0[/math]) и [math]-\pi + \operatorname{arctg}\ \frac{b}{a}[/math] (если [math]a \lt 0 \wedge b \lt 0[/math]).
При возведении комплексного числа в степень достаточно возвести только его модуль, а аргумент [math]\varphi[/math] домножить на показатель степени:
- [math]z^k = \left ({\left | z \right | \cdot (\cos \varphi + i \sin \varphi)}\right )^k = \left | z \right |^k \cdot (\cos k\varphi + i \sin k\varphi)[/math]
Показательная форма комплексного числа, открытая Эйлером: [math]z = r \cdot e^{i\varphi}[/math], где r — модуль комплексного числа, а [math]\varphi[/math] — его аргумент.
[править] Операции с комплексными числами
- Абрамович М. И., Стародубцев М. Т. Математика (геометрия и тригонометрические функции). М., 1976.
cyclowiki.org
Комплексные числа: определения и основные понятия
ОПРЕДЕЛЕНИЕ Комплексные числа – это числа вида , где – действительные числа, – мнимая единица, удовлетворяющая соотношению .Число называется действительной частью комплексного числа и имеет обозначение .
Число называется мнимой частью комплексного числа и имеет обозначение .
Например. — комплексное число, действительной частью которого является вещественное число , а мнимой частью – вещественное число .
Если действительная часть комплексного числа равна нулю комплексное число называется чисто мнимым.
Например. , где .
Комплексные числа являются расширением действительных (вещественных) чисел. Любое действительное число может быть записано в форме комплексного числа: .
Например. Комплексные числа обозначают действительное число .
Равенство комплексных чисел
ОПРЕДЕЛЕНИЕ Два комплексных числа и называются равными, если , т.е. равны их действительные и мнимые части.В противном случае комплексные числа называются неравными.
ПРИМЕР| Задание | Определить, при каких и два комплексных числа и являются равными. |
| Решение | По определению два комплексных числа являются равными, если равны их действительные и мнимые части, т.е. . |
| Ответ |
Комплексно сопряженные числа
ОПРЕДЕЛЕНИЕ Сопряженным (или комплексно сопряженным) числом к комплексному числу называется число . ПРИМЕР| Задание | Найти для комплексного числа его сопряженное число. |
| Решение | Комплексно сопряженным числом является число вида . Действительной частью комплексного числа является число , мнимой частью является .
Следовательно, сопряженное число имеет вид: . |
| Ответ |
Подробнее про комплексно сопряженные числа читайте в отдельной статье: Комплексно сопряженные числа.
Противоположные комплексные числа
ОПРЕДЕЛЕНИЕ Противоположным к комплексному числу является комплексное число . ПРИМЕР| Задание | Найти противоположное число к комплексному числу . |
| Решение | Действительной частью комплексного числа является число , мнимой частью – число .
Следовательно, противоположным числом будет являться число . |
| Ответ |
Формы записи комплексных чисел
Алгебраическая форма КЧ
Тригонометрическая форма КЧ
Показательная форма КЧ
Модуль комплексного числа
Комплексно сопряженные числа
ru.solverbook.com
Основы теории комплексных чисел — КиберПедия
Студент должен:
знать:-определение мнимой единицы;
— определение комплексного числа;
— формы комплексного числа;
—действия над комплексными числами;
— геометрическую интерпретацию комплексных чисел.
уметь: — вычислять степени мнимой единицы;
— переходить от одной формы записи комплексного числа к другой;
— выполнять действия над комплексными числами в алгебраической ,
тригонометрической и показательной формах ;
— изображать комплексное число в виде вектора.
Определение мнимой единицы. Степени мнимой единицы. Определение комплексного числа. Алгебраическая форма комплексного числа. Равенство комплексных чисел. Комплексно-сопряженные числа. Действия над комплексными числами в алгебраической форме. Геометрическая интерпретация комплексного числа. Тригонометрическая форма записи комплексного числа.. Действия над комплексными числами в тригонометрической форме. Показательная форма записи комплексного числа. Действия над комплексными числами в показательной форме.
Методические указания.
Данную тему рекомендуется начать с определения мнимой единицы и степеней мнимой единицы. Далее необходимо определить комплексное число в алгебраической форме. Изучить арифметические действия над комплексными числами в алгебраической форме. Перед изучением деления вводится понятие комплексно- сопряженного числа. Через геометрическую интерпретацию вводится тригонометрическая форма комплексного числа. Далее необходимо выделить алгоритм перехода от алгебраической формы к тригонометрической форме. В тригонометрической форме изучить умножение, деление, возведение в степень и извлечение корня. Перед введением показательной формы необходимо изучить формулы Эйлера. Отработать технику перехода от тригонометрической формы в показательную форму, показательной формы в тригонометрическую форму и алгебраическую форму. Перед изучением действий в показательной форме нужно повторить действия над степенями.
Вопросы для самоконтроля.
1.Дайте определение мнимой единицы.
2. Сформулируйте алгоритм вычисления степени мнимой единицы.
3. Дайте определение комплексного числа.
4.Что называют действительной (мнимой) частью комплексного числа?
5. Когда комплексные числа равны?
6. Как складываются комплексные числа?
7. Как найти разность комплексных чисел?
8. Как умножаются комплексные числа?
9. Какие числа называются комплексно-сопряженными?
10. Как изобразить комплексное число на координатной плоскости?
11. Что такое аргумент, модуль комплексного числа?
12. Как перейти из алгебраической формы в тригонометрическую форму?
13. Какие действия выполняем над комплексными числами в тригонометрической форме? Каким образом (формулы)?
14. Как записываются формулы Эйлера.
15. Сформулируйте правило перехода из тригонометрической формы в показательную форму.
16. Сформулируйте правило перехода из алгебраической формы в показательную форму и обратно.
17. Сформулируйте правила действия над комплексными числами в показательной форме.
Раздел 3
Основные понятия и методы математического анализа
Тема3.1 Функции, пределы, непрерывность
Студент должен:
знать:-определение функции;
— область определения и область значения функции;
—основные свойства функции;
—определения предела функции;
— замечательные пределы;
— непрерывность и точки разрыва функции..
уметь: — находить область определения функции;
— определять основные свойства заданной функции;
— вычислять предел функции ;
— раскрывать неопределенности;
— исследовать функцию на непрерывность и квалифицировать точки
разрыва;
Определение функции. Область определения и область значения функции. Четность нечетность функции. Промежутки знакопостоянства функции. Промежутки монотонности функции. Точки пересечения с координатными осями.
Определения предела функции. Односторонние пределы. Теоремы о пределах функции. Неопределенности. Бесконечно малые и бесконечно большие функции. Два замечательных предела. Вычисление пределов и раскрытие неопределенностей.
Непрерывность и точки разрыва функции.
Методические указания.
При изучении данной темы сначала рассматривают определение функции, ее свойства на примерах элементарных функций, затем уже обобщают понятия. Определение предела функции и его смысла рассматривать лучше графически. Для вычисления пределов и раскрытия неопределенностей используют алгебраические преобразования и эквивалентные функции, а так же два замечательных предела.
Вопросы для самоконтроля.
1. Дайте определение функции.
2. Дайте определение области определения и области значения функции.
3. Как исследовать функцию на четность нечетность?
4. Как найти точки пересечения с координатными осями?
5. Что такое промежутки знакопостоянства и монотонности функции?
6. Дайте определение предела функции.
7. Как находят левый и правый пределы функции?
8. Сформулируйте теоремы о пределах функции и следствия из них.
9. Что такое неопределенность. Какие неопределенности знаете?
10. Дайте определения бесконечно больших и бесконечно малых функции.
11. Какими свойствами они связаны?
12. Какие пределы называют замечательными?
13. Дайте определение непрерывной функции.
14.Как классифицируют точки разрыва функции?
cyberpedia.su
