| 1 | Найти точное значение | sin(30) | |
| 2 | Найти точное значение | sin(45) | |
| 3 | Найти точное значение | sin(30 град. ) | |
| 4 | Найти точное значение | sin(60 град. ) | |
| 5 | Найти точное значение | tan(30 град. ) | |
| 6 | Найти точное значение | arcsin(-1) | |
| 7 | Найти точное значение | sin(pi/6) | |
| 8 | Найти точное значение | cos(pi/4) | |
| 9 | Найти точное значение | sin(45 град.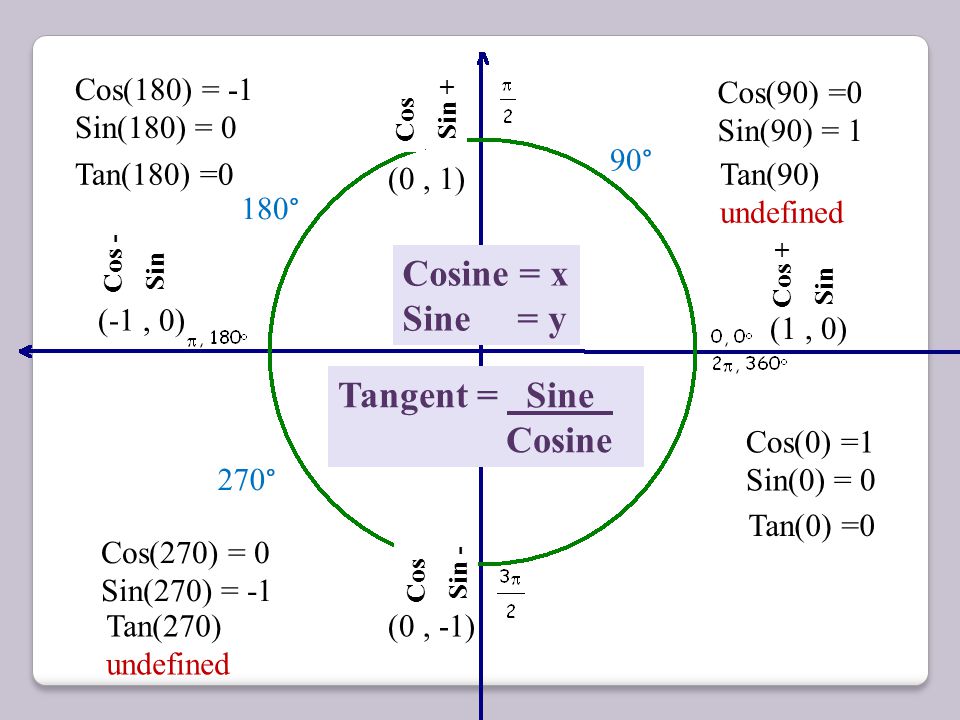 ) ) |
|
| 10 | Найти точное значение | sin(pi/3) | |
| 11 | Найти точное значение | arctan(-1) | |
| 12 | Найти точное значение | cos(45 град. ) | |
| 13 | Найти точное значение | cos(30 град. ) | |
| 14 | Найти точное значение | tan(60) | |
| 15 | Найти точное значение | csc(45 град. ) | |
| 16 | Найти точное значение | tan(60 град.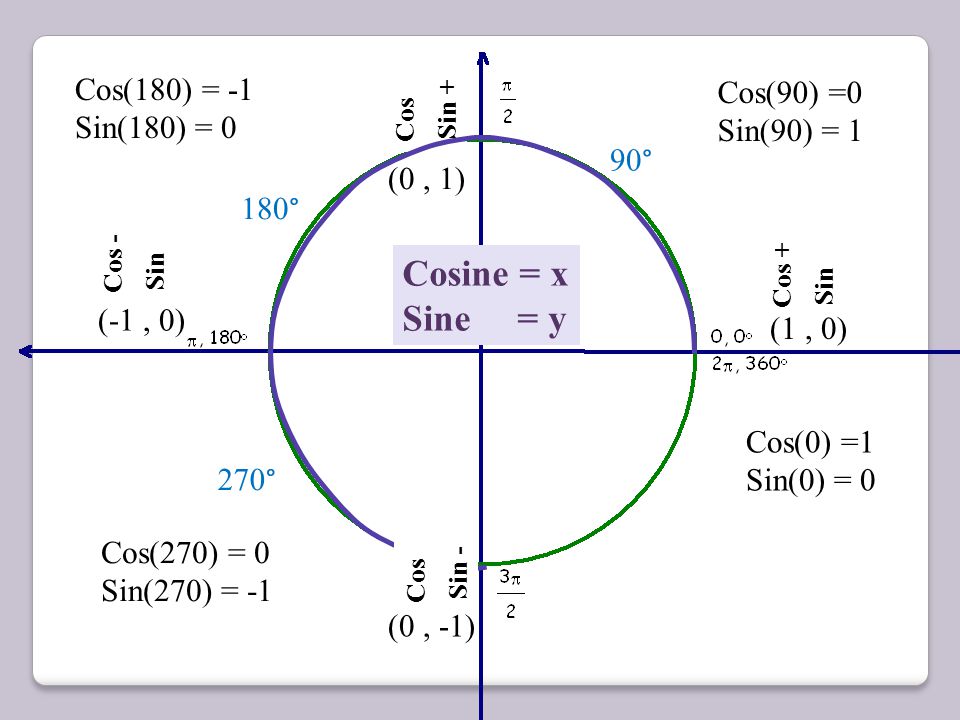 ) ) |
|
| 17 | Найти точное значение | sec(30 град. ) | |
| 18 | Найти точное значение | cos(60 град. ) | |
| 19 | Найти точное значение | ||
| 20 | Найти точное значение | sin(60) | |
| 21 | Найти точное значение | cos(pi/2) | |
| 22 | Найти точное значение | tan(45 град. ) | |
| 23 | Найти точное значение | arctan(- квадратный корень 3) | |
| 24 | Найти точное значение | csc(60 град. ) ) |
|
| 25 | Найти точное значение | sec(45 град. ) | |
| 26 | Найти точное значение | csc(30 град. ) | |
| 27 | Найти точное значение | sin(0) | |
| 28 | Найти точное значение | sin(120) | |
| 29 | Найти точное значение | cos(90) | |
| 30 | Преобразовать из радианов в градусы | pi/3 | |
| 31 | Найти точное значение | tan(30) | |
| 32 | Преобразовать из градусов в радианы | 45 | |
| 33 | Найти точное значение | cos(45) | |
| 34 | Упростить | sin(theta)^2+cos(theta)^2 | |
| 35 | Преобразовать из радианов в градусы | pi/6 | |
| 36 | Найти точное значение | cot(30 град.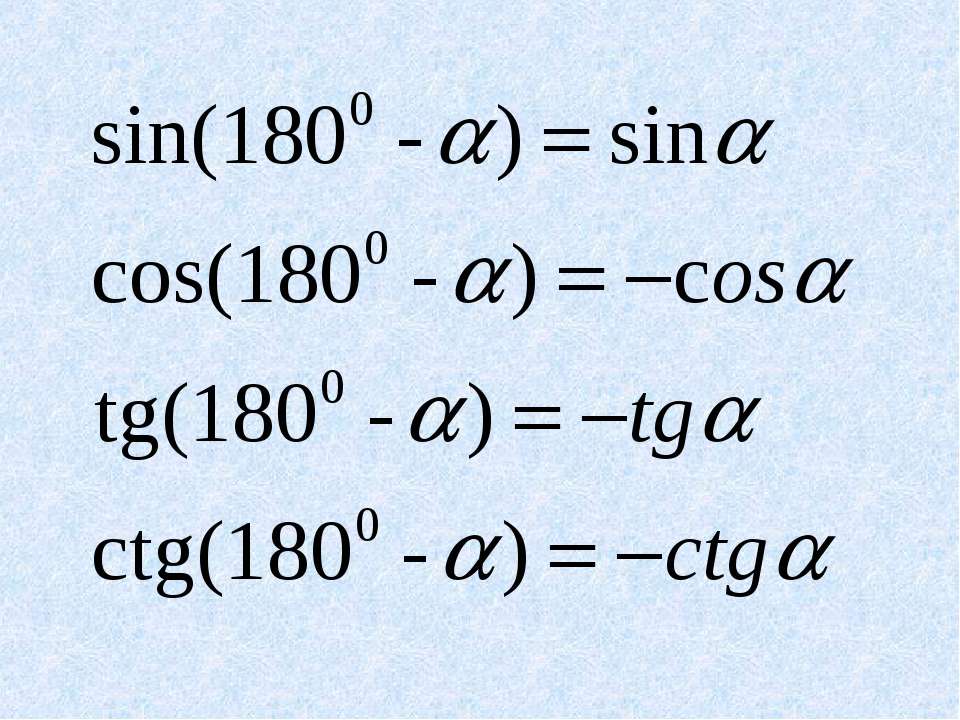 ) ) |
|
| 37 | Найти точное значение | arccos(-1) | |
| 38 | Найти точное значение | arctan(0) | |
| 39 | Найти точное значение | cot(60 град. ) | |
| 40 | Преобразовать из градусов в радианы | 30 | |
| 41 | Преобразовать из радианов в градусы | (2pi)/3 | |
| 42 | Найти точное значение | sin((5pi)/3) | |
| 43 | Найти точное значение | sin((3pi)/4) | |
| 44 | Найти точное значение | tan(pi/2) | |
| 45 | Найти точное значение | sin(300) | |
| 46 | Найти точное значение | cos(30) | |
| 47 | Найти точное значение | cos(60) | |
| 48 | Найти точное значение | cos(0) | |
| 49 | Найти точное значение | cos(135) | |
| 50 | Найти точное значение | cos((5pi)/3) | |
| 51 | Найти точное значение | cos(210) | |
| 52 | Найти точное значение | sec(60 град.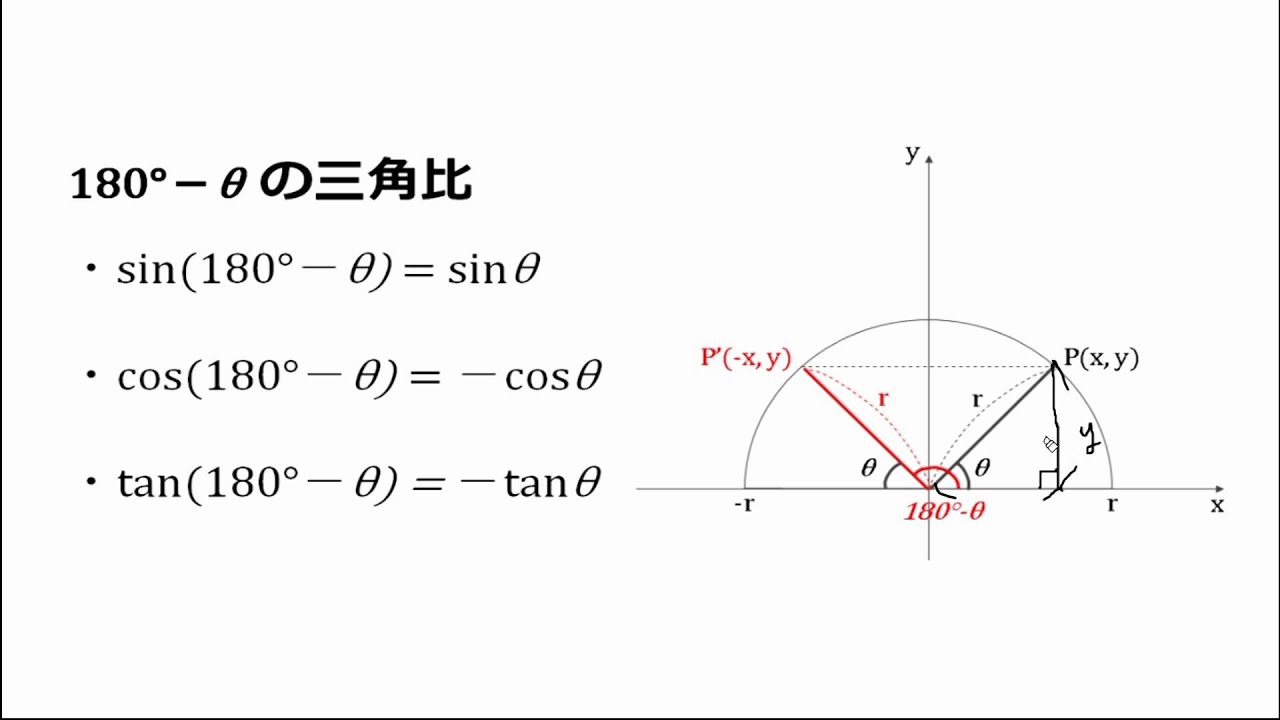 ) ) |
|
| 53 | Найти точное значение | sin(300 град. ) | |
| 54 | Преобразовать из градусов в радианы | 135 | |
| 55 | Преобразовать из градусов в радианы | 150 | |
| 56 | Преобразовать из радианов в градусы | (5pi)/6 | |
| 57 | Преобразовать из радианов в градусы | (5pi)/3 | |
| 58 | Преобразовать из градусов в радианы | 89 град. | |
| 59 | Преобразовать из градусов в радианы | 60 | |
| 60 | Найти точное значение | sin(135 град. ) ) |
|
| 61 | Найти точное значение | sin(150) | |
| 62 | Найти точное значение | sin(240 град. ) | |
| 63 | Найти точное значение | cot(45 град. ) | |
| 64 | Преобразовать из радианов в градусы | (5pi)/4 | |
| 65 | Найти точное значение | sin(225) | |
| 66 | Найти точное значение | sin(240) | |
| 67 | Найти точное значение | cos(150 град. ) ) |
|
| 68 | Найти точное значение | tan(45) | |
| 69 | Вычислить | sin(30 град. ) | |
| 70 | Найти точное значение | sec(0) | |
| 71 | Найти точное значение | cos((5pi)/6) | |
| 72 | Найти точное значение | csc(30) | |
| 73 | Найти точное значение | arcsin(( квадратный корень 2)/2) | |
| 74 | Найти точное значение | tan((5pi)/3) | |
| 75 | Найти точное значение | tan(0) | |
| 76 | Вычислить | sin(60 град. ) ) |
|
| 77 | Найти точное значение | arctan(-( квадратный корень 3)/3) | |
| 78 | Преобразовать из радианов в градусы | (3pi)/4 | |
| 79 | Найти точное значение | sin((7pi)/4) | |
| 80 | arcsin(-1/2) | ||
| 81 | Найти точное значение | sin((4pi)/3) | |
| 82 | Найти точное значение | csc(45) | |
| 83 | Упростить | arctan( квадратный корень 3) | |
| 84 | Найти точное значение | sin(135) | |
| 85 | Найти точное значение | sin(105) | |
| 86 | Найти точное значение | sin(150 град. ) ) |
|
| 87 | Найти точное значение | sin((2pi)/3) | |
| 88 | Найти точное значение | tan((2pi)/3) | |
| 89 | Преобразовать из радианов в градусы | pi/4 | |
| 90 | Найти точное значение | sin(pi/2) | |
| 91 | Найти точное значение | sec(45) | |
| 92 | Найти точное значение | cos((5pi)/4) | |
| 93 | cos((7pi)/6) | ||
| 94 | Найти точное значение | arcsin(0) | |
| 95 | Найти точное значение | sin(120 град. ) ) |
|
| 96 | Найти точное значение | tan((7pi)/6) | |
| 97 | Найти точное значение | cos(270) | |
| 98 | Найти точное значение | sin((7pi)/6) | |
| 99 | Найти точное значение | arcsin(-( квадратный корень 2)/2) | |
| 100 | Преобразовать из градусов в радианы | 88 град. |
Урок по теме «Формулы приведения». 9-й класс
Цели урока:
Учебная цель:
- научить применять формулы приведения для нахождения синусов, косинусов и тангенсов углов больших 900;
- повторить нахождение синусов, косинусов и тангенсов острых углов по таблице Брадиса, а также их значения для углов 00, 300, 450, 600, 900.

Развивающая цель:
- развитие внимания, мышления, памяти и воображения;
- работа над математической речью.
Воспитательная цель:
- развитие позитивной «Я-концепции» в каждом ученике;
- воспитание чувства ответственности, сопереживания, внимательного и терпеливого отношения к окружающим;
- умение сдерживать отрицательные эмоции и высказывать их тактично;
- формирование навыков умственного труда – поиск рационального пути выполнения задания.
Оборудование: учебник «Геометрия 7–9 » Л.С. Атанасяна, таблицы Брадиса, надписи с заданиями и ответами, таблица с единичными окружностями.
План урока:
- Рефлексия настроения
- Обсуждение темы и целей занятия
- Актуализация знаний, умений, навыков:
- обучающая самостоятельная работа с проверкой у доски
- формулировка правила
- чертеж – шпаргалка
- Закрепление формул приведения на примерах
- Психологическая разгрузка (стихотворение)
- Самостоятельная работа
- обучающая с проверкой у доски
- проверка знаний каждого ученика
- Итог урока
- Рефлексия результативности, настроения
 Рефлексия настроения
Рефлексия настроенияЗдравствуйте, ученики! Я рада вас видеть!
Желаю вам успехов на сегодняшнем непростом занятии – в освоении синусов, косинусов и тангенсов углов.
II. Обсуждение темы и целей занятияНа прошлом уроке мы познакомились с формулами приведения. Сегодня наша цель – научиться их применять. Откроем тетради, запишем число и тему урока.
Задание: на доске
а) используя таблицу Брадиса (стр. 52), найти:
| sin 20°, | ответ (0,3420) | |
| cos 70°, | ответ (0,3420) | |
| sin 30°, | ответ (0,5000) | |
| cos 60°. | ответ (0,5000) |
б) как можно найти по-другому:
| sin 30°, | ответ (1/2) | |
cos 60°. |
ответ (1/2) |
Для нахождения синусов, косинусов, тангенсов углов 00, 300, 450, 600, 900 можно воспользоваться таблицей, неплохо было бы ее запомнить.
в) найти:
sin 120°,
cos 210°.
Вот для этого случая и нужны формулы приведения. Вспомним их.
III Актуализация знаний, умений, навыков:
Вспомним звучание формул.
Чтобы найти синус, косинус, тангенс углов больших 900, надо
1) заменить этот угол суммой
90° + α; 180° + α; 270° + α; 360° + α…
(или разностью 180° — α; 270° — α; 360° — α…).
2) определить какой знак «+» или «-» имеет искомое значение в зависимости от нахождения в четверти.
3) изменить sinα на cosα, если есть 90° или 270°
cosα на sinα
tgα на сtgα
не менять функцию, если есть 180° или 360°.
Лучше сориентироваться поможет рисунок-шпаргалка. Вспомним основные моменты его построения.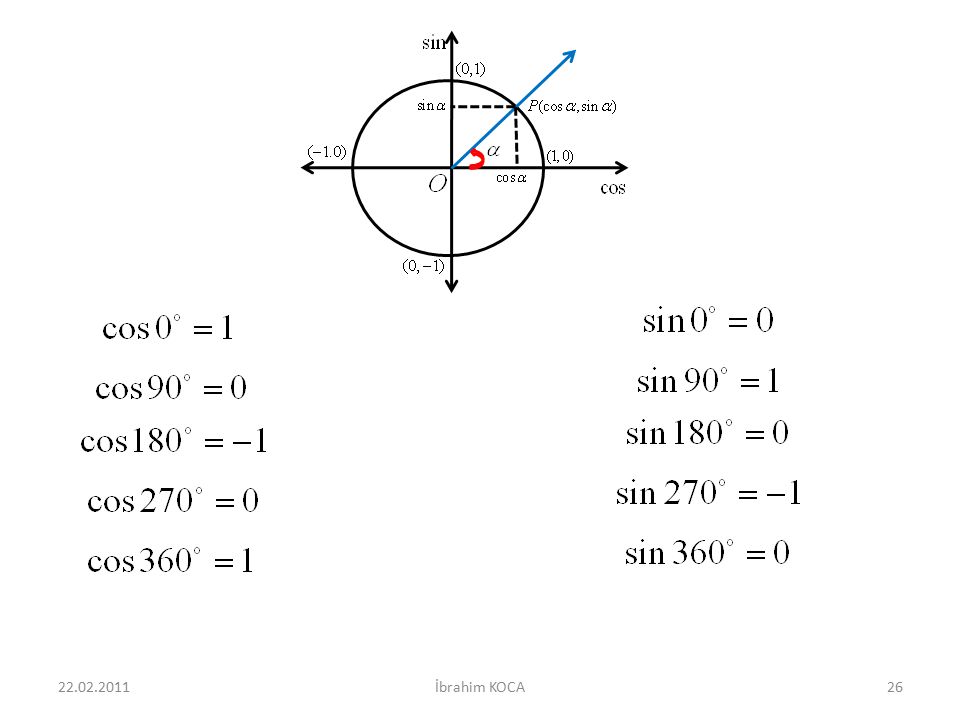
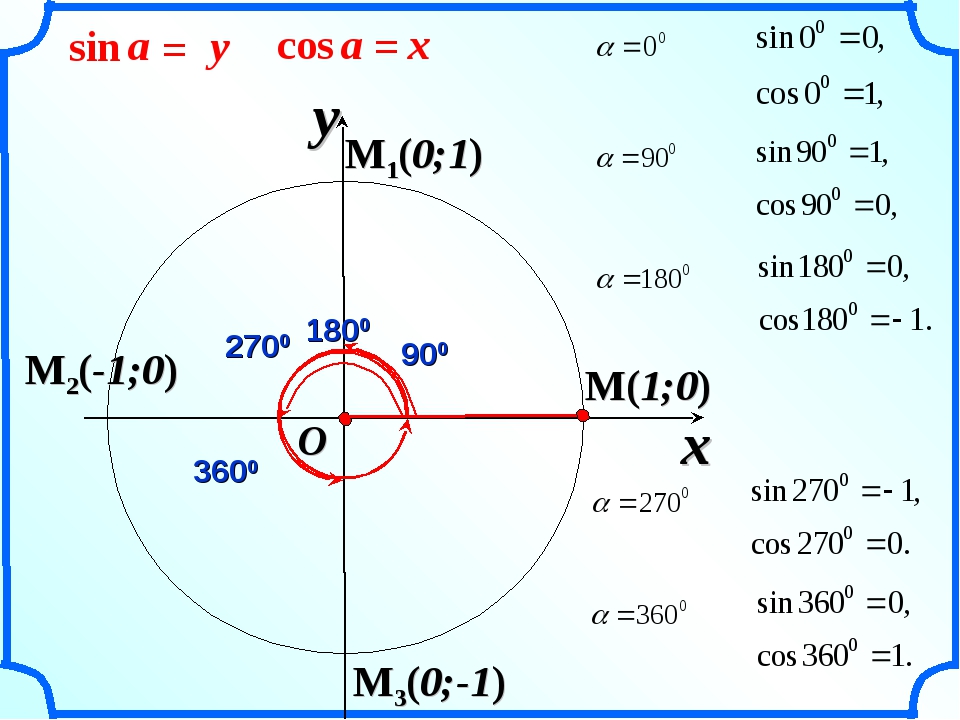
Рисунок – Единичная окружность и координаты точек
Вопросы к классу:
- Почему окружность называется единичной?
- Назвать координаты точек пересечения окружности с осями координат.
- Какие знаки имеют абсциссы и ординаты всех точек, лежащих в первой четверти, второй, третьей, четвертой?
- Какое местоположение точки считается начальным?
- Какой угол считаем положительным, а какой отрицательным?
- С какой координатой точки совпадает sinα, с какой – cosα?
Вернемся к заданию в).
I вариант решения: sin 120° = sin (90° + 30°) = +cos 30° = /2
II вариант решения: sin 120° = sin (180° 60°) = +sin 60° = /2
I вариант решения: cos 210° = cos (180° + 30°) = — cos 30° = — /2
II вариант решения: cos 210° = cos (270° — 60°) = — sin 60° = — /2
IV. Закрепление формул приведения на примерахВернемся к примеру в тетради и на доске. (Ученик выполняет под руководством учителя задание).
(Ученик выполняет под руководством учителя задание).
а) sin 110° = sin (90°+ 20°) = cos 20° ≈ 0,9397
или sin 110° = sin (180° — 70°) = sin 70°≈ 0,9397
б) cos 200° = cos (180° + 20°) = — cos 20°≈ — 0,9397
или cos 200° = cos (270° — 70°) = — sin 70° ≈ — 0,9397
V. Психологическая разгрузка (стихотворение)Научись встречать беду не плача:
Горький миг – не зрелище для всех.
Знай: душа растет при неудачах
И слабеет, если скор успех.
Мудрость обретают в трудном споре,
Предначертан путь нелегкий твой
По спирали радости и горя,
А не вверх взмывающей кривой.
Вдумайтесь в слова этого стихотворения и возьмите себе на вооружение.
VI. Самостоятельная работа1) обучающая работа с проверкой у доски
Учебник стр. 241 № 1016.
- cos 120° = cos (90° + 30°) = — sin 30° = — 1/2
- sin 120° = sin (90° + 30°) = cos 30° = /2
- tg 120° = tg (90° + 30°) = — ctg 30° = —
или
- cos 120° = cos (180° — 60°) = — cos 60° = — 1/2
- sin 120° = sin (180° — 60°) = sin 60° = /2
- tg 120° = tg (180° — 60°) = — tg 60° = —
2) проверка знаний каждого ученика
- cos 135° = cos (90° + 45°) = — sin 45° = — /2
- sin 135° = sin (90° + 45°) = cos 45° = /2
- tg 135° = tg (90° + 45°) = — ctg 45° = — 1
или
VII.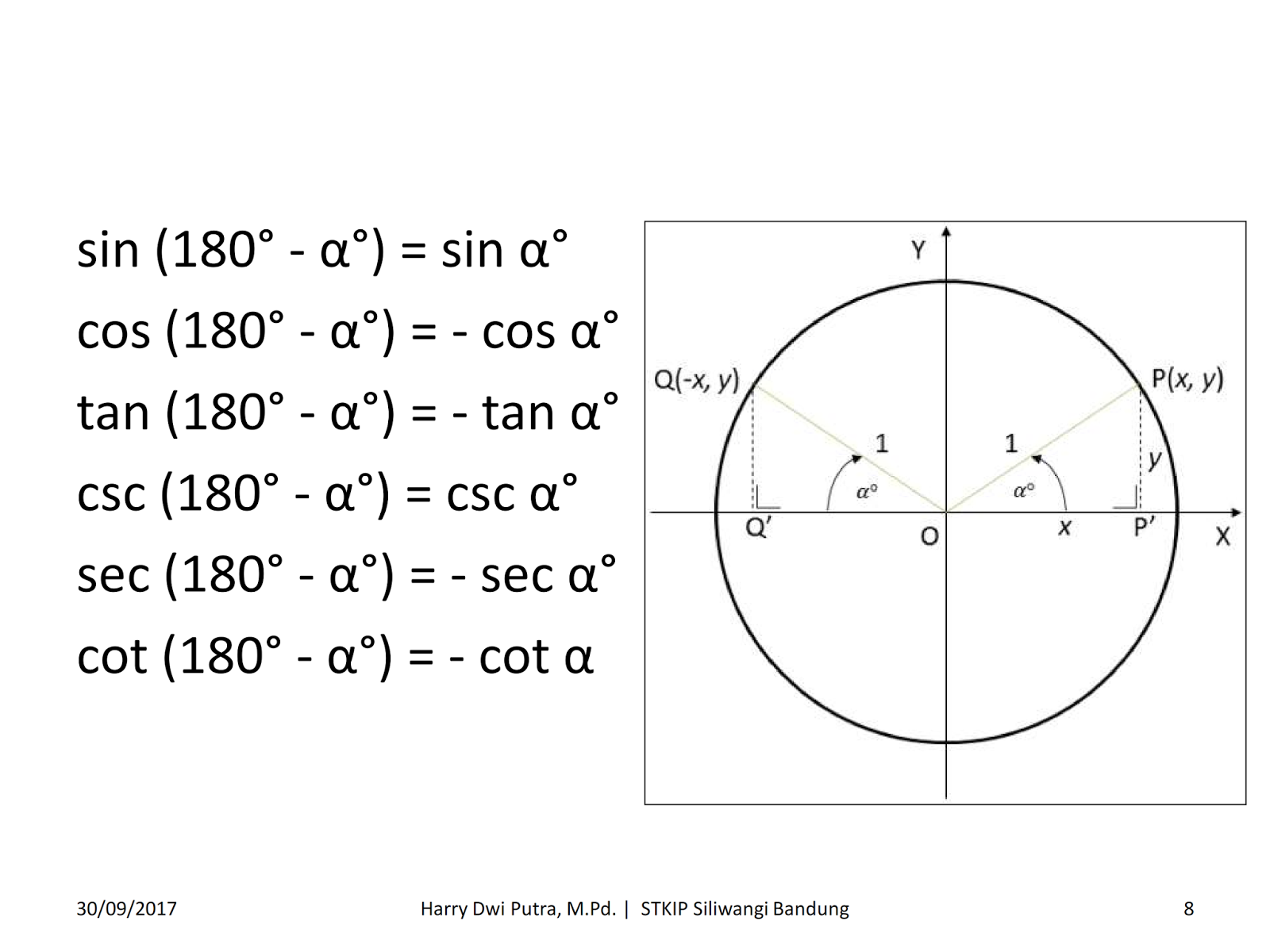 Итог урока
Итог урокаВремя урока подходит к концу. Ребята, давайте вспомним, какова была цель нашего занятия. Как вы думаете, мы достигли этой цели? На следующих уроках нам потребуется умение находить синусы, косинусы, тангенсы углов больших 900, не только в геометрии, но и на уроках алгебры и физики.
VIII. Рефлексия результативности, настроенияЯ благодарю вас за урок. Вы подарили мне хорошее настроение, я надеюсь, что я вам тоже. До новой встречи.
Синус, косинус и тангенс угла — урок. Геометрия, 9 класс.
В системе координат построим полуокружность радиуса \(1\) с центром в начале координат.
Как уже известно, в прямоугольном треугольнике синус острого угла определяется как отношение противолежащего катета к гипотенузе, а косинус острого угла определяется как отношение прилежащего катета к гипотенузе.
В треугольнике \(AOX\):
sinα=AXAO;cosα=OXAO.
Так как радиус полуокружности \(R = AO = 1\), то sinα=AX;cosα=OX.
Длина отрезка \(AX\) равна величине координаты \(y\) точки \(A\), а длина отрезка \(OX\) равна величине координаты \(x\) точки \(A\):
Acosα;sinα.
Следовательно, для углов 0°≤α≤180° видно, что −1≤cosα≤1;0≤sinα≤1.
В прямоугольном треугольнике тангенс острого угла равен отношению противолежащего катета к прилежащему катету, а значит,
tgα=AXOX=sinαcosα.
Используя единичную полуокружность и рассмотренную информацию, определим синус, косинус и тангенс для 0°;90°;180°.
sin0°=0;cos0°=1;tg0°=0;sin90°=1;cos90°=0;tg90° не существует;sin180°=0;cos180°=−1;tg180°=0.
Рассмотрим оба острых угла в треугольнике \(AOX\). Если вместе они образуют 90°, то оба выразим через α.
Если sinα=AXAO;cosα=OXAO, то sin90°−α=OXAO;cos90°−α=AXAO.
Видим, что справедливы равенства:
cos90°−α=sinα;sin90°−α=cosα.
Рассмотрим тупой угол, который также выразим через α.
Справедливы следующие равенства:
sin180°−α=sinα;cos180°−α=−cosα.
Эти формулы называются формулами приведения:
cos90°−α=sinα;sin90°−α=cosα.
sin180°−α=sinα;cos180°−α=−cosα.
Если в треугольнике \(AOX\) применить теорему Пифагора, получаем AX2+OX2=1. Заменив отрезки соответственно синусом и косинусом, мы напишем
Главное тригонометрическое тождество
sin2α+cos2α=1.
Это тождество позволяет вычислить величину синуса угла, если дан косинус
(как уже отмечено, синус для углов 0°≤α≤180° только 0 или положительный):
sin2α+cos2α=1;sin2α=1−cos2α;sinα=1−cos2α
— или величину косинуса угла, если дан синус:
sin2α+cos2α=1;cos2α=1−sin2α;cosα=±1−sin2α.
Для острых углов косинус положительный, а для тупых углов берём отрицательное значение.
Значения тригонометрических функций разных углов
- Главная
- Алгебра
- Тригонометрия
- Значения тригонометрических функций разных углов
Рассмотрим значения тригонометрических функций углов от 0° до 360°. Углы изобразим на единичной окружности с радиусом единица. Одна сторона угла всегда будет совпадать с положительным направлением оси абсцисс, а другая будет перемещаться при росте угла против часовой стрелки.
Углы изобразим на единичной окружности с радиусом единица. Одна сторона угла всегда будет совпадать с положительным направлением оси абсцисс, а другая будет перемещаться при росте угла против часовой стрелки.
Синус
Синус угла — это высота, на которой оказалась точка пересечения второй стороны угла с единичной окружностью.
Для изображённого угла высота этой точки — 0,6. Значит синус этого угла равен 0,6.
При изменении угла от 0° до 360° синус изменяется. Когда угол равен нулю, его стороны схлопываются, как книжка, и совпадают с положительным направлением оси абсцисс, и вторая сторона пересекает единичную окружность на высоте 0, т.е. синус 0° равен 0. С увеличением угла синус возрастает, и синус 90° равен 1. Затем синус начинает уменьшаться, и синус 180° уже снова равен 0. Потом синус продолжает уменьшаться, и синус 270° уже равен –1. А после этого с дальнейшим увеличением угла синус обратно возрастает до нуля, и синус 360° уже равен 0.
Косинус
Косинус угла — это абсцисса точки пересечения второй стороны с единичной окружностью.
Косинус изображённого угла равен 0,7.
При изменении угла от 0° до 360° значение косинуса изменяется. Если угол равен нулю, то обе его стороны совпадают с положительным направлением оси абсцисс и пересекает единичную окружность в самой правой точке, у которой абсцисса равна единице. Т.е. косинус 0° равен 1. При росте угла косинус уменьшается, и косинус 90° уже равен 0. Потом косинус уменьшается ещё дальше при увеличении угла, и косинус 180° равен –1. Затем косинус снова увеличивается, и косинус 270° уже равен 0. Косинус продолжает увеличиваться, и косинус 360° уже снова равен 1.## ТангенсТангенс — это синус делённый на косинус. Чтобы найти значение тангенса, нужно построить дополнительную прямую, которая называется ось тангенсов. И масштаб на этой прямой выбирается такой же, как и на оси синусов и косинусов, т.е. отрезок, равный радиусу окружности, принимается за 1. Так вот тангенс угла — это высота, на которой продолжение 2й стороны угла пересекает ось тангенсов.
Для изображённого угла тангенс равен примерно 1,4.
В отличие от синуса и косинуса тангенс не ограничен плюс и минус единицей, и может принимать любые значения от минус до плюс бесконечности. Посмотрим, как изменяется тангенс при изменении угла от 0° до 360°. Если угол равен нулю, то вторая сторона его так же, как и первая, пересекает ось тангенсов на высоте 0, и тангенс 0° равен 0. При увеличении угла тангенс всегда возрастает. И в первой четверти до 90° он возрастает от 0 до +∞. И наконец, тангенс 90° не определён, потому что продолжение стороны не пересекает ось тангенсов. А когда угол увеличивается снова, то сторону нужно продолжать в другом направлении. Тангенс продолжает возрастать уже от –∞ до 0, и наконец тангенс 180° равен 0. Снова возрастает угол и снова возрастает тангенс уже от 0 до +∞ и тангенс 270° опять не определён. И при увеличении угла тангенс снова возрастает от –∞ до 0, и тангенс 360° равен нулю.## КотангенсКотангенс — это косинус деленный на синус. Чтобы определить значение котангенса, нужно построить дополнительную прямую. Она называется ось котангенсов. И масштаб на этой прямой выбирается так же, как и на оси синусов и косинусов — отрезок, равный радиусу окружности, принимается за 1. Так вот котангенс угла это абсцисса, на которой продолжение 2й стороны пересекает ось котангенсов. И для изображённого угла котангенс равен примерно 1,3.
Она называется ось котангенсов. И масштаб на этой прямой выбирается так же, как и на оси синусов и косинусов — отрезок, равный радиусу окружности, принимается за 1. Так вот котангенс угла это абсцисса, на которой продолжение 2й стороны пересекает ось котангенсов. И для изображённого угла котангенс равен примерно 1,3.
Посмотрим как меняется котангенс при изменении угла от 0° до 360°. И сразу возникает особенность — когда угол равен нулю, обе его стороны совпадают с положительным направлением оси абсцисс, и вторая сторона не пересекает ось котангенсов, и котангенс 0° не определён. При возрастании угла котангенс всё время убывает, и в первой четверти котангенс убывает от +∞ до 0. И котангенс 90° равен 0. При возрастании угла котангенс продолжает убывать уже от 0 до –∞, и котангенс 180° снова не определён. Опять возрастает угол и опять убывает котангенс уже от +∞ до 0. И котангенс 270° равен 0. И снова возрастает угол и снова убывает котангенс уже от 0 до –∞ и котангенс 360° градусов снова не определён.
Учебник. Соотношения между сторонами и углами произвольного треугольника
Под косинусом тупого угла α (90° < α < 180°) будем понимать значение косинуса смежного с ним угла, взятого со знаком минус. Косинус прямого угла будем считать равным 0.
Под синусом тупого угла будем понимать синус смежного угла. Синус прямого угла будем считать равным 1.
Из этих определений следует, что для любых углов, таких, что 0 < α < 180° справедливы равенства
sin α = sin (180° – α) и cos α = –cos (180° – α).Действительно, если α = 90°, то имеем верные равенства.
sin 90° = sin (180° – 90°) и cos 90° = 0 = –cos (180° – 90°).Если α – острый угол, то 180° – α = β, 90° < α < 180° – тупой угол. Тогда по определению
sin β = sin (180° – β) или sin (180° – α) = sin (180° – (180° – α)) = sin α. cos β = –cos (180° – β) или cos (180° – α) = –cos (180° – (180° – α)) = –cos α.Отсюда получаем cos α = cos (180° – α).
Наконец, если α (90° < α < 180°) – тупой угол, то равенства видны по определению.
Теорема косинусов. Квадрат любой стороны треугольника равен сумме квадратов двух других сторон без удвоенного произведения этих сторон на косинус угла между ними.
Пусть угол α – между двумя сторонами AB и AC треугольника ABC равен 90°. Тогда треугольник ABC прямоугольный и по теореме Пифагора имеем
BC2 = AB2 + AC2.Но с другой стороны, так как cos 90° = 0
AB2 + AC2 = AB2 + AC2 – 2AB ⋅ AC cos 90° = BC2.Теорема верна.
На рис. 5.2.1 показаны три возможных случая, связанных с величиной угла α между известными сторонами. В первых двух случаях угол α – острый, в третьем – тупой. Пусть ABC – данный треугольник. Докажем, что
Докажем, что
Опустим из вершины B высоту BD на прямую (AC). Рассмотрим два возможных случая.
-
Пусть угол α – острый. Тогда, либо точка D лежит между точками A и C, либо точка C – между точками A и D. Поэтому справедливы следующие равенства:
AB2 = AD2 + BD2;
BC2 = CD2 + BD2;
AD = AB cos α;
CD = |AC – AD|. Из первых двух равенств, исключая BD2, получим BC2 = AB2 + CD2 – AD2. Подставляя из последнего равенства выражение для CD, имеем: BC2 = AB2 + (|AC – AD|)2 – AD2 = AB2 + AC2 – 2AC ⋅ AD. С учётом третьего равенства окончательно получаем требуемое равенство:
BC2 = AB2 + AC2 – 2AB ⋅ AC cos α.
С учётом третьего равенства окончательно получаем требуемое равенство:
BC2 = AB2 + AC2 – 2AB ⋅ AC cos α.
-
Пусть угол α – тупой. Тогда точка A лежит между точками D и C. Поэтому справедливы равенства:
AB2 = AD2 + BD2;
BC2 = CD2 + BD2;
AD = AB cos (180° – α);
CD = AC + AD. Имеем: BC2 = AB2 + CD2 – AD2. С учётом последнего равенства BC2 = AB2 + (AC + AD)2 – AD2 = AB2 + AC2 + 2AC ⋅ AD = AB2 + AC2 + 2AB ⋅ AC ⋅ cos (180° – α).
Так как угол α – тупой , то cos α = –cos (180° – α) и, с учётом этого, окончательно получаем
BC2 = AB2 + AC2 – 2AB ⋅ AC cos α.Теорема доказана.
К доказательству теоремы косинусовК доказательству теоремы косинусовТеорема синусов. Стороны треугольника пропорциональны синусам противолежащих углов, т. е.
asinα=bsinβ=csinγ.Пусть ABC – треугольник со сторонами a, b, c и соответственно противолежащими им углами α, β, γ. Докажем, что asinα=bsinβ=csinγ.
Опустим из вершины B высоту BD на прямую (AC).
- Пусть все углы Δ ABC острые. Тогда BD = a sin γ из прямоугольного треугольника BCD. Аналогично из треугольника ABD BD = c sin α. Приравнивая правые части, получаем a sin γ = c sin α или asinα=csinγ.

Аналогично, если опустить высоту CE из вершины C на прямую (AB), получим CE = b sin α из Δ ACE, CE = a sin β из Δ BCE. И, сравнивая эти равенства, имеем asinα=bsinβ.
Окончательно из полученных равенств имеем asinα=bsinβ=csinγ. -
Пусть один из углов (например, γ) тупой. Тогда BD = a sin (180° – γ) = a sin γ из Δ BCD, BD = c sin α из Δ ABD. Отсюда a sin γ = c sin α или asinα=csinγ.
Далее, опуская высоту CE из вершины C на прямую (AB) и рассуждая аналогично пункту 1, получим asinα=bsinβ и, окончательно, asinα=bsinβ=csinγ.
Теорема доказана.
Пусть даны два Δ ABC и A1B1C1 и углы при вершинах A, B и C одного треугольника равны углам при вершинах A1, B1, C1 соответственно, другого треугольника.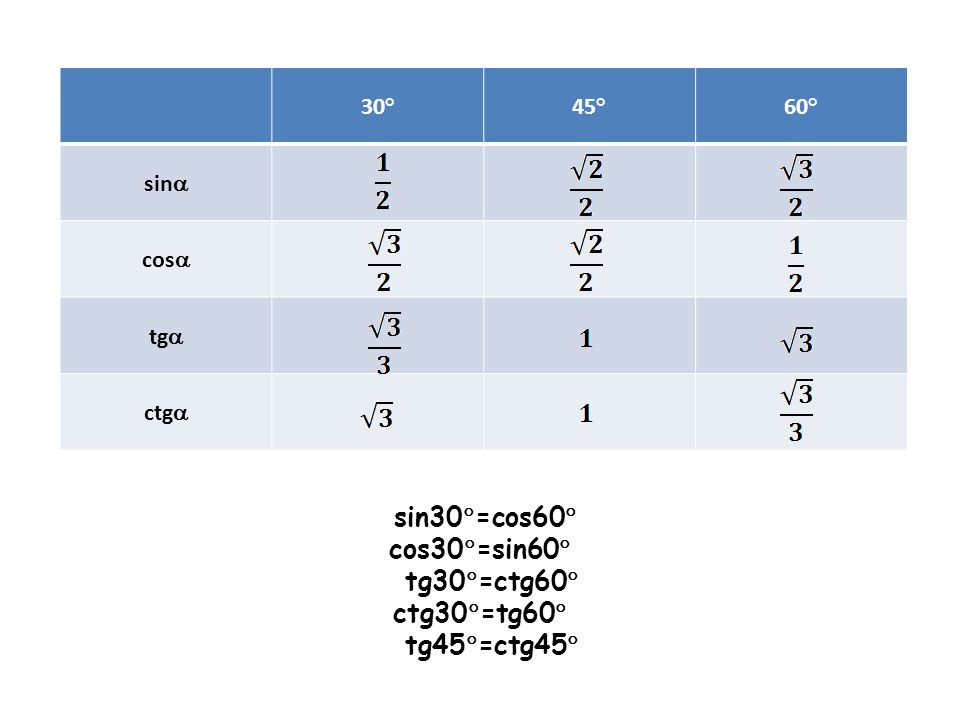 Тогда отношения длин сторон этих треугольников, лежащих против равных углов равны, то есть
A1B1AB=B1C1BC=A1C1AC.
Тогда отношения длин сторон этих треугольников, лежащих против равных углов равны, то есть
A1B1AB=B1C1BC=A1C1AC.
Действительно из Δ ABC по теореме синусов имеем
ABsin(∠ C)=BCsin(∠ A)=ACsin(∠ B).Аналогично из Δ A1B1C1 получим
A1B1sin(∠ C1)=B1C1sin(∠ A1)=A1C1sin(∠ B1).Деля входящие во второе равенство выражения на соответствующие выражения из первого равенства и учитывая, что синусы равных углов равны получим искомое равенство.
Пусть α и β – угловые величины двух острых углов, причём α < β. Тогда sin α < sin β
Отложим от луча AB в одну полуплоскость углы BAC и BAD так, что
∠ BAC=90∘-β, ∠ BAD=90∘-α. Точки B, C, D лежат на прямой a, которая перпендикулярна лучу AB. Так как (90∘-β)<(90∘-α), то луч AC лежит между сторонами угла BAD, следовательно, точка C лежит между точками B и D и BC < BD. Отрезки BC и BD являются проекциями наклонных AC и AD на прямую a, соответственно, поэтому, по свойству наклонных (см. параграф 5.1) AD > AC. Треугольники ABC и ABD прямоугольные (∠ B равен 90° по условию), поэтому ∠ ACB = β, ∠ ADB = α.
Отрезки BC и BD являются проекциями наклонных AC и AD на прямую a, соответственно, поэтому, по свойству наклонных (см. параграф 5.1) AD > AC. Треугольники ABC и ABD прямоугольные (∠ B равен 90° по условию), поэтому ∠ ACB = β, ∠ ADB = α.
По определению
sinβ=ABAC; sinα=ABAD,ноsinβsinα=ABAC⋅ADAB=ADAC>1.Отсюда
sin β > sin α, что и требовалось доказать.Заметим, что, если α – острый угол, то
sinα<1=sin90∘.К следствию 5.2В треугольнике против большего угла лежит большая сторона, против большей стороны лежит больший угол.
Если все углы треугольника – острые, то этот факт следует из результата леммы 5.1 и теоремы 5.4. Если же один из углов треугольника, например, для определенности γ – тупой, то γ = 180° – (α + β), но sin (180° – (α + β)) = sin (α + β) и по лемме 5. 2 sin (α + β) = sin γ > sin α и sin γ > sin β. Bторое утверждение следует из теоремы 5.4.
2 sin (α + β) = sin γ > sin α и sin γ > sin β. Bторое утверждение следует из теоремы 5.4.
Каковы бы ни были три точки, расстояние между любыми двумя из этих точек не больше суммы расстояний от них до третьей.
Пусть A, B, C – три данные точки. Если две точки из трёх или все три совпадают, то утверждение теоремы очевидно. Если все три точки различны, но лежат на одной прямой, одна из них лежит между двумя другими без ограничения общности, например, B. Тогда AB + BC = AC. Отсюда AB < AC < AC + BC, BC < AC < AC + BC, AC = AB + BC и утверждение теоремы верно.
Пусть точки A, B и C не лежат на одной прямой. Докажем, что AB < AC + BC.
Опустим перпендикуляр CD на прямую AB. Точки A, B, D лежат на данной прямой и по доказанному AB ≤ AD + BD. Но AD < AC и BD < BC по построению и свойству наклонной. Отсюда AB < AC + BC. Теорема доказана.
Но AD < AC и BD < BC по построению и свойству наклонной. Отсюда AB < AC + BC. Теорема доказана.
В любом треугольнике каждая сторона меньше суммы двух других сторон.
Таблица косинусов, полная таблица косинусов для студентов
Содержание:
Таблица косинусов — наровне с таблицей синусов изучается в самом начале тригонометрии (И вместе с таблицей синусов является основным материалом тригонометрии). Без понимания данного материала и без знания хотя бы части таблицы косинусов будет очень сложно изучать тригонометрию и применять тригонометричекие формулы. Даже в университетском курсе часто используется тригонометрия, при решении интегралов и производных. Пользуйте таблицей косинусов на здоровье.
Таблица косинусов 0° — 180°
|
|
|
Таблица косинусов 180° — 360°
|
|
|
На нашем сайте в основном автоматические находятся программы для решения задач по математике, но также
мы собрали много теоретического материала по математике и в частности по тригонометрии. Здесь Вы можете найти
таблицы тригонометрических функций:
таблицу косинусов,
таблицу синусов,
таблицу котангенсов и
таблицу тангенсов. Также для улучшения понимания материала по тригонометрии мы добавили
тригонометрические формулы, чтобы
вызывало меньше затруднений решение тригонометрических задач по математике. Пользуйтесь нашим сайтом и таблицей косинусов на здоровье.
Также для улучшения понимания материала по тригонометрии мы добавили
тригонометрические формулы, чтобы
вызывало меньше затруднений решение тригонометрических задач по математике. Пользуйтесь нашим сайтом и таблицей косинусов на здоровье.
Слишком сложно?
Таблица косинусов, таблица значений косинусов не по зубам? Тебе ответит эксперт через 10 минут!
Урок 22. формулы для вычисления площади правильного многоугольника, его стороны и радиуса вписанной окружности — Геометрия — 9 класс
Обозначим S площадь правильного n-угольника, an его сторону, Р периметр, r и R – радиусы соответственно вписанной и описанной окружностей.
Рассмотрим сначала доказательство, что площадь данного многоугольника будет равна: S = 1/2 P r
Выполним следующее построение
Проведем линии из центра многоугольника к его вершинам.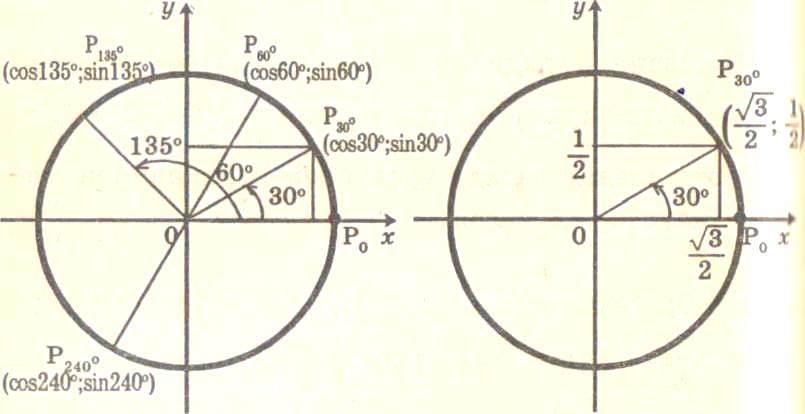 Многоугольник разбили на несколько треугольников. Применяя формулу площади треугольника запишем следующее равенство. Площадь каждого треугольника будет равна: S = 1/2 anr, где an – сторона многоугольника; r – радиус вписанной окружности, является высотой каждого рассматриваемого треугольника.
Многоугольник разбили на несколько треугольников. Применяя формулу площади треугольника запишем следующее равенство. Площадь каждого треугольника будет равна: S = 1/2 anr, где an – сторона многоугольника; r – радиус вписанной окружности, является высотой каждого рассматриваемого треугольника.
Так как все треугольники равны, то умножим количество треугольников на площадь треугольника:
S = n ∙ 1/2 anr, где n – количество треугольников.
После преобразований получим формулу: S = 1/2 (n ∙ an)r
Произведение в скобках отражает периметр рассматриваемого многоугольника. Таким образом, формула расчёта площади многоугольника выглядит следующим образом: S = 1/2 Pr
Выведем формулы для вычисления стороны правильного многоугольника и радиуса вписанной окружности.
Рассмотрим прямоугольный треугольник А1Н1О. Угол А1 рассматриваемого треугольника будет равен половине угла αn многоугольника (отмечен красным), т.к. сторона треугольника А1О является так же биссектрисой угла αn многоугольника.
Угол А1 рассматриваемого треугольника будет равен половине угла αn многоугольника (отмечен красным), т.к. сторона треугольника А1О является так же биссектрисой угла αn многоугольника.
По формуле вычисления угла α правильного многоугольника αn = (n — 2)/n ∙ 180° применяя простые преобразования получим равенство для угла А1 рассматриваемого треугольника: ∠A1 = αn/2 = (n — 2)/2n ∙ 180° = 90° — (180°)/n
Полагая, что сторона правильного многоугольника an будет равна an = 2A1H1 и, учитывая, что треугольник А1Н1О является прямоугольным, воспользуемся соотношениями между сторонами и углами прямоугольного треугольника.
Получим следующее равенство: an = 2A1H1 = 2 Rcos(90° — (180°)/n) = 2 R sin (180°)/n.
Итак, сторона правильного многоугольника an = 2 R sin (180°)/n
радиус вписанной окружности r = R cos (180°)/n
Формулы расчета сторон для правильного треугольника, квадрата и правильного шестиугольника.
Треугольник: a3 = 2 R sin(180°)/3 = 2 R sin60° = 2 R ∙ √3/2 = R√3
Квадрат: a4 = 2 R sin(180°)/4 = 2 R sin45° = 2 R∙√2/2 = R√2
Шестиугольник: a6 = 2 R sin(180°)/6 = 2 R sin30° = 2 R ∙ 1/2 = R
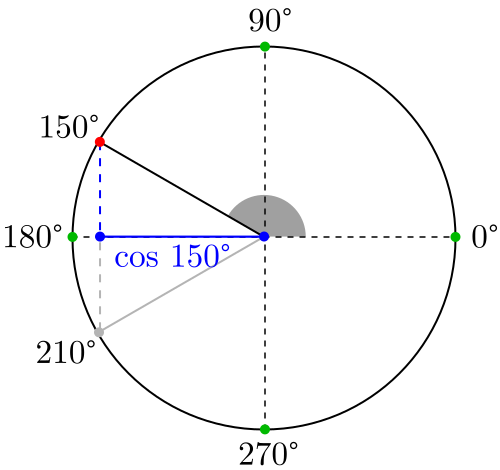
тригонометрия — Два способа найти косинус угла 180 градусов
тригонометрия — Два способа найти косинус угла 180 градусов — Mathematics Stack ExchangeСеть обмена стеков
Сеть Stack Exchange состоит из 177 сообществ вопросов и ответов, включая Stack Overflow, крупнейшее и пользующееся наибольшим доверием онлайн-сообщество, где разработчики могут учиться, делиться своими знаниями и строить свою карьеру.
- 0
- +0
- Авторизоваться Зарегистрироваться
Mathematics Stack Exchange — это сайт вопросов и ответов для людей, изучающих математику на любом уровне, и профессионалов в смежных областях.Регистрация займет всего минуту.
Зарегистрируйтесь, чтобы присоединиться к этому сообществуКто угодно может задать вопрос
Кто угодно может ответить
Лучшие ответы голосуются и поднимаются наверх
Спросил
Просмотрено 93k раз
$ \ begingroup $Я нашел вопрос, как найти значение cos 180, тогда мы все знаем, что его ответ равен cos 0, что дает нам 1 в качестве ответа.Я сам думаю, что идея cos 180 равна 1:
cos 180 = cos (180-0)
cos 180 = -cos 0 ", который равен cos (180-a) = - cos a"
cos 180 = - 1.
соз 180 = соз (270-90)
cos 180 = -sin 90 cos (270-a) = -sin a,
cos 180 = -1
Создан 04 сен.
Ягами17711 золотых знаков22 серебряных знака1414 бронзовых знаков
$ \ endgroup $ 1 $ \ begingroup $Во второй строке вы используете $ \ cos (AB) = \ cos A \ cos B + \ sin A \ sin B $, но проблема в том, что вы подразумеваете $ \ cos180 = 1 $ ($ \ sin180 = 0 $, поэтому эта часть отменяется), чтобы получить результат $ \ cos180 = 1 $, что делает ваше доказательство «правильным», но, очевидно, неверным.
Есть много других примеров, когда неверное предположение при использовании правильной личности может заставить вас «доказать» это предположение.
CiaPan11.6k11 золотых знаков1717 серебряных знаков5151 бронзовых знаков
Создан 04 сен.
имранфатимранфат9,67644 золотых знака1818 серебряных знаков3434 бронзовых знака
$ \ endgroup $ $ \ begingroup $Прошу прощения за неправильную формулу, я обнаружил, что:
cos 180 = cos (180-0) = -cos 0 = -1 (метод 1)
cos 180 = cos (270-90) = -sin 90 = -1 (метод 2)
Благодаря полуклассическому и прочему ответу. \ circ) = — \ cos (0) = -1 $
Создан 04 сен.
CiaPanCiaPan11.6k11 золотой знак1717 серебряных знаков5151 бронзовый знак
$ \ endgroup $ $ \ begingroup $cos180 = cos (90 + 90) Используя cos (A + B) = cosAcosB-sinAsinB
cos (90 + 90) = cos90cos90-sin90sin90
= 0 * 0-1 * 1
= -1
, следовательно, cos180 = -1
Создан 05 июля ’17 в 7: 552017-07-05 07:55
$ \ endgroup $ 1Не тот ответ, который вы ищете? Посмотрите другие вопросы с метками тригонометрия или задайте свой вопрос.
Mathematics Stack Exchange лучше всего работает с включенным JavaScriptВаша конфиденциальность
Нажимая «Принять все файлы cookie», вы соглашаетесь с тем, что Stack Exchange может хранить файлы cookie на вашем устройстве и раскрывать информацию в соответствии с нашей Политикой в отношении файлов cookie.
Принимать все файлы cookie Настроить параметры
Значение Cos 120 градусов и других тригонометрических углов
(i) Функция синуса (sin)
sin \ [\ theta \] = \ [\ frac {Opposite} {Hypotenuse} \]
(ii) Функция косинуса (cos)
cos \ [\ theta \] = \ [\ frac {Смежные} {Гипотенуза} \]
(iii) Функция касания (tan)
tan (\ [\ theta \]) = \ [\ frac {sin (\ theta)} {cos (\ theta)} \]
Квадрант и правило приведения
Как указано выше, углы, отличные от угла 90 градусов в прямоугольном треугольнике, являются острыми (т.е.д, менее 90 градусов). Чтобы найти значение функций для углов более 90 градусов, мы следуем набору правил, известных как правило приведения. Возьмем четыре оси, чтобы разделить 360 градусов на четыре квадранта. Углы всегда измеряются против часовой стрелки от положительной оси x. Данная диаграмма показывает 30 градусов от положительной оси абсцисс.
[Изображение будет скоро загружено]
Есть четыре квадранта, как показано на рисунке ниже. Каждый квадрант содержит диапазон углов:
Первый квадрант: все углы между 0⁰ и 90⁰ лежат в первом квадранте.Значения всех функций (Sin, Tan, Cos) в этом квадранте положительны. Обозначается буквой A (обозначает все) на второй диаграмме ниже.
Второй квадрант: все углы между 90⁰ и 180⁰ лежат во втором квадранте. Значение только Sin положительно в этом квадранте. Обозначается буквой S (представляет Sin) на второй диаграмме ниже.
Третий квадрант: все углы между 180⁰ и 270⁰ лежат в третьем квадранте. Значение только Tan положительно в этом квадранте.Обозначается буквой T (обозначает загар) на второй диаграмме ниже.
Четвертый квадрант: Все углы между 270⁰ и 360⁰ лежат в четвертом квадранте. Значение только Cos положительно в этом квадранте. Обозначается буквой C (обозначает Cos) на второй диаграмме ниже.
[Изображение будет загружено в ближайшее время]
Начиная с четвертого квадранта, мы можем сказать, что квадрант следует за серией CAST, где C — Cos, A — все, S — Sin, а T — Tan.
Связанные углы
Значения sin, cos и tan для некоторых углов равны значениям sin, cos и tan для других углов.Давайте возьмем для примера cos (-30⁰). Поскольку 30 градусов лежат в первом квадранте, мы можем сказать, что cos (-30⁰) равен cos (30⁰), потому что все углы в первом квадранте положительны. Аналогично, cos (390⁰) также равен cos (30⁰). На диаграммах ниже показаны заштрихованные углы sin, cos и tan, имеющие одинаковую величину.
Рис. 1: sin 30⁰ = 0,5
Рис. 2: sin 150⁰ = 0,5
Рис. 3: sin 210⁰ = -0,5
Рис. 4: sin 330⁰ = -0,5
[Изображение будет скоро загружено]
Следовательно эти углы называются связанными углами.На приведенном ниже изображении показаны значения всех углов cos.
[Изображение будет скоро загружено]
Cos 120
Значение Cos 120⁰ равно — ½. Это аддитивная величина, обратная величине косинуса 60⁰ или cos 60⁰. Косинус — одна из основных тригонометрических функций. Он выражается как отношение основания прямоугольного треугольника к его гипотенузе.
Как найти значение Cos 120?
Углы прямоугольного треугольника выражаются в единицах, кратных или кратных 180, или π в радианах.Следовательно, чтобы найти значение cos 120⁰, нам нужно будет выразить 120⁰ через 180⁰ или 90⁰.
Случай 1:
Выразим 120⁰ как (180-60) ⁰
cos 120⁰ = cos (180-60) ⁰
Поскольку, cos (180⁰ — x) = — cos x.
Следовательно, cos (180-60) ⁰ = — cos 60⁰
=> cos 120⁰ = -½
Случай 2:
Выразим 120⁰ как (90 + 30) ⁰
cos 120⁰ = cos (90 + 30) ⁰
Поскольку cos (90⁰ + x) = — sin x.
Следовательно, cos (90 + 30) ⁰ = -sin 30⁰
=> cos 120⁰ = — ½
Решенные примеры
Вопрос 1: Найдите точное значение cos (- 390⁰).
Решение: мы знаем, что cos (-x) = cos (x)
, следовательно, cos (- 390⁰) = cos (390⁰).
Так как угол 390 greater больше, чем угол 360⁰,
, мы находим угол t такой, что
t = 390 — (360) = 30⁰
Это означает, что Cos (390⁰) и cos (30 co) совпадают. .
Итак,
Cos (390⁰) = Cos (30⁰)
Мы знаем, что значение Cos 30⁰ равно \ [\ sqrt {\ frac {3} {2}} \]
Под каким углом находится cos?
Под каким углом находится cos?
Определение косинуса Косинус угла определяется как синус дополнительного угла.Дополнительный угол равен заданному углу, вычтенному из прямого угла, 90 °. Например, если угол равен 30 °, то его дополнение составляет 60 °.
Что такое cos 180 А?
Cos 180 ° = — sin 90 ° (Мы знаем, что cos (270 ° — a) = — sin a) Значение sin 90 градусов равно 1. Подставляем значение в приведенное выше соотношение, получаем. Cos 180 ° = — (1) = -1. Следовательно, значение cos 180 ° равно -1.
Как найти COS 180 Theta?
- Следовательно, sin (180 ° — θ) = sin θ, [поскольку cos (90 ° — θ) = sin θ]
- Следовательно, cos (180 ° — θ) = — cos θ, [поскольку sin (90 ° — θ) = cos θ]
- Следовательно, tan (180 ° — θ) = — tan θ, [поскольку cot (90 ° — θ) = tan θ]
- Следовательно, sec (180 ° — θ) = — sec θ
- Следовательно, детская кроватка (180 ° — θ) = — детская кроватка θ.
Почему грех тета, грех 180 тета?
Синус угла θ представлен значением y точки P на единичной окружности. Таким образом, поскольку sin θ = sin (180 — θ), мы отмечаем два равных интервала на графике. Следовательно, между 0 ° и 180 ° график симметричен относительно θ = 90 °. Точно так же между 180 ° и 360 ° график симметричен относительно θ = 270 °.
Что такое тета-значение sin 180?
Из значения sin 0 мы получим значение sin 180. Мы знаем, что точное значение степени sin 0 равно 0.Следовательно, значение sin 180 градусов = 0. Значение sin pi может быть получено из некоторых других тригонометрических углов и функций, таких как функции синуса и косинуса из таблицы тригонометрии.
Что такое SEC PI минус тета?
Пи минус тэта — это дополнение к тэте. Ну, синус разницы — это синус, косинус, косинус, синус. Синус пи, косинус тета, косинус пи, синус тета и синус минус остаются неизменными. Синус пи 0, косинус пи равен -1, поэтому получается, что синус пи минус тета равен синусу тета.
Что такое СОТ 90 минус тета?
tan (90 ° — θ) = cot θ csc (90 ° — θ) = sec θ sec (90 ° — θ) = csc θ cot (90 ° — θ) = tan θ Давайте посмотрим, как тригонометрические соотношения Определяются 90 градусов минус тета.
Почему TAN 90 — это бесконечность?
Здесь угол находится между лучом, соединяющим начало координат с точкой (x, y), и осью x (положительные углы измеряются против часовой стрелки). Используя этот метод, загар угла определяется как y / x. Так как любой угол, имеющий 90 °, будет на оси y, x будет равен нулю.Деление на ноль не определено, следовательно, это загар (90 °).
Почему определяется COT 90?
cot 90, который является обратной величиной tan90, есть не что иное, как 0. 1/0 не может считаться бесконечным, поскольку вы не можете извлечь что-то из ничего.
Чему равно Cos минус тета?
Отрицательным является только угол или тета. Если бы вы упростили отрицательные углы, тогда cos (-θ) = cos (θ) и sin (-θ) = -sin (θ). Прокомментируйте сообщение Стивена: «Негативным является только угол или тэта.
Cos — положительный или отрицательный?
Во втором квадранте (II) синус (и косинус) положительные. В третьем квадранте (III) тангенты (и котан) положительны. В четвертом квадранте (IV) cos (и sec) положительны. Они просто следуют из знака (+ или -) x или y для каждого квадранта, как мы видели выше.
Может ли Cos быть больше 1?
В тригонометрии базовой плоскости тригонометрические отношения синуса или косинуса угла могут иметь любое значение от -1 до +1, и они не могут быть больше 1 или меньше -1.Чтобы определить синус угла, это отношение перпендикуляра к гипотенузе, а косинус угла — это отношение основания к гипотенузе в прямоугольном треугольнике.
Почему cos положительный?
В первом квадранте (от 0 до 90 градусов) плечо, значения x и y положительны. Итак, sin m, cos m и tan m — все положительные значения в первом квадранте. Во втором квадранте (от 90 до 180 градусов) плечо и y положительны, а x отрицательны. Следовательно, косинус отрицательного угла изменится на положительное значение.
Что такое отрицательный косинус?
cos (-θ) = cos θ и sin (-θ) = — sin θ. Это тождества с отрицательным углом. Отрицательные угловые тождества также говорят нам о симметрии функций косинуса и синуса. Функция f даже если f (-x) = f (x) для каждого x в области определения f. Поскольку cos (-θ) = cos θ, мы заключаем, что косинус является четной функцией.
Чему равен отрицательный синус?
Инверсный синус равен функции cosec? Обратный синус или арксинус — это функция, обратная синусу, которая возвращает значение угла, для которого функция синуса равна противоположной стороне и коэффициенту гипотенузы.
Может ли косинусное подобие быть отрицательным?
Косинусное сходство можно рассматривать как метод нормализации длины документа во время сравнения. В случае поиска информации косинусное сходство двух документов будет варьироваться от 0 до 1, поскольку частоты терминов (с использованием весов tf – idf) не могут быть отрицательными.
Могут ли триггерные тождества быть отрицательными?
На основе единичной окружности тождества с отрицательным углом (также называемые «нечетными / четными» тождествами) говорят вам, как найти триггерные функции в точке -x в терминах триггерных функций в точке x.Например, sin (-x) = -sin (x), cos (-x) = cos (x) и tan (-x) = -tan (x). …
Что такое один минус тета?
1 — cos2θ. 1 — sin2θ. Они называются тождествами Пифагора, потому что, как мы увидим в их доказательстве, они представляют собой тригонометрическую версию теоремы Пифагора.
Какое значение имеет тета cos 2?
Cos2x = 2cos²x- 1 это другое значение для двойного угла Cos.
Что такое sinA * cosA?
sinA × cosA = 1/2 × sin2A. = sinAsin (pi / 2-2A)
Что такое 2cosacosb?
Формула 2cosacosb Мы знаем, что cos (A + B) = cos A cos B — sin A sin B….. (1) cos (A — B) = cos A cos B + sin A sin B… .. (2)
Что такое cos 270 минус тета? — AnswersToAll
Что такое cos 270 минус тета?
2) cos (270 − Θ) = cos [180+ (90 − Θ 270 — Θ) = cos [180 + (90 — Θ)] Но мы знаем, что cos (180 + Θ) = — cosΘ Θ) = — cos Θ) ∴ cos [180 + (90 -)] = — cos (90 − Θ Θ)] = — cos (90 — Θ) Но cos (90 -Θ) = sinΘ Θ) = sin Θ) ∴ cos ( 270 − Θ) = — sinΘ ––––––––––––––––––––––––––
Что такое cos (- theta?
Cos theta или cos θ — это отношение соседней стороны к гипотенузе, где θ — один из острых углов.Формула косинуса выглядит следующим образом: Cos \ Theta = \ frac {смежный} {Hypotenuse}
Как найти COS 180 Theta?
- Следовательно, sin (180 ° — θ) = sin θ, [поскольку cos (90 ° — θ) = sin θ]
- Следовательно, cos (180 ° — θ) = — cos θ, [поскольку sin (90 ° — θ) = cos θ]
- Следовательно, tan (180 ° — θ) = — tan θ, [поскольку cot (90 ° — θ) = tan θ]
- Следовательно, sec (180 ° — θ) = — sec θ
- Следовательно, детская кроватка (180 ° — θ) = — детская кроватка θ.
Что такое COS 1 в радианах?
Как вы можете видеть ниже, cos-1 (1) равен 270 ° или, в радианах, 3Π / 2.
Каковы 6 триггерных функций числа Пи?
1 ответ
- sin (π6) = 12csc (π6) = 2.
- cos (π6) = √32сек (π6) = 2√3.
- загар (π6) = 1√3cot (π6) = √3.
Является ли Cos Pi 2 неопределенным?
Значение cos (пи / 2) равно 0, поэтому секанс (пи) / 2 должен быть неопределенным.
Какие 6 тригонометрических функций?
Существует шесть тригонометрических соотношений: синус, косинус, тангенс, косеканс, секанс и котангенс. Эти шесть тригонометрических соотношений обозначаются как sin, cos, tan, csc, sec, cot.
Как PI используется в тригонометрии?
В тригонометрии круг равен 360 градусам, где каждый градус представляет угол. Углы могут быть преобразованы в радианы в качестве единицы измерения, которая используется в тригонометрии по формуле: один пи радиан равен 180 градусам. Преобразование радиана в градус: таким образом, два пи преобразуются в 360 градусов.
Почему пи радиан равен 180 градусам?
Ну, если весь круг равен 2π⋅r, половина будет только π⋅r, но половина круга соответствует 180 °, хорошо… Длина вашей дуги для полукруга, мы видели, что π⋅r делится на r… вы получаете π радиан !!!!!!
Как пи радианы равны 180 градусам?
Радианы и градусы
| Градусов | Радианы (точные) | радиан (приблизительно) |
|---|---|---|
| 90 ° | π / 2 | 1.571 |
| 180 ° | π | 3,142 |
| 270 ° | 3π / 2 | 4,712 |
| 360 ° | 2π | 6,283 |
Кто является мировым рекордсменом по запоминанию наибольшего числа цифр числа Пи?
Лу Чао
Сколько цифр Пи может запомнить средний человек?
Сегодня День Пи — день каждого года, 14 марта, который следует за первыми тремя цифрами числа Пи (3.14). И в этом году День числа Пи особенный: поскольку — в США — дата представлена как 14 марта 2015 г., у нас в календаре есть первые пять цифр числа Пи…. Сколько цифр числа Пи вам нужно запомнить. Быть особенным.
| УРОВЕНЬ ТОЧНОСТИ | ПРОЦЕНТ РЕСПОНДЕНТОВ |
|---|---|
| 3./td> | 7 |
| 3./td> | 5 |
Сколько цифр Пи вы можете назвать?
Поскольку число Пи — иррациональное число, то есть числа никогда не заканчиваются и никогда не повторяются, День Пи также отмечается конкурсами на декламацию числа Пи. {2} \ beta \ sin \ beta} \\ & = — \ frac {1} {\ sin \ beta} \\ & = — \ frac {1} {p} \ end {выровнять *}
\ (\ dfrac {\ cos (- \ text {120} °)} {\ tan \ text {150} °} + \ cos \ text {390} ° \)
\ begin {align *} & \ dfrac {\ cos (\ text {120} °)} {\ tan \ text {150} °} + \ cos \ text {390} ° \\ & = \ frac {\ cos (\ text {180} ° — \ text {60} °)} {\ tan (\ text {180} ° — \ text {30} °)} + \ cos (\ text {360 } ° + \ текст {30} °) \\ & = \ frac {- \ cos \ text {60} °} {- \ tan \ text {30} °} + \ cos \ text {30} ° \\ & = \ frac {\ sin \ text {30} °} {\ frac {\ sin \ text {30} °} {\ cos \ text {30} °}} + \ cos \ text {30} ° \\ & = \ cos \ text {30} ° + \ cos \ text {30} ° \\ & = 2 \ cos \ text {30} ° \\ & = 2 \ left (\ frac {\ sqrt {3}} {2} \ right) \\ & = \ sqrt {3} \ end {выровнять *}
\ ((1 — \ sin \ text {45} °) (1 — \ sin \ text {225} °) \)
\ begin {align *} & (1 — \ sin \ text {45} °) (1 — \ sin \ text {225} °) \\ & = 1 — \ sin \ text {45} ° — \ sin \ text {225} ° + (\ sin \ text {45} °) (\ sin \ text {225} °) \\ & = 1 — \ sin \ text {45} ° — \ sin (\ text {180} ° + \ text {45} °) + (\ sin \ text {45} °) (\ sin (\ text {180} ° + \ текст {45} °)) \\ & = 1 — \ sin \ text {45} ° + \ sin \ text {45} ° — \ sin ^ {2} \ text {45} ° \\ & = 1 — \ sin ^ {2} \ text {45} ° \\ & = 1 — \ left (\ frac {1} {\ sqrt {2}} \ right) ^ {2} \\ & = 1 — \ frac {1} {2} \\ & = \ frac {1} {2} \ end {выровнять *}
\ (\ tan ^ {2} \ beta — \ dfrac {1} {\ cos ^ {2} \ beta} \)
\ begin {align *} \ tan ^ {2} \ beta — \ dfrac {1} {\ cos ^ {2} \ beta} & = \ dfrac {\ sin ^ {2} \ beta} {\ cos ^ {2} \ beta} — \ dfrac {1} {\ cos ^ {2} \ beta} \\ & = \ dfrac {\ sin ^ {2} \ beta — 1} {\ cos ^ {2} \ beta} \\ & = \ dfrac {- (1 — \ sin ^ {2} \ beta)} {\ cos ^ {2} \ beta} \\ & = \ dfrac {- \ cos ^ {2} \ beta} {\ cos ^ {2} \ beta} \\ & = — \ текст {1} \ end {выровнять *}
\ (\ sin ^ {2} (\ text {90} ° + \ theta) \ tan ^ {2} \ theta + \ tan ^ {2} \ theta \ cos ^ {2} (\ text {90} ° — \ theta) \)
\ begin {align *} & \ sin ^ {2} (\ text {90} ° + \ theta) \ tan ^ {2} \ theta + \ tan ^ {2} \ theta \ cos ^ {2} (\ text {90} ° — \ тета) \\ & = \ cos ^ {2} \ theta \ tan ^ {2} \ theta + \ tan ^ {2} \ theta \ sin ^ {2} \ theta \\ & = \ tan ^ {2} \ theta \ left (\ cos ^ {2} \ theta + \ sin ^ {2} \ theta \ right) \\ & = \ tan ^ {2} \ theta \ left (1 \ right) \\ & = \ tan ^ {2} \ theta \ end {выровнять *}
\ (\ sin \ alpha \ cos \ alpha \ tan \ alpha — 1 \)
\ begin {align *} \ грех \ альфа \ соз \ альфа \ загар \ альфа -1 & = \ sin \ alpha \ cos \ alpha \ left (\ frac {\ sin \ alpha} {\ cos \ alpha} \ right) — 1 \\ & = \ sin ^ {2} \ alpha — 1 \\ & = — \ left (1 — \ sin ^ {2} \ alpha \ right) \\ & = — \ соз ^ {2} \ альфа \ end {выровнять *}
\ (\ tan ^ 2 \ theta + \ dfrac {\ cos ^ 2 \ theta — 1} {\ cos ^ 2 \ theta} \)
\ begin {align *} \ tan ^ 2 \ theta + \ dfrac {\ cos ^ 2 \ theta — 1} {\ cos ^ 2 \ theta} & = \ tan ^ 2 \ theta — \ dfrac {(1 — \ cos ^ 2 \ theta)} {\ cos ^ 2 \ theta} \\ & = \ tan ^ 2 \ theta — \ dfrac {\ sin ^ 2 \ theta} {\ cos ^ 2 \ theta} \\ & = \ tan ^ 2 \ theta — \ tan ^ 2 \ theta \\ & = \ текст {0} \ end {выровнять *}
Учитель математики Троя просит класс ответить на следующий вопрос.{2} \ theta \\ \ поэтому \ text {LHS} & = \ text {RHS} \ end {выровнять *}
Прокомментируйте ответ Троя и покажите правильный метод подтверждения личности.
Вопрос требует, чтобы Трой подтвердил личность. Однако, работая с обеими сторонами идентичности одновременно, он признал, что это правда. Правильный метод подтверждения личности — работать только с одной стороной за раз и показать, что одна сторона равна другой. Иногда необходимо сначала упростить одну сторону идентичности, а затем также упростить другую сторону, чтобы показать, что они равны.{2} \ theta} {\ cos \ theta (1+ \ sin \ theta)} \\ & = \ dfrac {\ cos \ theta} {1+ \ sin \ theta} \\ & = \ текст {LHS} \ end {выровнять *}
Ограничения: undefined, где \ (\ cos \ theta = \ text {0}, \ text {и} \ sin \ theta = — \ text {1} \).
Итак, \ (\ theta \ ne \ text {90} + k \ cdot \ text {180} ° \ text {и} \ theta \ ne — \ text {90} + k \ cdot \ text {360} ° \ ).
Следовательно, \ (\ theta \ ne \ text {90} ° + k \ cdot \ text {180} °, \ quad k \ in \ mathbb {Z} \).
ОРГАНЫ ОБЪЕКТА Базовые углы и тригонометрия.
Презентация на тему: «Базовые углы и тригонометрия окружности устройства» — стенограмма презентации:
ins [data-ad-slot = «4502451947»] {display: none! important;}} @media (max-width: 800px) {# place_14> ins: not ([data-ad-slot = «4502451947»]) {display: none! important;}} @media (max-width: 800px) {# place_14 {width: 250px;}} @media (max-width: 500 пикселей) {# place_14 {width: 120px;}} ]]>1 ОБЩАЯ КРУГЛОСТЬ МОДУЛЯ Базовые углы и тригонометрия
2 Использование тригонометрии в прямоугольном треугольнике
Мы были ограничены острыми углами. Мы можем расширить тригонометрию до углов любой меры, поместив эти углы в координатную плоскость. Мы делаем это, используя опорные углы, острые углы измеряются по оси x.
3 Сторона клемм повернута против часовой стрелки. Углы 135 ° размещены так, чтобы одна сторона, называемая начальной стороной, располагалась на положительной оси x.
4 Сторона клемм повернута против часовой стрелки. 135 ° 45 ° Базовый угол отсчитывается от оси x.
5 Сторона клемм повернута против часовой стрелки.225 ° 45 ° Базовый угол отсчитывается от оси x.
6 Сторона клемм повернута против часовой стрелки. 315 ° 45 ° Базовый угол отсчитывается от оси x.
7 Если сторона вывода повернута по часовой стрелке, размер угла будет
Отрицательный. 45 ° Базовый угол отсчитывается от оси x.Всегда позитивный. -45 °
8 Единичный Круг имеет радиус 1 единицу.
9 Unit Circle имеет радиус 1 единицу.
Cos + Sin + = y 45 ° x = косинус = x синус = y 1 45 °
10 Cos — Sin + Cos + Sin + 135 ° Базовый угол = 45 ° 45 °
11 135 ° 45 ° 225 ° 45 ° 45 ° 45 ° Базовый угол = 225 ° Cos — Sin + Cos +
12 135 ° 45 ° 45 ° 45 ° 45 ° 45 ° Базовый угол 315 ° 225 ° 315 ° Cos — Sin +
13 135 ° 45 ° 45 ° 45 ° 45 ° 45 ° 225 ° 315 ° Квадрант 2 Cos — Sin + Квадрант 1
14 Косинус = x Синус = y Касательная = Δy Δx Касательная = Синус Косинус tan = 1 45 °
Квадрант 1 Cos + Sin + tan = 1 Косинус = x Синус = y 45 ° 45 ° Касательная = Δy Δx Касательная = Синус косинус
15 загар = -1 загар = 1135 ° 45 ° 45 ° 45 ° 45 ° 45 ° 225 ° 315 ° загар = 1 загар = -1
Квадрант 2 Cos — Sin + Квадрант 1 загар = -1 Cos + Sin + загар = 1135 ° 45 ° 45 ° 45 ° 45 ° 45 ° 225 ° 315 ° Квадрант 3 Cos — Sin — Cos + Sin — Квадрант 4 tan = 1 tan = -1
16 Касательная = синус-косинус, квадрант 2 Cos — Sin + Tan — квадрант 1 Cos +
17 Cos + Sin + 30 ° 30 ° 1 Косинус = x Синус = y
18 150 ° 150 ° 30 ° 30 ° 30 ° 30 ° 30 ° 210 ° 330 ° Cos — Sin + Cos + Sin + Cos —
19 Касательная = синус-косинус 150 ° 30 ° 210 ° 330 ° Cos — Sin + Cos + Sin + Cos —
20 Cos + Sin + 60 ° 60 ° 1
21 год Cos + Sin + Cos + Sin + 60 ° 120 ° 120 ° 60 ° 60 °
22 Cos — Sin + Cos + Sin + 60 ° 120 ° 60 ° 60 ° 60 ° Cos — Sin — 240 °
23 60 ° 120 ° 60 ° 60 ° 60 ° 60 ° 240 ° 300 ° Cos — Sin + Cos + Sin + Cos — Sin —
24 Тангенс = синус-косинус 60 ° 120 ° 240 ° 300 ° Cos — Sin + Cos + Sin + Cos —
25 Косинус = x Синус = y Cos (180) = -1 Cos (90) = 0 Sin (180) = 0 Sin (90) = 1
90 ° (0, 1) 180 ° Cos — Sin Косинус = x Синус = y Cos + Sin (-1, 0) (1, 0) Cos (0) = 1 Sin (0) = 0 270 ° Cos (270) = 0 Sin (270) = -1 Cos Sin — (0, — 1)
26 год Косинус = x Синус = y Тангенс = Синус Косинус Cos (180) = -1 Sin (180) = 0
90 ° Tan (180) = 0 (0, 1) Tan (90) undefined 180 ° Cos — Sin косинус = x Sine = y Cos + Sin (-1, 0) (1, 0) Tangent = Sine Cosine Cos (0) = 1 Sin (0) = 0 270 ° Tan (0) = 0 Cos (270) = 0 Sin (270) = -1 Cos Sin — Tan (270) undefined (0, -1)
27 Вычислить тригонометрические функции для каждого действительного числа.

 С учётом третьего равенства окончательно получаем требуемое равенство:
BC2 = AB2 + AC2 – 2AB ⋅ AC cos α.
С учётом третьего равенства окончательно получаем требуемое равенство:
BC2 = AB2 + AC2 – 2AB ⋅ AC cos α.

 9994
9994 8988
8988 6428
6428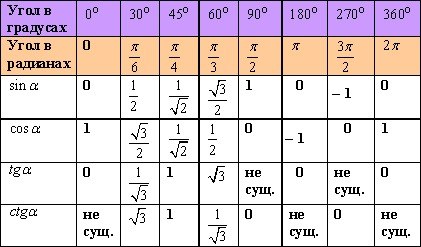 2924
2924 1219
1219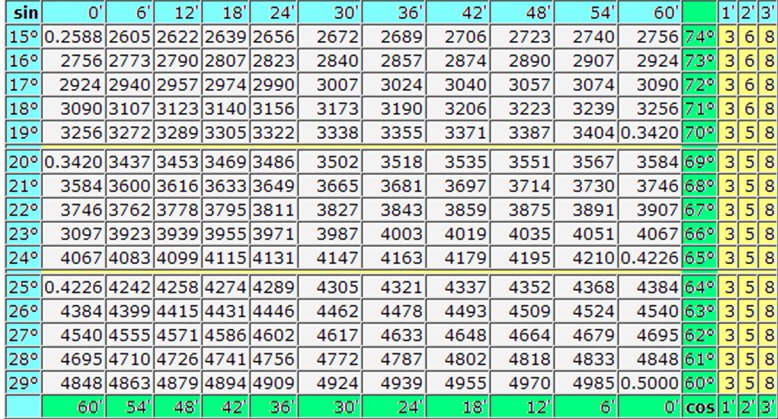 5
5 788
788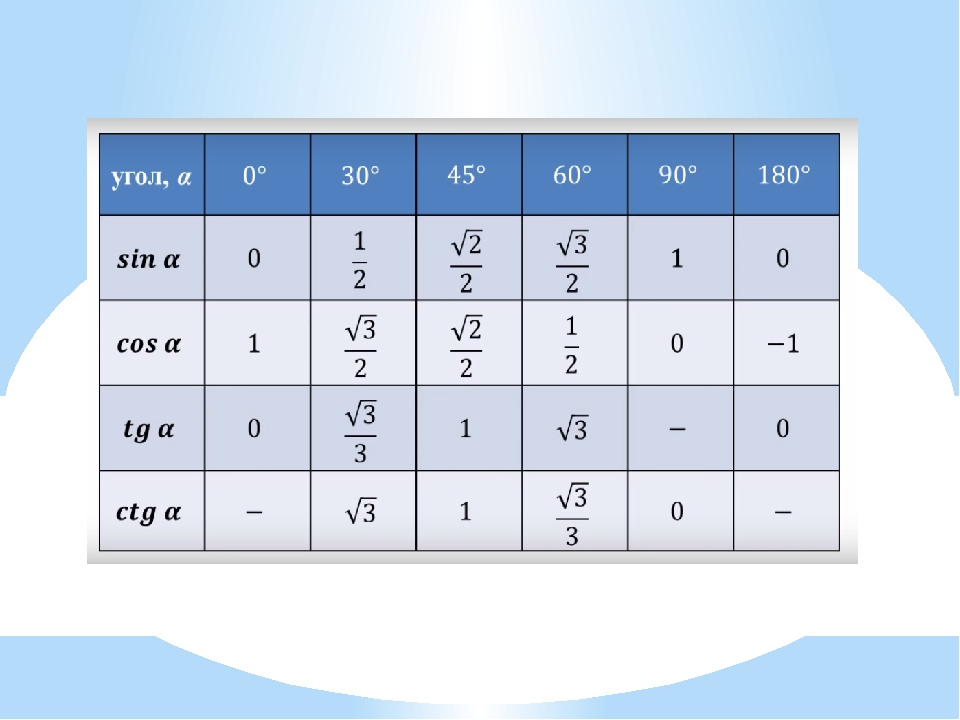 9659
9659 9962
9962 8829
8829 6293
6293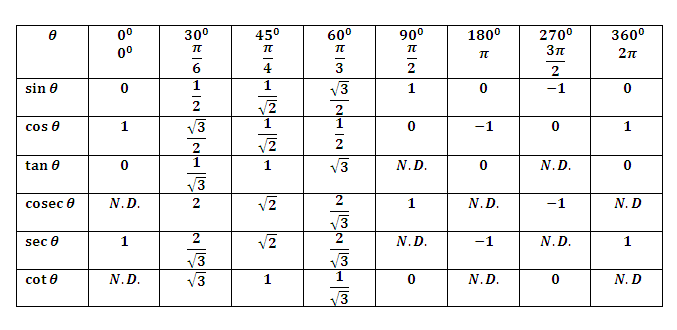 2924
2924 1045
1045 4848
4848 788
788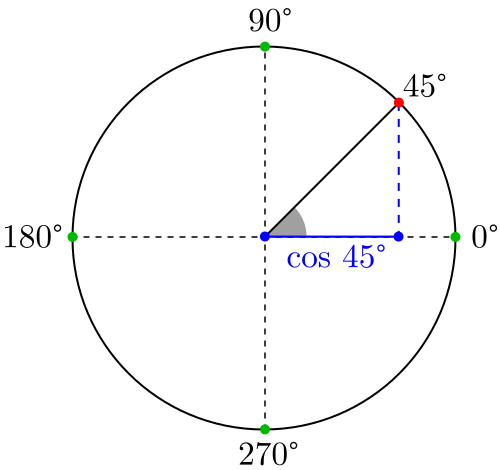 9659
9659