 2+n-72)=1/(n+9)
2+n-72)=1/(n+9)Функция y = sin x, свойства и график синуса с примерами
п.1. Развертка ординаты движения точки по числовой окружности в функцию от угла
При движении точки по числовой окружности её ордината является синусом соответствующего угла (см. §2 данного справочника).
Рассмотрим, как изменяется синус, если точка описывает полный круг, и угол x изменяется в пределах: 0≤x≤2π и построим график y=sinx на этом отрезке.
Если мы продолжим движение по окружности для углов x > 2π, кривая продолжится вправо; если будем обходить числовую окружность в отрицательном направлении (по часовой стрелке) для углов x<0, кривая продолжится влево.
В результате получаем график y=sinx для любого \(x\in\mathbb{R}\).
График y=sinx называют синусоидой.
Часть синусоиды для 0≤x≤2π называют волной синусоиды.
Часть синусоиды для 0≤x≤π называют полуволной или аркой синусоиды.
п.2. Свойства функции
y=sinx1. Область определения \(x\in\mathbb{R}\) — множество действительных чисел.
2. Функция ограничена сверху и снизу
$$ -1\leq sinx\leq 1 $$Область значений \(y\in[-1;1]\)
3. Функция нечётная
$$ sin(-x)=-sinx $$4. Функция периодическая с периодом 2π
$$ sin(x+2\pi k)=sinx $$5. Максимальные значения \(y_{max}=1\) достигаются в точках
$$ x=\frac\pi2+2\pi k $$Минимальные значения \(y_{min}=-1\) достигаются в точках
$$ x=-\frac\pi2+2\pi k $$Нули функции \(y_{0}=sinx_0=0\) достигаются в точках \(x_0=\pi k\)
6. Функция возрастает на отрезках
$$ -\frac\pi2+2\pi k\leq x\leq\frac\pi2+2\pi k $$Функция убывает на отрезках
$$ \frac\pi2+2\pi k\leq x\leq\frac{3\pi}{2}+2\pi k $$7. Функция непрерывна.
п.3. Примеры
Пример 1.Найдите наименьшее и наибольшее значение функции y=sinx на отрезке:
a) \(\left[\frac\pi6; \frac{3\pi}{4}\right]\) $$ y_{min}=sin\left(\frac\pi6\right)=\frac12,\ \ y_{max}=sin\left(\frac\pi2\right)=1 $$ б) \(\left[\frac{5\pi}{6}; \frac{5\pi}{3}\right]\) $$ y_{min}=sin\left(\frac{3\pi}{2}\right)=-1,\ \ y_{max}=sin\left(\frac{5\pi}{6}\right)=\frac12 $$
Пример 2. 2}{4}\right)\) (см. §29 справочника для 8 класса)
2}{4}\right)\) (см. §29 справочника для 8 класса)
Два корня: \(x_1=0,\ \ x_2=\pi\)
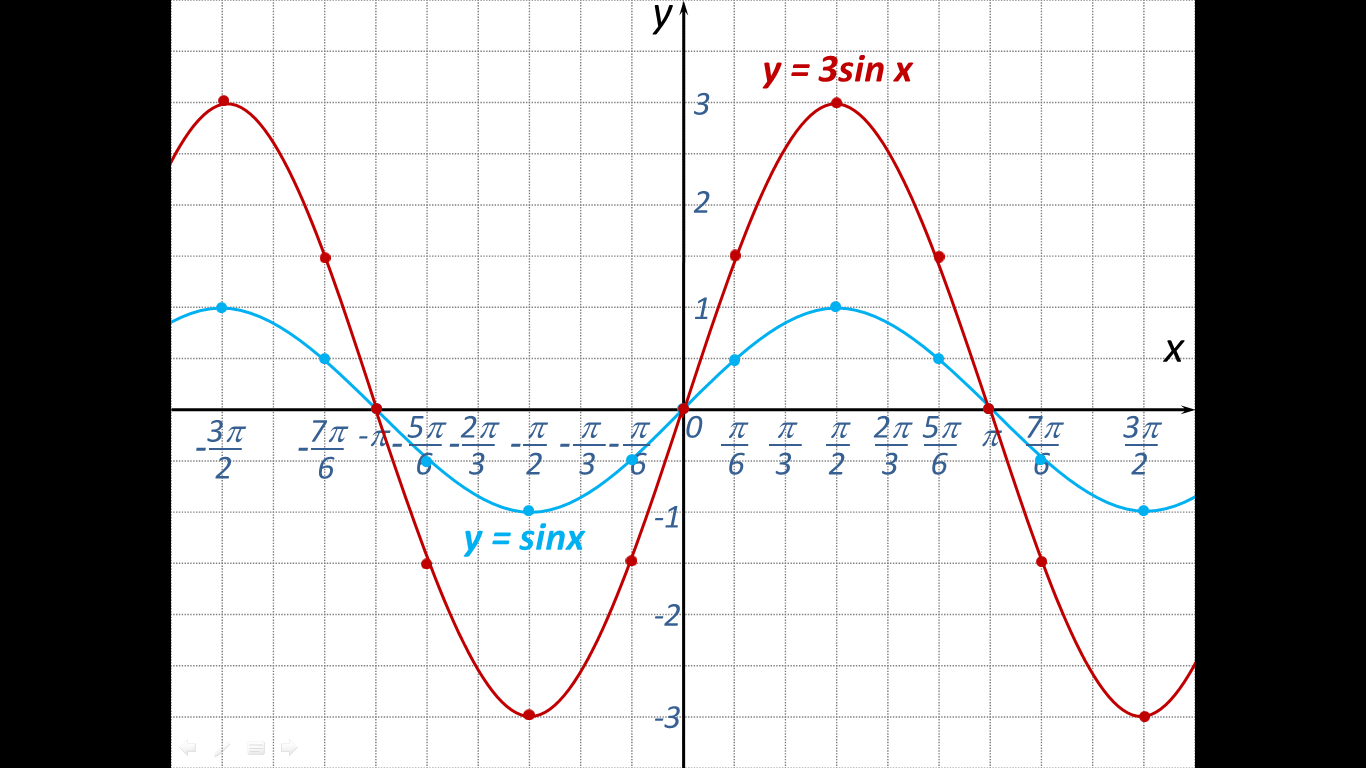
Пример 3. Постройте в одной системе координат графики функций $$ y=sinx,\ \ y=-sinx,\ \ y=2sinx,\ \ y=sinx+2 $$
\(y=-sinx\) – отражение исходной функции \(y=sinx\) относительно оси OX. Область значений \(y\in[-1;1]\).
\(y=2sinx\) – исходная функция растягивается в 2 раза по оси
\(y=sinx+2\) — исходная функция поднимается вверх на 2. Область значений \(y\in[1;3]\).
Пример 4. Постройте в одной системе координат графики функций $$ y=sinx,\ \ y=sin2x,\ \ y=sin\frac{x}{2} $$
Амплитуда колебаний у всех трёх функций одинакова, область значений \(y\in[-1;1]\).
Множитель под синусом изменяет период колебаний.
\(y=sin2x\) — период уменьшается в 2 раза, полная волна укладывается в отрезок \(0\leq x\leq \pi\).
\(y=sin\frac{x}{2}\) — период увеличивается в 2 раза, полная волна укладывается в отрезок \(0\leq x\leq 4\pi\).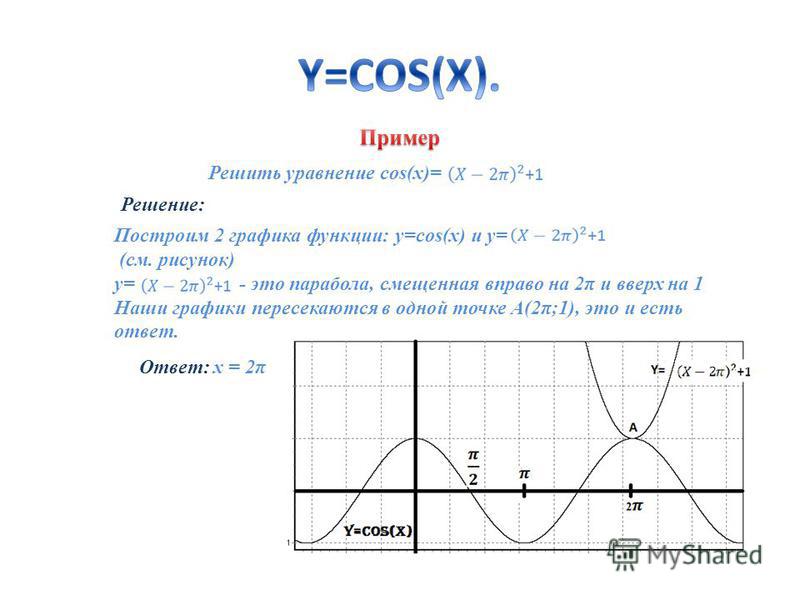
Построить график функции y sin 2. Построение и исследование графика тригонометрической функции y=sinx в табличном процессоре MS Excel. Задачи на синус для самостоятельного решения
Урок и презентация на тему: «Функция y=sin(x). Определения и свойства»
Дополнительные материалы
Уважаемые пользователи, не забывайте оставлять свои комментарии, отзывы, пожелания! Все материалы проверены антивирусной программой.
Пособия и тренажеры в интернет-магазине «Интеграл» для 10 класса от 1С
Решаем задачи по геометрии. Интерактивные задания на построение для 7-10 классов
Программная среда «1С: Математический конструктор 6.1»
Что будем изучать:
- Свойства функции Y=sin(X).
- График функции.
- Как строить график и его масштаб.
- Примеры.
Свойства синуса. Y=sin(X)
Ребята, мы уже познакомились с тригонометрическими функциями числового аргумента. Вы помните их?
Давайте познакомимся поближе с функцией Y=sin(X)
Запишем некоторые свойства этой функции:
1) Область определения – множество действительных чисел.
2) Функция нечетная. Давайте вспомним определение нечетной функции. Функция называется нечетной если
выполняется равенство: y(-x)=-y(x). Как мы помним из формул привидения: sin(-x)=-sin(x). Определение выполнилось, значит Y=sin(X) – нечетная функция.
3) Функция Y=sin(X) возрастает на отрезке и убывает на отрезке [π/2; π]. Когда мы движемся по первой четверти (против часовой стрелки), ордината увеличивается, а при движении по второй четверти она уменьшается.
4) Функция Y=sin(X) ограничена снизу и сверху. Данное свойство следует из того, что
-1 ≤ sin(X) ≤ 1
5) Наименьшее значение функции равно -1 (при х = — π/2+ πk). Наибольшее значение функции равно 1 (при х = π/2+ πk).
Давайте, воспользовавшись свойствами 1-5, построим график функции Y=sin(X). Будем строить наш график последовательно, применяя наши свойства. Начнем строить график на отрезке .
Особое внимание стоит обратить на масштаб. На оси ординат удобнее принять единичный отрезок равный 2 клеточкам, а на оси абсцисс — единичный отрезок (две клеточки) принять равным π/3 (смотрите рисунок).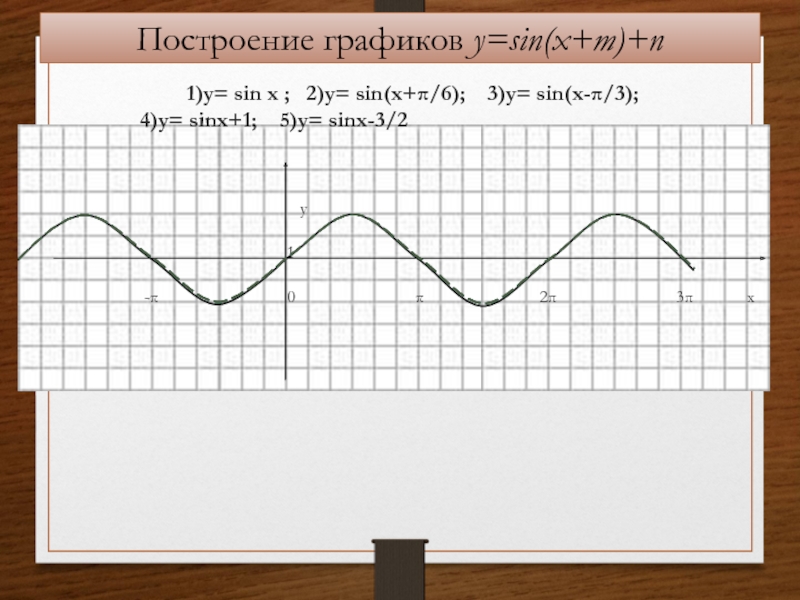
Построение графика функции синус х, y=sin(x)
Посчитаем значения функции на нашем отрезке:
Построим график по нашим точкам, с учетом третьего свойства.
Таблица преобразований для формул привидения
Воспользуемся вторым свойством, которое говорит, что наша функция нечетная, а это значит, что ее можно отразить симметрично относительно начало координат:
Мы знаем, что sin(x+ 2π) = sin(x). Это значит, что на отрезке [- π; π] график выглядит так же, как на отрезке [π; 3π] или или [-3π; — π] и так далее. Нам остается аккуратно перерисовать график на предыдущем рисунке на всю ось абсцисс.
График функции Y=sin(X) называют — синусоидой.
Напишем еще несколько свойств согласно построенному графику:
6) Функция Y=sin(X) возрастает на любом отрезке вида: [- π/2+ 2πk; π/2+ 2πk], k – целое число и убывает на любом отрезке вида: [π/2+ 2πk; 3π/2+ 2πk], k – целое число.
7) Функция Y=sin(X) – непрерывная функция. Посмотрим на график функции и убедимся что у нашей функции нет разрывов, это и означает непрерывность.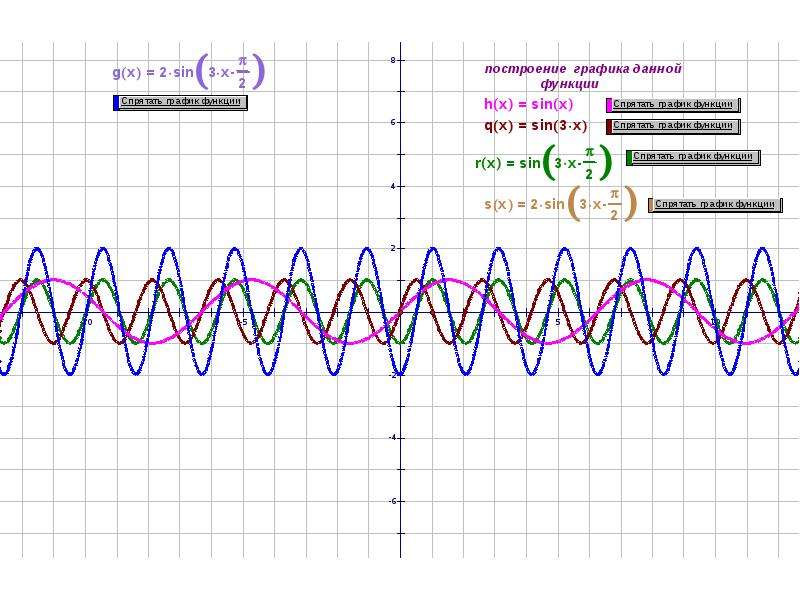
9) Функция Y=sin(X) — периодическая функция. Посмотрим опять на график и увидим, что функция принимает одни и те же значения, через некоторые промежутки.
Примеры задач с синусом
1. Решить уравнение sin(x)= x-π
Решение: Построим 2 графика функции: y=sin(x) и y=x-π (см. рисунок).
Наши графики пересекаются в одной точке А(π;0), это и есть ответ: x = π
2. Построить график функции y=sin(π/6+x)-1
Решение: Искомый график получится путем переноса графика функции y=sin(x) на π/6 единиц влево и 1 единицу вниз.
Решение: Построим график функции и рассмотрим наш отрезок [π/2; 5π/4].
На графике функции видно, что наибольшие и наименьшие значения достигаются на концах отрезка, в точках π/2 и 5π/4 соответственно.
Ответ: sin(π/2) = 1 – наибольшее значение, sin(5π/4) = наименьшее значение.
Задачи на синус для самостоятельного решения
- Решите уравнение: sin(x)= x+3π, sin(x)= x-5π
- Построить график функции y=sin(π/3+x)-2
- Построить график функции y=sin(-2π/3+x)+1
- Найти наибольшее и наименьшее значение функции y=sin(x) на отрезке
- Найти наибольшее и наименьшее значение функции y=sin(x) на отрезке [- π/3; 5π/6]
«Йошкар-Олинский техникум сервисных технологий»
Построение и исследование графика тригонометрической функции y=sinx в табличном процессоре MS Excel
/методическая разработка/
Йошкар – Ола
Тема . Построение и исследование графика тригонометрической функции y = sinx в табличном процессоре MS Excel
Построение и исследование графика тригонометрической функции y = sinx в табличном процессоре MS Excel
Тип урока – интегрированный (получение новых знаний)
Цели:
Дидактическая цель — исследовать поведение графиков тригонометрической функции
Обучающие:
1. Выяснить изменение графика тригонометрической функции y = sin x в зависимости от коэффициентов
2. Показать внедрение компьютерных технологий в обучение математике, интеграцию двух предметов: алгебры и информатики.
3. Формировать навыки использования компьютерных технологий на уроках математики
4. Закрепить навыки исследования функций и построения их графиков
Развивающие:
1. Развивать познавательный интерес учащихся к учебным дисциплинам и умение применять свои знания в практических ситуациях
2. Развивать умения анализировать, сравнивать, выделять главное
Развивать умения анализировать, сравнивать, выделять главное
3. Способствовать повышению общего уровня развития студентов
Воспитывающие :1. Воспитывать самостоятельность, аккуратность, трудолюбие
2. Воспитывать культуру диалога
Формы работы на уроке – комбинированная
Дидактическое оснащение и оборудование:
1. Компьютеры
2. Мультимедийный проектор
4. Раздаточный материал
5. Слайды презентации
Ход урока
I . Организация начала урока
· Приветствие студентов и гостей
· Настрой на урок
II . Целеполагание и актуализация темы
Для исследования функции и построения ее графика требуется много времени, приходится выполнять много громоздких вычислений, это не удобно, на помощь приходят компьютерные технологии.
Сегодня мы научимся строить графики тригонометрических функций в среде табличного процессора MS Excel 2007.
Тема нашего занятия «Построение и исследование графика тригонометрической функции
Из курса алгебры нам известна схема исследования функции и построения ее графика. Давайте вспомним как это сделать.
Слайд 2
Схема исследования функции
1. Область определения функции (D(f))
2. Область значения функции Е(f)
3. Определение четности
4. Периодичность
5. Нули функции (y=0)
6. Промежутки знакопостоянства (у>0, y
7. Промежутки монотонности
8. Экстремумы функции
III . Первичное усвоение нового учебного материала
Откройте программу MS Excel 2007.
Построим график функции y=sinx
Построение графиков в табличном процессоре MS Excel 2007
График данной функции будем строить на отрезке x Є [-2π; 2π]
Значения аргумента будем брать с шагом, чтобы график получился более точным.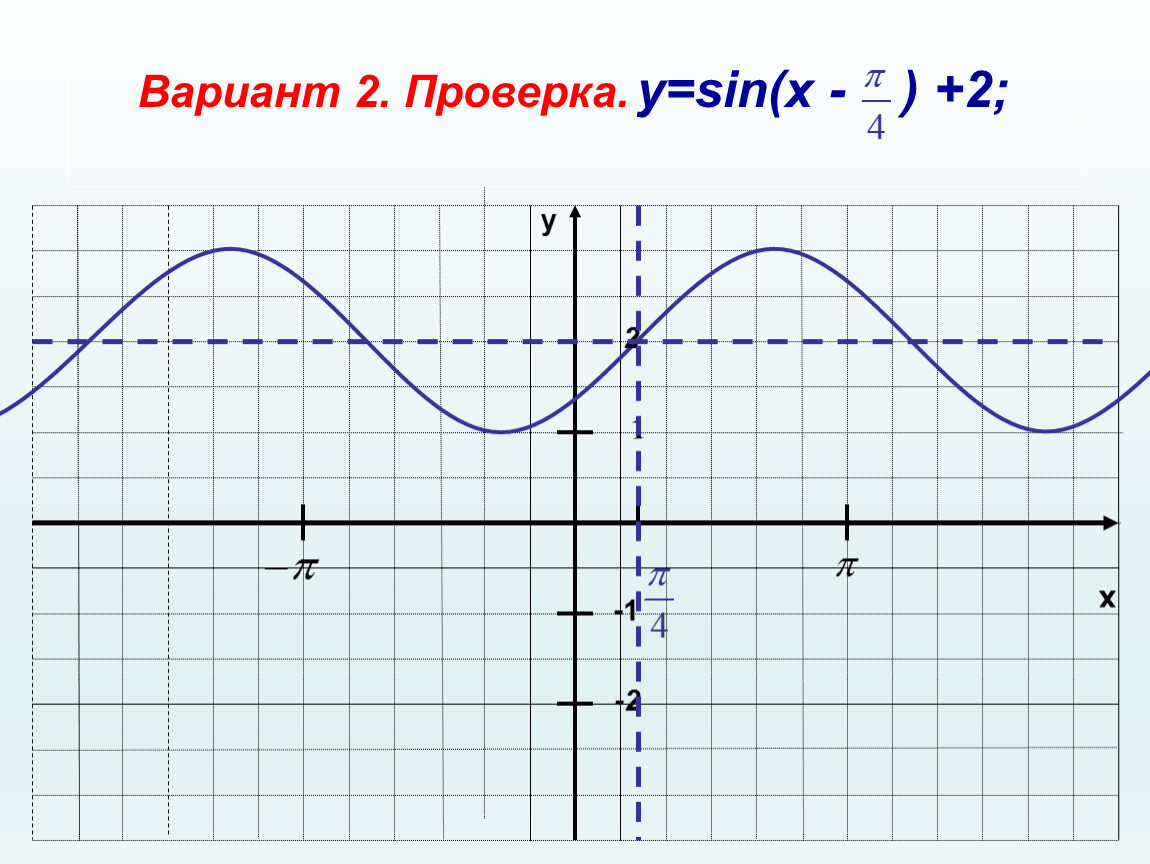
Т. к. редактор работает с числами, переведем радианы в числа, зная что П ≈ 3,14 . (таблица перевода в раздаточном материале).
1. Находим значение функции в точке х=-2П. Для остальных значение аргумента соответствующие значения функции редактор вычисляет автоматически.
2. Теперь у нас имеется таблица со значениями аргумента и функции. С помощью этих данных мы должны построить график этой функции с помощью мастера диаграмм.
3. Для построения графика надо выделить нужный диапазон данных, строки со значениями аргумента и функции
4..jpg»>
Выводы записываем в тетрадь (Слайд 5)
Вывод. График функции вида у=sinx+k получается из графика функции у=sinx с помощью параллельного переноса вдоль оси ОУ на k единиц
Если k >0, то график смещается вверх на k единиц
Если k
Построение и исследование функции вида у= k *sinx, k — const
Задание 2. На рабочем Листе2 в одной системе координат постройте графики функций y = sinx y =2* sinx , y = * sinx , на интервале (-2π; 2π) и проследите как изменяется вид графика.
На рабочем Листе2 в одной системе координат постройте графики функций y = sinx y =2* sinx , y = * sinx , на интервале (-2π; 2π) и проследите как изменяется вид графика.
(Чтобы заново не задавать значение аргумента давайте скопируем имеющиеся значения. Теперь вам надо задать формулу, и по полученной таблице построить график.)
Сравниваем полученные графики. Разбираем вместе с обучающимися поведение графика тригонометрической функции в зависимости от коэффициентов. (Слайд 6)
https://pandia.ru/text/78/510/images/image005_66.gif»>x , на интервале (-2π; 2π) и проследите как изменяется вид графика.
Сравниваем полученные графики. Разбираем вместе с обучающимися поведение графика тригонометрической функции в зависимости от коэффициентов. (Слайд 8)
https://pandia.ru/text/78/510/images/image008_35.jpg»>
Выводы записываем в тетрадь (Слайд 11)
Вывод. График функции вида у= sin(x+k) получается из графика функции у=sinx с помощью параллельного переноса вдоль оси ОХ на k единиц
График функции вида у= sin(x+k) получается из графика функции у=sinx с помощью параллельного переноса вдоль оси ОХ на k единиц
Если k >1, то график смещается вправо вдоль оси ОХ
Если 0
IV . Первичное закрепление полученных знаний
Дифференцированные карточки с заданием на построение и исследование функции при помощи графика
Y=6 *sin(x) | Y= 1-2 sin х | Y= — sin (3х+ ) | |
1. Область определения | |||
2. Область значения | |||
3. | |||
4. Периодичность | |||
5. Промежутки знакопостоянства | |||
6. Промежутки монотонности | |||
Функция возрастает | |||
Функция убывает | |||
7. Экстремумы функции | |||
Минимум | |||
Максимум |
V .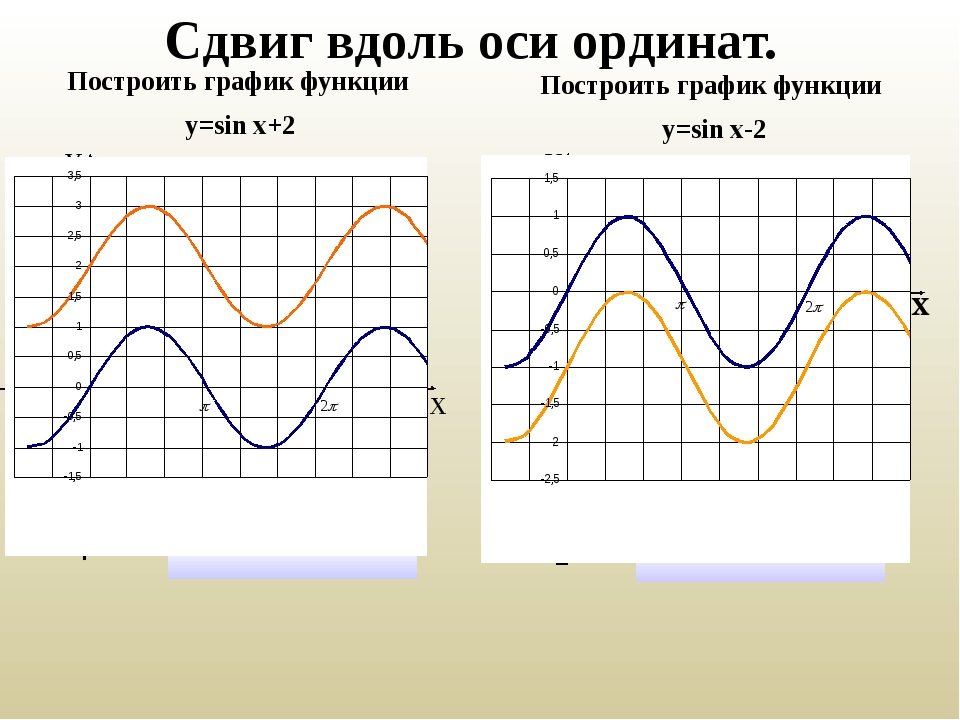 Организация домашнего задания
Организация домашнего задания
Построить график функции y=-2*sinх+1 , исследовать и проверить правильность построения в среде электронной таблицы Microsoft Excel. (Слайд 12)
VI . Рефлексия
Как построить график функции y=sin x? Для начала рассмотрим график синуса на промежутке .
Единичный отрезок берём длиной 2 клеточки тетради. На оси Oy отмечаем единицу.
Для удобства число π/2 округляем до 1,5 (а не до 1,6, как требуется по правилам округления). В этом случае отрезку длиной π/2 соответствуют 3 клеточки.
На оси Ox отмечаем не единичные отрезки, а отрезки длиной π/2 (через каждые 3 клеточки). Соответственно, отрезку длиной π соответствует 6 клеточек, отрезку длиной π/6 — 1 клеточка.
При таком выборе единичного отрезка график, изображённый на листе тетради в клеточку, максимально соответствует графику функции y=sin x.
Составим таблицу значений синуса на промежутке :
Полученные точки отметим на координатной плоскости:
Так как y=sin x — нечётная функция, график синуса симметричен относительно начала отсчёта — точки O(0;0).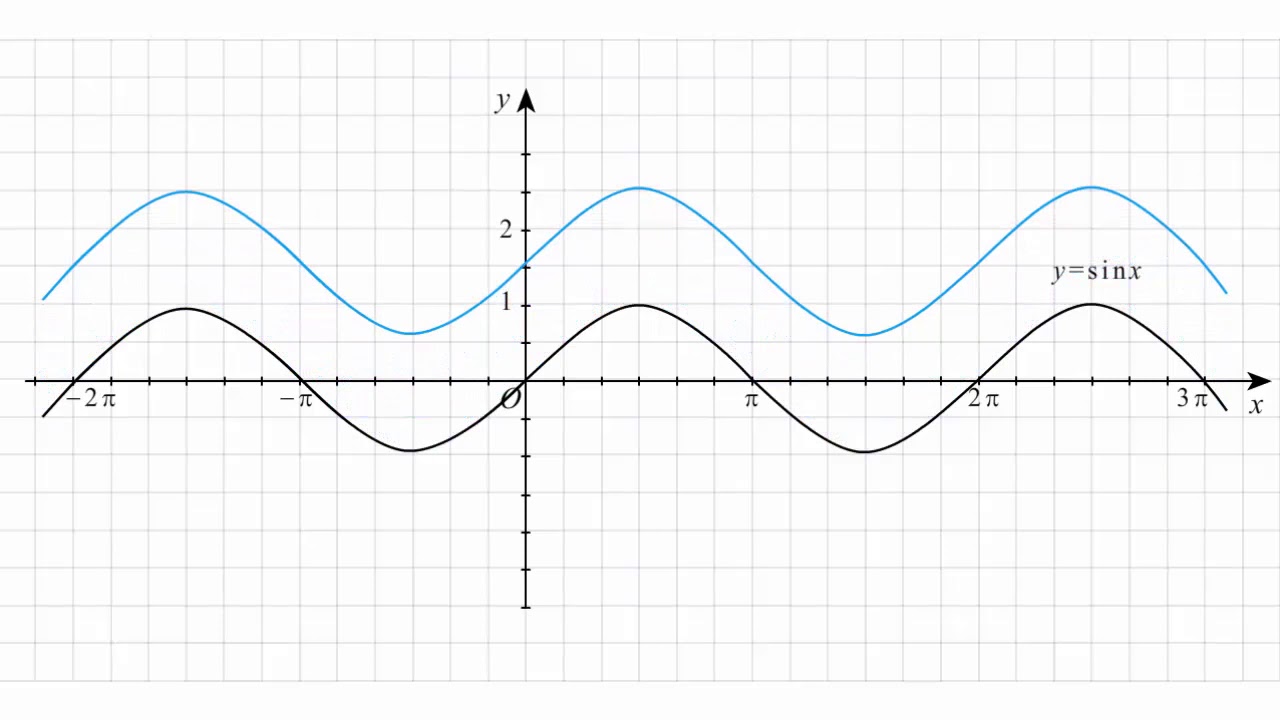 С учётом этого факта продолжим построение графика влево, то точки -π:
С учётом этого факта продолжим построение графика влево, то точки -π:
Функция y=sin x — периодическая с периодом T=2π. Поэтому график функции, взятый на на промежутке [-π;π], повторяется бесконечное число раз вправо и влево.
Теперь мы рассмотрим вопрос о том, как строить графики тригонометрических функций кратных углов ωx , где ω — некоторое положительное число.
Для построения графика функции у = sin ωx сравним эту функцию с уже изученной нами функцией у = sin x . Предположим, что при х = x 0 функция у = sin х принимает значение, равное у 0 . Тогда
у 0 = sin x 0 .
Преобразуем это соотношение следующим образом:
Следовательно, функция у = sin ωx при х = x 0 / ω принимает то же самое значение у 0 , что и функция у = sin х при х = x 0 . А это означает, что функция у = sin ωx повторяет свои значения в ω раз чаще, чем функция у
= sin x .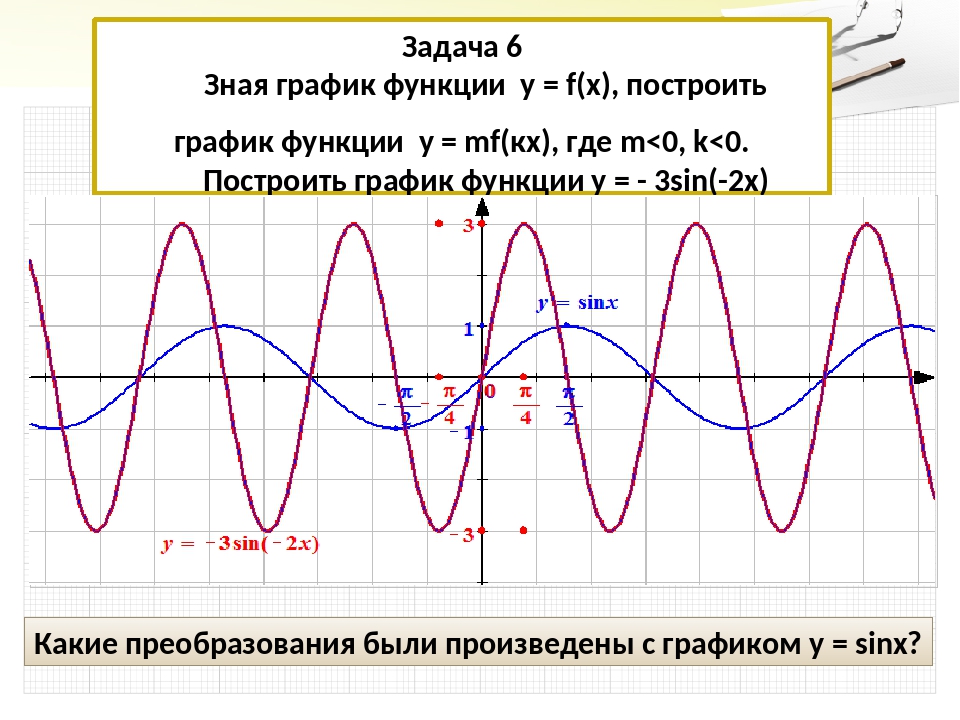 Поэтому график функции у = sin ωx получается путем «сжатия» графика функции у = sin x в ω раз вдоль оси х.
Поэтому график функции у = sin ωx получается путем «сжатия» графика функции у = sin x в ω раз вдоль оси х.
Например, график функции у = sin 2х получается путем «сжатия» синусоиды у = sin x вдвое вдоль оси абсцисс.
График функции у = sin x / 2 получается путем «растяжения» синусоиды у = sin х в два раза (или «сжатия» в 1 / 2 раза) вдоль оси х.
Поскольку функция у = sin ωx повторяет свои значения в ω раз чаще, чем функция
у = sin x , то период ее в ω раз меньше периода функции у = sin x . Например, период функции у = sin 2х равен 2π / 2 = π , а период функции у = sin x / 2 равен π
/ x / 2 = 4π .
Интересно провести исследование поведения функции у = sin аx на примере анимации, которую очень просто можно создать в программе Maple :
Аналогично строятся графики и других тригонометрических функций кратных углов. На рисунке представлен график функции у = cos 2х , который получается путем «сжатия» косинусоиды у = cos х в два раза вдоль оси абсцисс.
На рисунке представлен график функции у = cos 2х , который получается путем «сжатия» косинусоиды у = cos х в два раза вдоль оси абсцисс.
График функции у = cos x / 2 получается путем «растяжения» косинусоиды у = cos х вдвое вдоль оси х.
На рисунке вы видите график функции у = tg 2x , полученный «сжатием» тангенсоиды у = tg x вдвое вдоль оси абсцисс.
График функции у = tg x / 2 , полученный «растяжением» тангенсоиды у = tg x вдвое вдоль оси х.
И, наконец, анимация, выполненная программой Maple:
Упражнения
1. Построить графики данных функций и указать координаты точек пересечения этих графиков с осями координат. Определить периоды данных функций.
а). y = sin 4x / 3 г). y = tg 5x / 6 ж). y = cos 2x / 3
б). у= cos 5x / 3 д). у = ctg 5x / 3 з). у= ctg x / 3
у = ctg 5x / 3 з). у= ctg x / 3
в). y = tg 4x / 3 е). у = sin 2x / 3
2. Определить периоды функций у = sin (πх) и у = tg ( πх / 2 ).
3. Приведите два примера функции, которые принимают все значения от -1 до +1 (включая эти два числа) и изменяются периодически с периодом 10.
4 *. Приведите два примера функций, которые принимают все значения от 0 до 1 (включая эти два числа) и изменяются периодически с периодом π / 2 .
5. Приведите два примера функций, которые принимают все действительные значения и изменяются периодически с периодом 1.
6 *. Приведите два примера функций, которые принимают все отрицательные значения и нуль, но не принимают положительные значения и изменяются периодически с периодом 5.
Урок 4. свойства и график функции y=sinx — Алгебра и начала математического анализа — 11 класс
Алгебра и начала математического анализа, 11 класс
Урок №4. Свойства и график функции .
Свойства и график функции .
Перечень вопросов, рассматриваемых в теме
Глоссарий по теме
Синусоидой называется множество точек плоскости, которое в некоторой системе координат является графиком функции , где a≠0.
Число │a│ называется амплитудой.
Основная литература:
Колягин М.В. Ткачева Ю.М., Федорова Н.Е. и др., под ред. Жижченко А.Б. Алгебра и начала математического анализа (базовый и профильный уровни) 11 кл. М.: Просвещение, 2010.–336 с.
Дополнительная литература:
Шахмейстер, А.Х. Тригонометрия / А.Х. Шахмейстер.— СПб.: Петроглиф, 2014. — 750 с.
Открытые электронные ресурсы:
Открытый банк заданий ЕГЭ ФИПИ [Электронный ресурс].– Режим доступа: http://ege.fipi.ru/
Решу ЕГЭ образовательный портал для подготовки к экзаменам [Электронный ресурс]. – Режим доступа: https://ege.sdamgia.ru/
Теоретический материал для самостоятельного изучения
На прошлом уроке мы говорили о свойствах графика косинуса:
1) область определения функции – множество R всех действительных чисел;
2) Множество значений функции – отрезок [–1;1];
3) Функция косинуса периодическая, ;
4) Функция чётная;
5) Функция принимает:
- значение, равное 0, при ;
- наименьшее значение, равное –1, при
;
- наибольшее значение, равное 1, при ;
6) Функция
- возрастает на отрезке и на отрезках, получаемых сдвигами этого интервала на .

Давайте сравним их со свойствами графика синуса, а для начала определим следующие моменты:
- При движении точки до первой четверти ордината увеличивается;
- При движении точки по второй четверти ордината постепенно уменьшается;
- Функция возрастает на отрезке и убывает на отрезке .
Свойства функции :
1) D(y) =R;
2) E (y) =[–1;1];
3) Период функции равен ;
4) Функция чётная/нечётная;
5) Функция принимает:
6) Функция
- возрастает на отрезке и на отрезках, получаемых сдвигами этого отрезка на ;
- убывает на отрезке и на отрезках, получаемых сдвигами этого отрезка на .
Изменяя амплитуду и значение аргумента функции синуса график ведет себя следующим образом (рис.1)
Рис. 1 – графики синуса
Сдвиг графика влево/вправо вдоль оси абсцисс
Если к аргументу функции добавляется постоянная, то происходит сдвиг (параллельный перенос) графика вдоль оси Ох.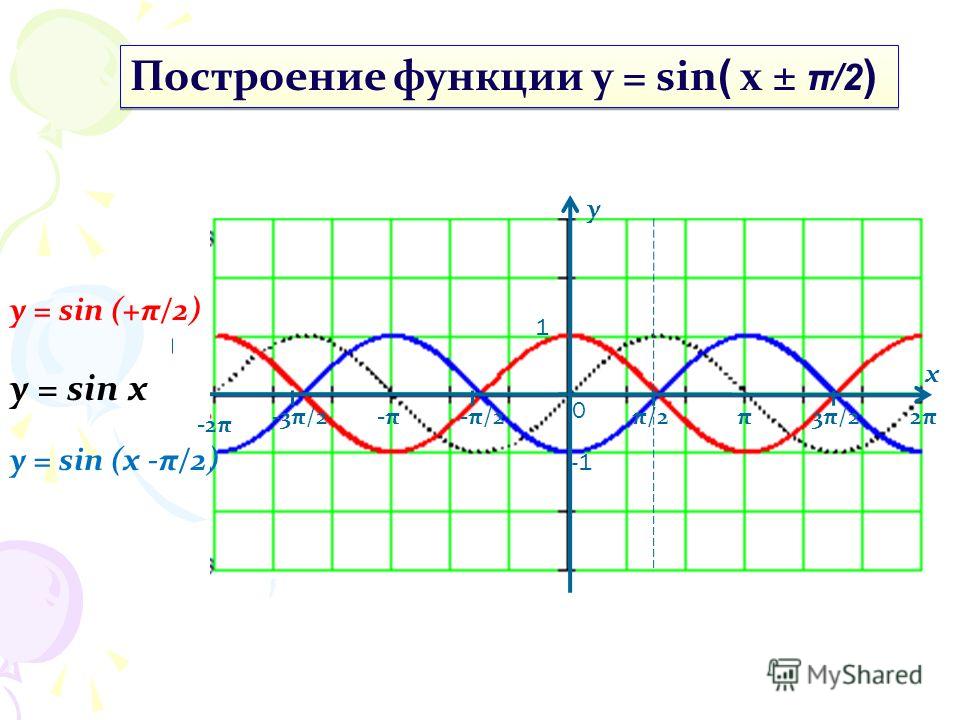
Правило:
1) чтобы построить график функции , нужно сдвинуть график вдоль оси Ох на b единиц влево;
2) чтобы построить график функции , нужно график сдвинуть вдоль оси ОХ на b единиц вправо.
Теоретический материал для самостоятельного изучения
Актуализация знаний
1. На следующие утверждения нужно ответить верно/неверно.
1) Тригонометрическая функция определена на всей числовой прямой.
2) График нечетной функции можно построить с помощью преобразования симметрии относительно оси Оу.
3) График тригонометрической функции можно построить, используя одну главную полуволну.
Ответ: верно, неверно, верно.
2. Вспомним, что мы уже знаем о функции , ответив на вопросы:
1) Какие значения может принимать переменная х. Какова область определения этой функции?
2) В каком промежутке заключены значения выражения . Назови наибольшее и наименьшее значения функции .
3) Функция синуса чётная или нечётная?
Ответ:1) 𝑥∈𝑅; 2) [–1;1]; 𝑦𝑚𝑎𝑥=3, 𝑦𝑚𝑖𝑛=–3; 3) чётная;
Примеры и разборы решения заданий тренировочного модуля:
Пример 1. Найдем все корни уравнения , принадлежащие отрезку .
Найдем все корни уравнения , принадлежащие отрезку .
Построим графики функций и (рис. 6)
Рис. 7 – графики функций и .
Графики пересекаются в четырёх точках, абсциссы которых являются корнями уравнения . На выбранном отрезке от корни уравнения симметричны: и . Из рисунка видно, что симметричность корней объясняется периодичностью функции: аналогично для
Ответ: ; .
Пример 2.Найти все решения неравенства , принадлежащие отрезку .
Из рисунка 7 видно, что график функции лежит выше графика функции на промежутках и и
Ответ: , ,
Преобразование графика функции y=sin x
Преобразование графика функции y = sin x
0 (положительная) для всех x ∈ (2π·k, π+2π·k), sin x (отрицательная) для всех x ∈ (π+2π·k, 2π+2π·k), Функция возрастает от −1 до 1 на промежутках: [- π /2+2 π k ; π /2+2 π k] Функция убывает от 1 до -1 на промежутках: [ π /2+2 π k ; 3 π /2+2 π k] Наибольшее значение функции sin x = 1 в точках: X= π /2 + 2 π k , Наименьшее значение функции sin x = −1 в точках: X= — π /2 + 2 π k , «- Область определения функции — множество R всех действительных чисел
- Множество значений функции — отрезок [-1; 1],
- синус — функция ограниченная .

- Функция нечетная: sin(−x)=−sin x для всех х ∈ R . График функции симметричен относительно начала координат.
- Функция периодическая с наименьшим положительным периодом 2π:sin(x+2π·k) = sin x, где k ∈ Z для всех х ∈ R .
- sin x = 0 при x = π·k, k ∈ Z .
- sin x 0 (положительная) для всех x ∈ (2π·k, π+2π·k),
- sin x (отрицательная) для всех x ∈ (π+2π·k, 2π+2π·k),
- Функция возрастает от −1 до 1 на промежутках: [- π /2+2 π k ; π /2+2 π k]
- Функция убывает от 1 до -1 на промежутках: [ π /2+2 π k ; 3 π /2+2 π k]
- Наибольшее значение функции sin x = 1 в точках: X= π /2 + 2 π k ,
- Наименьшее значение функции sin x = −1 в точках: X= — π /2 + 2 π k ,
- Область определения функции
- Множество значений функции
- Четность функции
- Ограниченность функции
- Промежутки знакопостоянства
- Монотонность функции
- Наибольшее и наименьшее значения функции
- R
- [-1 ;1 ]
- Нечетная.
 График симметричен относительно О.
График симметричен относительно О. - Ограниченная. Сверху прямой y=1 , снизу прямой y=-1 .
- sin x 0 (положительная) для всех x ∈ (2π·k, π+2π·k), sin x
- Функция возрастает от −1 до 1 на промежутках: [- π /2+2 π k ; π /2+2 π k] , Функция убывает от 1 до -1 на промежутках: [ π /2+2 π k ; 3 π /2+2 π k]
- Наибольшее значение функции sin x = 1 в точках: X= π /2 + 2 π k , Наименьшее значение функции sin x = −1 в точках: X= — π /2 + 2 π k ,
Растяжение от оси X с коэффициентом m : y=m sinx
График функции y=m sinx получается из графика функции
y= sinx умножением ординат соответствующих точек графика функции y= sinx на число m .
Если m1 – растяжение от оси X с коэффициентом m
Если 0сжатие к оси X с коэффициентом 1/ m
Построить график функции
У= 2 sin x
У= 1/2 sin x
1, то сжатие к оси Y с коэффициентом к Если 0 «Сжатие к оси ординат с коэффициентом k : y= sin(kx)
- График функции y= sin(kx) получается из графика функции
y= sinx путем уменьшения в k раз абсцисс соответствующих точек графика функции y= sinx
Если к 1, то сжатие к оси Y с коэффициентом к
Если 0
Сдвиг вдоль оси абсцисс: y= sin(x+ β )
- График функции y= sin(x+ β ) получается из графика функции
y= sin x путем параллельного переноса на β влево (вправо) вдоль оси X .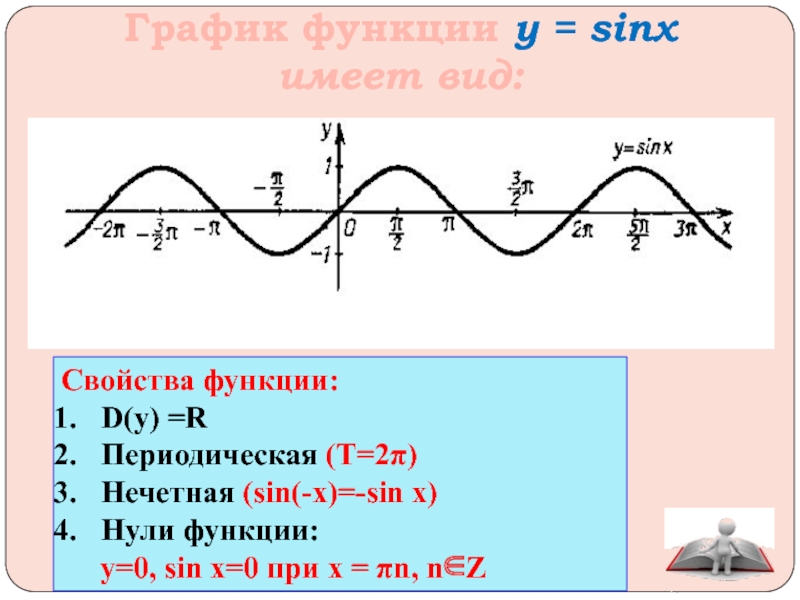
- Y=sin (x+ π /3)
- Y=sin (x – π /4)
сдвиг вдоль оси Y : Y = sinx + n
- График функции Y = sinx + n получается из графика функции
Y = sinx в результате параллельного переноса вдоль оси Y на n вверх (вниз).
Дети и учеба — Информационный портал
ГРАФИКИ ФУНКЦИЙ
Функция синус
— множество R всех действительных чисел.
Множество значений функции — отрезок [-1; 1], т.е. синус функция — ограниченная .
Функция нечетная: sin(−x)=−sin x для всех х ∈ R .
Функция периодическая
sin(x+2π· k) = sin x, где k ∈ Z для всех х ∈ R .
sin x = 0 при x = π·k , k ∈ Z .
sin x > 0 (положительная) для всех x ∈ (2π·k , π+2π·k ), k ∈ Z .
sin x (отрицательная) для всех x ∈ (π+2π·k
, 2π+2π·k
),
k ∈ Z .
Функция косинус
Область определения функции — множество R всех действительных чисел.
Множество значений функции — отрезок [-1; 1], т.е. косинус функция — ограниченная .
Функция четная: cos(−x)=cos x для всех х ∈ R .
Функция периодическая с наименьшим положительным периодом 2π :
cos(x+2π· k ) = cos x, где k ∈ Z для всех х ∈ R .
| cos x = 0 при | |
| cos x > 0 для всех | |
| cos x для всех | |
| Функция возрастает от −1 до 1 на промежутках: | |
| Функция убывает от −1 до 1 на промежутках: | |
| Наибольшее значение функции sin x = 1 в точках: | |
| Наименьшее значение функции sin x = −1 в точках: |
Множество значений функции — вся числовая прямая, т.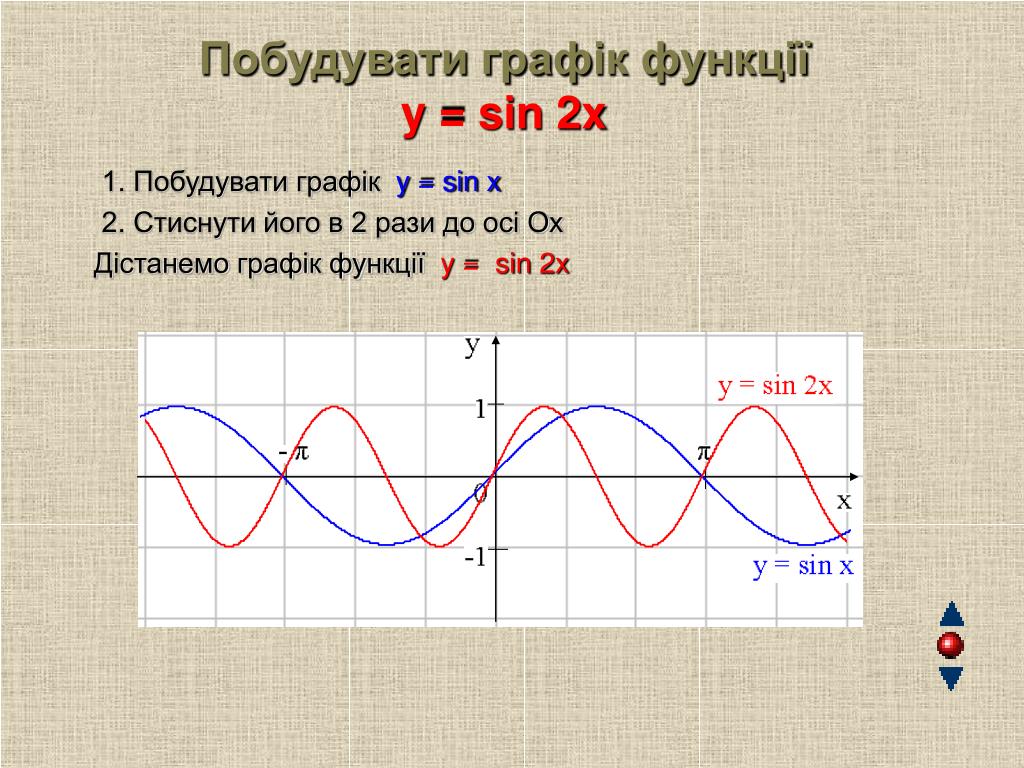 е. тангенс — функция неограниченная .
е. тангенс — функция неограниченная .
Функция нечетная: tg(−x)=−tg x
График функции симметричен относительно оси OY.
Функция периодическая с наименьшим положительным периодом π , т.е. tg(x+π· k ) = tg x, k ∈ Z для всех х из области определения.
Функция котангенс
Множество значений функции — вся числовая прямая, т.е. котангенс — функция неограниченная .
Функция нечетная: ctg(−x)=−ctg x для всех х из области определения.График функции симметричен относительно оси OY.
Функция периодическая с наименьшим положительным периодом π , т.е. ctg(x+π· k )=ctg x, k ∈ Z для всех х из области определения.
Функция арксинус
Область определения функции — отрезок [-1; 1]
Множество значений функции — отрезок -π /2 arcsin x π /2, т.е. арксинус — функция ограниченная .
Функция нечетная: arcsin(−x)=−arcsin x для всех х ∈ R .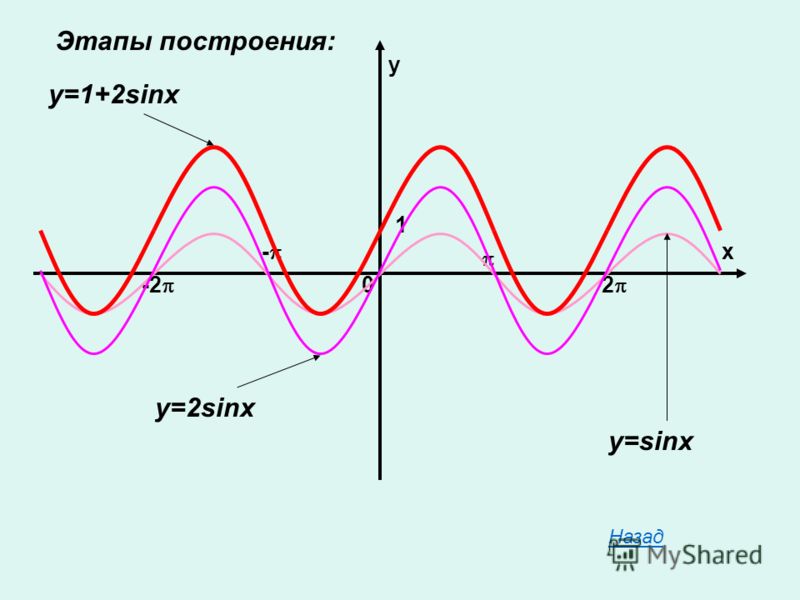
График функции симметричен относительно начала координат.
На всей области определения.
Функция арккосинус
Область определения функции — отрезок [-1; 1]
Множество значений функции — отрезок 0 arccos x π , т.е. арккосинус — функция ограниченная .
Функция является возрастающей на всей области определения.
Функция арктангенс
Область определения функции — множество R всех действительных чисел.
Множество значений функции — отрезок 0 π, т.е. арктангенс — функция ограниченная .
Функция нечетная: arctg(−x)=−arctg x для всех х ∈ R .
График функции симметричен относительно начала координат.
Функция является возрастающей на всей области определения.
Функция арккотангенс
Область определения функции — множество R всех действительных чисел.
Множество значений функции — отрезок 0 π, т. е. арккотангенс — функция ограниченная .
е. арккотангенс — функция ограниченная .
Функция не является ни четной, ни нечетной.
График функции несимметричен ни относительно начала координат, ни относительно оси Оy.
Функция является убывающей на всей области определения.
На этом уроке мы подробно рассмотрим функцию у = sin х, ее основные свойства и график. В начале урока дадим определение тригонометрической функции у = sin t на координатной окружности и рассмотрим график функции на окружности и прямой. Покажем периодичность этой функции на графике и рассмотрим основные свойства функции. В конце урока решим несколько простейших задач с использованием графика функции и ее свойств.
Тема: Тригонометрические функции
Урок: Функция y=sinx, её основные свойства и график
При рассмотрении функции важно каждому значению аргумента поставить в соответствие единственное значение функции. Этот закон соответствия и называется функцией.
Определим закон соответствия для .
Любому действительному числу соответствует единственная точка на единичной окружности У точки есть единственная ордината, которая и называется синусом числа (рис. 1).
Каждому значению аргумента ставится в соответствие единственное значение функции.
Из определения синуса вытекают очевидные свойства.
На рисунке видно, что т.к. это ордината точки единичной окружности.
Рассмотрим график функции . Вспомним геометрическую интерпретацию аргумента. Аргумент — это центральный угол, измеряемый в радианах. По оси мы будем откладывать действительные числа или углы в радианах, по оси соответствующие значения функции.
Например, угол на единичной окружности соответствует точке на графике (рис. 2)
Мы получили график функции на участке Но зная период синуса мы можем изобразить график функции на всей области определения (рис. 3).
Основным периодом функции является Это значит, что график можно получить на отрезке а затем продолжить на всю область определения.
Рассмотрим свойства функции :
1) Область определения:
2) Область значений:
3) Функция нечетная:
4) Наименьший положительный период:
5) Координаты точек пересечения графика с осью абсцисс:
6) Координаты точки пересечения графика с осью ординат:
7) Промежутки, на которых функция принимает положительные значения:
8) Промежутки, на которых функция принимает отрицательные значения:
9) Промежутки возрастания:
10) Промежутки убывания:
11) Точки минимума:
12) Минимум функции:
13) Точки максимума:
14) Максимум функции:
Мы рассмотрели свойства функции и её график. Свойства неоднократно будут использоваться при решении задач.
Список литературы
1. Алгебра и начала анализа, 10 класс (в двух частях). Учебник для общеобразовательных учреждений (профильный уровень) под ред. А. Г. Мордковича. -М.: Мнемозина, 2009.
2. Алгебра и начала анализа, 10 класс (в двух частях). Задачник для общеобразовательных учреждений (профильный уровень) под ред. А. Г. Мордковича. -М.: Мнемозина, 2007.
3. Виленкин Н.Я., Ивашев-Мусатов О.С., Шварцбурд С.И. Алгебра и математический анализ для 10 класса (учебное пособие для учащихся школ и классов с углубленным изучением математики).-М.: Просвещение, 1996.
4. Галицкий М.Л., Мошкович М.М., Шварцбурд С.И. Углубленное изучение алгебры и математического анализа.-М.: Просвещение, 1997.
5. Сборник задач по математике для поступающих во ВТУЗы (под ред. М.И.Сканави).-М.:Высшая школа, 1992.
6. Мерзляк А.Г., Полонский В.Б., Якир М.С. Алгебраический тренажер.-К.: А.С.К., 1997.
7. Саакян С.М., Гольдман А.М., Денисов Д.В. Задачи по алгебре и началам анализа (пособие для учащихся 10-11 классов общеобразов. учреждений).-М.: Просвещение, 2003.
8. Карп А.П. Сборник задач по алгебре и началам анализа: учеб. пособие для 10-11 кл. с углубл. изуч. математики.-М.: Просвещение, 2006.
Домашнее задание
Алгебра и начала анализа, 10 класс (в двух частях). Задачник для общеобразовательных учреждений (профильный уровень) под ред.
А. Г. Мордковича. -М.: Мнемозина, 2007.
№№ 16.4, 16.5, 16.8.
Дополнительные веб-ресурсы
3. Образовательный портал для подготовки к экзаменам ().
Как построить график функции y=sin x? Для начала рассмотрим график синуса на промежутке .
Единичный отрезок берём длиной 2 клеточки тетради. На оси Oy отмечаем единицу.
Для удобства число π/2 округляем до 1,5 (а не до 1,6, как требуется по правилам округления). В этом случае отрезку длиной π/2 соответствуют 3 клеточки.
На оси Ox отмечаем не единичные отрезки, а отрезки длиной π/2 (через каждые 3 клеточки). Соответственно, отрезку длиной π соответствует 6 клеточек, отрезку длиной π/6 — 1 клеточка.
При таком выборе единичного отрезка график, изображённый на листе тетради в клеточку, максимально соответствует графику функции y=sin x.
Составим таблицу значений синуса на промежутке :
Полученные точки отметим на координатной плоскости:
Так как y=sin x — нечётная функция, график синуса симметричен относительно начала отсчёта — точки O(0;0). С учётом этого факта продолжим построение графика влево, то точки -π:
Функция y=sin x — периодическая с периодом T=2π. Поэтому график функции, взятый на на промежутке [-π;π], повторяется бесконечное число раз вправо и влево.
Урок и презентация на тему: «Функция y=sin(x). Определения и свойства»
Дополнительные материалы
Уважаемые пользователи, не забывайте оставлять свои комментарии, отзывы, пожелания! Все материалы проверены антивирусной программой.
Пособия и тренажеры в интернет-магазине «Интеграл» для 10 класса от 1С
Решаем задачи по геометрии. Интерактивные задания на построение для 7-10 классов
Программная среда «1С: Математический конструктор 6.1»
Что будем изучать:
- Свойства функции Y=sin(X).
- График функции.
- Как строить график и его масштаб.
- Примеры.
Свойства синуса. Y=sin(X)
Ребята, мы уже познакомились с тригонометрическими функциями числового аргумента. Вы помните их?
Давайте познакомимся поближе с функцией Y=sin(X)
Запишем некоторые свойства этой функции:
1) Область определения – множество действительных чисел.
2) Функция нечетная. Давайте вспомним определение нечетной функции. Функция называется нечетной если
выполняется равенство: y(-x)=-y(x). Как мы помним из формул привидения: sin(-x)=-sin(x). Определение выполнилось, значит Y=sin(X) – нечетная функция.
3) Функция Y=sin(X) возрастает на отрезке и убывает на отрезке [π/2; π]. Когда мы движемся по первой четверти (против часовой стрелки), ордината увеличивается, а при движении по второй четверти она уменьшается.
4) Функция Y=sin(X) ограничена снизу и сверху. Данное свойство следует из того, что
-1 ≤ sin(X) ≤ 1
5) Наименьшее значение функции равно -1 (при х = — π/2+ πk). Наибольшее значение функции равно 1 (при х = π/2+ πk).
Давайте, воспользовавшись свойствами 1-5, построим график функции Y=sin(X). Будем строить наш график последовательно, применяя наши свойства. Начнем строить график на отрезке .
Особое внимание стоит обратить на масштаб. На оси ординат удобнее принять единичный отрезок равный 2 клеточкам, а на оси абсцисс — единичный отрезок (две клеточки) принять равным π/3 (смотрите рисунок).
Построение графика функции синус х, y=sin(x)
Посчитаем значения функции на нашем отрезке:
Построим график по нашим точкам, с учетом третьего свойства.
Таблица преобразований для формул привидения
Воспользуемся вторым свойством, которое говорит, что наша функция нечетная, а это значит, что ее можно отразить симметрично относительно начало координат:
Мы знаем, что sin(x+ 2π) = sin(x). Это значит, что на отрезке [- π; π] график выглядит так же, как на отрезке [π; 3π] или или [-3π; — π] и так далее. Нам остается аккуратно перерисовать график на предыдущем рисунке на всю ось абсцисс.
График функции Y=sin(X) называют — синусоидой.
Напишем еще несколько свойств согласно построенному графику:
6) Функция Y=sin(X) возрастает на любом отрезке вида: [- π/2+ 2πk; π/2+ 2πk], k – целое число и убывает на любом отрезке вида: [π/2+ 2πk; 3π/2+ 2πk], k – целое число.
7) Функция Y=sin(X) – непрерывная функция. Посмотрим на график функции и убедимся что у нашей функции нет разрывов, это и означает непрерывность.
8) Область значений: отрезок [- 1; 1]. Это также хорошо видно из графика функции.
9) Функция Y=sin(X) — периодическая функция. Посмотрим опять на график и увидим, что функция принимает одни и те же значения, через некоторые промежутки.
Примеры задач с синусом
1. Решить уравнение sin(x)= x-π
Решение: Построим 2 графика функции: y=sin(x) и y=x-π (см. рисунок).
Наши графики пересекаются в одной точке А(π;0), это и есть ответ: x = π
2. Построить график функции y=sin(π/6+x)-1
Решение: Искомый график получится путем переноса графика функции y=sin(x) на π/6 единиц влево и 1 единицу вниз.
Решение: Построим график функции и рассмотрим наш отрезок [π/2; 5π/4].
На графике функции видно, что наибольшие и наименьшие значения достигаются на концах отрезка, в точках π/2 и 5π/4 соответственно.
Ответ: sin(π/2) = 1 – наибольшее значение, sin(5π/4) = наименьшее значение.
Задачи на синус для самостоятельного решения
- Решите уравнение: sin(x)= x+3π, sin(x)= x-5π
- Построить график функции y=sin(π/3+x)-2
- Построить график функции y=sin(-2π/3+x)+1
- Найти наибольшее и наименьшее значение функции y=sin(x) на отрезке
- Найти наибольшее и наименьшее значение функции y=sin(x) на отрезке [- π/3; 5π/6]
Х y O Единичная тригонометрическая окружность
3 =180 3,14 рад R R О Р М R Рассмотрим окружность радиуса R. Построим MOP: МР = R 1 радиан Величина МОР равна 1 радиан МР =1рад МОР 57 17= 1рад Радианная мера угла
4 Длина окружности выражается формулой C=2 R, где R – радиус окружности. 3, Окружность, радиус которой равен 1, называется … Точки М,Р,К,N – назовем узловыми. Отметим точки А,В,С. Длину единичной окружности удобно измерять в радианах. Если R=1, то С=2 рад! Наименование радиан обычно опускают. y х К Р С В А Длина дуги половины окружности равна рад. М N рад – четверть длины окружности рад – три четверти длины окружности О 1 единичной Радианная мера угла
uk-badge uk-margin-small-right»> 5 Градусная мера Радианная мера0 Итак, величину угла поворота точки, а также величину дуги единичной окружности, можно задавать: I четверть II четверть III четверть IV четверть О в градусной мере в радианной мере Радианная мера угла 0 2 I четверть II четверть III четверть IV четверть О 2
6 «Размотаем» окружность как нить на координатный луч с началом в точке 0 Установим соответствие между множеством действительных чисел на числовой прямой и точками единичной окружности. Такое «разматывание» можно продолжать бесконечно. 3,14 0 Построение графика х y=sin x
13 Преобразование графиков Функция Преобразование 1 y= f (x) + mПараллельный перенос вдоль оси OY на m единиц 2 y= f (x – n)Параллельный перенос вдоль оси OX на n единиц 3 y=А f (x) Растяжение вдоль оси OY относительно оси OX в А раз 4 y= f (k x)Сжатие вдоль оси OX относительно оси OY в k раз 5 y= – f (x) Симметричное отражение относительно оси OX 6 y= f (– x) Симметричное отражение относительно оси OY y = f (x)
20 Построим график функции y= 3 sin(2x+ /3)–2 Этапы построения: 1. y= sin x – синусоида 3. y= sin(2x+ /3) – перенос на /3 единиц влево 4. y= 3 sin(2x+ /3) – растяжение в 3 раза вдоль оси Oy 2. y= sin 2x – сжатие в 2 раза вдоль оси Ох 5. y= 3 sin(2x+ /3)–2 – перенос на 2 единицы вниз
26 Преобразование графиков Функция Преобразование 1 y=sin(kx)Сжатие вдоль оси OX относительно оси OY в k раз 2 y=sin(x–m)Параллельный перенос вдоль оси OX на m единиц 3 y=А sin x Растяжение вдоль оси OY относительно оси OX в А раз 4 y=sin x+nПараллельный перенос вдоль оси OY на n единиц 5 y= – sin x Симметричное отражение относительно оси OX 6 y= sin (–x) Симметричное отражение относительно оси OY y = Asin(kx–n)+m
28 1.Функция y=sin x существует при всех действительных значениях x, причем, график ее является сплошной линией (без разрывов), т.е. функция непрерывна. 2.Функция y=sin x нечетная, ее график симметричен относительно начала координат 3.Наибольшие и наименьшие значения. Все возможные значения функции sinx ограничены неравенством -1 sinx 1, причем 4. Нули функции (точки пересечения графика функции с осью абсцисс): sinx=0, если x= n. (n Z) Некоторые свойства функции y=sinx sin x= – 1, если sin x=1, если
10 класс. Алгебра. Тригонометрические функции. Функции у=sinx, y=cosx, их свойства, графики, типовые задачи. — Функция y=sinx, ее основные свойства, график и типовые задачи.
Комментарии преподавателяФункция y=sint, её свойства и типовые задачи
На прошлом уроке мы рассмотрели основные свойства функции и сейчас используем их при решении задач.
Подробно рассмотрим поведение функции на промежутке и отметим основные точки (рис. 1).
Теперь те же точки поместим в числовую окружность на отрезке (рис. 2).
Отметим некоторые особенности функции при
1) Монотонное возрастание функции от до
2) Функция пробегает все свои возможные значения,
Рассмотрим несколько задач, при решении которых очень важное значение имеет монотонность функции.
Задача 1.
a) Найти наибольшее значение функции на отрезке
Решение:
Функция монотонно возрастает на указанном промежутке, значит, наибольшее значение принимает на правом конце отрезка, (рис. 3).
b) Найти наименьшее значение функции на отрезке
Решение:
Функция монотонно возрастает на указанном отрезке, значит, наименьшее значение принимает на его левом конце, (рис. 3).
Ответ: a) 1; b)
Задача 2. Если аргумент меняется в заданных пределах, то найдите, в каких пределах меняется функция . Найти наименьшее и наибольшее значение функции.
a)
Решение:
Функция монотонно возрастает на отрезке значит,
(рис. 4).
Ответ:
b)
Решение:
На заданном промежутке функция немонотонна (рис. 5).
На графике мы видим, что функция меняется в пределах
Ответ:
Задача 3. Найти количество решений уравнения на промежутке
Решение:
На заданном промежутке функция монотонна, значит, каждое свое значение она принимает при единственном значении аргумента (рис. 1). Поэтому уравнение на данном отрезке имеет единственное решение.
Важнейшая особенность функции на отрезке монотонность функции. Поэтому и прямая и обратная задачи тут имеют одно решение.
1. Прямая задача – заданному значению аргумента соответствует единственное значение функции.
Например:
2. Обратная задача – заданное значение монотонной функции достигается только при одном значении аргумента.
Например: Если
Если
Если
Задача 4. Построить график функции
Решение:
Построим график функции В силу периодичности достаточно будет рассмотреть график на участке
Для получения искомого графика кривую необходимо сдвинуть на вправо по оси x (рис. 6).
Вспомним общее правило: Кривая получается сдвигом кривой на вправо по оси x.
Задача 5. Найти наибольшее и наименьшее значения функции на отрезке
Решение (рис. 7).
Ответ:
Задача 6. Найти пределы изменения функции на отрезке
Решение (рис. 8).
Ответ:
Задача 7. Найти все значения параметра, при каждом из которых уравнения имеют хотя бы одно решение.
a)
b)
Решение:
a) Решим задачу графическим способом.
Построим график функции на участке Для этого необходимо построить график функции отобразить его симметрично относительно оси x и сдвинуть на 1 вверх по оси y (рис. 9).
Чтобы уравнение имело хотя бы одно решение, график должен пересекаться прямой хотя бы в одной точке.
Ответ:
b) Построим график функции (рис. 10).
Ответ:
Задача 8. Найти число решений уравнения
Решение:
Построим в одних координатных осях графики функций
График функции парабола , сдвинутая на вправо по оси x (рис. 11).
На промежутке возрастает, а убывает. Значит, на этом промежутке есть только одно решение уравнения .
На промежутке убывает, возрастает, значит, решение уравнения на этом промежутке также единственное. Всего уравнение имеет два решения.
Ответ: Два решения.
Задача 9. Решить уравнение
Решение:
Построим графики функций (рис. 12).
На рисунке видно, что построенные графики функций имеют только одну общую точку с абсциссой
Ответ:
Мы рассмотрели график функции подробно изучили особенности ее поведения на промежутке использовали особенности и свойства функции при решении задач, в том числе и задач с параметром.
ИСТОЧНИК
http://interneturok.ru/ru/school/algebra/10-klass/trigonometricheskie-funkcii/funktsiya-y-sinx-eyo-svoystva-grafik-i-tipovye-zadachi
http://www.youtube.com/watch?v=deeOFMi_uwM
http://powpt.ru/uploads/posts/2013-08/1377622534_5.png
http://dok.opredelim.com/pars_docs/refs/50/49678/img9.jpg
http://11book.ru/images/shcoolbook_ru/10/10_a_mord_baz.pdf
http://vklasse.org/10-klass/reshebniki/algebra/ag-mordkovich-2009-zadachnik
Графическая функция синуса
В тригонометрические соотношения также может рассматриваться как функция переменной, которая является мерой угла. Эту угловую меру можно указать в градусы или же радианы . Здесь мы будем использовать радианы.
График синус функция у знак равно грех ( Икс ) выглядит так:
Свойства синусоидальной функции, у знак равно грех ( Икс )Домен : ( — ∞ , ∞ )
Диапазон : [ — 1 , 1 ] или же — 1 ≤ у ≤ 1
у -перехват : ( 0 , 0 )
Икс -перехват : п π , где п целое число.
Период: 2 π
Непрерывность: непрерывно горит ( — ∞ , ∞ )
Симметрия: происхождение (нечетная функция)
Максимальное значение у знак равно грех ( Икс ) происходит, когда Икс знак равно π 2 + 2 п π , где п целое число.
Минимальное значение у знак равно грех ( Икс ) происходит, когда Икс знак равно 3 π 2 + 2 п π , где п целое число.
Амплитуда и период функции с моментаАмплитуда графика у знак равно а грех ( б Икс ) это величина, на которую он изменяется выше и ниже Икс -ось.
Амплитуда = | а |
Период синусоидальной функции — это длина самого короткого интервала на Икс -ось, по которой график повторяется.
Период = 2 π | б |
Пример:
Нарисуйте графики у знак равно грех ( Икс ) а также у знак равно 2 грех ( Икс ) .Сравните графики.
Для функции у знак равно 2 грех ( Икс ) , график имеет амплитуду 2 . С б знак равно 1 , график имеет период 2 π . Таким образом, он проходит один цикл от 0 к 2 π с одним максимумом 2 , и один минимум — 2 .
Обратите внимание на графики у знак равно грех ( Икс ) а также у знак равно 2 грех ( Икс ) . У каждого такое же Икс -перехватывает, но у знак равно 2 грех ( Икс ) имеет амплитуду, в два раза превышающую амплитуду у знак равно грех ( Икс ) .
Также см Тригонометрические функции .
SineFunction.html
Исследование синусоидальной функции
по
Тоня ДеДжордж
Начнем с основной функции синуса: y = sin x
Если бы мы построили график этой функции, мы бы получили:
Из этого графика мы видим, что график пересекает ось x- в точках 0, 2 и т. Д.Мы также видно, что амплитуда (высота каждой волны) равна единице, а период функция равна 2 ( время, необходимое для того, чтобы волна завершила один цикл). Однако функция может измениться в зависимости от по разным значениям параметров.
Например, мы можем переписать функцию y = sin x как y = a sin ( bx + c ), где a , b и c вещественные числа.В в данном конкретном случае a и b равны единице, а c равны нулю. В этом исследовании мы увидим, что происходит с функцией синуса, когда мы меняем значения a , b и c .
Что происходит, когда мы меняем значение на ?
Чтобы увидеть разницу, используя график функция калькулятора, мы должны построить функцию y = sin x и y = a sin ( bx + c ) на том же графике, изменяя значения на , в то время как сохраняя b равным единице и c равным 0.
Перед подключением различных значений и , мы должны сначала рассмотреть все возможные значения и . С вещественное число, существует три возможных диапазона значений: , , может быть больше нуля (, > 0), равный нулю ( a = 0) или меньше чем ноль ( a <0). Давайте сначала рассмотрим, когда a > 0.
Что происходит, когда a > 0?
Если подключить 2 на и в уравнение y = a sin ( bx + c ), мы получаем y = 2sin x , как показано ниже:
Из этого графика мы видим, что когда мы меняем значение a на 2, амплитуда функции увеличивается. Но работает ли это при любом положительном значении или ? Если мы выберем другое значение, например a = 10 ( y = 10sin x ), получаем:
Казалось бы, всякий раз, когда мы меняем значение на , амплитуда меняется. Однако если присмотреться к На графике видно, что амплитуда не только увеличивается, но и увеличивается до значения a . Для и = 2, амплитуда увеличилась до 2. Для a = 10 амплитуда увеличился до 10. Таким образом, мы можем Предположим, что для любого положительного значения a , амплитуда увеличивается до этого значения.
Что происходит, когда a = 0?
Если мы подключим ноль для и , мы видим, что функция y = a sin ( bx + c ) становится y = 0. Следовательно, функция больше не является синусоидальной функцией, а вместо этого стала линейной.Функция y = 0 имеет нулевой наклон и на графике лежит прямо на оси x-.
Что происходит, когда a <0?
Если подключить -2 для а в уравнение y = a sin ( bx + c ), мы получаем функцию y = -2sin x :
Отсюда видно, что амплитуда также увеличивается до 2.Аналогично, если мы установим a = -10, мы увидим, что амплитуда увеличивается до 10:
Таким образом, можно сделать вывод, что амплитуда функция увеличивается до | а |.
Но в чем разница между и и — а ?
Теперь вам может быть интересно, в чем разница между вставка положительного значения , и отрицательного значения , , когда амплитуда изменяется на | a | в обоих случаях. Что ж, давайте сравним, что происходит с графиком, когда a = 2 и a = -2:
.
Из этого графика мы можем видеть что знак на меняет график. Фиолетовая линия — это график функции y = 2sin x , а зеленая линия — график функция y = -2sin x. Мы можем видеть, что когда — это . отрицательный, он не только изменяет амплитуду функции, но также отражение функции y = 2 sin x . Мы также можем сравнить это для a = 10 и a = -10:
Отсюда видно, что мы получить такие же результаты. (Фиолетовая линия представляет y = 10sin x , а зеленая линия представляет y = -10sin x ).
Мы можем увидеть те же результаты, посмотрев на следующую анимацию, где a изменяется от -5 до 5:
Выводы о стоимости a :
* Если a > 0, амплитуда функции изменяется на значение на .
* Если a <0, амплитуда меняется на значение | a | и является отражением функция y = a sin x .
* Если a = 0, то функция меняется на линейная функция, y = 0.
Что происходит, когда меняем значение на ?
Как и при исследовании a , построим график функции y = sin x и y = a sin ( bx + c ) на том же графике, изменив значения b при сохранении a равным единице и c равным 0.
Так как b — настоящий числа, существует три возможных диапазона значений: b может быть больше нуля ( b > 0), равный нулю ( b = 0) или меньше чем ноль ( b <0). Давайте сначала рассмотрим, когда b > 0.
Что произойдет, если b > 0?
Если воткнуть 2 на б в уравнение y = a sin ( bx + c ), мы получаем y = sin (2 x ), как показано ниже:
Отсюда видно, что график функции выглядит как если бы он был сжат. Так что именно здесь произошло? Что ж, если мы снова взглянем на базовую синусоидальную функцию, мы увидим что период этой функции равен 2.
Однако, оглядываясь на предыдущий график:
Период функции y = sin2 x теперь равен из 2. Другими словами, функция теперь может соответствовать двум волнам за то же время, что и одна волна в основная функция синуса.Является ли это работает если поменять значение b на 3 (для y = sin (3 x ))? Получаем:
Отсюда мы видим, что теперь есть три полных волны в том же интервале, что и одна. Но как это выразить математически? Пока у нас:
б = 1 -> y = sin x -> период: 2
б = 2 -> y = sin (2 x ) -> точка: (или)
б = 3 -> y = sin (3 x ) -> период: (так как три волны в одной период по сравнению с функцией y = sin x )
Следовательно, для всех положительных значений b можно сделать вывод, что период функции y = sin bx будет.
Что произойдет, если b = 0?
Если мы подключим ноль для b , мы видим, что функция y = sin ( bx ) становится y = sin (0) x , которое затем становится y = sin (0). Если мы оценим это, мы увидим, что sin (0) равен 0 и, следовательно, уравнение принимает вид y = 0. Таким образом, когда b = 0, функция становится линейной.
Что произойдет, если b <0?
Давайте начнем с подключения -2 для b ( y = sin (-2 x )) и посмотрим, что мы получим:
Наблюдая за графиком, мы видим, что получаем то же самое результаты: период действия функции меняется.Как и в случае, когда b = 2, мы видим, что период сейчас. Посмотрим что происходит, когда b = -3 ( y = sin (-3 x )):
Опять же, мы видим, что период изменился.
б = 1 -> y = sin x -> период: 2
б = -2 -> y = sin (-2 x ) -> точка: (или)
б = -3 -> y = 3sin (-3 x ) -> период: (так как три волны в одной период по сравнению с функцией y = sin x )
Следовательно, для всех отрицательных значений b можно сделать вывод, что период функции y = sin ( bx ) будет .
Но в чем разница между b и — b ?
Опять же, вам может быть интересно, в чем разница между подключение положительного значения b и отрицательное значение b , когда период в обоих случаях меняется на. Что ж, давайте сравним, что происходит с графиком, когда b = 2 и b = -2:
.
Фиолетовый цвет представляет функцию y = sin2 x , а зеленый представляет функцию y = sin (-2 x ).Отсюда мы видим, что они являются отражением каждого Другие. Как и в случае со значением a , мы можем видеть, что отрицательное значение b является отражением y = sin ( bx ), когда b положительно.
Аналогичным образом, мы можем увидеть, как b изменяет график с помощью анимации ниже (где b находится в диапазоне от -5 до 5):
Выводы о стоимости b :
* Если b > 0, период функции изменения к .
* Если b <0, период функции изменяется на и является отражением функции y = sin ( bx) .
* Если b = 0, то функция меняется на линейная функция, y = sin (0), которая тогда становится y = 0.
Что происходит, когда меняем значение c ?
Снова построим график функции y = sin x и y = a sin ( bx + c ) на том же графике, изменение значений c при сохраняя a и b равными единице.
Так как c это настоящий числа, существует три возможных диапазона значений: c может быть больше нуля ( c > 0), равно нулю ( c = 0) или меньше чем ноль ( c <0). Давайте сначала рассмотрим, когда c > 0.
Что происходит, когда c > 0?
Если подключить 1 для c в уравнение y = a sin ( bx + c ), мы получаем y = sin ( x + 1), как показано ниже:
Отсюда видно, что график, кажется, сместился слева 1 единица, амплитуда и период совпадают.
Что произойдет, если мы изменим значение c на 2 ( y = sin ( x + 2))?
Снова мы видим, что график сместился влево, но на этот раз он сдвинул на две единицы . Точно так же мы видим, что он сдвигается три единицы, когда c = 3 ( y = sin ( x + 3)):
Следовательно, можно сделать вывод, что функция y = sin ( x + c ) смещается влево на c единиц.
Что происходит, когда c = 0?
Если мы подставим ноль в уравнение y = sin ( x + c ), мы получим y = sin x . Следовательно, когда c = 0, синусоидальная функция не смещается ни в одном направлении.
Что происходит, когда c <0?
Если воткнуть -1 для c в уравнение y = a sin ( bx + c ), мы получаем y = sin ( x — 1), который показан ниже:
Отсюда видно, что график, кажется, сместился на справа 1 стоимость единицы, с амплитуда и период одинаковые.
Что произойдет, если мы изменим значение c на -2 ( y = sin ( x — 2))?
Или для c = -3 ( y = sin ( x — 3))?
Таким образом, можно сделать вывод, что функция y = sin ( x + c ) переходит в право | c | единицы измерения.
Опять же, мы можем увидеть, что происходит, когда мы изменяем c (от -5 до 5), как функция изменяется в анимации ниже:
Выводы о стоимости c :
* Если c > 0 функция смещается влево c единицы измерения.
* Если c <0, функция переключается на право | c | единицы измерения.
* Если c = 0, функция не сдвигается в в любом направлении. (Когда c = 0, функция остается как y = sin x )
Окончательное заключение:
Из этого исследования мы увидели синусоидальную функцию изменяются в зависимости от различных значений на , b, и c .Давай положим все это информация вместе:
Для данной функции: y = a sin ( bx + c ):
При изменении значения на :
o Если a > 0, амплитуда функции изменяется до значения на .
о Если a <0, амплитуда меняется на значение | a | и является отражением функция y = a sin x .
о Если a = 0, тогда функция меняется на линейная функция, y = 0.
При изменении значения b :
о Если b > 0, период функции изменения к .
о Если b <0, период функции изменяется на и является отражением функции y = sin ( bx) .
о Если b = 0, то функция меняется на линейная функция, y = sin (0), которая тогда становится y = 0.
При изменении значения c :
o Если c > 0, функция переключается на осталось c шт.
o Если c <0, функция переключается на право | c | единицы измерения.
o Если c = 0, функция не сдвигается в в любом направлении. (Когда c = 0, функция остается как y = sin x )
ДомГрафический синус и косинус «Практические инструкции по тригонометрии» Ваш онлайн-источник для всех тригонометрических задач! Ознакомьтесь с нашей статьей в майском номере журнала «What’s Your Sine»! Как построить график функций СИНУС и КОСИНУС? На этом сайте вы научитесь технике рисования. графики функций синуса и косинуса.Графики синуса и косинуса функции можно определить как кривую. Для пример: Чтобы нарисовать графики основных функций синуса и косинуса, есть четыре основных ключевых термина, с которыми вам следует ознакомиться: период, горизонтальный сдвиг, вертикальный сдвиг и амплитуда. У нас есть базовая формула, которая поможет нам построить график. процесс: y = AsinB (x-C) + D или y = AcosB (x-C) + D Построение графика Функция синуса Амплитуда: Значение «A» влияет на амплитуду (половина расстояния между максимальным и минимальным значениями функции).Амплитуда иногда неформально называется высотой «горбов» графика. Изменение значения амплитуды будет приведет к вертикальному растяжению или сжатию графика. Например: y = 2sinx y = sinx y = ½sinx
Сдвиг по вертикали / по горизонтали Сдвиг: Значение C определяет горизонтальный сдвиг, а D влияет на вертикальный сдвиг. y = sinx + 1 Значение «D» изменилось с 0 на +1, который переместил исходный график, y = sinx, на одну единицу вверх. y = sin (x-90) Значение C изменилось с 0 на 90, который переместил исходный график, y = sinx, 90 единиц вправо. * Примечание: горизонтальный сдвиг имеет обратную зависимость, означает, что y = sin (x-1) переместит график вправо на одну единицу, а y = sin (x + 1) переместит график влево на одну единицу. Период: Период — это длина, необходимая для завершения одного полного цикл графика. Значение «B» определяет период. Чем больше «B», тем меньше становится период. Формула для определения периода: 2π / B в радианах или 360 / B в градусах. Например: y = sin2x Период изменился с 360 ° на 180 ° по формуле (360/2 = 180) Построение графика функции косинуса Построение графика функции косинуса в основном такое же, как отображение функции синуса, поскольку функция косинуса — это просто функция синуса, перемещенная на 90 ° (или π / 2 радиана) Слева! Это так просто, просто посмотрите на график! Итак, поскольку графики этих двух функций схожи, правила построения графиков синусоидальных функций применяются к графику косинусных функций.Для получения дополнительной информации о графиках и многом другом, ознакомьтесь с ними!
|
BioMath: тригонометрические функции
В этом разделе мы исследуем графики шести тригонометрических функций, начиная с графика функции косинуса.
Построение графика y = cos x
Чтобы нарисовать график y = cos x , мы можем составить таблицу значений, которые мы можем вычислить ровно:
Мы можем построить эти точки и нарисовать плавную кривую, проходящую через них:
Поскольку область определения функции косинуса — это все действительные числа, мы помещаем стрелки на график, чтобы указать, что график точно повторяется в обоих направлениях.Тот факт, что функция косинуса повторяется, означает, что она периодическая . В в частности, y = cos x периодичен с периодом 2π. Это означает, что если точка ( x , y ) лежит на графике, то точка ( x +2 k π, y ) также будет лежать на графике, где k — любое целое число. Например, ( x + 2π, y ) и ( x — 2π, y ) оба будут лежать на графике.
График y = sin x
Чтобы нарисовать график y = sin x , мы можем составить таблицу значений, которые мы можем вычислить. ровно:
Мы можем построить эти точки и нарисовать плавную кривую, проходящую через них:
Поскольку область определения синусоидальной функции — это действительные числа, мы помещаем стрелки на graph, чтобы указать, что график точно повторяется в обоих направлениях.Нравиться функция косинуса, функция синуса также периодична 2π.
График y = tan x
Чтобы нарисовать график y = tan x , мы можем составить таблицу значений, которые мы можем вычислить. ровно:
Обратите внимание, что теперь у нас есть несколько неопределенных функциональных значений; графически эти соответствуют вертикальным асимптотам.Мы можем набросать y = tan x следующим образом:
На приведенном выше графике пунктирными линиями обозначены вертикальные асимптоты. Мы размещаем стрелки на графике, указывающие, что функция возрастает до ∞. Например, tan x → ∞ как x → (π / 2) — . (т.е. поскольку x приближается к π / 2 слева) и загар x → −∞ как x → (π / 2) — (т.е. поскольку x приближается к π / 2 справа). В отличие от функций синуса и косинуса, касательная функция π периодична. То есть, если точка ( x , y ) лежит на графике y = tan x , то будет и точка ( x + k π, y ), где k любое целое число.
График y = sec x , y = csc x, и y = детская кроватка x
Напомним, что функции секанса, косеканса и котангенса являются обратными величинами функций косинуса, синуса и тангенса соответственно.Вы с меньшей вероятностью встретите эти графики при изучении наук о жизни. Мы включаем эти графики для полноты картины.
Преобразование y = cos x и y = sin x
Теперь мы рассмотрим графические преобразования y = cos x и y = sin x .Мы можно записать преобразованную функцию косинуса и синуса следующим образом:
y = a cos ( b ( x — d )) + c ,
y = a sin ( b ( x — d )) + c .
Звоним | a | амплитуда функции. Амплитуда — это расстояние от минимальное функциональное значение к максимальному функциональному значению, деленному на 2.В период вышеуказанных функций равен 2π / b (обратите внимание, когда b = 1, период равен 2π). Когда моделирование определенной величины или явления с помощью функции синуса или косинуса, амплитуда и период — две важные характеристики, определяющие поведение. Ты можете обратиться к разделу преобразований, чтобы изучить другие преобразования. ближе.
*****
В следующем разделе мы представим тригонометрические тождества.
Личности
графиков синусоидальной функции | mathtestpreparation.com
графики синусоидальной функции | mathtestpreparation.com вернуться к тригонометрии- График синусоидальной функции y = sin x
- Область y = sin x — это набор всех действительных чисел, а диапазон — это интервал [-1, 1], который имеет период 2pi, то есть sin (x + 2pi n) = sin x для все целое число n.Ключевые пять точек y = sin x: (0, 0), (pi / 2, 1), (pi, 0), (3pi / 2, -1), (2pi, 0). На основе y = sin x является нечетным и периодической функцией, вы можете нарисовать остальную часть кривой.
- График синусоидальной функции y = (3/2) sin x
- Область y = (3/2) sin x — это набор всех действительных чисел, а диапазон — это интервал [-3/2, 3/2], он имеет период 2pi. Ключевые пять точек: (0, 0), (pi / 2, 3/2), (пи, 0), (3pi / 2, — 3/2), (2pi, 0).На основе y = (3/2) sin x является нечетной функцией периода, вы можете нарисовать остальную часть кривой.
- График синусоидальной функции y = (2/3) sin (x + pi / 4)
- График y = (2/3) sin (x + pi / 4) — это график y = (2/3) sin x, переместившийся влево на pi / 4. Таким образом, нам нужно сначала нарисовать y = (2/3) sin x, а затем переместить его влево на единицу pi / 4.
- График синусоидальной функции y = (2/3) sin (x — pi / 4)
- График y = (2/3) sin (x — pi / 4) является графиком y = (2/3) sin x move right pi / 4.Таким образом, нам нужно сначала нарисовать y = (2/3) sin x, а затем переместить его вправо на единицу pi / 4.
- График синусоидальной функции y = sin x, y = sin 2x и y = — sin x / 2
- График y = — sin (x / 2) имеет период 4pi. График y = sin x имеет период 2pi. График y = sin2x имеет период пи.
- Постройте график y = A sin (Bx + C)
- Шагов:
- 1.Начните с рисования графика y = A sin x, его диапазон — [-A, A], период — 2pi.
- Постоянный коэффициент A — это амплитуда синусоидальной функции. Его пять ключевых точек: (0, 0), (pi / 2, A), (pi, 0), (3pi / 2, — A), (2pi, 0). Соединяем эти точки и расширяем его, получаем график y = A sin x.
- 2. (i). Если C> 0, переместите график y = A sin x влево на единицу C.
- (ii). Если C
- 3. (i). Если B> 1, все горизонтальные координаты сжимаются в 1 / B раз.
- (ii). Если B
- Оставить все вертикальные координаты неизменными.
- На этом этапе вы получаете график y = A sin (Bx + C) с периодом 2pi / B.
1. Графики y = a sin x и y = a cos x
М. Борна
(a) Синусоидальная кривая
y = a sin tМы видим синусоидальные кривые во многих естественных явлениях, таких как волны на воде.Когда волны имеют больше энергии, они поднимаются и опускаются более энергично. Мы говорим, что они имеют большую амплитуду .
Исследуем форму кривой y = a sin t и посмотрите, что означает понятие « амплитуда ».
Поиграйте со следующим интерактивом.
Синусоидальная кривая Interactive
Вы можете изменить радиус окружности (который изменяет амплитуду синусоидальной кривой) с помощью ползунка.
Масштаб по горизонтальной оси t (и по окружности) составляет радиан . Помните, что π радиан — это `180 °`, поэтому на графике значение «pi = 3,14» на оси t представляет «180 °», а «2pi = 6,28» эквивалентно «360 °».
Остановка
t = θ = 0
y = 70 sin (0) = 0
Авторские права © www.intmath.com Частота кадров: 0
Вы заметили?
- Форма синусоидальной кривой образует регулярный узор (кривая повторяется после того, как колесо повернет один раз).Мы говорим, что такие кривые периодические . Период — это время, необходимое для прохождения одного полного цикла.
- В интерактивном режиме, когда радиус круга составлял «50» единиц, кривая увеличивалась до «50» единиц и снижалась до «-50» по оси y . Эта величина синусоиды называется амплитудой графика. Это показывает, сколько энергии участвует в отображаемой величине. Более высокая амплитуда означает большую энергию.
- Угол поворота в радиан. совпадает со временем (в секундах). Подробнее о радианах. Все графики в этой главе относятся к углам в радианах. Радианы гораздо более полезны в инженерии и науке, чем ученые степени.
- Когда угол находится в первом и втором квадрантах, синус положительный, а когда угол в 3-м и 4-м квадрантах, синус отрицательный.
[Источники: Вышеупомянутая анимация в общих чертах основана на демонстрационном графике HumbleSoftware.]
Амплитуда
« a » в выражении y = грех x представляет амплитуду графика. Это показатель того, сколько энергии содержит волна.
Амплитуда — это расстояние от положения «покоя» (также известного как среднее значение или среднее значение ) кривой. В интерактивном режиме выше амплитуда может быть изменена от «10» до «100» единиц.
Амплитуда всегда равна положительной величине . Мы могли бы написать это, используя знаки абсолютного значения. Для кривой y = a sin x ,
амплитуда `= | a |`
График синуса
x — с переменной амплитудойНачнем с y = sin x .
Он имеет амплитуду `= 1` и период ` = 2pi`.
График `y = sin (x)` для `0 ≤ x ≤ 2pi`
Теперь посмотрим на график y = 5 sin x .
На этот раз амплитуда = 5, а период = 2 π . (Я использовал другой масштаб на оси и .)
График `y = 5sin (x)` для `0 ≤ x ≤ 2pi`
А теперь для y = 10 sin x .
Амплитуда = 10 и период = 2 π .
График `y = 10sin (x)` для `0 ≤ x ≤ 2pi`
Для сравнения, используя ту же шкалу осей и , вот графики
p ( x ) = sin x ,
q ( x ) = 5 sin x и
r ( x ) = 10 sin x
на одном комплекте осей.
Обратите внимание, что графики имеют тот же период (который равен «2pi»), но разные амплитуда .
Графики `p (x), q (x)` и `r (x)` для `0 ≤ x ≤ 2pi`
(б) График косинуса
x — с разными амплитудамиТеперь посмотрим, как выглядит график y = a cos x . На этот раз угол отсчитывается от положительной вертикальной оси.
Косинусная кривая Интерактивный
Подобно синусоидальному интерактиву вверху страницы, вы можете изменить амплитуду с помощью ползунка.
Нажмите «Пуск», чтобы увидеть анимацию.
Начало
t = θ = 0
y = 100 cos (0) = 0
Авторские права © www.intmath.com Частота кадров: 0
Вы заметили?
Графики синуса и косинуса почти идентичны, за исключением того, что кривая косинуса начинается с y = 1, когда t = 0 (тогда как синусоида начинается с y = 0). Мы говорим, что косинусоидальная кривая представляет собой синусоидальную кривую, которая на смещена влево на на `π / 2 \ (= 1.@) `.
Значение функции косинуса положительно в первом и четвертом квадрантах (помните, что на этой диаграмме мы измеряем угол от вертикальной оси) и отрицательно во 2-м и 3-м квадрантах.
Теперь посмотрим на график простейшей косинусной кривой, y = cos x (= 1 cos x ).
График `y = cos (x)` для `0 ≤ x ≤ 2pi`
Отметим, что амплитуда `= 1` и период ` = 2π`.
Аналогично тому, что мы сделали с y = sin x выше, теперь мы видим графики
- p ( x ) = cos x
- q ( x ) = 5 cos x
- r ( x) = 10 cos x
на одном комплекте осей, для сравнения:
Графики `p (x), q (x)` и `r (x)` для `0 ≤ x ≤ 2pi`
Примечание. Для косинусоидальной кривой, как и для синусоидальной кривой, период каждого графика одинаков («2pi»), но амплитуда изменилась.
Упражнения
Нарисуйте один цикл следующего без , используя таблица значений! (Важно знать форму из этих графики — не то, чтобы можно было соединять точки!)
Каждый имеет период «2 пи». Мы узнаем больше о периоде в следующем разделе Графики y = a sin bx.
В примерах используется t в качестве независимой переменной. В электронике переменная чаще всего составляет t .
1) i = sin t
Ответ
i = sin t
Мы видели эту кривую выше, за исключением того, что теперь мы используем i для тока и t для времени.Это очень распространенные переменные в тригонометрии.
График `i = sin (t)` для `0
Период = 2 π
Амплитуда `= 1`
2) v = cos t
Ответ
v = cos t
Мы снова видели эту кривую выше, за исключением того, что теперь мы используем v для напряжения и t для времени.
График `v = cos (t)` для `0
Период = 2 π
Амплитуда `= 1`
3) i = 3 грех т
Ответ
i = 3 sin t
График `i = 3sin (t)` для `0
Период = 2 π
Амплитуда `= 3`
4) E = −4 cos т
Ответ
E = −4 cos t
Переменная E используется для «электродвижущей силы», другого термина для напряжения.
График `E = -4cos (t)` для `0
Период = 2 π
Амплитуда `= 4`
Обратите внимание, что:
- Отрицательный знак перед косинусом приводит к переворачиванию кривой косинуса «вверх ногами». То есть это зеркальное отображение по горизонтальной оси t .
- Амплитуда — положительное число (это расстояние)
Построение функции y = f (x) в Python (с Matplotlib)
В нашем предыдущем уроке мы узнали, как построить прямую линию или линейные уравнения типа $ y = mx + c $. {3} $.3 здесь у = х ** 3 # установка осей в центре fig = plt.figure () ax = fig.add_subplot (1, 1, 1) ax.spines [‘влево’]. set_position (‘центр’) ax.spines [‘дно’]. set_position (‘центр’) ax.spines [‘правильно’]. set_color (‘нет’) ax.spines [‘вверху’]. set_color (‘нет’) ax.xaxis.set_ticks_position (‘снизу’) ax.yaxis.set_ticks_position (‘влево’) # построить функцию plt.plot (x, y, ‘g’) # показать сюжет plt.show ()
Тригонометрические функции
Здесь мы строим тригонометрическую функцию $ y = \ text {sin} (x) $ для значений $ x $ между $ — \ pi $ и $ \ pi $.У метода linspace () интервал установлен от $ — \ pi $ до $ \ pi $.
импортировать matplotlib.pyplot как plt
импортировать numpy как np
# 100 чисел с линейным интервалом
x = np.linspace (-np.pi, np.pi, 100)
# функция, которая здесь y = sin (x)
у = np.sin (х)
# установка осей в центре
fig = plt.figure ()
ax = fig.add_subplot (1, 1, 1)
ax.spines ['влево']. set_position ('центр')
ax.spines ['дно']. set_position ('центр')
топор.шипы ['право']. set_color ('нет')
ax.spines ['вверху']. set_color ('нет')
ax.xaxis.set_ticks_position ('снизу')
ax.yaxis.set_ticks_position ('влево')
# построить функцию
plt.plot (x, y, 'b')
# показать сюжет
plt.show ()
Построим его вместе с еще двумя функциями, $ y = 2 \ text {sin} (x) $ и $ y = 3 \ text {sin} (x) $. На этот раз мы помечаем функции.
import matplotlib.pyplot как plt
импортировать numpy как np # 100 чисел с линейным интервалом
x = np.linspace (-np.pi, np.pi, 100) # функция, которая здесь y = sin (x)
у = np.sin (х) # установка осей в центре
fig = plt.figure ()
ax = fig.add_subplot (1, 1, 1)
ax.spines ['влево']. set_position ('центр')
ax.spines ['дно']. set_position ('центр')
ax.spines ['правильно']. set_color ('нет')
ax.spines ['вверху']. set_color ('нет')
ax.xaxis.set_ticks_position ('снизу')
топор.yaxis.set_ticks_position ('влево') # построить график функций
plt.
 Четность
Четность 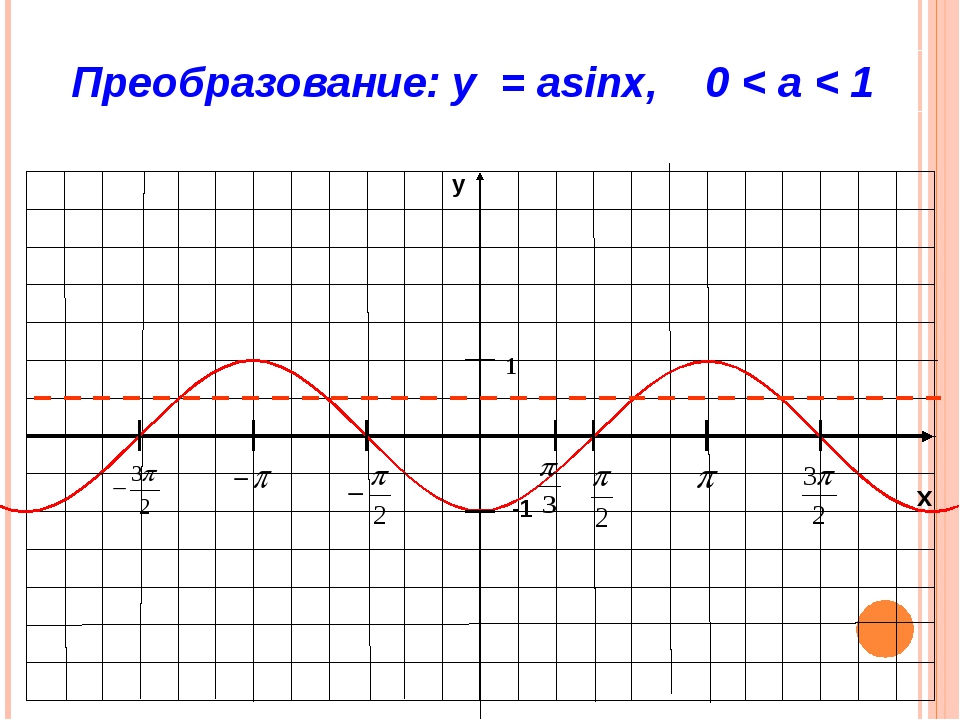
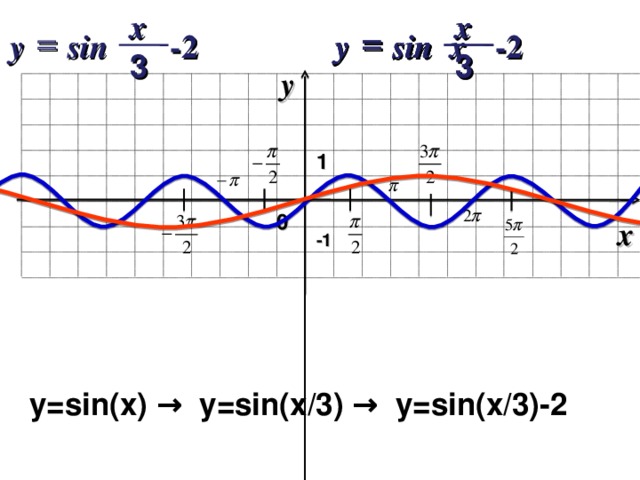
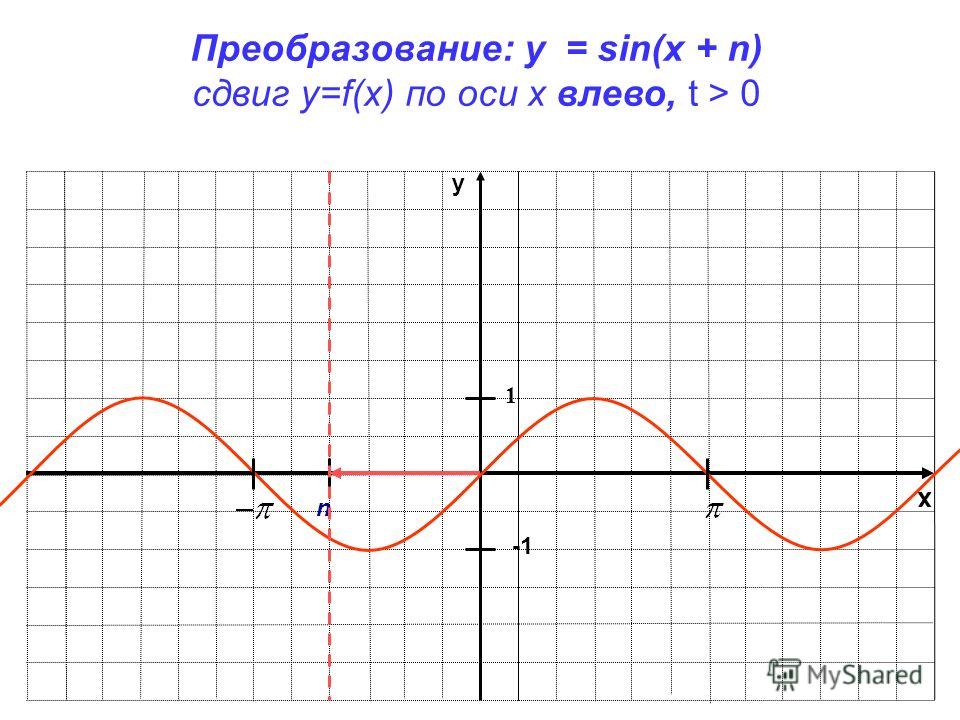 График симметричен относительно О.
График симметричен относительно О.