Y x 3 график и свойства: Функции вида y = x², y = x³ и их свойства – онлайн-тренажер для подготовки к ЕНТ, итоговой аттестации и ВОУД

404 — Страница не найдена

	Страницы Партнеры сайта _________________________________ 404: Запрошенная страница с адресом [http://primer. by/algebra/funkcii/funkcija-y-x3] не найдена. Если Вы уверены, что набрали ссылку корректно, напишите, пожалуйста, об этом на: меню пользователя Новости 30.11.16  17.03.15  25.03.14  29.08.13  05. 05.13
	primer. by 2013-2016

Степенная функция и ее свойства

Skip to content

22.03.2019 Artman Алгебра

Функция вида:

 у = хⁿ

называется степенной функцией с натуральным показателем.

График степенной функции онлайн можете построить в этом сервисе, например, чтобы построить график функции у=х³ введите так: Math.pow(x,3)

При  n=1 получаем функцию вида у = х

Рассмотрим свойства функции у = kx:

1. Область определения — D(f)=(-∞; +∞).
2.  Область значения — E(f)=(0; +∞).
3. Нечетная, так как f( — kх) = k ( — х)= — kx = -f(x)
4. При k > 0  функция возрастает,  а при k < 0 функция убывает на всей числовой прямой.

График линейной функции y=x

---

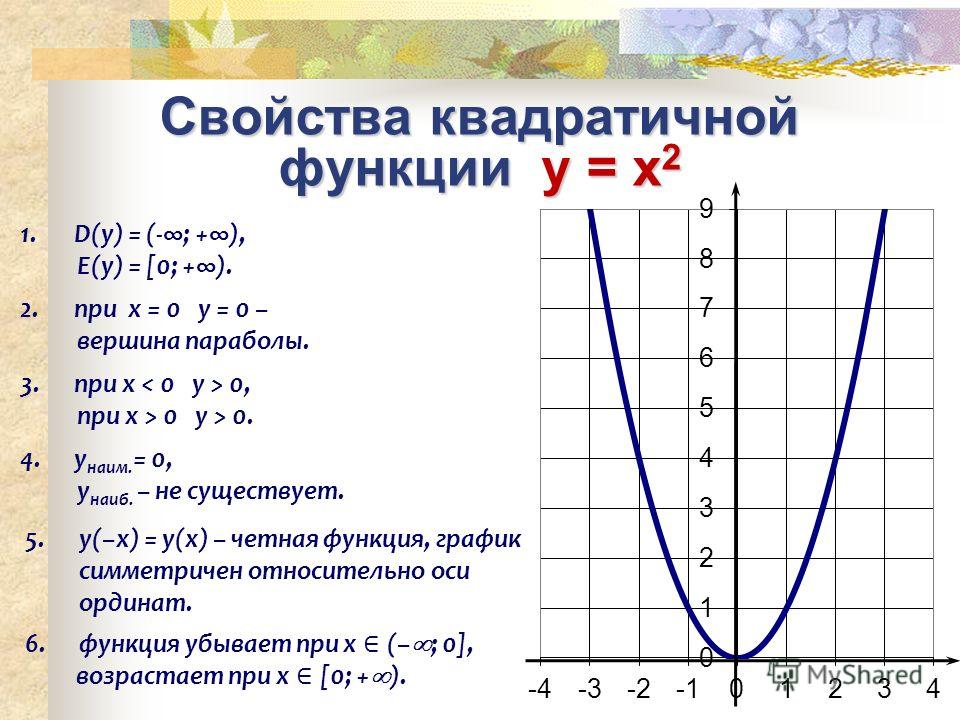
При  n=2 получаем функцию вида у = х² — эта функция называется параболой.

Рассмотрим свойства функции у =х² :

1. Область определения — D(f)=(-∞; +∞).
2.  Область значения E(f) y∈[0; +∞).
3. Чётная, так как f( — х) = ( — x)² = x² = f (х)
4. На промежутке (—∞; 0] функция убывает, а на промежутке [0; +∞) функция возрастает.
5. Корень x=0
6. Экстремумы функции — min при x=0.

График параболы y=x²

---

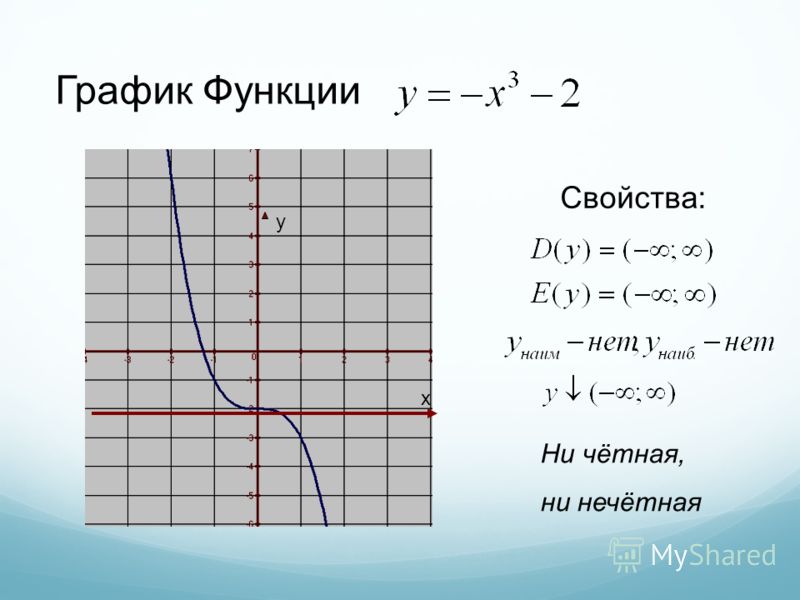
При  n=3 получаем функцию вида у = х³ — эта функция называется кубической параболой.

Рассмотрим свойства функции у = х³:

1. Область определения — D(f)=(-∞; +∞).
2.  Область значения — E(f)=(-∞; +∞).
3. Нечётная, так как f( — х) = ( — x)³ = —x³ = —f (х)
4. Функция возрастает на всей числовой прямой.
5. Корень x=0
6. Экстремумов нет. 2}}}$ 

   ---

   Рассмотрим элементарную функцию с корнем $y = \sqrt x $

   Свойства функции $y = \sqrt x $:

   1. Область определения — D(f)=[0; +∞).
   2.  Область значения — E(f)=[0; +∞).
   3. Функция ни чётная, ни нечётная.
   4. Функция возрастает на [0; +∞).
   5. Экстремумов нет.
   6. Корень x=0
   7. Экстремумы функции — min при x=0.

   37057

   3 6 Решить для ? cos(x)=1/2 7 Найти x sin(x)=-1/2 8 Преобразование градусов в радианы 225 9 Решить для ? cos(x)=(квадратный корень из 2)/2 10 Найти x cos(x)=(квадратный корень из 3)/2
   11 Найти x sin(x)=(квадратный корень из 3)/2 92=9 14 Преобразование градусов в радианы 120 градусов 15 Преобразование градусов в радианы 180 16 Найти точное значение желтовато-коричневый(195) 92-4 38 Найти точное значение грех(255) 39 Оценить лог база 27 из 36
   40 Преобразовать из радианов в градусы 2 шт. 92-3sin(x)+1=0 43 Найти x tan(x)+ квадратный корень из 3=0 44 Найти x sin(2x)+cos(x)=0 45 Упростить (1-cos(x))(1+cos(x)) 92=25 59 График f(x)=- натуральный логарифм x-1+3 60 Найдите значение с помощью единичного круга угловой синус(-1/2) 61 Найти домен квадратный корень из 36-4x^2 92=0 66 Найти x cos(2x)=(квадратный корень из 2)/2 67 График у=3 68 График f(x)=- логарифмическая база 3 x-1+3 92 71 Найти x квадратный корень из x+4+ квадратный корень из x-1=5 72 Решить для ? cos(2x)=-1/2 73 Найти x логарифмическая база x из 16=4 9х 75 Упростить (cos(x))/(1-sin(x))+(1-sin(x))/(cos(x)) 76 Упростить сек(х)sin(х) 77 Упростить кубический корень из 24 кубический корень из 18 92=0 96 Найти x 3x+2=(5x-11)/(8г) 97 Решить для ? sin(2x)=-1/2 98 Найти x (2x-1)/(x+2)=4/5 92+n-72)=1/(n+9)

   Линейные неравенства и полуплоскости

   Каждая линия на координатном графике делит график (или плоскость) на две полуплоскости. Эта линия называется граничной линией (или граничной линией ). График линейного неравенства всегда является полуплоскостью. Прежде чем построить график линейного неравенства, вы должны сначала найти или использовать уравнение линии, чтобы построить граничную линию.

   Открытая полуплоскость

   Если неравенство представляет собой «>» или «<», то график будет открытой полуплоскостью. Открытая полуплоскость не включает граничную линию, поэтому граничная линия записывается на графике как пунктирная линия .

   Пример 1

   Изобразите неравенство y < x – 3. <"), как показано на рис. 1. 

   Рис. 1. График граничной линии для y < x – 3.

   
   x
   y
    | 3  | 0
    | 0  | -3
    | 4  | 1

   Теперь заштрихуйте нижнюю полуплоскость, как показано на рис. 2, начиная с y < x – 3. 

   проверьте, правильно ли вы заштриховали полуплоскость, подставьте пару координат — часто бывает хорошим выбором пара (0, 0). Если выбранные вами координаты составляют неравенство верное утверждение при подключении, тогда вы должны заштриховать полуплоскость , содержащую эти координаты. Если выбранные вами координаты не делают неравенство верным, закрасьте полуплоскость , не содержащую этих координат.

   Поскольку точка (0, 0) не делает это неравенство верным,

   y < x – 3

   0 < 0 – 3 неверно.

   Вы должны заштриховать ту сторону, которая не содержит точки (0, 0).

   Этот метод проверки часто используется просто как метод, чтобы решить, какую полуплоскость заштриховать.

   Замкнутая полуплоскость

   Если неравенство «≤» или «≥», то график будет замкнутой полуплоскостью . Замкнутая полуплоскость включает граничную линию и изображается сплошной линией и штриховкой.

   Пример 2

   Нарисуйте неравенство 2 x – y ≤ 0. 

   Сначала преобразуйте неравенство так, чтобы y было левым членом.

   No related posts.