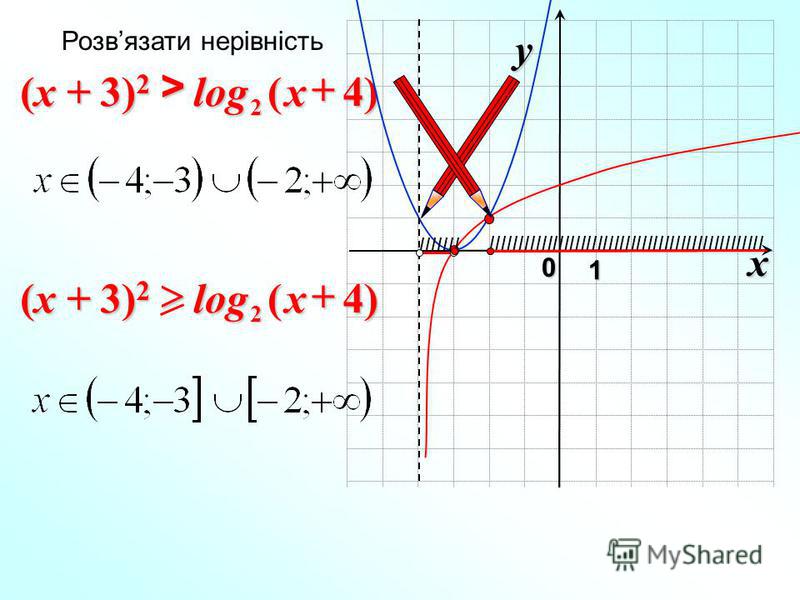
Площадь криволинейной трапеции.
Алгебра. 11 класс. Параграф 56. Тест 2.
Если f(x) непрерывная и неотрицательная на отрезке [a; b] функция, а F — ее первообразная на этом отрезке, то площадь S соответствующей криволинейной трапеции равна приращению первообразной на отрезке [a; b], т.е. S = F(b) — F(a).
Вариант 1.
Вычислить площадь S криволинейной трапеции, ограниченной линиями:
1. f(x)=x2; x=3; x=6; y=0.
A) 18; B) 24; C) 36; D) 63.
2. y=(x-1)2; y=0; x=0. В ответе укажите значение 6·S.
A) 12; B) 6; C) 2; D) 3.
3. y=(x+3)2-4 и у=0.
4. y=1-2sinx; x=π; x=3π/2; y=0.
A) π; B) 2π; C) π/2 + 2; D) π + 2.
5. y=x2+4x+7 и y=x+7.
A) 6; B) 4,5; C) 9; D) 5,5.
7. у=(х+2)2; х=0; у=0. В ответе указать значение 6·S.
A) 10; B) 12; C) 16; D) 14.
8. y=x2-x и y=0. В ответе указать значение 3·S.
A) 2; B) 1,5; C) 1; D) 0,5.
9. y=4x-x2; y=0; x=5. Указание: применить формулы 1) и 2).
A) 10; B) 11; C)
12; D) 13.
10. y=x2; y=4; y=9; x=0. Указание: применить формулу 4).
11. При каких значениях а площадь фигуры, ограниченной линиями y=x2; у=0; х=а, равна 9?
A) 3; B) 6; C) 9; D) 12.
Найдите объем тела, полученного при вращении вокруг оси абсцисс криволинейной трапеции, ограниченной линиями y=(x-3)2; x=4; x=5. Указание: применить формулу 6).
A) 6π; B) 6,2π; C) 6,5π; D) 7,5π.
Вариант 2.
Вычислить площадь S криволинейной трапеции, ограниченной линиями:
1. f(x)=x3; x=2; x=4; y=0.
A)
2. y=(x-2)2; y=0; x=0. В ответе укажите значение 3·S.
A) 8; B) 6; C) 4; D) 10.
3. y=(x-2)2-1 и у=0. В ответе укажите значение 12·S.
A) 14; B) 12; C) 14; D) 16.
4. y=2-sinx; x=3π/2; x=2π; y=0.
A) π; B) π+1; C) π/2 +1; D) π — 1.
5. y=x2-2x+3 и y=x+3.
A) 6; B) 4,5; C) 9; D) 5,5.
7. у=(х-3)2; х=0; у=0.
A) 7; B) 8; C) 6; D) 9.
8. y=x2-2x и y=0. В ответе указать значение 3·S.
A) 4; B) 2,5; C) 3; D) 4,5.
9. y=-x2-2х+3; y=0; x=2. Указание: применить формулы 1) и 2).
A)10; B) 11; C)12; D) 13.
10. y=x2; y=9; y=16; x=0. Указание: применить формулу 4).
11. При каких значениях а площадь фигуры, ограниченной линиями y=x3; у=0; х=а, равна 4?
A) 3; B) 1; C)
12. Найдите объем тела, полученного при вращении вокруг оси абсцисс криволинейной трапеции, ограниченной линиями y=(x-2)2; x=3; x=5. Указание: применить формулу 6).
A) 48,4π; B) 46,2π; C) 42,5π; D) 44,6π.
Сверить ответы.
Поделиться новостью в соцсетях
Метки: алгебра 11 класс, интеграл, криволинейная трапеция
Графики и симметрия
Графики и симметрия
I.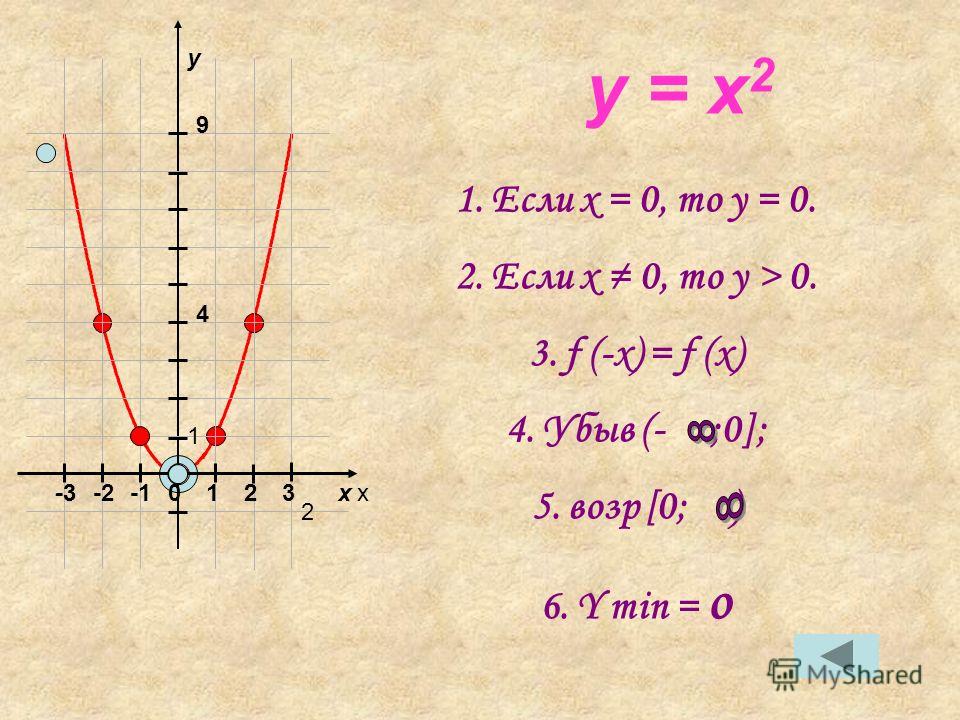
Домашнее задание
II. Симметрия (Геометрия)
Мы говорим, что граф симметричен относительно оси у , если для каждая точка (a,b) на графике, также есть точка (-a,b) на графике. Визуально мы видим, что ось Y действует как зеркало для графика. Мы продемонстрирует несколько функций для проверки симметрии графически, используя графического калькулятора.
Мы говорим, что граф симметричен относительно оси x , если для каждая точка (a,b) на графике, также есть точка (a,-b) на графике. Визуально мы видим, что ось x действует как зеркало для графика. Мы продемонстрирует несколько функций для проверки симметрии графически, используя графического калькулятора.
Мы говорим, что граф симметричен относительно начала координат , если для
каждая точка (a,b) на графике, также есть точка (-a,-b) на графике.
Визуально у нас есть точка P на графике, если мы нарисуем линию
сегмент PQ через P и начало координат так, что начало координат является средней точкой
PQ, то Q также находится на графике.
Воспользуемся графическим калькулятором
проверить все три симметрии.
IV. Симметрия (алгебра)
Чтобы алгебраически проверить, симметричен ли график относительно оси x, мы замените все y на -y и посмотрите, получим ли мы эквивалентное выражение.
Примеры:
A) Для x – 2y = 5 заменим x – 2(-y) = 5. Упрощая мы получили
x + 2y = 5, что не эквивалентно исходному выражению.
Б) Для х 3 — у 2 = 2 заменяем на x 3 — (-y) 2 = 2, что эквивалентно исходное выражение, так что x 3 — y 2 = 2 симметрично относительно оси х.
Чтобы алгебраически проверить, симметричен ли график относительно оси y, мы заменим все x на -x и посмотрим, получим ли мы эквивалентное выражение.
Пример:
А) Для y = x 2 заменяем на y =
(-x) 2 = x 2 так что y =
x 2 симметрична относительно оси y.
B) Для y = x 3 заменяем на y = (-x) 3 = — x 3 , так что y = x 3 не симметрично относительно к оси у.
Алгебраически проверить, симметричен ли граф относительно начала координат мы заменяем оба x и y на -x и -y и смотрим, эквивалентен ли результат к исходному выражению.
Примеры:
A) Для y = x 3 мы заменяем на (-y) = (-x) 3 , поэтому что -y = -x 3 или y = x 3 . Следовательно, у = x 3 симметрична относительно начала координат.
B) Для y = x 2 мы заменяем на -y = (-x) 2 так что -y = x 2
Мы будем делать другие примеры в классе в группе.
В.
Перехваты
Мы определяем х точек пересечения как точки на графике, где график пересекает ось х. Если точка находится на оси x, то координата y точки равно 0. Следовательно, чтобы найти точки пересечения x, мы устанавливаем y = 0 и решать.
Пример: Найти x пересечений
у = х 2 + х — 2
Положим у = 0, так что
0 = х 2 + х — 2 = (х + 2)(х — 1)
Следовательно, точки пересечения x находятся в точках (-2,0) и (1,0)
Мы определяем y точек пересечения графа как точки, в которых граф пересекает ось у. В этих точках координата x равна 0, следовательно, хорошо перехватывает y, мы устанавливаем x = 0 и находим y.
Пример: Найдите точки пересечения y y = x 9{ 2 } — 4 x — 5 = 0
Тригонометрия
4 \sin \theta \cos \theta = 2 \sin \theta
Линейное уравнение
y = 3x + 4
Арифметика 3 5 9 0 9 * 90 90
Матрица
\left[ \begin{array} { l l } { 2 } & { 3 } \\ { 5 } & { 4 } \end{array} \right] \left[ \begin{array} { l l l } { 2 } & { 0 } & { 3 } \\ { -1 } & { 1 } & { 5 } \end{массив} \right]
Одновременное уравнение
\left.