Параллелограмм. Признаки параллелограмма 8 класс онлайн-подготовка на Ростелеком Лицей
Тема 1: Четырехугольники
- Видео
- Тренажер
- Теория
Заметили ошибку?
Параллелограмм. Признаки параллелограмма.
Параллелограмм – четырехугольник, у которого каждые две противоположные стороны параллельны.
Основные свойства параллелограмма:
-
∠ВАD = ∠BCD, ∠ABC = ∠CDA (противоположные углы равны).
-
AB = DC, BC = AD (противоположные стороны равны).
Первые два свойства следуют из равенства треугольников ABC и ACD, а также треугольников ABD и BCD.
-
AO = OC, BO = OD (диагонали точкой пересечения делятся пополам).
Третье свойство следует из равенства треугольников BOC и AOD.
-
∠BAD + ∠ABC = 180° (сумма углов, прилежащих к одной стороне, равна 180°).

Четвертое свойство следует из параллельности прямых BC и AD, а также AB и CD.
Первый признак параллелограмма. Если в четырехугольнике две противоположные стороны равны и параллельны, то этот четырехугольник – параллелограмм.
Дано: АВ||CD, AB = CD.
Доказать: ABCD – параллелограмм.
Доказательство: проведем в четырехугольнике диагональ, она разобьет его на два треугольника. Запишем, что мы знаем об этих треугольниках:
AB = CD по условию.
BD – диагональ параллелограмма, является общей стороной для треугольников АВD и BCD.
∠АВD = ∠ВDС как накрест лежащие.
Значит, треугольник АВD равен треугольнику BCD по первому признаку равенства треугольников.
Из равенства указанных треугольников следует, что ∠СВD = ∠АDB, а значит, АD||BC по признаку параллельности прямых при пересечении их секущей. Имеем, что AB||CD и AD||BC, значит АВСD – параллелограмм по определению.
Второй признак параллелограмма. Если в четырехугольнике каждые две противоположные стороны равны, то этот четырехугольник – параллелограмм.
Дано: АВ = СD, AD = BC.
Доказать: ABCD – параллелограмм.
Доказательство: проведем в четырехугольнике диагональ BD, она разобьет его на два треугольника. Запишем, что мы знаем об этих треугольниках:
АВ = СD по условию.
AD = BC по условию.
BD – общая сторона.
Значит, треугольник АВD равен треугольнику CBD по третьему признаку равенства треугольников.
Из равенства треугольников следует, что ∠СВD = ∠АDB, ∠АВD = ∠ВDС, а значит, АD||BC и AB||DC по признаку параллельности прямых при пересечении их секущей. Получаем AD||BC и AB||DC, значит АВСD – параллелограмм по определению.
Заметили ошибку?
Расскажите нам об ошибке, и мы ее исправим.Признаки параллелограмма. Формулировка и доказательства
Признаки параллелограмма. а) Если в выпуклом четырёхугольнике две противоположные стороны равны и параллельны, то такой четырёхугольник — параллелограмм. б) Если в выпуклом четырёхугольнике противоположные стороны попарно равны, то такой четырёхугольник — параллелограмм. в) Если диагонали выпуклого четырёхугольника, пересекаясь, делятся пополам, то такой четырёхугольник — параллелограмм.
а) Если в выпуклом четырёхугольнике две противоположные стороны равны и параллельны, то такой четырёхугольник — параллелограмм. б) Если в выпуклом четырёхугольнике противоположные стороны попарно равны, то такой четырёхугольник — параллелограмм. в) Если диагонали выпуклого четырёхугольника, пересекаясь, делятся пополам, то такой четырёхугольник — параллелограмм.
Доказательство первого признака параллелограмма. Если в выпуклом четырёхугольнике две противоположные стороны равны и параллельны, то такой четырёхугольник — параллелограмм. Доказательство. Вот наш четырёхугольник, и известно, что стороны AB и CD равны и параллельны. И надо доказать, что ABCD — параллелограмм. Рассмотрим треугольники ABC и ADC. В них AC — общая сторона, стороны AB и CD равны, и углы BAC и DCA равны как накрест лежащие при ПАРАЛЛЕЛЬНЫХ и СЕКУЩЕЙ. Значит, треугольники равны по первому признаку. Значит, их соответственные углы BCA и DAC равны, а эти углы накрест лежащие при параллельных боковых сторонах и секущей диагонали. То есть боковые стороны тоже параллельны, то есть четырёхугольник — параллелограмм. ЧТД.
То есть боковые стороны тоже параллельны, то есть четырёхугольник — параллелограмм. ЧТД.
Доказательство второго признака параллелограмма. Если в выпуклом четырёхугольнике противоположные стороны попарно равны, то такой четырёхугольник — параллелограмм. Доказательство. Вот наш четырёхугольник ABCD. И про него известно, что AB=CD и BC=AD. И надо доказать, что этот четырёхугольник ABCD — параллелограмм.Рассмотрим треугольники ABC и ADC. У них AC — общая сторона, AB=CD и BC=AD значит, треугольники равны по третьему признаку, а значит углы DCA и BAC равны, а они накрест лежащие при верхней и нижней сторонах и секущей диагонали, а значит верхняя и нижняя стороны параллельны. Также углы DAC и BCA равны, а они накрест лежащие при боковых сторонах и секущей диагонали. Значит, и боковые стороны четырёхугольника тоже параллельны, значит четырёхугольник ABCD — параллелограмм, ЧТД.
Доказательство третьего признака параллелограмма. Если диагонали выпуклого четырёхугольника точкой своего пересечения делятся пополам, то такой четырёхугольник — параллелограмм. Доказательство. Вот наш четырёхугольник ABCD и про него известно, что его диагонали BD и AC точкой своего пересечения E делятся на равные половинки, то есть AE=CE и BE=DE. И надо доказать, что этот четырёхугольник ABCD — параллелограмм. Чтобы доказать, мы рассмотрим треугольники ADE и CBE. В этих треугольниках углы BEC и DEA равны как вертикальные. Стороны BE и DE равны по условию, и стороны AE и CE — тоже равны по условию. Значит, треугольники равны по 1-му признаку. Это значит, что их соответственные углы BCE и DAE равны, а эти углы являются накрест лежащими при двух боковых сторонах и секущей AC, следовательно, боковые стороны четырёхугольника — AD и BC — параллельны. Теперь рассмотрим треугольники EAB и ECD. В этих треугольниках углы BEA и DEC равны, как вертикальные. Стороны BE и DE равны по условию и стороны AE и CE — равны по условию. Следовательно и эти треугольники тоже равны по первому признаку. Это значит, что их соответственные углы BAE и DCE равны, а эти углы являются накрест лежащими при верхней и нижней сторонах AB и CD и секущей диагонали AC.
Доказательство. Вот наш четырёхугольник ABCD и про него известно, что его диагонали BD и AC точкой своего пересечения E делятся на равные половинки, то есть AE=CE и BE=DE. И надо доказать, что этот четырёхугольник ABCD — параллелограмм. Чтобы доказать, мы рассмотрим треугольники ADE и CBE. В этих треугольниках углы BEC и DEA равны как вертикальные. Стороны BE и DE равны по условию, и стороны AE и CE — тоже равны по условию. Значит, треугольники равны по 1-му признаку. Это значит, что их соответственные углы BCE и DAE равны, а эти углы являются накрест лежащими при двух боковых сторонах и секущей AC, следовательно, боковые стороны четырёхугольника — AD и BC — параллельны. Теперь рассмотрим треугольники EAB и ECD. В этих треугольниках углы BEA и DEC равны, как вертикальные. Стороны BE и DE равны по условию и стороны AE и CE — равны по условию. Следовательно и эти треугольники тоже равны по первому признаку. Это значит, что их соответственные углы BAE и DCE равны, а эти углы являются накрест лежащими при верхней и нижней сторонах AB и CD и секущей диагонали AC. Значит, стороны AB и CD тоже параллельны, то есть четырёхугольник ABCD — параллелограмм, ЧТД.
Значит, стороны AB и CD тоже параллельны, то есть четырёхугольник ABCD — параллелограмм, ЧТД.
← Предыдущий урок
Оглавление
Следующий урок →
Когда четырехугольник является параллелограммом?
Я думаю о четырехугольнике, у которого одна пара противоположных сторон параллельна и конгруэнтна. Назовите этот четырехугольник.
Я думаю о четырехугольнике, у которого две пары противоположных сторон равны. Назовите этот четырехугольник.
Я думаю о четырехугольнике, у которого обе пары противоположных углов равны. Назовите этот четырехугольник.
Я думаю о четырехугольнике, диагонали которого пересекаются пополам. Назовите этот четырехугольник.
Если вы ответили «параллелограмм» на все вышеперечисленное, вы правы! Конечно, вы уже знаете, что недостаточно заявить, что я думаю о параллелограмме. В машине есть сомневающиеся, так что придется доказывать.
Противоположные стороны конгруэнтны и параллельны
Ваша первая подсказка «Назови этот четырехугольник» заключалась в том, что одна пара противоположных сторон параллельна и конгруэнтна.
Рисунок 16.1 Четырехугольник ABCD с ¯BC и ¯BC ~= ¯AD.
- Теорема 16.1 : Если одна пара противоположных сторон четырехугольника параллельна и конгруэнтна, то четырехугольник является параллелограммом.
Вот план игры. Предположим, что ¯BC ¯AD и ¯BC ~= ¯AD. По определению, параллелограмм — это четырехугольник, у которого две пары противоположных сторон параллельны. Вы уже знаете, что одна пара противоположных сторон параллельна. Вам нужно показать, что другая пара противоположных сторон параллельна. Другими словами, нужно показать, что ¯AB ¯CD.
Вы можете посмотреть на этот четырехугольник двумя способами. Первый способ — сосредоточиться на отрезках ¯BC и ¯AD, пересекаемых секущей ¯AC. Тогда BCA и DAC являются альтернативными внутренними углами и равны, так как ¯BC ¯AD. Второй способ — перевернуть его на бок.
| Заявления | Причины | ||
|---|---|---|---|
| 1. | Четырехугольник ABCD с ¯BC ¯AD и ¯BC ~= ¯AD. | Дано | |
| 2. | ¯BC ¯AD пересечение секущей ¯AC | Определение секущей | |
| 4 s ACD 90 и внутренние углы BAC 0040 Определение альтернативных внутренних углов | |||
| 4. | БКА ~= ЦАП | Теорема 10.2 | |
| 5. | ¯AC ~= ¯AC | Рефлексивное свойство ~= | |
| 6. | DAC0 Постулат | ||
7. | БАК ~= ACD | CPOCTAC | |
| 8. | ¯AB и ¯CD — два отрезка, пересекаемые секущей ¯AC | . чередующиеся внутренние углы | Определение параллельных внутренних углов |
| 10. | ¯AB ¯CD | Теорема 10.8 | |
| 11. |
Теперь, когда вы правильно назвали этот четырехугольник, вы можете перейти к следующему четырехугольнику.
Две пары конгруэнтных сторон
Во второй игре «Назови этот четырехугольник» у четырехугольника было две пары конгруэнтных сторон. Давайте запишем это как теорему и отложим ее.
- Теорема 16.2 : Если обе пары противоположных сторон четырехугольника конгруэнтны, то этот четырехугольник является параллелограммом.
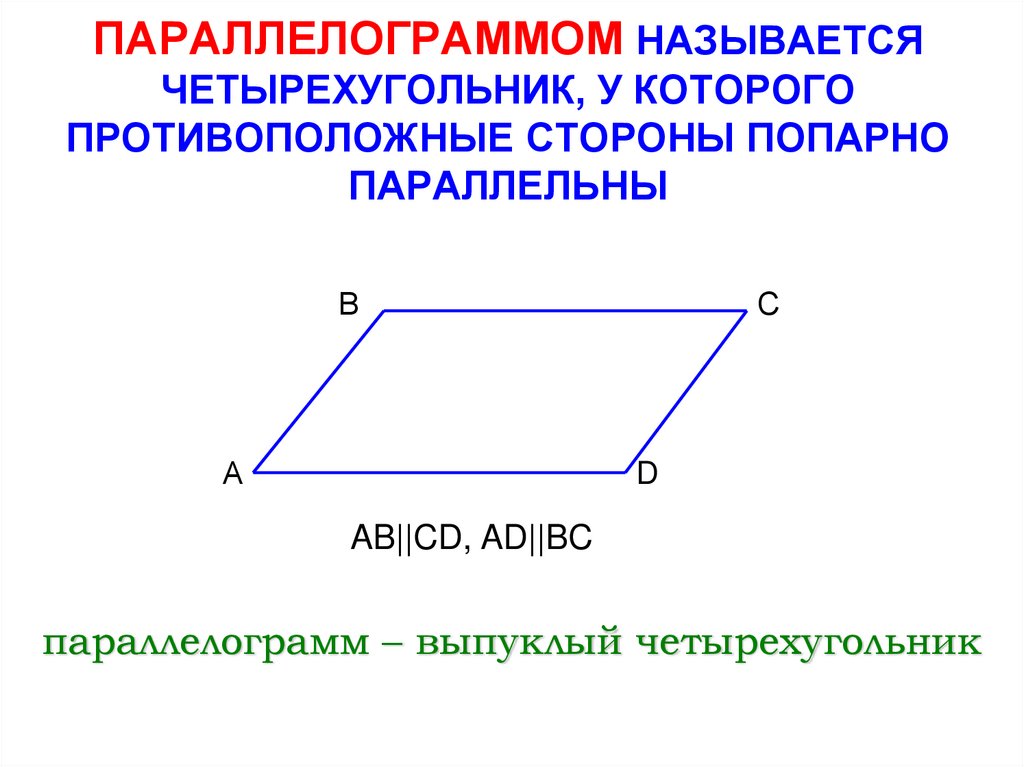
У нас есть визуал на рис. 16.2. У нас есть параллелограмм ABCD с ¯AB ~= ¯CD и ¯BC ~= ¯AD. План игры состоит в том, чтобы разделить четырехугольник на два треугольника с помощью диагонали ¯AC. Используйте постулат SSS, чтобы показать, что два треугольника конгруэнтны, и используйте CPOCTAC, чтобы сделать вывод, что альтернативные внутренние углы конгруэнтны, а противоположные стороны должны быть параллельны. Если мы покажем это для обеих пар противоположных сторон, то получим параллелограмм по определению. Пришло время написать подробности.
Используйте постулат SSS, чтобы показать, что два треугольника конгруэнтны, и используйте CPOCTAC, чтобы сделать вывод, что альтернативные внутренние углы конгруэнтны, а противоположные стороны должны быть параллельны. Если мы покажем это для обеих пар противоположных сторон, то получим параллелограмм по определению. Пришло время написать подробности.
Рисунок 16.2 Четырехугольник ABCD с ¯AB ~= ¯CD и ¯BC ~= ¯AD
| Утверждения | Причины | ||||
|---|---|---|---|---|---|
| 1. | Четырехугольник ABCD с ¯AB ~= ¯CD и ¯BC ~= ¯AD | Дано 31 | 2. | ¯AC ~= ¯AC | Рефлексивное свойство ~= |
| 3. | ABC ~= CDA | SSS Постулат | |||
| 4. | BAC ~= DAC | CPOCTAC | |||
| 5. | ¯BC и ¯AD два отрезка, разделенные секущей ¯AC | Определение поперечной | |||
| 6. | Определение альтернативного внутренние углы | ||||
7. | ¯BC ¯AD | Теорема 10.8 поперечный | |||
| 9. | BAC и ACD — альтернативные внутренние углы. | ||||
| 11. | Четырехугольник ABCD параллелограмм | Определение параллелограмма |
И снова сладкий вкус победы! Вы правильно назвали этот четырехугольник. Следующий!
Две пары равных углов
Третье описание четырехугольника включало конгруэнтность обеих пар противоположных углов. Я сформулирую теорему и воспользуюсь рис. 16.3, чтобы провести вас через доказательство.
Рисунок 16.3 Четырехугольник ABCD, где A ~= C и B ~= D.
- Теорема 16.3 : Если обе пары противоположных углов четырехугольника равны, то четырехугольник является параллелограммом.
Начать нужно с углов. Поскольку суммы внутренних углов четырехугольника в сумме составляют 360º, можно показать, что mA + mB = 180º, или что A и B являются дополнительными углами.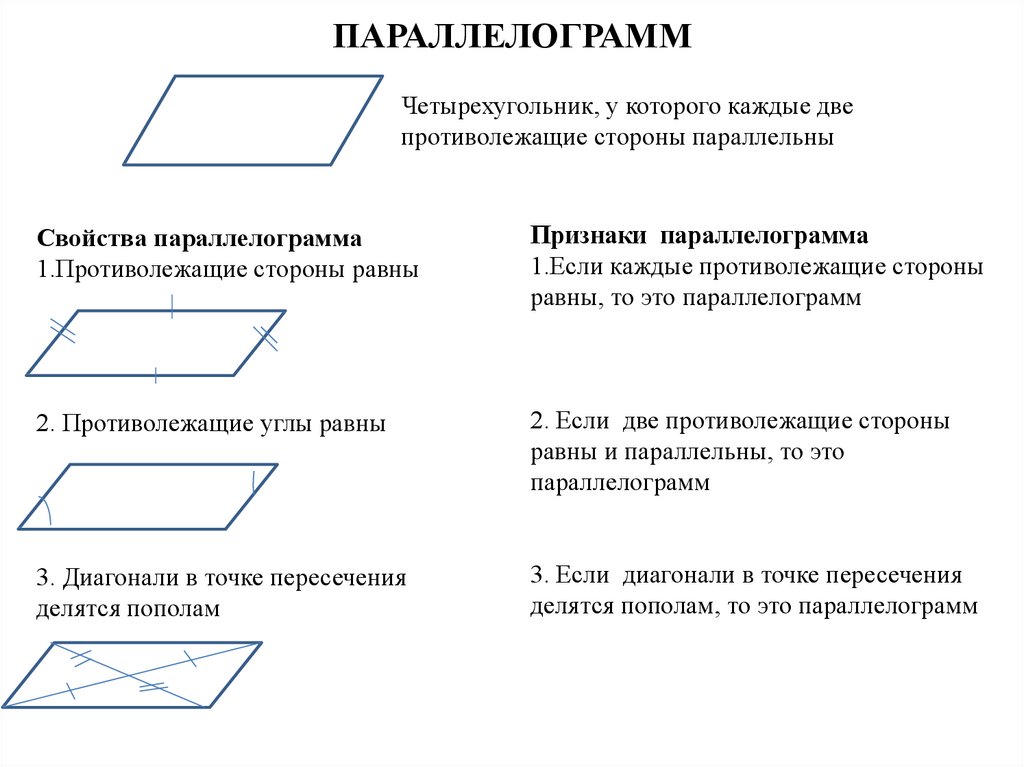
1
н.э.| Утверждения | Причины | ||||
|---|---|---|---|---|---|
| 1. | Четырехугольник ABCD с A ~= C и B ~= D | Дано | мА + мБ + мКл + мД = 360º | Внутренние углы четырехугольника в сумме дают 360º | |
| 3. | мА + мБ + мА + мБ = 360º | Замена (шаги 1 и 2) | |||
| 4. | мА + мБ = 180º | Алгебра | |||
| 5. | A и B являются дополнительными углами | ||||
6. | ¯BC и ¯AD два отрезка, разделенные секущей ¯AB | Определение секущей | |||
| 7. | ¯ до н.э. ¯ | Теорема 10.10 | |||
| 8. | ¯AB и ¯CD — два отрезка, пересекаемые секущей ¯AD | Определение поперечного сечения | |||
| 9. | мА + мД = 180º | Замена (шаги 1 и 4) | |||
| 10. | A и D являются дополнительными углами | Определение дополнительных углов | |||
| 11. | ¯AB ¯CD | Теорема 10.10 | |||
| 12. | Четырехугольник ABCD является параллелограммом | Определение параллелограмма |
Диагонали, делящиеся пополам
Ах, последняя игра этой серии! Если у вас есть четырехугольник, диагонали которого делят друг друга пополам, то ваш четырехугольник является параллелограммом. На рис. 16.4 показан параллелограмм ABCD с диагоналями ¯AC и ¯BD, пересекающимися в точке M и делящими друг друга пополам.
16.4 показан параллелограмм ABCD с диагоналями ¯AC и ¯BD, пересекающимися в точке M и делящими друг друга пополам.
Рисунок 16.4 Четырехугольник ABCD с диагоналями ¯AC и ¯BD, пересекающимися в точке M и делящими друг друга пополам.
- Теорема 16.4 : Если диагонали четырехугольника делят друг друга пополам, то четырехугольник является параллелограммом.
Если вы посмотрите на рис. 16.4, план игры для доказательства этой теоремы должен прозвучать громко и ясно. Вы воспользуетесь теоремой 16.2: пары противоположных сторон параллелограмма равны. Две диагонали делят параллелограмм на четыре треугольника. Поскольку диагонали делят друг друга пополам, ¯AM ~= ¯MC и ¯BM ~= ¯MD. Поскольку вертикальные углы конгруэнтны, вы можете использовать постулат SAS, чтобы показать, что AMB ~= BMC и AMB ~= DMC. Отсюда нужно применить CPOCTAC, чтобы показать, что обе пары противоположных сторон конгруэнтны.
.| Заявления | Причины | |
|---|---|---|
1. | Четырехугольник ABCD с диагоналями ¯AC и ¯BD, которые пересекаются в точке M и делят друг друга пополам | Дано |
| 2. | ¯AM ~= ¯MC и ¯BM ~= ¯MD | Определение деления пополам |
| 3. | AMB ~= CMD и AMD ~= BMC | Теорема 8.1 |
| 4. | драм ~= BMC и AMB ~= DMC | Постулат САС |
| 5. | ¯BC ~= ¯AD и ¯AB ~= ¯CD | КПОКТАК |
| 6. | Четырехугольник ABCD является параллелограммом | Теорема 16.2 |
Выдержки из Полное руководство идиота по геометрии © 2004 Дениз Сечеи, доктор философии. Все права защищены, включая право на полное или частичное воспроизведение в любой форме. Используется по договоренности с Alpha Books , член Penguin Group (USA) Inc.
Чтобы заказать эту книгу непосредственно у издателя, посетите веб-сайт Penguin USA или позвоните по телефону 1-800-253-6476. Вы также можете приобрести эту книгу на Amazon.com и в Barnes & Noble.
Вы также можете приобрести эту книгу на Amazon.com и в Barnes & Noble.
Определение, типы, свойства, формы, примеры
Параллелограмм — это особый тип четырехугольника, у которого обе пары противоположных сторон параллельны и равны.
На данном рисунке изображен параллелограмм ABCD, у которого AB II CD и AD II BC. Кроме того, AD = BC и AB = CD.
Когда мы оглядываемся вокруг, мы можем видеть множество параллелограммных форм и объектов в виде зданий, плиток или бумаги.
Здания : Многие здания построены в форме параллелограмма. Знаменитой реальной иллюстрацией является офисное здание Dockland в Гамбурге, Германия.
Плитка : Плитка бывает разных форм и размеров. Одной из наиболее часто встречающихся форм плитки является параллелограмм.
Ластик : Всем знаком классический ластик. Ластики тоже бывают разных форм и размеров, один из них имеет форму параллелограмма. Грани этого ластика имеют форму параллелограмма.
Площадь параллелограмма определяется по формуле A = bh , где b — длина основания, а «h» — высота.
Периметр параллелограмма равен сумме длин четырех сторон. Поскольку противоположные стороны параллелограмма равны, его периметр также может быть выражен как удвоенная сумма смежных сторон, т. е. 2 (AB + BC)
SplashLearn преобразует образование для детей начальной школы от детского сада до 5 класса. SplashLearn мотивирует детей изучать математику с помощью увлекательных и персонализированных программ. Доступный на всех цифровых платформах, он был использован более чем 40 миллионами детей по всему миру. Чтобы узнать больше о параллелограммах, нажмите здесь.
На рисунке ниже ABCD представляет собой параллелограмм, где ∠DAB = 75° и ∠CBD = 60°. Вычислите ∠BDC.
Как известно, противоположные углы параллелограмма равны. Следовательно, ∠DCB = ∠DAB = 75°.
Найдите площадь этого параллелограмма с основанием 15 см и высотой 6 см.
1 Каков периметр параллелограмма ABCD, две смежные стороны которого равны 12 м и 8 м соответственно?40 м 20 м 4 м 30 м Правильный ответ: 40 м 2 Какой из следующих параллелограммов не является параллелограммом?Прямоугольник Ромб Квадрат Трапеция Правильный ответ: Трапеция 3 В параллелограмме ABCD, если ∠A = 60°, то ∠D равно140° 130° 120° 2 Ответ: 110° Противоположные углы параллелограмма равны. Итак, ∠A = ∠C = 60°, а также ∠B = ∠D Кроме того, ∠A + ∠B + ∠C + ∠D = 360° 60° + ∠B + 60° + ∠D = 360° 120 ° + ∠B + ∠D = 360° ∠B + ∠D = 240° и ∠B = ∠D Следовательно, ∠D = 120° |
Является ли трапеция параллелограммом?
Нет, трапеция не является параллелограммом, потому что у параллелограмма две пары параллельных сторон, а у трапеции только одна пара параллельных сторон.
Все ли прямоугольники параллелограммы?
Да, все прямоугольники являются параллелограммами, потому что прямоугольник имеет два набора параллельных сторон и две пары противоположных сторон, которые равны. Следовательно, он соблюдает все свойства параллелограмма.
Все ли параллелограммы прямоугольники?
Нет, параллелограмм не всегда является прямоугольником.